6.1.1. Вычисление предела дробно – рациональной функции при ![]()
Пусть ![]() и
и ![]() – многочлены соответственно степеней
– многочлены соответственно степеней ![]() и
и ![]() .
.
Выражение  при
при ![]() может не представлять собой неопределённости или быть отношением двух бесконечно малых. При вычислении
может не представлять собой неопределённости или быть отношением двух бесконечно малых. При вычислении  могут представляться следующие случаи.
могут представляться следующие случаи.
А. Выражение  не представляет собой неопределённости, если
не представляет собой неопределённости, если ![]() – не является корнем знаменателя, то есть
– не является корнем знаменателя, то есть ![]() . В этом случае используют теорему об арифметических действиях над функциями, имеющими предел в точке:
. В этом случае используют теорему об арифметических действиях над функциями, имеющими предел в точке:

Б. Не представляет никакого труда вычисление предела и в случае, если ![]() – корень знаменателя, но не является корнем числителя, то есть
– корень знаменателя, но не является корнем числителя, то есть ![]() ,
, ![]() . В этом случае отношение
. В этом случае отношение  При
При ![]() является бесконечно большой функцией, поэтому
является бесконечно большой функцией, поэтому  .
.
В. Если же ![]() является и корнем числителя и корнем знаменателя:
является и корнем числителя и корнем знаменателя: ![]() ,
, ![]() , то выражение
, то выражение  При
При ![]() представляет собой неопределённость типа
представляет собой неопределённость типа ![]() . В этом случае в числителе и в знаменателе можно выделить общий множитель наибольшей степени
. В этом случае в числителе и в знаменателе можно выделить общий множитель наибольшей степени ![]() и сократить на него. Выделить такой множитель можно либо с помощью деления многочленов на
и сократить на него. Выделить такой множитель можно либо с помощью деления многочленов на ![]() «в столбик», либо путём группировки слагаемых. После сокращения на
«в столбик», либо путём группировки слагаемых. После сокращения на ![]() приходим либо к случаю А, либо к случаю Б.
приходим либо к случаю А, либо к случаю Б.
Пример 1. Вычислить ![]() .
.
Решение. Число ![]() не является корнем знаменателя:
не является корнем знаменателя: ![]() (случай А), поэтому
(случай А), поэтому
 .
.
Пример 2. Вычислить 
Решение. Здесь ситуация такая же: число 2 не является корнем знаменателя (хотя и является корнем числителя).

Пример 3. Вычислить 
Решение. В данном случае число ![]() является корнем знаменателя, но не является корнем числителя (случай Б)
является корнем знаменателя, но не является корнем числителя (случай Б)

Пример 4. Вычислить ![]()
Решение. В этом случае ![]() является корнем и числителя, и знаменателя, а значит выражение представляет собой неопределённость
является корнем и числителя, и знаменателя, а значит выражение представляет собой неопределённость ![]() . В знаменателе следует выделить множетель
. В знаменателе следует выделить множетель ![]() . Возможно этот множитель будет входить в некоторой степени (если корни кратные). В числителе выделить такой множитель несложно:
. Возможно этот множитель будет входить в некоторой степени (если корни кратные). В числителе выделить такой множитель несложно:
![]()
Для того чтобы выделить такой множитель в знаменателе удобно разделить знаменатель на ![]() “в столбик”. Такое деление возможно без остатка по следствию из теоремы Безу. Действительно:
“в столбик”. Такое деление возможно без остатка по следствию из теоремы Безу. Действительно:

Теперь знаменатель можно представить как произведение:
![]()
Окончательно: 
6.1.2 Вычисление предела дробно – рациональной функции при ![]()
Пусть при ![]() дробно-рациональная функция представляет собой неопределённость типа
дробно-рациональная функция представляет собой неопределённость типа ![]() . Тогда при вычислении
. Тогда при вычислении  полезно учитывать, что при
полезно учитывать, что при ![]()
![]()
![]()
Поэтому

Пример 6.

![]() ;
;
Пример 7.

![]() ;
;
Пример 8.
 .
.
Если многочлены в числителе и знаменателе не представлены в стандартном виде, нужно внимательно отнестись к определению старшей степени. Например, выражение ![]() является многочленом третьей, а не четвёртой степени.
является многочленом третьей, а не четвёртой степени.
| < Предыдущая | Следующая > |
|---|
Вычисление пределов. Пределы с неопределенностью
Прежде чем рассказать о вычислении пределов с неопределенностью, хочется верить, что у вас уже есть понимание того, что такое предел и как вычислить элементарные пределы. Если такого понимания нет, то сначала прочитайте статью “Пределы. Понятие пределов. Вычисление пределов”.
Теперь перейдем к рассмотрению пределов с неопределенностью.
Существует группа пределов, когда x , а функция представляет собой дробь, подставив в которую значение х = получим неопределенность вида .
Необходимо вычислить предел
Воспользуемся нашим правилом №1 и подставим в функцию. Как видно мы получаем неопределенность .
В числителе находим х в старшей степени, которая в нашем случае = 2:
То же самое проделаем со знаменателем:
Здесь также старшая степень = 2.
Далее надо из двух найденных степеней выбрать самую старшую. В нашем случае степень числителя и знаменателя совпадают и =2.
Итак, для раскрытия неопределенности нам потребуется разделить числитель и знаменатель на х в старшей степени, т.е. на x 2 :
Существуют также пределы с другой неопределенностью – вида . Отличие от предыдущего случая лишь в том, что х стремится уже не к , а к конечному числу.
Необходимо вычислить предел .
Снова воспользуемся правилом №1 и подставим в место х число -1:
Мы получили неопределенность , для раскрытия которой необходимо разложить числитель и знаменатель на множители, для чего в свою очередь обычно решается квадратное уравнение или используются формулы сокращенного умножения.
В нашем случае решаем уравнение:
.
Если корень не извлекается целый вероятней всего D вычислен неправильно.
Теперь находим корни уравнения:
В знаменателе у нас х + 1, что итак является простейшим множителем.
Тогда наш предел примет вид:
х + 1 красиво сокращается:
Теперь подставим вместо х значение -1 в функцию и получаем:
Рассмотрим основные положения, применяемые при решении различного рода задач с пределами:
-
Предел суммы 2-х или более функций равен сумме пределов этих функций:
Предел постоянной величины равен самой постоянной величине:
За знак предела можно выносить постоянный коэффициент:
Предел произведения 2-х и более функций равен произведению пределов этих функций ( последние должны существовать):
Предел отношения 2-х функций равен отношению пределов этих функций (в том случае, если предел знаменателя 0:
Степень функции, находящейся под знаком предела, применима к самому пределу этой функции (степень должна быть действительным числом):
На этом с вычислением пределов с неопределенностью всё. Еще в статье “Замечательные пределы: Первый и второй замечательный предел” мы отдельно рассматриваем интересную группу пределов. Статья вставит еще один блок для решения большинства пределов, встречающихся не просторах обучения.
Решение пределов с дробями из многочленов
Здесь мы рассмотрим примеры и методы решения пределов функций, составленных из отношений многочленов. Это дроби из многочленов и разности дробей. Обзор и обоснование методов решения таких пределов изложены в разделе Раскрытие неопределенностей с дробями.
Методы решения пределов с дробями из многочленов
1. Рассмотрим предел функции, которая является отношением многочленов:
, где
(1) ,
и – многочлены степеней m и n , соответственно:
;
.
1.1. Пусть есть бесконечность:
.
Тогда возникает неопределенность вида . Для ее раскрытия, нужно числитель и знаменатель дроби разделить на x s , где s – наибольшее из чисел m и n . Примеры ⇓
1.2. Пусть есть конечное число. Найдем значение знаменателя дроби, подставив :
.
1.2.1. Если , то неопределенности нет. Функция определена и непрерывна при . Значение предела равно значению функции в точке :
. Пример ⇓
1.2.2. Если знаменатель равен нулю, а числитель нет: ,
то неопределенность также отсутствует. Предел равен бесконечности:
. Пример ⇓
1.2.3. Пусть теперь и числитель, и знаменатель равны нулю:
.
В этом случае у нас возникает неопределенность вида 0/0 . Для ее раскрытия, делим числитель и знаменатель на . Деление можно выполнять либо уголком, либо в уме, приравнивая коэффициенты при одинаковых степенях переменной x . Примеры ⇓
2. Теперь рассмотрим пределы от суммы или разности отношений многочленов. В этом случае, может возникнуть неопределенность вида бесконечность плюс-минус бесконечность: . Для ее раскрытия, нужно привести дроби к общему знаменателю. В результате получим предел от функции вида (1), методы решения которого мы уже рассмотрели. Пример ⇓
Примеры решений
Все примеры Далее мы приводим подробные решения пределов дробей из многочленов.
⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓ ⇓
Пределы при x стремящемся к бесконечности
Пример 1
Все примеры ⇑ Найти предел отношения многочленов при x стремящемся к бесконечности:
.
Разделим числитель и знаменатель дроби на . При имеем:
.
На основании свойств степенной функции, при . Применяя арифметические свойства предела функции, находим:
.
Пример 2
Все примеры ⇑ Найти предел функции, которая является отношением многочленов:
.
Разделим числитель и знаменатель дроби на . При имеем:
.
Применяя арифметические свойства предела функции, находим:
.
Пример 3
Разделим числитель и знаменатель дроби на . При имеем:
.
Применим арифметические свойства предела функции к числителю и знаменателю:
;
.
Применим свойства бесконечно малых и бесконечно больших функций:
.
Мы получили правильную величину предела: . Но бесконечно удаленная точка может включать в себя два частных случая: и . Как , так и являются . Если и, для достаточно больших |x| , , то . Если, для достаточно больших |x| , то .
Выясним, имеет ли наш предел определенный знак? Для этого преобразуем знаменатель и переведем бесконечно большую часть в числитель:
;
.
Поскольку , то . Тогда
.
Пределы в конечной точке
Пример 4. Непрерывные функции
Все примеры ⇑ Найти пределы функции
a) при ; б) при .
а) Найдем значение знаменателя в точке :
.
Поскольку знаменатель не обращается в нуль, то функция непрерывна в точке . Поэтому предел функции равен ее значению при :
.
б) Найдем значение знаменателя в точке :
.
Здесь также знаменатель не обращается в нуль. Функция непрерывна. Ее предел при равен значению при :
.
Пример 5. Бесконечно большие функции
Все примеры ⇑ Задана функция в виде отношения многочленов:
.
Найти односторонние пределы:
а) ; б) .
Найдем значение знаменателя дроби в точке :
.
Знаменатель равен нулю. Поэтому функция не является непрерывной при . Выясним, есть ли неопределенность вида 0/0 ? Для этого найдем значение числителя в этой точке:
.
Числитель не равен нулю. Поэтому неопределенности вида 0/0 нет. Предел при равен бесконечности:
.
Но нам нужно найти односторонние пределы. Для этого выделим из многочлена в знаменателе множитель . То есть представим знаменатель в следующем виде:
.
Раскрываем скобки:
.
Сравнивая левую и правую части, находим:
.
Отсюда ,
;
.
Функция непрерывна в точке , поскольку знаменатель дроби не обращается в нуль. При , имеем:
.
Тогда
;
при .
а) Подставим :
.
б) Подставим :
.
Примечание.
Если бы знаменатель дроби не равнялся нулю при , то функция была бы непрерывной в точке . В этом случае, пределы слева и справа были бы равны:
.
Неопределенность вида 0/0
Пример 6
Найдем значение знаменателя дроби при :
.
Знаменатель дроби равен нулю. Поэтому функция не определена и, следовательно, не является непрерывной в точке .
Найдем значение числителя при :
.
Числитель дроби также равен нулю. Мы имеем неопределенность вида 0/0 . Для ее раскрытия, выделим в многочленах множитель .
Ищем разложение знаменателя в виде:
.
Раскрываем скобки и группируем члены с одинаковыми степенями x :
.
Сравнивая левую и правую части, находим:
.
Отсюда ,
.
На практике, нет необходимости выписывать неопределенные коэффициенты разложения, а затем решать систему уравнений. Подобные вычисления легко проводить в уме. Для числителя имеем:
.
Пример 7
Все примеры ⇑ Найти предел отношения многочленов:
.
Найдем значение знаменателя при :
.
Знаменатель равен нулю. Поэтому функция не является непрерывной в точке .
Найдем значение числителя дроби при :
.
Числитель дроби также равен нулю. У нас неопределенность вида 0/0 . Для ее раскрытия, выделим в многочленах множитель .
Вычисления делаем в уме:
,
.
Делим числитель и знаменатель на . Тогда при имеем:
.
Снова находим значения числителя и знаменателя при : ;
.
Опять неопределенность 0/0 . Снова выделяем множитель :
;
.
При имеем:
.
Функция непрерывна в точке , поскольку знаменатель дроби не равен нулю при . Поскольку функции и отличаются только в одной точке ( определена и непрерывна при , а не определена), то их пределы в любой точке равны (см. «Влияние значений функции в конечном числе точек на величину предела»). Находим искомый предел:
.
Пример 8. Неопределенность вида ∞±∞
Все примеры ⇑ Найти предел разности дробей из многочленов:
.
При имеем:
;
;
;
.
Поскольку знаменатель каждой из дробей равен нулю, а числители отличны от нуля, то при , каждая из дробей стремится к бесконечности:
при .
То есть мы имеем неопределенность вида “бесконечность минус бесконечность”.
Для раскрытия неопределенности, приводим дроби к общему знаменателю. Чтобы упростить выкладки, предварительно выделим в знаменателях дробей множитель .
;
;
;
.
Таким образом, задача свелась к вычислению предела от дроби многочленов:
.
Применяем описанные выше методы.
Находим значения числителя и знаменателя при :
;
.
Поскольку числитель и знаменатель равны нулю, то это неопределенность вида 0/0 . В знаменателе множитель уже выделен. Выделим этот множитель в числителе:
.
Находим предел:
.
Автор: Олег Одинцов . Опубликовано: 23-01-2019
Пределы с иррациональностями. Первая часть.
Пределы, содержащие иррациональности (или, попросту говоря, корни) крайне популярны у составителей типовых расчётов и контрольных работ по высшей математике. Обычно рассматриваются три группы неопределённостей:
- Неопределённость вида $frac<0><0>$. Пример: $lim_frac<sqrt<7-x>-2><4-sqrt<13+x>>$.
- Неопределенность вида $frac<infty><infty>$. Пример: $lim_frac<9cdot sqrt[3]<5x^4-x^2+1>+7cdotsqrt[4]><11cdot sqrt[6]+4x-10>$.
- Неопределенность вида $infty-infty$. Пример: $lim_left( sqrt-sqrt right)$.
В данной теме мы рассмотрим все три перечисленные выше группы пределов с иррациональностями. Начнём с пределов, содержащих неопределенность вида $frac<0><0>$.
Раскрытие неопределенности $frac<0><0>$.
Схема решения стандартных примеров такого типа обычно состоит из двух шагов:
- Избавляемся от иррациональности, вызвавшей неопределенность, домножая на так называемое “сопряжённое” выражение;
- При необходимости раскладываем выражение в числителе или знаменателе (или и там и там) на множители;
- Сокращаем множители, приводящие к неопределённости, и вычисляем искомое значение предела.
Термин “сопряжённое выражение”, использованный выше, будет детально пояснён в примерах. Пока что останавливаться на нём подробно нет резона. Вообще, можно пойти иным путём, без использования сопряжённого выражения. Иногда от иррациональности может избавить удачно подобранная замена. Такие примеры редки в стандартных контрольных работах, поэтому на использование замены рассмотрим лишь один пример №6 (см. вторую часть данной темы).
Нам понадобится несколько формул, которые я запишу ниже:
Кроме того, предполагаем, что читатель знает формулы для решения квадратных уравнений. Если $x_1$ и $x_2$ – корни квадратного трёхчлена $ax^2+bx+c$, то разложить его на множители можно по следующей формуле:
Формул (1)-(5) вполне хватит для решения стандартных задач, к которым мы сейчас и перейдём.
Найдём отдельно пределы числителя и знаменателя:
В заданном пределе мы имеем неопределённость вида $frac<0><0>$. Раскрыть эту неопределённость нам мешает разность $sqrt<7-x>-2$. Для того, чтобы избавляться от подобных иррациональностей, применяют умножение на так называемое “сопряжённое выражение”. Как действует такое умножение мы сейчас и рассмотрим. Умножим $sqrt<7-x>-2$ на $sqrt<7-x>+2$:
Чтобы раскрыть скобки применим формулу №1, подставив в правую часть упомянутой формулы $a=sqrt<7-x>$, $b=2$:
Как видите, если умножить числитель на $sqrt<7-x>+2$, то корень (т.е. иррациональность) в числителе исчезнет. Вот это выражение $sqrt<7-x>+2$ и будет сопряжённым к выражению $sqrt<7-x>-2$. Однако мы не вправе просто взять и умножить числитель на $sqrt<7-x>+2$, ибо это изменит дробь $frac<sqrt<7-x>-2>$, стоящую под пределом. Умножать нужно одовременно и числитель и знаменатель:
Теперь вспомним, что $(sqrt<7-x>-2)(sqrt<7-x>+2)=3-x$ и раскроем скобки. А после раскрытия скобок и небольшого преобразования $3-x=-(x-3)$ сократим дробь на $x-3$:
Неопределенность $frac<0><0>$ исчезла. Сейчас можно легко получить ответ данного примера:
Замечу, что сопряжённое выражение может менять свою структуру – в зависимости от того, какую именно иррациональность оно должно убрать. В примерах №4 и №5 (см. вторую часть данной темы) будет использован иной вид сопряжённого выражения.
Запишем пределы числителя и знаменателя:
Мы имеем дело с неопределённостью вида $frac<0><0>$. Избавимся от иррациональности в знаменателе данной дроби. Для этого доможим и числитель и знаменатель дроби $frac<3x^2-5x-2><sqrt-sqrt<7x^2-19>>$ на выражение $sqrt+sqrt<7x^2-19>$, сопряжённое к знаменателю:
Вновь, как и в примере №1, нужно использовать формулу №1 для раскрытия скобок. Подставив в правую часть упомянутой формулы $a=sqrt$, $b=sqrt<7x^2-19>$, получим такое выражение для знаменателя:
Вернёмся к нашему пределу:
В примере №1 практически сразу после домножения на сопряжённое выражение произошло сокращение дроби. Здесь перед сокращением придётся разложить на множители выражения $3x^2-5x-2$ и $x^2-4$, а уж потом перейти к сокращению. Чтобы разложить на множители выражение $3x^2-5x-2$ нужно использовать формулу №5. Для начала решим квадратное уравнение $3x^2-5x-2=0$:
Подставляя $x_1=-frac<1><3>$, $x_2=2$ в формулу №5, будем иметь:
$$ 3x^2-5x-2=3cdotleft(x-left( -frac<1><3>right)right)(x-2)=3cdotleft(x+frac<1><3>right)(x-2)=left(3cdot x+3cdotfrac<1><3>right)(x-2) =(3x+1)(x-2). $$
Теперь настал черёд разложить на множители выражение $x^2-4$. Воспользуемся формулой №1, подставив в неё $a=x$, $b=2$:
Используем полученные результаты. Так как $x^2-4=(x-2)(x+2)$ и $3x^2-5x-2=(3x+1)(x-2)$, то:
Сокращая на скобку $x-2$ получим:
Всё! Неопределённость исчезла. Ещё один шаг и мы приходим к ответу:
В следующем примере рассмотрим случай, когда иррациональности будут присутствовать как в числителе, так и в знаменателе дроби.
Найдём пределы числителя и знаменателя:
Имеем неопределённость вида $frac<0><0>$. Так как в данном случае корни наличествуют и в знаменателе, и в числителе, то дабы избавиться от неопределённости придется домножать сразу на две скобки. Во-первых, на выражение $sqrt+sqrt$, сопряжённое числителю. А во-вторых на выражение $sqrt-sqrt<5x-9>$, сопряжённое знаменателю.
Раскрывая скобки с помощью формулы №1, получим:
Возвращаясь к рассматриваемому пределу, имеем:
Осталось разложить на множители выражения $-x^2+x+20$ и $x^2-8x+15$. Начнем с выражения $-x^2+x+20$. Чтобы разложить его на множители требуется решить уравнение $-x^2+x+20=0$, а затем воспользоваться формулой №5:
Для выражения $x^2-8x+15$ получим:
Подставляя полученные разожения $-x^2+x+20=-(x-5)(x+4)$ и $x^2+8x+15=(x-3)(x-5)$ в рассматриваемый предел, будем иметь:
В следующей (второй) части рассмотрим ещё пару примеров, в которых сопряжённое выражение будет иметь иной вид, нежели в предыдущих задачах. Главное, помните, что цель использования сопряжённого выражения – избавиться от иррациональности, вызывающей неопределённость.
[spoiler title=”источники:”]
http://1cov-edu.ru/mat-analiz/reshenie-predelov/drobi-iz-mnogochlenov/
http://math1.ru/education/limits/limitirraz.html
[/spoiler]
Простое объяснение принципов решения пределов 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения пределов
Пределом называется значение функции, вычисленное в точке к которой стремиться независимый аргумент.
Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Примеры решений пределов
Задача
Найти предел:
Решение
Заменим в выражении аргумент
его предельным значением:
Ответ
Задача
Найти предел:
Решение
Заменим в выражении аргумент
его предельным значением:
Ответ
Задача
Найти предел:
Решение
Заменим в выражении аргумент
его предельным значением:
Ответ
Задача
Найти предел:
Решение
Проверяем, не обращается ли в нуль знаменатель дробно-рациональной функции при предельном значении аргумента. Для этого подставим значение в
Вычисляем передел:
Ответ
Задача
Найти предел:
Решение
Проверяем, не обращается ли в нуль знаменатель дробно-рациональной функции при предельном значении аргумента. Для этого подставим значение в
Вычисляем предел:
Ответ
Задача
Найти предел:
Решение
Проверяем, не обращается ли в нуль знаменатель дробно-рациональной функции при предельном значении аргумента. Для этого подставим значение в
Вычисляем предел:
Ответ
Задача
Найти предел:
Решение
В данном примере знаменатель обращается в нуль при предельном значении аргумента
Преобразуем выражение
Ответ
Задача
Найти предел:
Решение
При числитель и знаменатель дроби обращаются в нуль. Для решения задачи необходимо сделать подстановку
Число
является наименьшим общим кратным показателей корней.
Разделим числитель и знаменатель дроби
на
В итоге получим:
Ответ
Задача
Найти предел:
Решение
При знаменатель дроби
обращается в нуль, поэтому вычислить непосредственно предел нельзя.
Рассмотрим обратную дробь
и её предел при
Т.к.
, то при функция
является бесконечно малой, поэтому
при
является бесконечно большой, а
Ответ
Задача
Найти предел:
Решение
Разделим числитель и знаменатель дроби на – высшую степень
, встречающуюся в дроби
При
поэтому
Ответ
В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.
- Определение предела функции
-
Решение пределов
- С заданным числом
- С бесконечностью
- С неопределенностью (икс стремится к бесконечности)
- С неопределенностью (икс стремится к конкретному числу)
Определение предела функции
Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.
Запись предела:
- предел обозначается значком lim;
- под ним добавляется, к какому значению стремится аргумент (переменная) функции. Обычно, это x, но не обязательно, например: “x→1″;
- затем справа дописывается сама функция, например:

Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):
![]()
Читается как “предел функции при икс, стремящемся к единице”.
x→1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).
Решение пределов
С заданным числом
Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x→1):
![]()
Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).
С бесконечностью
В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:
![]()
Если x→∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:
- 3 – 1 = 2
- 3 – 10 = -7
- 3 – 100 = -97
- 3 – 1000 – 997 и т.д.
Другой более сложный пример
![]()
Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.
- При x = 1, y = 12 + 3 · 1 – 6 = -2
- При x = 10, y = 102 + 3 · 10 – 6 = 124
- При x = 100, y = 1002 + 3 · 100 – 6 = 10294
Таким образом при “икс”, стремящемся к бесконечности, функция x2 + 3x – 6 неограниченно растет.
С неопределенностью (икс стремится к бесконечности)
![]()
В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.
Пример: давайте вычислим предел ниже.
![]()
Решение
Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:
![]()
Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:
1. Находим x в старшей степени для числителя (в нашем случае – это два).

2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).

3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.

4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.

С неопределенностью (икс стремится к конкретному числу)
![]()
И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.
В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.
Пример: Найдем предел функции ниже.
![]()
Решение
1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.
![]()
2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.
В нашем случаем корнями выражения в числителе (2x2 – 5x + 3 = 0) являются числа 1 и 1,5. Следовательно его можно представить в виде: 2(x-1)(x-1,5).
Знаменатель (x – 1) изначально является простым.
3. Получаем вот такой видоизмененный предел:
![]()
4. Дробь можно сократить на (x – 1):
![]()
5. Остается только подставить число 1 в выражение, получившееся под пределом:
![]()
Пределы дробно-рациональных функций с квадратичными выражениями
В случае
неопределённости
![]() следует разложить квадратичное выражение
следует разложить квадратичное выражение
на множители. Для этого можно
а)
воспользоваться тождеством
![]() ,
,
где![]() и
и![]() – корни уравнения
– корни уравнения![]() ,
,
найденные по формуле![]() ;
;
б)
учесть, что, когда
![]() ,
,
то![]() – один из корней, и другой корень
– один из корней, и другой корень![]() можно найти по теореме Виета, например,
можно найти по теореме Виета, например,
из равенства![]() ,
,
где![]() ;
;
в)
применить равенство
![]() ,
,
где
![]() .
.
Пример 7.
![]()
![]()
(решили уравнения
![]() и
и![]() и применили 1-й способ).
и применили 1-й способ).
Пример 8.
![]()
![]() .
.
В уравнении
![]() свободный коэффициент –10 разделили на
свободный коэффициент –10 разделили на
коэффициент, стоящий перед![]() (число 4). Результат разделили на известный
(число 4). Результат разделили на известный
корень 2. Получили 2-й корень![]() .
.
Затем в уравнении
![]() нашли 2-й корень из условия
нашли 2-й корень из условия![]() ,
,
где 2 – известный корень, а 6 – свободный
коэффициент (Теорема Виета).
Пример 9.
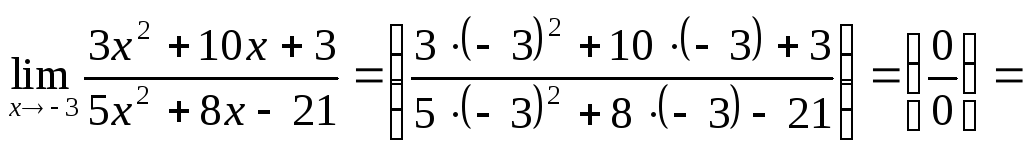
![]() .
.
Скобка
![]() получена как
получена как![]() ,
,
а остальные найдены 3-м способом.
ПР6. Раскройте
неопределённость
![]() ,
,
разложив дробь на множители:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)![]() ;
;
4) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)![]() .
.
Пример 10.
![]()
![]() .
.
Предел дробно-рациональной функции в бесконечности
Пусть дана функция
![]() (см. стр. 16) и надо найти
(см. стр. 16) и надо найти![]() .
.
Оказывается, при![]() вся дробь ведёт себя так, как отношение
вся дробь ведёт себя так, как отношение
старших степеней:
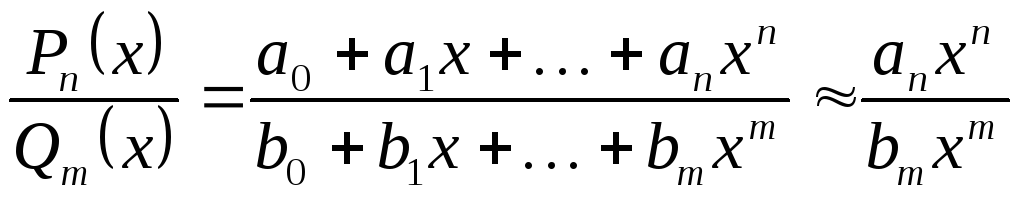 .
.
Тогда
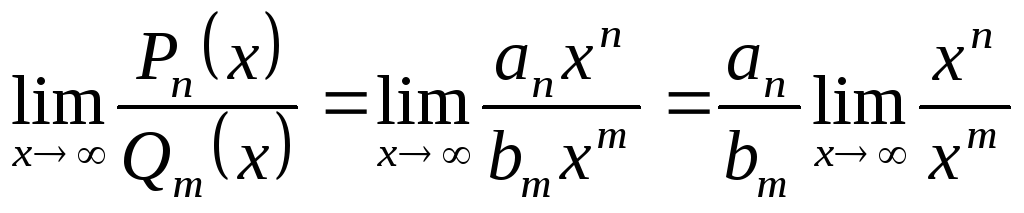 .
.
Обозначим![]() .
.
Возможны 3 случая:
1)
![]() ,
,
тогда![]() ,
,
где
![]()
(![]() );
);
2)
![]() ,
,
тогда![]() ,
,
где
![]()
(![]() );
);
3)
![]() ,
,
тогда![]() .
.
Таким образом,
предел равен
а) бесконечности,
если степень числителя больше, чем
степень знаменателя;
б) 0 в противоположном
случае;
в) отношению
старших коэффициентов, если степени
равны.
ПР7.
Найдите пределы
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ; д)
; д)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
д)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
д)![]() ;
;
ПР8.
Найдите пределы
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() .
.
Пример 11. Оставив
в числителе и в знаменателе старшие
степени, находим
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Пример 12.
Оставив старшие степени, видим, что
а)
![]() ;
;
б)
![]() ;
;
в)
![]() .
.
Обратите внимание,
что знак бесконечности (если таковая
получается) в ответе не указывается.
Тем не менее, если обе старшие степени
– чётные (или если обе нечётные), очевидно,
их отношение всегда положительно, что
можно учесть.
ПР9. Найдите
пределы функций
![]() в точках
в точках![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
а также при![]() .
.
![]() .
.
Пределы иррациональных функций
Если функция
содержит корень, подставляем, как обычно,
предельную точку. Сложности связаны с
неопределённостью
![]() ,
,
когда приходится умножать числитель и
знаменатель насопряжённое
выражение.
Выражения сопряжены
относительно
разности квадратов,
если их произведение превращается в
разность квадратов по формуле
![]() .
.
Примеры сопряжённых выражений
а)
![]() сопряжено с
сопряжено с![]() ,
,
при этом![]() ;
;
б)
![]() сопряжено с
сопряжено с![]() ,
,
и тогда![]() ;
;
в)
![]() сопряжено с
сопряжено с![]() ,
,
поскольку
![]() ,
,
причём под корнем
всё остаётся без изменений;
г)
![]() сопряжено с
сопряжено с![]() :
:
![]() .
.
ПР10. Найдите
пределы иррациональных функций простой
подстановкой:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
4) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() .
.
Пример 13.
Подставив указанные точки, находим
значения
а)
![]() ;
;
б)
![]() .
.
ПР11. Раскройте
неопределённость
![]() ,
,
умножив числитель и знаменатель дроби
на подходящее сопряжённое выражение и
сократив одинаковые скобки:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
4) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г)
![]() ; д)
; д)![]() ; е)
; е)![]() .
.
Пример 14.
![]()
![]() .
.
Пример 15.
![]()
![]()
![]() .
.
Пример 16.
![]()
![]()
![]()
![]() .
.
ПР12. Умножьте
числитель и знаменатель на выражение,
сопряжённое к числителю, а затем – на
выражение, сопряжённое к знаменателю.
Сократив скобки, раскройте неопределённость
![]() :
:
1) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)![]() ;
;
2) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ; г)
; г)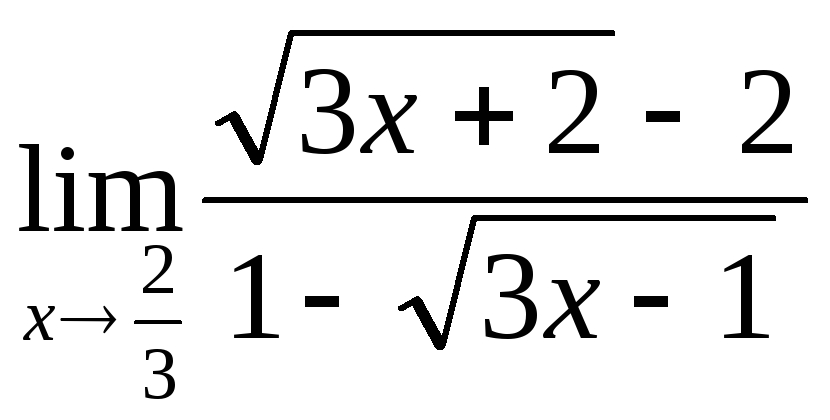 ;
;
3) а)
![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
4) а)
![]() ; б)
; б)![]() ; в)
; в)![]() .
.
Пример 17.
Умножим, чтобы получить разность
квадратов:
![]()
![]()
![]() .
.
Пример 18.
Так же, как в примере 17,
![]()
![]()
![]()
![]()
![]()
![]() .
.
Иррациональные
пределы при
![]() в случае неопределённости
в случае неопределённости![]() находят подобно рациональным, при помощи
находят подобно рациональным, при помощи
старших степеней, а в случае неопределённости![]() сводят её к
сводят её к![]() при помощи сопряжённого выражения.
при помощи сопряжённого выражения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
