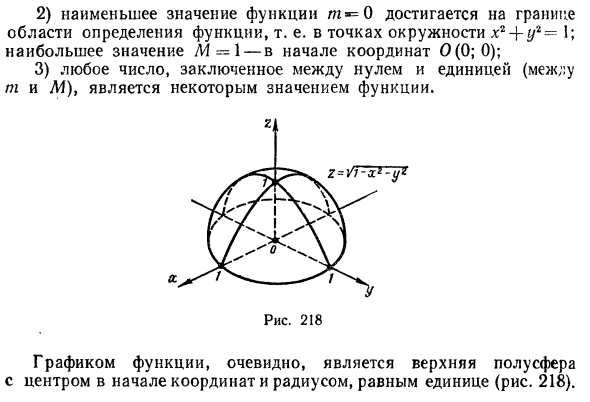
Содержание:
Множества точек n-мерного евклидова пространства:
Назовем n-мерным координатным пространством и обозначим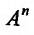 
Координатное пространство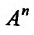 
называется n-мерным евклидовым пространством и обозначается 
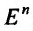, если между двумя любыми точками 
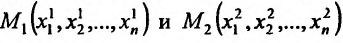пространства 
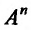определено расстояние, обозначаемое 
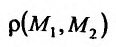и вычисляемое по формуле:
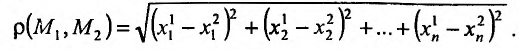
Опишем важнейшие типы множеств n-мерного евклидова пространства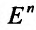 
.
Множество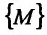 
всевозможных точек М пространства 
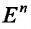, координаты которых удовлетворяют:
- а) неравенству
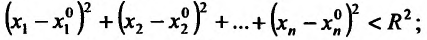
- б) неравенству
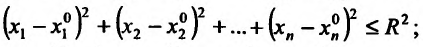
- в) равенству
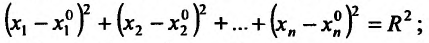
- г) неравенствам
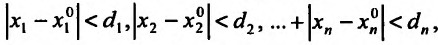
где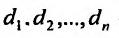 
– некоторые положительные числа, называется:
- а) открытым n-мерным шаром;
- б) замкнутым n-мерным шаром;
- в) n-мерной сферой радиуса R с центром в точке
- г) открытым n-мерным координатным параллелепипедом с центром в точке
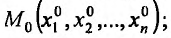
Открытый n-мерный шар раднуса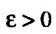 
с центром в точке 
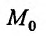будем называть 
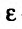-окрестностью точки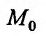 
Множество {М} точек пространства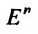
называется ограниченным, если найдется n-мерный шар, содержащий все точки этого множества.
Определение функции n переменных, двух переменных
Определение 15.2.1. Пусть задано множество точек {М} n-мерного евклидова пространства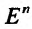 
. Если каждой точке М из множества {М) ставится в соответствие по известному закону некоторое число и, то говорят, что на множестве {м} задана функция u = u(х) или 
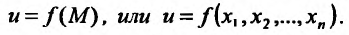. При этом множество {M} называют областью задания функции 
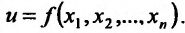. Число u соответствующее данной точке М из множества {M}, называется частным значением функции в точке М. Совокупность {м} всех частных значений функции 
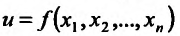называется множеством значений этой функции.
Частным случаем функции n переменных является функция двух переменных, которую можно определить следующим образом.
Если каждой паре (х, у) значений двух независимых друг от друга переменных величин х и у. принадлежащих области D, соответствует по известному закону определенное значение величины z, то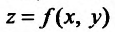 
называется функцией двух независимых переменных х и у, определенной в области D. D называется областью определения функции z = f(x, у).
Функция двух независимых переменных может быть задана:
- аналитически, то есть с помощью формул;
- при помощи таблицы, в которой указываются частные значения х и y, и соответствующие значения z;
- при помощи компьютерной программы, в которой определен алгоритм получения значений функции z для частных значений х и y
Для определения частных значений функции двух переменных должны быть заданы значения независимых переменных: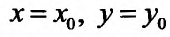 
И поэтому ясно, что функция z =f(х, у) может быть определена на всей плоскости или в некоторой ее части, то есть в некоторой области. Область определения как всякое множество может быть открытой (незамкнутой) или замкнутой.
Рассмотрим функцию 
определенную в области D на плоскости Оху и систему прямоугольных декартовых координат Oxyz. В каждой точке (x, у) восстановим перпендикуляр к плоскости Оху и на ней отложим отрезок, равный f(x,y). Тогда получим точку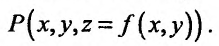 
Геометрическое место точек Р, координаты которых удовлетворяют (15.2.1), называется графиком функции двух переменных. Но уравнение (15.2.1) определяет некоторую поверхность, следовательно, графиком функции двух переменных является поверхность, проектирующаяся на плоскость Оху в область определения функции.
Например, областью задания функции двух переменных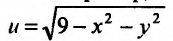 
является круг радиуса 3 с центром в начале координат, а множество значений представляет собой отрезок
.
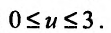Область задания функции n переменных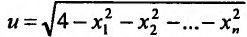 
служит n-мерный шар радиуса 2 с центром в точке O(0,0…..0). Множеством значений рассматриваемой функции является отрезок [0;2],
Из приведенных примеров, видим, что область задания функции n переменных представляет собой некоторое множество точек n-мерного евклидова пространства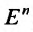 
, а множество всех значений этой функции- множество одномерного евклидова пространства 
.
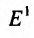Предел функции двух переменных
Определение 15.3.1. (предел функции по Кохии) Число А называется пределом функции z = f(M) в точке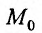 
(или при 
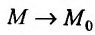). если для любого положительного числа 
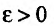найдется такое положительное число 
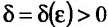, что для любой точки М из множества 
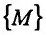задания этой функции, удовлетворяющей условию 
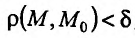, справедливо неравенство 
.
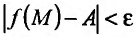Для обозначения предела функции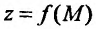 
в точке используется символика: 
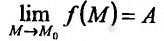или если точка имеет координаты 
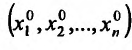,тo 
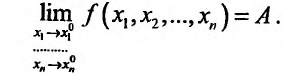Отметим, что в определении не указывается закон стремления точки М к точке Л , поэтому он может быть любым. Функция 
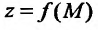называется бесконечно малой в точке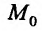 
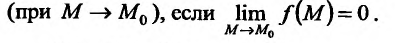Например, функция 
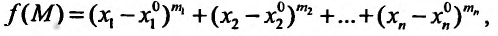где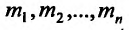 
– положительные числа, является бесконечно малой в точке
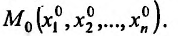Если функция 
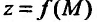имеет предел А в точке 
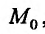, то ее можно представить в виде суммы предела и бесконечно малой функции в этой точке: 
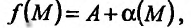где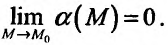 
Для функции 
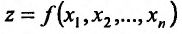можно определить понятие повторного предела, то есть предела по одной из переменных 
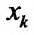при фиксированных значениях остальных переменных. Рассмотрим повторный предел для функции двух переменных 
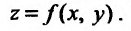Пусть функция 
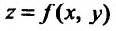задана в прямоугольной окрестности 
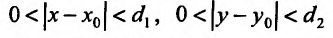точки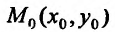 
и пусть для каждого фиксированного 
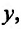удовлетворяющего условию 
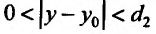существует предел функции
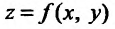одной пе ременной х в точке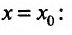 
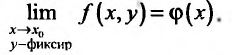Тогда, если существует предел А функции 
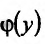в точке 
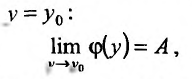то он называется 
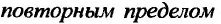для функции 
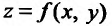в точке 
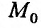, который обозначается следующим образом:
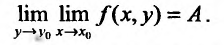Аналогично определяется повторный предел: 
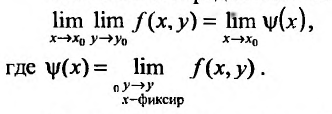Отметим, что если в точке 
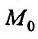функция 
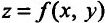имеет пре дел равный 
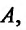и существуют пределы 
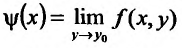и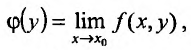 
то повторные пределы 
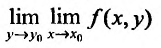и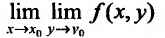 
существуют и оба равны А. Однако из существования повторных пределов еще не следует существования предела функции
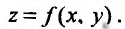Так, например, функция 
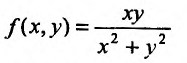не имеет предела в точке 
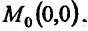хотя можно указать такие законы стремления точки 
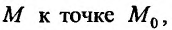, что повторные пределы будут равны: 
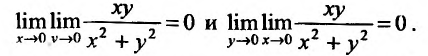Но если точка М стремится к точке
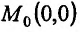по прямой 
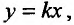, то значение повторного предела будет зависеть от значения 
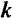, что и свидетельствует об отсутствии предела рассматриваемой функции в точке (О,О).
Может оказаться, что оба повторных предела существуют, но различны. Нетрудно заметать, что для функции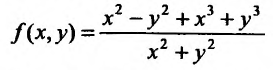 
будем иметь различные повторные пределы:
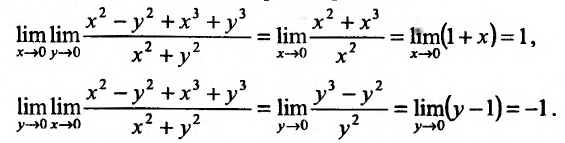
Поэтому, можно сделать вывод, что если для любого закона движения точки М к точке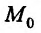 
повторные пределы существуют и они равны между собой, тогда и предел функции z = f(x, у) существует и равен этим повторным пределам.
Непрерывность функции двух переменных
Рассмотрим функцию п переменных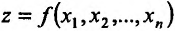 
, заданную на некотором множестве 
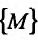пространства 
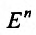. Пусть 
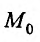-произвольная точка 
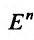, принадлежащая множеству 
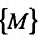и такая, что в любой 
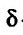-окрестности точки 
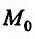содержатся точки множества 
.
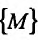Будем говорить, что функция z = f(М) непрерывна в точке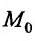 
, если предел этой функции в точке 
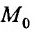существует и равен частному значению
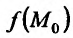. Символически непрерывность функции z = f(М) в точке 
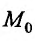можно записать в виде: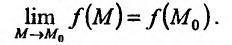 
В частности, для функции двух переменных: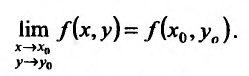 
что поскольку 
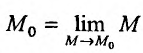, то условие непрерывности можно записать в виде:
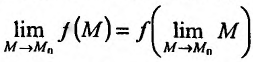
Значит, для непрерывной функции в точке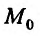 
символ lim предела и символ 
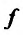характеристики функции можно менять местами.
Точки пространства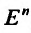 
, в которых функция z = f(м) не обладает свойством непрерывности, называются точками разрыва этой функции.
Используя определение предела функции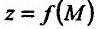 
в точке 
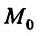по Коши, можно сформулировать определения непрерывности функции по Коши.
Если обозначить через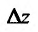 
полное приращение функции 
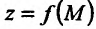, определяемое по формуле 
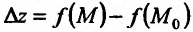, где М произвольная точка из области задания функции, то для непрерывности функции z = f(M) в точке 
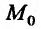необходимо и достаточно, чтобы ее приращение представляло в точке 
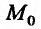бесконечно малую функцию, то есть
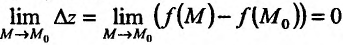
Аналогичным образом определяется непрерывность функции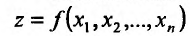 
по одной из переменных. Для этого вводятся частные приращения:
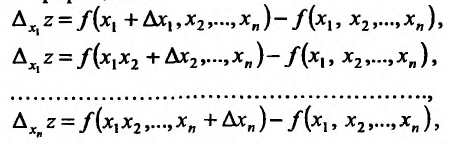
и тогда если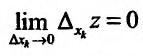 
, то функция 
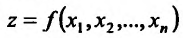называется непрерывной по переменной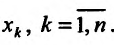 
Очевидно, что из условия непрерывности функции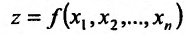 
в данной точке 
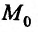вытекает непрерывность этой функции в точке 
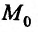по каждой из переменных 
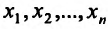. Однако, из непрерывности функции в точке 
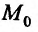по каждой из переменных 
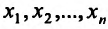не вытекает, вообще говоря, непрерывность функции в этой точке.
Для непрерывности функции n переменных справедливы многие аналогичные свойства непрерывных функций одной переменной: непрерывность сложной функции, устойчивость знака непрерывной функции, о прохождении через любое промежуточное значение, теоремы Вейрштраса и т.д.
Частные производные первого и высших порядков функции двух переменных
Пусть функция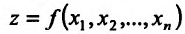 
n переменных задана на множестве {м} и точка 
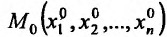– внутренняя точка данного множества. Зафиксируем все аргументы, кроме 
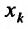, которому придадим произвольное приращение
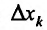, такое, чтобы точка с координатами 
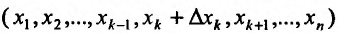находилась в области задания функции. Определим соответствующее частное приращение функции в точке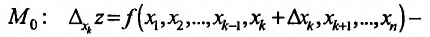 
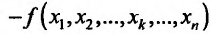. Составим отношение частного приращения 
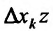к соответствующему приращению аргумента 
:
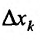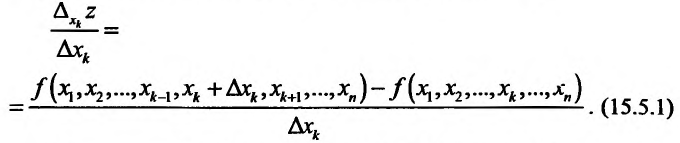
Отношение (15.5.1) представляет собой функцию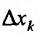 
, определенную для всех отличных от нуля значений 
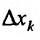, для которых точка 
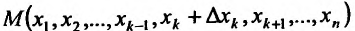принадлежит области задания функции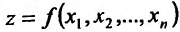 
Определение 15.5.1. Если существует предел отношения (15.5.1) частного приращения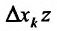 
функции к соответствующему приращению 
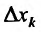аргумента 
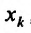, при стремлении 
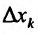к нулю, то тот предел называется частной производной функции 
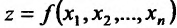в точке
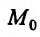по аргументу 
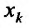и обозначается одним из символов:
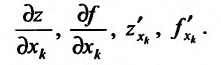
Таким образом,
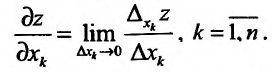(15.5.2)
В частности, для функции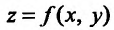 
двух переменных можно определить частные производные по х и у:
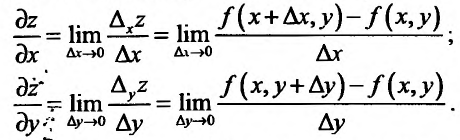
Из определения 15.5.1 следует, что частная производная функции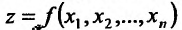 
по аргументу
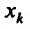представляет собой обыкновенную производную функции одной переменной 
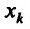при фиксированных значениях остальных переменных. Поэтому вычисление частных производных производится с использованием правил вычислений производных функций одной переменной и таблицы производных.
- Заказать решение задач по высшей математике
Пример:
Вычислить частные производные функций:
a)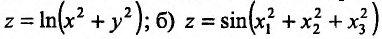
Решение:
Для вычисления частных производных воспользуемся правилами вычисления производных функции одной переменной, при этом, вычисляя частную производную по одной из переменных, другую считаем постоянной величиной.
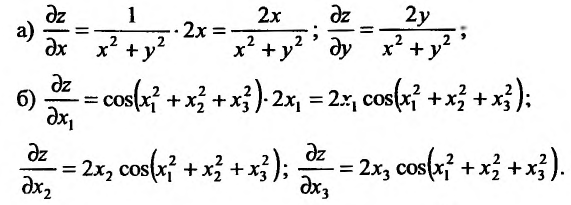
Предположим, что частная производная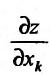 
по аргументу 
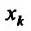функции 
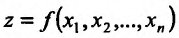, определенной на множестве 
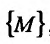, существует в каждой точке этого множества
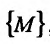. Тогда указанная частная производная представляет собой функцию n переменных, определенную на множестве {М}. Если эта функция 
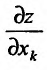имеет частную производную по аргументу 
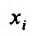в некоторой точке 
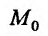множества {м), то она называется частной производной второго порядка функции
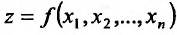в точке 
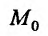сначала по аргументу хк, а затем по аргументу х, и обозначается одним из символов: 
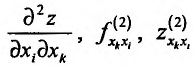. При этом, если 
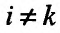, то частная производная 
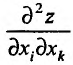называется смешанной частной производной второго порядка. После того как нами введено понятие второй частной производной, последовательно вводится понятие третьей частной производной, четвертой и т.д. Частную производную функции 
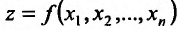П0 одному из аргументов в некоторой точке 
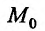от частной производной (n-l)-ro порядка по аргументам 
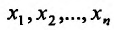(отдельные или даже все номера которых могут совпадать) называется частной производной n-го порядка функции 
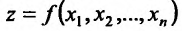в точке 
.
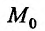В частности для функции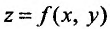 
двух переменных частные производные второго порядка определяются следующим образом.
Пусть частная производная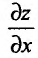 
по аргументу х функции z = f(х, у), определенной в области D. существует в каждой точке области D. В этом случае указанная частная производная представляет собой функцию двух переменных, также определенную в области D.
Тогда если эта функция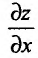 
имеет частную производную по аргументу х в некоторой точке 
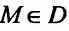, то указанную частную производную по х называют второй частной производной или частной производной второго порядка функции 
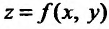в точке М по аргументу х и обозначают одним из символов: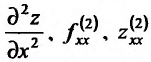 
Аналогично определяется частная производная второго порядка по аргументу у.
Частная производная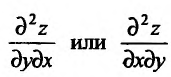 
называется смешанной производной второго порядка, т.е.
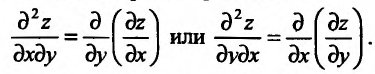
После того как введено понятие второй частной производной, можно последовательно ввести понятие третьей частной производной, затем четвертой и т.д.
Так как частная производная функции по аргументу х (у) определяется как обыкновенная производная функции одной переменной х (у)при фиксированном значении другой переменной, то методика вычисления частных производных высших порядков предполагает умение вычислять только обыкновенные производные первого порядка.
Пример:
Вычислить частные производные второго порядка функции
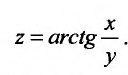
Решение:
Применив правило вычисления частных производных, получим: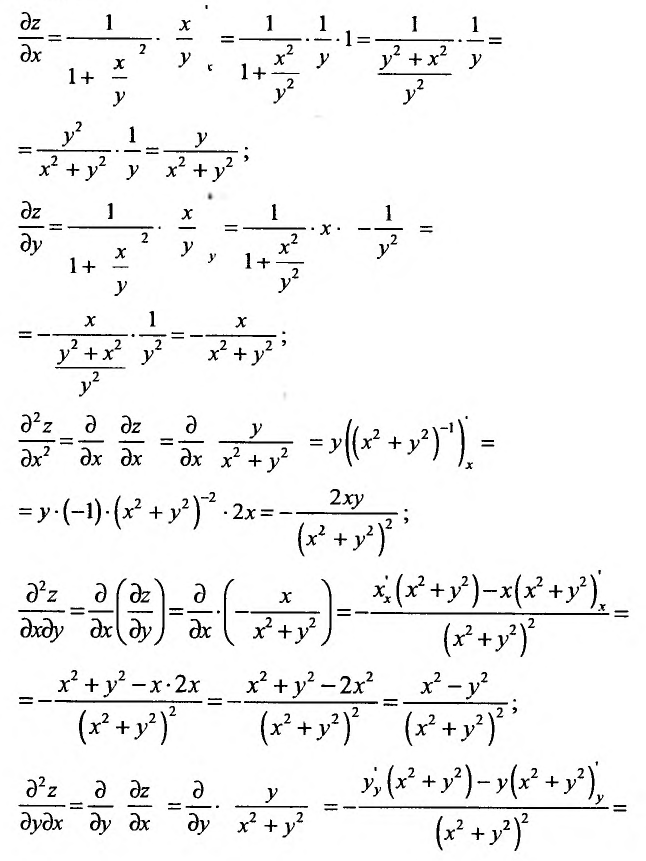 
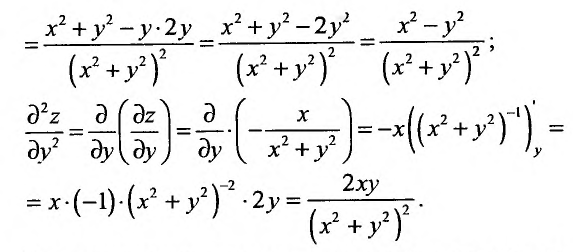
В рассмотренном примере смешанные частные производные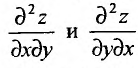 
равны друг другу. Вообще говоря, значения смешанных производных зависят от порядка, в котором производятся последовательные вычисления производных.
Достаточные условия независимости порядка вычисления производных определяются следующей теоремой.
Теорема 15.5.1. Пусть функция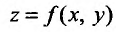 
в точке
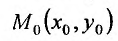имеет непрерывные частные производные второго порядка, тогда в этой точке частные производные 
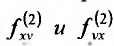равны.
Более того имеет место такая же теорема о независимости значений любой смешанной частной производной n-го порядка от порядка, в котором производятся вычисления частных производных.
Теорема 15.5.2. Пусть функция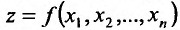 
имеет непрерывные частные производные n-го порядка в точке 
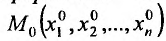Тогда в этой точке значение любой смешанной частной производной n-го порядка не зависит от порядка, в котором производится вычисление производных.
- Дифференцируемость функции нескольких переменных
- Несобственные интегралы
- Дифференциальные уравнения первого порядка
- Линейные дифференциальные уравнения второго порядка
- Функция одной переменной
- Производная функции одной переменной
- Приложения производной функции одной переменной
- Исследование поведения функций
-
Предел и непрерывность функции двух переменных
2.1. Предел функции
Для функции двух
(и большего числа) переменных вводится
понятие предела функции и непрерывности,
аналогично случаю функции одной
переменной. Введем понятие окрестности
точки. Множество всех точек
плоскости, координаты которых удовлетворяют
неравенству
,
называется-окрестностью
точки
.
Другими словами,-окрестность
точки
– это все внутренние точки круга с
центром
и радиусом
(рис. 2).
Рис. 2
Пусть функция
определена в некоторой окрестности
точки
,
кроме, быть может, самой этой точки.
Число А называетсяпределом
функции
при
(или, что то же самое, при
),
если для любого
существует
такое, что для всех
и удовлетворяющих неравенству
выполняется неравенство
Записывают:
Из определения
следует, что если предел существует, то
он не зависит от пути, по которому М
стремиться к М0
(число таких направлений бесконечно;
для функции одной переменной
по
двум направлениям: справа и слева).
Геометрический
смысл предела функции двух переменных
состоит в следующем. Каково бы ни было
число
,
найдется-окрестность
точки
,
что во всех её точках
,
отличных от
,
аппликаты соответствующих точек
поверхности
отличаются от числа А по модулю меньше,
чем на.
Пример 1.
Найти предел
Решение:
Будем приближаться к 0(0;0) по прямой
,
гдеk
– некоторое
число. Тогда
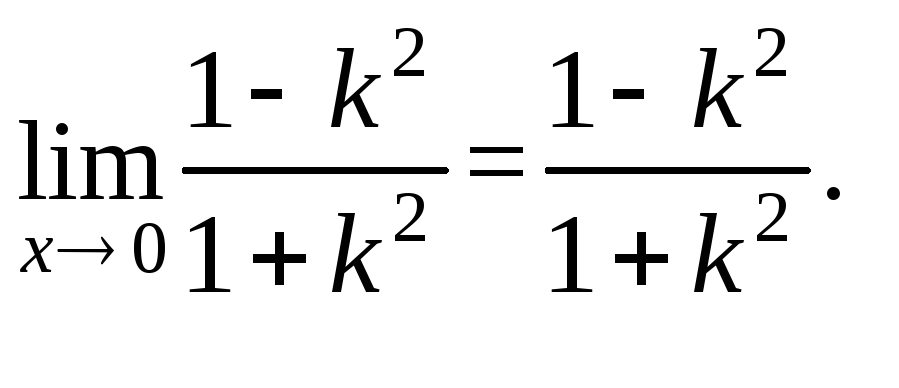
Функция
в
точке 0(0;0) предела не имеет, т. к. при
разных значенияхk
предел функции не одинаков (функция
имеет различные предельные значения).
Предел функции
двух переменных обладает свойствами,
аналогичными свойствами предела функции
одной переменной. Это означает, что
справедливы утверждения: если функции
определены на множествеD
и имеют в точке
этого множества пределы А и В соответственно,
то и функции
имеют
в точке М0
пределы, которые соответственно равны
-
Непрерывность
функции двух переменных
Функция
(илиf(M))
называется непрерывной
в точке
,
если она: а) определена в этой точке
и некоторой её окрестности;
б) имеет предел
в) этот предел
равен значению функции z
в точке М0,
т. е.
или
Функция, непрерывная
в каждой точке некоторой области,
называется
непрерывной в этой области.
Точки, в которых непрерывность нарушается
(не выполняется хотя бы одно из условий
непрерывности функции в точке), называются
точками
разрыва
этой функции. Точки разрыва
могут образовывать целыелинии
разрыва. Так,
функция
имеет линию разрыва
Можно дать другое,
равносильное приведенному выше,
определение непрерывности функции
в точке. Обозначим
.
Величины
называютсяприращениями
аргументов х и у, а
–полным
приращением функции
в точке
.
Функция
называется непрерывной в точке
если выполняется равенство
т.
е. полное приращение функции в этой очке
стремится к нулю, когда приращения её
аргументовх
и у
стремятся к нулю.
Пользуясь
определением непрерывности и теоремами
о пределах, можно доказать, что
арифметические операции над непрерывными
функциями и построение сложной функции
из непрерывных функций приводит к
непрерывным функциям – подобные теоремы
имели место для функций одной переменной.
-
Свойства функций,
непрерывных в ограниченной замкнутой
области
Приведем свойства
функций, непрерывных в ограниченной
замкнутой области (они аналогичны
свойствам непрерывных на отрезке функций
одной переменной). Предварительно
уточним понятие области.
Областью
называется
множество точек плоскости, обладающих
свойствами открытости и связности.
Свойство
открытости: каждая
точка принадлежит ей вместе с некоторой
окрестностью этой точки.
Свойство связности:
любые две
точки области можно соединить непрерывной
линией, целиком лежащей в этой области.
Точка N0
называется
граничной
точкой области
D,
если она не принадлежит D,
но в любой окрестности её лежат точки
этой области. Совокупность граничных
точек области D
называется границей
D.
Область D
с присоединенной к ней границей называется
замкнутой
областью,
обозначается
.
Область называетсяограниченной,
если все её
точки принадлежат некоторому кругу
радиуса R.
В противном случае область называется
неограниченной.
Примером неограниченной области может
служить множество точек первого
координатного угла, а примером ограниченной
–
-окрестность
точки
.
Теорема.
Если функция
непрерывна в ограниченной замкнутой
области, то она в этой области: а)
ограничена, т. е. существует такое числоR
> 0, что для всех точек N
в этой области выполняется неравенство
б)
имеет точки, в которых принимает
наименьшееm
и наибольшее M
значения; в) принимает хотя бы в одной
точке области любое численное значение,
заключенной между m
и M
(дается без доказательства).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
-
Предел функции в точке.
Начать изучение
-
Предел по множеству.
Начать изучение
-
Повторные пределы. Бесконечные пределы.
Начать изучение
Предел функции в точке.
Напомним, что окрестностью (O(x^0)) точки (x^0) в метрическом пространстве (X) называется любое множество, для которого точка (x^0) является внутренней. Проколотая окрестность (dot{O}(x^0)) получается из (O(x^0)) удалением самой точки (x^0), то есть (dot{O}(x^0)=O(x^0)backslash{x^0}).
Будем рассматривать функции (f: Mrightarrow R), где (M) есть некоторое множество, принадлежащее метрическому пространству (X). Если (X=R^n), то функция (f: Mrightarrow R) называется функцией многих переменных и обозначается обычно следующим образом:
$$
f(x)=f(x_1,ldots,x_n),quad xin M.nonumber
$$
Например, функция (displaystyle sqrt{1-x_1^2-x_2^2}) определена в единичном круге пространства (R^2) с центром в точке ((0,0)), а функция (operatorname{ln}(x_1^2+x_2^2)) определена в любой проколотой окрестности точки ((0,0)).
Определение 1.
Пусть функция (f(x)) определена в проколотой окрестности (dot{O}(x^0)) точки (x^0) метрического пространства (X). Говорят, что число (A) есть предел функции (f(x)) при (xrightarrow x_0), если (forall varepsilon > 0 exists delta > 0) такое, что для (forall xindot{O}(x^0)), удовлетворяющего условию (rho(x,x^0) < delta), выполнено неравенство (|f(x)-A| < varepsilon).
Определение 2.
Говорят, что функция (f(x)), определенная в (dot{O}(x^0)), имеет при (xrightarrow x_0) предел (A), если для любой последовательности (x^{(k)}indot{O}(x^0)) такой, что (displaystylelim_{krightarrowinfty}x^{(k)}=x^0), выполнено равенство (displaystylelim_{krightarrowinfty}f(x^{(k)})=A).
Эквивалентность двух определений предела доказывается так же, как и для функций одной переменной.
Если число (A) есть предел функции (f(x)) при (xrightarrow x_0), то будем писать
$$
A=lim_{xrightarrow x^0}f(x).nonumber
$$
Если функция двух переменных (f(x,y)) определена в (dot{O}((a,b))), a число (A) есть ее предел при ((x,y)rightarrow(a,b)), то пишут
$$
A=lim_{xrightarrow a,yrightarrow b}f(x,y)nonumber
$$
и называют иногда число (A) двойным пределом.
Аналогично, для функции (n) переменных наряду с обозначением (A=displaystylelim_{xrightarrow x^0}f(x)) будем использовать обозначение
$$
A=lim_{xrightarrow x_1^0,ldots,x_nrightarrow x_n^0}f(x_1,ldots,x_n).nonumber
$$
Лемма 1.
Пусть функции (f(x)) и (varphi(x)) определены в (dot{O}(x^0)) и (|f(x)|leq varphi(x)) в (dot{O}(x^0)). Если (displaystylelim_{xrightarrow x^0}varphi(x)=0), то и (displaystylelim_{xrightarrow x^0}f(x)=0).
Доказательство.
(circ) Так как (displaystylelim_{xrightarrow x^0}varphi(x)=0), то для любого (varepsilon > 0) найдется шар (S_{delta}(x^0)) такой, что для всех (xin S_{delta}(x^0)) выполнено неравенство (|varphi(x)| < varepsilon). Тем более для всех (xin S_{delta}(x^0)) выполнено неравенство (|f(x)| < varepsilon), то есть (displaystylelim_{xrightarrow x^0}f(x)=0). (bullet)
Пример 1.
Доказать, что (displaystylelim_{xrightarrow 0,yrightarrow 0}(x^2+y^2)^a=0), если (a > 0).
Решение.
(triangle) Возьмем любое (varepsilon > 0). Положим (delta=varepsilon^{1/(2a)}). Пусть ((x,y)in S_delta(0, 0)), тогда
$$
(x^2+y^2)^a < delta^{2a} < varepsilon,nonumber
$$
то есть
$$
lim_{xrightarrow 0,yrightarrow 0}(x^2+y^2)^a=0.nonumber
$$
Что и требовалось доказать. (blacktriangle)
Пример 2.
Показать, что (displaystyle lim_{xrightarrow 0,yrightarrow 0}frac{|x|^{alpha}|y|^{beta}}{(x^2+y^2)^{gamma}}=0), если (alpha+beta-2gamma > 0).
Решение.
(triangle) Так как
$$
|x| < sqrt{x^2+y^2},qquad |y| < sqrt{x^2+y^2},nonumber
$$
то при (x^2+y^2 > 0) имеем неравенства
$$
0leq f(x,y)=frac{vert xvert^alphavert yvert^beta}{(x^2+y^2)^gamma}leqfrac{(x^2+y^2)^{alpha/2}(x^2+y^2)^{beta/2}}{(x^2+y^2)^gamma}=\(x^2+y^2)^{(alpha+beta-2gamma)/2}=varphi(x,y).nonumber
$$
В силу примера выше (displaystylelim_{xrightarrow 0,yrightarrow 0}varphi(x,y)=0.), так как (alpha+beta-2gamma > 0). Применяя лемму 1, получаем, что
$$
lim_{xrightarrow 0,yrightarrow 0}f(x,y)=0.nonumber
$$
Что и требовалось доказать. (blacktriangle)
Пример 3.
Функция
$$
f(x,y)=frac{2xy}{x^2+y^2}label{ref1}
$$
не имеет предела при ((x,y)rightarrow (0,0)).
Решение.
(triangle) Рассмотрим последовательность точек ((x_n,y_n)=displaystyleleft(frac{1}{n},frac{1}{n}right)). Тогда (f(x_n,y_n)=1) и, следовательно, (displaystyle lim_{nrightarrowinfty}f(x_n,y_n)=1). Если же взять последовательность точек ((x_n’,y_n’)=displaystyleleft(frac{1}{n},-frac{1}{n}right)), то (displaystyle lim_{nrightarrowinfty}f(x_n’,y_n’)=-1).
Так как при любом (nin mathbb{N}) точки ((x_n,y_n)) и ((x_n’,y_n’)) не совпадают с точкой ((0,0)), а последовательности точек ((x_n,y_n)) и ((x_n’,y_n’)) сходятся к точке ((0,0)), то, используя определение 2 предела, получаем, что функция (f(x,y)) не имеет предела при ((x,y)rightarrow (0,0)). (blacktriangle)
Пример 4.
Функция
$$
f(x,y)=frac{2x^2y}{x^4+y^2}label{ref2}
$$
не имеет предела при ((x,y)rightarrow (0,0)).
Решение.
(triangle) Повторяя рассуждения примера 3, построим две последовательности точек ((x_n,y_n)=displaystyleleft(frac{1}{n},frac{1}{n}right)) и ((x_n’,y_n’)=displaystyleleft(frac{1}{n},frac{1}{n^2}right)). Так как ((x_n,y_n)rightarrow(0,0)) и ((x_n’,y_n’)rightarrow(0,0)), а (displaystylelim_{nrightarrowinfty}f(x_n,y_n)=0) и (displaystylelim_{nrightarrowinfty}f(x_n’,y_n’)=1), то двойной предел функции (f(x,y)) при ((x,y)rightarrow(0,0)) не существует. (blacktriangle)
Предел по множеству.
Предел (displaystylelim_{xrightarrow x^0}f(x)) был определен ранее для функции, заданной в (dot{O}(x^0)). Расширим определение предела, введя понятие предела по множеству.
Определение 3.
Пусть (M) есть подмножество области определения функции (f(x)), (x^0) — предельная точка множества (M). Будем говорить, что число (A) есть предел функции (f(x)) по множеству (M) при (xrightarrow x^0), если (forallvarepsilon > 0 exists delta > 0) такое, что (forall xin{dot S}_delta(x^0)cap M) выполнено неравенство (|f(x)-A| < varepsilon). В этом случае пишут
$$
A=lim_{xrightarrow x^0, xin M}f(x).nonumber
$$
Пусть функция двух переменных (f(x,y)) определена в проколотой окрестности (dot{O}(x_0,y_0)). Пределом функции (f(x,y)) в точке ((x_0,y_0)) по направлению (l=(cosalpha,sinalpha)) будем называть выражение
$$
lim_{trightarrow+0}f(x_0+tcosalpha, y_0+tsinleft(alpharight))=lim_{begin{array}{c}(x,y)rightarrow(x_0,y_0)\(x,y)indot O(x_0,y_0)cap L\end{array}}f(x,y),nonumber
$$
где (L) есть луч, выходящий из точки ((x_0,y_0)) в направлении (l).
Пример 5.
Показать, что предел функции (f(x,y)=displaystyle frac{2xy}{x^2+y^2}) в точке ((0,0)) по любому направлению (l=(cosalpha, sinalpha)) существует и равен (sin 2alpha).
Решение.
(triangle) Так как при (t > 0) выполнено равенство
$$
f(tcosalpha, tsinalpha)=2sinalphacosalpha=sin 2alpha,nonumber
$$
то
$$
lim_{trightarrow 0}f(tcosalpha, tsinalpha)=sin 2alpha.quadblacktrianglenonumber
$$
Пример 6.
Показать, что предел функции (f(x,y)=displaystyle frac{2x^2y}{x^4+y^2}) в точке ((0,0)) по любому направлению (l=(cosalpha, sinalpha)) существует и равен нулю.
Решение.
(triangle) При (t > 0) справедливо равенство
$$
f(tcosalpha, tsinalpha)=frac{2tcos^2alphasinalpha}{t^2cos^4alpha+sin^2alpha}.nonumber
$$
Если (sinalpha=0), то (f(tcosalpha, tsinalpha)=0) и, следовательно,
$$
lim_{trightarrow +0}f(tcosalpha, tsinalpha)=0.nonumber
$$
Если (sinalphaneq 0), то
$$
lim_{trightarrow +0}f(tcosalpha, tsinalpha)=0.quadblacktrianglenonumber
$$
Ясно, что из существования (displaystylelim_{xrightarrow x^0, xin M}f(x)) следует существование (displaystylelim_{xrightarrow x^0, xin M’}f(x)) для любого подмножества (M’subset M), для которого (x’) есть предельная точка. В частности, из существования двойного предела функции (f(x,y)) при ((x,y)rightarrow (x_0,y_0)) следует существование предела функции (f(x,y)) в точке ((x_0,y_0)) по любому направлению и равенство этих пределов двойному пределу функции (f(x,y)) при ((x,y)rightarrow (x_0,y_0)).
Из результатов примеров 4 и 6 следует, что из существования и равенства пределов по любому направлению в точке ((x_0,y_0)) не вытекает существование в этой точке предела функции.
Предел функции (f(x)) в точке (x^0in R^n) по направлению (l=(l_1,ldots,l_n)), где (l_1^2+ldots+l_n^2=1), определяется по аналогии со случаем функции двух переменных.
Повторные пределы. Бесконечные пределы.
Пусть функция двух переменных (f(x,y)) определена на множестве
$$
Pi={(x,y):quad 0 < |x-x_0| < a,quad 0 < |y-y_0| < b}.nonumber
$$
Пусть (forall xin (x_0-a, x_0+a), xneq x_0), существует (displaystylelim_{yrightarrow y_0}f(x,y)=g(x)), а функция (g(x)) определена в проколотой окрестности точки (x_0). Если существует (displaystylelim_{xrightarrow x_0}g(x)=lim_{xrightarrow x_0}lim_{yrightarrow y_0}f(x,y)), то этот предел называется повторным. Аналогично определяется другой повторный предел (displaystylelim_{yrightarrow y_0}lim_{xrightarrow x_0}f(x,y)).
Как показывают простые примеры, из существования двойного предела не следует существование повторных пределов, а из существования и равенства повторных пределов не следует существование двойного предела.
Так для функции (displaystyle f(x,y)=frac{2xy}{x^2+y^2}) примера 3 двойной предел при ((x,y)rightarrow (0,0)) не существует, но оба повторных предела равны нулю, так как
$$
lim_{xrightarrow0}f(x,y)=lim_{yrightarrow0}f(x,y)=0.nonumber
$$
Для функции
$$
f(x,y)=left{begin{array}{lc}xsinfrac1y,&yneq0,\0,&y=0,end{array}right.nonumber
$$
справедливо неравенство (|f(x,y)|leq|x|). В силу леммы 1 двойной предел этой функции при ((x,y)rightarrow (0,0)) равен нулю. Но при (xneq 0) не существует
$$
lim_{yrightarrow0}xsinfrac1y,nonumber
$$
а поэтому не существует и соответствующий повторный предел.
Бесконечные пределы для функций многих переменных определяются по той же схеме, что и для функций одной переменной. Например, (displaystylelim_{xrightarrow x^0}f(x)=+infty), если для любого числа (C > 0) число (delta > 0), что для всех (x) из проколотой окрестности (dot{O}(x^0)) точки (x^0) выполнено неравенство (f(x) > C).
Пример 7.
Показать, что
$$
lim_{xrightarrow +infty,yrightarrow +infty}(x^2+y^2)e^{-(x+y)}=0.nonumber
$$
Решение.
(triangle) Так как при (x > 0, y > 0) справедливо неравенство
$$
0leq (x^2+y^2)e^{-(x+y)}leq(x+y)^2e^{-(x+y)}nonumber
$$
и (displaystylelim_{trightarrow +infty}t^2e^{-t}=0), то (forall varepsilon > 0 existsdelta > 0) такое, что (forall t > delta) выполнено неравенство (t^2e^{-t} < varepsilon). Но тогда (forall x > displaystylefrac{delta}{2}) и (forall y > displaystylefrac{delta}{2}) справедливо неравенство
$$
0leq(x^2+y^2)e^{-(x+y)} < varepsilon.quadblacktrianglenonumber
$$
До сих пор мы рассматривали функции одной переменной, т. е. функции, значения которых зависят от значений одной независимой переменной.
При рассмотрении многих вопросов естествознания приходится иметь дело с такими зависимостями между переменными величинами, в которых числовые значения одной из них полностью определяются значениями нескольких других. Так, например, температура тела в данный момент времени t может изменяться от точки к точке. Каждая точка тела определяется тремя координатами х, у и z, поэтому температура зависит от трех переменных х, у и z, а если еще учитывать зависимость температуры от времени t, то значения ее будут уже определяться значениями четырех переменных х, у, z и t. Площадь прямоугольника со сторонами, длины которых равны хну, определяется значениями двух переменных х и у, а объем прямоугольного параллелепипеда с ребрами, длины которых равны х, у, z, — значениями трех переменных х, у и z. Примеров таких зависимостей можно привести сколько угодно.
Эта часть курса и посвящается рассмотрению такого рода зависимостей. С этой целью вводится понятие функции нескольких переменных и развивается аппарат для исследования таких функций.
Определение функции двух и более переменных
Аналогично функции одной переменной вводится понятие функции двух переменных.
Определение:
Пусть X, Y и Z — некоторые числовые множества. Функцией двух переменных называется множество f упорядоченных троек чисел (х; у; z) таких, что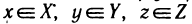 
и каждая упорядоченная пара чисел (х; у) входит в одну и только одну тройку этого множества, а каждое z входит, по крайней мере, в одну тройку. При этом говорят, что упорядоченной паре чисел (х; у) поставлено в соответствие число z, и пишут z=f(x; у). Число z называется значением функции f в точке (х; у). Переменную z называют зависимой переменной, а переменные х и у — независимыми переменными (или аргументами); множество {(x; у)} —областью определения функции, а множество Z — множеством значений функции.
Функцию двух переменных обозначают также следующими символами: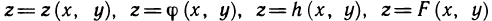 
и т. д.
Так как каждой упорядоченной паре чисел (х; у) при фиксированной прямоугольной системе координат соответствует единственная точка М плоскости и, обратно, каждой точке М соответствует единственная упорядоченная пара чисел (х; у), то функцию двух переменных можно рассматривать как функцию точки М и вместо z=f(x; у) писать z=f(M). Областью определения функции в этом случае является некоторое множество {M} точек плоскости. В дальнейшем будем использовать эти два обозначения функции двух переменных.
Способы задания функции двух переменных, как и в случае одной переменной, могут быть различными. В примерах мы используем, как правило, аналитический способ задания, когда функция задается с помощью формулы. Областью определения функции, в этом случае считается множество всех точек плоскости, для которых эта формула имеет смысл.
Примеры функций двух переменных
1. 
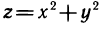. Область определения этой функции — множество {М} всех пар чисел (х; у), т. е. вся плоскость Оху, а множество значений — промежуток 
.
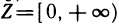2. 
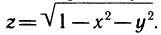Областью определения данной функции является множество всех точек, для которых выражение 
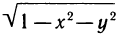определено, т. е. множество точек, для которых 
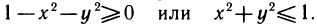Множество всех таких точек образует круг с центром в начале координат и радиусом, равным единице. Множество значений функции представляет собой отрезок [0,1].
3. 
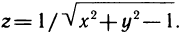Область определения этой функции — множество точек, координаты которых удовлетворяют неравенству 
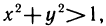т. е. множество точек, лежащих вне круга с радиусом 1 и центром в начале координат, а множество значений представляет собой промежуток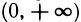 
Из рассмотренных примеров следует, что областью определения функции двух переменных может быть вся плоскость Оху или ее часть.
Из аналитической геометрии известно, что множество всех упорядоченных троек чисел (х; у; z) образует координатное пространство. При этом каждой тройке (х; у; z) в пространстве соответствует точка М (х; у; z), и наоборот. Если вместо множества (М) точек плоскости взять множество {M} точек пространства, то аналогично можно дать определение функции трех переменных u=f(M) или u=f(x; y; z). Областью определения функции трех переменных является все пространство или его часть. Так, например, функция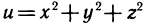 
определена во всем пространстве, а функция 
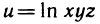— на множестве точек пространства, координаты которых удовлетворяют неравенству xyz>0. В первом случае множеством значений функции является промежуток 
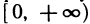, а во втором — 
.
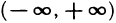Аналогично можно дать определение функции четырех переменных u=f(x, у, z, t). В этом случае множество упорядоченных четверок чисел (х; у: z; t) образуют так называемое четырехмерное пространство, а каждая четверка (z; y; z; t) называется точкой этого пространства. Однако область определения функции четырех переменных уже не имеет наглядного геометрического истолкования. Аналогично можно ввести понятия функции пяти и вообще n переменных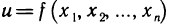 
.
Далее подробно рассмотрены функции двух переменных; следует иметь в виду, что обобщение определений и полученных результатов на функции трех и более переменных не содержит принципиальных отличий.
Геометрическое изображение функции двух переменных
Как известно, функция одной переменной изображается на плоскости в виде линии, определенной уравнением y=f(x). Функция двух переменных изображается в пространстве в виде поверхности, которая определяется уравнением z=f(x, у), т. е. сама формула, задающая функцию, и есть уравнение этой поверхности.
В аналитической геометрии рассматриваются различные поверхности и их уравнения. Так, например, уравнение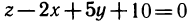 
является уравнением плоскости. Данная плоскость есть график функции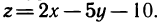 
Уравнение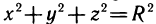 
является уравнением сферы радиуса R с центром в начале координат. С другой стороны, сфера есть объединение графиков двух функций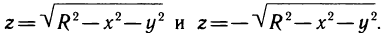 
Построение графиков функций двух переменных во многих случаях представляет значительные трудности. Поэтому существует еще один способ изображения функции двух переменных, основанный на сечении поверхности z=f(x, у) плоскостями z=c, где с —любое число, т. е. плоскостями, параллельными плоскости Оху.
Назовем линией уровня функции z=f(x, у) множество точек (х; у) плоскости Оху, в которых функция принимает одно и то же значение с. Очевидно, при различных с получаются различные линии уровня для данной функции.
Если взять числа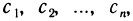 
образующие арифметическую прогрессию с разностью h, то получим ряд линий уровня, по взаимному расположению которых можно получить представление о графике функции, т. е. о форме поверхности. Там, где линии располагаются «гуще», функция изменяется быстрее (поверхность идет круче), а в тех местах, где линии уровня располагаются реже, функция изменяется медленнее (поверхность более пологая) (рис. 162). Ясно, что чем меньше h, тем полнее представление о графике функции.
Термин «линии уровня» заимствован из картографии. Там линии уровня — это линии, на которых высота точек земной поверхности над уровнем моря постоянна. По ним можно судить не только о высоте над уровнем моря определенной точки местности, но и о характере рельефа, что особенно важно, если местность гористая.
Пример:
Построить линии уровня функции 
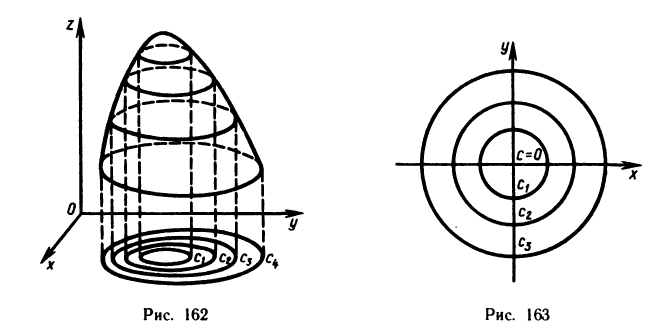
Решение:
Линии уровня данной функции определяются уравнением 
Давая с различные значения, получаем семейство линий уровня, представляющих собой концентрические окружности. При с=0 окружность вырождается в точку (0; 0) (рис. 163).
Так как в данном случае линии уровня — окружности с центрами в начале координат, то графиком данной функции должна быть поверхность вращения вокруг оси Oz. Действительно, из аналитической геометрии известно, что уравнение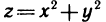 
определяет параболоид вращения.
Предел функции двух переменных
Введем понятие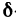 
-окрестности данной точки 
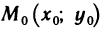и понятие сходящейся последовательности точек плоскости.
Определение:
Множество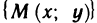 
всех точек, координаты х и у которых удовлетворяют неравенству 
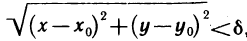или, короче, 
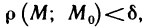называется 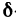-окрестностью точки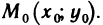 
Другими словами, 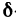-окрестность точки 
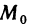— это все точки, лежащие внутри круга с центром 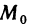радиуса .
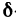Рассмотрим последовательность точек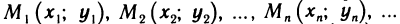 
Будем кратко обозначать эту последовательность символом 
.
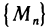Определение:
Последовательность точек 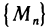называется сходящейся к точке 
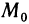, если для любого 
существует номер N такой, что при n>N выполняется неравенство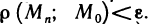 
При этом точка 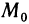, называется пределом последовательности .
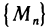Обозначение: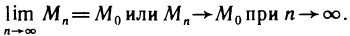 
Заметим, что понятие сходящейся последовательности точек плоскости является обобщением понятия сходящейся числовой последовательности. Действительно, задание последовательности 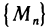точек на прямой равносильно заданию числовой последовательности 
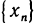и неравенство 
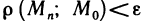переходит в этом случае в неравенство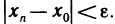 
Теперь определим предел функции двух переменных. Его определение аналогично определению предела функции одной переменной.
Пусть функция z=f(M) определена на некотором множестве {М} и точка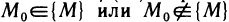 
, но обладает тем свойством, что в любой 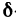-окрестности этой точки содержится хотя бы одна точка множества {М}, отличная от 
.
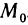Определение:
Число А называется пределом функции z=f(М) в точке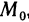 
, если для любой сходящейся к 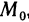последовательности точек 
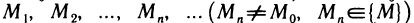соответствующая последовательность значений функции 
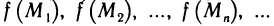сходится к А.
Обозначение: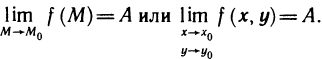 
Так, например, функция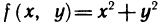 
определена на всей плоскости. Найдем предел этой функции в точке 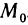(1; 2). Для любой последовательности точек , сходящейся к точке , имеем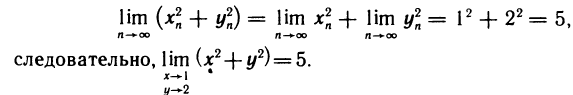 
Приведем пример функции, не имеющей предела в некоторой точке. Функция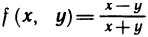 
определена всюду, кроме точек прямой х+у=0. Покажем, что она не имеет предела в точке (0; 0). Для этого выберем две сходящиеся к точке (0; 0) последовательности точек 
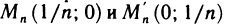; тогда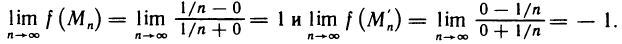 
Таким образом, двум различным последовательностям точек, сходящимся к началу координат, соответствуют две последовательности значений функции, которые имеют разные пределы. Следовательно, по определению 3 данная функция не имеет предела в точке (0; 0).
Приведенное определение предела функции двух переменных дано с помощью понятия предела последовательности. Так же, как для функции одной переменной, можно дать эквивалентное определение, используя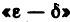 
терминологию.
Определение:
Число А называется пределом функции z=f(AM) в точке 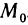если для любого 
существует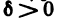 
такое, что для всех точек 
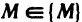, удовлетворяющих условию 
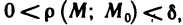выполняется неравенство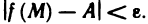
Используя логические символы, данное определение можно записать в виде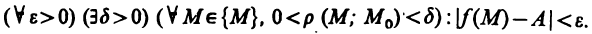 
Доказательство эквивалентности определений 3 и 4 проводится точно так же, как и в случае функции одной переменной. Следует только в доказательстве теоремы 4.1 заменить последовательность 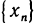последовательностью точек 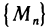, точку 
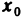— точкой 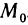разности 
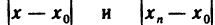— соответственно расстояниями 
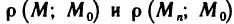, а числовую последовательность 
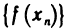— числовой последовательностью 
.
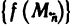Используя определение предела функции двух переменных, можно перенести основные теоремы о пределах для функции одной переменной на функции двух переменных. Например, имеет место следующая теорема.
Теорема:
Пусть функции f(М) и g(М) определены на одном и том же множестве {M} и имеют в точке 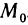пределы В и С. Тогда функции 
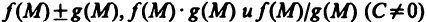имеют в точке 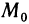пределы, равные соответственно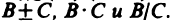 
Доказательство этой теоремы аналогично доказательству теоремы 4.3 и может быть получено из него формальной заменой букв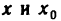 
буквами 
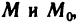, только вместо определения 1 предела функции одной переменной следует использовать определение 3 предела функции двух переменных.
Определение:
Функция z=f(M) называется бесконечной малой в точке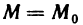 
(или при 
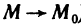), если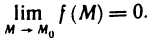 
Если функция z=f(M) имеет в точке 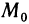предел, равный А, то функция 
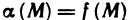— A является бесконечно малой в точке 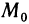. Действительно, 
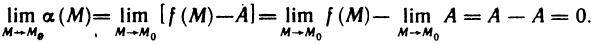Отсюда получаем специальное представление для функции, имеющей в точке 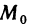предел, равный 
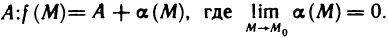При этом говорят, что функция f(M) в окрестности точки 
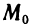отличается от числа А на бесконечно малую функцию.
Сравнение бесконечно малых функций двух переменных производится точно так же, как и бесконечно малых функций одной переменной, причем, как и в случае одной переменной, под символом о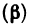
будем понимать любую бесконечно малую в данной точке 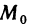функцию более высокого порядка малости, чем бесконечно малая в точке 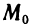функция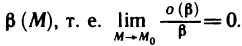 
Непрерывность функции двух переменных
Понятие непрерывности функции двух переменных вводится на основе понятия предела.
Определение непрерывности функции двух переменных
Пусть на некотором множестве {M} определена функция f(M), точка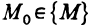 
и любая 
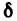-окрестность точки 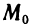содержит точки множества {M}.
Определение:
Функция z=f(M) называется непрерывной в точке 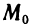, если предел функции в этой точке существует и равен значению функции в этой точке, т. е.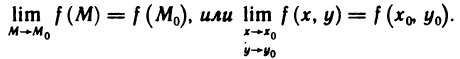 
Согласно определению предела функции в терминах последовательностей данное определение непрерывности функции в точке 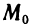равносильно тому, что для любой последовательности 
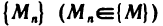такой, что 
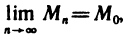, последовательность 
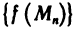сходится и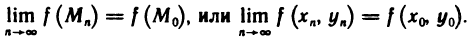 
Точки, в которых функция не обладает свойством непрерывности, называются точками разрыва этой функции.
Например, функция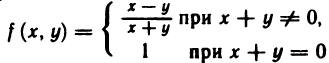
разрывна в точке (0; 0), так как предел этой функции при 
, 
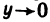не существует; функция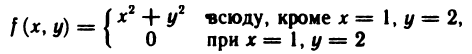 
в точке (1; 2) разрывна, так как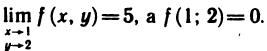 
Сформулируем определение непрерывности функции, используя определение предела функции в терминах 
Определение:
Функция z=f(М) называется непрерывной в точке 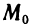, если для любого
существует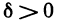 
такое, что для всех точек 
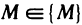, удовлетворяющих условию 
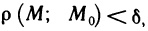выполняется неравенство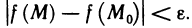 
Используя символы, определение 2 можно записать в виде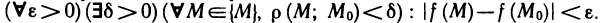
Так же как для функции одной переменной, используя данные определения непрерывности и соответствующие теоремы о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложных функций из непрерывных функций приводят к непрерывным функциям.
В дальнейшем используется определение 1 непрерывности функции, записанное в другом виде.
Назовем полным приращением функции z=f(M) в точке 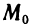функцию 
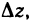определяемую формулой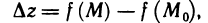 
где М — любая точка из области определения функции. Пусть точки 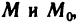имеют соответственно координаты 
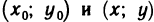. Обозначим 
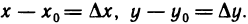Используя эти обозначения, для 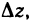получаем следующее выражение: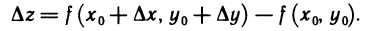 
Определение 3. Функция z f (М) называется непрерывной в точке 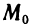, если ее полное приращение в этой точке есть бесконечно малая при 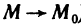функция, т. е.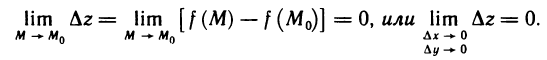 
Это условие, очевидно, равносильно условию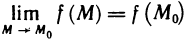 
из определения 1.
Пример:
Функция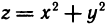 
непрерывна в любой точке (x; у)-Действительно, полное приращение данной функции в точке (x; у) имеет вид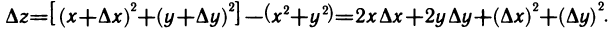 
Очевидно,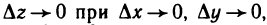 
т. е. согласно определению 3 функция 
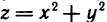непрерывна в точке (х; у).
Функция z=f(М) называется непрерывной на некотором множестве {М}, если она непрерывна в каждой точке этого множества.
Основные свойства непрерывных функций двух переменных
Приведем без доказательства основные свойства непрерывных функций двух переменных, поскольку они в основном аналогичны доказательствам соответствующих свойств функций одной переменной. Предварительно введем ряд понятий для множеств {М} точек плоскости.
Определение:
Множество {М} точек плоскости называется связным, если любые две точки этого множества можно соединить непрерывной линией, состоящей из точек данного множества. Например, круг — связное множество, а множество, состоящее из двух кругов, не имеющих общих точек, не является связным.
Определение:
Точка М называется внутренней точкой множества {М}, если существует 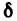-окрестность этой точки, состоящая из точек данного множества.
Определение:
Множество {М}, состоящее лишь из внутренних точек, называется открытым множеством.
Определение:
Связное открытое множество {М} точек называется открытой областью, или короче, областью. Простейшими областями являются: внутренность треугольника, круга, эллипса и т. п.
Определение:
Точка М называется граничной точкой области, если в любой ее 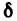-окрестности есть точки как принадлежащие, так и не принадлежащие этой области. Множество всех граничных точек области называется границей этой области.
Например, для области, которая состоит из точек, лежащих внутри круга, границей является окружность.
Определение:
Множество {М} точек, образованное областью и ее границей, называется замкнутой областью.
Определение:
Множество {М} называется ограниченным, если существует круг, внутри которого оно содержится.
Отрезок и треугольник — ограниченные множества. Прямая не является ограниченным множеством.
Замкнутая ограниченная область, в которой определена функция двух переменных, является аналогом отрезка для функции одной переменной.
Теперь сформулируем основные свойства непрерывных функций двух переменных:
1°. Если функция z=f(M) непрерывна в замкнутой ограниченной области, то она ограничена в этой области, т. е. существует число k такое, что для всех точек области выполняется неравенство
2°. Если функция z=f(M) непрерывна в замкнутой ограниченной области, то она достигает в этой области своих точных граней.
3°. Если функция z=f(M) непрерывна в области, то она принимает все промежуточные значения между любыми двумя своими значениями, т. е. если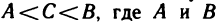 
— какие-то значения функции f(М) в данной области, то в этой области существует точка 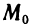, в которой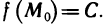 
Отсюда, в частности, следует, что если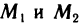 
— точки данной области и 
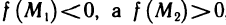, то в области существует точка 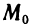, в которой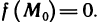
4°. Если функция z=f(M) непрерывна в замкнутой ограниченной области, то она равномерно-непрерывна в этой области, т. е. для любого существует 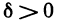такое, что для любых двух точек М’ и М» области, удовлетворяющих условию
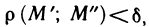выполняется неравенство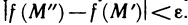 
В заключение отметим, что понятия предела, непрерывности и перечисленные свойства функций двух переменных легко обобщаются на функции трех и более переменных.
Предел функции нескольких переменных. Непрерывность функции и точки разрыва
Смотрите также:
- Решение задач по высшей математике
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Предел функции двух переменных в точке
Содержание:
- Предел функции двух переменных в точке
- Предел функции двух переменных
- Непрерывность функции двух переменных в точке
Предел функции двух переменных в точке
Предел и непрерывность функции двух переменных – это число А называется пределом функции в точке (или при и ), если для любого сколь угодно малого положительного числа найдется положительное число такое, что для всех точек , отстоящих от точки на расстояние, меньшее чем , выполняется неравенство.
Предел функции двух переменных
Для функции двух переменных можно ввести понятие предела и непрерывности в точке M0 (x0, y0). Пусть функция z = f (x, y) задана в окрестности точки M0 (x0, y0) (рис. 8). Под δ-окрестностью точки M0 будем понимать множество точек плоскости Оxy, которые удовлетворяют неравенства 
< δ или 
Рис. 8.
Определение 3. Число b называется пределом функции z = f (x, y) при 
если для любого ε > 0 существует такое δ > 0, что как только 
< δ , то 
< ε.
Символически это можно записать так: 
(5,1)
Очевидно, что предел функции не должен зависеть от способа приближения точки M к точке M0 .
Пример 1. Найти предел функции 
в точке О (0; 0).
Решение. Найдем сначала предел функции, когда y = 0, x → 0:
Теперь найдем предел функции, когда x = 0, y → 0:
Очевидно, что в этом случае предела функции не существует, поэтому что при приближении к точке O (0; 0) по различным направлениям получаются различные пределы.
Непрерывность функции двух переменных в точке
Определение 4. Функция z = f (x, y) называется непрерывной в точке M0 (x0; y0), если она задана в этой точке и некоторой ее окрестности и выполняется условие:
(5.2)
Для непрерывных функций двух переменных справедливы те же теоремы, что и для функции одной переменной.
Пример 2. Исследовать на непрерывность функцию
в точке O (0; 0).
Решение. Найдем повторные пределы:
Будем приближаться к точке О (0,0) по произвольной прямой y = kx, тогда:
Из того, что все пределы равны и совпадают со значением функции в точке O (0; 0), следует непрерывность функции в этой точке.
Аналогично вводим понятие предела и непрерывности в точке для функции u = f (x1, x2, …, xn) .
Лекции:
- Степенной ряд сходимость: пример решения
- Как решать пределы: пример решения
- Площадь, ограниченная кривой
- Декартова система координат: примеры решения
- Реляционная модель данных
- Как решать пределы с корнями: в числителе
- Уравнение касательной. Угловой коэффициент
- Вычислить криволинейный интеграл
- Перпендикулярность плоскостей
- Решение задач на нахождение пределов
