Пределы со степенями: показательная, степенная и показательно-степенная функции
Пределы со степенями бывают различных видов в зависимости от положения неизвестной $x$ в пределе. Рассмотрим примеры решений для следующих ситуаций:
- Показательная функция
$$limlimits_{xto a} a^{f(x)} = a^{limlimits_{xto a} f(x)} $$ - Степенная функция
$$ limlimits_{xto a} (f(x))^a = bigg(limlimits_{xto a} f(x) bigg)^a $$ - Показательно-степенная функция
$$limlimits_{xto a} bigg(f(x)bigg)^{g(x)} = limlimits_{xto a} frac{ln(f(x))}{frac{1}{g(x)}} $$
| Пример 1 |
| Найти предел показательной функции $limlimits_{xto 2} 2^{frac{x^2-4}{x-2}}$ |
| Решение |
|
Подставив точку $x=2$ в предел получим неопределенность $2^{big(frac{0}{0}big)}$. Итак, перенесем знак предела в показатель и попробуем его вычислить путем разложения числителя по формуле разности квадратов $a^2-b^2 = (a-b)(a+b)$. $$limlimits_{xto 2} 2^{frac{x^2-4}{x-2}} = 2^{limlimits_{xto 2} frac{(x-2)(x+2)}{x-2}} = $$ Сокращаем числитель со знаменателем на $x-2$ и вычисляем предел степени. $$ =2^{limlimits_{xto 2} (x+2)} = 2^{2+2} = 2^4 = 16 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$limlimits_{xto 2} 2^{frac{x^2-4}{x-2}} = 16$$ |
| Пример 2 |
| Решить предел степенной функции $limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3$ |
| Решение |
|
Внесем знак предела внутрь скобок, а степень останется при этом снаружи. $$limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3 = bigg(limlimits_{xto 0} frac{sin x^2}{1-cos x}bigg)^3 = $$ При подстановке точки $x=0$ в предел получаем неопределенность $frac{0}{0}$. Для её устранения воспользуемся таблицей эквивалентностей пределов. $$sin x^2 sim x^2$$ $$ 1-cos x sim frac{x^2}{2}$$ Подставляем эквивалентные функции в предел и сокращаем $x$. $$ = bigg(limlimits_{xto 0} frac{x^2}{frac{x^2}{2}}bigg)^3 = bigg(limlimits_{xto 0} frac{2x^2}{x^2} bigg)^3 = 2^3 = 8$$ |
| Ответ |
| $$limlimits_{xto 0} bigg(frac{sin x^2}{1-cos x}bigg)^3 = 8$$ |
| Пример 3 |
| Вычислить предел показательно-степенной функции $limlimits_{xto 0} (tg x)^{sin x} $ |
| Решение |
|
Если подставим $x=0$, то получим предел ноль в степени ноль $(0^0)$. Превратим это в другую неопределенность $(frac{infty}{infty})$ с помощью третьей формулы. $$limlimits_{xto 0} (tg x)^{sin x} = limlimits_{xto 0} frac{ln (tg ;x)}{frac{1}{sin x}} = frac{infty}{infty} = $$ Используем правило Лопиталя для продолжения решения. По нему, как известно, предел отношения функций равен пределу отношения производных от этих функций. $$ = limlimits_{xto 0} frac{(ln (tg ;x))’}{(frac{1}{sin x})’} = limlimits_{xto 0} frac{frac{frac{1}{cos^2 x}}{tg ;x}}{-frac{cos x}{sin^2 x}} = $$ Преобразуем числитель в нормальный вид с помощью формулы $tg ; x = frac{sin x}{cos x}$ и выполняем все необходимые сокращения. $$ = limlimits_{xto 0} frac{frac{1}{sin x cos x}}{-frac{cos x}{sin^2 x}} = -limlimits_{xto 0} frac{sin x}{cos^2 x} = $$ Теперь подставляя точку $x=0$ возможно получить окончательный ответ. $$ = – frac{sin 0}{cos^2 x} = -frac{0}{1} = 0 $$ |
| Ответ |
| $$limlimits_{xto 0} (tg x)^{sin x} = 0$$ |
Вычисление пределов степенно-показательных функций
Пусть функции
![]()
и
![]()
заданы на множестве
![]()
и функция
![]()
на нем положительна. Функция
![]()
называется степенно
– показательной.
Предположим, что
![]()
– точка сгущения множества
![]()
и существуют конечные пределы
![]() ,
,
![]() ,
,
где
![]() .
.
Нужно найти
![]() .
.
Воспользовавшись
тождествами
![]() ,
,
запишем исходное выражение в виде
![]() .
.
В силу теоремы 6.1
получим
![]() .
.
При заданных
значениях пределов будем иметь
![]() .
.
Из проведенного
рассуждения видно, что предположение
о существовании конечных пределов
![]()
и
![]()
можно отбросить. Действительно, для
нахождения предела выражения
![]()
достаточно знать предел произведения
![]()
(конечный или бесконечный).
1) Пусть
![]() .
.
Тогда
![]() .
.
2) Если
![]() ,
,
то
![]() .
.
3) Если
![]() ,
,
то
![]() .
.
Заметим, что
произведение
![]()
может оказаться неопределенностью типа
![]() .
.
Тогда и исходное выражение
![]()
представляет собой неопределенность.
Перечислим возникающие здесь
неопределенности.
1) Если
![]() ,
,
то вычисление предела
![]()
приводит к неопределенности типа
![]() .
.
2) Если
![]() ,
,
то вычисление предела
![]()
приводит к неопределенности типа
![]() .
.
3) Если
![]() ,
,
то вычисление предела
![]()
приводит к неопределенности типа
![]() .
.
Во всех указанных
случаях (![]() ,
,
![]() ,
,
![]() )
)
можно раскрыть неопределенность
![]()
в показателе степени, преобразуя ее к
типу
![]()
и используя соответствующие эквивалентные
бесконечно малые.
Замечание 8.3.
Приведенные выше рассуждения справедливы
и для вычисления предела степенно-показательной
функции в бесконечно удаленной точке:
![]() .
.
Пример 8.2.
Вычислить
![]() .
.
Решение.
Здесь
![]() ,
,
![]() ,
,
поэтому имеем неопределенность типа
![]() .
.
Преобразуем выражение под знаком
предела:
![]() .
.
В показателе
степени имеем неопределенность типа
![]() .
.
Заменой
![]()
при
![]()
на эквивалентную бесконечно малую
![]()
раскрываем ее:
![]() .
.
Таким образом,
![]() .
.
Замечание 8.4.
Аналогично доказывается равенство
![]() .
.
Пределы
![]() ,
,
![]()
образуют две формы
одного и того же равенства, которое
также является замечательным
пределом
и часто служат определением числа
![]() .
.
Задачи к §8
Задача
1. Вычислить
 .
.
Решение.
Здесь имеем
неопределенность типа
![]() .
.
Преобразуем числитель дроби к форме
произведения:
 .
.
Затем
заменим бесконечно малую в точке
![]()
функцию

эквивалентной бесконечно малой
![]() .
.
Тогда
получим

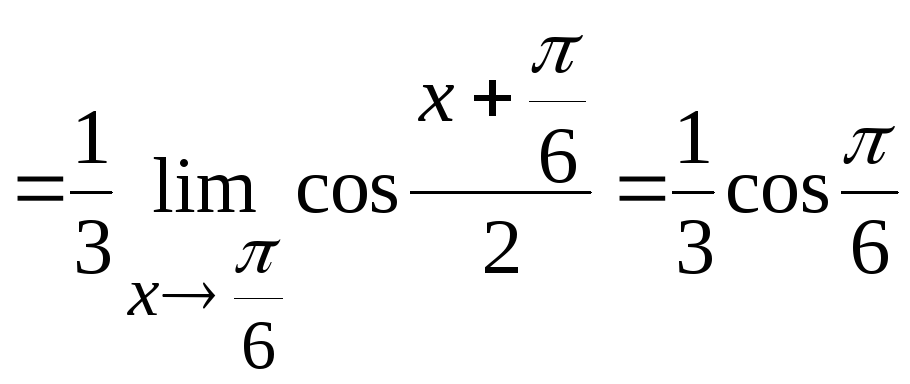 .
.
Ответ:
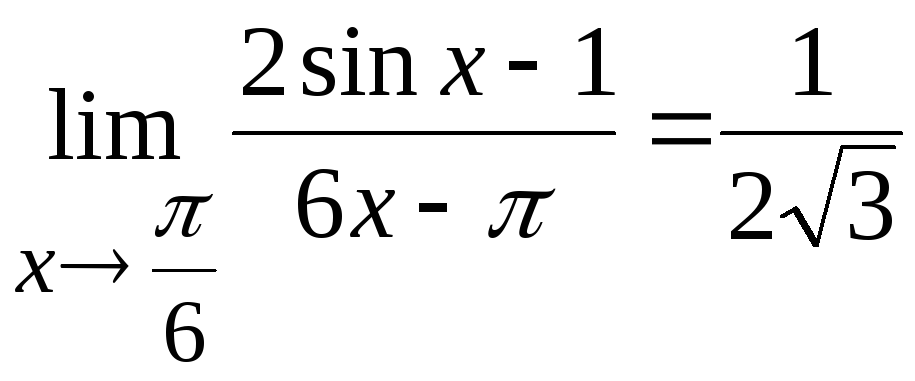 .
.
Задача
2. Вычислить
![]() .
.
Решение.
Здесь возникает неопределенность типа
![]() .
.
Преобразуем знаменатель, воспользовавшись
свойствами логарифмической функции, и
выделим в аргументе логарифма слагаемое,
равное 1:
![]() .
.
Заменим
бесконечно малую в точке
![]()
функцию
![]()
эквивалентной бесконечно малой
![]() .
.
Числитель разложим на множители:
![]() .
.
Тогда
получим:
 .
.
Ответ:
![]() .
.
Задача
3. Вычислить
![]() .
.
Решение.
Здесь возникает неопределенность типа
![]() .
.
Представим числитель в виде:
![]() .
.
Затем
заменим его эквивалентной бесконечно
малой в точке
![]()
функцией
![]() .
.
Функцию
![]()
в точке
![]()
тоже заменим на эквивалентную бесконечно
малую
![]() .
.
Тогда
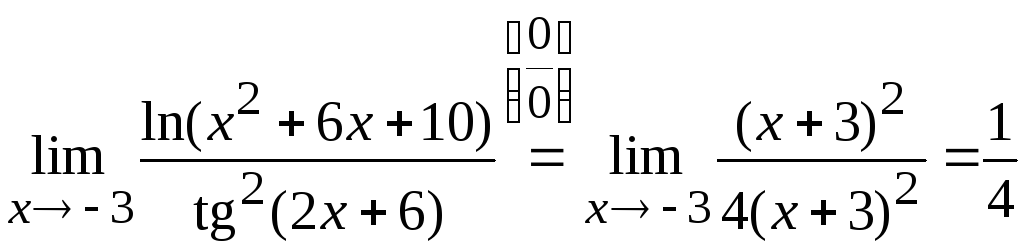 .
.
Ответ:
![]() .
.
Задача
4. Вычислить
![]() .
.
Решение.
Здесь возникает неопределенность типа
![]() .
.
Представим числитель в виде:
![]() .
.
Затем
заменим его эквивалентной бесконечно
малой в точке
![]()
функцией
![]() .
.
Преобразуем
знаменатель:
![]()
и
заменим его на эквивалентную бесконечно
малую
![]() .
.
Тогда получим
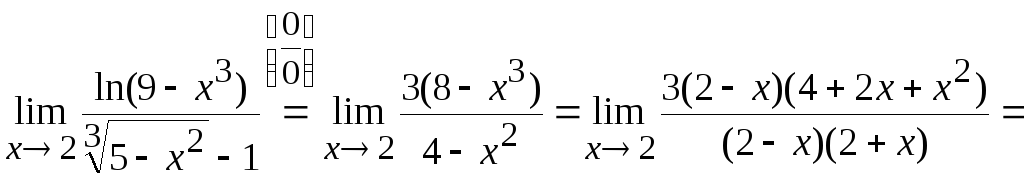
![]() .
.
Ответ:
![]() .
.
Задача
5. Вычислить
![]() .
.
Решение.
Здесь возникает неопределенность типа
![]() .
.
Числитель
![]()
можно заменить эквивалентной бесконечно
малой
![]() .
.
Чтобы
воспользоваться соотношением (8.4),
преобразуем знаменатель:
![]()
![]()
и
заменим его эквивалентной бесконечно
малой
![]() .
.
Тогда
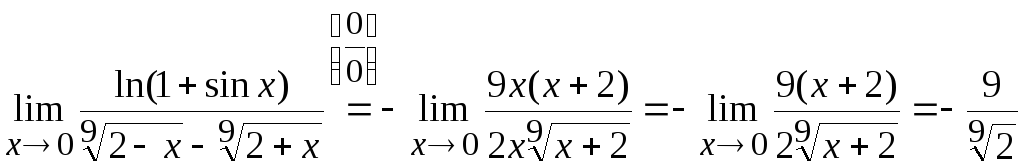 .
.
Ответ:
![]() .
.
Задача
6. Вычислить
![]() .
.
Решение.
Здесь имеем неопределенность типа
![]() .
.
Чтобы применить к выражению
![]()
соотношение (8.3), представим его в виде:
![]() ,
,
и
заменим бесконечно малую функцию
![]()
эквивалентной бесконечно малой
![]() .
.
Знаменатель же представим в виде:
![]()
и,
используя соотношения (8.2) и (8.8), заменим
его эквивалентной бесконечно малой
![]() .
.
Учитывая проведенные выкладки и
соотношение (8.4), получим:
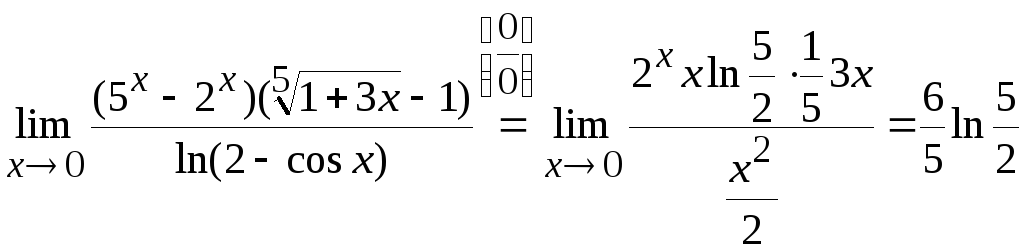 .
.
Ответ:
![]() .
.
Задача
7. Вычислить
![]() .
.
Решение.
Здесь имеем неопределенность типа
![]() .
.
Используя ряд приемов, примененных в
задачах 1–7, получим
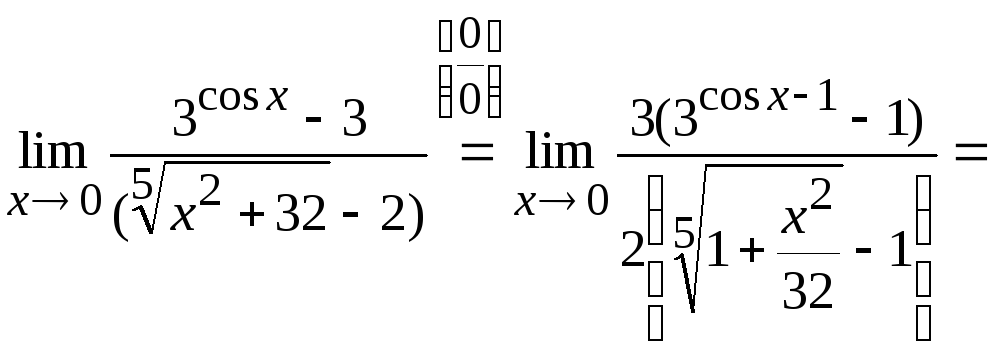
![]() .
.
Ответ:
![]() .
.
Задача
8. Вычислить
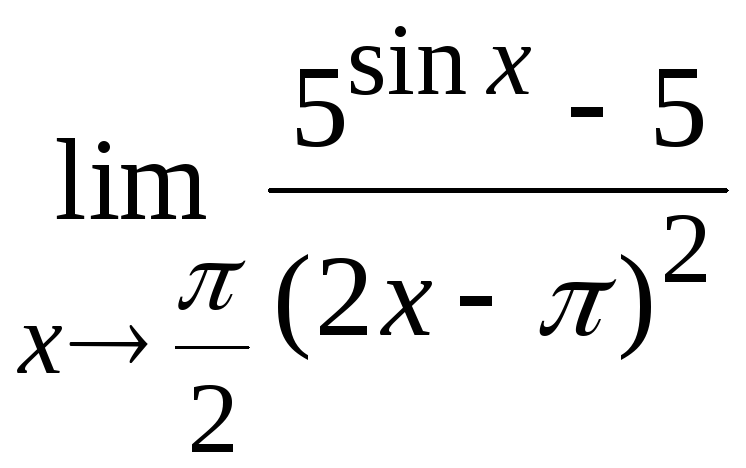 .
.
Решение.
Здесь имеем неопределенность типа
![]() .
.
Используя ряд приемов, примененных в
задачах 1–7 и формулы приведения для
тригонометрических функций, получим
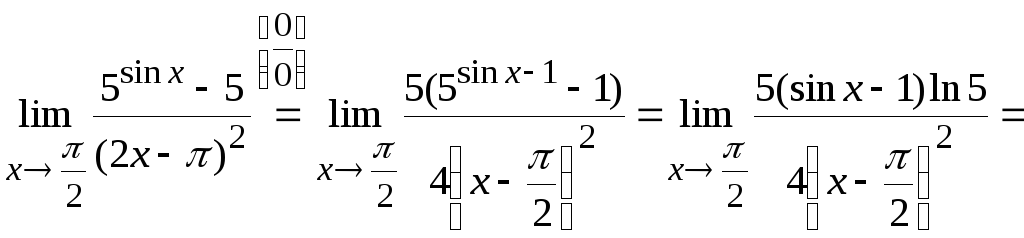
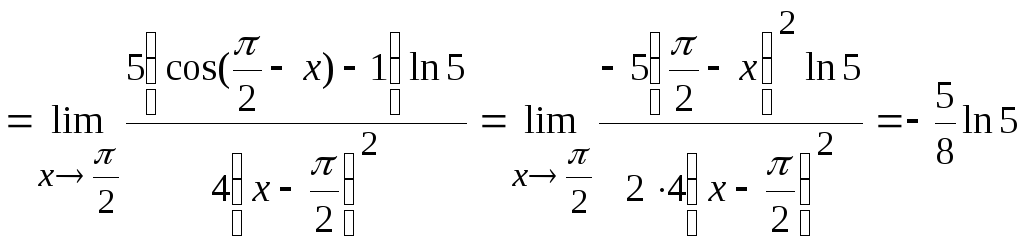 .
.
Ответ:
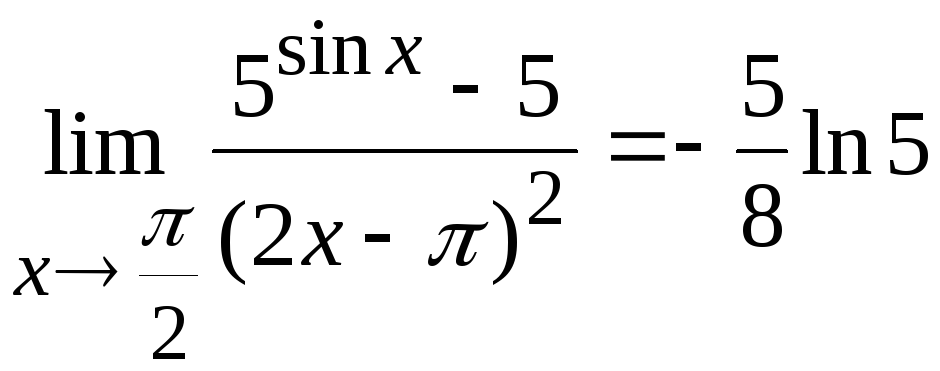 .
.
Задача
9. Вычислить
![]() .
.
Решение.
Здесь имеем неопределенность типа
![]() .
.
Чтобы применить к числителю соотношение
(8.2), преобразуем его следующим образом:
![]()
![]() .
.
Теперь
числитель согласно соотношению (8.2)
можно заменить эквивалентной бесконечно
малой
![]() .
.
Преобразуем
знаменатель
![]() .
.
Заменяем,
используя соотношение (8.1),
![]()
эквивалентной бесконечно малой
![]() .
.
Тогда
 .
.
Ответ:
![]() .
.
Задача
10. Вычислить
![]() .
.
Решение.
Здесь имеем неопределенность типа
![]() .
.
Используя приемы, описанные выше, получим



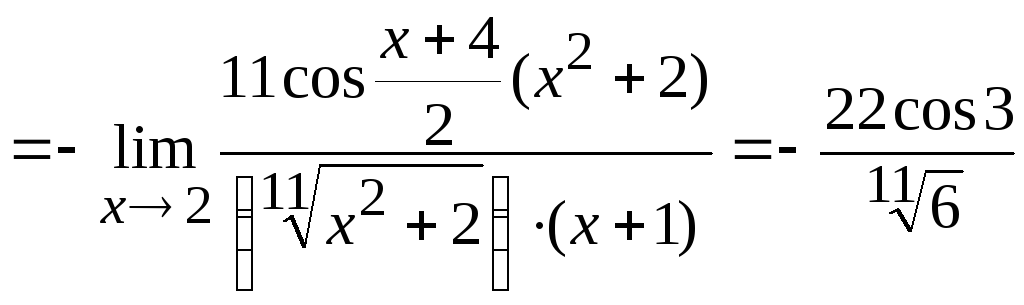 .
.
.
Ответ:
![]() .
.
Задача
11. Вычислить
 .
.
Решение.
Здесь имеем неопределенность типа
![]() .
.
Используя теоремы 6.2 и 6.1, получим

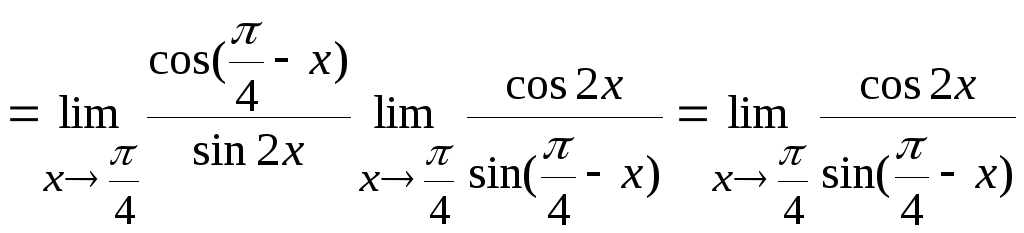 .
.
Получили
неопределенность типа
![]() .
.
Преобразуем выражение с помощью формул
приведения, затем переходим к эквивалентным
бесконечно малым. В итоге получим
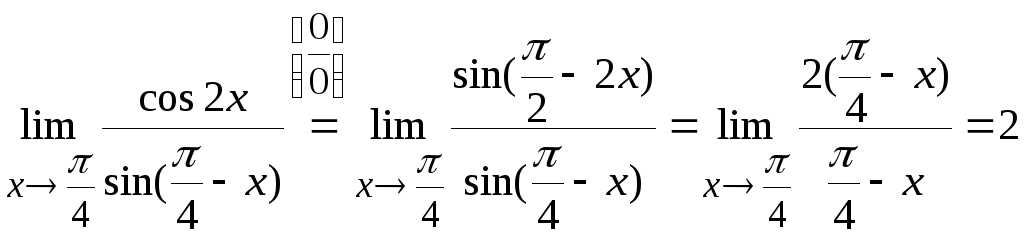 .
.
Ответ:
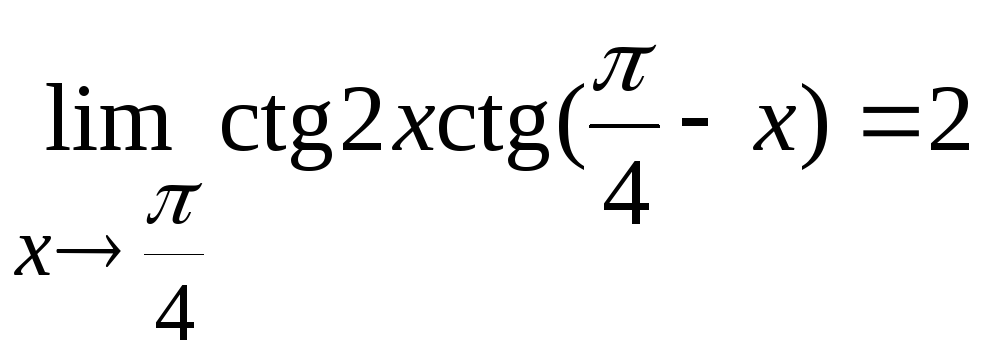 .
.
Задача
12. Вычислить
![]() .
.
Решение.
Здесь имеем неопределенность типа
![]() .
.
Выделим
![]()
в основании степени:
![]() .
.
Заметим,
что
![]()
при
![]() .
.
Справедлива
цепочка равенств
 .
.
Заменяя
логарифм эквивалентной бесконечно
малой согласно соотношению (8.2) и используя
замечание 6.4 для раскрытия неопределенности,
получим
![]()
.
Ответ:
![]() .
.
Задача
134.
Вычислить
![]() .
.
Решение.
Здесь имеем неопределенность типа
![]() .
.
Введем переменную
![]() .
.
Если
![]() ,
,
то
![]() .
.
![]() .
.
Выделим
![]()
в основании степени:
![]() ,
,
тогда
![]() .
.
Заметим,
что
![]()
при
![]() .
.
Заменим функцию
![]()
эквивалентной бесконечно малой
![]() ,
,
будем иметь
![]() .
.
Используя
теорему 7.3, окончательно получим
![]() .
.
Ответ:
![]() .
.
Задача
14. Вычислить
![]() .
.
Решение.
Здесь возникает неопределенность типа
![]() .
.
Поскольку
![]() ,
,
вычислим
сначала
![]() .
.
Мы имеем дело с неопределенностью типа
![]() .
.
Воспользовавшись
последовательно соотношениями (8.2) и
(8.1), будем иметь
![]() .
.
Ответ:
![]() .
.
Задача
15. Вычислить
![]() .
.
Решение.
Здесь возникает неопределенность типа
![]() .
.
Воспользуемся формулой
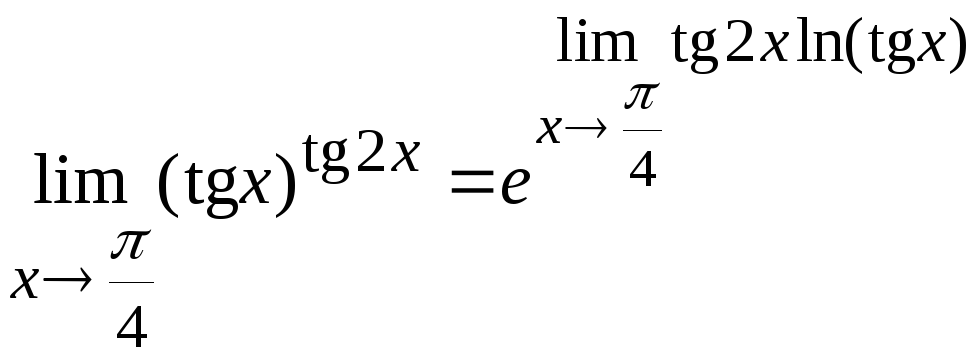 .
.
Вычислим
предел, стоящий в показателе степени.
Для этого требуется раскрыть
неопределенность типа
![]() .
.
Преобразуем ее в неопределенность типа
![]()
и воспользуемся эквивалентностью
бесконечно малых:
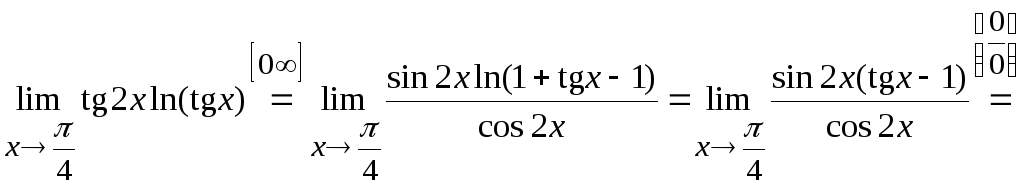
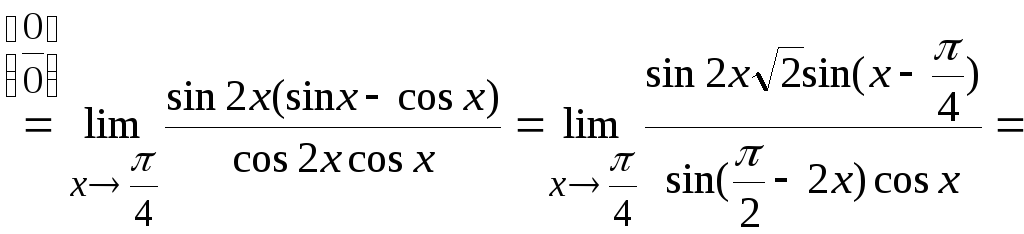
 .
.
Ответ:
![]() .
.
Задача
16. Вычислить
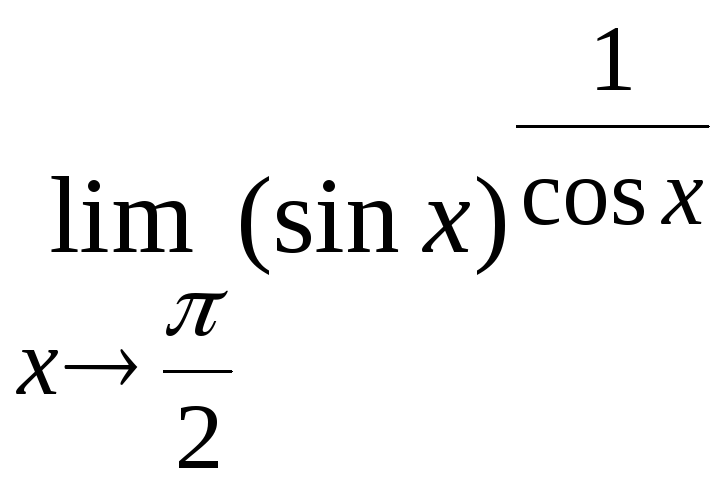 .
.
Решение.
Здесь возникает неопределенность типа
![]() .
.
Преобразуем исходное предельное
выражение
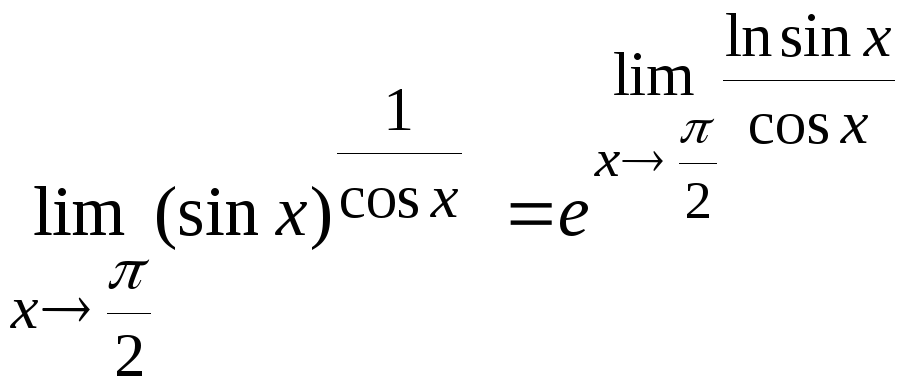 .
.
Вычислим
предел, стоящий в показателе степени.

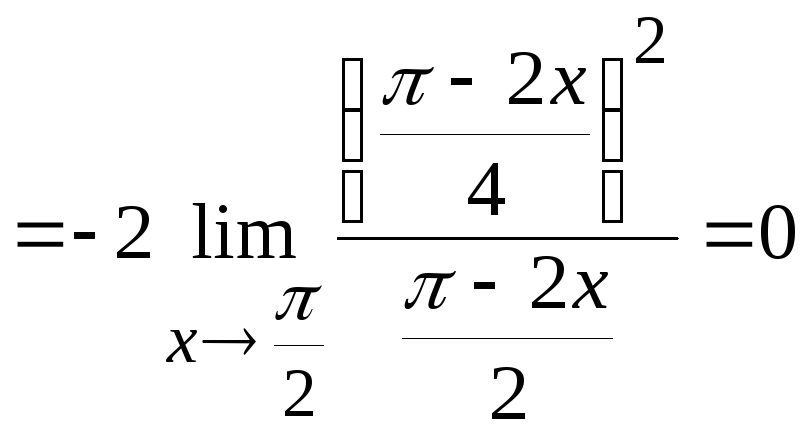 .
.
Ответ:
 .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
При вычислении пределов от показательно-степенной функции пользуются либо формулой 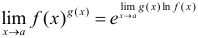 , либо вторым замечательным пределом.
, либо вторым замечательным пределом.

Пример №1.
Вычислить 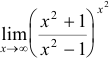 .
.
Решение:
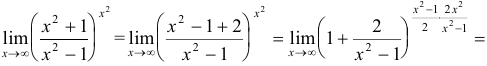
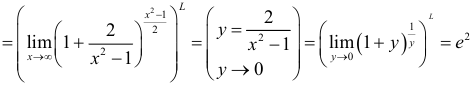 , так как
, так как
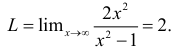
Пример №1.
Вычислить 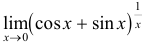 .
.
Решение:
Заметим, что 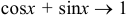 , а
, а 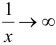 при
при 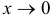 . Следовательно, имеется неопределенность вида
. Следовательно, имеется неопределенность вида 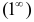 . Для ее раскрытия воспользуемся вторым замечательным пределом. Получим, что
. Для ее раскрытия воспользуемся вторым замечательным пределом. Получим, что
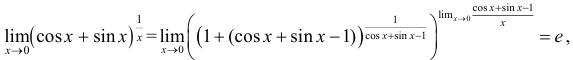
так как
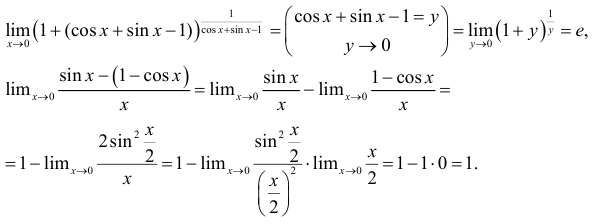
Пример №2.
Вычислить 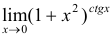 .
.
Решение:
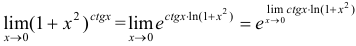 в силу непрерывности
в силу непрерывности 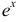 . Вычислим
. Вычислим
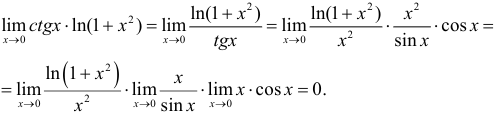
Следовательно, 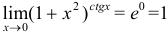 .
.
Пример №3.
Вычислить 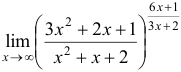 .
.
Решение:
Так как 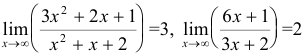 , то в данном случае отсутствует неопределенность и
, то в данном случае отсутствует неопределенность и
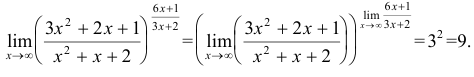
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:

Содержание:
- Примеры с решением
Вы знакомы с функциями  и т.д. Все эти функции являются частными случаями степенной функции, т.е. функции
и т.д. Все эти функции являются частными случаями степенной функции, т.е. функции 
где р — заданное действительное число.
Свойства и график степенной функции (1) существенно зависят от свойств степени с действительным показателем и, в частности, от того, при каких значениях х и р имеет смысл степень  .
.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Перейдем к подробному рассмотрению различных случаев в зависимости от показателя степени р.

1. Показатель  — четное натуральное число.
— четное натуральное число.
В этом случае степенная функция  , где
, где  — натуральное число, обладает следующими свойствами:
— натуральное число, обладает следующими свойствами:
— является убывающей на промежутке  и возрастающей — на промежутке
и возрастающей — на промежутке  График функции
График функции  имеет такой же вид, как, например, график функции
имеет такой же вид, как, например, график функции  (рис. 13, а).
(рис. 13, а).
Возможно вам будут полезны данные страницы:
2. Показатель  — нечетное натуральное число.
— нечетное натуральное число.

В этом случае степенная функция  , где
, где  — натуральное число, обладает следующими свойствами:
— натуральное число, обладает следующими свойствами:
- — область определения — множество
 ;
; - — множество значений — множество
 ;
; - — функция
 — нечетная, так как
— нечетная, так как 
- — является возрастающей на всей действительной оси.
График функции  имеет такой же вид, как, например, график функции
имеет такой же вид, как, например, график функции  (рис. 13, 6).
(рис. 13, 6).
3. Показатель  — натуральное число.
— натуральное число.
В этом случае степенная функция  обладает следующими свойствами:
обладает следующими свойствами:
График функции  имеет такой же вид, как, например, график функции
имеет такой же вид, как, например, график функции  (рис. 14, а).
(рис. 14, а).
4. Показатель  — натуральное число.
— натуральное число. 
В этом случае степенная функция  обладает следующими свойствами: |у=_т
обладает следующими свойствами: |у=_т
График функции  имеет такой же вид, как, например, график функции
имеет такой же вид, как, например, график функции  = (рис. 14, б).
= (рис. 14, б).
5. Показатель р — положительное действительное нецелое число.
В этом случае функция  обладает следующими свойствами:
обладает следующими свойствами:
- — область определения — неотрицательные числа
 ;
; - — множество значений — неотрицательные числа
 ;
; - — является возрастающей на промежутке
 .
.
График функции  — положительное нецелое число, имеет такой же вид, как, например, график функции
— положительное нецелое число, имеет такой же вид, как, например, график функции  (при
(при  ) или, как, например, график функции
) или, как, например, график функции  (рис. 15, а—6).
(рис. 15, а—6).

6. Показатель р — отрицательное действительное нецелое число.

В этом случае функция  обладает следующими свойствами:
обладает следующими свойствами:
- — область определения — положительные числа
 ;
; - — множество значений — положительные числа у > 0;
- — является убывающей на промежутке х > 0.
График функции  , где р — отрицательное
, где р — отрицательное
нецелое число, имеет такой же вид, как, например, график функции (рис. 15, в).
(рис. 15, в).
Примеры с решением
Задача 1.
Решить неравенства:  1) Неравенство
1) Неравенство  имеет смысл при
имеет смысл при  . При х = 0 неравенство не выполняется. При х > 0, возводя неравенство в куб, получаем
. При х = 0 неравенство не выполняется. При х > 0, возводя неравенство в куб, получаем
Так как  откуда
откуда  . Следовательно,
. Следовательно, 
2) Аналогично, возводя неравенство  при
при  в куб, получаем
в куб, получаем  Так как
Так как 
Ответ. 
Решение этой задачи показывает, что график функции  лежит выше графика функции у = х при
лежит выше графика функции у = х при  и ниже — при х > 1 (рис. 16, а); график функции
и ниже — при х > 1 (рис. 16, а); график функции  лежит выше графика функции у = х при
лежит выше графика функции у = х при  и ниже — при
и ниже — при  (рис. 16, 6).
(рис. 16, 6).

Задача 2.
Сравнить числа 
Д Так как  Функция
Функция  убывает на промежутке х > 0. Поэтому
убывает на промежутке х > 0. Поэтому

Задача 3*.
Найти точки пересечения графиков функций 
Для нахождения точек пересечения этих графиков решим уравнение  Левая часть этого уравнения имеет смысл при всех х, а правая — только при
Левая часть этого уравнения имеет смысл при всех х, а правая — только при 
При  функция
функция  совпадает с функцией
совпадает с функцией  , поэтому уравнение можно представить в следующем виде:
, поэтому уравнение можно представить в следующем виде:

Возводя это уравнение (при  ) в куб, получаем
) в куб, получаем

откуда 
Ответ. (0; 0), (1; 1).
Задача 4*.
Построить график функции
Д Заметим, что эта функция четная, так как  Поэтому достаточно построить ее график для х > 0, а затем симметрично отразить его относительно оси ординат.
Поэтому достаточно построить ее график для х > 0, а затем симметрично отразить его относительно оси ординат.
При  имеем
имеем  . Строим график функции
. Строим график функции  (при
(при  ), сдвигаем его вверх на единицу и отражаем полученный график относительно оси ординат (рис. 17).
), сдвигаем его вверх на единицу и отражаем полученный график относительно оси ординат (рис. 17).
 Если каждому значению х из некоторого множества действительных чисел поставлено в соответствие по определенному правилу число у, то говорят, что на этом множестве определена функция.
Если каждому значению х из некоторого множества действительных чисел поставлено в соответствие по определенному правилу число у, то говорят, что на этом множестве определена функция.
При этом х называют независимой переменной или аргументом, а у — зависимой переменной или функцией.
Множество значений х, для которых определены значения z/(x), называют областью определения функции.
Для обозначения функции обычно используют буквы  т.д. Например, говорят: дана функция
т.д. Например, говорят: дана функция  , или функция
, или функция  или функция
или функция  .
.
Функции могут быть заданы формулами, графиками, таблицами. В 7—9 классах вы познакомились с некоторыми функциями, изучили их свойства и строили графики. Нижеприведенная таблица напомнит вам о них.
В § 6 степень была определена для любого положительного основания и любого действительного показателя. Пусть основание степени а > 0. Тогда каждому  соответствует одно определенное число
соответствует одно определенное число  . Тем самым задана функция
. Тем самым задана функция  . Если а = 1, то функция
. Если а = 1, то функция  принимает одно и то же значение у = 1 при всех х. Функцию
принимает одно и то же значение у = 1 при всех х. Функцию 
где а > 0,  , называют показательной функцией. Такое название функции объясняется тем, что ее аргументом является показатель степени.
, называют показательной функцией. Такое название функции объясняется тем, что ее аргументом является показатель степени.
Показательная функция обладает следующими свойствами:
Это свойство следует из того, что степень с положительным основанием определена для любого действительного значения показателя.
- Свойство 2. Множество значений показательной функции
 — множество положительных чисел.
— множество положительных чисел.
Второе свойство следует из того, что если  , то уравнение
, то уравнение  имеет корень при любом
имеет корень при любом  , т.е. функция принимает любое положительное значение. Это доказывается в курсе высшей математики. При
, т.е. функция принимает любое положительное значение. Это доказывается в курсе высшей математики. При  уравнение
уравнение  не имеет корней, так как
не имеет корней, так как  при любом х.
при любом х.
Третье свойство следует из теоремы и следствия 1.
Задача 1.
Построить график функции 
Составим таблицу:
 Построим эти точки и проведем через них кривую, учитывая, что функция
Построим эти точки и проведем через них кривую, учитывая, что функция  возрастает (рис. 6). А
возрастает (рис. 6). А
Вообще график показательной функции  , где а > 1, имеет вид, представленный на рисунке 7.
, где а > 1, имеет вид, представленный на рисунке 7.
Этот график расположен выше оси Ох, так как  при
при  . С возрастанием аргумента значения функции увеличиваются, так как
. С возрастанием аргумента значения функции увеличиваются, так как  — возрастающая функция, если а > 1.
— возрастающая функция, если а > 1.
Задача 2.
Построить график функции 
Составим таблицу:
 Построим эти точки и проведем через них кривую (рис. 8).
Построим эти точки и проведем через них кривую (рис. 8).

Вообще график показательной функции  , имеет вид, представленный на рисунке 9.
, имеет вид, представленный на рисунке 9.
Этот график расположен выше оси Ох, так как  при
при  . С увеличением аргумента значения функции уменьшаются, так как
. С увеличением аргумента значения функции уменьшаются, так как 
Из свойств 2 и 3 следует, что уравнение 
 , имеет единственный корень т.е. по заданному значению b степени ах показатель степени х однозначно определяется. Геометрически это означает, что прямая
, имеет единственный корень т.е. по заданному значению b степени ах показатель степени х однозначно определяется. Геометрически это означает, что прямая  пересекает график функции в одной точке, абсцисса которой является корнем уравнения
пересекает график функции в одной точке, абсцисса которой является корнем уравнения  (рис. 10).
(рис. 10).
Задача 3.
Решить графически уравнение 
А Построим графики функций  (рис. 11). Из рисунка 7 видно, что графики этих функций пересекаются в одной точке. Следовательно, данное уравнение имеет один корень — абсциссу этой точки. Из рисунка видно, что х = 1.
(рис. 11). Из рисунка 7 видно, что графики этих функций пересекаются в одной точке. Следовательно, данное уравнение имеет один корень — абсциссу этой точки. Из рисунка видно, что х = 1.
Проверка показывает, что х = 1 является корнем уравнения.
Показательная функция часто используется при описании различных физических процессов. Так, радиоактивный распад описывается формулой: 
где  — массы радиоактивного вещества соответственно в момент времени t и в начальный момент времени
— массы радиоактивного вещества соответственно в момент времени t и в начальный момент времени  — период полураспада (промежуток времени, за который первоначальное количество вещества уменьшается вдвое).
— период полураспада (промежуток времени, за который первоначальное количество вещества уменьшается вдвое).
 С помощью показательной функции выражается давление воздуха в зависимости от высоты и подъема, ток самоиндукции в катушке после включения постоянного напряжения и т.д.
С помощью показательной функции выражается давление воздуха в зависимости от высоты и подъема, ток самоиндукции в катушке после включения постоянного напряжения и т.д.
Задача 4*.
Альпинист, находясь на высоте  м над уровнем моря определил, что давление воздуха
м над уровнем моря определил, что давление воздуха  мм рт. ст., а температура 15°С. Каково давление воздуха на высоте
мм рт. ст., а температура 15°С. Каково давление воздуха на высоте  = 2300 м при той же температуре?
= 2300 м при той же температуре?
А Известно, что давление  находится по следующей барометрической формуле:
находится по следующей барометрической формуле:

Подставляя в эту формулу данные из условий задачи, имеем 
Выполнив вычисления с помощью микрокалькулятора, получим  ~ 639 мм рт. ст.
~ 639 мм рт. ст.
Задача 5*.
Период полураспада плутония равен 140 сут. Сколько плутония останется через 10 лет, если его начальная масса 8 г?
А Воспользуемся формулой (1). В данной задаче  = 8 г, t = 10 • 365 (считаем, что в году 365 дней). Т = 140. Тогда
= 8 г, t = 10 • 365 (считаем, что в году 365 дней). Т = 140. Тогда
 Выполнив вычисления с помощью микрокалькулятора, получим
Выполнив вычисления с помощью микрокалькулятора, получим 


Лекции:
- Теория сплайнов примеры решения
- Жорданова форма матрицы
- Скрещивающиеся прямые
- Несобственный интеграл примеры решения
- Определенный интеграл и объем фигур вращения
- Производная функции
- Найдите наименьшее значение функции на отрезке
- Собственные числа матрицы
- Системы линейных дифференциальных уравнений
- Свойства пределов функции
Предел показательно степенной функции, примеры нахождения
В процессе нахождения предела показательно-степенной функции типа lim x → x 0 ( f ( x ) ) g ( x ) часто работаем с такими степенными неопределенностями, как 1 ∞ , 0 0 , ∞ 0 .
Для их раскрытия необходимо задействовать логарифмирование a = e ln ( a ) , свойство логарифма a · ln ( b ) = ln ( b a ) и применение его предела заданной непрерывной функции, причем ее знак разрешено менять местами.
Для этого производятся преобразования вида:
lim x → x 0 ( f ( x ) ) g ( x ) = e ln lim x → x 0 f ( x ) ) g ( x ) = e lim x → x 0 ( ln ( f ( x ) ) g ( x ) = e lim x → x 0 ( g ( x ) ln ( f ( x ) ) ) = = e lim x → x 0 ln ( f ( x ) ) 1 g ( x )
Отсюда видно, что задание приводится к нахождению предела заданной функции вида e lim x → x 0 ln ( f ( x ) ) 1 g ( x ) = ∞ ∞ или 0 0 .
Данный случай рассматривает методы:
- непосредственного вычисления;
- использования правила Лопиталя;
- с заменой эквивалентных бесконечно малых функций;
- применение первого замечательного предела.
Для того, чтобы неопределенность была раскрыта, необходимо применять второй замечательный предел, при наличии 1 ∞ .
Рассмотрим теорию на элементарных примерах заданий.
Найти предел заданной функции lim x → 0 ( x 3 + 2 x + 1 ) 3 2 x 3 + x .
Для решения необходимо произвести подстановку. Получаем :
lim x → 0 ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = ( 0 3 + 2 · 0 + 1 ) 3 2 ( 0 3 + 0 ) = 1 ∞
Получение единицы в степени бесконечность называют неопределенностью, значит, необходимо решить другим методом.
Следует произвести преобразования данного предела. Получаем:
lim x → 0 ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = e ln lim x → 0 ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = = e lim x → 0 ln ( x 3 + 2 x + 1 ) 3 2 ( x 3 + x ) = e lim x → 0 3 ln ( x 3 + 2 x + 1 ) 2 ( x 3 + x )
Видим, что преобразование сводится к пределу вида lim x → 0 3 ln ( x 3 + 2 x + 1 ) 2 ( x 3 + x ) .
lim x → 0 3 ln ( x 3 + 2 x + 1 2 ( x 3 + x ) = 0 0 = 3 2 lim x → 0 ln ( x 3 + 2 x + 1 ) x 3 + x = = 3 2 lim x → 0 x 3 + 2 x x 3 + x = 3 2 lim x → 0 x 2 + 2 x 2 + 1 = 3 2 · 0 2 + 2 0 2 + 1 = 3
Данные преобразования были выполнены при помощи применения замены логарифма на эквивалентную бесконечно малую функцию.
Тогда исходный предел принимает вид lim x → 0 ( x 2 + 2 x + 1 ) 3 2 ( x 3 + x ) = e 3 .
Вычисление данного предела возможно с применением второго замечательного предела. Тогда получаем:
lim x → 0 ( x 2 + 2 x + 1 ) 3 2 ( x 3 + x ) = lim x → 0 ( 1 + ( x 3 + 2 x ) 1 x 3 + 2 x ( x 3 + 2 x ) 3 2 ( x 3 + x ) = = lim x → 0 ( 1 + ( x 3 + 2 x ) ) 1 x 3 + 2 x 3 ( x 3 + 2 x ) 2 ( x 3 + x ) = lim x → 0 1 + ( x 3 + 2 x ) ) 1 x 3 + 2 x 3 ( x 2 + 2 ) 2 ( x 2 + 1 ) = = lim x → 0 ( 1 + ( x 3 + 2 x ) 1 x 3 + 2 x 3 = e 3
Найти и вычислить предел lim x → π 2 ( t g x ) 2 c o s x
Если произведем подстановку, в результате получим ответ в виде бесконечности в степени ноль, а это является знаком, что необходимо применить другой метод для преобразования. Получаем:
lim x → π 2 ( t g x ) 2 c o s x = ∞ 0 = e ln lim x → π 2 ( t g x ) 2 cos x = = e 2 lim x → π 2 ( t g x ) 2 cos x = e lim x → π 2 ( 2 cos x · ln · ( t g x ) ) = = e 2 lim x → π 2 ln ( t g x ) 1 cos x
Отсюда видно, что решение сводится к переделу lim x → π 2 ln ( t g x ) 1 cos x = ∞ ∞ .
Для дальнейшего преобразования применим правило Лопиталя, так как получили неопределенность в виде частного бесконечностей. Видим, что
lim x → π 2 ln ( t g x ) 1 cos x = ∞ ∞ = lim x → π 2 = ln ( t g x ) ‘ 1 cos ( x ) ‘ = = lim x → π 2 1 t g ( x ) · 1 cos 2 ( x ) sin ( x ) cos 2 ( x ) = lim x → π 2 cos ( x ) sin 2 ( x ) = cos π 2 sin 2 π 2 = 0 1 2 = 0
Отсюда следует, что пределом показательно-степенной функции является результат, полученный при вычислении. Имеем вы предел вида lim x → π 2 ( t g x ) 2 cos x = e 2 · 0 = e 0 = 1 .
Второй замечательный предел
Обычно второй замечательный предел записывают в такой форме:
Число $e$, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: $eapprox718281828459045>$. Если сделать замену $t=frac$, то формулу (1) можно переписать в следующем виде:
Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной $x$ в формуле (1) или вместо переменной $t$ в формуле (2). Главное – выполнение двух условий:
- Основание степени (т.е. выражение в скобках формул (1) и (2)) должно стремиться к единице;
- Показатель степени (т.е. $x$ в формуле (1) или $frac$ в формуле (2)) должен стремиться к бесконечности.
Говорят, что второй замечательный предел раскрывает неопределенность $1^infty$. Заметьте, что в формуле (1) мы не уточняем, о какой именно бесконечности ($+infty$ или $-infty$) идёт речь. В любом из этих случаев формула (1) верна. В формуле (2) переменная $t$ может стремиться к нулю как слева, так и справа.
Отмечу, что есть также несколько полезных следствий из второго замечательного предела. Примеры на использование второго замечательного предела, равно как и следствий из него, очень популярны у составителей стандартных типовых расчётов и контрольных работ.
Сразу отметим, что основание степени (т.е. $frac$) стремится к единице:
При этом показатель степени (выражение $4x+7$) стремится к бесконечности, т.е. $lim_(4x+7)=infty$.
Основание степени стремится к единице, показатель степени – к бесконечности, т.е. мы имеем дело с неопределенностью $1^infty$. Применим формулу (1) для раскрытия этой неопределённости. В основании степени формулы (1) расположено выражение $1+frac$, а в рассматриваемом нами примере основание степени таково: $frac$. Посему первым действием станет формальная подгонка выражения $frac$ под вид $1+frac$. Для начала прибавим и вычтем единицу:
Следует учесть, что просто так добавить единицу нельзя. Если мы вынуждены добавить единицу, то её же нужно и вычесть, дабы не изменять значения всего выражения. Для продолжения решения учтём, что
Продолжим «подгонку». В выражении $1+frac$ формулы (1) в числителе дроби находится 1, а в нашем выражении $1+frac$ в числителе находится $6$. Чтобы получить $1$ в числителе, опустим $6$ в знаменатель с помощью следующего преобразования:
Итак, основание степени, т.е. $1+frac>$, подогнано под вид $1+frac$, который требуется в формуле (1). Теперь начнём работать с показателем степени. Заметьте, что в формуле (1) выражения, стоящие в показатели степени и в знаменателе, одинаковы:

Значит, и в нашем примере показатель степени и знаменатель нужно привести к одинаковой форме. Чтобы получить в показателе степени выражение $frac$, просто домножим показатель степени на эту дробь. Естественно, что для компенсации такого домножения, придется тут же домножить на обратную дробь, т.е. на $frac$. Итак, имеем:
Отдельно рассмотрим предел дроби $frac$, расположенной в степени:
Согласно формуле (1) имеем $lim_left(1+frac>right )^>=e$. Кроме того, $lim_frac=8$, поэтому возвращаясь к исходному пределу, получим:
Полное решение без промежуточных пояснений будет иметь такой вид:
Кстати сказать, вовсе не обязательно использовать первую формулу. Если учесть, что $fracto$ при $xtoinfty$, то применяя формулу (2), получим:
Выражение, стоящее в основании степени, т.е. $7-6x$, стремится к единице при условии $xto$, т.е. $lim_>(7-6x)=7-6cdot1=1$. Для показателя степени, т.е. $frac$, получаем: $lim_>frac=infty$. Итак, здесь мы имеем дело с неопределенностью вида $1^infty$, которую раскроем с помощью второго замечательного предела.
Для начала отметим, что в формуле (1) переменная $x$ стремится к бесконечности, в формуле (2) переменная $t$ стремится к нулю. В нашем случае $xto$, поэтому имеет смысл ввести новую переменную, чтобы она стремилась или к нулю (тогда применим формулу (2)), или к бесконечности (тогда применим формулу (1)). Введение новой переменной, вообще говоря, не является обязательным, это будет сделано просто для удобства решения. Проще всего новую переменную $y$ ввести так: $y=x-1$. Так как $xto$, то $to$, т.е. $yto$. Подставляя $x=y+1$ в рассматриваемый пример, и учитывая $yto$, получим:
Применим формулу (2). Выражение в основании степени в формуле (2), т.е. $1+t$, соответствует форме выражения в основании степени нашего примера, т.е. $1+(-6y)$ (выражение $-6y$ играет роль $t$). Формула (2) предполагает, что показатель степени будет иметь вид $frac$, т.е. в нашем случае в показателе степени следует получить $frac$. Домножим показатель степени на выражение $frac$. Для компенсации такого домножения нужно домножить показатель степени на обратную дробь, т.е. на выражение $frac=-6y$:
Полное решение без пояснений таково:
Так как $lim_>(cos)=1$ и $lim_>frac>=infty$ (напомню, что $sinto$ при $uto$), то мы имеем дело с неопределённостью вида $1^infty$. Преобразования, аналогичные рассмотренным в примерах №1 и №2, укажем без подробных пояснений, ибо они были даны ранее:
Так как $sin^2x=frac>$, то $cos-1=-2sin^2x$, поэтому:
Здесь мы учли, что $lim_>frac>>=frac$. Подробное описание того, как находить этот предел, дано в соответствующей теме.
Так как при $x>0$ имеем $ln(x+1)-ln=lnleft(fracright)$, то:
Раскладывая дробь $frac$ на сумму дробей $frac=1+frac$ получим:
Так как $lim_>(3x-5)=6-5=1$ и $lim_>frac=infty$, то мы имеем дело с неопределенностью вида $1^infty$. Подробные пояснения даны в примере №2, здесь же ограничимся кратким решением. Сделав замену $t=x-2$, получим:
Можно решить данный пример и по-иному, используя замену: $t=frac$. Разумеется, ответ будет тем же:
Выясним, к чему стремится выражение $frac$ при условии $xtoinfty$:
Таким образом, в заданном пределе мы имеем дело с неопределенностью вида $1^infty$, которую раскроем с помощью второго замечательного предела:
Заметили ошибку, опечатку, или некорректно отобразилась формула? Отпишите, пожалуйста, об этом в данной теме на форуме (регистрация не требуется).
Замечательные пределы: Первый и второй замечательный предел.
Понятие замечательных пределов используется на просторах бывшего Советского Союза для обозначения хорошо известных математических тождеств со взятием предела. Замечательны они потому, что они уже доказаны великими математиками и нам нам остается лишь пользоваться ими для удобства нахождения пределов. Из них наиболее известны первый и второй замечательные пределы. Дальнейшее чтение статье будет намного интереснее, если вы уже знакомы с понятием пределов. Если для вас lim , это то что новое, то рекомендуем к прочтению статью «Пределы. Понятие пределов. Вычисление пределов.»
Теперь со спокойной душой переходим к рассмотрению замечательных пределов.
Первый замечательный предел имеет вид .
Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к 0.
Необходимо вычислить предел
Как видно, данный предел очень похож на первый замечательный, но это не совсем так. Вообще, если Вы замечаете в пределе sin, то надо сразу задуматься о том, возможно ли применение первого замечательного предела.
Согласно нашему правилу №1 подставим вместо х ноль:
Получаем неопределенность .
Теперь попробуем самостоятельно организовать первый замечательный предел. Для этого проведем нехитрую комбинацию:
Таким образом мы организовываем числитель и знаменатель так, чтобы выделить 7х. Вот уже и проявился знакомый замечательный предел. Желательно при решении выделять его:
Подставим решение первого замечательного примера и получаем:
Как видите – все очень просто.
Второй замечательный предел имеет вид , где e = 2,718281828… – это иррациональное число.
Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к .
Необходимо вычислить предел
Здесь мы видим наличие степени под знаком предела, значит возможно применение второго замечательного предела.
Как всегда воспользуемся правилом №1 – подставим вместо х:
Видно, что при х основание степени
, а показатель – 4x >
, т.е. получаем неопределенность вида
:
Воспользуемся вторым замечательным пределом для раскрытия нашей неопределенности, но сначала надо его организовать. Как видно – надо добиться присутствия в показателе, для чего возведем основание в степень 3х, и одновременно в степень 1/3x, чтобы выражение не менялось:
Не забываем выделять наш замечательный предел:
Дальше знак предела перемещаем в показатель:
Вот такие действительно замечательные пределы!
Если у вас остались какие то вопросы по первому и второму замечательным пределам, то смело задавайте их в комментариях.
Всем по возможности ответим.
Также вы можете позаниматься с педагогом по этой теме.
Мы рады предложить вам услуги подбора квалифицированного репетитора в вашем городе. Наши партнеры оперативно подберут для вас хорошего преподавателя на выгодных для вас условиях.
