Suppose that the function is defined on the intervals
#(a_1,a_2) cup (a_2,a_3) cup … cup (a_{n-1},a_n)#
where the interals can be open or closed, and #a_1# and/or #a_n# are possibly #pminfty#, and inside each interval #(a_i, a_{i+1})# #f(x)# is defined as #f_i(x)#.
There are two cases: if you need to compute #lim_{x to c} f(x)#, where #c in (a_i, a_{i+1})# for some #i#, then you simply compute #lim_{x to c} f_i(x)#, as if it was a “normal” function.
The only special case is when you want to compute the limit with #x# tending towards a border point. In this case, you simply compute the left and right limits, using the correct definitions: if you have #f_{i-1}(x)# in #(a_{i-1},a_i)# and #f_i(x)# in #(a_i,a_{i+1})#, you have
#lim_{xto a_i} f(x) = lim_{xto a_i^-}f_{i-1}(x) = lim_{xto a_i^+}f_i(x)#
So, the limit exists if and only if the left limit of #f_i(x)# and the right limit of #f_{i-1}# exist and are the same.
Непрерывность и
построение графиков кусочно-заданных
функций – сложная тема. Учиться строить
графики лучше непосредственно на
практическом занятии. Здесь в основном
показано исследование на непрерывность.
Известно,
что элементарная
функция (см.
с. 16) непрерывна во всех точках, в которых
определена. Поэтому нарушение непрерывности
у элементарных функций возможно только
в точках двух типов:
а) в точках, где
функция «переопределяется»;
б) в точках, где
функция не существует.
Соответственно
только такие точки и проверяются при
исследовании на непрерывность, что
показано в примерах.
Для неэлементарных
функций исследование сложнее. Например,
функция
![]() (целая часть числа) определена на всей
(целая часть числа) определена на всей
числовой оси, но терпит разрыв при каждом
целомx.
Подобные вопросы выходят за рамки
пособия.
Перед изучением
материала следует повторить по лекции
или учебнику, какими (какого рода) бывают
точки разрыва.
Исследование кусочно-заданных функций на непрерывность
Функция задана
кусочно,
если она на разных участках области
определения задаётся разными формулами.
Основная
идея при исследовании таких функций –
выяснить, задана ли функция в тех точках,
в которых переопределяется, и как. Затем
проверяется, совпадают ли значения
функции слева и справа от таких точек.
Пример 1.
Покажем, что функция
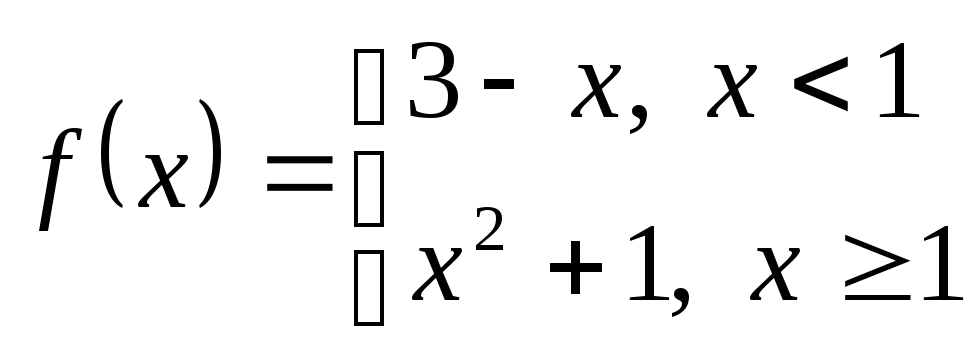 непрерывна.
непрерывна.
Функция
![]() элементарна и потому непрерывна в тех
элементарна и потому непрерывна в тех
точках, в которых определена. Но, очевидно,
она определена во всех точках.
Следовательно, во всех точках она и
непрерывна, в том числе при![]() ,
,
как требует условие.
То же справедливо
для функции
![]() ,
,
и при![]() она непрерывна.
она непрерывна.
В таких случаях
непрерывность может нарушаться только
там, где функция переопределяется. В
нашем примере это точка
![]() .
.
Проверим её, для чего найдём пределы
слева и справа:
а)
![]() ;
;
б)
![]() .
.
Пределы слева и
справа совпадают. Остаётся узнать:
а) определена ли
функция в самой точке
![]() ;
;
б) если да, то
совпадает ли
![]() со значениями пределов слева и справа.
со значениями пределов слева и справа.
По условию, если
![]() ,
,
то![]() .
.
Поэтому![]() .
.
Видим, что
![]() (все равны числу 2). Это означает, что в
(все равны числу 2). Это означает, что в
точке![]() функция
функция
непрерывна.
Итак, функция непрерывна на всей оси,
включая точку
![]() .
.
Замечания к
решению
а) При вычислениях
не играло роли, подставляем
мы в конкретную формулу число
![]() или
или![]() .
.
Обычно это важно, когда получается
деление на бесконечно малую величину,
поскольку влияет на знак бесконечности.
Здесь же![]() и
и![]() отвечают только завыбор
отвечают только завыбор
функции;
б) как правило,
обозначения
![]() и
и![]() равноправны, то же касается обозначений
равноправны, то же касается обозначений![]() и
и![]() (и справедливо для любой точки, а не
(и справедливо для любой точки, а не
только для![]() ).
).
Дальше для краткости применяются
обозначения вида![]() ;
;
в) когда пределы
слева и справа равны, для проверки на
непрерывность фактически остаётся
посмотреть, будет ли одно из неравенств
нестрогим.
В примере таковым оказалось 2-е неравенство.
Пример 2.
Исследуем на непрерывность функцию
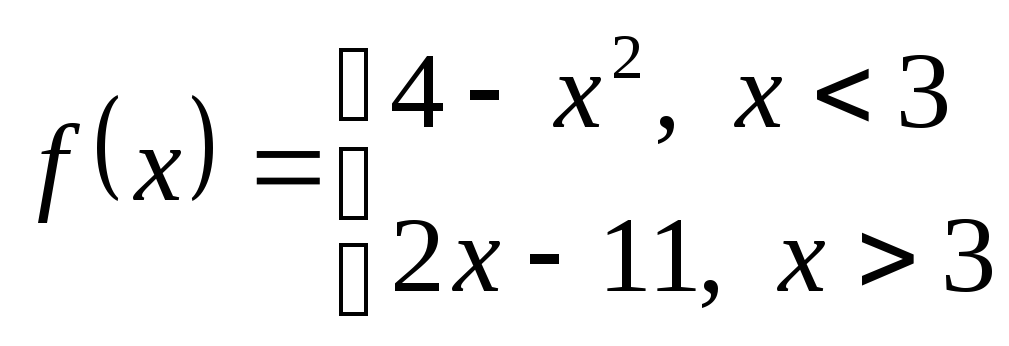 .
.
По тем же причинам,
что в примере 1, непрерывность может
нарушаться только в точке
![]() .
.
Проверим:
а)
![]() ;
;
б)
![]() .
.
Пределы слева и
справа равны, но в самой точке
![]() функция не определена (неравенства
функция не определена (неравенства
строгие). Это означает, что![]() – точкаустранимого
– точкаустранимого
разрыва.
«Устранимый
разрыв» означает, что достаточно или
сделать любое из неравенств нестрогим,
или придумать для отдельной точки
![]() функцию, значение которой при
функцию, значение которой при![]() равно –5, или просто указать, что
равно –5, или просто указать, что![]() ,
,
чтобы вся функция![]() стала непрерывной.
стала непрерывной.
Ответ:
точка
![]() – точка устранимого разрыва.
– точка устранимого разрыва.
Замечание 1.
В литературе устранимый разрыв обычно
считается частным случаем разрыва 1-го
рода, однако студентами чаще понимается
как отдельный тип разрыва. Во избежание
разночтений будем придерживаться 1-й
точки зрения, а «неустранимый» разрыв
1-го рода оговаривать особо.
Пример 3.
Проверим, непрерывна ли функция
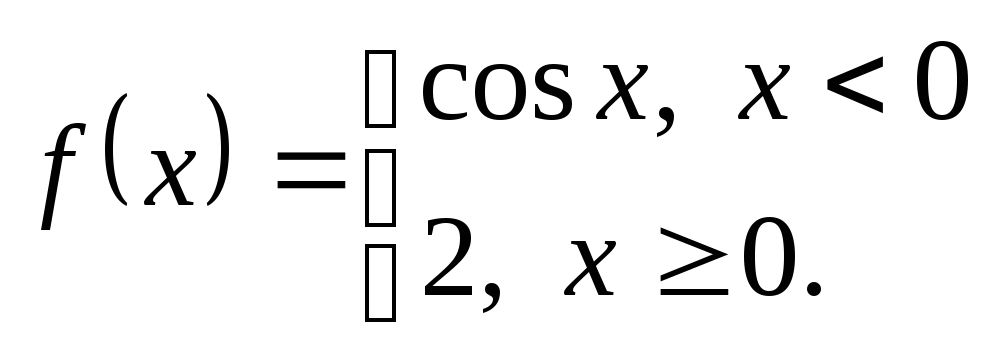
В точке
![]()
а)
![]() ;
;
б)
![]() .
.
Пределы слева и
справа различны:
![]() .
.
Независимо от того, определена ли функция
при![]() (да) и если да, то чему равна (равна 2),
(да) и если да, то чему равна (равна 2),
точка![]() –точка
–точка
неустранимого разрыва 1-го рода.
В точке
![]() происходитконечный
происходитконечный
скачок (от
1 к 2).
Ответ:
точка
![]() – точка неустранимого разрыва 1-го рода.
– точка неустранимого разрыва 1-го рода.
Замечание 2.
Вместо
![]() и
и![]() обычно пишут
обычно пишут![]() и
и![]() соответственно.
соответственно.
Возможен вопрос:
чем отличаются функции
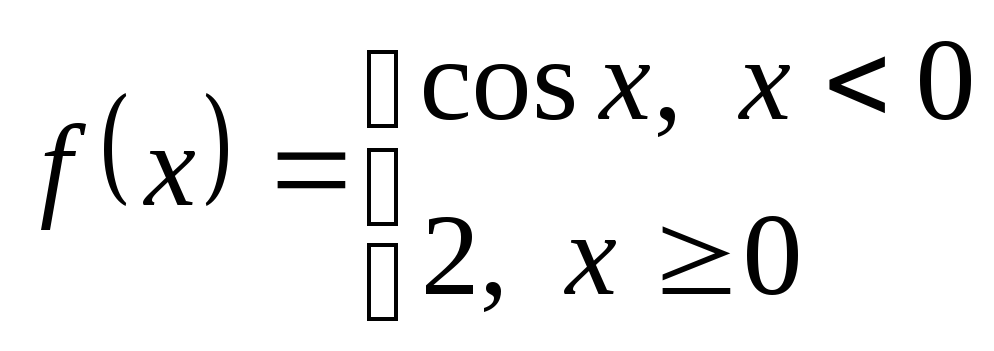 и
и
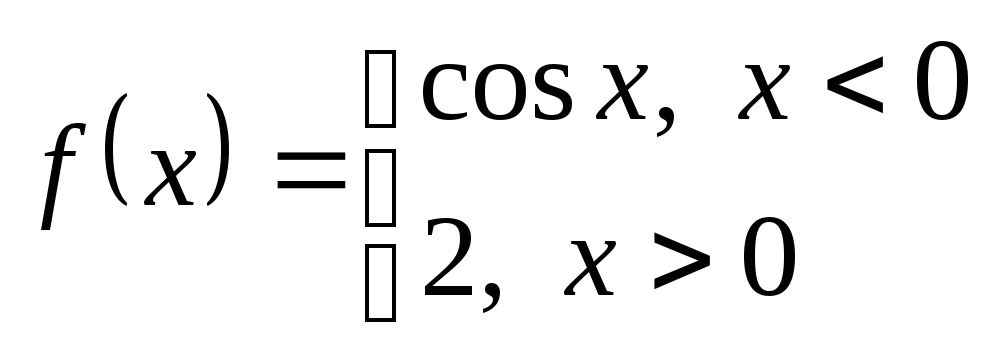 ,
,
а также их графики?
Правильный ответ:
а) 2-я функция не
определена в точке
![]() ;
;
б) на графике 1-й
функции точка
![]() «закрашена», на графике 2-й – нет
«закрашена», на графике 2-й – нет
(«выколотая точка»).
Точка
![]() ,
,
где обрывается график![]() ,
,
не закрашена на обоих графиках.
Сложнее исследовать
функции, по-разному определённые на
трёх
участках.
Пример 4.
Непрерывна ли функция
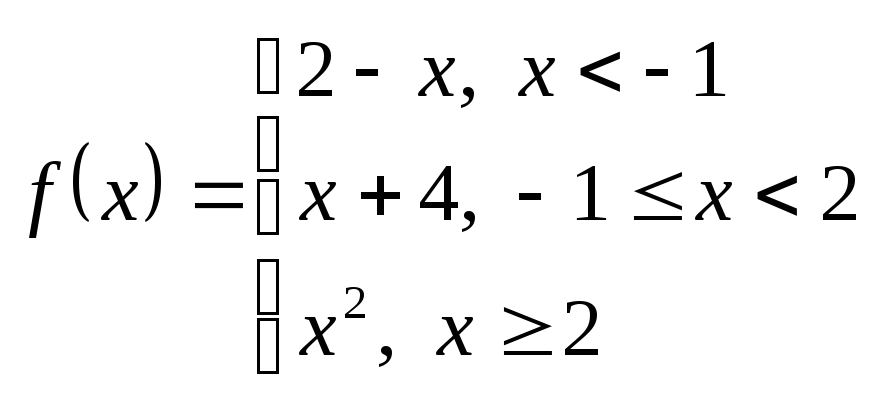 ?
?
Так же, как в
примерах 1 – 3, каждая из функций
![]() ,
,![]() и
и![]() непрерывна на всей числовой оси, в том
непрерывна на всей числовой оси, в том
числе – на участке, на котором задана.
Разрыв возможен только в точке![]() или (и) в точке
или (и) в точке![]() ,
,
где функция переопределяется.
Задача распадается
на 2 подзадачи: исследовать на непрерывность
функции
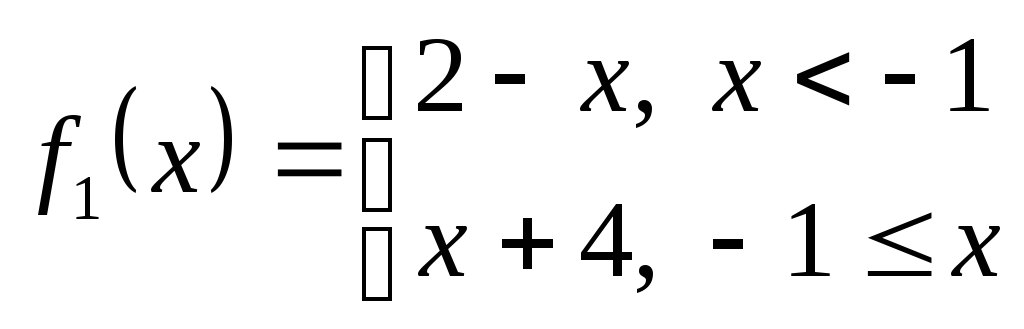 и
и
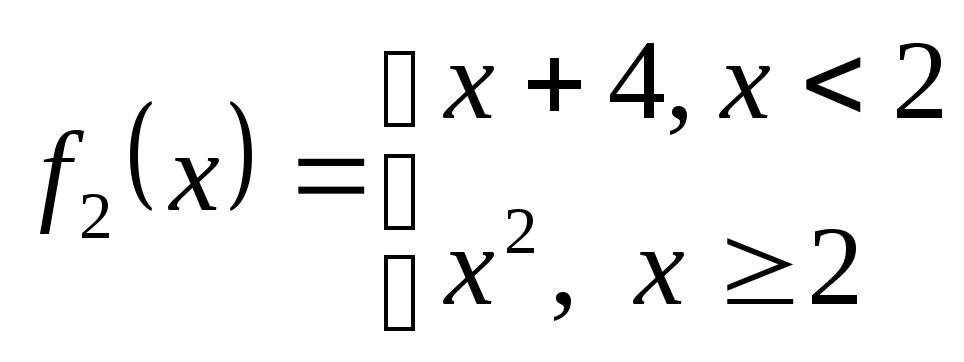 ,
,
причём точка
![]() не представляет интереса для функции
не представляет интереса для функции![]() ,
,
а точка![]() – для функции
– для функции![]() .
.
1-й
шаг. Проверяем
точку
![]() и функцию
и функцию![]() (индекс не пишем):
(индекс не пишем):
а)
![]() ;
;
б)
![]() .
.
Пределы совпадают.
По условию,
![]() (если пределы слева и справа равны, то
(если пределы слева и справа равны, то
фактически функция непрерывна, когда
одно и из неравенств нестрогое). Итак,
в точке![]() функция непрерывна.
функция непрерывна.
2-й
шаг. Проверяем
точку
![]() и функцию
и функцию![]() :
:
а)
![]() ;
;
б)
![]() .
.
Поскольку
![]() ,
,
точка![]() – точка разрыва 1-го рода, и значение
– точка разрыва 1-го рода, и значение![]() (и то, есть ли оно вообще) уже не играет
(и то, есть ли оно вообще) уже не играет
роли.
Ответ:
функция непрерывна во всех точках, кроме
точки
![]() ,
,
где имеет место неустранимый разрыв
1-го рода – скачок от 6 к 4.
Пример 5.
Найти точки разрыва функции
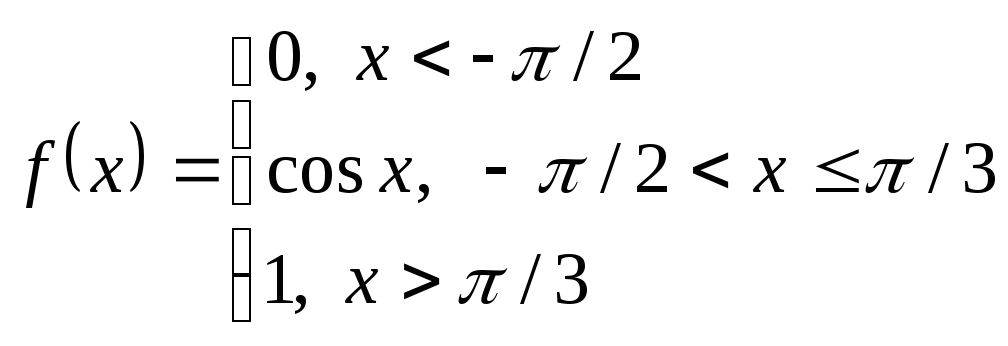 .
.
Действуем по той
же схеме, что в примере 4.
1-й
шаг. Проверяем
точку
![]() :
:
а)
![]() ,
,
поскольку слева от![]() функция постоянна и равна 0;
функция постоянна и равна 0;
б)
![]() (
(![]() – чётная функция).
– чётная функция).
Пределы совпадают,
но при
![]() функция по условию не определена, и
функция по условию не определена, и
получается, что![]() – точка устранимого разрыва.
– точка устранимого разрыва.
2-й
шаг. Проверяем
точку
![]() :
:
а)
![]() ;
;
б)
![]() – значение функции не зависит от
– значение функции не зависит от
переменной.
Пределы различны:
![]() ,
,
точка![]() – точка неустранимого разрыва 1-го рода.
– точка неустранимого разрыва 1-го рода.
Ответ:
![]() – точка устранимого разрыва,
– точка устранимого разрыва,![]() – точка неустранимого разрыва 1-го рода,
– точка неустранимого разрыва 1-го рода,
в остальных точках функция непрерывна.
Пример 6.
Непрерывна ли функция
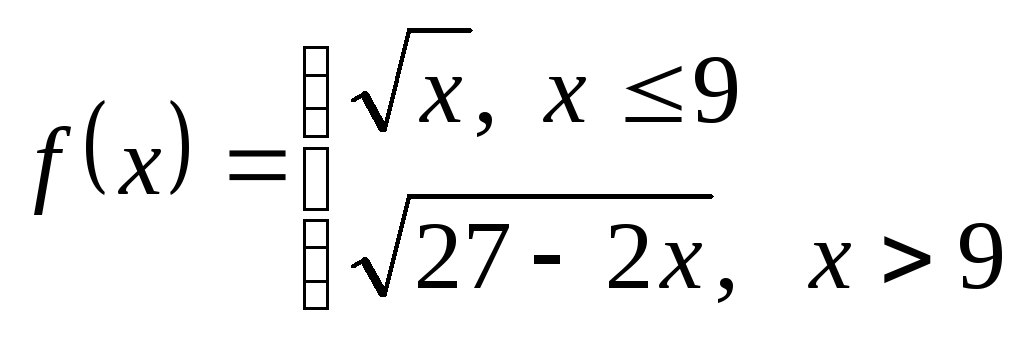 ?
?
Функция
![]() определена при
определена при![]() ,
,
поэтому условие![]() превращается в условие
превращается в условие![]() .
.
С другой стороны,
функция
![]() определена при
определена при![]() ,
,
т.е. при![]() .
.
Значит, условие![]() превращается в условие
превращается в условие![]() .
.
Получается, что
должно выполняться условие
![]() ,
,
и область определения всей функции –
отрезок![]() .
.
Сами по себе
функции
![]() и
и![]() элементарны и потому непрерывны во всех
элементарны и потому непрерывны во всех
точках, в которых определены – в
частности, и при![]() .
.
Остаётся проверить,
что происходит в точке
![]() :
:
а)
![]() ;
;
б)
![]() .
.
Поскольку
![]() ,
,
смотрим, определена ли функция в точке![]() .
.
Да, 1-е неравенство – нестрогое относительно![]() ,
,
и этого достаточно.
Ответ:
функция определена на отрезке
![]() и непрерывна на нём.
и непрерывна на нём.
Более сложные
случаи, когда одна из составляющих
функций неэлементарна или не определена
в какой-либо точке своего отрезка,
выходят за рамки пособия.
НФ1. Постройте
графики функций. Обратите внимание,
определена ли функция в той точке, в
которой переопределяется, и если да –
каково значение функции (слово
«если» в определении функции для
краткости пропущено):
1) а)
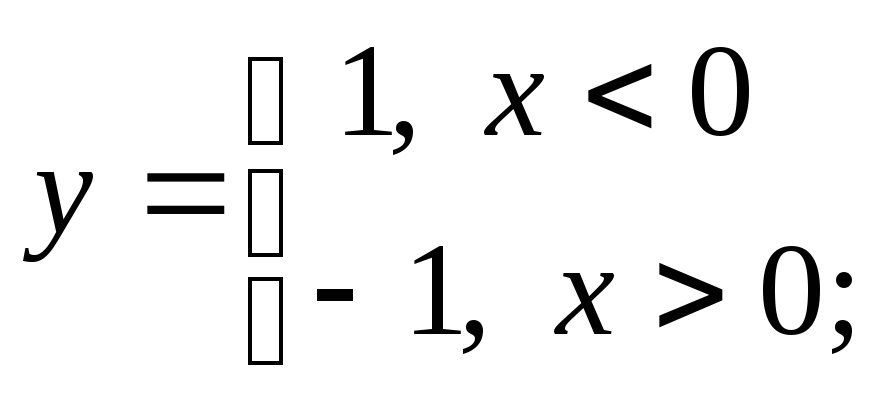 б)
б)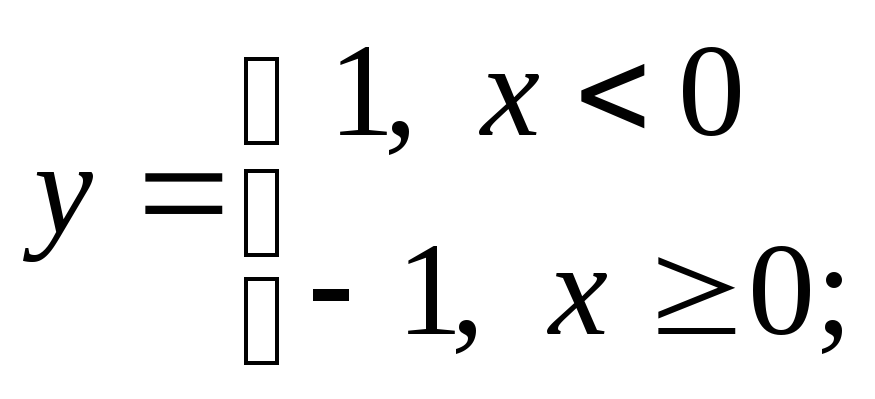 в)
в)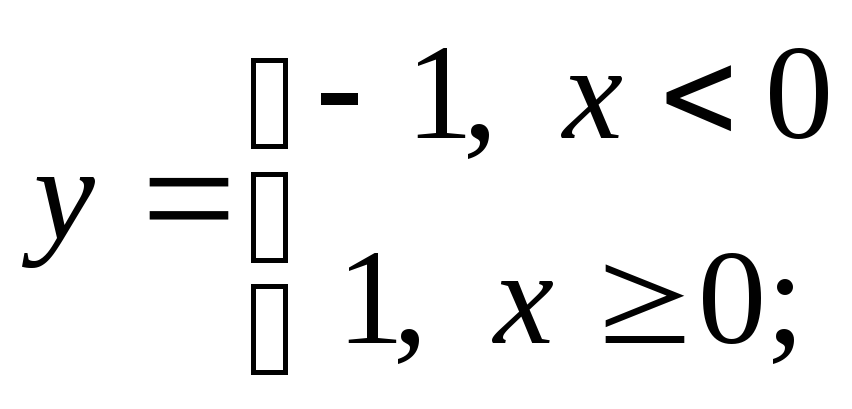 г)
г)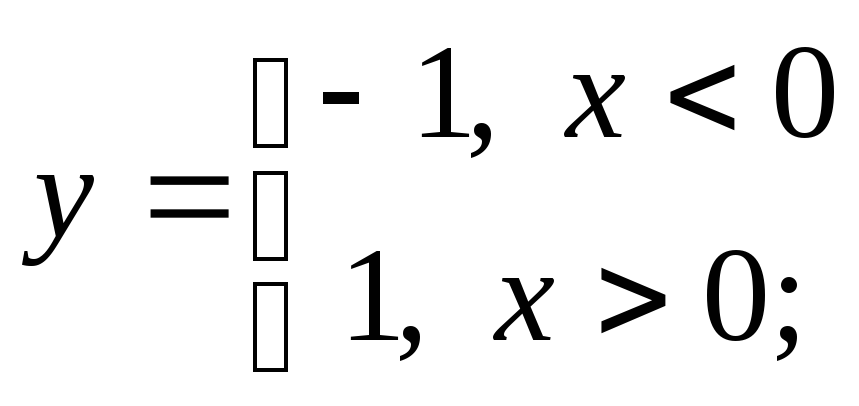
2) а)
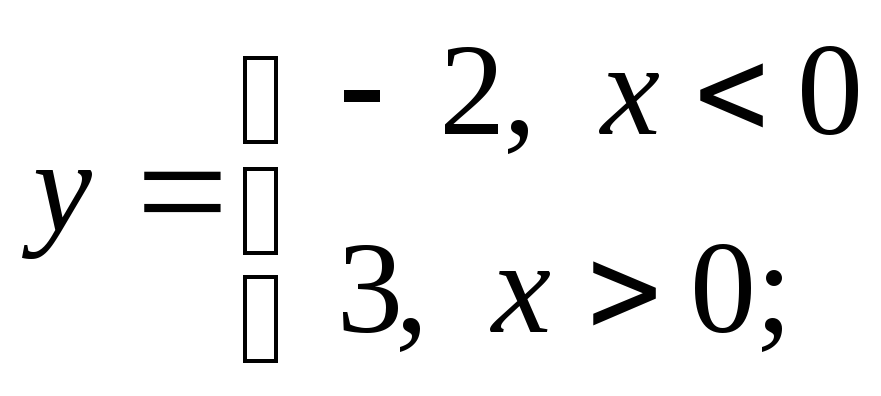 б)
б)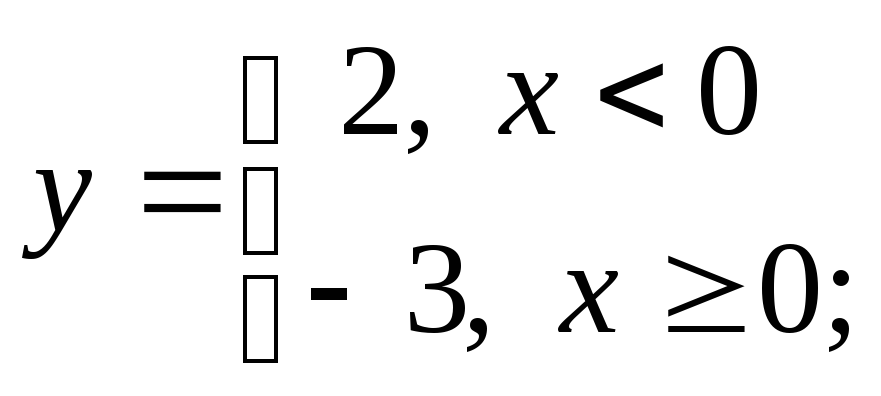 в)
в)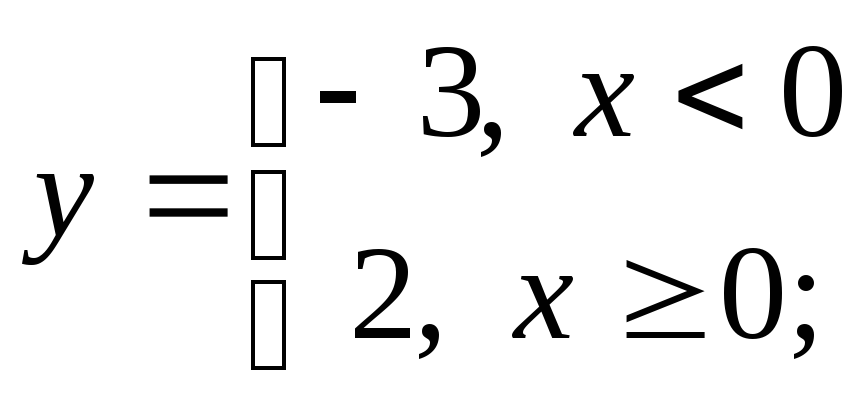 г)
г)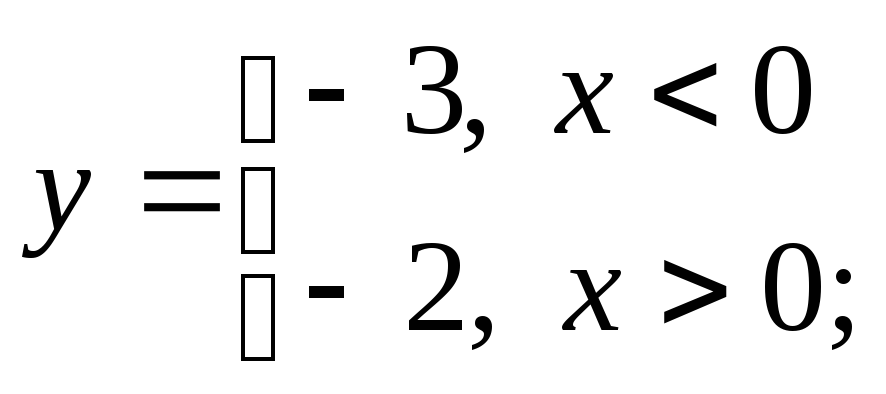
3) а)
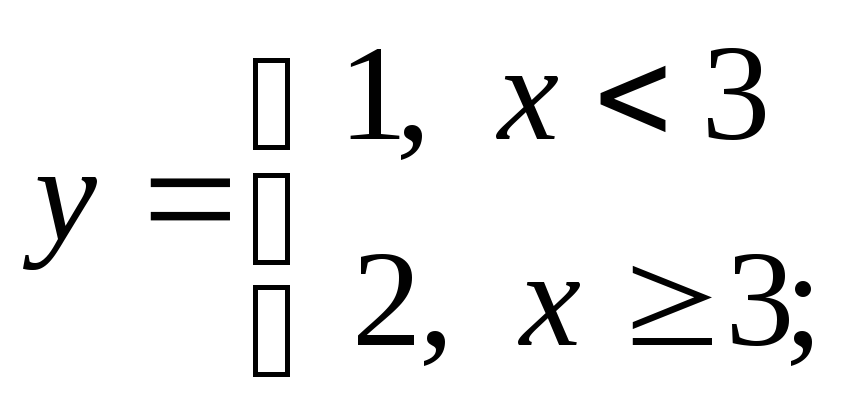 б)
б)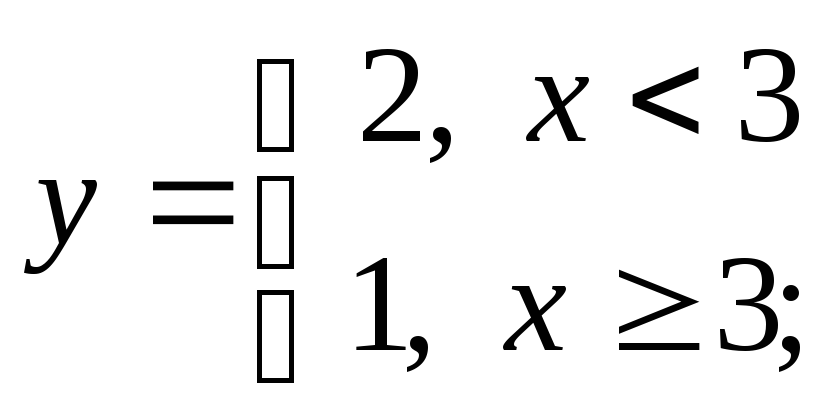 в)
в)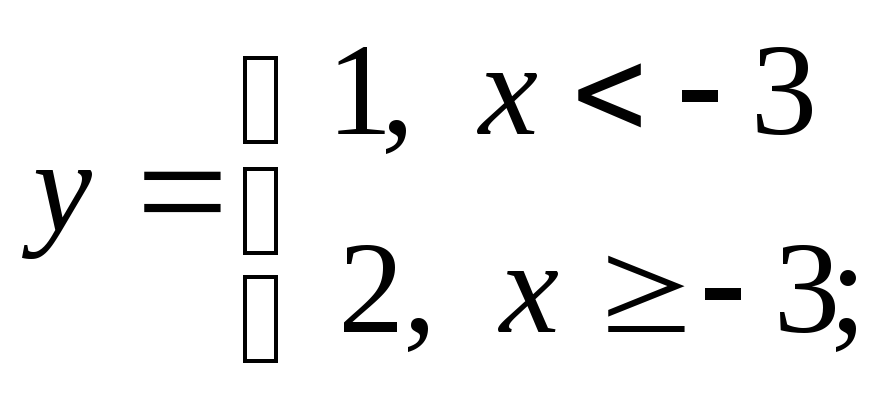 г)
г)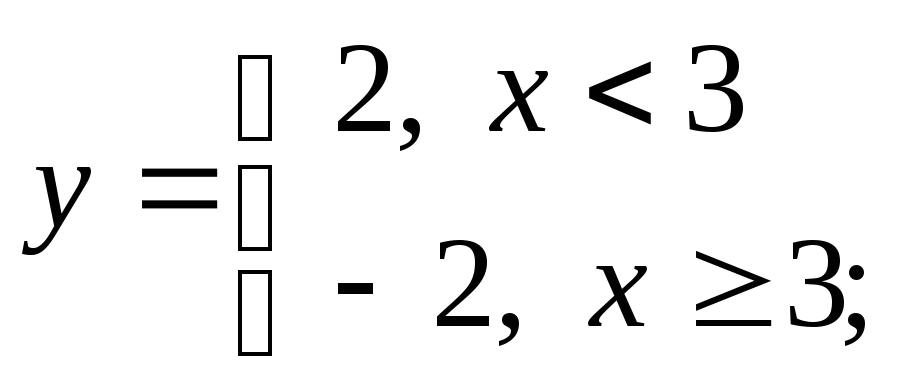
4) а)
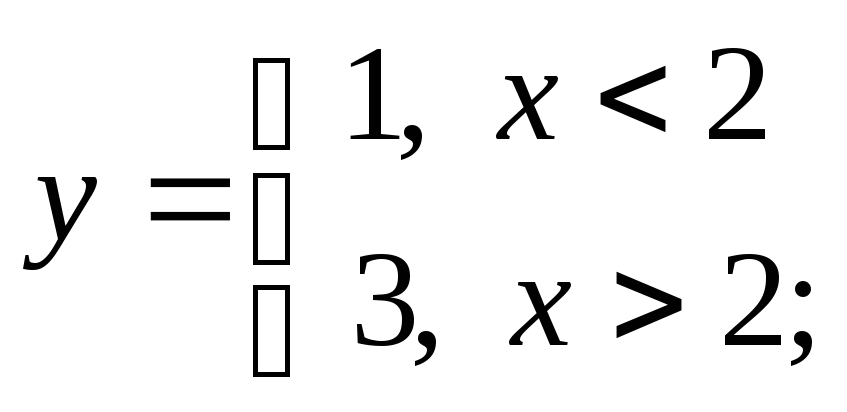 б)
б) в)
в)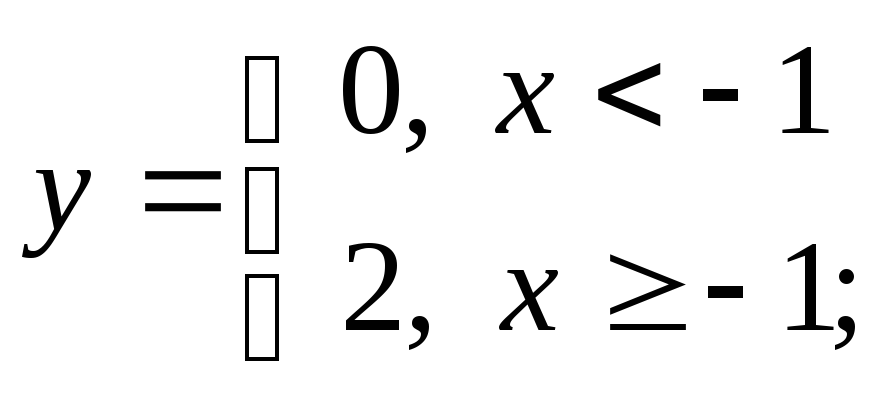 г)
г)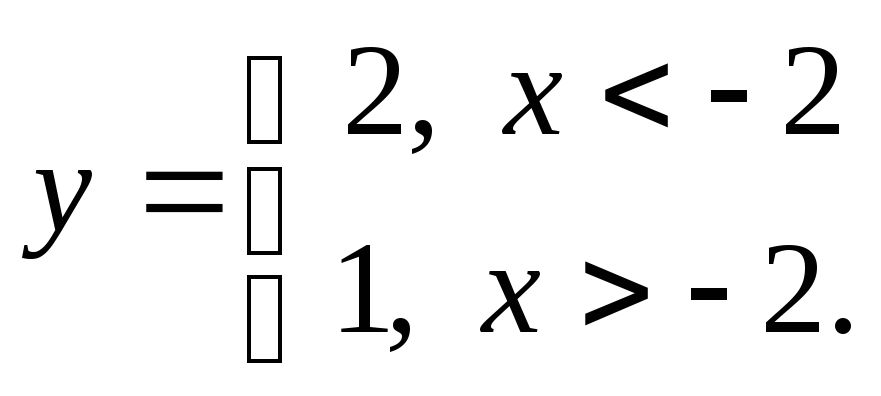
Пример 7.
Пусть
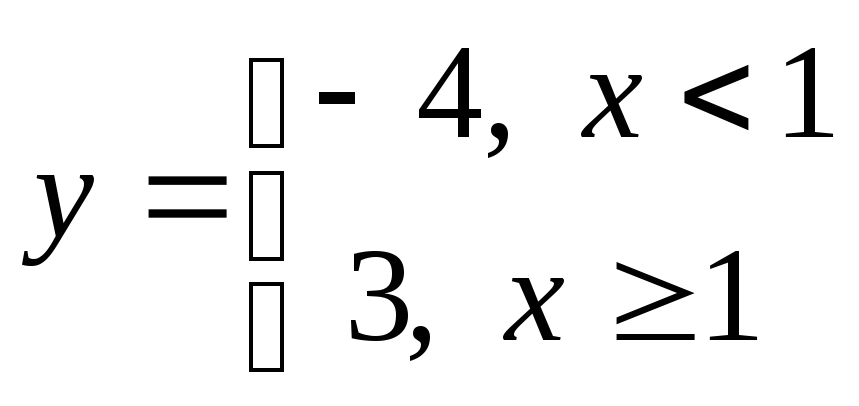 .
.
Тогда на участке![]() строим горизонтальную прямую
строим горизонтальную прямую![]() ,
,
а на участке![]() строим горизонтальную прямую
строим горизонтальную прямую![]() .
.
При этом точка с координатами![]() «выколота», а точка
«выколота», а точка![]() «закрашена». В точке
«закрашена». В точке![]() получается разрыв 1-го рода («скачок»),
получается разрыв 1-го рода («скачок»),
и![]() .
.
НФ2. Исследуйте
на непрерывность
функции, по-разному определённые на 3-х
интервалах. Постройте графики:
1) а)
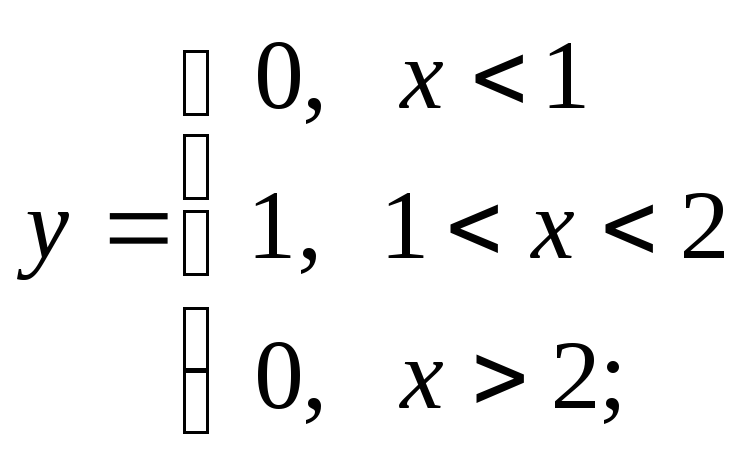 б)
б)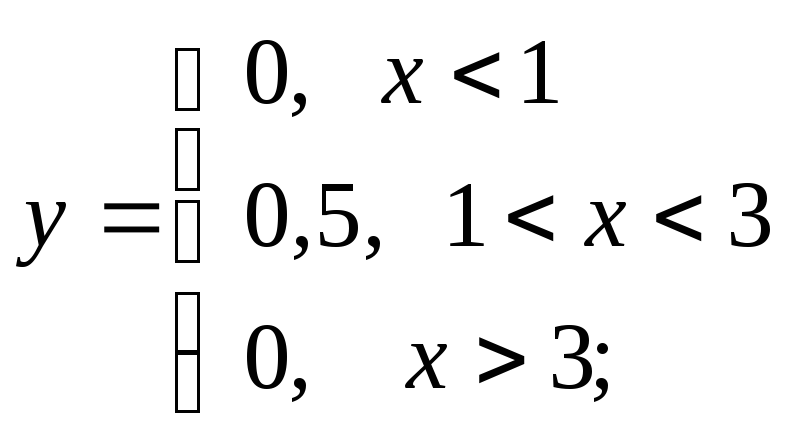 в)
в)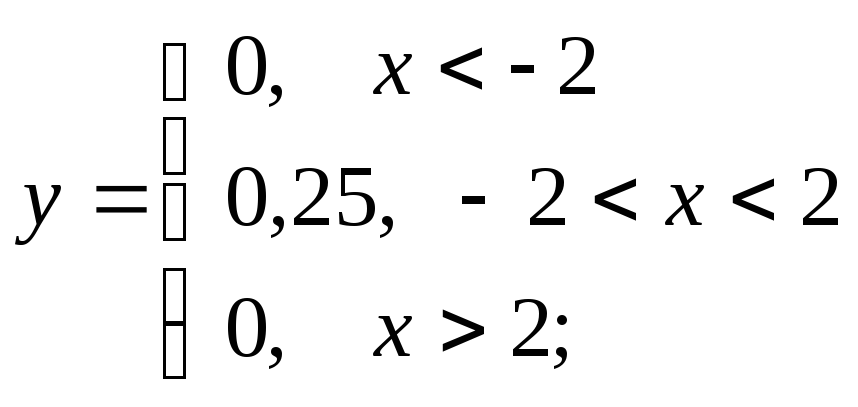
г)
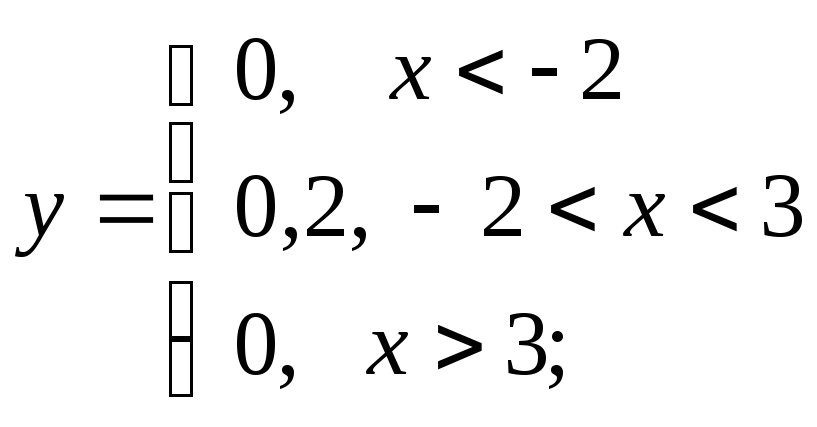 д)
д)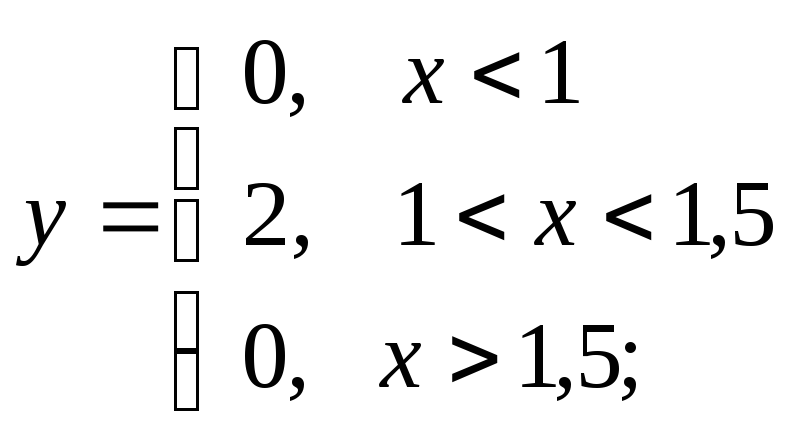 е)
е)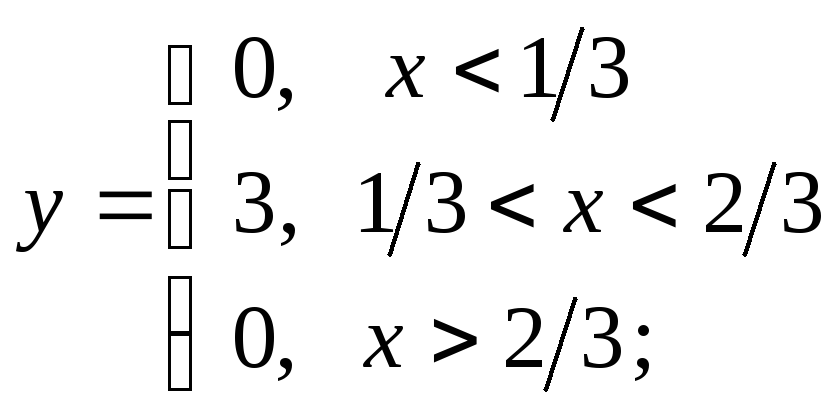
2) а)
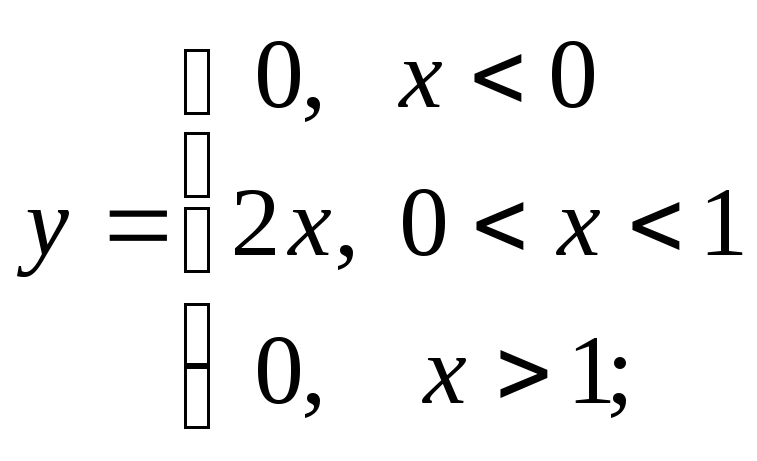 б)
б)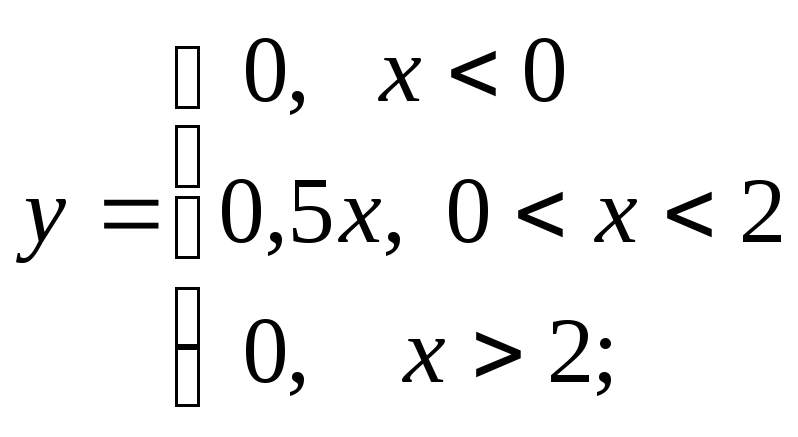 в)
в)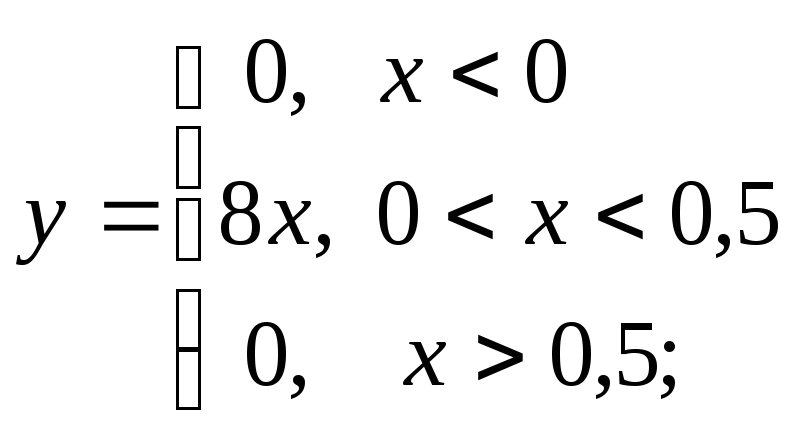
г)
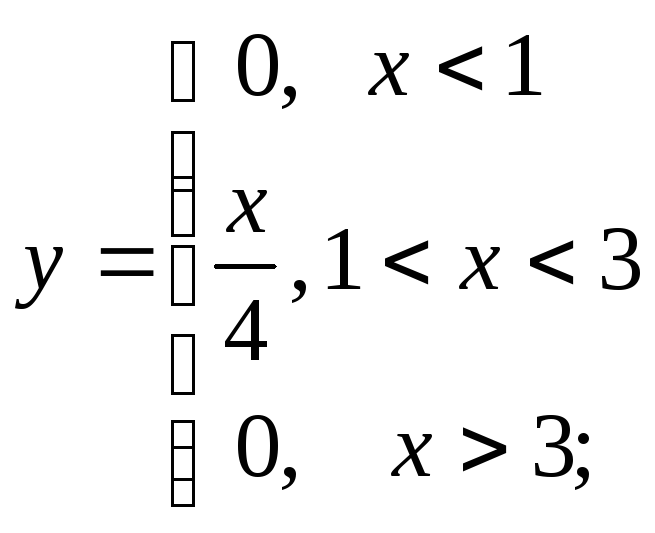 д)
д)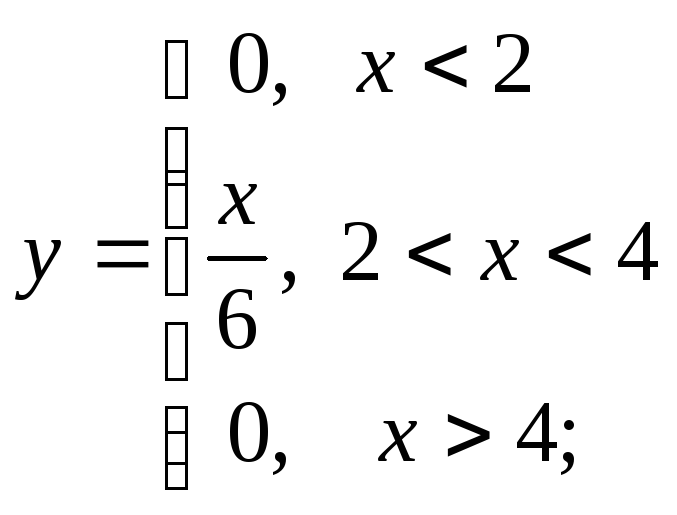 е)
е)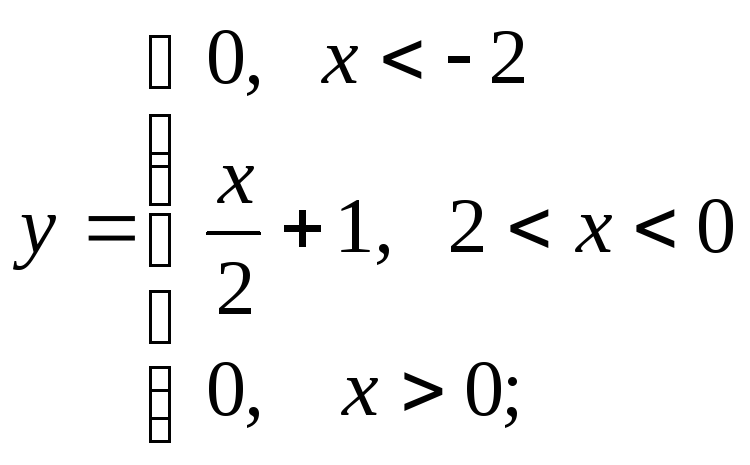
3) а)
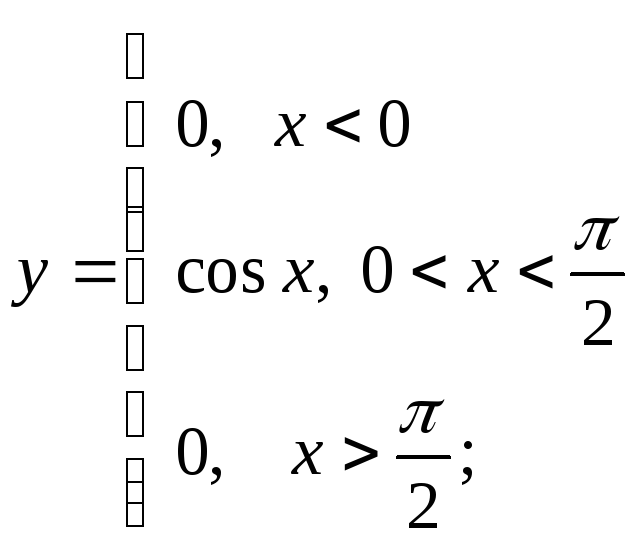 б)
б)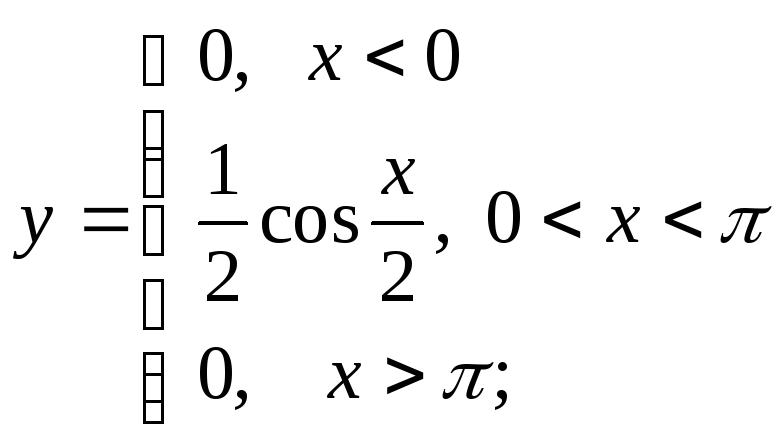 в)
в)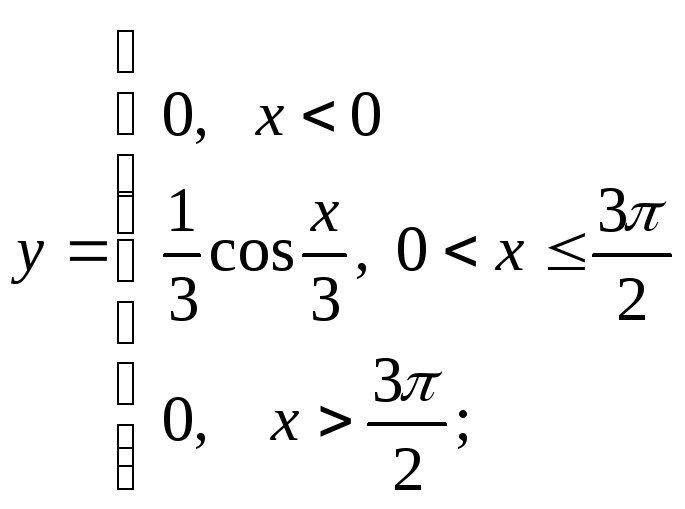
г)
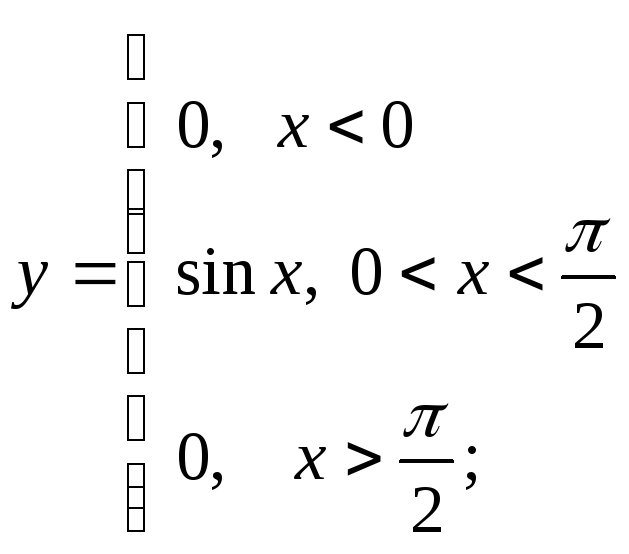 д)
д)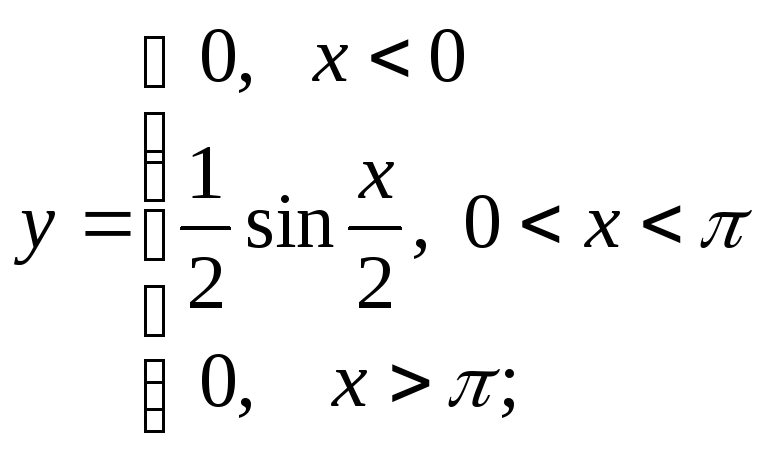 е)
е)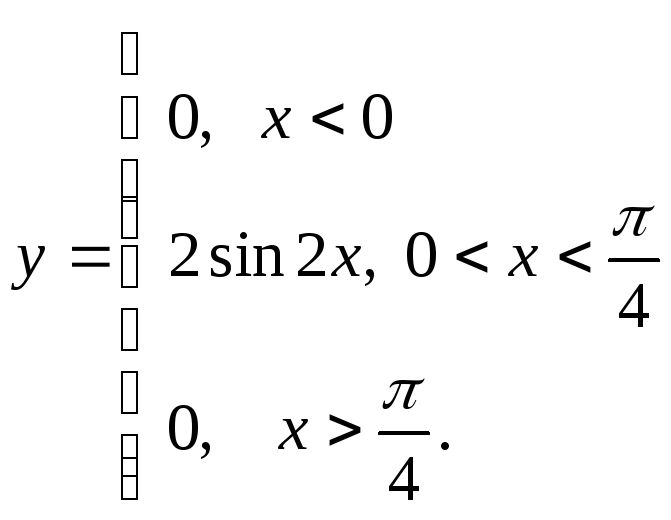
Пример 8.
Пусть
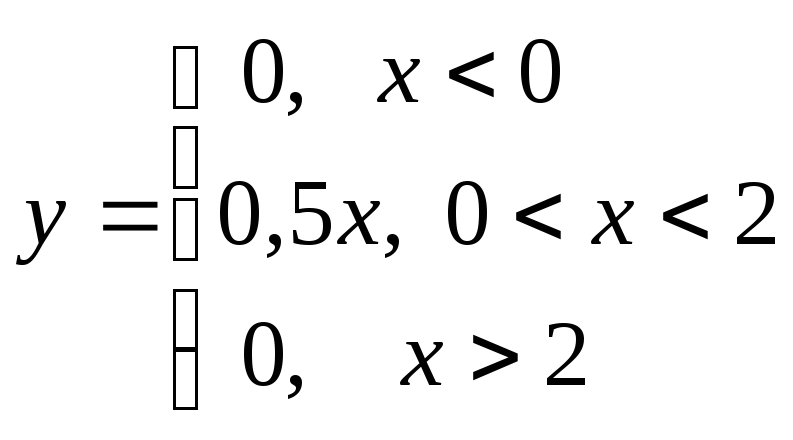 .
.
На участке![]() строим прямую
строим прямую![]() ,
,
для чего находим![]() и
и![]() .
.
Соединяем точки![]() и
и![]() отрезком. Сами точки не включаем,
отрезком. Сами точки не включаем,
поскольку при![]() и
и![]() функция по условию не определена.
функция по условию не определена.
На участке
![]() и
и![]() обводим осьOX
обводим осьOX
(на ней
![]() ),
),
однако точки![]() и
и![]() «выколоты». В точке
«выколоты». В точке![]() получаем устранимый разрыв, а в точке
получаем устранимый разрыв, а в точке![]() – разрыв 1-го рода («скачок»).
– разрыв 1-го рода («скачок»).
НФ3.
Постройте графики функций и убедитесь
в их непрерывности:
1) а)
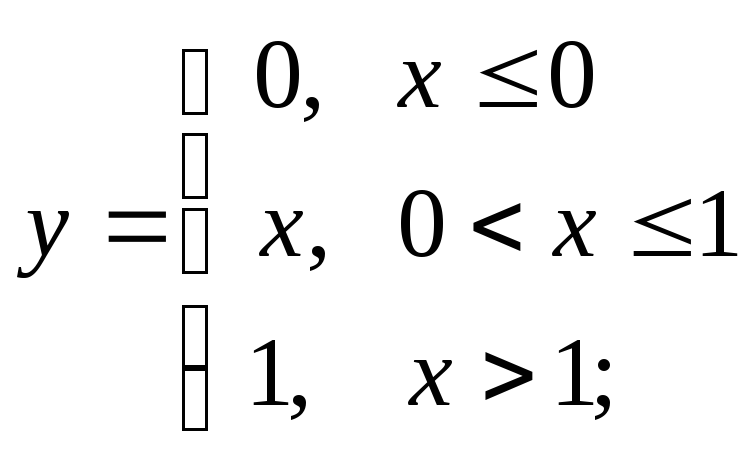 б)
б)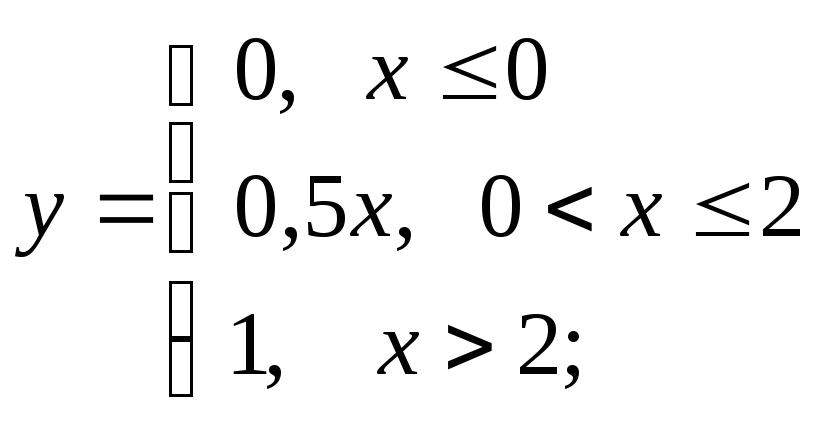 в)
в)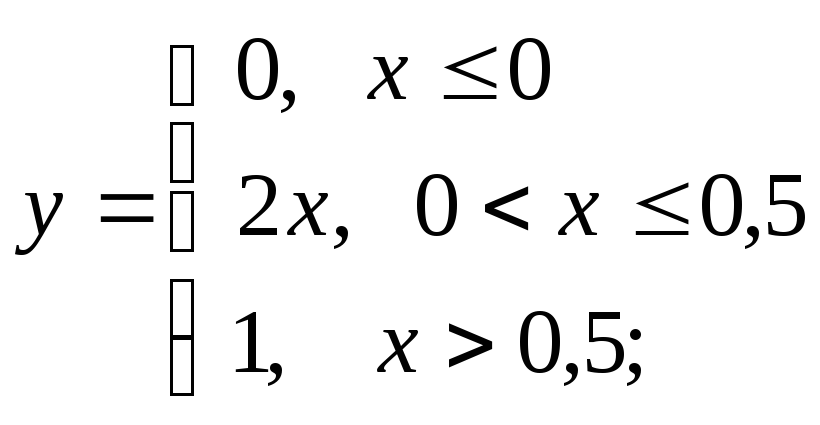
г)
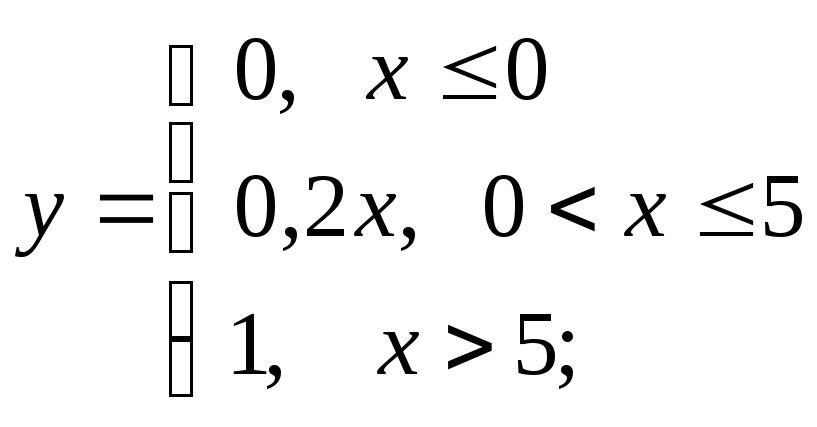 д)
д)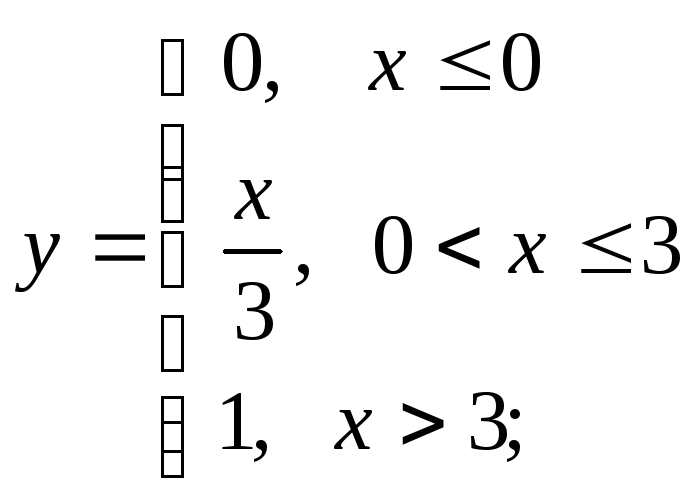 е)
е)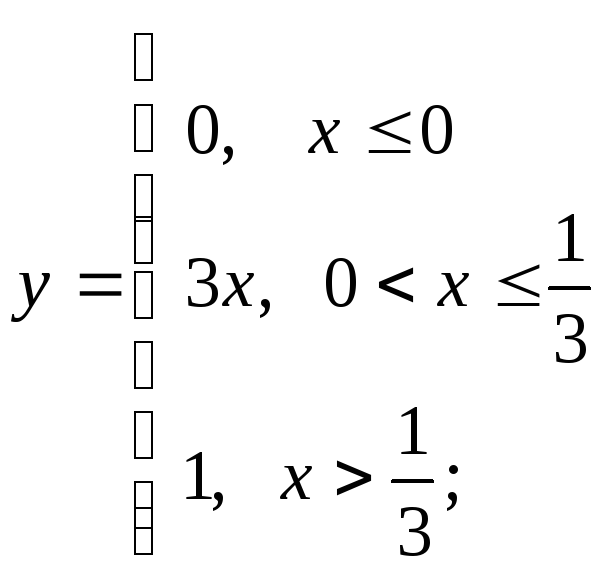
2) а)
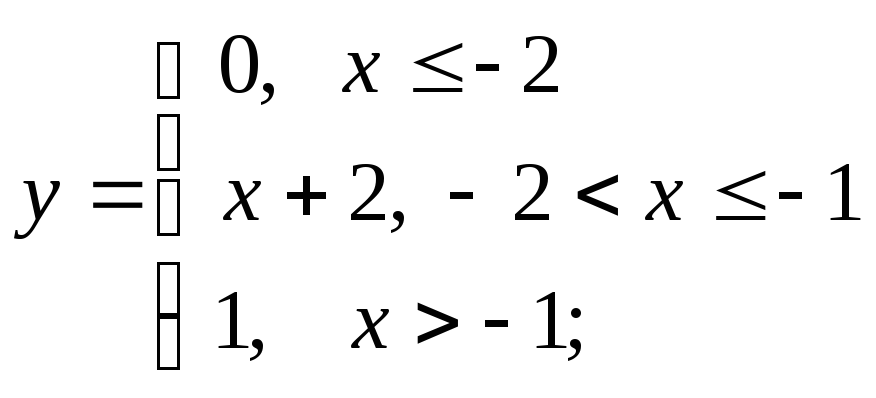 б)
б)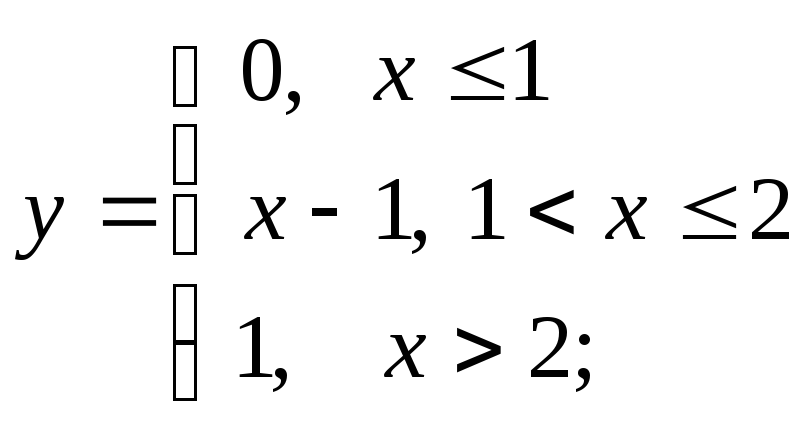 в)
в)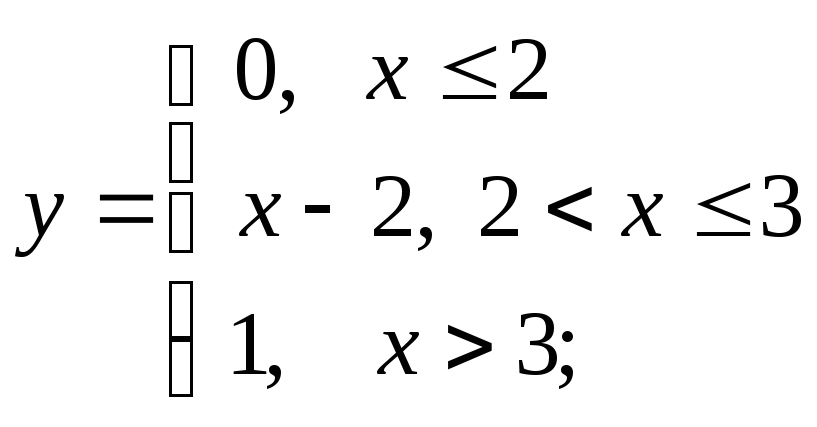
г)
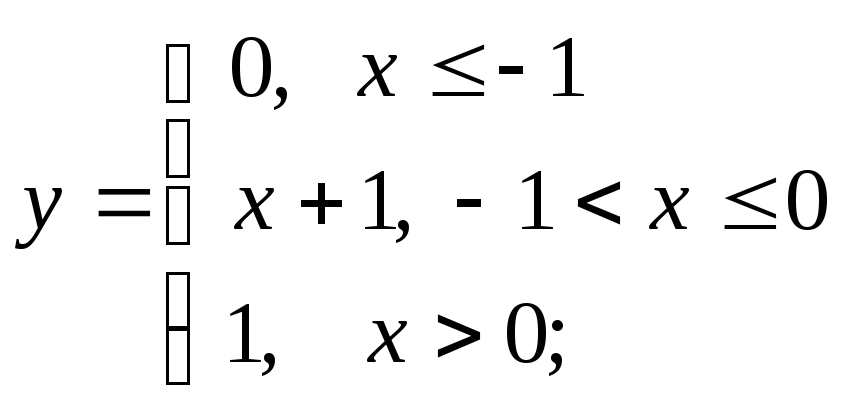 д)
д)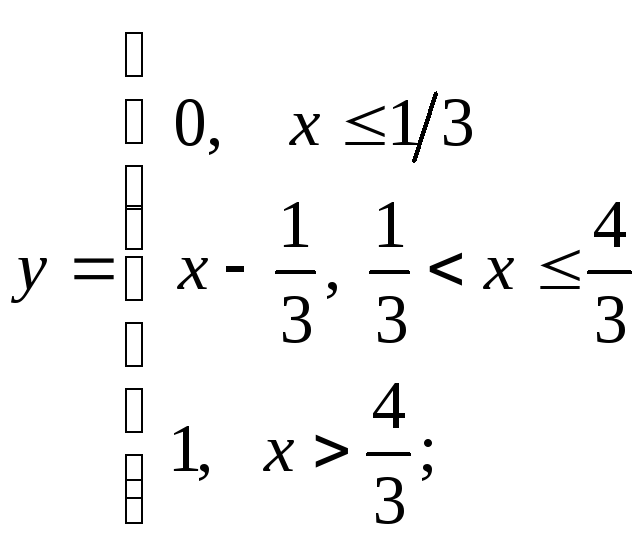 е)
е)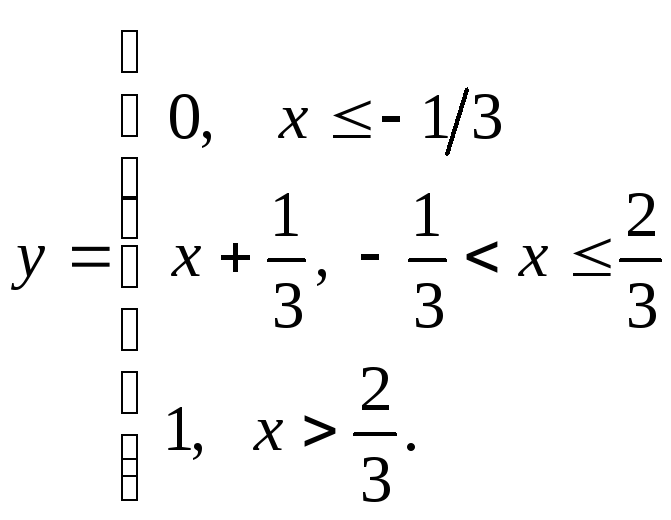
НФ4.
Убедитесь в непрерывности функций и
постройте их графики:
1) а)
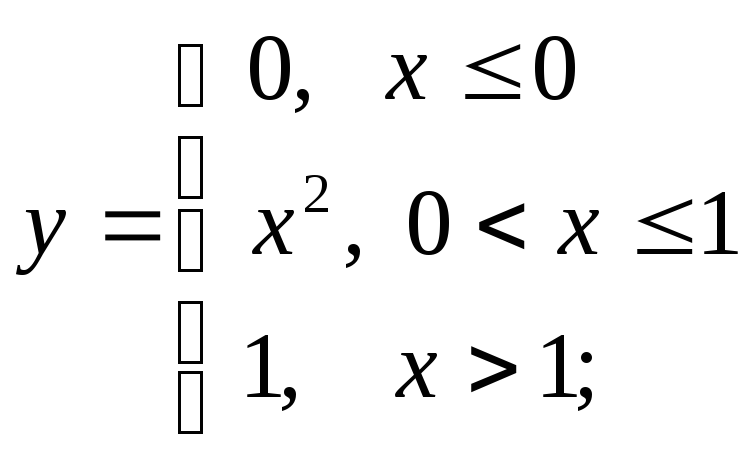 б)
б)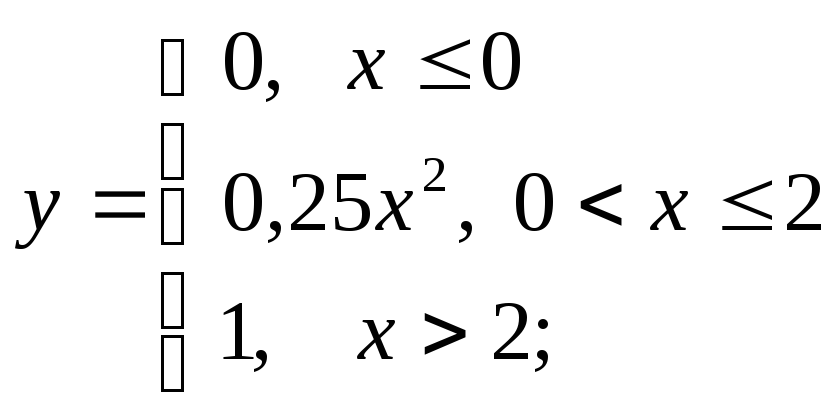 в)
в)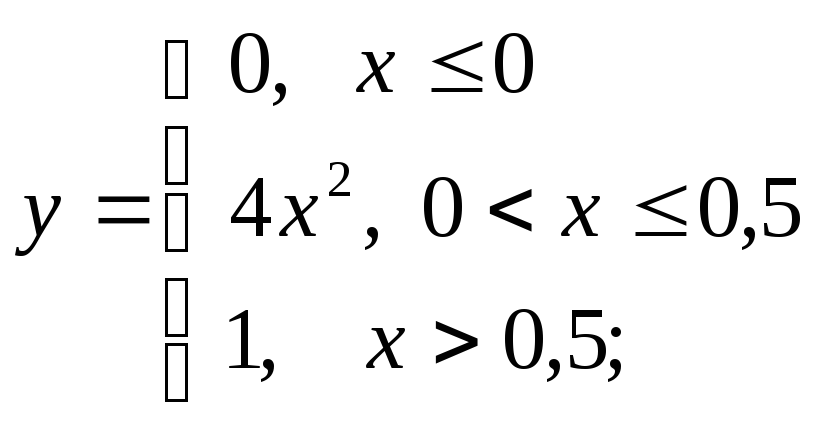
2 а)
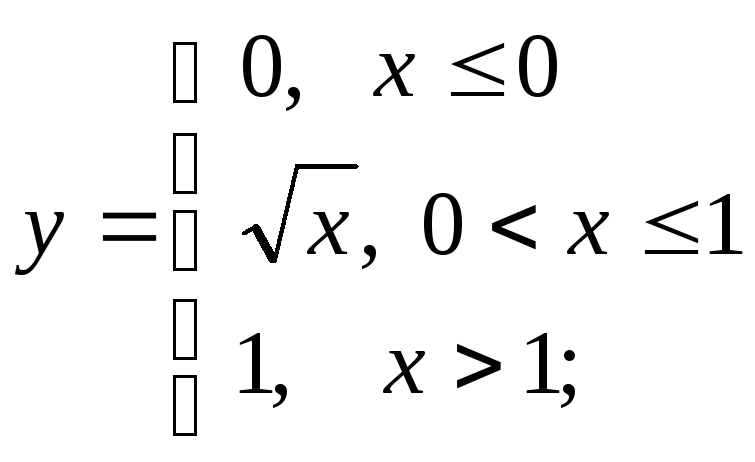 б)
б)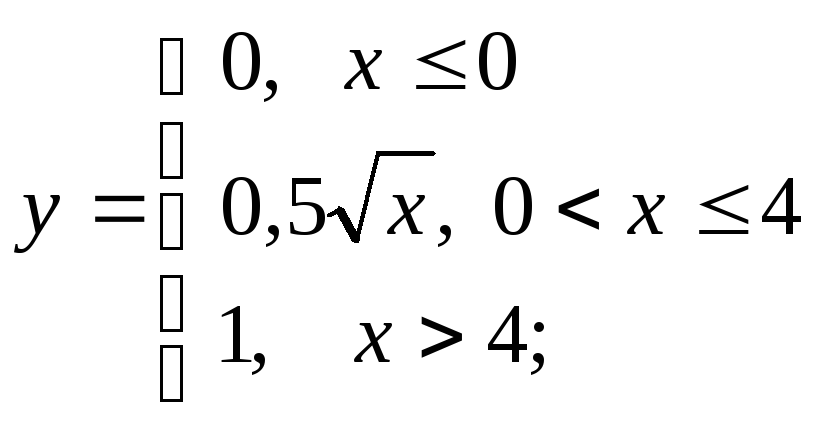 в)
в)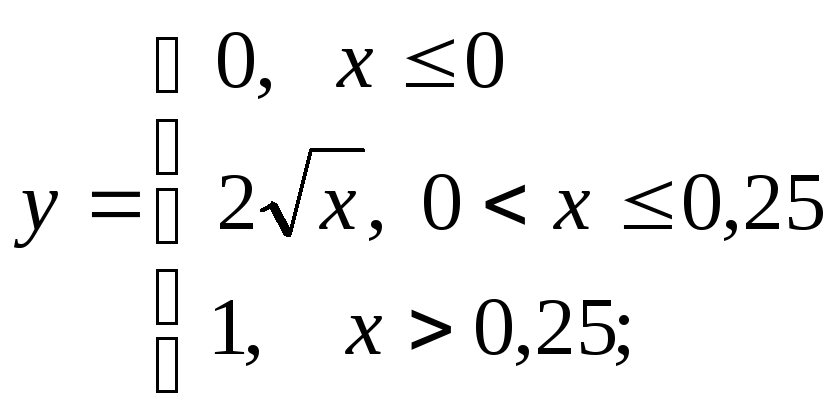
3) а)
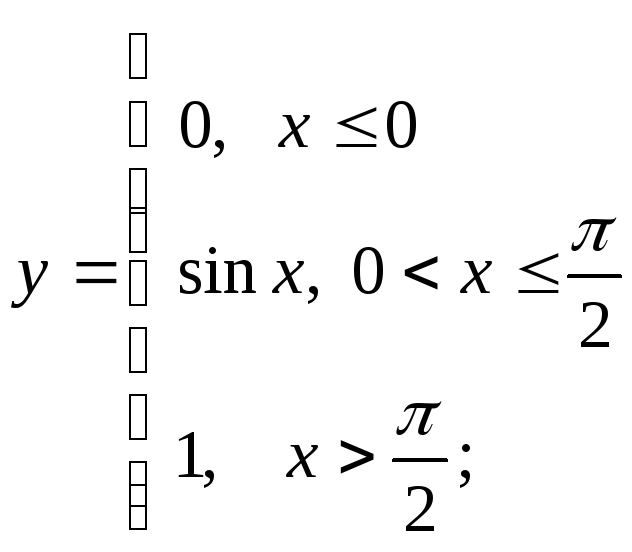 б)
б)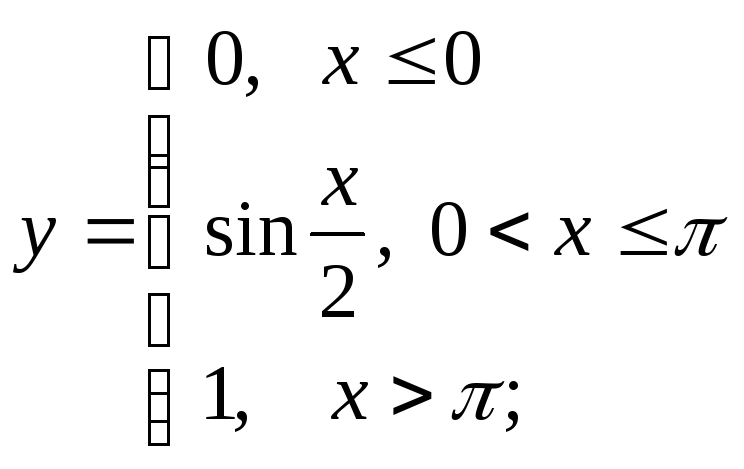 в)
в)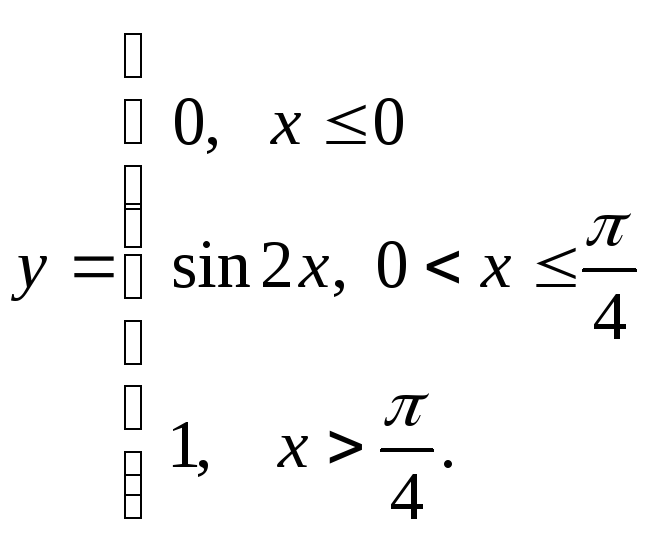
НФ5.
Постройте графики функций. Обратите
внимание на непрерывность:
1) а)
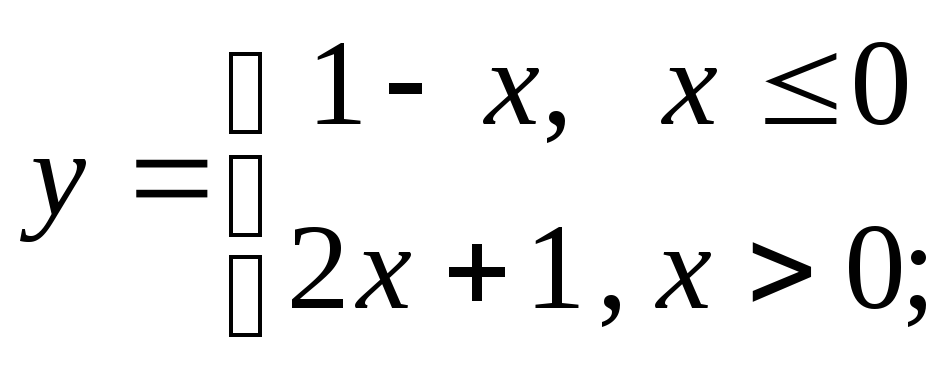 б)
б)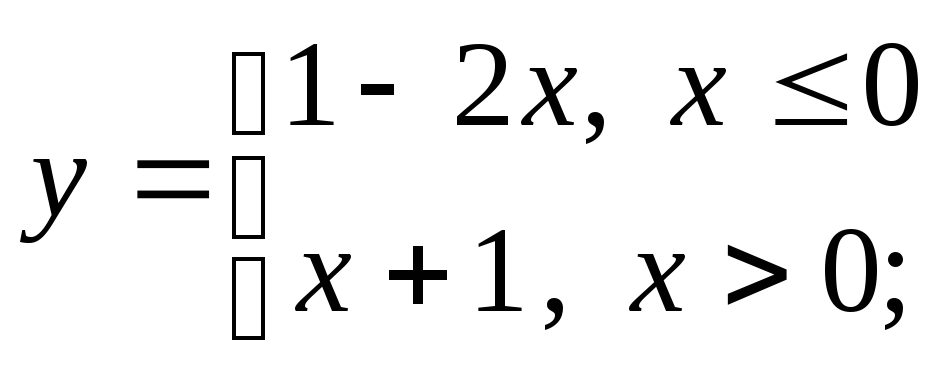 в)
в)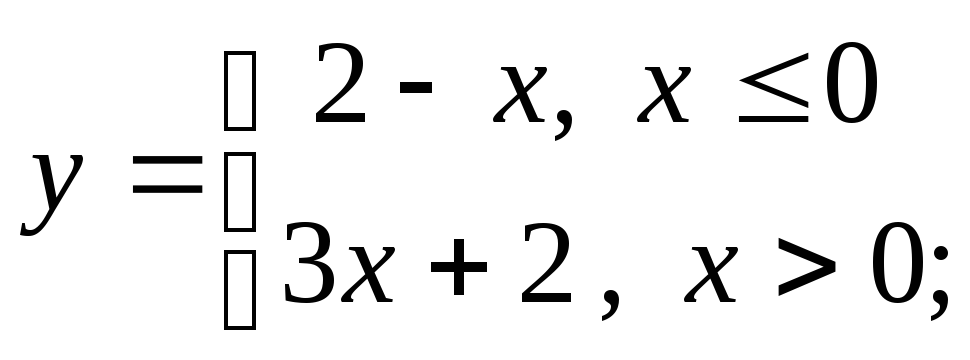
г)
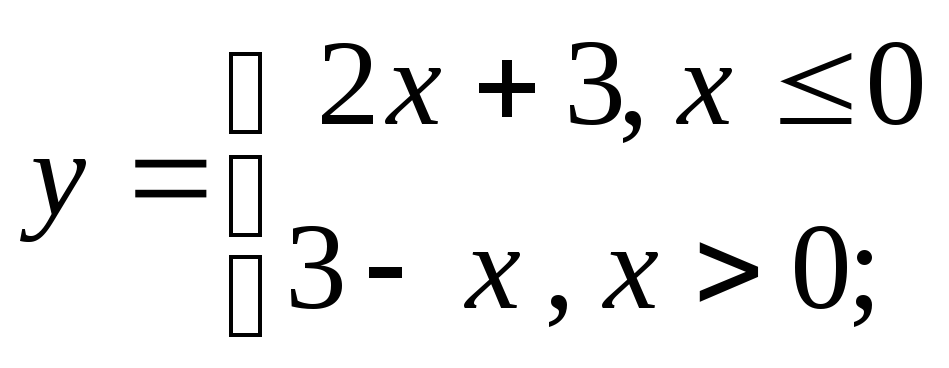 д)
д)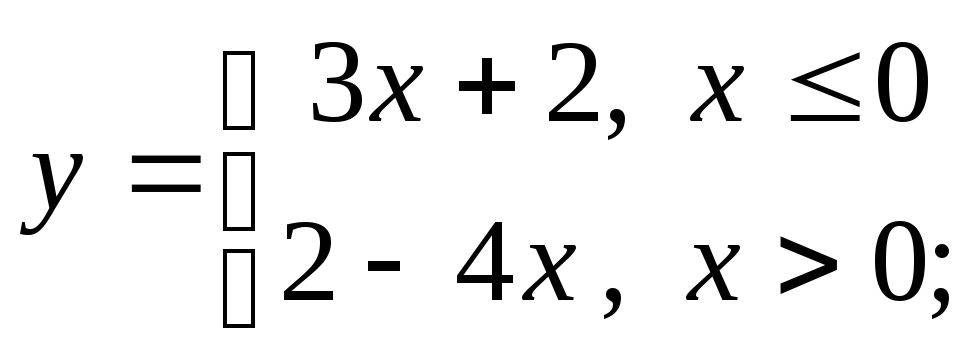 е)
е)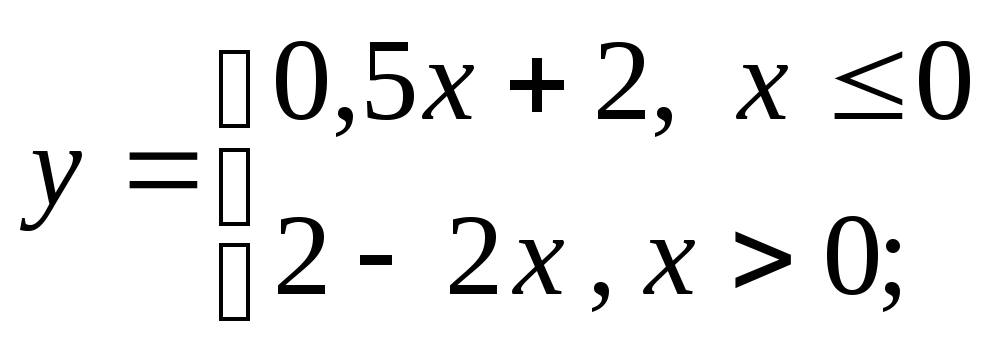
2) а)
 б)
б)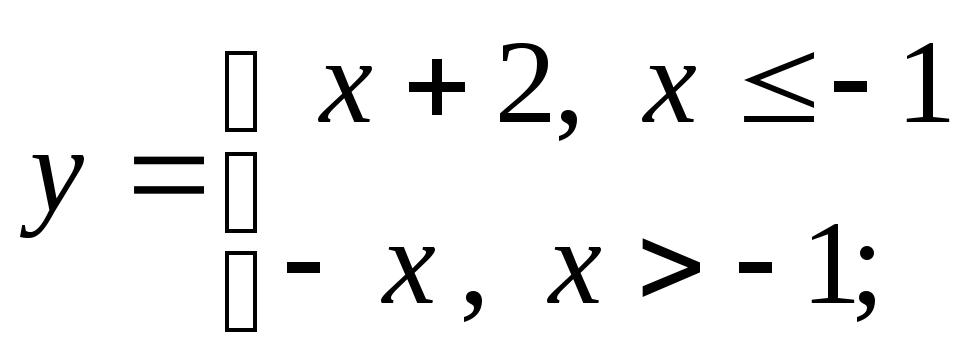 в)
в)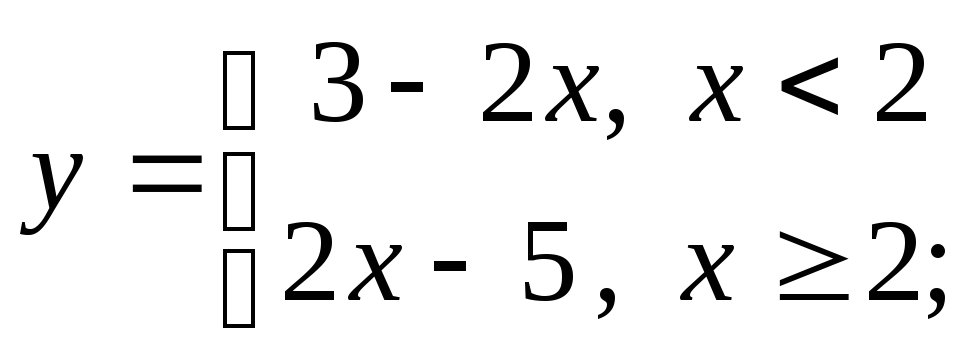
г)
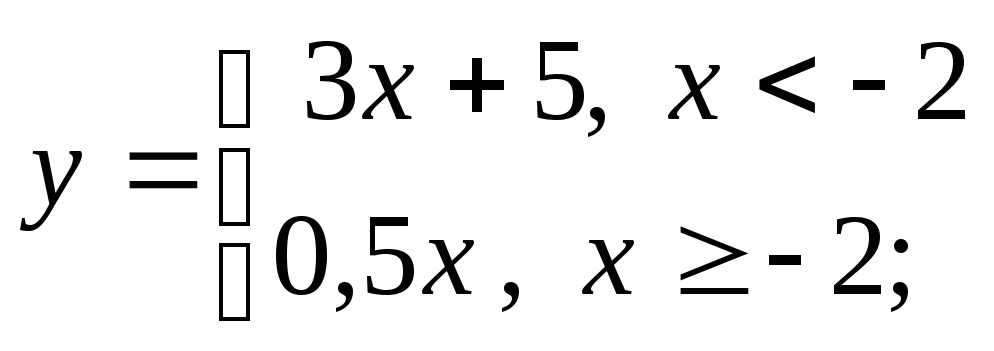 д)
д)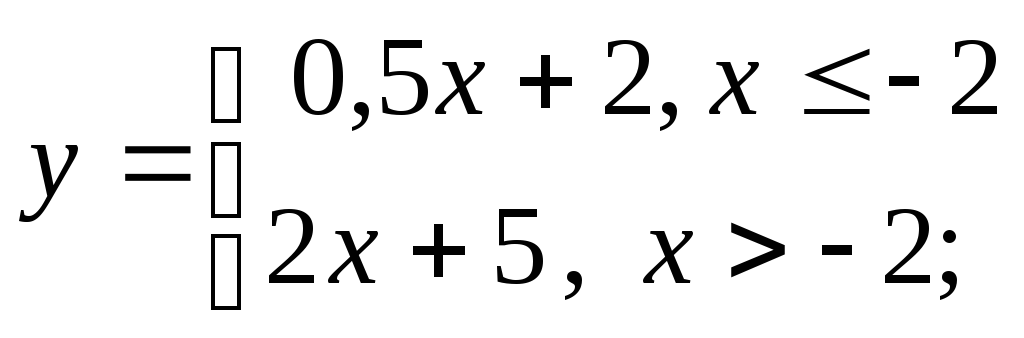 е)
е)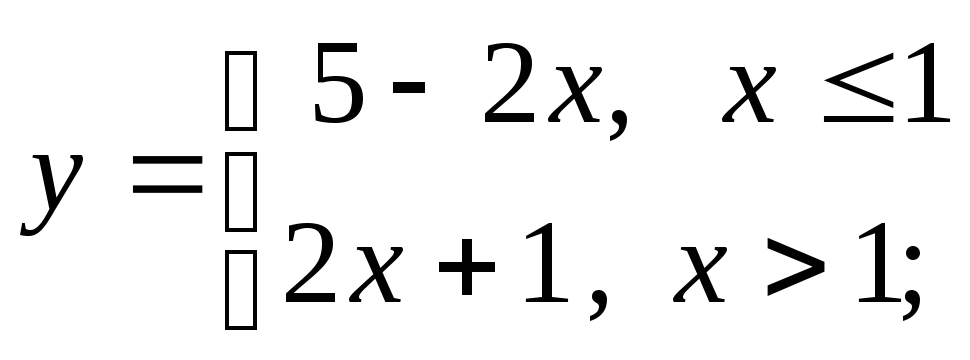
3) а)
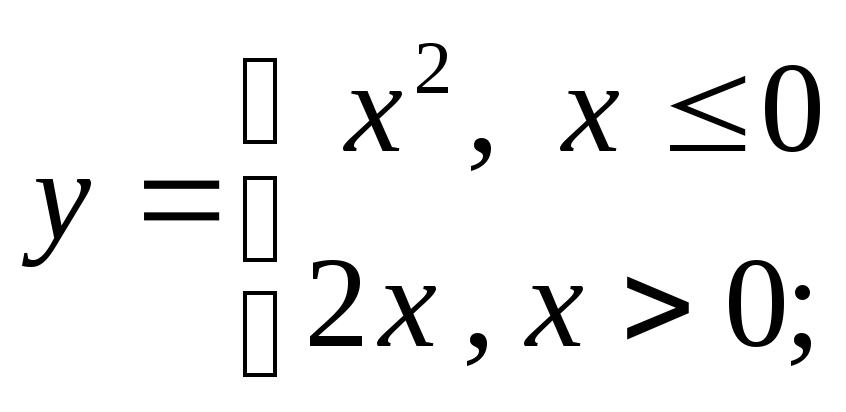 б)
б)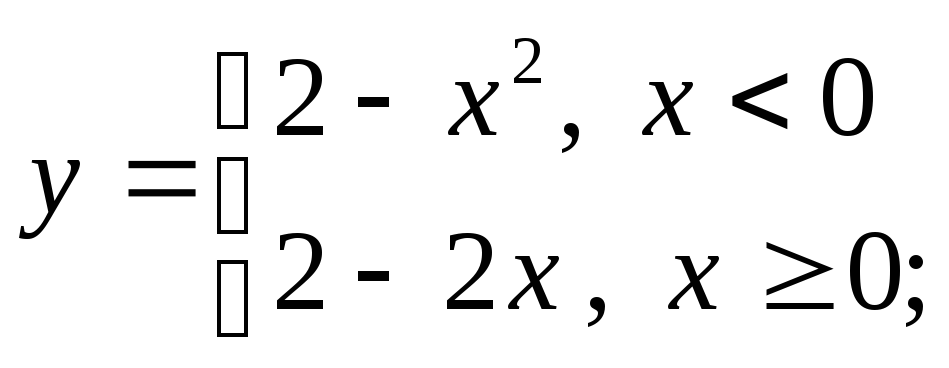 в)
в)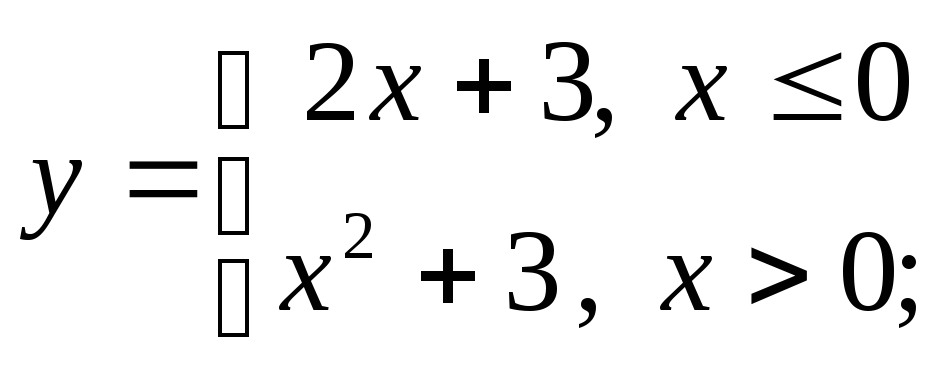
г)
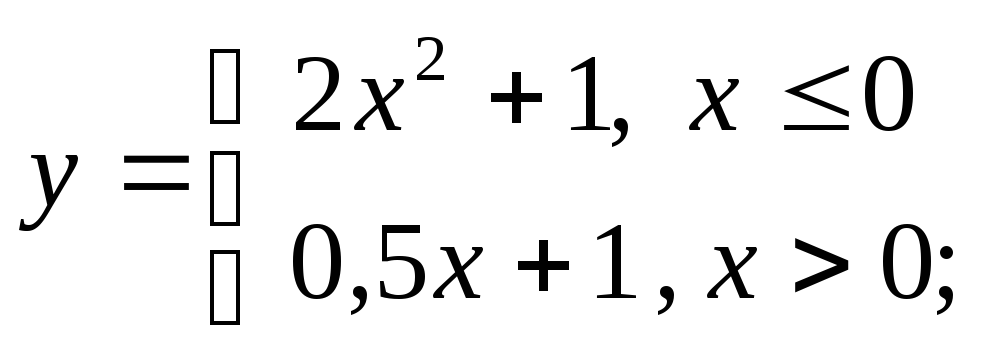 д)
д)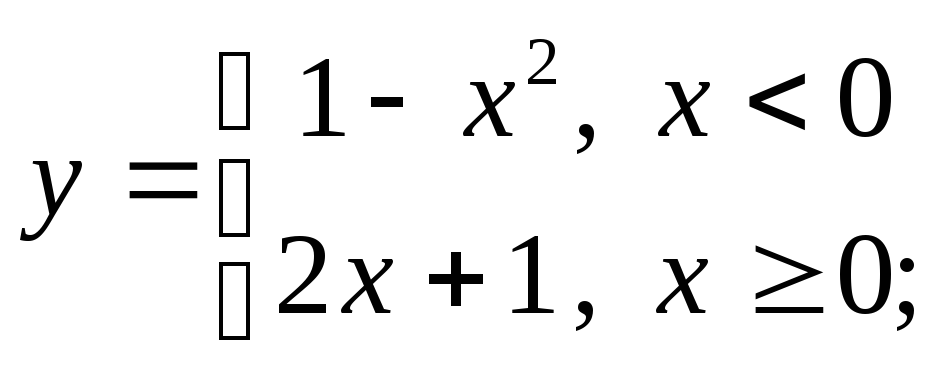 е)
е)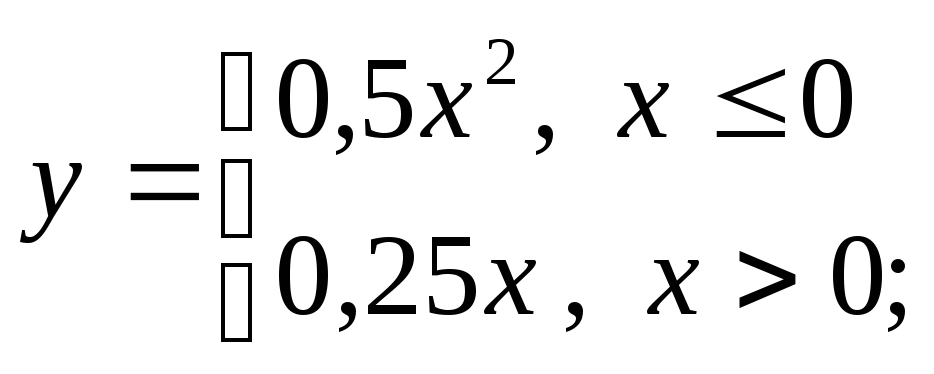
4) а)
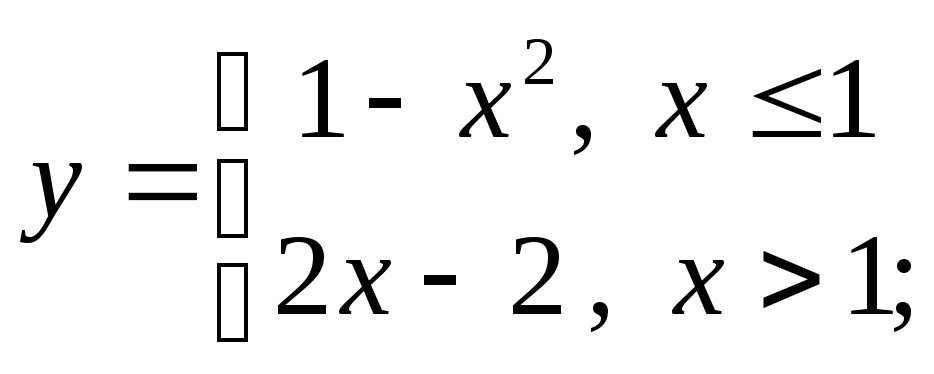 б)
б)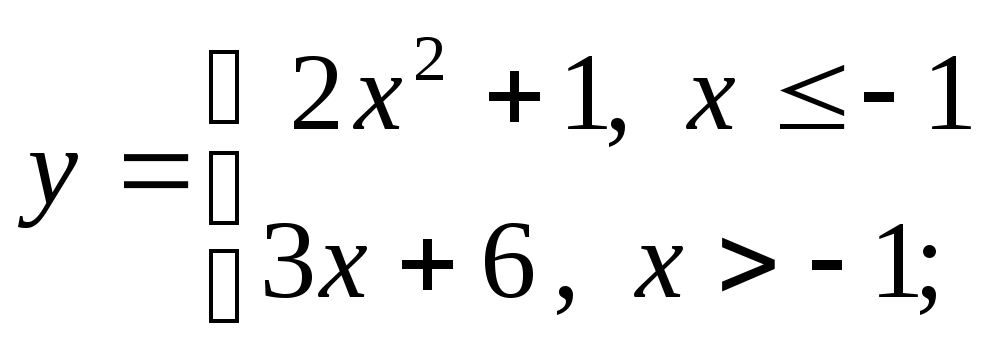 в)
в)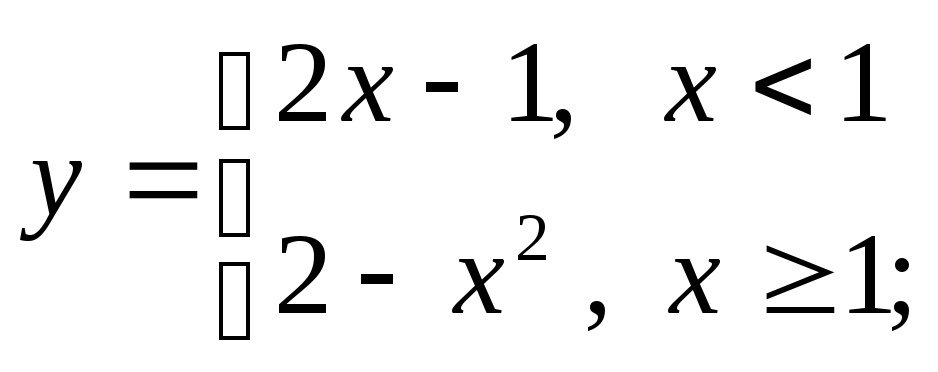
г)
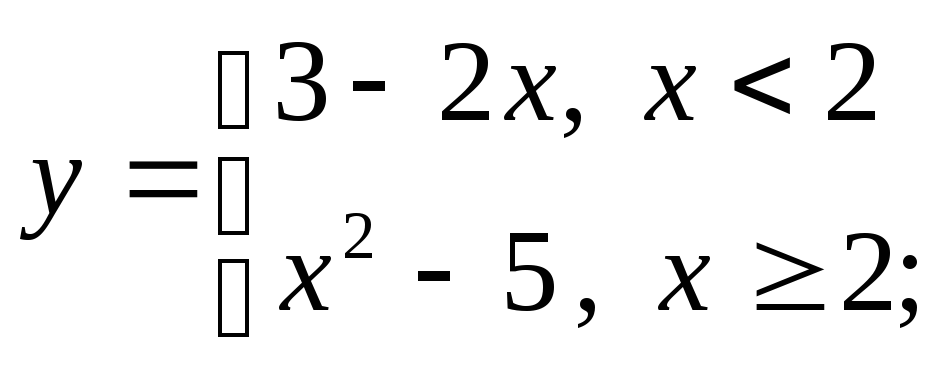 д)
д)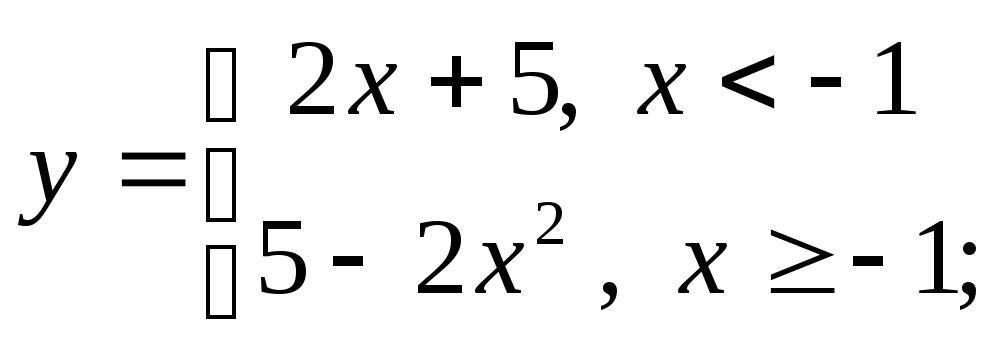 е)
е)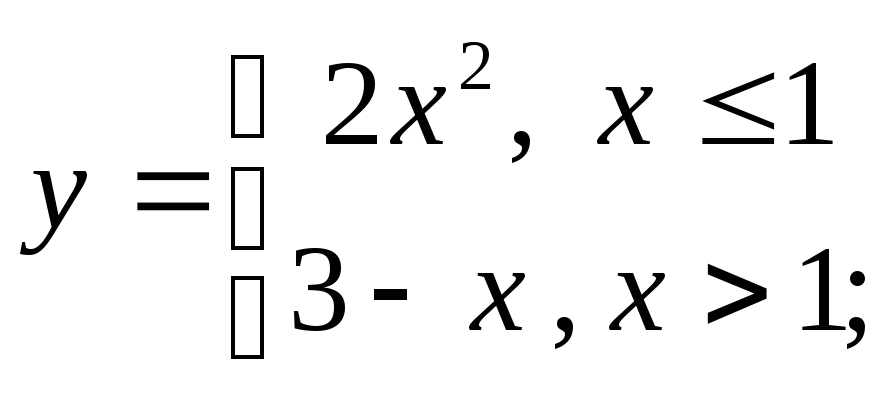
5) а)
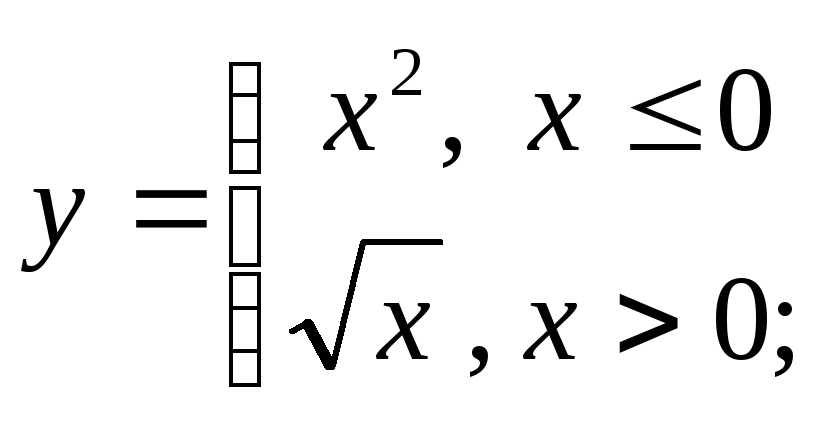 б)
б)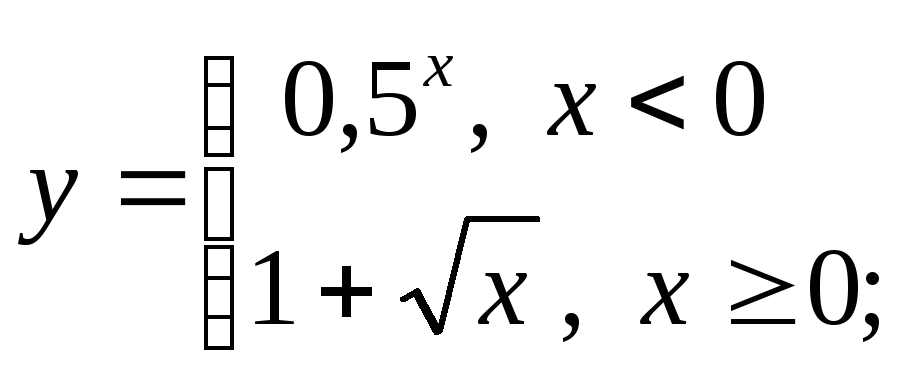 в)
в)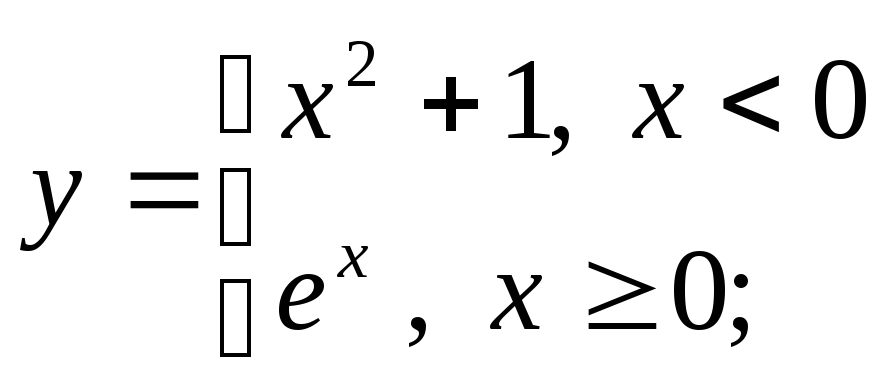
г)
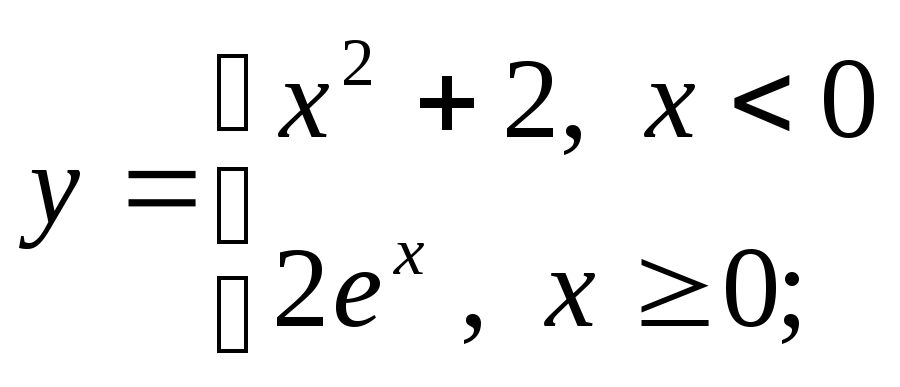 д)
д)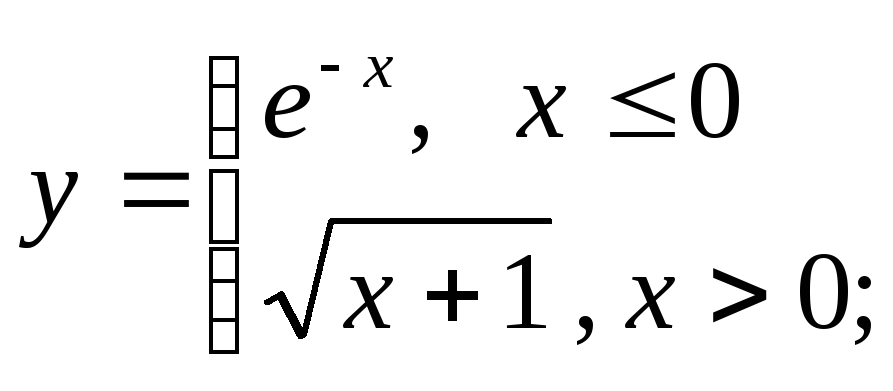 е)
е)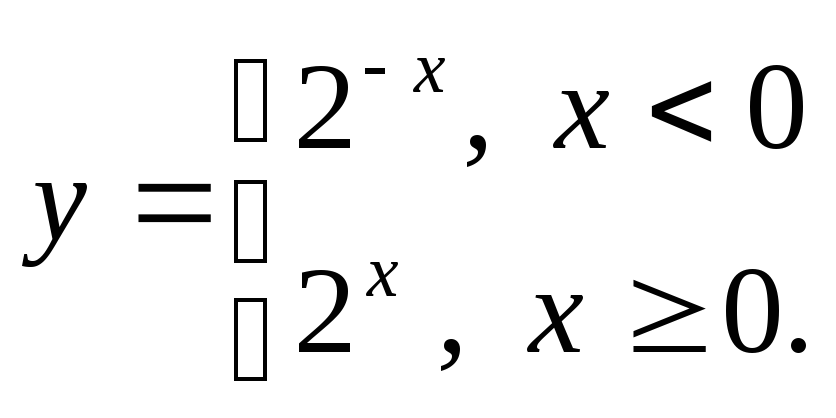
НФ6.
Постройте графики разрывных функций.
Обратите внимание на значение функции
в той точке, где функция переопределяется
(и существует ли оно):
1) а)
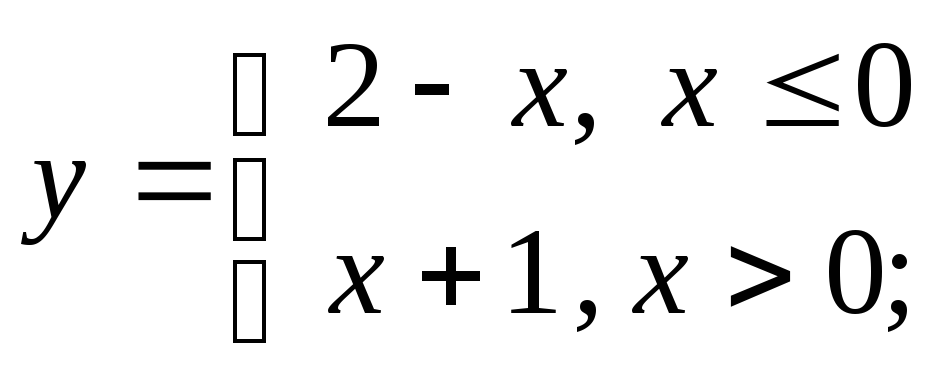 б)
б) в)
в)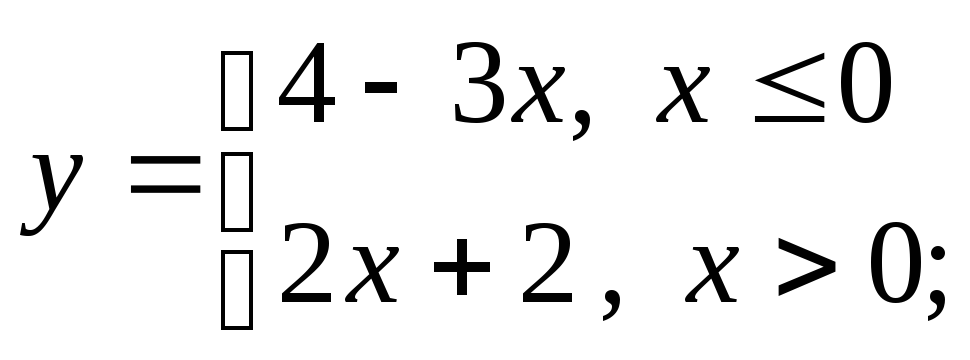
г)
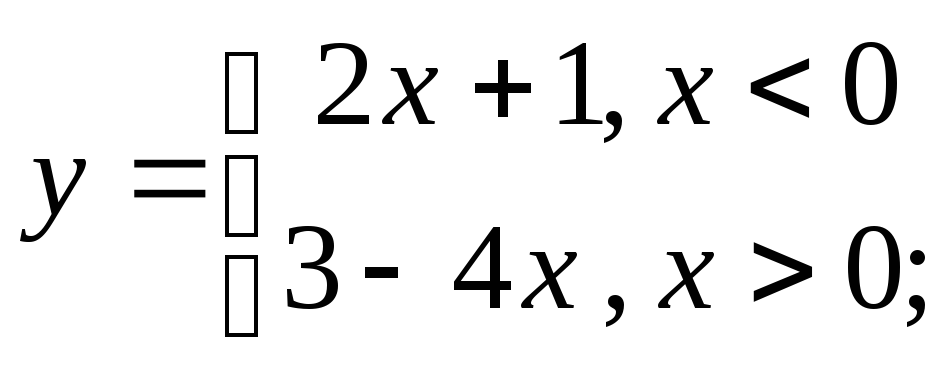 д)
д)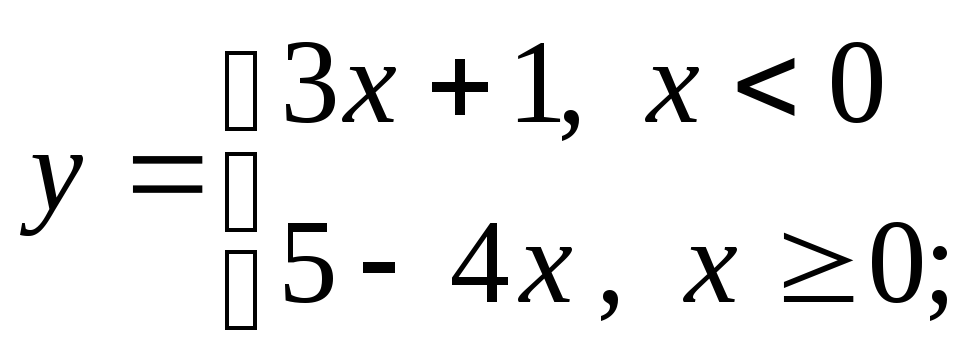 е)
е)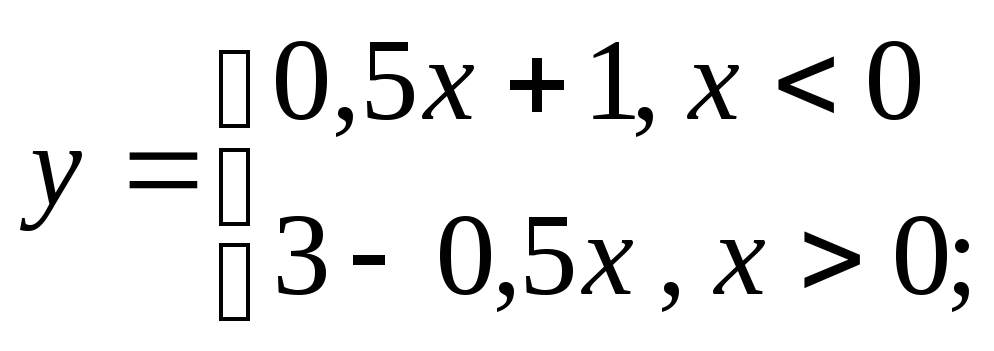
2) а)
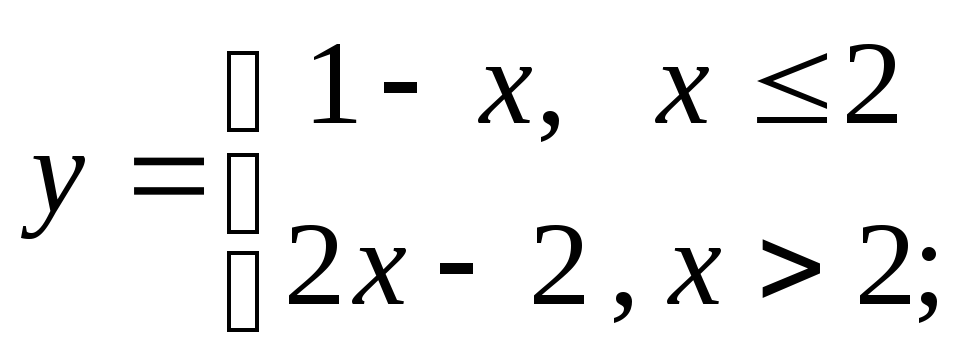 б)
б)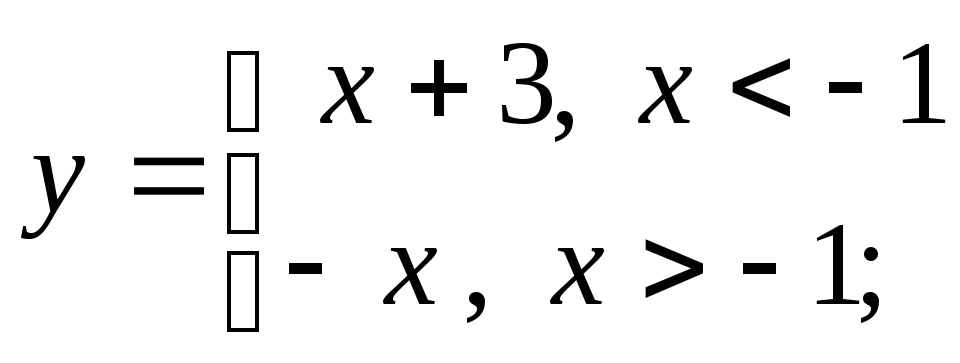 в)
в)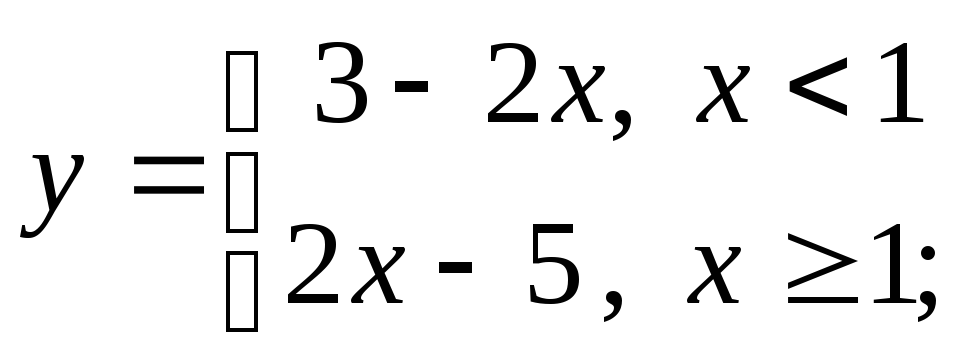
г)
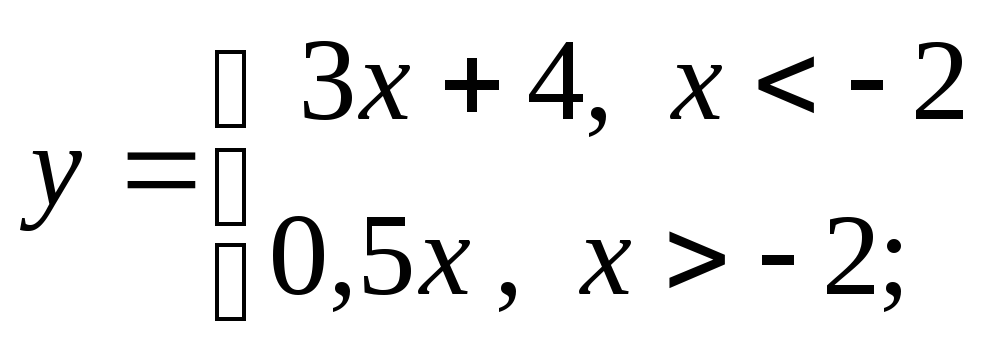 д)
д)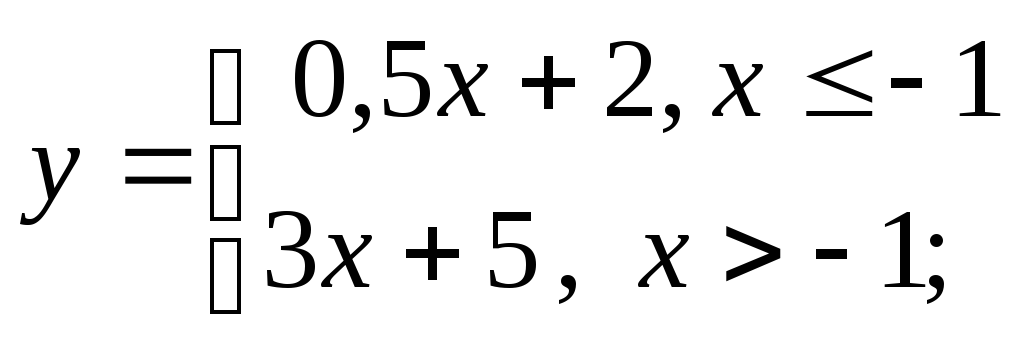 е)
е)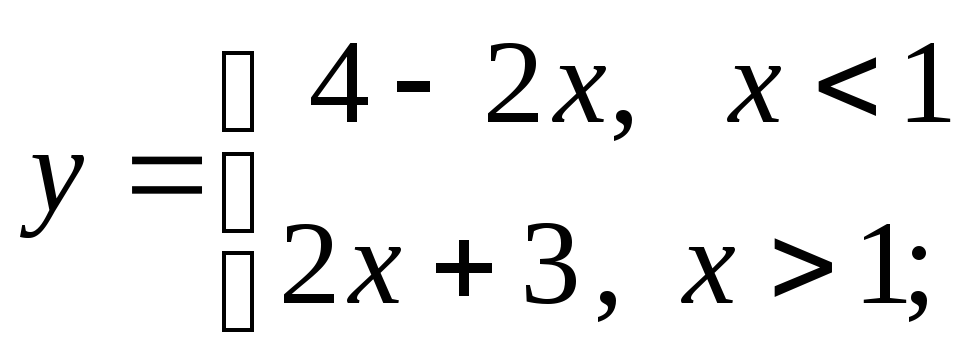
3) а)
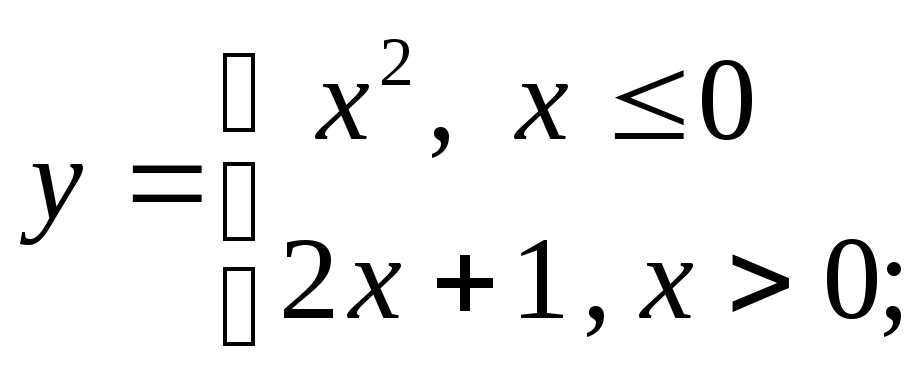 б)
б)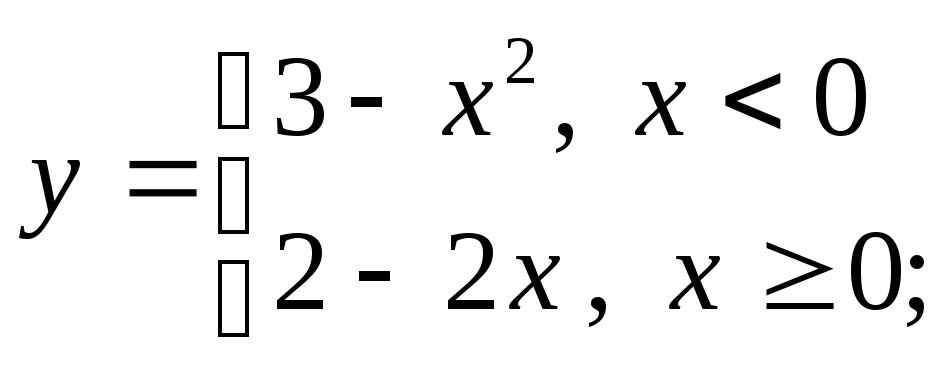 в)
в)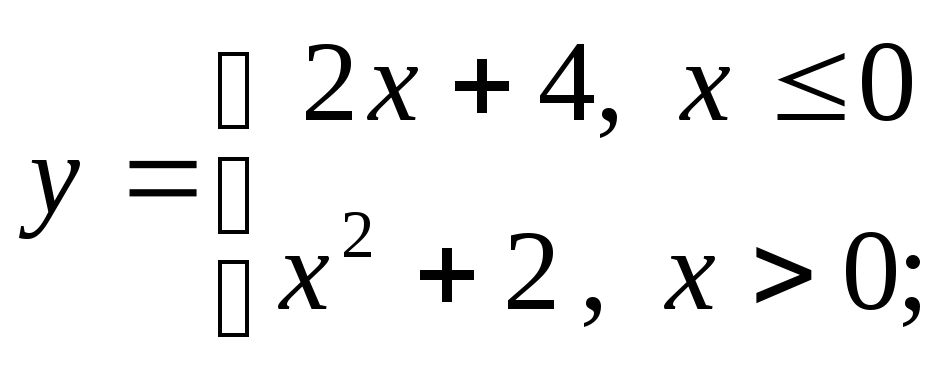
г)
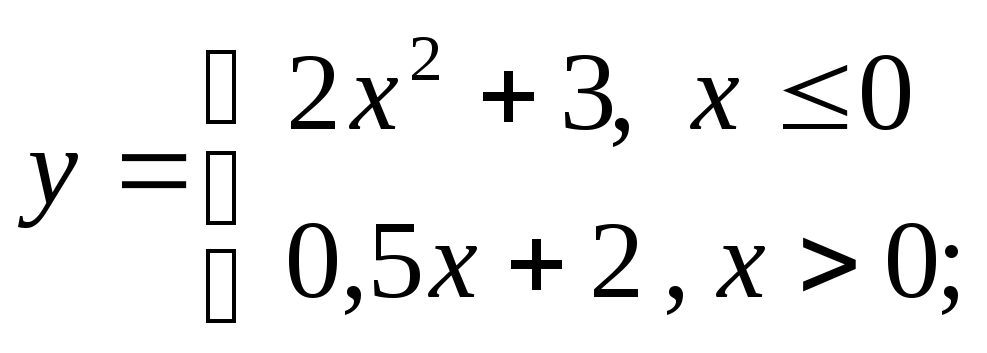 д)
д)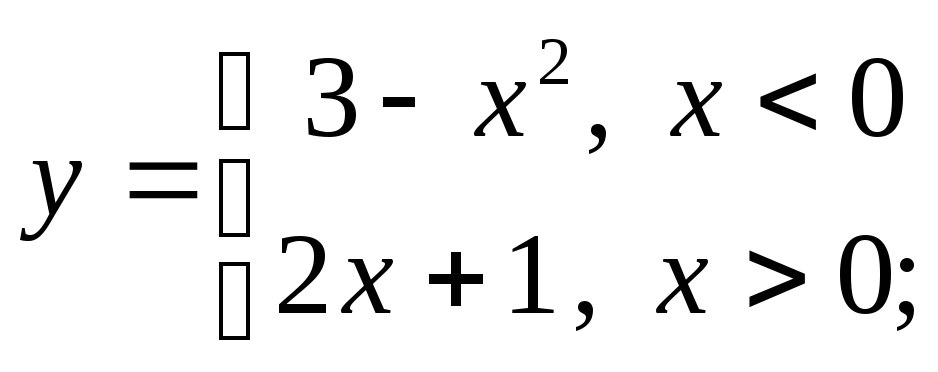 е)
е)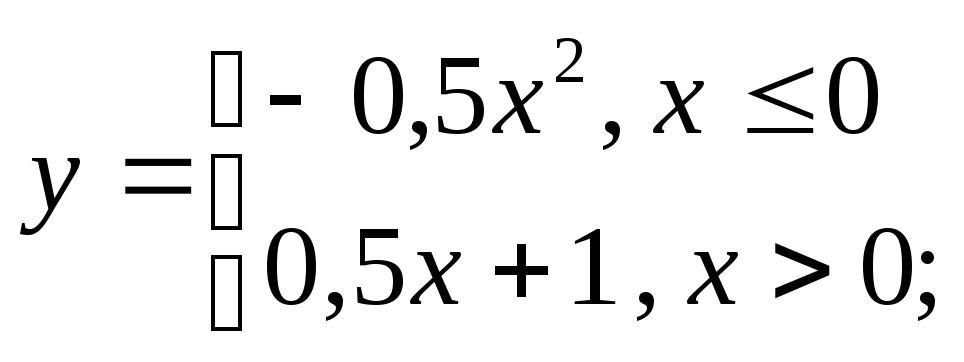
4) а)
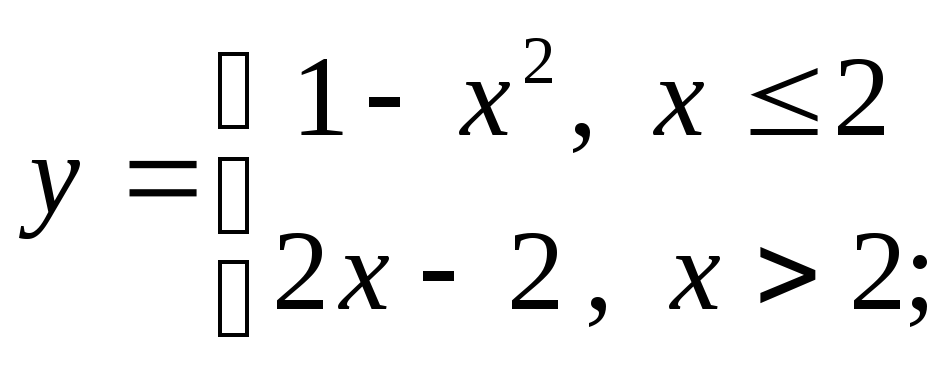 б)
б)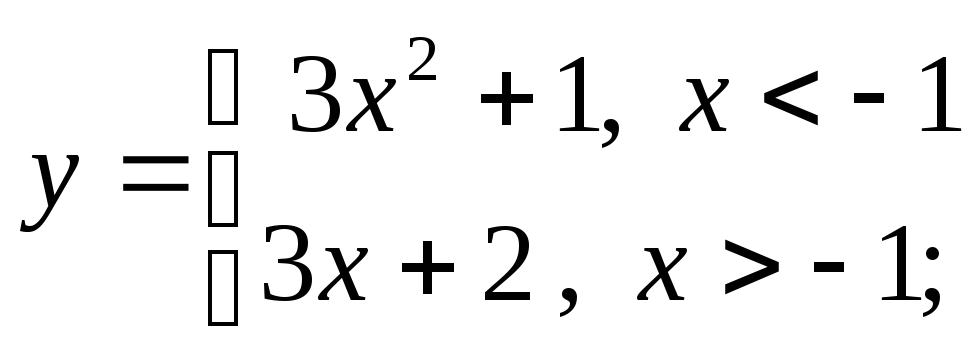 в)
в)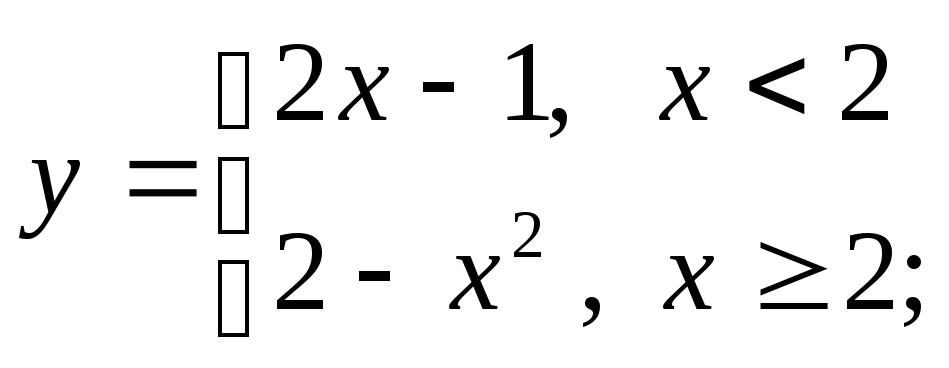
г)
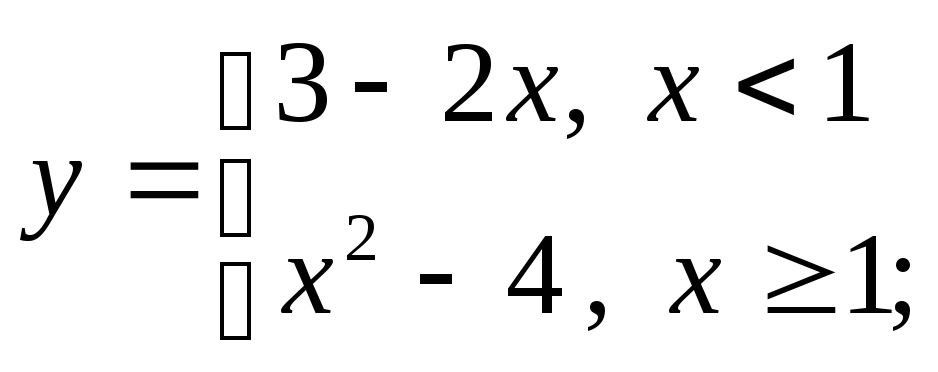 д)
д)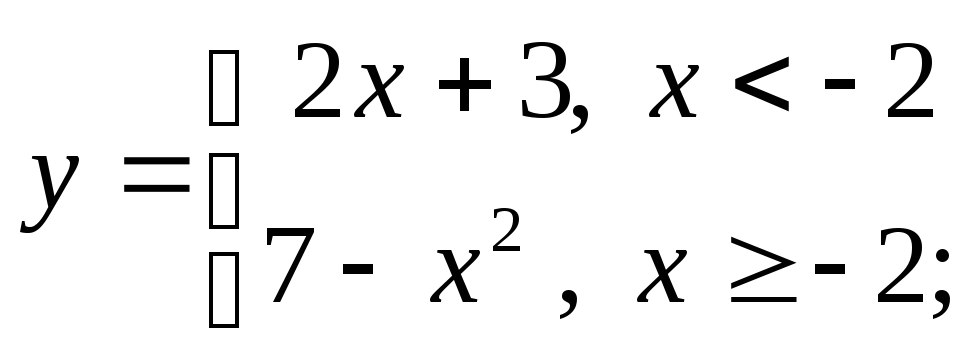 е)
е)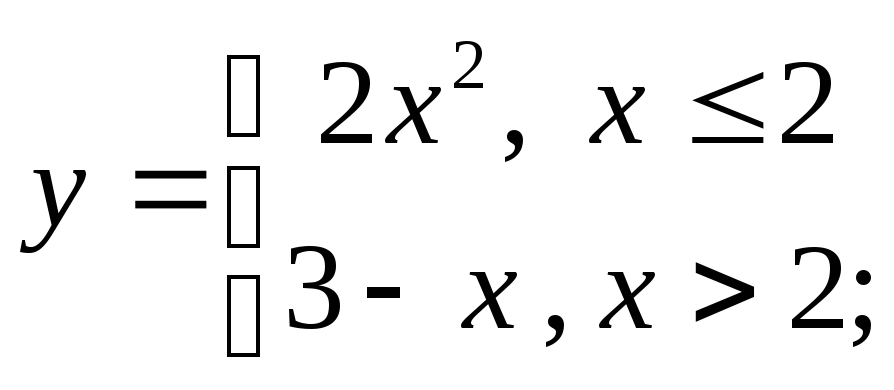
5) а)
 б)
б)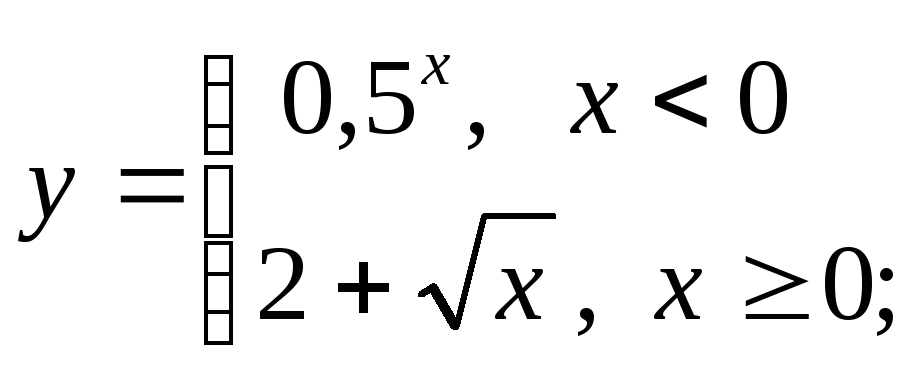 в)
в)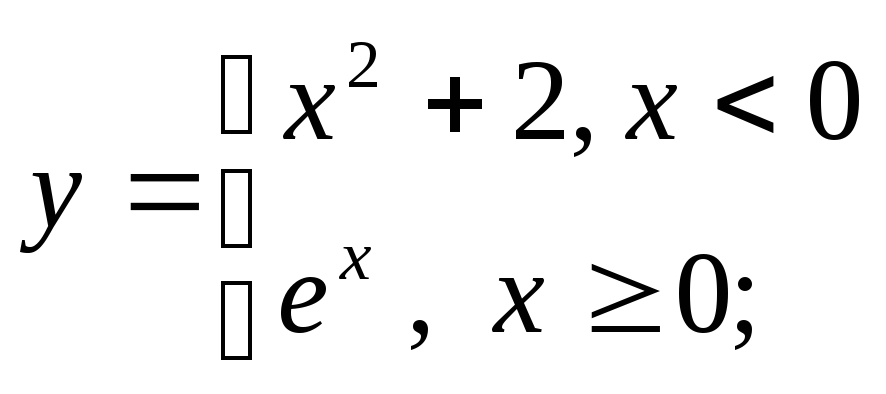
г)
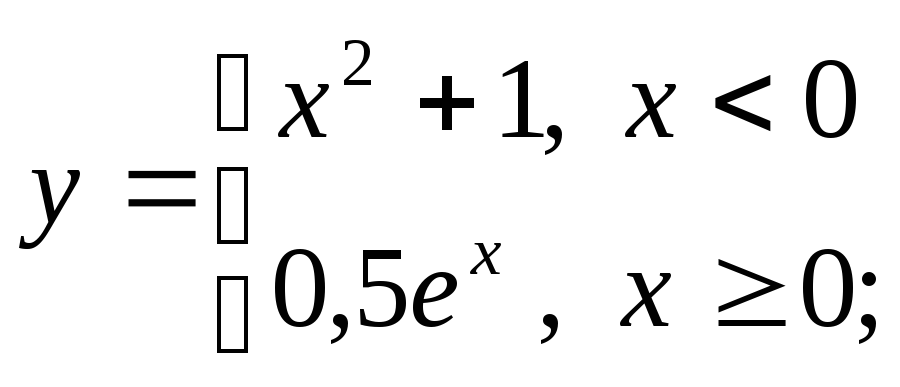 д)
д)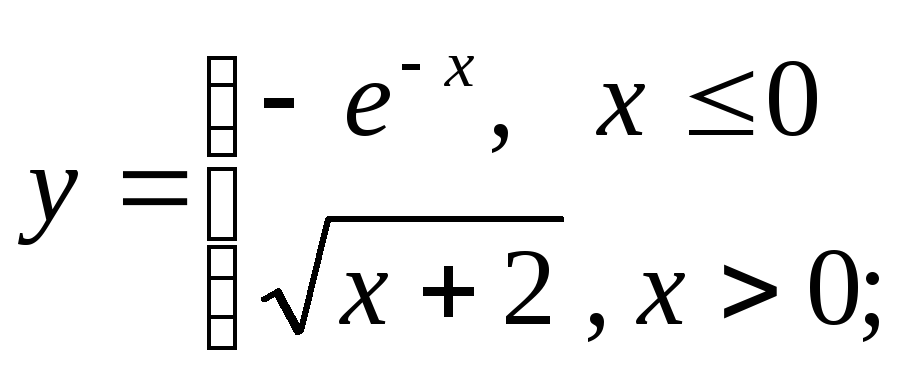 е)
е)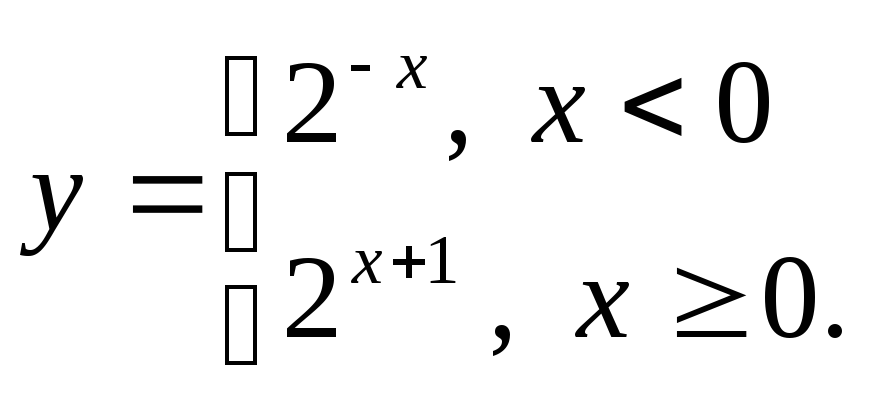
НФ7.
То же задание, что и в НФ6:
1) а)
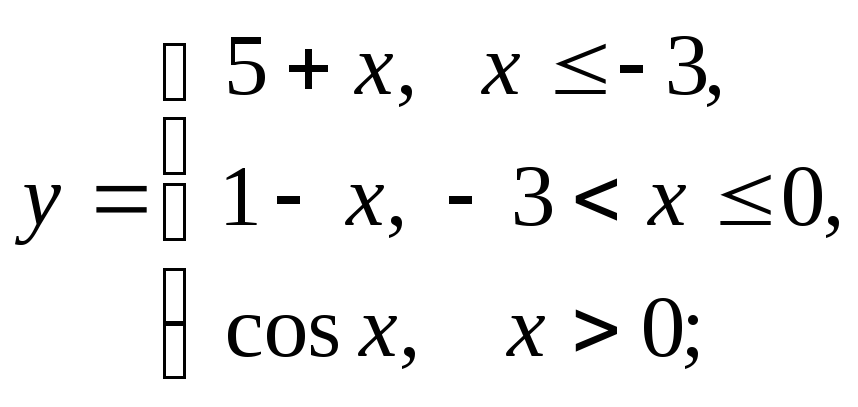 б)
б)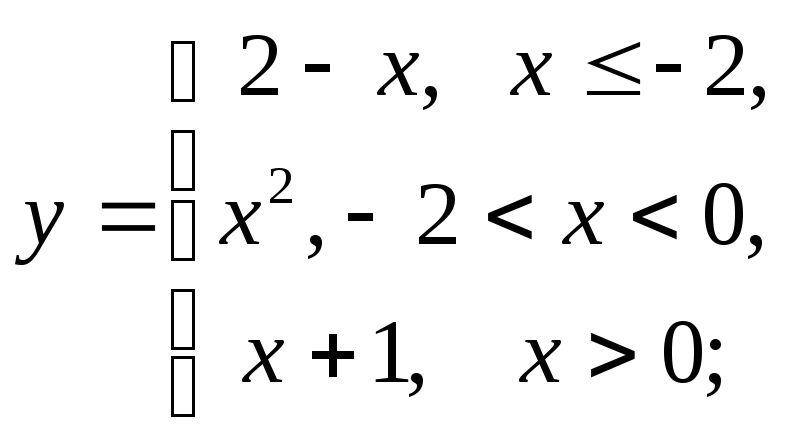 в)
в)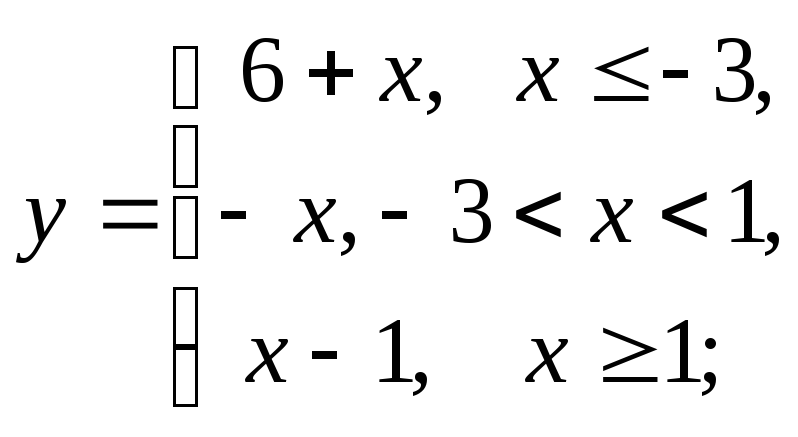
г)
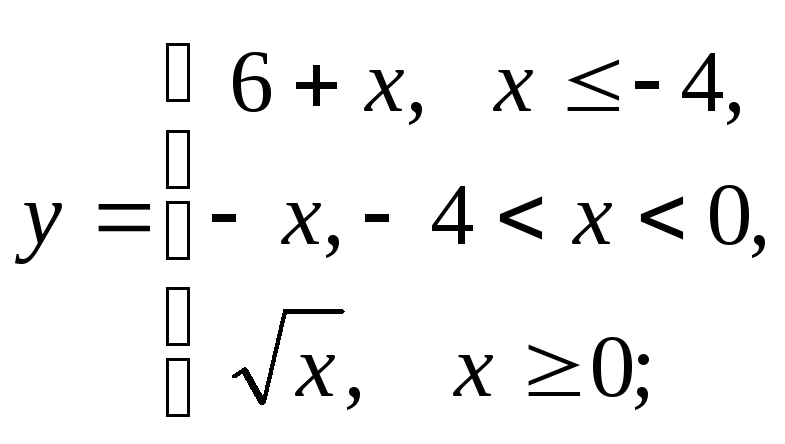 д)
д)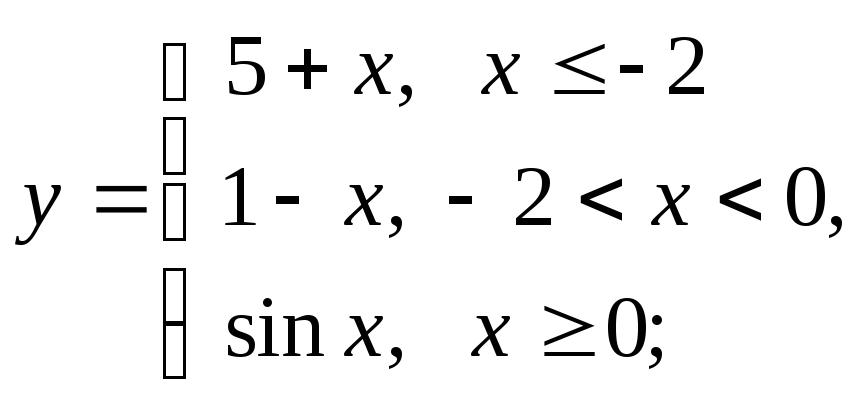 е)
е)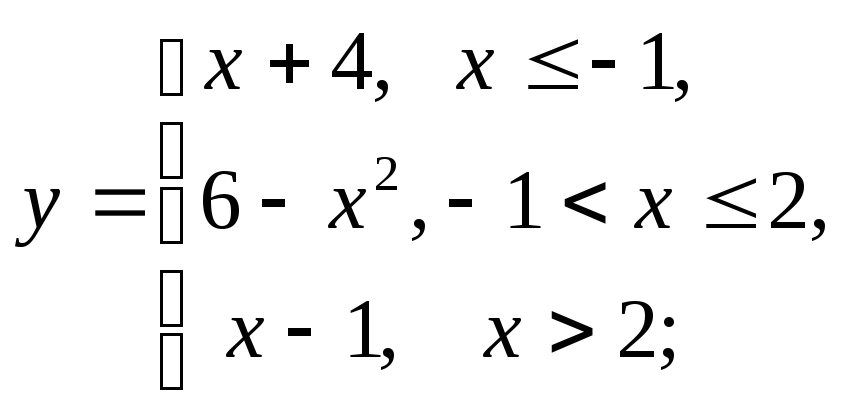
2) а)
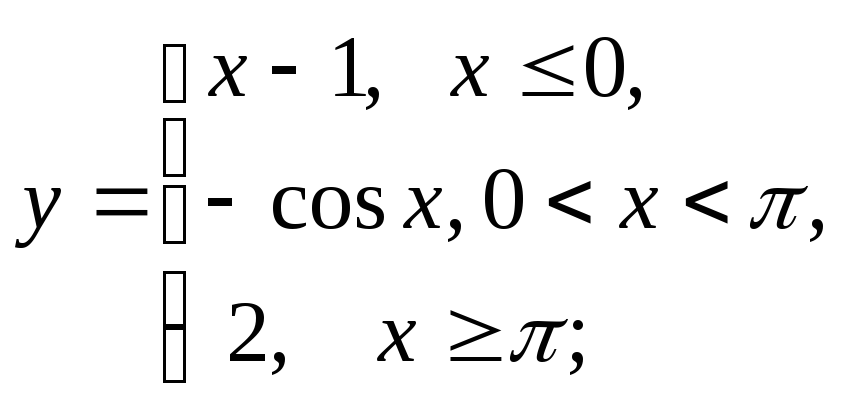 б)
б)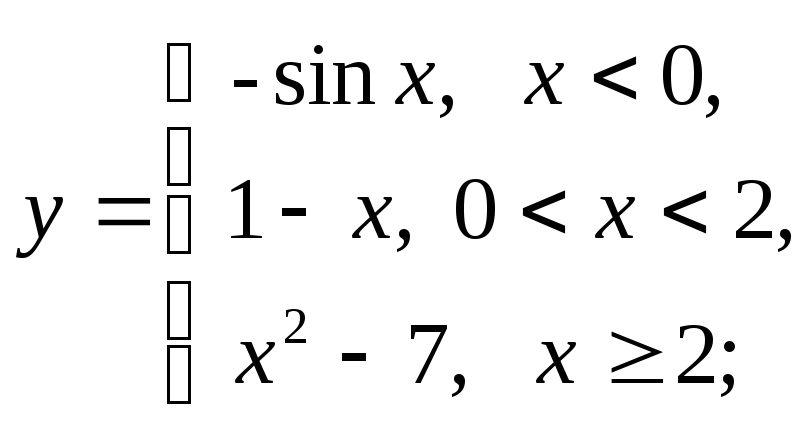 в)
в)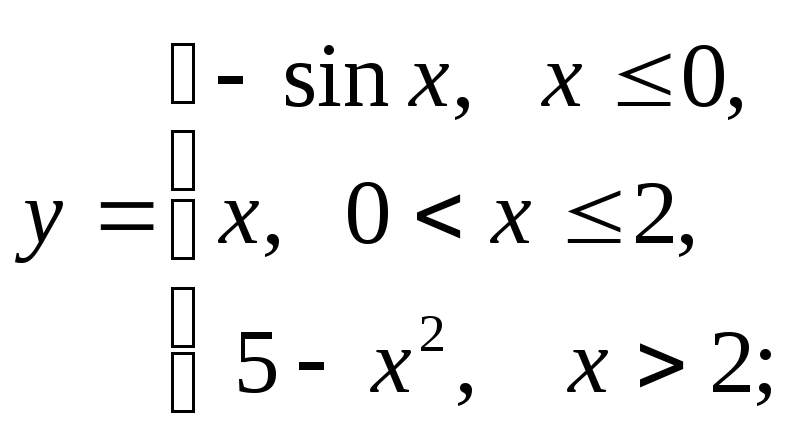
г)
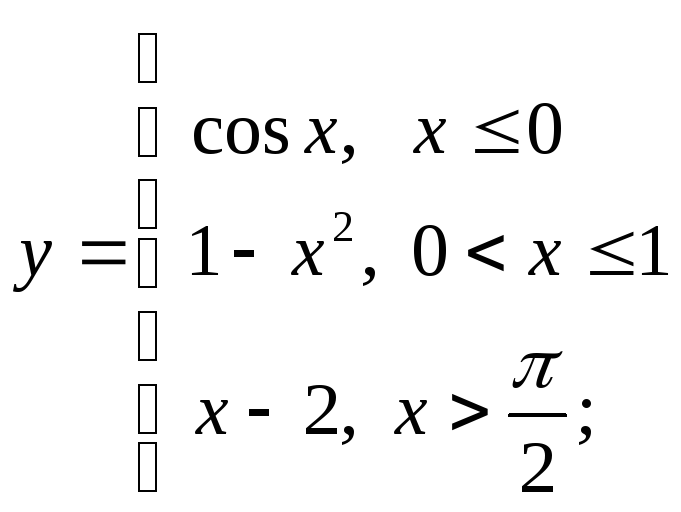 д)
д) е)
е)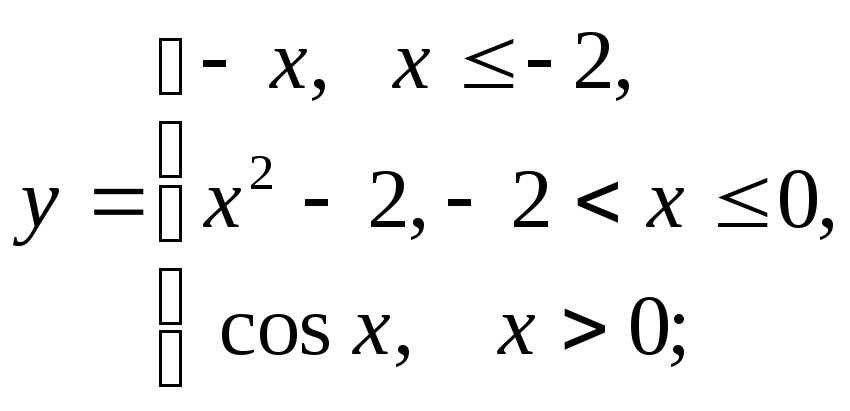
3) а)
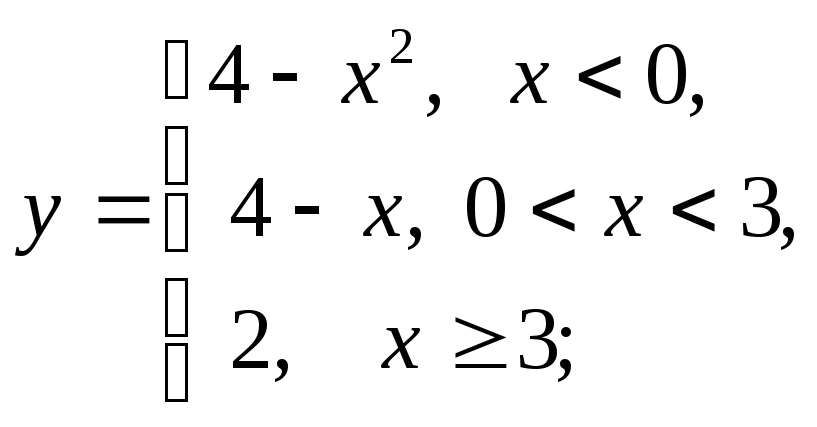 б)
б)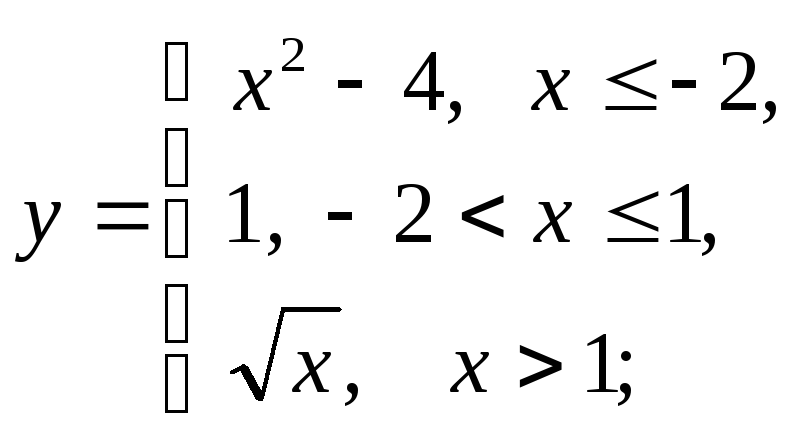 в)
в)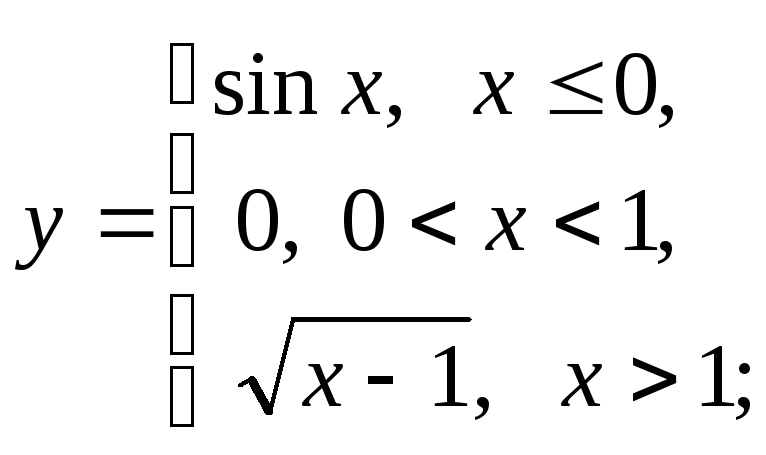
г)
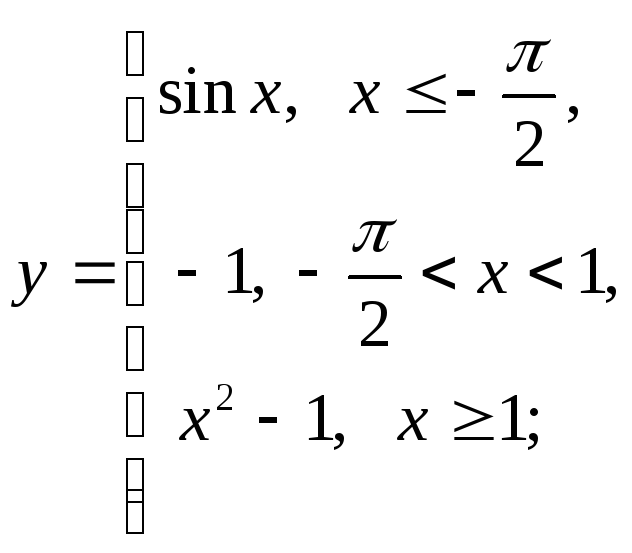 д)
д)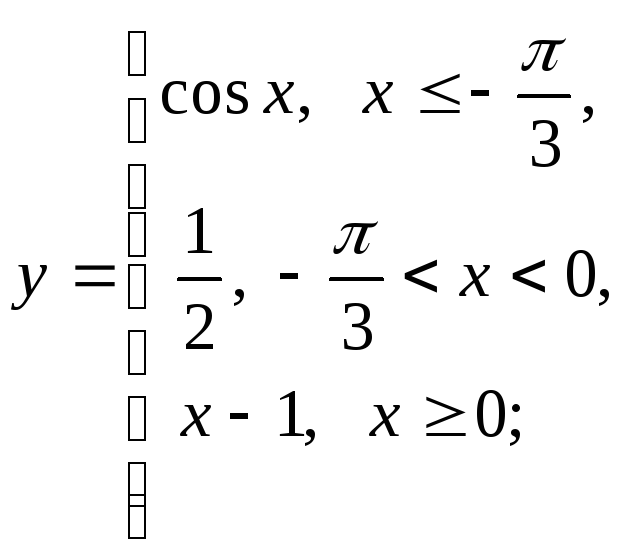 е)
е)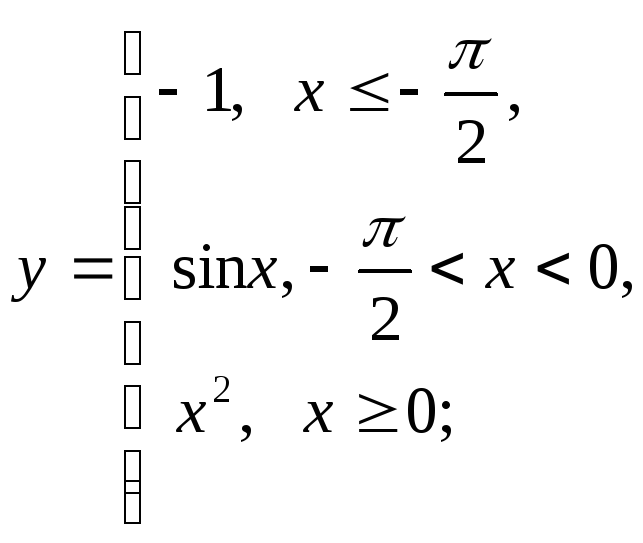
4) а)
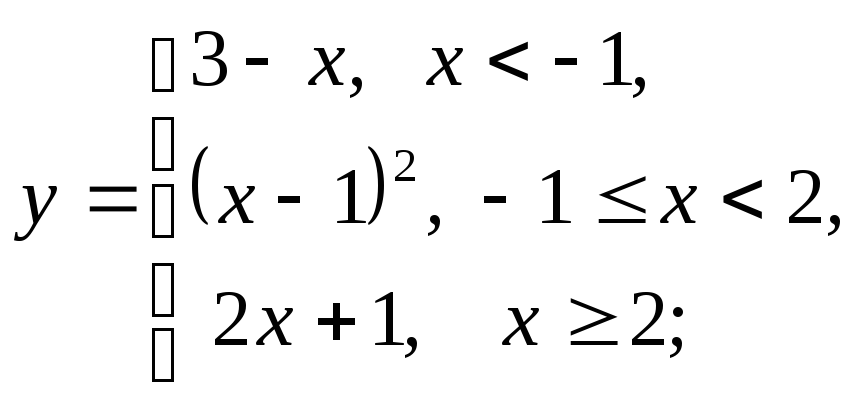 б)
б)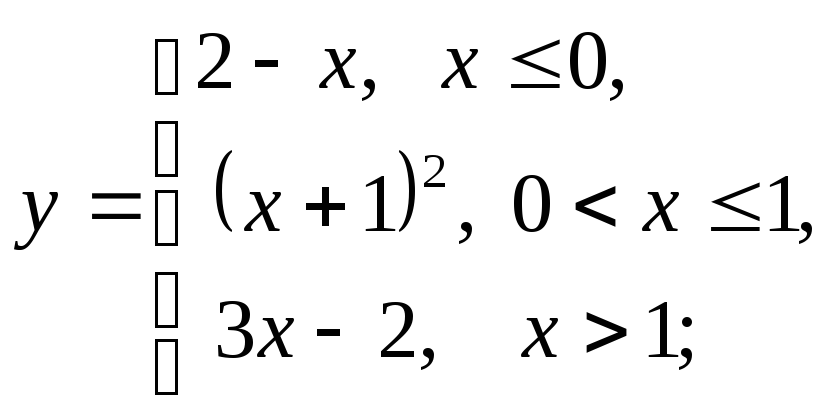 в)
в)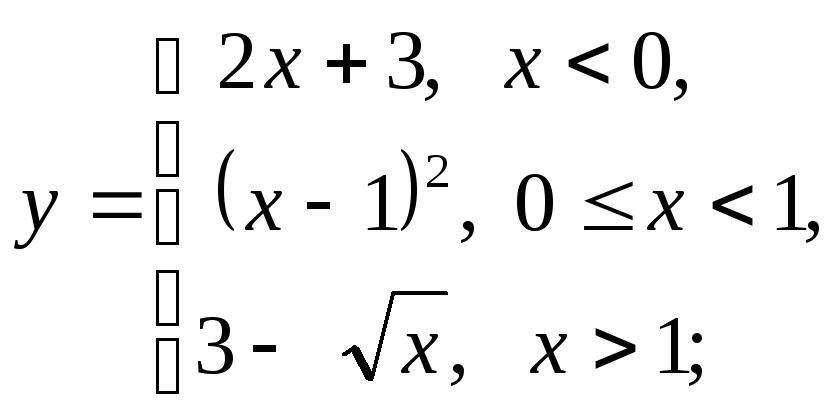
г)
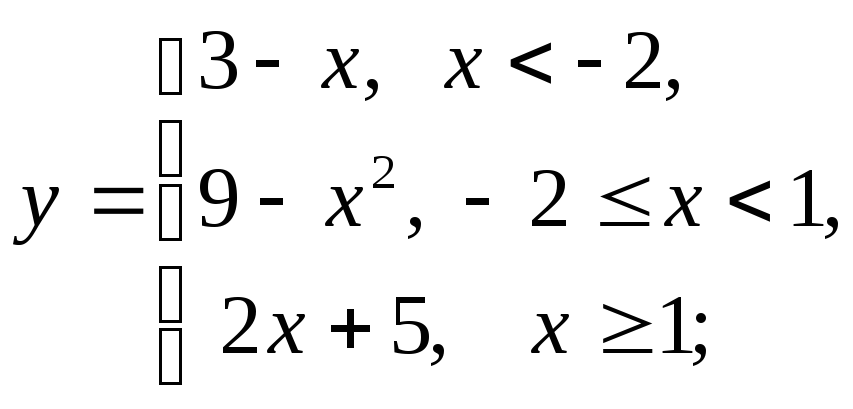 д)
д)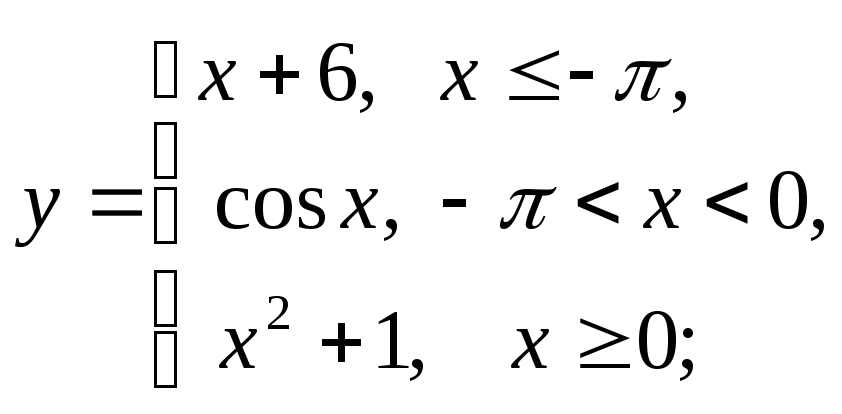 е)
е)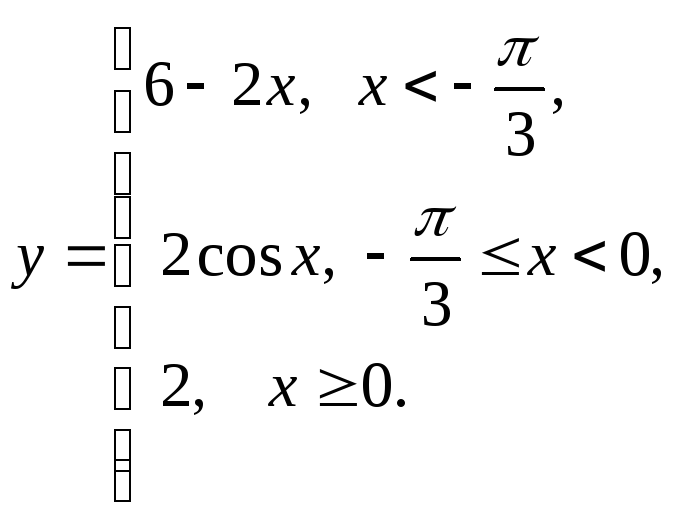
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
|
0 / 0 / 0 Регистрация: 12.11.2018 Сообщений: 4 |
|
|
1 |
|
Найти предел кусочной функции19.11.2018, 10:44. Показов 3498. Ответов 5
Прошу помощи в поиску предела кусочной функции в MathCad. Миниатюры
0 |
|
8701 / 6308 / 3384 Регистрация: 14.01.2014 Сообщений: 14,473 |
|
|
19.11.2018, 10:55 |
2 |
|
У меня то же самое, видимо Mathcad не любит кусочно заданные функции.
1 |
|
6630 / 4733 / 1975 Регистрация: 02.02.2014 Сообщений: 12,683 |
|
|
19.11.2018, 11:38 |
3 |
|
mathcad prime тоже морщится…
1 |
|
0 / 0 / 0 Регистрация: 12.11.2018 Сообщений: 4 |
|
|
20.11.2018, 00:03 [ТС] |
4 |
|
MathCad не может искать предел функции заданной с помощью элементов панели программирование.
0 |
|
6630 / 4733 / 1975 Регистрация: 02.02.2014 Сообщений: 12,683 |
|
|
20.11.2018, 01:22 |
5 |
|
Решение
функции заданной с помощью элементов панели программирование. дело не в панели программирования, а в условно-“кусочности” функции Кликните здесь для просмотра всего текста
1 |
|
0 / 0 / 0 Регистрация: 12.11.2018 Сообщений: 4 |
|
|
20.11.2018, 09:53 [ТС] |
6 |
|
Благодарю за данное уточнение.
0 |
-
Функция
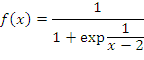
определена на всей числовой оси за исключением точки x = 2, которая является точкой разрыва этой функции.
Найдем односторонние пределы
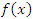 в этой точке.
в этой точке.
Если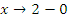 , то
, то
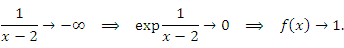
Если
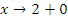 , то
, то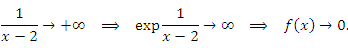
Функция претерпевает скачок на конечную величину и, следовательно, x = 2 является точкой разрыва первого рода.
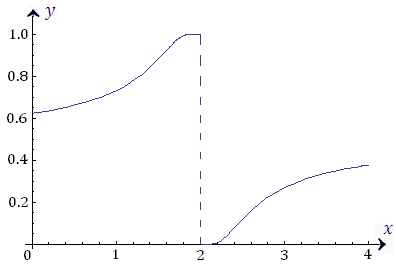
Рис. 17. График функции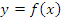 в окрестности точки x = 2.
в окрестности точки x = 2.
***
-
Непрерывность функции
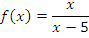
нарушается в точке x = 5.
Эта точка является точкой разрыва второго рода, поскольку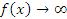 при x → 5.
при x → 5.
***
-
Рассмотрим кусочно-заданную функцию

Поскольку функции
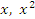 определены на всей числовой оси, то непрерывность функции
определены на всей числовой оси, то непрерывность функции 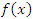 может нарушаться только в точках “сшивания” x = 0 и x = 1.
может нарушаться только в точках “сшивания” x = 0 и x = 1.
В точке x = 0 функция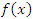 непрерывна, поскольку односторонние пределы совпадают между собой и со значением функции в нуле:
непрерывна, поскольку односторонние пределы совпадают между собой и со значением функции в нуле: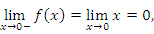
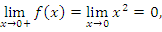
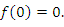
Найдем односторонние пределы в точке x = 1:
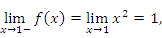
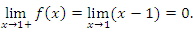
Конечное значение скачка функции
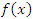 означает, что x = 1 является точкой разрыва первого рода.
означает, что x = 1 является точкой разрыва первого рода.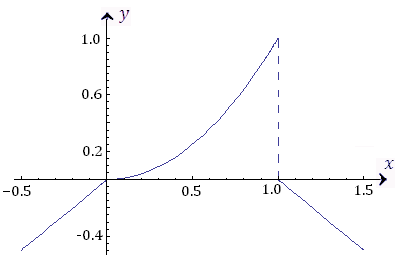
Рис. 18. График кусочно-заданной функции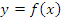 .
.
Мы определим сейчас некоторый класс функций, которым часто пользуются в теоретических исследованиях.
Определение. Функция  определенная на измеримом множестве
определенная на измеримом множестве  , называется кусочно-постоянной на этом множестве, если она принимает на g лишь конечное или счетное множество значений.
, называется кусочно-постоянной на этом множестве, если она принимает на g лишь конечное или счетное множество значений.
Пусть  различные значения, принимаемые функцией
различные значения, принимаемые функцией  на g, причем среди этих значений могут быть значения
на g, причем среди этих значений могут быть значения
 . Для измеримости
. Для измеримости  очевидно, необходимо и достаточно, чтобы множества точек
очевидно, необходимо и достаточно, чтобы множества точек  на которых
на которых  равно
равно  были при всех k измеримыми [42]. В дальнейшем мы будем рассматривать только измеримые кусочно-постоянные функции.
были при всех k измеримыми [42]. В дальнейшем мы будем рассматривать только измеримые кусочно-постоянные функции.
Введем новое понятие. Если g — некоторое множество точек, то характеристической функцией этого множества назовем такую функцию  определенную на всей плоскости, что
определенную на всей плоскости, что  если Р принадлежит
если Р принадлежит  если Р не принадлежит §. Кусочно-постоянная функция
если Р не принадлежит §. Кусочно-постоянная функция  есть линейная комбинация характеристических функций:
есть линейная комбинация характеристических функций:

причем Р принадлежит  . Поскольку
. Поскольку  не имеют общих точек
не имеют общих точек  различные числа) в написанной сумме только одно слагаемое отлично от нуля, кроме случая, когда
различные числа) в написанной сумме только одно слагаемое отлично от нуля, кроме случая, когда  соответствующее выбранной точке
соответствующее выбранной точке  равно нулю. В последнем случае все слагаемые равны нулю.
равно нулю. В последнем случае все слагаемые равны нулю.
Характеристическая функция  измерима, очевидно, в том и только в том случае, если
измерима, очевидно, в том и только в том случае, если  — измеримое множество.
— измеримое множество.
Мы покажем сейчас возможность получения измеримых функций как пределов кусочно-постоянных функций. Мы ограничимся при этом случаем неотрицательных функций.
Теорема 1. Для всякой неотрицательной ограниченной и измеримой на измеримом множестве  функции существует возрастающая последовательность
функции существует возрастающая последовательность  неотрицательных измеримых кусочно-постоянных на
неотрицательных измеримых кусочно-постоянных на  функций с конечным числом значений, которая равномерно на
функций с конечным числом значений, которая равномерно на  стремится к
стремится к  в каждой точке
в каждой точке  .
.
В силу ограниченности  имеется такое положительное число L, что
имеется такое положительное число L, что  Промежуток
Промежуток  делим на
делим на  равных частей точками
равных частей точками

Введем в рассмотрение измеримые множества

и построим последовательность функций  следующим образом:
следующим образом:

Нетрудно проверить, что последовательность  удовлетворяет всем требованиям теоремы. Каждая из функций
удовлетворяет всем требованиям теоремы. Каждая из функций  принимает на
принимает на  конечное число значений. Далее при переходе от
конечное число значений. Далее при переходе от  к
к  каждый промежуток
каждый промежуток

разобьется на два:

и

и тем самым каждое из множеств  разобьется на два множества:
разобьется на два множества:

На множестве  функция
функция  равна тому же числу
равна тому же числу  , что и функция
, что и функция  на всем множестве
на всем множестве  , а на множестве
, а на множестве  функция
функция  равна
равна

и, следовательно, последовательность функций  есть возрастающая последовательность. Далее, на любом множестве имеем
есть возрастающая последовательность. Далее, на любом множестве имеем

и

Тем самым

во всех точках  , принадлежащих g, откуда и следует, что последовательность
, принадлежащих g, откуда и следует, что последовательность  стремится к
стремится к  равномерно на g. В следующей теореме мы рассмотрим тот случай, когда
равномерно на g. В следующей теореме мы рассмотрим тот случай, когда  может быть неограниченной.
может быть неограниченной.
Теорема 2. Для всякой неотрицательной, принимающей конечные значения и измеримой на множестве g, функции  существует возрастающая последовательность
существует возрастающая последовательность  неотрицательных кусочно-постоянных на g функций, которая равномерно на g стремится к
неотрицательных кусочно-постоянных на g функций, которая равномерно на g стремится к 
В данном случае делим на части бесконечный промежуток  при помощи точек
при помощи точек

Определяем опять множества  и функции
и функции


 Сообщение было отмечено Taigar как решение
Сообщение было отмечено Taigar как решение

