Как найти предел от косинуса - Сайт, где вы сможете решить свои вопросы

Уважаемые студенты!
Заказать решение задач можно у нас всего за 10 минут.

Как решать пределы с синусами и косинусами?

Чтобы решать пределы с синусами и косинусами необходимо уметь выполнять элементарные преобразования под первый замечательный предел, а также знать основные тригонометрические формулы. Так же применимо правило Лопиталя для вычисления с помощью производной. Рассмотрим примеры решений.

Пример 1

Вычислить предел с синусом $ lim_{x to 0} frac{5x}{sin 7x} $

Решение

Воспользуемся формулой первого замечательного предела $$ lim_{x to 0} frac{sin x}{x} = 1 $$ Подстраиваем дробь под знаком предела путем элементарных преобразований. Одновременно умножаем и делим на 7 числитель со знаменателем: $$ lim_{xto 0} frac{7 cdot 5x}{7sin 7x} = $$

Выносим множители из числителя и знаменателя за знак предела $$ = frac{5}{7} lim_{xto 0} frac{7x}{sin 7x} = $$ Переворачиваем подпредельную дробь под вид общей формулы первого замечательного предела $$ = frac{5}{7} lim_{x to 0} frac{1}{frac{sin 7x}{7x}} = frac{5}{7} cdot 1 = frac{5}{7} $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ lim_{xto 0} frac{5x}{sin 7x} = frac{5}{7} $$

Пример 2

Решить пределы с косинусом $ lim_{xto 0} frac{cos 3x – cos x}{x^2} $

Решение

Используем тригонометрическую формулу разности косинусов: $$ cos alpha – cos beta = -2 sin frac{alpha – beta}{2} sin frac{alpha + beta}{2} $$

Выполняем преобразование разности косинусов в произведение синусов $$ cos 3x – cos x = -2 sin frac{3x-x}{2} sin frac{3x+x}{2} = -2 sin x sin 2x $$ Записываем предел с новым числителем $$ lim_{xto 0} frac{-2 sin x sin 2x}{x^2} = $$

Разбиваем предел на два, чтобы воспользоваться первым замечательным пределом: $$ = -2lim_{xto 0} frac{sin x}{x} cdot lim_{xto 0} frac{sin 2x}{x} = $$ Первый предел равен единице, поэтому остаётся разобраться со вторым. Подгоним его под формулу замечательного предела путем домножения числителя и знаменателя на число равное аргументу синуса $$ = -2 lim_{xto 0} frac{sin 2x}{x} = -4 lim_{xto 0} frac{sin 2x}{2x} = -4 $$

Ответ

$$ lim_{xto 0} frac{cos 3x – cos x}{x^2} = -4 $$

Пример 3

Взять предел с косинусом $ lim_{xto 0} frac{1-cos x}{x^2} $

Решение

В данном случае целесообразно прибегнуть к таблице эквивалентных элементарных функций, а именно $$ 1- cos x = frac{x^2}{2} $$

Подставляем в предел и получаем $$ lim_{x to 0} frac{1-cos x}{x^2} = lim_{x to 0} frac{x^2}{2x^2} $$ Осталось выполнить сокращение числителя на знаменатель, чтобы записать ответ $$ lim_{x to 0} frac{x^2}{2x^2} = frac{1}{2} $$

Ответ

$$ lim_{x to 0} frac{x^2}{2x^2} = frac{1}{2} $$

Источник

Простое объяснение принципов решения пределов тригонометрических функций и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения пределов тригонометрических функций

Для тригонометрических функций существует много разных пределов, но как правило, все они вычисляются, опираясь на первый замечательный предел и его следствия.

Первый замечательный предел выглядит следующим образом:

$[lim_{xrightarrow 0}frac{sinx}{x}=1]$

Следствия первого замечательного предела

Главным следствием первого замечательного предела считают:

$[lim_{xrightarrow 0}frac{tgx}{x}=1]$

Также следствиями являются:

$[lim_{xrightarrow 0}frac{1 - cosx}{x^2}=1]$

$[lim_{xrightarrow 0}frac{arcsinx}{x}=1]$

$[lim_{xrightarrow 0}frac{arctgx}{x}=1]$

Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Цена работы

Примеры решения пределов тригонометрических функций

Задание

Найти предел функции:

$[lim_{xrightarrow 0}frac{sin(10x)}{3x}=]$

Решение

Заменим значение х на число, к которому стремится функция:

$[lim_{xrightarrow 0}frac{sin(10x)}{3x}=begin{bmatrix}0\0end{bmatrix}=?]$

Так как мы пришли на неопределённость вида 0/0, преобразуем синус так, чтобы он стал вида первого замечательного предела:

$[lim_{xrightarrow 0}frac{frac{sin(10x)}{10x}cdot 10x}{3x}=lim_{xrightarrow 0}frac{frac{sin(10x)}{10x}cdot 10}{3}]$

Мы знаем, что первый замечательный предел равен единице, следовательно

$[lim_{xrightarrow 0}frac{sin(10x)}{10x}=1]$

Таким образом найдём предел функции:

$[lim_{xrightarrow 0}frac{frac{sin(10x)}{10x}cdot 10}{3}=frac{1cdot 10}{3}=frac{10}{3}]$

Задание

Найти предел функции:

$[lim_{xrightarrow 0}frac{3x^2-5x}{sin3x}=]$

Решение

При замене х на число, к которому он стремится, снова получаем неопределённость

$[lim_{xrightarrow 0}frac{3x^2-5x}{sin3x}=begin{bmatrix}frac{0}{0}end{bmatrix}]$

Данную задачу можно решить, применив правило Лопиталя.

Найдём производные числителя и знаменателя функции и решим задачу:

$[lim_{xrightarrow 0}frac{6x-5}{3cos3x}=frac{0-5}{3cdot 1}=-frac{5}{3}]$

Задание

Найти предел функции:

$[lim_{xrightarrow 0}frac{1-cos2x}{4x^2}]$

Решение

При подстановке нуля получим неопределённость типа 0/0:

$[lim_{xrightarrow 0}frac{1-cos2x}{4x^2}=frac{1-1}{0}=frac{0}{0}]$

Воспользуемся свойством

$[frac{1-cost}{2}=sin^2left(frac{t}{2} right)]$

Преобразуем функцию и упростим её:

$[lim_{xrightarrow 0}frac{1-cos2x}{4x^2}=lim_{xrightarrow 0}frac{frac{2cdot (1-cos2x)}{2}}{4x^2}=lim_{xrightarrow 0}frac{2sin^2x}{4x^2}=lim_{xrightarrow 0}frac{sin^2x}{2x^2}]$

Вынесем константу ½ за лимит и, пользуюсь свойством первого замечательного предела, найдём передел данной функции:

$[lim_{xrightarrow 0}frac{sin^2x}{2x^2}=frac{1}{2}lim_{xrightarrow 0}left(frac{sinx}{x} right)^2=frac{1}{2}cdot 1^2=frac{1}{2}cdot 1=frac{1}{2}]$

Задание

Найти предел функции:

$[lim_{xrightarrow 0}frac{sin7x}{x^2+pi x}=]$

Решение

Если заменить x на число, придём к неопределённости 0/0:

$[lim_{xrightarrow 0}frac{sin7x}{x^2+pi x}=left[ frac{0}{0}right]]$

Для решения данного примера применим правило Лопиталя и заменим х на число в производных:

$[lim_{xrightarrow 0}frac{7cos7x}{2x+pi}=left[ frac{7cos0}{2 cdot0 + pi } =frac{7cdot 1}{pi }right]=frac{7}{pi}]$

Задание

Вычислить предел функции:

$[lim_{xrightarrow 0}frac{cosx-cos5x}{2x^2}=]$

Решение

Для решения данного примера воспользуемся свойством разности косинусов:

$[cosalpha -cosbeta =-2cdot sinfrac{alpha +beta }{2}cdot sinfrac{alpha -beta }{2}]$

и получим

$[lim_{xrightarrow 0}frac{-2cdot sin3xcdot sin2x}{2x^2}=]$

Вынесем минус за лимит, дабы не потерять и продолжим решение. Для решения задачи приведём функцию к виду первого замечательного предела. Для этого нужно разделить дробь на множители и добавить в знаменатель коэффициент, равный коэффициенту в числителе. А потом упростим выражение:

$[-lim_{xrightarrow 0}frac{sin3x}{x}cdot frac{sin2x}{x}=-lim_{xrightarrow 0}frac{sin3x}{frac{3x}{3}}cdot frac{sin2x}{frac{2x}{2}}=-lim_{xrightarrow 0}frac{3sin3x}{3x}cdot frac{2sin2x}{2x}=]$

Снова вынесем константы за лимит и получим вид первого замечательного предела, с помощью которого приходим к искомому решению:

$[-6lim_{xrightarrow 0}frac{sin3x}{3x}cdot frac{sin2x}{2x}=-6cdot 1cdot 1=-6]$

Задание

Вычислить предел функции:

$[lim_{xrightarrow 0}frac{sinx-tgx}{x^3}=]$

Решение

При подстановке х снова получаем неопределённость

$[lim_{xrightarrow 0}frac{sinx-tgx}{x^3}=left[ frac{0}{0} right]]$

Значит будем искать передел путём приведения к виду первого замечательного предела.

Представим тангенс в виде частного синуса х и косинуса х

$[lim_{xrightarrow 0}frac{sinx-tgx}{x^3}=lim_{xrightarrow 0}frac{sinx-frac{sinx}{cosx}}{x^3}=lim_{xrightarrow 0}frac{sinx(1-frac{1}{cosx})}{x^3}=]$

Приведём к общему знаменателю и разделим выражение на множители следующим образом:

$[lim_{xrightarrow 0}frac{sinx(1-frac{1}{cosx})}{x^3}=lim_{xrightarrow 0}frac{sinx}{x}cdot lim_{xrightarrow 0}frac{1-frac{1}{cosx}}{x^2}]$

Мы видим первый замечательный предел, а значит, можем упростить до:

$[lim_{xrightarrow 0}frac{sinx}{x}=1]$

Далее снова приведём числитель к общему знаменателю:

$[lim_{xrightarrow 0}frac{1-frac{1}{cosx}}{x^2}=lim_{xrightarrow 0}frac{frac{cosx-1}{cosx}}{x^2}=lim_{xrightarrow 0}frac{cosx-1}{x^2cdot cosx}=]$

Вновь разделим на множители и подставим значение х во второй косинус:

$[lim_{xrightarrow 0}frac{cosx-1}{x^2}cdot lim_{xrightarrow 0}frac{1}{cosx}=lim_{xrightarrow 0}frac{cosx-1}{x^2}cdot 1=]$

Таким образом нам остаётся разобраться с первым числителем. Поменяем местами 1 и косинус и вынесем минус за лимит.

Далее воспользуемся формулой понижения степени и найдём решение:

$[-lim_{xrightarrow 0}frac{1-cosx}{x^2}=-lim_{xrightarrow 0}frac{2sin^2frac{x}{2}}{x^2}=-lim_{xrightarrow 0}2cdot left( frac{sinfrac{x}{2}}{x}right)^2=-2lim_{xrightarrow 0}left( frac{sinfrac{x}{2}}{frac{2x}{2}}right)^2=-frac{1}{2}cdot 1^2=-frac{1}{2}]$

Задание

Вычислить предел функции:

$[lim_{xrightarrow 0}frac{sin3x}{tg2x}]$

Решение

При простом вычислении получаем неопределённость

$[lim_{xrightarrow 0}frac{sin3x}{tg2x}=left[frac{0}{0} right ]]$

Следовательно, будем вычислять предел, опираясь на правило первого замечательного предела. Приведём тангенс к виду частного синуса и косинуса:

$[lim_{xrightarrow 0}frac{sin3x}{tg2x}=lim_{xrightarrow 0}frac{sin3x}{frac{sin2x}{cos2x}}=lim_{xrightarrow 0}frac{sin3x cdot cos2x}{sin2x}=]$

Разделим пример на множители.

Приведём синусы к виду первого замечательного предела и получим ответ:

$[lim_{xrightarrow 0}frac{sin3x}{sin2x}cdot lim_{xrightarrow 0}cos2x=lim_{xrightarrow 0}frac{frac{3xcdot sin3x}{3x}}{frac{2xcdot sin2x}{2x}}cdot 1=lim_{xrightarrow 0}frac{3x}{2x}cdot frac{frac{sin3x}{3x}}{frac{sin2x}{2x}}=frac{3}{2}cdotfrac{1}{1}=frac{3}{2}]$

Задание

Найти предел функции:

$[lim_{xrightarrow 0}frac{sin^2x-tg^2x}{x^4}=]$

Решение

При подставлении числа на место х приходим к неопределённости типа 0/0:

$[lim_{xrightarrow 0}frac{sin^2x-tg^2x}{x^4}=left[frac{0}{0} right ]]$

Преобразуем tg, приведем выражение к общему знаменателю cos x, вынесем общий множитель – sin x за скобку:

$[lim_{xrightarrow 0}frac{sin^2x-tg^2x}{x^4}=lim_{xrightarrow 0}frac{sin^2x-frac{sin^2x}{cos^2x}}{x^4}=lim_{xrightarrow 0}frac{frac{sin^2xcdot cos^2x-sin^2x}{cos^2x}}{x^4}=]$

$[= lim_{xrightarrow 0}frac{frac{-sin^2x(1-cos^2x)}{cos^2x}}{x^4}=]$

Используя следствие из первого замечательного предела, преобразим выражение и избавимся от тангенса.

Затем вновь приведем функцию к следствию первого замечательного предела и найдем ответ:

$[lim_{xrightarrow 0}frac{-tg^2x}{x^2}cdot frac{frac{1-cos^2x}{cos^2x}}{x^2}=lim_{xrightarrow 0}- left(frac{tgx}{x} right)^2cdot frac{frac{sin^2x}{cos^2x}}{x^2}=]$

$[= lim_{xrightarrow 0} left(-1^2 cdot frac{tg^2x}{x^2} right)=lim_{xrightarrow 0}left(-left(frac{tgx}{x} right)^2 right)=lim_{xrightarrow 0}left(-left(1 right )^2 right )=-1]$

Задание

Найти предел функции:

$[lim_{xrightarrow 0} left(1-x right) cdot tgfrac{pi x}{2}]$

Решение

При подстановке числа видим неопределённость.

$[lim_{xrightarrow 0} left(1-x right) cdot tgfrac{pi x}{2}=left[ 0 cdot infty right ]]$

Следовательно, искать предел будем, опираясь на правило первого замечательного предела. Для этого заменим переменную, которая будет стремиться к нулю:

Подставим в функцию:

$[lim_{trightarrow 0}tcdot tgfrac{pileft(1-t right)}{2}=lim_{trightarrow 0}t cdot tg left(frac{pi}{2}-frac{pi t}{2} right)=]$

Опираясь на свойства тригонометрии, заменим тангенс.

$[lim_{trightarrow 0}t cdot tg left(frac{pi}{2}-frac{pi t}{2} right)=lim_{trightarrow 0}t cdot ctg left(frac{pi t}{2} right)=lim_{trightarrow 0}frac{t cdot cos left(frac{pi t}{2} right )}{sin left(frac{pi t}{2} right )}=]$

Зная, что предел косинуса нуля = 1, преобразуем пример и приведём к виду первого замечательного предела.

Найдём ответ.

$[lim_{trightarrow 0}frac{t cdot cos left(frac{pi t}{2} right )}{sin left(frac{pi t}{2} right )}=lim_{trightarrow 0}frac{t cdot 1 cdot frac{pi}{2} cdot frac{2}{pi}}{sin left(frac{pi t}{2} right )}=frac{2}{pi}lim_{trightarrow 0}left(frac{sinleft(frac{pi t}{2} right )}{frac{pi t}{2}} right )^{-1}=frac{2}{pi} cdot left(1 right )^{-1}=frac{2}{pi}]$

Задание

Вычислить предел функции:

$[lim_{trightarrow 0}frac{arcsin3x}{2x}=]$

Решение

Здесь так же получим неопределённость:

$[lim_{trightarrow 0}frac{arcsin3x}{2x}=left[frac{0}{0} right ]]$

Значит, введём новую переменную t:

$[x=frac{1}{3}sint]$

Подставим получившиеся значения в пример и найдём предел:

$[lim_{trightarrow 0}frac{t}{2 cdot sin3x}=lim_{trightarrow 0}frac{t}{2 cdot frac{1}{3}sint}=frac{3}{2}lim_{trightarrow 0}left( frac{sint}{t}right )^{-1}=frac{3}{2}]$

Источник

Определение непрерывности функции в точке и передела функции на бесконечности и на использовании свойств предела непрерывной функции способствует непосредственному вычислению пределов.

Определение 1

Значение предела в точке непрерывности определено значением функции в этой точке.

При опоре на свойства основные элементарные функции имеют предел в любой точке из области определения, вычисляется как значение соответствующей функции в этих точках.

Пример 1

Произвести вычисление предела функции limx→5arctg35·x

Решение

Функция арктангенса отличается непрерывностью на всей своей области определения. Отсюда получим, что в точке x0=5 функция является непрерывной. Из определения имеем, что для нахождения предела является значением этой же функции. Тогда необходимо произвести подстановку. Получим, что

limx→5arctg35·x=arctg35·5=arctg3=π3

Ответ: π3.

Для вычисления односторонних пределов необходимо использовать значения точек границ предела. У акрксинуса и акрккосинуса имеются такие значения x0=-1 или x0=1.

При x→+∞ или x→-∞ вычисляются пределы функции, заданные на бесконечностях.

Для упрощения выражений применяют свойства пределов:

Определение 2

limx→x0(k·f(x))=k·limx→x0f(x), k является коэффициентом.
limx→x0(f(x)·g(x))=limx→x0f(x)·limx→x0g(x), применяемое при получении неопределенности предела.
limx→x0(f(g(x)))=flimx→x0gx,используемое для непрерывных функций, где знак функции и предельного перехода можно менять местами.

Для того, чтобы научиться вычислять переделы, необходимо знать и разбираться в основных элементарных функциях. Ниже приведена таблица, в которой имеются переделы этих функций с приведенными разъяснениями и подробным решением. Для вычисления необходимо основываться на определении предела функции в точке и на бесконечности.

Таблица пределов функции

Для упрощения и решения пределов используется данная таблица основных пределов.

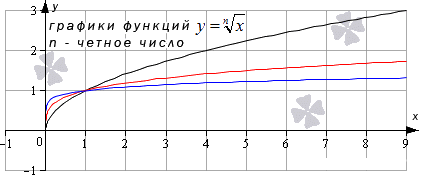
Функция корень n-ой степени

y=xn, где n=2, 4, 6 …

limx→∞xn=+∞n=+∞

Для любых x0 из опрелеления

limx→x0xn=x0n

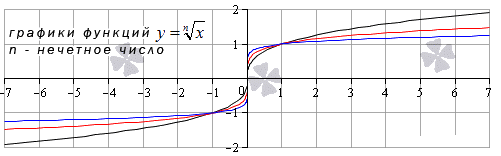
Функция корень n-ой степени

y=xn, где n=3, 5, 7 …

limx→∞xn=+∞n=+∞limx→∞xn=-∞n=-∞

limx→x0xn=x0n

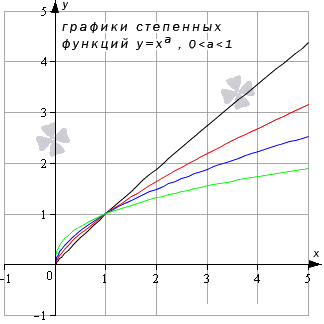
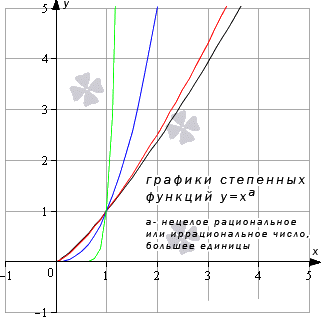
Степенная функция y=xa , a>0

Для любого положительного числа a
limx→∞xa=+∞a=+∞
Если a=2, 4, 6 …, то
limx→∞xa=-∞a=+∞
Если a=1, 3, 5, …, то
limx→∞xa=-∞a=-∞
Для любых x0, из области определния
limx→x0xa=(x0)a

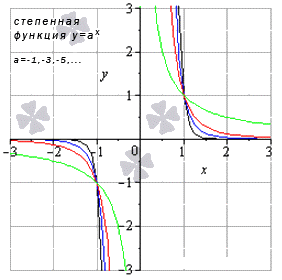
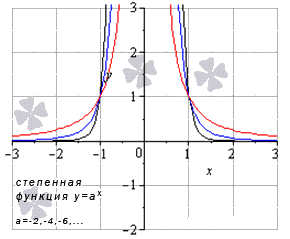
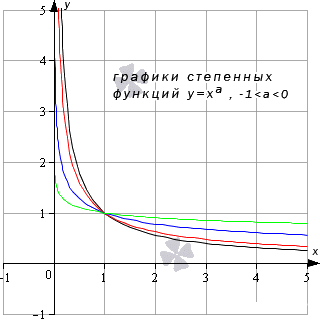
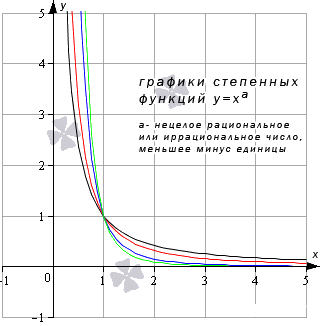
Степенная функция y=xa, a<0

Для любого отрицательного числа a
limx→∞xa=(+∞)a=+0limx→0+0=(0+0)a=+∞
Если a=-2, -4, -4, …, то
limx→∞xa=-∞a=+0limx→0-0xa=(0-0)a=+∞
Если a=-1, -3, -5, …, то
limx→∞xa=-∞a=-0limx→0-0xa=(0-0)a=-∞
Для любых x0 из области определения
limx→x0xa=(x0)a

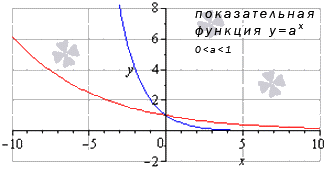
Показательная функия

y=ax, 0<a<1

limx→∞ax=a-∞=+∞limx→∞ax=a+∞=+0

Для любых x0 из области опреления limx→x0ax=ax0

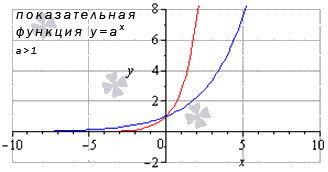
Показательная функия

y=ax, a>1limx→∞ax=a-∞=+0limx→x0ax=a+∞=+∞

Для любых знвчений x0 из област опредения limx→x0ax=ax0

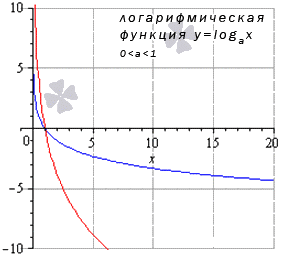
Логарифмическая функция

y=loga(x), 0<a<1

limx→0+0logax=loga(0+0)=+∞limx→∞logax=loga(+∞)=-∞

Для любых x0 из области опрелеленияlimx→x0logax=logax0

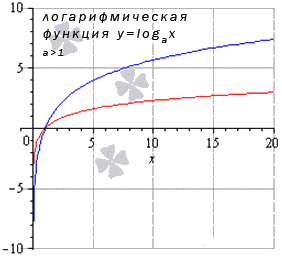
Логарифмическая функция

y=loga(x), a>1

limx→0+0logax=loga(0+0)=-∞limx→∞logax=loga(+∞)=+∞

Для любых x0 из области опрелеления

limx→x0logax=logax0

Тригонометрические функции

Синус
limx→∞ sin x не существует
Для любых x0 из области опрелеления
limx→x0sin x=sin x0
Тангненсlimx→π2-0+π·ktg x=tgπ2-0+π·k=+∞limx→π2+0+π·ktg x=tgπ2+0+π·k=-∞

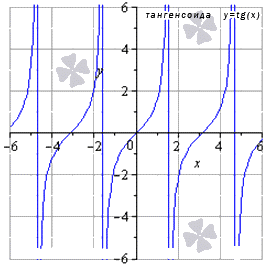
limx→∞tg x не существует

Для любых x0 из области опрелеления

limx→x0tg x=tg x0

Тригонометрические функции

Косинус
limx→∞cos x не существует
Для любых x0 из области опрелеления
limx→x0cos x=cos x0
Котангенсlimx→-0+π·kctg x=ctg(-0+π·k)=-∞limx→+0+π·kctg x=ctg(+0+π·k)=+∞

limx→∞ctg x не существует

Для любых x0 из области опрелеления
limx→x0сtg x=сtg x0

Обратные тригонометрические функции

Арксинус
limx→-1+0arcsin x=-π2limx→1-0arcsin x=π2

Для любых x0 из области опрелеления

limx→x0arcsin x=arcsin x0

Арккосинус
limx→-1+0arccos (x)=πlimx→1-0arccos (x)=0

Для любых x0 из области опрелеления

limx→x0arccis x=arccos x0

Обратные тригонометрические функции

Арктангес
limx→-∞ arctg (x)=-π2limx→+∞ arctg (x)=π2

Для любых x0 из области опрелеления

limx→x0arctg x=arctg x0

Арккотангенс
limx→-∞arcctg (x)=πlimx→+∞arcctg (x)=0

Для любых x0 из области опрелеления

limx→x0arcctg x=arcctg x0

Пример 2

Произвести вычисление предела limx→1×3+3x-1×5+3.

Решение

Для решения необходимо подставить значение х=1. Получаем, что

limx→1×3+3x-1×5+3=13+3·1-115+3=34=32

Ответ: limx→1×3+3x-1×5+3=32

Пример 3

Произвести вычисление предела функции limx→0(x2+2,5)1×2

Решение

Для того, чтобы раскрыть предел, необходимо подставить значение х, к которому стремится предел функции. В данном случае нужно произвести подстановку х=0. Подставляем числовое значение и получаем:

x2+2.5x=0=02+2.5=2.5

Предел записывается в виде limx→0(x2+2.5)1×2=limx→02.51×2. Далее необходимо заняться значением показателя. Он является степенной функцией 1×2=x-2. В таблице пределов, предоставленной выше, имеем, что limx→0+01×2=limx→0+0x-2=+∞ и limx→0+01×2=limx→0+0x-2=+∞, значит, имеем право записать как limx→01×2=limx→0x-2=+∞

Теперь вычислим предел. Получит вид limx→0(x2+2.5)1×2=limx→02.51×2=2.5+∞

По таблице пределов с показательными функциями, имеющими основание больше 1 получаем, что

limx→0(x2+2.5)1×2=limx→02.51×22.5+∞=+∞

Ответ: limx→0(x2+2.5)1×2=+∞

Когда задан более сложный предел, то при помощи таблицы не всегда получится получать целое или конкретное значение. Чаще получаются разные виды неопределенностей, для разрешения которых необходимо применять правила.

Рассмотрим графическое разъяснение приведенной выше таблицы пределов основных элементарных функций.

Предел константы

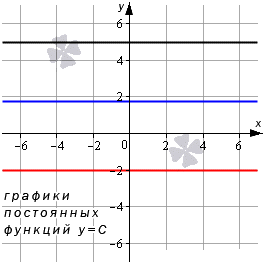
Из рисунка видно, что функция у=С имеет предел на бесконечности. Такой же предел при аргументе, который стремится к х0. Он равняется числу C.

Предел функции корень n-ой степени

Четные показатели корня применимы для limx→+∞xn=+∞n=+∞, а нечетные, равные больше, чем значение 1, – для limx→+∞xn=+∞n=+∞, limx→-∞xn=-∞n=-∞. Область определения может принимать абсолютно любое значение х предела заданной функции корня n-ой степени, равного значению функции в заданной точке.

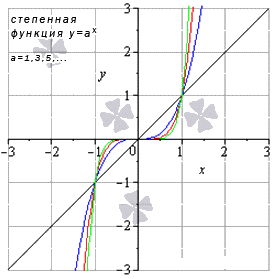
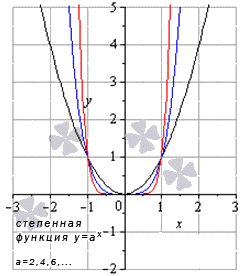
Предел степенной функции

Необходимо разделить все степенные функции по группам, где имеются одинаковые значения пределов, исходя из показателя степени.

Когда a является положительным числом, тогда limx→+∞xa=+∞a=+∞ и limx→-∞xa=-∞a=-∞. Когда x принимает любое значение, тогда предел степенной функции равняется значению функции в точке. Иначе это записывается как limx→∞xa=(∞)a=∞.

Когда a является положительным четным числом, тогда получаем limx→+∞xa=(+∞)a=+∞ и limx→-∞xa=(-∞)a=+∞, причем x из данной области определения является пределом степенной функции и равняется значением функции в этой точке. Предел имеет вид limx→∞xa=∞a=+∞.

Когда a имеет другие значения, тогда limx→+∞xa=(+∞)a=+∞, а область определения x способствует определению предела функции в заданной точке.

Когда a имеет значение отрицательных чисел, тогда получаем limx→+∞xa=+∞a=+0, limx→-∞xa=(-∞)a=-0, limx→0-0xa=(0-0)a=-∞,limx→0+0xa=0+0a=+∞, а значения x может быть любым из заданной области определения и равняется функции в заданной точке. Получаем, что limx→∞xa=∞a=0 иlimx→0xa=0a=∞.

Когда a является отрицательным четным числом, тогда получаем limx→+∞xa=(+∞)a=+0, limx→-∞xa=-∞a=+0, limx→0-0(0-0)a=+∞, limx→0+0xa=(0+0)a=+∞, а любое значение x на области определения дает результат предела степенной функции равным значению функции в точке. Запишем как limx→∞xa=(∞)a=+0 и limx→0xa=(0)a=+∞.

Когда значение a имеет другие действительные отрицательные числа, тогда получим limx→+∞xa=+∞a=+0 и limx→0+0xa=0+0a=+∞, когда x принимает любое значение из своей области определения, тогда предел степенной функции равняется значению функции в этой точке.

Предел показательной функции

Когда 0<a<1, имеем, что limx→-∞ax=a-∞=+∞, limx→+∞ax=(a)+∞=+∞, любое значение x из области определения дает пределу показательной функции значению функции в точке.

Когда a>1, тогда limx→-∞ax=(a)-∞=+0, limx→+∞ax=(a)+∞=+∞, а любое значение x из области определения дает предел функции равный значению этой функции в точке.

Предел логарифмической функции

Когда имеем 0<a<1, тогда limx→0+0logax=loga(0+0)=+∞, limx→+∞logax=loga(+∞)=-∞ , для всех остальных значений x из заданной области определения предел показательной функции равняется значению заданной функции в точках.

Когда a>1, получаем limx→0+0logax=loga(0+0)=-∞, limx→+∞logax=loga(+∞)=+∞,остальные значения x в заданной области определения дают решение предела показательной функции равному ее значению в точках.

Предел тригонометрических функций

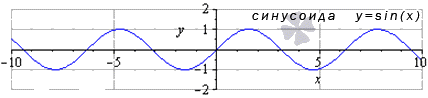
Предел бесконечности не существует для таких функций как y=sin x, y=cos x. Любое значение x, входящее в область определения, равняется значению функции в точке.

Функция тангенса имеет предел вида limx→π2-0+π·ktg(x)=+∞, limx→π2+π·ktg(x)=∞ или limx→π2+π·ktg(x)=∞, тогда остальные значения x, принадлежащие области определения тангенса, равняется значению функции в этих точках.

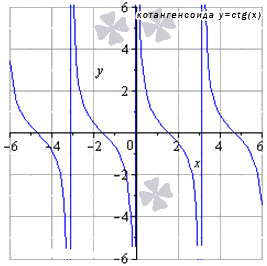
Для функции y=ctg x получаем limx→-0+π·kctg(x)=-∞, limx→+0+π·kctg(x)=+∞ или limx→π·kctg (x)=∞, тогда остальные значения x, принадлежащие области определения, дают предел котангенса, равный значению функции в этих точках.

Предел обратных тригонометрических функций

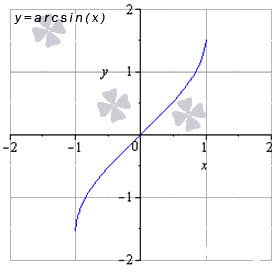
Функция арксинус имеет предел вида limx→-1+0arcsin(x)=-π2 и limx→1-0arcsin (x)=π2, остальные значения x из области определения равняются значению функции в заданной точке.

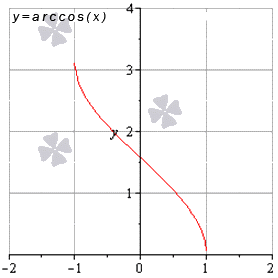
Функция арккосинус имеет предел вида limx→-1+0arccos(x)=π и limx→1-0arccos(x)=0, когда остальные значения x, принадлежащие области определения, имеют предел арккосинуса, равного значению функции в этой точке.

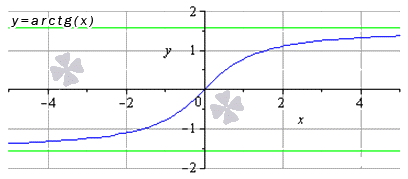
Функция арктангенс имеет предел вида limx→-∞arctg(x)=-π2 и limx→+∞arctg(x)=π2, причем другие значения x, входящие в область определения, равняется значению функции в имеющихся точках.

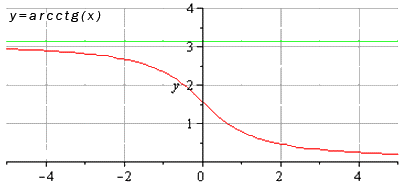
Функция котангенса имеет предел вида limx→-∞arcctg(x)=π и limx→+∞arctg(x)=0, где x принимает любое значение из своей заданной области определения, где получаем предел арккотангенса, равного значению функции в имеющихся точках.

Все имеющееся значения пределов применяются в решении для нахождения предела любой из элементарных функций.

Источник

Добавил:

Upload

Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Предмет:

Файл:

Скачиваний:

Добавлен:

09.02.2015

Размер:

510.96 Кб

Скачать

=[tg x x, sin x x ï ðè x →0]= lim	x	− lim	x	= lim	1	− lim	1	=[∞ −∞].

x→0 x3	x→0 x3	x→0 x2	x→0 x2

При вычислении пределов, содержащих тригонометрические функции, как правило, приходится обращаться к таблице эквивалентностей, предварительно преобразовав выражение с помощью тригонометрических формул.

sin

2 x

Пример 2.20. Вычислить

lim

x→0 arcsin

2 x

sin

Решение.

lim

x→0 arcsin

= sin

ï ðè x →0 = lim

= 1 .

, arcsin

= lim

2 2

x→0

x→0 x2

Пример 2.21. Вычислить

lim tg x −sin x .

x→0

Решение. Вычислить этот предел в 2.4 не удалось. Рассмотрим другой путь рассуждений. С помощью преобразований перейдем в числителе от разности бесконечно малых к произведению бесконечно малых и заменим эквивалентными в произведении.

sin x

lim tg x −sin x =

= lim cos x −sin x =

lim sin x −sin xcos x =

x→0

x3 cos x

sin x(1 −cos x)

при x →0]= lim

= lim

sin x x, 1 −cos x

x3 cos x

x→0

x→0 x3 cos x

= lim

= 1 .

2cos x

x→0

В некоторых случаях применение тригонометрических преобразований позволяет раскрыть неопределенность, не обращаясь к таблице эквивалентностей.

cos

−sin

Пример 2.22. Вычислить

lim

cos x

x→2

Решение. Так как cos

−sin π

−

= 0

и cos

= 0 , то имеем неоп-

ределенность 00 . Имеет смысл преобразовать знаменатель по формуле

cos x = cos2 2x −sin2 2x , а потом разложить знаменатель на множители как раз-

ность квадратов. После сокращения общего множителя в числителе и знаменателе, неопределенность уйдет:

cos

−sin

cos

−sin

lim

= lim

cos x

x→π2

x→π2 cos2

−sin2

cos

−sin

= limπ

x→2 cos

−sin

cos

+sin

x→2 cos

+sin

− x

tg x .

Пример 2.23. Вычислить lim

x→

Решение.

Известно,

что

lim tg x = ∞.

Выражение, стоящее под знаком

x→π

предела, дает неопределенность 0 ∞ при x → π2 . Уничтожить неопределен-

ность только посредством преобразований, как это было сделано примере 2.22, не удастся. Сделаем замену переменной так, чтобы новая переменная

стремилась к нулю. Положим y = x −	π	, y →0	при	x →	π	, а	x = y +	π	. Да-
	2						2			2
				π	= −ctg y :
лее воспользуемся формулой приведения tg y +	2

lim

∞]=

y = x −

, y →0

= lim

− x tg x =[0

(−y)tg y +

x→π 2

y→0

= lim y ctg y = lim	y cos y	=[sin y y, y →0]= lim	y cos y	= lim cos y =1.
sin y	y
y→0	y→0	y→0	y→0

Замечание. Предел lim sin 3x также вычисляется путем замены пере- x→πsin 2x

менной: y = x −π и последующим применением формул приведения. Однако было бы ошибкой сразу прибегнуть к таблице эквивалентностей: sin 3x 3x, sin 2x 2x . Дело в том, что аргументы данных функций – 2x и 3x не являются бесконечно малыми при x → π.

2.6.Пределы выражений, содержащих показательную, логарифмическую и степенную функции

Пример 2.24. Вычислить lim 3x −3−x . x→0 x

Решение. Так как 30 =1, то выражение, стоящее под знаком предела, при x →0 дает неопределенность 00 . Воспользуемся свойствами показательной

функции: ax a y = ax+y ,

a−x =

и преобразуем числитель дроби следую-

3x 3x −1

32x −1

щим образом: 3x −3−x =

3x −

. Тогда

lim

3x −3−x

32x −1

2xln 3 при x →0]= lim

2xln 3

= lim

x→0

x→0 3x x

= lim 2 ln 3

= 2 ln 3

= 2ln 3 .

x→0 3x

x ln (x + 2)

Пример 2.25. Вычислить

lim

−ln x .

x→∞

Решение. В скобках воспользуемся свойством логарифмической функ-

ции: loga N1 −loga N2 = loga N1 и выделим в аргументе логарифма единицу:

ln (x + 2)−ln x = ln	x + 2			2				2
	= ln 1	+		Легко видеть, что	ln 1	+		→ln1 = 0 , а
x
			x				x

выражение α(x) = 2x →0 при x →∞. По таблице эквивалентностей имеем:

при x →∞,

lim

x ln (x + 2)−ln x =

ln 1

x→∞

x + 2

=[∞ 0]= lim x

= lim xln

= lim xln 1 +

= 2 .

x→∞

Пример 2.26. Вычислить lim

ln x −1 .

x→e

x −e

Решение. Поскольку по определению логарифма ln e =1, надо раскрыть

неопределенность

0 . Введем новую переменную, так чтобы она стремилась

к нулю и сделаем замену в пределе:

ln (y +e)−1

lim

ln x −1

= 0

=[y = x −e, y →0 при x →е, x = y + e]= lim

x −e

x→e

y→0

[

ln e =1 =

lim

ln (y +e)−ln e

ln N −ln N

= ln

]

y→0

при y

lim

= ln

→0

= lim

y→0

Пример 2.27. Вычислить lim

3 x4

−1

5 x

−1

x→1

	y +e
	ln
e
lim		=
	y
y→0

= e−1.

Решение. Применим к степенным выражениям соотношение

= x n

и сделаем в пределе замену

y = x −1 с целью воспользоваться эквивалентно-

стью (y +1)m −1 m y при y →0 . Тогда lim

3 x4 −1

x→1

5 x −1

−1

(y +1)

−1 =

= lim

=[y = x −1, y →0 ï ðè x →1, x = y +1]= lim

−1

y→0

−1

x→1 x5

(y +1)5

4 y

4 5

= (y +1)3 −1

(y +1)5

−1

y ï ðè y →0

= lim

y→0

Соседние файлы в папке 1k2s_all

Источник

Предел по-шагам

Примеры пределов

Пределы от рациональных дробей на бесконечности
```
(x - 1)/(x + 1)
```
```
(x^3 + 2*x - 1)/(-7*x^3 - 4*x^2)
```
Пределы от рациональных дробей в конечной точке
```
(x - 1)/(sqrt(x) - 1)
```
Пределы от дроби в нуле
```
log(x)/x
```
Первый замечательный предел
```
sin(7*x)/x
```
```
(1 - cos(x)^2)/x^2
```
Второй замечательный предел
```
(1 - 7/x)^x
```
```
(1 + x/2)^((5*x + 3)/x)
```
Пределы с квадратными корнями
```
sqrt(x + 5) - sqrt(x + 2)
```
```
x - sqrt(x^2 - 7)
```
Правило Лопиталя
```
(e^(x) - x^e)/(x - e)
```
```
log(1+2*x^2)/x
```

Что умеет калькулятор пределов?

Детальное решение для указанных методов:
- Правило Лопиталя
- Теорема о двух милиционерах
- Второй замечательный предел
- Разложение функции на множители
- Использование замены
- Первый замечательный предел
Типы пределов:
- От одной переменной
- На бесконечности
- Односторонние пределы
Строит график функции и её предела
Предлагает другие пределы

Подробнее про Предел функции.

Указанные выше примеры содержат также:

модуль или абсолютное значение: absolute(x) или |x|
квадратные корни sqrt(x),
кубические корни cbrt(x)
тригонометрические функции:
синус sin(x), косинус cos(x), тангенс tan(x), котангенс ctan(x)
показательные функции и экспоненты exp(x)
обратные тригонометрические функции:
арксинус asin(x), арккосинус acos(x), арктангенс atan(x),
арккотангенс acot(x)
натуральные логарифмы ln(x),
десятичные логарифмы log(x)
гиперболические функции:
гиперболический синус sh(x), гиперболический косинус ch(x),
гиперболический тангенс и котангенс tanh(x), ctanh(x)
обратные гиперболические функции:
гиперболический арксинус asinh(x), гиперболический арккосинус acosh(x),
гиперболический арктангенс atanh(x), гиперболический арккотангенс acoth(x)
другие тригонометрические и гиперболические функции:
секанс sec(x), косеканс csc(x), арксеканс asec(x),
арккосеканс acsc(x), гиперболический секанс sech(x),
гиперболический косеканс csch(x), гиперболический арксеканс asech(x),
гиперболический арккосеканс acsch(x)
функции округления:
в меньшую сторону floor(x), в большую сторону ceiling(x)
знак числа:
sign(x)
для теории вероятности:
функция ошибок erf(x) (интеграл вероятности),
функция Лапласа laplace(x)
Факториал от x:
x! или factorial(x)
Гамма-функция gamma(x)
Функция Ламберта LambertW(x)
Тригонометрические интегралы: Si(x),
Ci(x),
Shi(x),
Chi(x)

Правила ввода

Можно делать следующие операции

2*x: – умножение
3/x: – деление
x^2: – возведение в квадрат
x^3: – возведение в куб
x^5: – возведение в степень
x + 7: – сложение
x – 6: – вычитание
Действительные числа: вводить в виде 7.5, не 7,5

Постоянные

pi: – число Пи
e: – основание натурального логарифма
i: – комплексное число
oo: – символ бесконечности

Источник

Как решать пределы с синусами и косинусами?

Алгоритм решения пределов тригонометрических функций

Примеры решения пределов тригонометрических функций

Таблица пределов функции

Предел константы

Предел функции корень n-ой степени

Предел степенной функции

Предел показательной функции

Предел логарифмической функции

Предел тригонометрических функций

Предел обратных тригонометрических функций

2.6.Пределы выражений, содержащих показательную, логарифмическую и степенную функции

Предел по-шагам

Примеры пределов

Что умеет калькулятор пределов?

Правила ввода

Постоянные

Вам также может понравиться

Как найти палето бэй в гта 5

Молитва как найти машину

Как найти кардинату точки

Добавить комментарий Отменить ответ