Назначение сервиса. Данный сервис предназначен для решения пределов, используя правило Лопиталя. Результаты вычисления оформляются в формате Word (см. пример).
Это поле предназначено для ввода числителя дроби.
Правила ввода функций:
Например, x2+3x, записываем как x^2+3*x; ln(1+sin2x) ≡ ln(1+sin(x)^2)
Это поле предназначено для ввода знаменателя дроби. Если знаменатель отсутствует, можно оставить это поле пустым или указать 1.
Правила ввода функций:
Пример. Найти 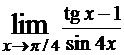
Решение.Сначала убедимся, что правило Лопиталя применить можно. Действительно, величины, стоящие в числителе и знаменателе при x → π/4 являются бесконечно малыми, то есть имеем неопределенность вида 0/0, следовательно можно воспользоваться правилом Лопиталя:
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
Лопиталь:lim_{xto0}(frac{9-sqrt{81-5x}}{x})
-
Лопиталь:lim_{ntoinfty}(frac{n+3}{n-1})
-
Лопиталь:lim_{xtoinfty}(frac{5x^{3}+4}{3x+2})
-
Лопиталь:lim_{xtoinfty}(frac{sqrt{x+1}}{x})
- Показать больше
Описание
Пошаговое определение пределов по правилу Лопиталя
limit-lhopital-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Advanced Math Solutions – Limits Calculator, L’Hopital’s Rule
In the previous posts, we have talked about different ways to find the limit of a function. We have gone over…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Правило Лопиталя

Примеры нахождения пределов функций по правилу Лопиталя
- Пределы от рациональных дробей на бесконечности
-
(x - 1)/(x + 1)
-
(x^3 + 2*x - 1)/(-7*x^3 - 4*x^2)
- Пределы от рациональных дробей в конечной точке
-
(x - 1)/(sqrt(x) - 1)
- Пределы от дроби в нуле
-
log(x)/x
- Первый замечательный предел
-
sin(7*x)/x
-
(1 - cos(x)^2)/x^2
- Пределы с квадратными корнями
-
sqrt(x + 5) - sqrt(x + 2)
-
x - sqrt(x^2 - 7)
- С экспонентой
-
(e^(x) - x^e)/(x - e)
- С логарифмом
-
log(1+2*x^2)/x
Калькулятор ниже находит предел функции по правилу Лопиталя (через производные числителя и знаменателя). Описание правила смотри ниже.
Предел функции в точке — правило Лопиталя
Допустимые операции: + – / * ^
Константы: pi
Функции: sin cosec cos tg ctg sech sec arcsin arccosec arccos arctg arcctg arcsec exp lb lg ln versin vercos haversin exsec excsc sqrt sh ch th cth csch
Точка в которой необходимо посчитать предел
Точность вычисления
Знаков после запятой: 2
Правило Лопиталя
Если выполняются следующие условия:
Тогда существует предел отношения функций f(x) и g(x):
,
И он равен пределу отношения производной функции f(x) к производной функции g(x):
В формуле допускается использование числа пи (pi), экспоненты (e), следующих математических операторов:
+ — сложение
– — вычитание
* — умножение
/ — деление
^ — возведение в степень
и следующих функций:
- sqrt — квадратный корень
- rootp — корень степени p, например root3(x) – кубический корень
- exp — e в указанной степени
- lb — логарифм по основанию 2
- lg — логарифм по основанию 10
- ln — натуральный логарифм (по основанию e)
- logp — логарифм по основанию p, например log7(x) — логарифм по основанию 7
- sin — синус
- cos — косинус
- tg — тангенс
- ctg — котангенс
- sec — секанс
- cosec — косеканс
- arcsin — арксинус
- arccos — арккосинус
- arctg — арктангенс
- arcctg — арккотангенс
- arcsec — арксеканс
- arccosec — арккосеканс
- versin — версинус
- vercos — коверсинус
- haversin — гаверсинус
- exsec — экссеканс
- excsc — экскосеканс
- sh — гиперболический синус
- ch — гиперболический косинус
- th — гиперболический тангенс
- cth — гиперболический котангенс
- sech — гиперболический секанс
- csch — гиперболический косеканс
- abs — абсолютное значение (модуль)
- sgn — сигнум (знак)
Предел функции при ( x to x_0 )
Пусть функция ( f(x) ) определена на некотором множестве (X) и пусть точка ( x_0 in X ) или ( x_0 notin X )
Возьмем из (X) последовательность точек, отличных от (x_0) :
(x_1 ;, ; x_2 ;, ; x_3 ;, …, ; x_n ; , ; … tag{1} )
сходящуюся к (x^*).
Значения функции в точках этой последовательности также образуют числовую последовательность
( f(x_1) ;, ; f(x_2) ;, ; f(x_3) ;, …, ; f(x_n) ; , ; … tag{2} )
и можно ставить вопрос о существовании ее предела.
Определение. Число (A) называется пределом функции (f(x)) в точке ( x = x_0 ) (или при ( x to x_0 ) ), если для
любой сходящейся к (x_0) последовательности (1) значений аргумента (x), отличных от (x_0) соответствующая
последовательность (2) значений функции сходится к числу (A).
Символически это записывается так:
$$ lim_{xto x_0}{ f(x)} = A $$
Функция (f(x)) может иметь в точке (x_0) только один предел. Это следует из того, что последовательность ( left{ f(x_n) right} )
имеет только один предел.
Существует другое определение предела функции.
Определение Число (A) называется пределом функции (f(x)) в точке (x_0), если для любого числа ( varepsilon > 0 )
существует число ( delta > 0 ) такое, что для всех ( x in X, ; x neq x_0 ), удовлетворяющих неравенству ( |x-x_0| < delta ),
выполняется неравенство ( |f(x)-A| < varepsilon )
Используя логические символы, это определение можно записать в виде
( (forall varepsilon > 0) (exists delta > 0) (forall x in X, ; x neq x_0, ; |x-x_0| < delta): |f(x)-A| < varepsilon )
Отметим, что неравенства ( x neq x_0, ; |x-x_0| < delta ) можно записать в виде ( 0 < |x-x_0| < delta )
<>Первое определение основано на понятии предела числовой последовательности, поэтому его часто называют определением
«на языке последовательностей».
Второе определение называют определением «на языке ( varepsilon – delta )».
Эти два определения предела функции эквивалентны и можно использовать любое из них в зависимости от того, какое более
удобно при решении той или иной задачи.
Заметим, что определение предела функции «на языке последовательностей» называют также определением предела функции по Гейне,
а определение предела функции «на языке ( varepsilon – delta )» — определением предела функции по Коши.
Предел функции при ( x to x_{0-} ) и при ( x to x_{0+} )
В дальнейшем будут использованы понятия односторонних пределов функции, которые определяются следующим образом.
Определение Число (A) называется правым (левым) пределом функции (f(x)) в точке (x_0), если для любой сходящейся
к (x_0) последовательности (1), элементы (x_n) которой больше (меньше) (x_0), соответствующая
последовательность (2) сходится к (A).
Символически это записывается так:
$$ lim_{x to x_{0+}} f(x) = A ; left( lim_{x to x_{0-}} f(x) = A right) $$
Можно дать равносильное определение односторонних пределов функции «на языке ( varepsilon – delta )»:
Определение число (A) называется правым (левым) пределом функции (f(x)) в точке (x_0), если для любого
( varepsilon > 0 ) существует ( delta > 0 ) такое, что для всех (x), удовлетворяющих неравенствам
( x_0 < x < x_0 + delta ; (x_0 -delta < x < x_0 ) ) , выполняется неравенство ( |f(x)-A| < varepsilon ).
Символические записи:
( (forall varepsilon > 0) (exists delta > 0) (forall x, ; x_0 < x < x_0 + delta ): |f(x)-A| < varepsilon )
( (forall varepsilon > 0) (exists delta > 0) (forall x, ; x_0 -delta < x < x_0 ): |f(x)-A| < varepsilon )
Связь между односторонними пределами и пределом функции устанавливает следующая теорема.
Теорема
Функция (f(x)) имеет в точке (x_0) предел тогда и только тогда, когда в этой точке существуют как правый, так и левый пределы,
и они равны. В этом случае предел функции равен односторонним пределам.
Предел функции при ( x to infty ), при ( x to -infty ) и при ( x to +infty )
Кроме рассмотренных понятий предела функции при ( x to x_0 ) и односторонних пределов существует также понятие предела функции
при стремлении аргумента к бесконечности.
Определение. Число (A) называется пределом функции (f(x)) при ( x to infty ), если для любой бесконечно большой
последовательности (1) значений аргумента соответствующая последовательность (2) значений функции сходится к (A).
Символическая запись:
$$ lim_{x to infty} f(x) = A $$
Определение. Число (A) называется пределом функции (f(x)) при ( x to +infty ; (x to -infty) ) , если для любой бесконечно
большой последовательности значений аргумента, элементы (x_n) которой положительны (отрицательны), соответствующая
последовательность значений функции сходится к (A).
Символическая запись:
$$ lim_{x to +infty} f(x) = A ; left( lim_{x to -infty} f(x) = A right) $$
Теоремы о пределах функций
Определение предела функции «на языке последовательностей» дает возможность перенести доказанные выше теоремы о пределах
последовательностей на функции. Покажем это на примере двух теорем.
Теорема. Пусть функции (f(x)) и (g(x)) имеют в точке (x_0) пределы (B) и (C). Тогда функции ( f(x) pm g(x) ; , ; f(x) cdot g(x) ) и
( frac{f(x)}{g(x)} ) (при ( C neq 0 ) ) имеют в точке (x_0) пределы, равные соответственно ( B pm C ; , ; B cdot C ), и ( frac{B}{C} ).
Теорема. Пусть функции ( f(x) ; , ; g(x) ) и ( h(x) ) определены в некоторой окрестности точки (x_0), за исключением, быть
может, самой точки (x_0), и функции ( f(x) ; , ; h(x) ) имеют в точке (x_0) предел, равный (A), т.е.
$$ lim_{x to x_0} f(x) = lim_{x to x_0} h(x) = A $$
Пусть, кроме того, выполняются неравенства ( f(x) leqslant g(x) leqslant h(x) ).
Тогда $$ lim_{x to x_0} g(x) = A $$
Теорема Лопиталя. Если $$ lim_{x to x_0} f(x) = lim_{x to x_0} g(x) = 0 $$ или (infty ), (f(x)) и (g(x))
дифференцируемы в окрестности (x_0) , и ( g'(x) neq 0 ) в окрестности (x_0) ,
и существует $$ lim_{x to x_0} frac{f'(x)}{g'(x)} $$ то существует $$ lim_{x to x_0} frac{f(x)}{g(x)} = lim_{x to x_0} frac{f'(x)}{g'(x)} $$
Т.е. теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Теорема Лопиталя позволяет раскрывать неопределённости вида ( frac{0}{0} ) и ( frac{infty}{infty} ).
Первый замечательный предел
$$ lim_{x to 0} frac{sin x}{x} = 1 $$
Второй замечательный предел
$$ lim_{x to infty} left( 1+ frac{1}{x} right)^x = e $$


