Как найти предел числовой последовательности
Числовая последовательность ${x_n}$ – это правило, по которому каждому натуральному числу $n = 1,2,3,…$ устанавливается соответствующее число $x_n$, называющееся энным членом. Далее будем считать, что имеются в виду только действительные числа. Введём понятие и запишем определение.
Пределом числовой последовательности ${x_n}$ называется число $a$, такое что для любого положительного $varepsilon$ существует натуральное $N = N(varepsilon)$, при котором для всех $n > N$ выполняется неравенство $$|x_n – a| < varepsilon .$$
Обозначается он в математическом виде $$lim limits_{nto infty} x_n = a. $$ Аналогичная короткая форма записи принимает вид $$x_n to a text{ при } n to infty. $$
Чтобы успешно вычислить предел последовательности нужно знать основные равенства:
- При $k > 0$ справедливо $limlimits_{n to infty} frac{1}{n^k} = 0$
- При $k > 0$ справедливо $limlimits_{n to infty} n^k = infty $
- При $|a|<1$ справедливо $limlimits_{n to infty} a^n = 0 $
- При $|a|>1$ справедливо $limlimits_{n to infty} a^n = infty $
- У последовательности $-1,1,-1,1,…$, заданной как $x_n = (-1)^n$ нет предела.
Так же потребуется выучить основные свойства пределов последовательности:
- Сумма $limlimits_{nto infty} (a_n+b_n) = limlimits_{nto infty} a_n + limlimits_{nto infty} b_n = a+b $
- Разность $limlimits_{nto infty} (a_n-b_n) = limlimits_{nto infty} a_n – limlimits_{nto infty} b_n = a-b $
- Произведение $limlimits_{nto infty} (a_n cdot b_n) = limlimits_{nto infty} a_n cdot limlimits_{nto infty} b_n = a cdot b $
- Частное $limlimits_{nto infty} frac{a_n}{b_n} = frac{limlimits_ {nto infty} a_n}{limlimits_{nto infty} b_n} = frac{a}{b} $, если $limlimits_{nto infty} b_n neq 0 $
- Непрерывная функция $limlimits_{nto infty} f(a_n) = f (limlimits_{nto infty} a_n) = f(a) $.
| Пример 1 |
| Найти предел последовательности $limlimits_{nto infty} frac{3^{n+2}+2^{2n+1}}{5+4^{n+2}}$. |
| Решение |
|
Подставляем бесконечность в дробь вместо $n$ и получаем неопределенность вида $frac{infty}{infty}$. Чтобы от неё избавиться нужно вынести из числителя и знаменателя член с наивысшей степенью. Но прежде воспользуемся свойствами степеней для упрощения выражений. $$limlimits_{nto infty} frac{3^{n+2}+2^{2n+1}}{5+4^{n+2}} = limlimits_{n to infty} frac{9 cdot 3^n + 2 cdot 4^n}{5+16 cdot 4^n} = $$ Видим, что самые большие слагаемые содержат $4^n$, поэтому именно их выносим за скобки, не забывая за соответствующие множители перед ними. $$ = limlimits_{n to infty} frac{2 cdot 4^n( frac{9}{2} cdot (frac{3}{4})^n + 1)}{16 cdot 4^n (frac{5}{16} cdot frac{1}{4^n} +1)} = $$ Воспользовавшись первым равенством из теории замечаем, что $(frac{3}{4})^n = 0$ и $frac{1}{4^n} = 0$ при $nto infty$. Не забываем сократить дробь на $4^n$ и получаем окончательный ответ. $$ = frac{2 cdot (0 + 1)}{16 cdot (0 + 1)} = frac{2}{16} = frac{1}{8}$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ limlimits_{nto infty} frac{3^{n+2}+2^{2n+1}}{5+4^{n+2}} = frac{1}{8} $$ |
| Пример 2 |
| Вычислить предел последовательности $limlimits_{nto infty} frac{(5-n)^2+(5+n)^2}{(5-n)^2-(5+n)^2} $. |
| Решение |
|
Выносим из каждой скобки $n$ не забывая про квадрат. А далее выполним сокращение числителя и знаменателя на $n^2$. $$limlimits_{nto infty} frac{(5-n)^2+(5+n)^2}{(5-n)^2-(5+n)^2} = limlimits_{nto infty} frac{n^2(frac{5}{n}-1)^2 + n^2(frac{5}{n}+1)^2}{n^2(frac{5}{n}-1)^2-n^2(frac{5}{n}+1)^2} = $$ $$ = limlimits_{nto infty} frac{(frac{5}{n}-1)^2 + (frac{5}{n}+1)^2}{(frac{5}{n}-1)^2-(frac{5}{n}+1)^2} = frac{(0-1)^2 + (0+1)^2}{(0-1)^2-(0+1)^2} = $$ Нули в скобках появились из-за первого правила, согласно которому $limlimits_{nto infty} frac{1}{n^k} = 0$ при $k>0$. $$ = frac{1+1}{1-1} = frac{2}{0} = infty $$ Обратим внимание на то, что число в числителе деленное на ноль в знаменателе даёт бесконечность. |
| Ответ |
| $$limlimits_{nto infty} frac{(5-n)^2+(5+n)^2}{(5-n)^2-(5+n)^2} = infty$$ |
| Пример 3 |
| Найти предел числовой последовательности $limlimits_{nto infty} sqrt{n^2+2n}-n$. |
| Решение |
|
Подставим бесконечность вместо $n$ и получим неопределенность. $$limlimits_{nto infty} sqrt{n^2+2n}-n = infty – infty $$ Для устранения такой неопределенности нужно избавиться от иррациональности, то есть от корней. Сделаем это с помощью умножения и одновременного деления на сопряженное выражение. Оно отличается только противоположным знаком. $$limlimits_{nto infty} sqrt{n^2+2n}-n = limlimits_{nto infty} frac{(sqrt{n^2+2n}-n)(sqrt{n^2+2n}+n)}{sqrt{n^2+2n}+n} = $$ Теперь благодаря формуле $a^2-b^2 = (a-b)(a+b)$ сворачиваем выражение в числителе. $$ = limlimits_{nto infty} frac{n^2 + 2n – n^2}{sqrt{n^2+2n}+n} = limlimits_{nto infty} frac{2n}{sqrt{n^2+2n}+n} = $$ Если в лоб подставим вместо $n$ бесконечность, то найти решение не получится. Вылезет неопределенность $frac{infty}{infty}$. Чтобы этого не допустить вынесем старшую степень из знаменателя и сократим на $n$. $$ = limlimits_{n to infty} frac{2n}{n(sqrt{1+frac{2}{n}}+1)} = frac{2}{sqrt{1+0}+1} = 1$$ |
| Ответ |
| $$ limlimits_{nto infty} sqrt{n^2+2n}-n = 1 $$ |
Теория пределов – раздел математического анализа. Наряду с системами линейных уравнений и диффурами пределы доставляют всем студентам, изучающим математику, немало хлопот. Чтобы решить предел, порой приходится применять массу хитростей и выбирать из множества способов решения именно тот, который подойдет для конкретного примера.
В этой статье мы не поможем вам понять пределы своих возможностей или постичь пределы контроля, но постараемся ответить на вопрос: как понять пределы в высшей математике? Понимание приходит с опытом, поэтому заодно приведем несколько подробных примеров решения пределов с пояснениями.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Понятие предела в математике
Первый вопрос: что это вообще за предел и предел чего? Можно говорить о пределах числовых последовательностей и функций. Нас интересует понятие предела функции , так как именно с ними чаще всего сталкиваются студенты. Но сначала – самое общее определение предела:
Допустим, есть некоторая переменная величина. Если эта величина в процессе изменения неограниченно приближается к определенному числу a, то a – предел этой величины.
Для определенной в некотором интервале функции f(x)=y пределом называется такое число A, к которому стремится функция при х, стремящемся к определенной точке а. Точка а принадлежит интервалу, на котором определена функция.
Звучит громоздко, но записывается очень просто:
Lim – от английского limit – предел.
Существует также геометрическое объяснение определения предела, но здесь мы не будем лезть в теорию, так как нас больше интересует практическая, нежели теоретическая сторона вопроса. Когда мы говорим, что х стремится к какому-то значению, это значит, что переменная не принимает значение числа, но бесконечно близко к нему приближается.
Приведем конкретный пример. Задача – найти предел.
Чтобы решить такой пример, подставим значение x=3 в функцию. Получим:
Кстати, если Вас интересуют базовые операции над матрицами, читайте отдельную статью на эту тему.
В примерах х может стремиться к любому значению. Это может быть любое число или бесконечность. Вот пример, когда х стремится к бесконечности:
Интуитивно понятно, что чем больше число в знаменателе, тем меньшее значение будет принимать функция. Так, при неограниченном росте х значение 1/х будет уменьшаться и приближаться к нулю.
Как видим, чтобы решить предел, нужно просто подставить в функцию значение, к которому стремиться х. Однако это самый простой случай. Часто нахождение предела не так очевидно. В пределах встречаются неопределенности типа 0/0 или бесконечность/бесконечность. Что делать в таких случаях? Прибегать к хитростям!
Неопределенности в пределах
Неопределенность вида бесконечность/бесконечность
Пусть есть предел:
Если мы попробуем в функцию подставить бесконечность, то получим бесконечность как в числителе, так и в знаменателе. Вообще стоит сказать, что в разрешении таких неопределенностей есть определенный элемент искусства: нужно заметить, как можно преобразовать функцию таким образом, чтобы неопределенность ушла. В нашем случае разделим числитель и знаменатель на х в старшей степени. Что получится?
Из уже рассмотренного выше примера мы знаем, что члены, содержащие в знаменателе х, будут стремиться к нулю. Тогда решение предела:
Для раскрытия неопределенностей типа бесконечность/бесконечность делим числитель и знаменатель на х в высшей степени.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Еще один вид неопределенностей: 0/0
В таких случаях рекомендуется раскладывать числитель и знаменатель на множители. Но давайте посмотрим на конкретный пример. Нужно вычислить предел:
Как всегда, подстановка в функцию значения х=-1 дает 0 в числителе и знаменателе. Посмотрите чуть внимательнее и Вы заметите, что в числителе у нас квадратное уравнение. Найдем корни и запишем:
Сократим и получим:
Итак, если Вы сталкиваетесь с неопределенностью типа 0/0 – раскладывайте числитель и знаменатель на множители.
Чтобы Вам было проще решать примеры, приведем таблицу с пределами некоторых функций:
Правило Лопиталя в пределах
Еще один мощный способ, позволяющий устранить неопределенности обоих типов. В чем суть метода?
Если в пределе есть неопределенность, берем производную от числителя и знаменателя до тех пор, пока неопределенность не исчезнет.
Наглядно правило Лопиталя выглядит так:
Важный момент: предел, в котором вместо числителя и знаменателя стоят производные от числителя и знаменателя, должен существовать.
А теперь – реальный пример:
Налицо типичная неопределенность 0/0. Возьмем производные от числителя и знаменателя:
Вуаля, неопределенность устранена быстро и элегантно.
Надеемся, что Вы сможете с пользой применить эту информацию на практике и найти ответ на вопрос “как решать пределы в высшей математике”. Если нужно вычислить предел последовательности или предел функции в точке, а времени на эту работу нет от слова «совсем», обратитесь в профессиональный студенческий сервис за быстрым и подробным решением.
Предел последовательности
- Определение последовательности
- Предел последовательности
- Как доказать сходимость последовательности к пределу?
- Ограниченные и неограниченные последовательности
- Как доказать неограниченность последовательности?
- Примеры
п.1. Определение последовательности
С понятием «последовательность» мы уже познакомились, когда изучали прогрессии (см. §24 справочника для 9 класса). По определению:
Числовой последовательностью называют функцию натурального аргумента (y_n=f(n), ninmathbb{N}).
Значения (y_1,y_2,…,y_n,…) называют членами последовательности.
В символе (y_n) число (n) называют индексом последовательности.
Т.е., числовая последовательность – это некий набор чисел с присвоенными им порядковыми номерами. Это набор можно задать формулой, описанием или просто перечислением.
Например:
1) Формула (y_n=frac1n, ninmathbb{N}) задает бесконечную последовательность дробей:
| (1,) | (frac12,) | (frac13,) | (…,) | (frac1n,) | (…) |
| 1 | 2 | 3 | … | n | … |
2) Формула (y_n=(-1)^n, ninmathbb{N}) задает бесконечную последовательность «прыгающих» единиц:
| -1, | 1, | -1, | 1, | -1, | 1, | … |
| 1 | 2 | 3 | 4 | 5 | 6 | … |
3) Рекуррентная формула (y_1=1, y_2=1, y_(n+2)=y_(n+1)+y_n) задает бесконечную последовательность чисел Фибоначчи:
| 1, | 1, | 2, | 3, | 5, | 8, | … |
| 1 | 2 | 3 | 4 | 5 | 6 | … |
4) Описание «число π точностью до (10^{-n})» задает бесконечную последовательность все более «подробных» значений числа π:
| 3,1; | 3,14; | 3,141; | 3,1415; | 3,14159; | 3,141592; | … |
| 1 | 2 | 3 | 4 | 5 | 6 | … |
Этот ряд можно также задать формулой (y_n=frac{[picdot 10^n]}{10^n}), где квадратные скобки обозначают целую часть от числа.
п.2. Предел последовательности
Поведение последовательности «на длинных дистанциях» может быть неочевидным. Чтобы лучше понять, возрастает или убывает заданный ряд чисел, ограничен ли он какой-либо величиной или уходит на бесконечность, проще всего построить график.
Например:
В приведенных примерах мы видим, что последовательность (y_n=frac1n) сходится к 0, а приближение числа π (y_n=frac{[picdot 10^n]}{10^n}) конечно же сходится к π.
Говорят, что у таких последовательностей есть конечный предел, и записывают это так: $$ lim_{nrightarrowinfty}frac1n=0, lim_{nrightarrowinfty}frac{[picdot 10^n]}{10^n}=pi $$
Последовательность, имеющая предел, называется сходящейся.
Последовательность, не имеющая предела, называется расходящейся.
Если предел последовательности (lim_{nrightarrowinfty}y_n=0), последовательность называется бесконечно малой.
Число (binmathbb{R}) называют пределом последовательности (left{y_nright}), если последовательность (left{y_n-bright}) является бесконечно малой, т.е. все её элементы, начиная с некоторого номера (N_{varepsilon}), меньше по модулю любого заранее взятого положительного числа (varepsilongt 0): $$ lim_{nrightarrowinfty}y_n=bLeftrightarrow forallvarepsilongt 0 exists N_{varepsilon}inmathbb{N}: ngeq NRightarrow |a_n-b|lt varepsilon $$
Промежуток ((b-varepsilon; b+varepsilon)) $$ b-varepsilonlt y_nlt b+varepsilon $$ называют ε-окрестностью точки b.
п.3. Как доказать сходимость последовательности к пределу?
Разберем данное выше определение предела на конкретном примере.
Пусть (y_n=frac{1}{n+4}). Докажем, что предел этой последовательности b=0.
Найдем номер (N_{varepsilon}) члена последовательности, который первым окажется меньше одной тысячной. Т.е. «заранее взятое число» у нас ε=0,001, а ε-окрестность окружает точку предела (b=0: -varepsilonlt y_nltvarepsilon).
Решаем неравенство (|y_n-b|ltvarepsilon): begin{gather*} left|frac{1}{n+4}-0right|lt 0,001Rightarrow frac{1}{n+4}lt 0,001Rightarrow n+4gt frac{1}{0,001}=1000\ ngt 996Rightarrow N_{varepsilon}=997 end{gather*} Значит, начиная с (N_{varepsilon}=997), все (y_n=frac{1}{n+4}, ngeq N_{varepsilon}=997) будут меньше ε=0,001.
Если попробовать еще больше приблизиться к пределу b=0, например с ε=0,00001, стартовый номер (N_{varepsilon}) для членов последовательности, которые умещаются в 100 раз меньшей ε-окрестности, очевидно, увеличится.
Теперь найдем общую формулу зависимости (N_{varepsilon}) для последовательности (y_n=frac{1}{n+4}) с пределом b=0: begin{gather*} left|frac{1}{n+4}-0right|lt varepsilon Rightarrow frac{1}{n+4}lt varepsilonRightarrow n+4gt frac{1}{varepsilon}\ ngtfrac1varepsilon-4Rightarrow N_{varepsilon}=left[frac1varepsilon-4right]+1 end{gather*} где квадратные скобки обозначают целую часть от числа.
| (varepsilon) | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| (N_{varepsilon}) | 7 | 97 | 997 | 9997 | 99997 | 999997 |
| (lg varepsilon) | -1 | -2 | -3 | -4 | -5 | -6 |
| (lg N_{varepsilon}) | 0,845 | 1,987 | 2,999 | 4,000 | 5,000 | 6,000 |
И построим график (в логарифмическом масштабе):
Мы видим, что чем меньше ε, тем больше (N_{varepsilon}). Но главное – мы всегда можем его указать.
Таким образом, мы доказали, что действительно (lim_{nrightarrowinfty}frac{1}{n+4}=0)
Ведь для любого сколь угодно малого (varepsilongt 0) мы можем указать такой номер (N_{varepsilon}=left[frac1varepsilon-4right]+1), начиная с которого, для всех членов последовательности с номерами (ngeq N_{varepsilon}) разность (left|frac{1}{n+4}-0right|), т.е. эти члены не выйдут за переделы ε окрестности предела b=0.
Построенный график интересен еще и тем, что показывает одно из важных практических применений логарифмов: если разбросы по шкалам очень велики, отличаются на порядки, то графики удобней строить в десятичных логарифмах.
Такие графики часто можно увидеть у физиков-ядерщиков, копающих вглубь, от нанометров до планковских длин; или у астрономов, всматривающихся вдаль, от тысяч километров до гигапарсек.
п.4. Ограниченные и неограниченные последовательности
Последовательность (left{y_nright}) называется ограниченной сверху, если существует такое число (Minmathbb{R}), что для любого номера (n, y_nleq M).
Последовательность (left{y_nright}) называется ограниченной снизу, если существует такое число (minmathbb{R}), что для любого номера (n, y_ngeq m).
Последовательность (left{y_nright}) называется ограниченной, если она ограничена сверху и ограничена снизу, т.е. для любого номера (n, mleq y_nleq M).
Последовательность (left{y_nright}) называется неограниченной, если для любого сколь угодно большого (Mgt 0) найдется такой номер (N_M), что для любого (ngeq N_Mcdot|y_n|gt M)
Например:
1) последовательность (y_n=frac1n) ограничена сверху (M=y_1=1) и ограничена снизу (m=lim_{nrightarrowinfty}y_n=0). Т.е. (0lt y_nleq 1, forall n) – последовательность ограничена.
2) последовательность (y_n=(-1)^n) ограничена сверху (M=1) и ограничена снизу (m=-1). Т.е. (-1leq y_nleq 1, forall n) – последовательность ограничена.
3) последовательность чисел Фибоначчи (y_1=1, y_2=1, y_{n+2}=y_{n+1}+y_n) ограничена снизу (m=1), но неограничена сверху. Т.е. последовательность неограничена: (lim_{nrightarrowinfty}=+infty)
Неограниченную последовательность также называют бесконечно большой (стремящейся к бесконечности) и в зависимости от знаков (y_n) при (nrightarrow infty) используют запись: $$ lim_{nrightarrowinfty}y_n=+infty text{или} lim_{nrightarrowinfty}y_n=-infty $$
п.5. Как доказать неограниченность последовательности?
Разберем данное выше определение неограниченности (стремления к бесконечности) на конкретном примере.
Пусть (y_n=n^2). Докажем, что последовательность неограничена.
Найдем номер (N_M) члена последовательности, который первым окажется больше (M=100) – нашего «сколько угодно большого числа».
Согласно определению, подставляем значения в неравенство (|y_n|gt M): begin{gather*} |n^2|gt 100Rightarrow n^2gt 100Rightarrow ngt 10\ N_M=11 end{gather*} Т.е. все (y_n), начиная с 11-го, будут больше 100.
Выведем общую формулу для (N_M): begin{gather*} |n^2|gt MRightarrow n^2gt MRightarrow ngtsqrt{M}\ N_M=[sqrt{M}]+1 end{gather*} где квадратные скобки обозначают целую часть числа.
Например:
| (M) | 10 | 100 | 1 000 | 10 000 | 100 000 | 1 000 000 |
| (N_M) | 4 | 11 | 33 | 101 | 317 | 1001 |
Таким образом, мы доказали, что действительно (lim_{nrightarrowinfty}n^2=+infty)
Ведь для любого сколь угодно большого (Mgt 0) мы можем указать такой номер (N_M=[sqrt{M}]), начиная с которого, для всех членов последовательности с номерами (ngeq N_M, y_n=n^2gt M), т.е. члены последовательности становятся ещё больше.
п.6. Примеры
Пример 1. Используя определение предела последовательности, докажите, что:
a) ( lim_{nrightarrowinfty}frac{n+1}{3-2n}=-frac12 )
По условию: $$ y_n=frac{n+1}{3-2n}, b=-frac12 $$ Находим (N_{varepsilon}) для произвольного ε>0 из неравенства (|y_n-b|ltvarepsilon)
$$ left|frac{n+1}{3-2n}+frac12right|ltvarepsilonRightarrow left|frac{2n+2+3-2n}{2(3-2n)}right| lt varepsilonRightarrow frac52left|frac{1}{3-2n}right|lt varepsilon $$ Знаменатель у дроби под модулем при (ngeq 2) отрицательный . Поэтому, раскрывая модуль, получаем: begin{gather*} frac52left|frac{1}{3-2n}right|=frac{5}{2(2n-3)}lt varepsilonRightarrow 2n-3gt frac{5}{2varepsilon}Rightarrow ngtfrac12left(frac{5}{2varepsilon}+3right)\ N_{varepsilon}=left[frac12left(frac{5}{2varepsilon}+3right)right]+1 end{gather*} Например:
| ε | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| (N_{varepsilon}) | 15 | 128 | 1253 | 12503 | 125003 | 1250003 |
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности (N_{varepsilon}=left[frac12left(frac{5}{2varepsilon}+3right)right]+1), начиная с которого
(left|frac{n+1}{3-2n}+frac12right|ltvarepsilon, ngeq N_{varepsilon}geq 2).
Что и требовалось доказать.
б) ( lim_{nrightarrowinfty}frac{n^2+1}{3n^2+n+1}=frac13 )
По условию: $$ y_n=frac{n^2+1}{3n^2+n+1}, b=frac13 $$ Записываем неравенство (|y_n-b|ltvarepsilon):
$$ left|frac{n^2+1}{3n^2+n+1}-frac13right|ltvarepsilonRightarrow left|frac{3n^2+3-3n^2-n-1}{3(3n^2+n+1)}right| lt varepsilonRightarrow frac13left|frac{2-n}{3n^2+n+1}right|lt varepsilon $$ Раскрываем модуль: $$ frac13cdot left|frac{2-n}{3n^2+n+1}right|=frac{n-2}{3(3n^2+n+1)}lt varepsilon $$ Усилим неравенство, чтобы было легче найти (N_{varepsilon}). Заметим, что для (ngeq 3): begin{gather*} frac{n-2}{3(3n^2+n+1)}geqfrac{1}{3(3n^2+n+1)} = frac{1}{9left(n^2+frac n3+frac13right)}gtfrac{1}{9(n^2+2n+1)}=frac{1}{9(n+1)^2}\ frac{1}{9(n+1)^2}ltfrac{n-2}{3(3n^2+n+1)}lt varepsilonRightarrowfrac{1}{9(n+1)^2}lt varepsilonRightarrow (n+1)^2gtfrac{1}{9varepsilon}\ n+1gtfrac{1}{3sqrt{varepsilon}}Rightarrow ngtfrac{1}{3sqrt{varepsilon}}-1\ N_{varepsilon}=left[frac{1}{3sqrt{varepsilon}}-1right]+1 =left[frac{1}{3sqrt{varepsilon}}right], N_{varepsilon}geq 3 end{gather*} Например:
| ε | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| (N_{varepsilon}) | 3 | 3 | 11 | 33 | 105 | 333 |
Показанный приём с усилением неравенства часто применяется в математическом анализе. Найденное (N_{varepsilon}) немного больше «точного» значения, которое следует из исходной дроби (frac{n-2}{3(3n^2+n+1)}), но наша задача в том, чтобы обоснованно построить любое выражение для стартового номера (N_{varepsilon}) в зависимости от ε.
Если найденный номер будет немного больше исходного – не страшно; главное, чтобы он 1) был обоснован; 2) гарантировал размещение всех последующих (y_n, ngeq N_{varepsilon}) в ε окрестности предела b.
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности (N_{varepsilon}=left[frac{1}{3sqrt{varepsilon}}right]), начиная с которого (left|frac{n^2+1}{3n^2+n+1}-frac13right|ltvarepsilon, ngeq N_{varepsilon}geq 3).
Что и требовалось доказать.
в) ( lim_{nrightarrowinfty}frac{3^n+1}{3^n}=1 )
По условию: $$ y_n=frac{3^n+1}{3^n}, b=1 $$ Записываем неравенство (|y_n-b|ltvarepsilon):
begin{gather*} left|frac{3^n+1}{3^n}-1right|ltvarepsilonRightarrow left|frac{3^n+1-3^n}{3^n}right|ltvarepsilonRightarrow frac{1}{3^n}lt varepsilonRightarrow 3^ngt frac1varepsilon\ ngtlog_3frac1varepsilonRightarrow ngt -log_3varepsilon\ N_{varepsilon}=left[-log_3varepsilonright]+1 end{gather*} Например:
| ε | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| (N_{varepsilon}) | 3 | 5 | 7 | 9 | 11 | 14 |
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности (N_{varepsilon}=left[-log_3varepsilonright]), начиная с которого (left|frac{3^n+1}{3^n}-1right|ltvarepsilon, ngeq N_{varepsilon}).
Что и требовалось доказать.
г) ( lim_{nrightarrowinfty}frac{sqrt{n}}{5sqrt{n}+1}=frac15 )
По условию: $$ y_n=frac{sqrt{n}}{5sqrt{n}+1}, b=frac15 $$ Записываем неравенство (|y_n-b|ltvarepsilon):
begin{gather*} left|frac{sqrt{n}}{5sqrt{n}+1}-frac15right|ltvarepsilonRightarrow frac15left|frac{sqrt{n}-sqrt{n}-1}{sqrt{n}+1}right|ltvarepsilon Rightarrow frac{1}{5(sqrt{n}+1)}ltvarepsilonRightarrow sqrt{n}+1gtfrac{1}{5varepsilon}\ sqrt{n}gtfrac{1}{5varepsilon}-1Rightarrow ngtleft(frac{1}{5varepsilon-1}right)^2\ N_{varepsilon}=left[left(frac{1}{5varepsilon}-1right)^2right]+1 end{gather*} Например:
| ε | 0,1 | 0,01 | 0,001 | 0,0001 | 0,00001 | 0,000001 |
| (N_{varepsilon}) | 2 | 362 | 39602 | 3996002 | 4·108 | 4·1010 |
Таким образом, для любого сколь угодно малого ε>0 найдется номер в последовательности (N_{varepsilon}=left[left(frac{1}{5varepsilon}-1right)^2right]), начиная с которого (left|frac{sqrt{n}}{5sqrt{n}+1}-frac15right|ltvarepsilon, ngeq N_{varepsilon}).
Что и требовалось доказать.
Пример 2. Используя определения неограниченной последовательности, докажите, что:
a) ( lim_{nrightarrowinfty}2^n=+infty )
По условию: (y_n=2^n)
Записываем неравенство (|y_n|gt M):
begin{gather*} 2^ngt MRightarrow ngt log_2M\ N_M=left[log_2Mright]+1 end{gather*} Например:
| M | 10 | 100 | 1 000 | 10 000 | 100 000 | 1 000 000 |
| NM | 4 | 8 | 11 | 14 | 18 | 21 |
Таким образом, для любого сколь угодно большого (Mgt 0) мы можем указать такой номер (N_M=left[log_2Mright]+1), начиная с которого, для всех членов последовательности с номерами (ngeq N_M, y_n=2^ngt M).
Что и требовалось доказать.
б) ( lim_{nrightarrowinfty}sqrt{n+1}=+infty )
По условию: (y_n=sqrt{n+1})
Записываем неравенство (|y_n|gt M):
begin{gather*} sqrt{n+1}gt MRightarrow n+1gt M^2Rightarrow ngt M^2 -1\ N_M=left[M^2-1right]+1=left[M^2right] end{gather*} знак целой части оставляем, т.к. (Minmathbb{R}) – не обязательно целое.
Например:
| M | 10 | 100 | 1 000 | 10 000 | 100 000 | 1 000 000 |
| NM | 100 | 10 000 | 1 000 000 | 108 | 1010 | 1012 |
Таким образом, для любого сколь угодно большого (Mgt 0) мы можем указать такой номер (N_M=left[M^2right]), начиная с которого, для всех членов последовательности с номерами (ngeq N_M, y_n=sqrt{n+1}gt M).
Что и требовалось доказать.
Пределы числовых последовательностей
Содержание
Предел числовой последовательности
ОПРЕДЕЛЕНИЕ 1. Число a называют пределом числовой последовательности
a1 , a2 , … an , …
если для любого положительного числа ε найдется такое натуральное число N , что при всех n > N выполняется неравенство
| an – a | < ε .
Условие того, что число a является пределом числовой последовательности
a1 , a2 , … an , … ,
записывают с помощью обозначения
и произносят так: «Предел an при n , стремящемся к бесконечности, равен a ».
То же самое соотношение можно записать следующим образом:
an → a при .
Словами это произносится так: «an стремится к a при n , стремящемся к бесконечности».
ЗАМЕЧАНИЕ. Если для последовательности
a1 , a2 , … an , …
найдется такое число a , что an → a при , то эта последовательность ограничена.
ОПРЕДЕЛЕНИЕ 2. Говорят, что последовательность
a1 , a2 , … an , …
стремится к бесконечности, если для любого положительного числа C найдется такое натуральное число N , что при всех n > N выполняется неравенство
| an| > C .
Условие того, что числовая последовательность
a1 , a2 , … an , … ,
стремится к бесконечности, записывают с помощью обозначения
или с помощью обозначения
при
.
ПРИМЕР 1. Для любого числа k > 0 справедливо равенство
ПРИМЕР 2 . Для любого числа k > 0 справедливо равенство
ПРИМЕР 3. Для любого числа a такого, что | a | < 1, справедливо равенство
ПРИМЕР 4. Для любого числа a такого, что | a | > 1, справедливо равенство
ПРИМЕР 5 . Последовательность
– 1 , 1 , – 1 , 1 , … ,
заданная с помощью формулы общего члена
an = (– 1)n ,
предела не имеет.
Свойства пределов числовых последовательностей
Рассмотрим две последовательности
a1 , a2 , … an , … , и b1 , b2 , … bn , … .
Если при существуют такие числа a и b , что
и
,
то при существуют также и пределы суммы, разности и произведения этих последовательностей, причем
Если, кроме того, выполнено условие
то при существует предел дроби
причем
Для любой непрерывной функции f (x) справедливо равенство
Вывод формулы для суммы членов бесконечно убывающей геометрической прогрессии
Рассмотрим геометрическую прогрессию
b1 , b2 , … bn , … ,
знаменатель которой равен q .
Для суммы первых n членов геометрической прогрессии
Sn = b1 + b2 + … + bn , n = 1, 2, 3, …
справедлива формула
Если для суммы всех членов бесконечно убывающей геометрической прогрессии ввести обозначение
S = b1 + b2 + … + bn + … ,
то будет справедлива формула
В случае бесконечно убывающей геометрической прогрессии знаменатель q удовлетворяет неравенству
| q | < 1 ,
поэтому, воспользовавшись cвойствами пределов числовых последовательностей и результатом примера 3, получаем
Итак,
Примеры вычисления пределов последовательностей. Раскрытие неопределенностей
ОПРЕДЕЛЕНИЕ 3. Если при нахождении предела дроби выясняется, что и числитель дроби, и знаменатель дроби стремятся к , то вычисление такого предела называют раскрытием неопределенности типа
.
Часто неопределенность типа удается раскрыть, если и в числителе дроби, и в знаменателе дроби вынести за скобки «самое большое» слагаемое. Например, в случае, когда в числителе и в знаменателе дроби стоят многочлены, «самым большим» слагаемым будет член с наивысшей степенью.
ПРИМЕР 6. Найти предел последовательности
РЕШЕНИЕ. Сначала преобразуем выражение, стоящее под знаком предела, воспользовавшись свойствами степеней:
ОТВЕТ.
ПРИМЕР 7 . Найти предел последовательности
ОТВЕТ.
В следующих двух примерах показано, как можно раскрыть неопределенности типа.
ПРИМЕР 8 . Найти предел последовательности
РЕШЕНИЕ. Сначала преобразуем выражение, стоящее под знаком предела, приводя дроби к общему знаменателю:
Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое в каждой из скобок знаменателя дроби:
Теперь, используя cвойства пределов последовательностей и результат примера 1, получаем
ОТВЕТ.
ПРИМЕР 9. Найти предел последовательности
РЕШЕНИЕ. В рассматриваемом примере неопределенность типа возникает за счет разности двух корней, каждый из которых стремится к
. Для того, чтобы раскрыть неопределенность, умножим и разделим выражение, стоящее под знаком предела, на сумму этих корней и воспользуемся формулой сокращенного умножения «разность квадратов».
Из-за большого размера формул подробные вычисления видны только на устройствах с разрешением экрана по ширине не менее 768 пикселей (например, на стационарных компьютерах, ноутбуках и некоторых планшетах). На Вашем мобильном устройстве отображается только результат описанных операций.
Преобразуем дробь, вынося за скобки «самое большое» слагаемое в числителе дроби и «самое большое» слагаемое из-под каждого корня в знаменателе дроби, а затем сокращая дробь на n2:
Теперь, используя cвойства пределов последовательностей и результат примера 1, получаем
ОТВЕТ.
ПРИМЕР 10. Найти предел последовательности
РЕШЕНИЕ. Замечая, что для всех k = 2, 3, 4, … выполнено равенство
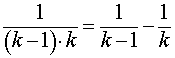
получаем
ОТВЕТ. 1 .
Число e. Второй замечательный предел
Рассмотрим последовательность
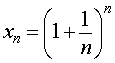 |
(1) |
В дисциплине «Математический анализ», которую студенты естественнонаучных и технических направлений высших учебных заведений изучают на 1 курсе, доказывают, что последовательность (1) монотонно возрастает и ограничена сверху. Из теоремы Вейерштрасса о монотонных и ограниченных последовательностях, доказательство которой выходит за рамки школьного курса математики, вытекает, что последовательность (1) имеет конечный предел. Этот предел принято обозначать буквой e.
Таким образом, справедливо равенство
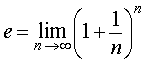 |
(2) |
причем расчеты показывают, что число
e = 2,718281828459045…
и является иррациональным и трансцендентным числом.
Число e играет исключительно важную роль в естествознании и, в частности, служит основанием натуральных логарифмов и основанием показательной функции
y = e x,
которую называют «экспонента».
Число e также является пределом последовательности
|
|
(3) |
что позволяет вычислять число e с любой точностью. Конечно же, доказательство формулы (3) выходит за рамки школьного курса математики.
ЗАМЕЧАНИЕ. Предел (2), в котором для последовательностей раскрывается неопределенность типа , называют вторым замечательным пределом. В разделе нашего справочника «Пределы функций» можно ознакомиться со вторым замечательным пределом для функций.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 сентября 2021 года; проверки требует 1 правка.
Предел числовой последовательности — предел последовательности элементов числового пространства. Числовое пространство — это метрическое пространство, расстояние в котором определяется как модуль разности между элементами. Поэтому, число 






В случае комплексных чисел существование предела последовательности равносильно существованию пределов соответствующих последовательностей вещественных и мнимых частей комплексных чисел.
Предел (числовой последовательности) — одно из основных понятий математического анализа. Каждое вещественное число может быть представлено как предел последовательности приближений к нужному значению. Система счисления предоставляет такую последовательность уточнений. Целые и рациональные числа описываются периодическими последовательностями приближений, в то время как иррациональные числа описываются непериодическими последовательностями приближений.[1] В численных методах, где используется представление чисел с конечным числом знаков, особую роль играет выбор системы приближений. Критерием качества системы приближений является скорость сходимости. В этом отношении, оказываются эффективными представления чисел в виде цепных дробей.
История[править | править код]
Понятие предела последовательности использовалось ещё Ньютоном во второй половине XVII века и математиками XVIII века, такими как Эйлер и Лагранж, однако они понимали предел интуитивно. Первые строгие определения предела последовательности дали Больцано в 1816 году и Коши в 1821 году.
Определение[править | править код]
Число 


- (для всякого малого эпсилон найдётся номер, начиная с которого элементы последовательности будут отличаться от предела меньше чем на эпсилон)
Если число 



Если никакое вещественное число не является пределом последовательности 
Для некоторых последовательностей предел полагают равным бесконечности.
А именно, говорят, что последовательность 
Формально,
Кроме того, если все элементы стремящейся к бесконечности последовательности, начиная с некоторого номера, имеют положительный знак, то говорят, что предел такой последовательности равен плюс бесконечности.
Если же элементы стремящейся к бесконечности последовательности, начиная с некоторого номера, имеют отрицательный знак, то говорят, что предел такой последовательности равен минус бесконечности.
Любая последовательность, стремящаяся к бесконечности — неограниченная. Однако обратное неверно.
Частичный предел последовательности — это предел одной из её подпоследовательностей.
Верхний предел последовательности — это наибольшая из её предельных точек (что равносильно, наибольший частичный предел).
Нижний предел последовательности — это наименьшая из её предельных точек.
Обозначения[править | править код]
Тот факт, что последовательность 

или
Свойства[править | править код]
Существуют определённые особенности для предела последовательностей вещественных чисел.[2]
Можно дать альтернативные определения предела последовательности. Например, называть пределом число, в любой окрестности которого содержится бесконечно много элементов последовательности, в то время, как вне таких окрестностей содержится лишь конечное число элементов. Таким образом, пределом последовательности может быть только предельная точка множества её элементов. Это определение согласуется с общим определением предела для топологических пространств.
Это определение обладает неустранимым недостатком: оно объясняет, что такое предел, но не даёт ни способа его вычисления, ни информации о его существовании. Всё это выводится из приводимых ниже (доказуемых по определению) свойств предела.
Свойства[править | править код]
- Единственность предела.

Арифметические свойства[править | править код]
Свойства сохранения порядка[править | править код]
- Если все элементы сходящейся последовательности, начиная с некоторого номера, не превышают некоторого числа, то и предел этой последовательности также не превышает этого числа.
- Если некоторое число не превышает все элементы сходящейся последовательности, начиная с некоторого номера, то оно также не превышает и предела этой последовательности.
- Если некоторое число строго превышает все элементы сходящейся последовательности, начиная с некоторого номера, то предел этой последовательности не превышает этого числа.
- Если все элементы сходящейся последовательности, начиная с некоторого номера, строго превышают некоторое число, то это число не превышает предела этой последовательности.
- Если, начиная с некоторого номера, все элементы одной сходящейся последовательности не превышают соответствующих элементов другой сходящейся последовательности, то и предел первой последовательности не превышает предела второй.
- Для числовых последовательностей справедлива теорема о двух милиционерах (принцип двустороннего ограничения).
Другие свойства[править | править код]
- Сходящаяся числовая последовательность имеет только один предел.
- Замкнутость. Если все элементы сходящейся числовой последовательности лежат на некотором отрезке, то на этом же отрезке лежит и её предел.
- Предел последовательности из одного и того же числа равен этому числу.
- Замена или удаление конечного числа элементов в сходящейся числовой последовательности не влияет на её предел.
- У возрастающей ограниченной сверху последовательности есть предел. То же верно для убывающей ограниченной снизу последовательности.
- Произведение бесконечно большой и ограниченной снизу последовательности является бесконечно большой последовательностью.
- Имеет место теорема Штольца.
Примеры[править | править код]
Случай комплексных чисел[править | править код]
Комплексное число 






Последовательность 



Примеры[править | править код]
Не у всякой ограниченной последовательности существует предел. Например, если взять в качестве пространства множество вещественных чисел со стандартной топологией, а в качестве 


См. также[править | править код]
- Частичный предел
- Замечательные пределы
- Фундаментальная последовательность
- Ряд
- Предел функции
- Неопределённости пределов
- Сравнение бесконечно малых величин
- Последовательность
Примечания[править | править код]
- ↑ Здесь подразумевается повторение чисел в записи числа в некоторой фиксированной системе счисления.
- ↑ В. А. Ильин, В. А. Садовничий, Бл. Х. Сендов. Глава 3. Теория пределов // Математический анализ / Под ред. А. Н. Тихонова. — 3-е изд., перераб. и доп. — М.: Проспект, 2006. — Т. 1. — С. 68—105. — 672 с. — ISBN 5-482-00445-7.

















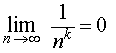
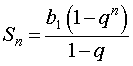
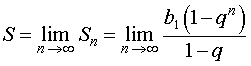

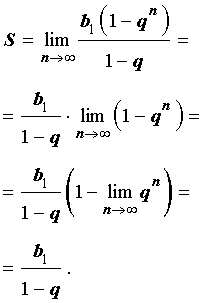
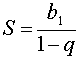
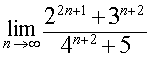
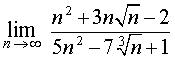
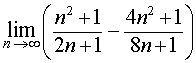


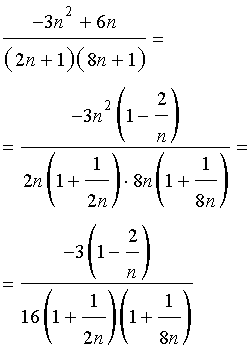
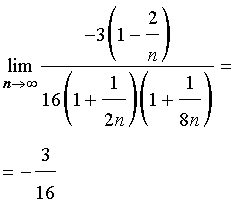






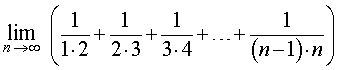











![x_n ~ xrightarrow[n to infty]{} ~ a](https://wikimedia.org/api/rest_v1/media/math/render/svg/dca29e2afe97f630d6adbac6cd34cbf9b249d3c1)







![forall n in N colon x_n in [a,~b] ~ Rightarrow ~ lim_{n to infty} x_n in [a,~b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/27a2ce0ddf926779c16d4ad74adab533a8a854ec)



![lim_{n to infty} sqrt[n]{n} = 1](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad8399b997df7368a350c447667a7003822626e1)


![lim_{n to infty} x_n = x ~ Rightarrow ~ lim_{n to infty} sqrt[n]{prod_{k = 1}^{n} x_k} = x](https://wikimedia.org/api/rest_v1/media/math/render/svg/dc5bb922a2a09d19904ad72ede143d98304c072c)
![forall n in N colon x_n > 0 ~ Rightarrow ~ lim_{n to infty} frac{x_{n+1}}{x_n} = lim_{n to infty} sqrt[n]{x_n}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3d8c2d4839dc08ba93add5d353960cf9e51ad2a6)


