Как найти предел последовательности с факториалами

Уважаемые студенты!
Заказать задачи по физике, информатике, экономике, праву, химии, теормеху, сопромату и другим предметам можно здесь всего за 10 минут.

Пределы с факториалами

Факториал числа $n!$ равен произведению чисел от 1 до $n$. Например, $5! = 1cdot 2cdot 3cdot 4cdot 5$. Для решения примеров на пределы с факториалами понадобится знать и понимать формулу разложения на множители. $$ (n+1)! = n!(n+1) qquad (1) $$

Например, $5! = 4! cdot 5 $, или $5! = 3! cdot 4 cdot 5$, а можно еще так $5! = 2! cdot 3 cdot 4 cdot 5 $.

Основная суть идеи:

1. Выносим наименьший факториал числа за скобки в числителе и знаменателе
2. Сокращаем факториалы, избавляя тем самым предел от них
3. Вычисляем предел подходящим способом

Пример 1

Вычислить предел с факториалами $limlimits_{xto infty} frac{n!}{(n+1)!} $

Решение

Подставляя $x=infty$ в предел получаем неопределенность бесконечность делить на бесконечность. Избавимся от факториалов. Для этого используем формулу (1) для их разложения на множители. $ (n+1)! = n! (n+1) $ Подставляем в предел полученное выражение и сокращаем на $n!$ числитель со знаменателем. $$ limlimits_{xto infty} frac{n!}{n! (n+1)} = limlimits_{nto infty} frac{1}{n+1} $$ Теперь подставляя бесконечность в предел вычисляем ответ. $$ limlimits_{nto infty} frac{1}{n+1} = (frac{1}{infty}) = 0 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$limlimits_{xto infty} frac{n!}{(n+1)!} = 0 $$

Пример 2

Решить предел с факториалом $ limlimits_{xto infty} frac{(2n+1)! + (2n+2)!}{(2n+3)!} $

Решение

Определяем наименьший факториал $(2n+1)!$. Его нужно вынести за скобки. Но перед этим нужно разложить остальные факториалы на множители, одним из которых будет $(2n+1)!$. Для этого воспользуемся формулой (1). $$(2n+2)! = (2n+1)! cdot (2n+2) $$ $$ (2n+3)! = (2n+1)! cdot (2n+2)cdot(2n+3) $$ Выполняем замену в пределе на полученные выражения. $$limlimits_{xto infty} frac{(2n+1)! + (2n+1)! (2n+2)}{(2n+1)!(2n+2)(2n+3)} = $$ Выносим общий множитель с факториалом в числителе за скобки и выполняем сокращение со знаменателем. $$ limlimits_{x to infty} frac{(2n+1)! (1+ (2n+2))}{(2n+1)!(2n+2)(2n+3)} = limlimits_{xto infty} frac{1+ (2n + 2)}{(2n+2)(2n+3)} = $$ Раскрываем полученные скобки и сокращаем на $2n+3$. $$ = limlimits_{x to infty} frac{2n+3}{(2n+2)(2n+3)} = limlimits_{xto infty} frac{1}{2n+2} = (frac{1}{infty}) = 0$$

Ответ

$$ limlimits_{xto infty} frac{(2n+1)! + (2n+2)!}{(2n+3)!} = 0 $$

Пример 3

Найти предел $limlimits_{xto infty} frac{3(n+1)!}{2(n+1)!-n!} $

Решение

Понятно, что предел имеет неопределенность $frac{infty}{infty}$. Попробуем её устранить избавившись от факториалов. Сразу находим среди них наименьший $n!$. Его нужно будет вынести за скобки. Но перед этим остальные факториалы нужно разложить по формуле (1) и затем подставить в предел. $$ (n+1)! = n! (n+1) $$ $$ limlimits_{xto infty} frac{3n! (n+1)}{2n!(n+1) – n!} = limlimits_{xto infty} frac{3(n+1)}{2(n+1)-1} = $$ Далее раскрываем скобки, попутно упрощая выражения, и затем выносим $n$. $$ = limlimits_{xto infty} frac{3n+3}{2n+1} = limlimits_{xto infty} frac{n(3+frac{3}{n})}{n(2+frac{1}{n})} = $$ Осталось выполнить сокращение на $n$ и получить ответ. $$ = limlimits_{xto infty} frac{3+frac{3}{n}}{2+frac{1}{n}} = frac{3+0}{2+0} = frac{3}{2} $$

Ответ

$$limlimits_{xto infty} frac{3(n+1)!}{2(n+1)!-n!} = frac{3}{2} $$

I assume your limits are $n to infty$.

For those examples, it might be easier to note that…

• … in the first, $n!$ grows way faster than $n-1$, so obviously the limit would be $0$. Alternatively, apply the definition of factorial:

$$frac{n-1}{n!} = frac{n-1}{n(n-1)(n-2)(n-3)cdots(2)(1)} = frac{1}{n cdot (n-2)!}$$

• … in the second, the contribution from $2$ would be completely outweighed by that of $n!$. That is, for large $n$, intuitively, $n! – 2 approx n!$, making the limit obviously $1$. You could also do some cancellation here, since breaking up the fraction yields
  $$frac{n! – 2}{n!} = frac{n!}{n!} – frac{2}{n!} = 1 – frac{2}{n!}$$
  which has an obvious limit.

Beyond that, I’m not sure how to help you with some factorial-based limits. Many limits you have to take as they come; there is no single rule or practice to handle them all. Personally, my favorite is Stirling’s approximation,

$$n! sim sqrt{2 pi n} cdot left( frac n e right)^n$$

which is an approximation that gets better and better for larger and larger $n$. In fact, this establishes an “asymptotic equivalence” between the two which means, often times, you can exchange these two expressions equivalently in infinite limits, which can often make things easier to see or derive.

Задачи на нахождение пределов числовых последовательностей при движении номера их общего члена до бесконечности занимают важное место в высшей математике и могут многое рассказать об их сходимости.

Основная суть в нахождении таких границ заключается в выделении из числителя и знаменателя крупнейшего слагаемого или множителя. После этого числитель и знаменатель делят на это значение и получают конечный результат.

Рассмотрим задачи из сборника задач Дубовика В.П., Юрика И.И. “Высшая математика”.

———————————–

Пример 1.

Найти пределы.

1) (4. 285)

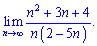
2) (4. 291)

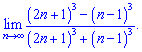
3) (4. 293)

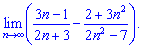
4) (4. 295)

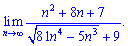
5) (4. 298)

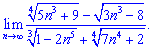
6) (4. 301)

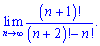
7) (4. 302)

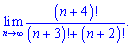
8) (4. 304)

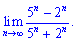
9) (4. 307)

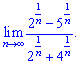
Решение.

1) Из числителя и знаменателя выделяем множитель который вносит наибольший вклад и сокращаем на него

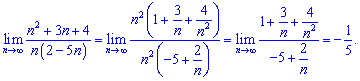
2) Выделяем множители содержащие третью степень и сокращаем на них

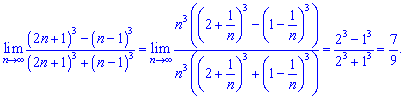
3) Разбиваем данный пример на сумму двух границ

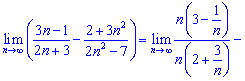
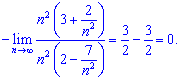
4) В такого типа примерах нужно вынести в знаменателе из-под корня множитель в наибольшей степени

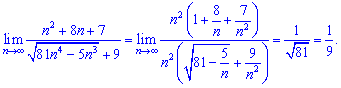
5) В этом примере и подобных нужно найти слагаемое с максимальным степенью

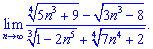
В числителе переменная 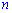находится в степенях 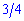и 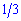. Переменная в знаменателе находится в степенях 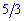и 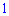. Поскольку наибольший степень знаменателя 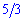является большим от степени числителя 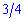то знаменатель растет быстрее за числитель. В таком случае граница

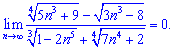
Если бы было наоборот, то предел был бы равен бесконечности (). В случае одинаковых показателей переменной, числитель и знаменатель сокращаем на нее и получаем константу.

6) Границы с факториалами занимают особое место среди числовых последовательностей. При их нахождении числитель и знаменатель раскладывают до наибольшего общего факториала

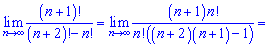
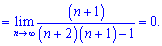
Граница равна нулю, так как степень знаменателя 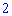больше от числителя .

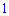7) Как и в предыдущем примере раскладываем до наибольшего общего факториала

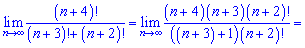
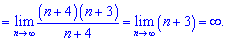
8) К примерам в которых переменная 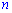выступает в качестве показателя надо относиться с особым вниманием. Незнание закономерностей поведения степенных функций часто приводит к ошибкам в решении. В данном примере 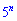растет значительно быстрее 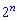поэтому его выделяем как самый множитель

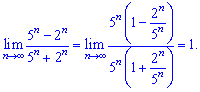
9) Величины 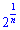и 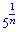стремятся к нулю при . На основе этого вычисляем предел

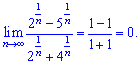
Подобных примеров можно найти немало и решения большинства из них заключается в нахождении доминирующего множителя. Если он в числителе то граница направляется к бесконечности, в знаменателе – к нулю. И только когда и там и там можно сократить на этот множитель дробь и получить предел в виде константы.

———————————–

Посмотреть материалы:

• Числовая последовательность и ее предел
• Вычисление пределов по правилу Лопиталя
• Предел функции
• Замечательные пределы на примерах
• Эквивалентные бесконечно малые функции при вычислении пределов

Пусть даны две
последовательности

,

и

.
Рассмотрим отношение этих последовательностей.
О пределе этого отношения последовательностей
заранее ничего определенного сказать
нельзя, так как в зависимости от самих
последовательностей предел их отношения
может принимать различные значения.
Например:

если
,

,
то

;

если
,

,
то

;

если
,

,
то

;

если
,

,
то

,

а этот предел не
существует.

Таким образом, для
нахождения предела последовательности

недостаточно знать, что

,

.
Нужны еще дополнительные сведения о
характере изменения

и

.

Для нахождения этого
предела в каждом конкретном случае
требуются специальные приемы.

Возникают неопределенности
различного вида.

1. Если

   ,

   ,
   то говорят, что выражение
   

   представляет собой неопределенность
   вида
   
   .

2. Если
   
   ,
   
   ,
   то выражение

   также представляет собой неопределенность
   и ее называют неопределенностью вида
   
   .

3. Если

   ,

   ,
   то для выражения
   

   получаем неопределенность вида
   
   .

4. Если

   ,
   
   ,
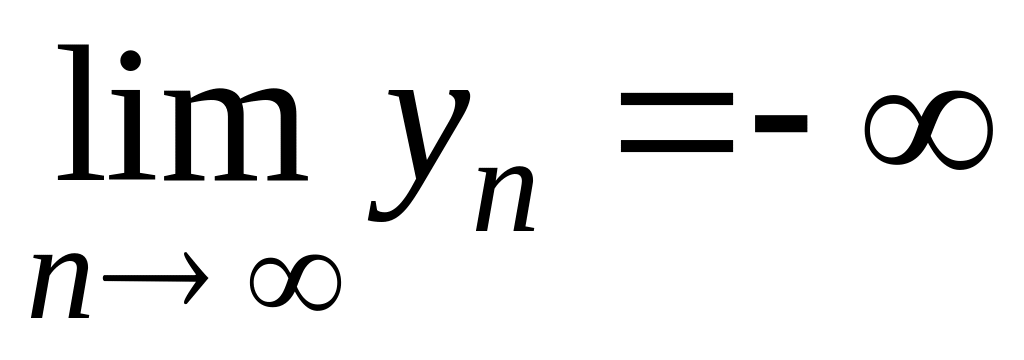
   то выражение
   

   представляет собой неопределенность
   вида
   
   .

Раскрыть соответствующую
неопределенность – это значит найти
предел (если он существует) соответствующего
выражения.

§3. Неопределенность вида

Правило. Чтобы
раскрыть неопределенность вида

надо числитель и знаменатель почленно
разделить на переменную величину в
наибольшей степени.

Пример 1.

Вычислить предел
числовой последовательности

.

Решение.

Дробь


– есть отношение
двух бесконечно больших величин, о
котором без исследования ничего
определенного сказать нельзя
–неопределенность вида

.
Здесь также нельзя применить теорему
о пределе частного, так как в условии
этой теоремы предполагается, что пределы
числителя и знаменателя существуют, а
в нашем случае при

.

В этом случае поступают
так: числитель и знаменатель дроби
делят на наивысшую степень n,встречающуюся
в членах дроби (в данном случае на n
).

.

.

Ответ:

.

Пример 2.

Вычислить предел
числовой последовательности

.

Решение.

Здесь неопределенность
вида

.
Разделим числитель и знаменатель дроби
на наивысшую степень n,
встречающуюся в дроби, т.е. на 
:

.

.

Ответ:

.

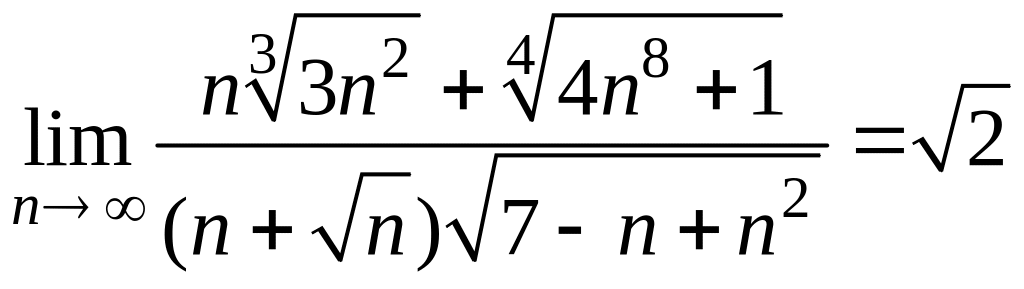
Пример 3.

Вычислить предел

.

Решение.

При

,

т.е. возникает
неопределенность вида

.

Последовательность
sin n
ограничена (
).

Разделим числитель и
знаменатель дроби на n

=

,

т.к.

бесконечно
малая последовательность при

и произведение бесконечно малой
последовательности на ограниченную –
есть бесконечно малая последовательность,
поэтому

при

.

Ответ:

.

§4. Неопределенность вида

в случае арифметической, геометрической
прогрессий и факториалов

Правило 1.

Чтобы раскрыть
неопределенность вида

в случае арифметической прогрессии
надо воспользоваться формулой суммы
первых n
членов арифметической прогрессии:

.

Пример 1.

Вычислить предел
числовой последовательности

.

Решение.

В знаменателе стоит
сумма членов арифметической прогрессии.
Воспользуемся формулой суммы первых n
членов арифметической
прогрессии.

В нашем случае

,
тогда

.

Получаем,

=
.

Ответ:

.

Правило 2.

Чтобы раскрыть
неопределенность вида

в случае геометрической прогрессии
надо воспользоваться формулой суммы
первых n
членов геометрической прогрессии:

.

Пример 2.

Вычислить предел
числовой последовательности

.

Решение.

Данная последовательность
представляет собой сумму двух
геометрических прогрессий:

.

Применим формулу суммы
первых n
членов геометрической прогрессии. Для
первой прогрессии

для второй прогрессии

.

Имеем,

=

=

т.к. если число

то

при

Ответ:

.

Правило 3.

Чтобы раскрыть
неопределенность вида

в случае факториалов надо выразить все
факториалы последовательности через
наименьший и сократить на него.

Пример 3.

Вычислить предел
числовой последовательности

.

Решение.

По определению

,

,

.

Поэтому, числитель и
знаменатель стремятся к

,
т.е. мы имеем неопределенность вида

.
Выберем наименьший факториал и выразим
через него все остальные. В нашем примере
наименьшим будет

.
Тогда

,

.
Имеем

Здесь

при

.

Ответ:

.

§5. Неопределенность вида

Правило.

Неопределенность
вида

,
получающаяся
в результате алгебраической суммы
иррациональных выражений, устраняется
или приводится к типу

путем домножения и деления на одно и то
же выражение, приводящее к формулам
сокращенного умножения. В случае
квадратных
корней
последовательность домножается на
сопряженное выражение и применяется
формула

.
В случае кубических
корней
последовательность домножается на
неполный квадрат суммы или разности и
применяется формула

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Здравствуйте, начал изучать Математический анализ и столкнулся с непонятной задачей.
Если возможно объясните, как такое решать? (если возможно подробное решение, я так лучше пойму)

Задача на: “Вычислить предел числовой последовательности”

lim = n!(n + 1)!/((8 + 85(n!)^2)(n+1))
x->00

или так будет понятнее:

n!(n + 1)!
_____________
((8 + 85(n!)^2)(n+1))

Я по аналогии с другими задачами все сократил и пришел к формату: 1/ (8 + 85(n!)) т.е. по идее = 0
(так как 1/Б.Б. = Б.М.)

Но при проверке в калькуляторе получаю: 1 / 85
Может кто нибудь подсказать? Как он мог до этого дойти или мой ответ тоже верен?