$begingroup$
How I can find a limit for this recursively defined sequence?
$$a_0>0, a_{n+1}=frac{a_{n}+2}{3a_{n}+2}$$
I’m particularly interested in answers involving concepts like contractive sequences and fixed points.
Many thanks.
Mike Spivey
54.3k17 gold badges174 silver badges277 bronze badges
asked Jan 21, 2013 at 22:30
$endgroup$
$begingroup$
There are two fixed points, $frac23$ and $-1$. Let’s look at the stability near each of these.
Let
$$
f(x)=frac{x+2}{3x+2}tag{1}
$$
Then
$$
f'(x)=-frac43frac1{(3x+2)^2}tag{2}
$$
Since $f’left(frac23right)=-frac13$ and $f'(-1)=-frac43$, $frac23$ is a stable fixed point, $|f'(x)|lt1$, and $-1$ is an unstable fixed point, $|f'(x)|>1$.
Let’s investigate the stable fixed point. The recursive definition centered on $frac23$ becomes
$$
left(a_n-tfrac23right)=-frac{left(a_{n-1}-tfrac23right)}{3left(a_{n-1}-tfrac23right)+4}tag{3}
$$
Note that if $a_{n-1}gt0$, then $3left(a_{n-1}-tfrac23right)+4gt2$. Thus, $(3)$ implies that
$$
left|a_n-tfrac23right|lttfrac12left|a_{n-1}-tfrac23right|tag{4}
$$
$(4)$ guarantees convergence.
answered Jan 22, 2013 at 3:35
robjohn♦robjohn
336k34 gold badges445 silver badges830 bronze badges
$endgroup$
5
$begingroup$
A little playing shows that the limit “should” be $frac{2}{3}$. So it is natural to compute $a_{n+1}-frac{2}{3}$.
We get
$$a_{n+1}-frac{2}{3}=frac{a_n+2}{3a_n+2}-frac{2}{3}=frac{frac{2}{3}-a_n}{3a_n+2}.$$
Thus
$$left|a_{n+1}-frac{2}{3}right|=left|a_n-frac{2}{3}right|frac{1}{3a_n+2}.$$
In particular,
$$left|a_{n+1}-frac{2}{3}right|lt frac{1}{2}left|a_n-frac{2}{3}right|.$$
So with each iteration our distance from $frac{2}{3}$ shrinks by a factor of at least $frac{1}{2}$. It follows that $lim_{ntoinfty}a_n=frac{2}{3}$.
answered Jan 21, 2013 at 22:53
André NicolasAndré Nicolas
499k47 gold badges537 silver badges969 bronze badges
$endgroup$
3
$begingroup$
Use the recurrence relation
$$ a_{n+1} – a_{n} = frac{a_n +2 }{ 3 a_n +2} – frac{a_{n-1} +2}{3 a_{n-1} +2 } = frac{4(a_{n-1} -a_{n})}{(3 a_{n-1} +2)(3 a_n +2)}. $$
Since
$$
3 a_n = 3 frac{a_{n-1} +2 }{3 a_{n-1} +2} > 1 + frac{1}{a_{n-1}+1} >1, quadforall ngeq 1,
$$
it follows that
$$
|a_{n+1} – a_{n}| < frac{4}{9} |a_{n} – a_{n-1}|.
$$
Iteration gives
$$
|a_{n+1} – a_{n}| < left(frac{4}{9}right)^n |a_{1} – a_{0}|.
$$
The series $sum_{n=1}^infty (a_{n+1}-a_n)$, of positive terms, is dominated by the convergent series $|a_1-a_0| sum_{n=1}^infty (4/9)^n$ and so converges. We have $sum_{n=1}^infty (a_{n+1}-a_n)= lim_{nto infty} a_n – a_1$ which shows that the limit exists.
Then, to find to fixed points we can pass to the limit in the recurrence relation
$$
a_{infty}= frac{a_{infty}+2}{3 a_{infty} +2},
$$
which leads to $a_{infty}= 2/3.$
answered Jan 21, 2013 at 22:45
BerkheimerBerkheimer
2,05815 silver badges30 bronze badges
$endgroup$
6
$begingroup$
$1$. First show that $a_n in (0,1)$ using induction.
$2$. Now if $a_0 < dfrac23$, using induction, show that $a_n$ is a monotone increasing sequence bounded above by $dfrac23$.
$3$. $vert vert vert^{ly}$, if $a_0 > dfrac23$, using induction, show that $a_n$ is a monotone decreasing sequence bounded below by $dfrac23$.
$4$. Now recall the completeness of $mathbb{R}$/ monotone sequence theorem, to conclude that the limit exists.
$5$. Now make use of limit laws to show that if $lim_{n to infty} a_n = L$, then
$$L = dfrac{L+2}{3L+2}$$
$6$. Solve the quadratic to get that $L = dfrac23$.
answered Jan 21, 2013 at 22:39
$endgroup$
6
$begingroup$
Fix $cin(0,3^{-1})$ and show that the map
$$
varphi_c:[c,+infty)to[c,+infty):xmapstofrac{x+2}{3x+2}
$$
is well defined and what is more
$$
|varphi_c(x)-varphi_c(y)|leqfrac{4}{(3c+2)^2}|x-y|
$$
Hence you can apply Banach fixed point theorem to show that $varphi_c$ have unique fixed point on $[c,+infty)$ and this is point is $2/3$.
Since this fixed point is the same for all $c$ and $f|_{[c,+infty)}=varphi_c$, then $f$ has unique fixed point on $(0,+infty)$
answered Jan 21, 2013 at 22:57
NorbertNorbert
55.7k8 gold badges108 silver badges201 bronze badges
$endgroup$
7
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
1. Вычислить пять
первых членов последовательности
=
Решение. Подставив
вместо n
последовательно 1, 2, 3, 4, 5, получим
.
2. Написать общий член последовательности натуральных чисел, каждое из которых при делении на 3 дает остаток, равный 1.
Решение. Для того
чтобы число при делении на-3 давало
остаток 1, оно должно иметь вид 3n+1;
следовательно, общий член последовательности
=3n+1.
3. Последовательность задана рекуррентным соотношением . Найти первые члены последовательности.
Решение. Зададим
первый член последовательности: пусть
.
Полагая
в рекуррентном соотношении n=2,
получим
При n =3,
4, 5 соответственно находим
. В
результате получаем последовательность
2, 7, 22, 67, 202, … .
4.
Доказать,
что последовательность с общим членом
=
монотонно убывает.
Решение. Для
убывающей последовательности выполняется
неравенство
,
или
.Запишем
(
)-й
член последовательности:
Тогда
,
так как
<
при любом натуральном п.
Следовательно, данная последовательность
является убывающей.
5. Доказать, что последовательность ограничена снизу и сверху.
Решение. Очевидно,
> 1, т. е. последовательность ограничена
снизу. С другой стороны имеем
,
где
–
правильная дробь, и, следовательно,
1+
<2,
т. е. последовательность ограничена
сверху.
2.3. Предел числовой последовательности
Определение
1: Число
называется пределом
последовательности
, если
для любого сколь угодно малого
положительного числа
найдется такое натуральное число N,
зависящее от
,
что
при всех п
> N выполняется
неравенство
.
Неравенство
равносильно двойному неравенству
а-
<
<а+
.
Интервал (а-
,а+
)
называют
–
окрестностью точки
а.
Тот факт, что число а
есть предел последовательности
,
геометрически означает, что в любой
–
окрестности точки а
находятся
все члены последовательности
,
начиная
с некоторого номера, а вне её может
находиться лишь конечное число членов.
Последовательность
может иметь только один предел.
Определение
2:
Если последовательность имеет предел,
то такую последовательность называют
сходящейся;
последовательность,
не имеющую предела, называют расходящейся.
Если
последовательность
имеет пределом число а,
то
пишут
.
В
этом
случае говорят, что последовательность
сходится к числу а.
2.4. Теоремы о пределах
Теорема
Вейерштрасса:
Если
последовательность монотонна и
ограничена, то она имеет предел.
Другими словами
ограниченность последовательности
является необходимым условием сходимости.
Теорема I. Если
последовательности
и
сходятся, то
Теорема II. Если
последовательности
и
сходятся, то
Следствие.
Постоянный множитель можно выносить
за знак предела:
Теорема III. Если
последовательности
и
сходятся и предел последовательности
отличен от нуля, то
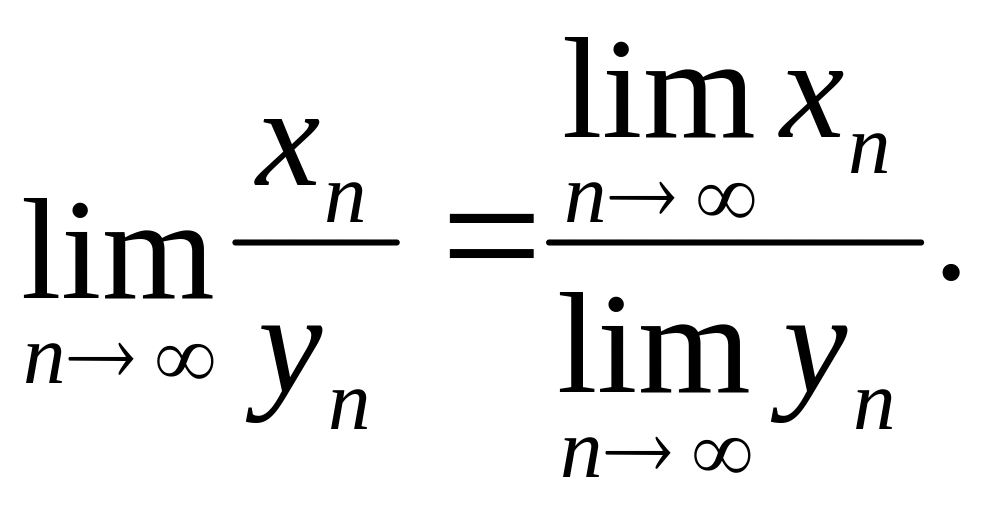
2.5. Предельный переход в неравенствах
Рассмотрим
последовательности
Теорема IV. Если
и, начиная с некоторого номера n,
выполняется неравенство
,
то
.
Теорема V. . Если
и, начиная с некоторого номера n,
справедливо неравенство
,
то
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Получились только первые 2 пункта
Найдём явную формулу a_n (не рекуррентную) (решала при помощи статьи “Общий член рекуррентной последовательности” с сайта Yagubov.ru)
1)
Составим характеристическое уравнение. Это будет r^(n+2) -2r^(n+1)-3r^n = 0;
Чуть упрощаем и получаем: r^2 – 2r -3 = 0; Отсюда получаем 2 корня этого уравнения: -1 и 3. Тогда общей формулой будет a_n = C1 * (-1)^(n-1) + C2 * 3^(n-1)
Найдём коэффициенты C1 и C2.
a0 = 1 = -C1 + C2 / 3
a1 = -5 = C1 + C2
Получаем C1 = -2, C2 = -3. Тогда a_n = 2 * (-1)^n – 3^n
Теперь ищем предел. (-1)^n – ограниченная, -3^n стремится к -бесконечности
Ответ: -бесконечность.
2)
Характеристич. уравнение: r^2 + 2r + 1 = 0; Отсюда r = -1 (кратность 2). Тогда общая формула: a_n = C1 * (-1)^(n-1) + C2 * n * (-1)^(n-1)
Найдём коэффициенты:
0 = -C1
5 = C1 + C2
C1 = 0; C2 = 5; a_n = 5n*(-1)^(n-1)
Тогда предела нет, тк n стремится к +бесконечности, а (-1)^(n-1) постоянно меняет знак
3) Тут, у меня не очень получилось ((
Характеристич. уравнение: 9r^3 = 15r^2 – 5r – 1
Корни: r1 = 1; r2,3 = (1 +- корень из 2)/3
Общая формула: a_n = C1*r1^(n-1) + C2*r2^(n-1) + C3*r3^(n-1), то есть a_n = C1 + C2*r2^(n-1) + C3*r3^(n-1)
Ищем коэффициенты.
