Как найти предел прочности при растяжении

Как найти предел прочности при растяжении

Использование материалов в строительстве невозможно без учёта их характеристик. Одна из важнейших — предел прочности при растяжении. Если не брать во внимание этот показатель, возведённое здание разрушится, так как конструктивные элементы не смогут выдержать нагрузку. Знать о свойстве стройматериала недостаточно, нужно уметь применять его на практике.

Предел прочности материала при растяжении — формула, характеристики и расчеты

Значение термина

Предел прочности материала при растяжении сокращённо обозначается ПП. Также допускается использовать выражение «временное сопротивление». Для обозначения предела прочности применяют буквы R или σ В (сигма). Единица измерения — мегапаскаль (МПа). Показатель означает допустимую величину силы, которая может воздействовать на объект до того, как он начнёт разрушаться. Речь идёт о механическом воздействии, но следует учитывать, что химические факторы способны изменить первоначальные свойства материала, в том числе повлиять на ПП. К немеханическим нагрузкам относят следующие:

  • нагревание;
  • охлаждение;
  • погодные условия (ветер, осадки, влажность);
  • агрессивная среда.

Предел прочности материала при растяжении — формула, характеристики и расчеты

Формула предела прочности при растяжении записывается так: R=0,64 (P/F), где F — площадь поверхности раскола предмета, а P — разрушающая нагрузка. При проектировании нельзя опираться на крайние значения, поэтому инженеры оставляют допуски на различные факторы, а также на период эксплуатации. Это значит, что при строительстве используется материал, у которого ПП превышает расчётное напряжение.

Изначально способность элемента выдерживать нагрузки определяли опытным путём. Материал использовали, не зная, как он себя поведёт во время эксплуатации, а после поломки заменяли более прочным. Со временем перешли к экспериментам и испытаниям, и по-прежнему самый точный способ найти предел прочности при натяжении и разрыве остаётся эмпирический.

Исследования проводят в лабораторных условиях, с использованием точной техники. Приборы фиксируют характеристики материала и то, как они изменяются под нагрузкой разной величины. Как правило, прочность измеряется так: предмет жёстко закрепляют и оказывают на него воздействие.

Предел прочности материала при растяжении — формула, характеристики и расчеты

Сначала закреплённый элемент растягивают. Он становится длиннее, при этом в одном месте образуется перешеек, и именно здесь заготовка разорвётся. Так ведут себя не все материалы, а только вязкие. Чугун, сталь и другие хрупкие сплавы растягиваются незначительно. При увеличении нагрузки они трескаются и разрушаются по наклонным плоскостям. Шейки не образуются.

Сила, прикладываемая в каждый момент, измеряется с точностью до тысячных долей ньютона. Одновременно определяют размер и характер деформации. Данные сверяют с таблицами.

Второй способ — математический анализ. Он заключается в том, что прочность определяют с помощью сложных вычислений. Однако без испытаний данные, полученные расчётным путём, нельзя считать полными. Дело в том, что на практике вещество может повести себя по-другому.

Классификация параметра

Материал обладает временным сопротивлением в ответ на воздействия разного характера, поэтому характеристику классифицируют на несколько групп. Усилия, которым подвергается заготовка или конструктивный элемент:

  • Растяжение. Изделие тянут за края с помощью специальной машины.
  • Кручение. Предмет помещается в условия, при которых работает крутящий вал.
  • Изгиб. Заготовку сгибают и разгибают в нескольких направлениях.
  • Сжатие. На материал давят попеременно с разных сторон.

Предел прочности материала при растяжении — формула, характеристики и расчеты

У одного и того же материала ПП может различаться. В качестве примера можно привести сталь. Она используется чаще, чем другие сплавы, потому что стальные конструкции показали себя как наиболее прочные, долговечные и устойчивые к неблагоприятным факторам. При этом они надёжны и не выделяют в атмосферу вредных веществ.

Существует несколько марок стали. Они производятся по разным технологиям, и в зависимости от этого различаются характеристики заготовок и конструкций. У обычных марок ПП составляет 300 Мпа. По мере увеличения содержания углерода прочность увеличивается. Самые твёрдые марки имеют показатель 900 МПа. Факторы, от которых зависят прочностные характеристики:

  • количество полезных и нежелательных примесей;
  • способ термической обработки (криообработка, закалка, отжиг).

Временное сопротивление и усталость

Между ПП и временным сопротивлением различным нагрузкам есть прямая связь. Второй показатель в документации и технической литературе обозначают символом Т. Он показывает, сколько длится деформация образца, когда на него воздействует постоянная нагрузка. Когда временное сопротивление прекращается, кристаллическая решётка вещества перестраивается. Это характерно для твёрдых материалов. В результате вещество становится более прочным, чем было до этого. Это явление называется самоупрочнением.

Ещё одна важная характеристика — усталость металла. Говоря о стали, применяют выражение «предел выносливости». Для обозначения используют символ R. Эта характеристика показывает, воздействие какой силы материал может переносить постоянно, а не разово. Во время эксперимента на образец оказывают давление заданной силы. Число воздействий составляет 107. За время испытаний материал не должен деформироваться или утратить исходные характеристики.

Предел прочности материала при растяжении — формула, характеристики и расчеты

На проведение таких экспериментов уходит много времени, поэтому их проводят не всегда. Часто обходятся математическими вычислениями, рассчитывая все важные коэффициенты.

Пределом пропорциональности называют максимальную нагрузку, при которой сохраняется соотношение, определяемое законом Гука. Согласно ему, тело деформируется прямо пропорционально величине оказываемого на него воздействия. Каждый материал обладает определённой степенью упругости. Она может быть классической и абсолютной. Изменения могут быть обратимыми и необратимыми. Пример первого типа — пружина: пока на неё воздействуют, она сжимается, а когда нажатие прекращается, расправляется.

Определение характеристик

Материалы обладают не только прочностным пределом, но и другими характеристиками. В случае со сталью это твёрдость и способность воспринимать ударные нагрузки. Испытания проводят следующим образом: в заготовку вдавливают алмазный конус или шар. Алмаз — эталон твёрдости. Размер следа зависит от того, насколько крепок испытуемый образец. Чем от мягче, тем больше отпечаток, и наоборот.

Прочность на удар рассчитывают так: на образце делают срез, затем ударяют. Результаты показывают характеристику для участка, который наиболее уязвим. Другие механические свойства, для которых получают данные эмпирическим путём:

  • Пластичность. Она показывает, до какой степени образец может изменять форму, сохраняя исходную структуру.
  • Усталость. Эта категория отображает, как долго материал не теряет свойства, испытывая длительные нагрузки.
  • Ударная вязкость. Характеристика означает, в какой степени вещество способно сопротивляться ударному воздействию.

Предел прочности материала при растяжении — формула, характеристики и расчеты

По прочности вещества делятся на классы. Они различаются по одной или нескольким характеристикам. Так, для двух классов показатели ПП могут быть одинаковыми, а значения относительного удлинения или текучести — разными.

Удельная прочность — величина, производная от предельной. Её получают путём деления исходного показателя на плотность материала. Практическая ценность расчёта состоит в том, что знание характеристики позволяет применять материал для различных целей, а не просто располагать данными о ПП. Показатель меняется в зависимости от объёма, толщины и веса изделия. Пример: тонкий лист легче деформировать, чем толстый.

Предел прочности и пластичность тесно связаны. Чем меньше второй параметр, тем быстрее разрушается образец. Материалы, у которых высокая пластичность, лучше поддаются обработке, они пригодны для изготовления деталей путём штамповки. Пример: элементы кузова штампуют из листов стали. Если у сплава невысокая пластичность, он относится к хрупким, хотя может быть иметь отличные показатели твёрдости. Одно из таких веществ — титан. Он плохо изгибается и тянется, но по твёрдости превосходит многие другие сплавы.

Для улучшения прочностных характеристик в материалы вводят добавки. Другой способ — термообработка.

Источник

Пределом прочности называют характеристику материала указывающую величину механических напряжений соответствующую максимальному значению нагрузки при испытаниях на растяжение.

Обозначение — σпч
Размерность — Паскаль [Па], либо кратные значения [МПа].
Синоним предела прочности — временное сопротивление (σв).

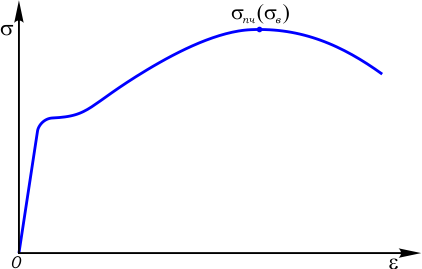
Предел прочности

Рис. 1. Предел прочности на диаграмме напряжений

Определяется экспериментально, как наивысшая точка условной диаграммы напряжений (рис. 1).

Либо по диаграмме растяжения как отношение максимальной продольной силы Fmax к начальной площади A0 поперечного сечения испытуемого образца:

σпч=Fmax/A0

Предел прочности является предельным напряжением при расчете допустимых напряжений для хрупких материалов.

Предел упругости >
Примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Решение задач и лекции по технической механике, теормеху и сопромату

Источник

Расчет на прочность при растяжении

2.4. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ РАСТЯЖЕНИИ Основной задачей расчета конструкции на растяжение является обеспечение ее прочности в условиях эксплуатации. Условие прочности – оценка прочности элемента конструкции, сводящаяся к сравнению расчетных напряжений с допускаемыми: σ≤рσ[р ]; σ с ≤[ с],σ (2.9) где σр и σс – наибольшие расчетные растягивающие и сжимающие напряжения; [σр] и [σс] – допускаемые напряжения при растяжении и сжатии. Допускаемое напряжение – наибольшее напряжение, которое можно допустить в элементе конструкции при условии его безопасной, долговечной и надежной работы: Здесь σпред – предельное напряжение (состояние), при котором конструкция перестает удовлетворять эксплуатационным требованиям; им мо- гут быть предел текучести, предел прочности, предел выносливости, пре- дел ползучести и др. Для конструкций из пластичных материалов при определении допускаемых напряжений используют предел текучести σт (рис. 2.4, а). Это связано с тем, что в случае его превышения деформации резко возрастают при незначительном увеличении нагрузки и конструкция перестает удовлетворять условиям эксплуатации. Допускаемое напряжение в этом случае определяют как Для хрупких материалов (чугун, бетон, керамика) где σвр и σвс – пределы прочности при растяжении и сжатии (рис. 2.4, б). Здесь [n] – нормативный коэффициент запаса прочности. В зависимости от той предельной характеристики, с которой сравнивают расчетное напряжение σ, различают [nт] – нормативный коэффициент запаса прочности по отношению к пределу текучести σт и [nв] – нормативный коэффициент запаса прочности по отношению к пределу прочности σв. Запас прочности – отношение предельно допустимой теоретической нагрузки к той нагрузке, при которой возможна безопасная работа конструкции с учетом случайных перегрузок, непредвиденных дефектов и недостоверности исходных данных для теоретических расчетов. Нормативные коэффициенты запаса прочности зависят: − от класса конструкции (капитальная, временная), − намечаемого срока эксплуатации, − условий эксплуатации (радиация, коррозия, загнивание), − вида нагружения (статическое, циклическое, ударные нагрузки) − неточности задания величины внешних нагрузок, − неточности расчетных схем и приближенности методов расчета − и других факторов. Нормативный коэффициент запаса прочности не может быть единым на все случаи жизни. В каждой отрасли машиностроения сложились свои подходы, методы проектирования и приемы технологии. В изделиях общего машиностроения принимают [nт] = 1,3 – 2,2; [nв] = 3 – 5. Вероятность выхода из строя приближенно можно оценить с помощью коэффициента запаса в условии прочности: n = 1 соответствует вероятности невыхода из строя 50 %; n = 1,2 соответствует вероятности невыхода из строя 90 %; n = 1,5 соответствует вероятности невыхода из строя 99 %; n = 2 соответствует вероятности невыхода из строя 99,9 %. Для неответственных деталей n = 2 много. Для ответственных – мало. Так для каната подъемного лифта это означает на 1000 подъемов одно падение. При расчете конструкций на прочность встречаются три вида задач, которые вытекают из условия прочности а) поверочный расчет (проверка прочности). Известны усилие N и площадь A. Вычисляют σ = N/A и, сравнивая его с предельным σт или σв (для пластичного и хрупкого материалов соответственно), находят фактический коэффициент запаса прочности который затем сопоставляют с нормативным [n]; б) проектный расчет (подбор сечения). Известны внутреннее усилие N и допускаемое напряжение [σ]. Определяют требуемую площадь поперечного сечения стержня в) определение грузоподъемности (несущей способности). Известны площадь А и допускаемое напряжение [σ]. Вычисляют внутреннее усилие N≤N[ ] = ⋅[σ]A, (2.15) а затем в соответствие со схемой нагружения – величину внешней нагрузки F ≤ [F].

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 марта 2021 года; проверки требуют 2 правки.

Преде́л про́чности — механическое напряжение sigma _{B}, выше которого происходит разрушение материала. Иначе говоря, это пороговая величина, превышая которую механическое напряжение разрушит некое тело из конкретного материала. Следует различать статический и динамический пределы прочности. Также различают пределы прочности на сжатие и растяжение.

Величины предела прочности[править | править код]

Статический предел прочности[править | править код]

Статический предел прочности, также часто называемый просто пределом прочности есть пороговая величина постоянного механического напряжения, превышая который постоянное механическое напряжение разрушит некое тело из конкретного материала. Согласно ГОСТ 1497-84 «Методы испытаний на растяжение», более корректным термином является временное сопротивление разрушению — напряжение, соответствующее наибольшему усилию, предшествующему разрыву образца при (статических) механических испытаниях. Термин происходит от представления, по которому материал может бесконечно долго выдержать любую статическую нагрузку, если она создаёт напряжения, меньшие статического предела прочности, то есть не превышающие временное сопротивление. При нагрузке, соответствующей временному сопротивлению (или даже превышающей её — в реальных и квазистатических испытаниях), материал разрушится (произойдет дробление испытываемого образца на несколько частей) спустя какой-то конечный промежуток времени (возможно, что и практически сразу, — то есть не дольше чем за 10 с).

Динамический предел прочности[править | править код]

Динамический предел прочности есть пороговая величина переменного механического напряжения (например при ударном воздействии), превышая которую переменное механическое напряжение разрушит тело из конкретного материала. В случае динамического воздействия на это тело время его нагружения часто не превышает нескольких секунд от начала нагружения до момента разрушения. В такой ситуации соответствующая характеристика называется также условно-мгновенным пределом прочности, или хрупко-кратковременным пределом прочности.

Предел прочности на сжатие[править | править код]

Предел прочности на сжатие есть пороговая величина постоянного (для статического предела прочности) или, соответственно, переменного (для динамического предела прочности) механического напряжения, превышая который механическое напряжение в результате (за конечный достаточно короткий промежуток времени) сожмет тело из конкретного материала — тело разрушится или неприемлемо деформируется.

Предел прочности на растяжение[править | править код]

Предел прочности на растяжение есть пороговая величина постоянного (для статического предела прочности) или, соответственно, переменного (для динамического предела прочности) механического напряжения, превышая который механическое напряжение в результате (за конечный достаточно короткий промежуток времени) разорвет тело из конкретного материала. (На практике, для детали какой либо конструкции достаточно и неприемлемого истончения детали.)

Другие прочностные параметры[править | править код]

Мерами прочности также могут быть предел текучести, предел пропорциональности, предел упругости, предел выносливости, предел прочности на сдвиг и др. так как для выхода конкретной детали из строя (приведения детали в негодное к использованию состояние) часто достаточно и чрезмерно большого изменения размеров детали. При этом деталь может и не разрушиться, а лишь только деформироваться. Эти показатели практически никогда не подразумеваются под термином «предел прочности».

Прочностные особенности некоторых материалов[править | править код]

Значения предельных напряжений (пределов прочности) на растяжение и на сжатие у многих материалов обычно различаются.

У композитов предел прочности на растяжение обычно больше предела прочности на сжатие. Для керамики (и других хрупких материалов) — наоборот, характерно многократное превышение пределом прочности на сжатие предела прочности на растяжение. Для металлов, металлических сплавов, многих пластиков, как правило, характерно равенство предела прочности на сжатие и предела прочности на растяжение. В большей степени это связано не с физикой материалов, а с особенностями нагружения, схемами напряженного состояния при испытаниях и с возможностью пластической деформации перед разрушением.

Прочность твёрдых тел обусловлена в конечном счёте силами взаимодействия между атомами, составляющими тело. При увеличении расстояния между атомами они начинают притягиваться, причем на критическом расстоянии сила притяжения по абсолютной величине максимальна. Напряжение, отвечающее этой силе, называется теоретической прочностью на растяжение и составляет σтеор ≈ 0,1E, где E — модуль Юнга . Однако на практике наблюдается разрушение материалов значительно раньше, это объясняется неоднородностями структуры тела, из-за которых нагрузка распределяется неравномерно.

Некоторые значения прочности на растяжение sigma _{0} в МПа (1 кгс/мм² = 100 кгс/см² ≈ 10 МН/м² = 10 МПа) (1 МПа = 1 Н/мм² ≈ 10 кгс/см²)[1]:

Материалы sigma _{0}, МПа sigma _{0}/E
Бор 5700 0,083
Графит (нитевидный кристалл) 2401 0,024
Сталь 60С2А рессорно-пружинная 1570 (после термообработки) 0,0074
Сапфир (нитевидный кристалл) 1500 0,028
Железо (нитевидный кристалл) 1300 0,044
Тянутая проволока из высокоуглеродистой стали 420 0,02
Тянутая проволока из вольфрама 380 0,009
Стекловолокно 360? 0,035
Сталь Ст0 обыкновенного качества 300 0,0017
Нейлон 50 0,0025

См. также[править | править код]

  • Теоретический предел прочности

Примечания[править | править код]

  1. ↑ Диапазон пределов прочности для стали составляет 500—3000 МПа (Б. Н. Арзамасов, В. А. Брострем, Н. А. Буше и др. Конструкционные материалы. Справочник. — М.: Машиностроение, 1990. — 688 с.).
Источник

From Wikipedia, the free encyclopedia

Two vises apply tension to a specimen by pulling at it, stretching the specimen until it fractures. The maximum stress it withstands before fracturing is its ultimate tensile strength.

Ultimate tensile strength (also called UTS, tensile strength, TS, ultimate strength or {displaystyle F_{text{tu}}} in notation)[1][2][3] is the maximum stress that a material can withstand while being stretched or pulled before breaking. In brittle materials the ultimate tensile strength is close to the yield point, whereas in ductile materials the ultimate tensile strength can be higher.

The ultimate tensile strength is usually found by performing a tensile test and recording the engineering stress versus strain. The highest point of the stress–strain curve is the ultimate tensile strength and has units of stress. The equivalent point for the case of compression, instead of tension, is called the compressive strength.

Tensile strengths are rarely of any consequence in the design of ductile members, but they are important with brittle members. They are tabulated for common materials such as alloys, composite materials, ceramics, plastics, and wood.

Definition[edit]

The ultimate tensile strength of a material is an intensive property; therefore its value does not depend on the size of the test specimen. However, depending on the material, it may be dependent on other factors, such as the preparation of the specimen, the presence or otherwise of surface defects, and the temperature of the test environment and material.

Some materials break very sharply, without plastic deformation, in what is called a brittle failure. Others, which are more ductile, including most metals, experience some plastic deformation and possibly necking before fracture.

Tensile strength is defined as a stress, which is measured as force per unit area. For some non-homogeneous materials (or for assembled components) it can be reported just as a force or as a force per unit width. In the International System of Units (SI), the unit is the pascal (Pa) (or a multiple thereof, often megapascals (MPa), using the SI prefix mega); or, equivalently to pascals, newtons per square metre (N/m2). A United States customary unit is pounds per square inch (lb/in2 or psi). Kilopounds per square inch (ksi, or sometimes kpsi) is equal to 1000 psi, and is commonly used in the United States, when measuring tensile strengths.

Ductile materials[edit]

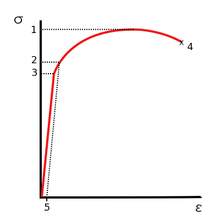
Figure 1: “Engineering” stress–strain (σ–ε) curve typical of aluminum

  1. Ultimate strength
  2. Yield strength
  3. Proportional limit stress
  4. Fracture
  5. Offset strain (typically 0.2%)

Many materials can display linear elastic behavior, defined by a linear stress–strain relationship, as shown in figure 1 up to point 3. The elastic behavior of materials often extends into a non-linear region, represented in figure 1 by point 2 (the “yield point”), up to which deformations are completely recoverable upon removal of the load; that is, a specimen loaded elastically in tension will elongate, but will return to its original shape and size when unloaded. Beyond this elastic region, for ductile materials, such as steel, deformations are plastic. A plastically deformed specimen does not completely return to its original size and shape when unloaded. For many applications, plastic deformation is unacceptable, and is used as the design limitation.

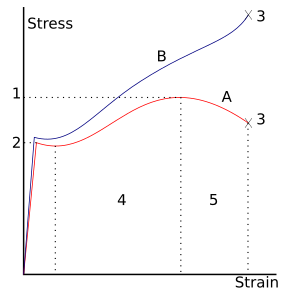
After the yield point, ductile metals undergo a period of strain hardening, in which the stress increases again with increasing strain, and they begin to neck, as the cross-sectional area of the specimen decreases due to plastic flow. In a sufficiently ductile material, when necking becomes substantial, it causes a reversal of the engineering stress–strain curve (curve A, figure 2); this is because the engineering stress is calculated assuming the original cross-sectional area before necking. The reversal point is the maximum stress on the engineering stress–strain curve, and the engineering stress coordinate of this point is the ultimate tensile strength, given by point 1.

Ultimate tensile strength is not used in the design of ductile static members because design practices dictate the use of the yield stress. It is, however, used for quality control, because of the ease of testing. It is also used to roughly determine material types for unknown samples.[4]

The ultimate tensile strength is a common engineering parameter to design members made of brittle material because such materials have no yield point.[4]

Testing[edit]

Round bar specimen after tensile stress testing

The “cup” side of the “cup–cone” characteristic failure pattern

Some parts showing the “cup” shape and some showing the “cone” shape

Typically, the testing involves taking a small sample with a fixed cross-sectional area, and then pulling it with a tensometer at a constant strain (change in gauge length divided by initial gauge length) rate until the sample breaks.

When testing some metals, indentation hardness correlates linearly with tensile strength. This important relation permits economically important nondestructive testing of bulk metal deliveries with lightweight, even portable equipment, such as hand-held Rockwell hardness testers.[5] This practical correlation helps quality assurance in metalworking industries to extend well beyond the laboratory and universal testing machines.

Typical tensile strengths[edit]

Typical tensile strengths of some materials

Material Yield strength
(MPa) 		Ultimate tensile strength
(MPa) 		Density
(g/cm3)
Steel, structural ASTM A36 steel 250 400–550 7.8
Steel, 1090 mild 247 841 7.58
Chromium-vanadium steel AISI 6150 620 940 7.8
Steel, 2800 Maraging steel[6] 2617 2693 8.00
Steel, AerMet 340[7] 2160 2430 7.86
Steel, Sandvik Sanicro 36Mo logging cable precision wire[8] 1758 2070 8.00
Steel, AISI 4130,
water quenched 855 °C (1570 °F), 480 °C (900 °F) temper[9]		 951 1110 7.85
Steel, API 5L X65[10] 448 531 7.8
Steel, high strength alloy ASTM A514 690 760 7.8
Acrylic, clear cast sheet (PMMA)[11] 72 87[12] 1.16
High-density polyethylene (HDPE) 26–33 37 0.85
Polypropylene 12–43 19.7–80 0.91
Steel, stainless AISI 302[13] 275 620 7.86
Cast iron 4.5% C, ASTM A-48 130 200 7.3
“Liquidmetal” alloy[citation needed] 1723 550–1600 6.1
Beryllium[14] 99.9% Be 345 448 1.84
Aluminium alloy[15] 2014-T6 414 483 2.8
Polyester resin (unreinforced)[16] 55 55  
Polyester and chopped strand mat laminate 30% E-glass[16] 100 100  
S-Glass epoxy composite[17] 2358 2358  
Aluminium alloy 6061-T6 241 300 2.7
Copper 99.9% Cu 70 220[citation needed] 8.92
Cupronickel 10% Ni, 1.6% Fe, 1% Mn, balance Cu 130 350 8.94
Brass 200 + 500 8.73
Tungsten 941 1510 19.25
Glass   33[18] 2.53
E-Glass — 1500 for laminates,
3450 for fibers alone		 2.57
S-Glass — 4710 2.48
Basalt fiber[19] — 4840 2.7
Marble — 15 2.6
Concrete — 2–5 2.7
Carbon fiber — 1600 for laminates,
4137 for fibers alone		 1.75
Carbon fiber (Toray T1100G)[20]
(the strongest human-made fibres)		   7000 fibre alone 1.79
Human hair 140–160 200–250[21]  
Bamboo fiber   350–500 0.4–0.8
Spider silk (see note below) 1000 1.3
Spider silk, Darwin’s bark spider[22] 1652
Silkworm silk 500   1.3
Aramid (Kevlar or Twaron) 3620 3757 1.44
UHMWPE[23] 24 52 0.97
UHMWPE fibers[24][25] (Dyneema or Spectra) 2300–3500 0.97
Vectran   2850–3340 1.4
Polybenzoxazole (Zylon)[26] 2700 5800 1.56
Wood, pine (parallel to grain)   40  
Bone (limb) 104–121 130 1.6
Nylon, molded, 6PLA/6M [27] 75-85 1.15
Nylon fiber, drawn[28] 900[29] 1.13
Epoxy adhesive — 12–30[30] —
Rubber — 16  
Boron — 3100 2.46
Silicon, monocrystalline (m-Si) — 7000 2.33
Ultra-pure silica glass fiber-optic strands[31] 4100
Sapphire (Al2O3) 400 at 25 °C,
275 at 500 °C,
345 at 1000 °C		 1900 3.9–4.1
Boron nitride nanotube — 33000 2.62[32]
Diamond 1600 2800
~80–90 GPa at microscale[33]		 3.5
Graphene — intrinsic 130000;[34]
engineering 50000–60000[35]		 1.0
First carbon nanotube ropes ? 3600 1.3
Carbon nanotube (see note below) — 11000–63000 0.037–1.34
Carbon nanotube composites — 1200[36] —
High-strength carbon nanotube film — 9600[37] —
Iron (pure mono-crystal) 3 7.874
Limpet Patella vulgata teeth (goethite whisker nanocomposite) 4900
3000–6500[38]
^a Many of the values depend on manufacturing process and purity or composition.
^b Multiwalled carbon nanotubes have the highest tensile strength of any material yet measured, with one measurement of 63 GPa, still well below one theoretical value of 300 GPa.[39] The first nanotube ropes (20 mm in length) whose tensile strength was published (in 2000) had a strength of 3.6 GPa.[40] The density depends on the manufacturing method, and the lowest value is 0.037 or 0.55 (solid).[41]
^c The strength of spider silk is highly variable. It depends on many factors including kind of silk (Every spider can produce several for sundry purposes.), species, age of silk, temperature, humidity, swiftness at which stress is applied during testing, length stress is applied, and way the silk is gathered (forced silking or natural spinning).[42] The value shown in the table, 1000 MPa, is roughly representative of the results from a few studies involving several different species of spider however specific results varied greatly.[43]
^d Human hair strength varies by ethnicity and chemical treatments.

Typical properties of annealed elements[edit]

Typical properties for annealed elements[44]

Element Young’s
modulus
(GPa) 		Yield
strength
(MPa) 		Ultimate
strength
(MPa)
Silicon 107 5000–9000
Tungsten 411 550 550–620
Iron 211 80–100 350
Titanium 120 100–225 246–370
Copper 130 117 210
Tantalum 186 180 200
Tin 47 9–14 15–200
Zinc 85–105 200–400 200–400
Nickel 170 140–350 140–195
Silver 83 170
Gold 79 100
Aluminium 70 15–20 40–50
Lead 16 12

See also[edit]

  • Flexural strength
  • Strength of materials
  • Tensile structure
  • Toughness
  • Failure
  • Tension (physics)
  • Young’s modulus

References[edit]

  1. ^ “Generic MMPDS Mechanical Properties Table”. stressebook.com. 6 December 2014. Archived from the original on 1 December 2017. Retrieved 27 April 2018.
  2. ^ Degarmo, Black & Kohser 2003, p. 31
  3. ^ Smith & Hashemi 2006, p. 223
  4. ^ a b “Tensile Properties”. Archived from the original on 16 February 2014. Retrieved 20 February 2015.
  5. ^ E.J. Pavlina and C.J. Van Tyne, “Correlation of Yield Strength and Tensile Strength with Hardness for Steels”, Journal of Materials Engineering and Performance, 17:6 (December 2008)
  6. ^ “MatWeb – The Online Materials Information Resource”. Archived from the original on 15 December 2013. Retrieved 20 February 2015.
  7. ^ “MatWeb – The Online Materials Information Resource”. Archived from the original on 21 February 2015. Retrieved 20 February 2015.
  8. ^ “MatWeb – The Online Materials Information Resource”. Archived from the original on 21 February 2015. Retrieved 20 February 2015.
  9. ^ “MatWeb – The Online Materials Information Resource”. Archived from the original on 28 March 2017. Retrieved 20 February 2015.
  10. ^ “USStubular.com”. Archived from the original on 13 July 2009. Retrieved 27 June 2009.
  11. ^ [1] Archived 23 March 2014 at the Wayback MachineIAPD Typical Properties of Acrylics
  12. ^ strictly speaking this figure is the flexural strength (or modulus of rupture), which is a more appropriate measure for brittle materials than “ultimate strength.”
  13. ^ “Stainless Steel – Grade 302 (UNS S30200)”. AZoM.com. 25 February 2013. Retrieved 2 February 2023.
  14. ^ “MatWeb – The Online Materials Information Resource”. Archived from the original on 21 February 2015. Retrieved 20 February 2015.
  15. ^ “MatWeb – The Online Materials Information Resource”. Archived from the original on 21 February 2015. Retrieved 20 February 2015.
  16. ^ a b “Guide to Glass Reinforced Plastic (fibreglass) – East Coast Fibreglass Supplies”. Archived from the original on 16 February 2015. Retrieved 20 February 2015.
  17. ^ “Properties of Carbon Fiber Tubes”. Archived from the original on 24 February 2015. Retrieved 20 February 2015.
  18. ^ “Soda-Lime (Float) Glass Material Properties :: MakeItFrom.com”. Archived from the original on 3 July 2011. Retrieved 20 February 2015.
  19. ^ “Basalt Continuous Fibers”. Archived from the original on 3 November 2009. Retrieved 29 December 2009.
  20. ^ “Toray Properties Document”. Archived from the original on 17 September 2018. Retrieved 17 September 2018.
  21. ^ “Tensile Testing Hair”. instron.us. Archived from the original on 28 September 2017.
  22. ^
  23. ^ Oral, E; Christensen, SD; Malhi, AS; Wannomae, KK; Muratoglu, OK (2006). “PubMed Central, Table 3”. J Arthroplasty. 21 (4): 580–91. doi:10.1016/j.arth.2005.07.009. PMC 2716092. PMID 16781413.
  24. ^ “Tensile and creep properties of ultra high molecular weight PE fibres” (PDF). Archived from the original (PDF) on 28 June 2007. Retrieved 11 May 2007.
  25. ^ “Mechanical Properties Data”. www.mse.mtu.edu. Archived from the original on 3 May 2007.
  26. ^ “MatWeb – The Online Materials Information Resource”. Archived from the original on 21 February 2015. Retrieved 20 February 2015.
  27. ^ https://advancednylons.co.za/Materialproperties.pdf[bare URL PDF]
  28. ^ “Nylon Fibers”. University of Tennessee. Archived from the original on 19 April 2015. Retrieved 25 April 2015.
  29. ^ “Comparing aramids”. Teijin Aramid. Archived from the original on 3 May 2015.
  30. ^ “Uhu endfest 300 epoxy: Strength over setting temperature”. Archived from the original on 19 July 2011.
  31. ^ “Fols.org” (PDF). Archived from the original (PDF) on 25 July 2011. Retrieved 1 September 2010.
  32. ^ “What is the density of Hydrogenated Boron Nitride Nanotubes (H-BNNT)?”. space.stackexchange.com. Archived from the original on 13 April 2017.
  33. ^ Dang, Chaoqun; et al. (1 January 2021). “Achieving large uniform tensile elasticity in microfabricated diamond”. Science. 371 (6524): 76–78. Bibcode:2021Sci…371…76D. doi:10.1126/science.abc4174. PMID 33384375.
  34. ^ Lee, C.; et al. (2008). “Measurement of the Elastic Properties and Intrinsic Strength of Monolayer Graphene”. Science. 321 (5887): 385–8. Bibcode:2008Sci…321..385L. doi:10.1126/science.1157996. PMID 18635798. S2CID 206512830. Archived from the original on 19 February 2009.
    • Phil Schewe (28 July 2008). “World’s Strongest Material”. Inside Science News Service. American Institute of Physics. Archived from the original on 25 February 2009.

  35. ^ Cao, K. (2020). “Elastic straining of free-standing monolayer graphene”. Nature Communications. 11 (284): 284. Bibcode:2020NatCo..11..284C. doi:10.1038/s41467-019-14130-0. PMC 6962388. PMID 31941941.
  36. ^ IOP.org Z. Wang, P. Ciselli and T. Peijs, Nanotechnology 18, 455709, 2007.
  37. ^ Xu, Wei; Chen, Yun; Zhan, Hang; Nong Wang, Jian (2016). “High-Strength Carbon Nanotube Film from Improving Alignment and Densification”. Nano Letters. 16 (2): 946–952. Bibcode:2016NanoL..16..946X. doi:10.1021/acs.nanolett.5b03863. PMID 26757031.
  38. ^ Barber, A. H.; Lu, D.; Pugno, N. M. (2015). “Extreme strength observed in limpet teeth”. Journal of the Royal Society Interface. 12 (105): 105. doi:10.1098/rsif.2014.1326. PMC 4387522. PMID 25694539.
  39. ^ Yu, Min-Feng; Lourie, O; Dyer, MJ; Moloni, K; Kelly, TF; Ruoff, RS (2000). “Strength and Breaking Mechanism of Multiwalled Carbon Nanotubes Under Tensile Load”. Science. 287 (5453): 637–640. Bibcode:2000Sci…287..637Y. doi:10.1126/science.287.5453.637. PMID 10649994.
  40. ^ Li, F.; Cheng, H. M.; Bai, S.; Su, G.; Dresselhaus, M. S. (2000). “Tensile strength of single-walled carbon nanotubes directly measured from their macroscopic ropes”. Applied Physics Letters. 77 (20): 3161. Bibcode:2000ApPhL..77.3161L. doi:10.1063/1.1324984. Archived from the original on 28 December 2012.
  41. ^ K.Hata. “From Highly Efficient Impurity-Free CNT Synthesis to DWNT forests, CNTsolids and Super-Capacitors” (PDF). Archived (PDF) from the original on 12 June 2010.
  42. ^ Elices; et al. “Finding Inspiration in Argiope Trifasciata Spider Silk Fibers”. JOM. Archived from the original on 15 January 2009. Retrieved 23 January 2009.
  43. ^ Blackledge; et al. (2005). “Quasistatic and continuous dynamic characterization of the mechanical properties of silk from the cobweb of the black widow spider Latrodectus hesperus”. Journal of Experimental Biology. The Company of Biologists. 208 (10): 1937–1949. doi:10.1242/jeb.01597. PMID 15879074. S2CID 9678391. Archived from the original on 1 February 2009. Retrieved 23 January 2009.
  44. ^ A.M. Howatson, P. G. Lund, and J. D. Todd, Engineering Tables and Data, p. 41

Further reading[edit]

  • Giancoli, Douglas, Physics for Scientists & Engineers Third Edition (2000). Upper Saddle River: Prentice Hall.
  • Köhler T, Vollrath F (1995). “Thread biomechanics in the two orb-weaving spiders Araneus diadematus (Araneae, Araneidae) and Uloboris walckenaerius (Araneae, Uloboridae)”. Journal of Experimental Zoology. 271: 1–17. doi:10.1002/jez.1402710102.
  • T Follett, Life without metals
  • Min-Feng Y, Lourie O, Dyer MJ, Moloni K, Kelly TF, Ruoff RS (2000). “Strength and Breaking Mechanism of Multiwalled Carbon Nanotubes Under Tensile Load” (PDF). Science. 287 (5453): 637–640. Bibcode:2000Sci…287..637Y. doi:10.1126/science.287.5453.637. PMID 10649994. Archived from the original (PDF) on 4 March 2011.
  • George E. Dieter, Mechanical Metallurgy (1988). McGraw-Hill, UK
Источник

Добавить комментарий