Как найти предел в maple - Сайт, где вы сможете решить свои вопросы

limit

calculate limit

Limit

inert form of limit

Calling Sequence

Parameters

Options

Description

Examples

References

Compatibility

Calling Sequence

limit(f, x=a)	limx→a⁡f
Limit(f, x=a)	limx→a⁡f
limit(f, x=a, dir, parametric=p)
Limit(f, x=a, dir)

Parameters

f	–	algebraic expression
x	–	name
a	–	algebraic expression; limit point, possibly infinity, or -infinity
dir	–	(optional) symbol; direction chosen from: left, right, real, or complex
p	–	(optional) either true or false (default)

Options

•	parametric=p

If parametric=true, or just parametric, is specified, then limit tries to compute an answer that is correct for all real values of any parameter(s) appearing in a. Typically, the result is a piecewise expression.

Description

•	The limit(f, x=a, dir) function attempts to compute the limiting value of f as x approaches a.

•	You can enter the command limit using either the 1-D or 2-D calling sequence.

•	If dir is not specified, the limit is the real bidirectional limit, except in the case where the limit point is infinity or -infinity, in which case the limit is from the left to infinity and from the right to -infinity. For help with directional limits, see limit/dir.

•	The output from limit can be a range (meaning a bounded result) or an algebraic expression, possibly containing infinity. For further help with the return type, see limit/return.

•	To compute a limit in a multidimensional space, specify a set of points as the second argument. For more information, see limit/multi.

•	Most limits are resolved by computing series. By increasing the value of the global variable Order, the ability of limit to solve problems with significant cancellation improves.

•	If Maple cannot find a closed form for the limit, the function calling sequence is returned.

Note: The limit function always assumes that the limit variable approaches the limit point along (one or more) continuous paths (e.g., along the real axis from the left or from the right). It is not currently possible to compute limits where the limit variable takes only discrete or integer values.

Also, the limit function ignores any assumptions on the limit variable made via assume or assuming.

•	If f is a function not known to Maple, the limit function assumes that f is regular at a finite expansion point.

•	The capitalized function name Limit is the inert limit function, which returns unevaluated. It appears gray so that it is easily distinguished from a returned limit calling sequence.

Note: Since Limit does not try to evaluate or check the existence of the limit of the expression, it can lead to incorrect transformations. Therefore, the use of limit is more reliable. This is demonstrated by the last two examples.

Examples

The inert Limit function returns unevaluated.

limx→01x

limx→0⁡1x

(1)

>	limx→−∞ln⁡x2

limx→−∞⁡ln⁡x2

(2)

limx→31x

(3)

limx→∞x2

∞

(4)

>	limx→0sin⁡xx

(5)

>	limx→∞&ExponentialE;x

∞

(6)

>	limx→−∞&ExponentialE;x

(7)

>	limx→∞&ExponentialE;x2⁢1−erf⁡x

(8)

limx→∞1x

(9)

To use the real and complex arguments, the limit command must be written in 1-D or 2-D command form and not in mathematical notation. See Entering Commands in 2-D Math for more information.

>	limit⁡1x,x=0,real

undefined

(10)

>	limit⁡1x,x=0,complex

∞+∞⁢I

(11)

Directional limits are possible. For more information see limit/dir.

limx→0+1x

∞

(12)

limx→0−1x

−∞

(13)

>	g ≔ piecewise⁡x<3,x2−6,3≤x,2⁢x−1

g≔x2−6x<32⁢x−13≤x

(14)

limx→3g

undefined

(15)

limx→3+g

(16)

limx→3−g

(17)

Unknown functions are assumed to be regular at a finite expansion point.

limx→af⁡x

f⁡a

(18)

Limits with parameters may only be computable when the domain for the parameters is limited via assumptions:

>	limx→∞sin⁡a⁢xx

limx→∞⁡sin⁡a⁢xx

(19)

>	limx→∞sin⁡a⁢xxassuminga::real

(20)

limx→∞xa

limx→∞⁡xa

(21)

>	limx→∞xaassuminga<0

(22)

>	limx→∞xaassuming0<a

∞

(23)

Examples for the parametric option:

limx→∞xa

limx→∞⁡xa

(24)

limx→∞xa

0a<01a=0∞0<alimx→∞⁡xaotherwise

(25)

limx→0xa

limx→0⁡xaa<01a=000<alimx→0⁡xaotherwise

(26)

>	limit⁡xa,x=0,'right','parametric'

∞a<01a=000<alimx→0+⁡xaotherwise

(27)

>	limit⁡xa,x=0,'left','parametric'

&ExponentialE;I⁢π⁢a⁢∞a<01a=000<alimx→0−⁡xaotherwise

(28)

>	limx→0tan⁡x+a⁢Pi2assuminga::integer

limx→0+⁡tan⁡x+π⁢a2

(29)

>	limit⁡tan⁡x+a⁢Pi2,x=0,'right','parametric'assuminga::integer

0a::even−∞a::odd

(30)

The use of the inert Limit function can lead to mathematically incorrect results.

>	combine⁡limx→01x⁢limx→0x

limx→0⁡1

(31)

>	combine⁡limx→01x⁢limx→0x

undefined

(32)

References

Geddes, K. O., and Gonnet, G. H. “A New Algorithm for Computing Symbolic Limits Using Hierarchical Series.” In Proceedings of ISSAC ’88, pp. 490-495. Edited by Patrizia M. Gianni. Berlin: Springer-Verlag, 1988.

Compatibility

•	The limit command was updated in Maple 2016; see Advanced Math.

•	The limit command was updated in Maple 2020.

•	The parametric option was introduced in Maple 2020.

•	For more information on Maple 2020 changes, see Updates in Maple 2020.

Предел функции

Непрерывность

Методические указания
к практическим занятиям по теме :

MAPLE^
В КУРСЕ МАТЕМАТИЧЕСКОГО АНАЛИЗА

Составители: Агарева
О.Ю.

Введенская
Е. В.

Осипенко
К. Ю.

Москва
1999

Введение

Цель
данных методических указаний –
познакомить студентов и преподавателей
с
математическим
пакетом MAPLE, научить, как с помощью этого
пакета решать
задачи,
возникающие при изучении стандартного
курса математического анализа
для
инженерных специальностей.

Настороженное
отношение к использованию компьютерных
технологий в изучении
математических
дисциплин связано прежде всего с далеко
не наивным вопросом
–
не заменит ли “нажатие
клавиш”
творческий процесс постижения
фундаментальных
основ изучаемых дисциплин? Авторы
убеждены, что, если
рассматривать
математические пакеты как мощные
вычислительные средства,
помогающие
избежать рутинных вычислений и
освобождающие тем самым время для
более
серьезного, качественного подхода к
изучаемому курсу, как средства,
позволяющие
наглядно демонстрировать глубокие
математические результаты
(например,
сходимость рядов Фурье), такой замены
не произойдет. Кроме
прививания глубоких
теоретических знаний, преподаватели
должны научить будущих
инженеров
при необходимости за короткое время
получать ответ на
вычислительные
задачи из математического анализа.
Безусловно, студент,
успешно
изучивший курс математического анализа,
будет в состоянии и через
довольно
продолжительный отрезок времени
самостоятельно вычислить,
например,
какой-либо интеграл. Он будет вспоминать,
какие замены
переменных
можно использовать для вычисления этого
интеграла, или смотреть
в
справочниках. Но не лучше ли дать ему
возможность мгновенно получить
ответ.

В
этой части работы рассматриваются
задачи вычисления пределов (включая
односторонние
пределы), исследования на непрерывность
и вычисления
производных функций одной переменной.
Все
разделы
устроены по единой схеме. Сначала
приводится краткий теоретический
материал (как правило, основные
определения), а затем на примерах показаны
способы
решения задач из соответствующих
разделов «вручную» и с помощью пакета
MAPLE.

Работа
частично поддержана федеральной
программой “Интеграция”
[проект
N
480].

Предел
функции

Вычисление
пределов с помощью пакета Maple

Пакет
Maple
V предоставляет широкие возможности
для вычисления пределов функций одной
переменной как односторонних, так и
двусторонних, в точке или в бесконечности.

Для
вычисления двустороннего предела
функции в точке следует в окне команд
после приглашения Maple (“>”) ввести
следующую команду:

limit(<функция>,<точка>);

здесь
<функция>
– некоторое выражение, содержащее
переменную, например,

((x^2-2*x+1)/(x^3-x)),

а
<точка>
– значение переменной, при котором
вычисляется предел, например,

x=0

После
нажатия клавиши
Enter
команда
будет обработана и Maple
выведет ответ. Пример команды для
нахождения этого предела:

limit(x^2+2*x+1,x=0);

Если
требуется найти предел функции в
бесконечности, в выражении <точка>
следует написать

x=infinity
или

x=-infinity

взависимости
от знака бесконечности, например,

limit(x^3+x,x=infinity);

В
случае одностороннего предела, команда
выглядит следующим образом:

limit(<функция>,<точка>,<сторона>);

Поле
<сторона>
содержит слово
left
в случае
левого предела, или right
в случае правого. Пример вычисления
одностороннего предела:

limit(1/x,x=0,left);

Основные
определения

Определение
1. Пусть
функция
определена в некоторой окрестности
точки.
Число– предел функциив точке,
если для любогосуществует такое,
что изследует неравенство.

Рис.
1. Предел функции в точке

пределение 2.
Число
– предел функциив точкесправа (слева)

,
если
определена в некоторой окрестности
точкии для любогосуществует такое,
что из неравенстваследует неравенство.

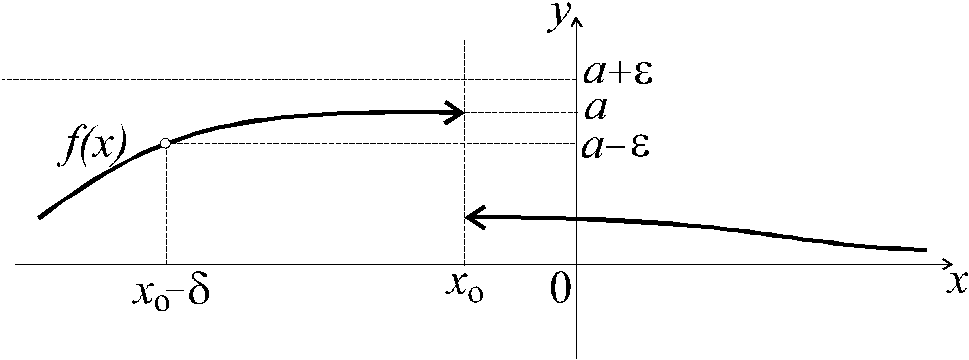
Рис.
2.
Предел слева

Замечательные
пределы:

Рис.
3.
Предел справа

.
.

Пример
вычисления замечательных пределов с
помощью пакета Maple:

>limit(sin(x)/x,x=0);

>limit((1+1/x)^x,x=infinity);

exp(1)

Следствия
из II
замечательного предела:

Пример
проверки с использованием Maple:

>limit(ln(1+x)/x,x=0);

>limit((exp(x)-1)/x,x=0);

Определение
3.
Функция
называется бесконечно малой при(обозначается),
если.

Определение
4.
Бесконечно
малые при
функциииназываются эквивалентными (обозначается),
если.

Таблица
эквивалентных бесконечно малых при
функций:

;	;
;	;
;	;
;	;
;	;
;	.

Методы
вычисления пределов

Функция
преобразуется к виду, для которого
предел легко найти.

Пример
1.

;

Пример
решения с использованием Maple:

>limit((x^2-2*x+1)/(x^3-x),x=1);

Пример
2.

Пример
решения с использованием Maple:

>limit(tan(3*x)/x,x=0);

В
пределах, содержащих иррациональные
выражения :

вводят
новую переменную для получения
рационального выражения.

Пример
3.

Пример
решения с использованием Maple:

>limit((sqrt(x-1)-3)/(x-10),x=10);

1/6

переводят
иррациональность из знаменателя в
числитель или наоборот.

Источник

федеральное государственное
образовательное

учреждение Высшего
профессионального образования

«Южный федеральный университет»

А.А.
Новакович

«Использование
современного пакета компьютерной
алгебры Maple
в физическом образовании бакалавров»

(учебно-методическое
пособие)

Ростов-на-Дону

2008

Новакович А.А.

Использование современного
пакета компьютерной алгебры Maple
в физическом образовании бакалавров:
Учебно-методическое пособие. –
Ростов-на-Дону, 2008. – 46
c.

Учебно-методическое
пособие «Использование
современного пакета компьютерной
алгебры Maple
в физическом образовании бакалавров»
предназначено для проведения
лабораторных занятий по дисциплинам:
«Программирование
и вычислительная физика»
и «Вычислительная
практика» для
студентов 2-го курса, обучающихся
по программе подготовки
бакалавров в департаменте физики ЮФУ
по направлению «Физика».
Настоящее пособие ставит
своей целью оказать помощь студентам
в освоении современного математического
пакета символьных вычислений Maple
11 применительно к решению математических
задач прикладного характера, встречающихся
в физических теориях, таких как
«Теоретическая
механика»,
«Статистическая
физика» и «Теория
электричества и магнетизма».
В пособии детально изложен материал
по использованию основных команд пакета
Maple,
предназначенных для нахождения
пределов, обыкновенных и
частных производных функций и выражений,
вычисления однократных, двойных и
тройных интегралов
от элементарных и специальных функций,
разложения функций в степенные и
асимптотические ряды, и суммирования
рядов. Каждый модуль пособия и его
разделы содержат проектные задания,
ряд которых предваряется изложением
дополнительного материала, необходимого
для решения конкретной поставленной
задачи.

Оглавление

№	Наименование	Стр.
	Введение	4
	Модуль 1	7
	Содержание модуля 1	7
1.	Нахождение пределов	7
	Проектное задание	7
	Дидактические тесты рубежного контроля №1	8
	Модуль 2	10
	Содержание модуля 2	10
2.	Дифференцирование выражений и функций	10
2.1	Обыкновенные производные	10
	Проектные задания	12
2.2	Частные производные	16
	Проектное задание	16
	Дидактические тесты рубежного контроля №2	17
	Модуль 3	19
	Содержание модуля 3	19
3.	Вычисление интегралов	19
3.1	Интегрирование элементарных функций	19
	Проектные задания	21
3.2	Интегрирование специальных функций	26
	Проектные задания	27
3.3	Двойные интегралы	29
	Проектное задание	30
3.4	Тройные интегралы	30
	Проектное задание	31
	Дидактические тесты рубежного контроля №3	32
	Модуль 4	34
	Содержание модуля 4	34
4.	Разложение в ряды	34
5.	Проектные задания Дидактические тесты рубежного контроля №4 Модуль 5 Содержание модуля 5 Суммирование рядов Проектное задание Дидактические тесты рубежного контроля №5 Литература	35 40 42 42 42 43 44 46

Введение

Учебно-методическое
пособие «Использование
современного пакета компьютерной
алгебры Maple
в физическом образовании бакалавров»
предназначено
для проведения лабораторных занятий
по дисциплинам: «Программирование
и вычислительная физика»
и «Вычислительная
практика» для
студентов 2-го курса, обучающихся
по программе подготовки
бакалавров в департаменте физики ЮФУ
по направлению «Физика».
Настоящее пособие ставит
своей основной целью
оказать помощь студентам в освоении
современного математического пакета
символьных вычислений Maple
11 применительно к решению математических
задач прикладного характера, встречающихся
в физических теориях, таких как
«Теоретическая
механика»,
«Статистическая
физика» и «Теория
электричества и магнетизма».
В пособии детально изложен материал
по использованию основных команд пакета
Maple,
предназначенных для нахождения
пределов, обыкновенных и
частных производных функций и выражений,
вычисления однократных, двойных и
тройных интегралов
от элементарных и специальных функций,
разложения функций в степенные и
асимптотические ряды, и суммирования
рядов. Каждый модуль пособия и его
разделы содержат проектные задания,
ряд которых предваряется изложением
дополнительного материала, необходимого
для решения конкретной поставленной
задачи. После изучения
материала модулей, представленных в
предлагаемом пособии, необходимо
выполнить предложенные проектные
задания и ответить на вопросы теста
рубежного контроля. Переход к изучению
материала следующего модуля желателен
только после успешного выполнения
предложенных контрольных материалов.
Уровень подготовки студента
предполагает его знакомство с основными
численными методами, излагаемыми в
одноименном лекционном курсе.

Мысль о том, что инженерная
деятельность – это всегда вычисления
– не нова. Однако “старая” школа
инженеров вкладывала в это совсем другой
смысл. Подразумевались, в первую очередь,
символьные вычисления, а на последнем
этапе численные оценки. Прогресс в
познании мира потребовал решения задач
либо очень сложных, либо не решаемых
аналитически. В вузах появились такие
дисциплины, как “Численные методы”,
“Численный анализ” и т.п. Развитие
вычислительной техники способствовало
созданию мегабайтных программ,
“взламывающих” сложные задачи. За
методами потянулись алгоритмы и
программы, на создание или поиск которых
растрачивалась уйма “золотого” времени.
К тому же специалисты, втянутые в эту
гонку, отмечают, что за массой чисел,
таблиц и графиков легко потерять
понимание реальности результатов
решения.

В последнее десятилетие
XX
века “программное” зло породило “добро”
– стали появляться универсальные пакеты
для численных методов: MatLab,
MathCAD,
электронные таблицы и многое другое.
Все они снимали с инженера половину
“головной боли”- поиск алгоритмов и
программ. Первым откровением для
специалистов стал пакет символьных
вычислений DERIVE,
который выполнял упрощения довольно
сложных алгебраических выражений,
оперировал с символьными матрицами,
дифференцировал и интегрировал выражения
в общем виде. Вслед за ним в России
появился знаменитый пакет “Mathematica”,
рассчитанный на математиков-профессионалов,
являющийся главным конкурентом пакету
символьных вычислений Maple,
разработанного в университете Ватерлоо
(Канада).

Пакет символьных вычислений
Maple
модифицируется и совершенствуется уже
свыше 25 лет, его версия, модифицированная
под ОС Windows,
поистине стала ярким бриллиантом среди
подобного класса программных пакетов.
С одной стороны, его интерфейс интуитивно
понятен, а правила работы предельно
просты, с другой же стороны – возможности
внушительны и увеличиваются с каждой
новой версией пакета. Появившись в
России, Maple
стал любимым средством для решения
задач у математиков-профессионалов,
инженеров, и автора настоящего
методического пособия. В студенческой
же среде он вызывает определенную
эйфорию, так как легко справляется с
труднейшими преобразованиями и
вычислениями при дипломном проектировании
и в курсовых заданиях. В настоящее время
изданы несколько справочных пособий
на русском языке по различным версиям
пакета Maple
[1,2,3,4].

Хотя мы и будем работать
с конкретным пакетом символьных
вычислений Maple
11,
этот пакет будет для нас просто
инструментом, а не предметом изучения.
Данный пакет достаточно универсален
(только базовая библиотека Maple
11 содержит
в себе более 3000 команд) и обновляется
примерно раз в три года, поэтому, детальное
изучение всего пакета достаточно
бессмысленно. Таким
образом,
мы
не преследуем цель заменить пособие
для программистов по пакету (среде)
Maple
11,
и будем довольствоваться краткими
описаниями и разъяснениями.
Автор надеется,
что данное методическое пособие окажется
полезным читателю для общения с пакетом
XXI
века Maple.

МОДУЛЬ
1

Комплексная цель:
изучение команды нахождения
пределов функций и выражений в среде
Maple.

Краткое изложение
программного материала: в
модуле рассмотрен конкретный пример
нахождения предела варианты в двух
возможных формах ее синтаксиса: выражения
и функции. Указан способ доступа к
встроенной справочной информации о
команде нахождения пределов, содержащей
ряд примеров ее использования.

Содержание модуля 1

Нахождение пределов.

Среду Maple
можно использовать для нахождения
пределов различных выражений и функций.
Например, чтобы найти предел выражения

,
следует использовать команду Maple
limit,
как указано ниже

>
limit(sin(3*x)/x,x=0);

В случае нахождения
пределов функций, следует сначала
определить саму функцию, а затем вычислить
ее предельное значение

>
y:=x->sin(3*x)/x;
limit(y(x),x=0);

Для вывода на экран дисплея
справочной информации о команде limit
с набором сопровождающих примеров,
используйте следующую команду:

>?limit

Проектное задание
1.1

Вычислить предел

двумя различными способами,
описанными выше.

Тест рубежного контроля
№1

Тест содержит 4 задания;
даны четыре варианта ответа
на каждый вопрос, из которых необходимо
выбрать один верный. На
выполнение каждого задания отводится
3 минуты. Выберите наиболее правильный,
по Вашему мнению, вариант ответа и
отметьте его любым значком в бланке
ответов. Тест оценивается по 5-балльной
системе: отлично – 4 правильных ответа;
хорошо – 3 правильных ответа;
удовлетворительно – 2 правильных ответа;
неудовлетворительно – менее 2 правильных
ответов.

Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и вычисляет значение
предела

?
1. >lim(x=0,sin^2(x)/x^2);
2. >lim(sin(x)^2/x^2,x=0);
3. >limit(sin(x)^2/x^2,x=0);
4. >limit(x=0,sin(x)^2/x^2);
Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и вычисляет значение
предела

?
1. >lim(a=0,x^a-1/a);
2. >lim((x^a-1)/a,a=0);
3. >limit((x^a-1)/a,a=0);
4. >limit(a=0,(x^a-1)/a);
Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и вычисляет значение
предела

?
1. >limit(n^1/2*((n+1)^1/2-n^1/2),n=∞);
2. >limit(n^1/2*((n+1)^1/2-n^1/2),n=infinity);
3. >limit(n^(1/2)*((n+1)^(1/2)-n^(1/2)),n=infinity);
4. >limit(n^(1/2)*(n+1)^(1/2)-n^(1/2),n=infinity);
Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и вычисляет значение
предела функции
?
1. >limit(x->sin(x)^3/x^3,x=0);
2. >limit(y(x),x=0); y:=x->sin(x)^3/x^3;
3. >y:=x->sin(x)^3/x^3;
  limit(y(x),x=0);
4. >y(x):=sin(x)^3/x^3;
  limit(y(x),x=0);

Бланк ответов

№	1	2	3	4
1)
2)
3)
4)

МОДУЛЬ 2

Комплексная цель:
изучение команды вычисления
производных функций и выражений в среде
Maple.

Краткое изложение
программного материала: в
модуле рассмотрены конкретные примеры
вычисления производных варианты в двух
возможных формах ее синтаксиса: выражения
и функции:

– обыкновенные производные
(выражения и функции);

– частные производные
(функции нескольких аргументов).

В каждый подраздел модуля
включен ряд проектных заданий
для самостоятельной работы.

Содержание модуля 2

Дифференцирование
выражений и функций.

В среде Maple
можно легко найти обыкновенные и частные
производные, как элементарных функций,
так и специальных функций, использующихся
в различных физических теориях.

2.1.
Обыкновенные производные.

В этом разделе мы
познакомимся с двумя командами
дифференцирования. Первая команда
используется для дифференцирования
функций и выражений, а вторая только
для функций. Рассмотрим сначала
дифференцирование выражений на примере
вычисления производных 1-го, 2-го и 3-го
порядков тангенса. Вы можете использовать
команду diff
и сразу получить результат, или
последовательно две команды Diff
и value
для получения того же
результата. Последний вариант не менее
полезен, так как он дает возможность
проверки правильности набора
дифференцируемого выражения.

>
diff(tan(x),x);

>
diff(tan(x),x$2);

> d:=Diff(tan(x),x$3);

>
d:=value(d);

>
d:=simplify(d);

Теперь
рассмотрим пример дифференцирования
функций.

>
f:=x->tan(x)/x;

Команда Diff
не работает
при ее применении к функциям. Вместо
нее необходимо использовать команду
D.
Это очень мощная команда, несмотря на
ее небольшой размер. С ее помощью можно
находить производные любого порядка
функций нескольких переменных, но мы
ограничимся случаем функции одной
переменной. (Для вызова справки о работе
с данной командой наберите в строке
ввода >?D).
Найдем первую производную функции f.

>
fp:=D(f);

Заметим, что
в результатом является функция fp(x).
Существует несколько способов нахождения
высших производных, но мы здесь рассмотрим
наиболее общий.

>
fpp:=D[1$2](f);

Единица в
квадратных скобках означает, что
дифференцирование проводится по первому
аргументу (в данном случае единственному),
а $2 означает, что дифференцирование
проводится дважды. Для лучшего усвоения
данного раздела вам предлагается
несколько упражнений для практики.

Проектное задание
2.1.1

Вычислить
производные, перечисленные ниже.
Используйте форму дифференцирования
выражений для вариантов (б,в,д,е,ж) и
форму дифференцирования функций для
вариантов (а,г). Попытайтесь упростить
результат дифференцирования, используя
команду simplify.
Вы обнаружите, что данная команда не
работает при ее применении к функциям.
Эта проблема может быть разрешена
следующим образом. Выделите мышью
выражение, которое вы хотите упростить,
скопируйте его в буфер обмена и свяжите
его с новой переменной, отрежьте
нежелательные аргументы. Затем следует
выполнить команду упростить. После
этого следует восстановить производную
функции, используя пункт меню Edit: вырезать
и вставить. Такое сочетание команд Maple
и редактирования является хорошим
способом устранения ошибок в алгебраических
преобразованиях.

(а)

(б)

(в)

(г)

(д)
(е)
(ж)

Здесь K(k)-полный
эллиптический интеграл первого рода.
В среде Maple для него используется
обозначение EllipticK.

Проектное задание
2.1.2

Задача нахождения минимумов
и максимумов функций часто встречается
в физических приложениях математического
анализа. Рассмотрим функцию
.
(Термин функция здесь используется в
математическом смысле, а не в смысле
формы определения функции в среде
Maple). Для решения данной задачи
предпочтительней использовать в среде
Maple
работу с выражениями. Сначала построим
график указанной функции на интервале
[0,10] изменения аргумента. Посмотрим на
ее график и найдем приближенно значения
аргумента x, при значениях которых
функция имеет минимум или максимум.
Вычислим производную данной функции в
форме выражения и присвоим результат
переменной f. Для точного нахождения
положения экстремума воспользуемся
командой fsolve,
предназначенной для численного решения
алгебраических уравнений. Например,
для нахождения положения экстремума,
расположенного в окрестности значения
аргумента x=1.1, наберите в строке ввода
команду

>fsolve(f,x=1.1);

Проектное задание
2.1.3

Из курса
теории электричества и
магнетизма известно,
что электрический потенциал заряженной
полусферы радиуса R с постоянной
поверхностной плотностью заряда σ имеет
следующую зависимость от z-координаты,
если ось z направлена вдоль оси симметрии
полусферы от центра к ее куполу:

>
V:=-1/2*sigma*R*(-sqrt(R^2+z^2)+sqrt((z-R)^2))/(z*e0);

Здесь диэлектрическая
постоянная ε₀
обозначена как e0. Компоненты вектора
напряженность электрического поля
можно получить, дифференцируя потенциал.
Попробуйте вычислить z-компоненту
напряженности поля
,
используя среду Maple, и упростите полученное
выражение. Вы увидите, что результат
содержит незнакомую функцию csgn.
Обратитесь к справке о
данной функции, введя команду >?csgn
и убедитесь, что вы понимаете,
для чего она предназначена.

Присвоим переменным
значения σ=1, R=1,
e0=1,
и построим график зависимости потенциала
V и z-компоненты
напряженности поля E_z
от координаты z
в диапазоне от -4 до 4. Участок графика
величины E_z
в окрестности z=R
(R=1)
имеет форму ступеньки, что согласуется
с известной теоремой теории электромагнитного
поля о том, что когда пересекается
поверхностная плотность заряда,
нормальная составляющая напряженности
электрического поля испытывает скачек
величиной σ/ε₀.

Вы можете заметить, что
в выражении для потенциала было
использовано обозначение e0
вместо ε₀.
Это было сделано умышленно. Опыт работы
в среде Maple показывает, что следует по
возможности избегать использования
переменных с индексами, поскольку они
воспринимаются как элементы массива
или таблицы. Сравните на графике величину
скачка E_z
с величиной σ/ε₀.
На вашем графике положительные значения
координаты z в диапазоне от 0 до R
соответствуют положению точки внутри
полусферы, а в диапазоне от R до
бесконечности, или отрицательные,
соответствуют положению точки вне
полусферы. Дайте физическую интерпретацию
построенным графикам.

Проектное задание
2.1.4

Среда Maple
позволяет вычислять производные функций,
заданных в неявном виде. Предположим,
что задано уравнение, связывающее
функцию y и ее аргумент x, например

. Мы
хотим
найти
производную

не
используя явный вид функции
.
Для этого следует просто продифференцировать
неявное уравнение. В результате получим
новое уравнение
,
которое следует разрешить относительно
искомой производной
.
Среда Maple выполнит дифференцирование,
но только при условии, что вы сами
подскажете, что y зависит от x. Например

> restart;

>
eq:=x^2
+ y(x)^3 = 3;

>
deq:=diff(eq,x);

>
dydx:=solve(deq,diff(y(x),x));

Если вы не
хотите каждый раз в командной строке
набирать y(x), можно использовать команду
alias,
и набирать просто у. В этом случае среда
Maple автоматически заменит символ y на
y(x) повсюду, где он встретится.

> restart;

>
alias(y=y(x));

>
eq:=x^2
+ y^3 = 3;

>
deq:=diff(eq,x);

>
dydx:=solve(deq,diff(y,x));

Рассмотрим
физический пример. Дисперсионное
соотношение для электромагнитной волны
в плазме имеет вид:,
где wp-плазменная
частота. Фазовая скорость волны равна

,
а ее групповая скорость выражается
через производную
.
В качестве первого задания, используя
Maple, найдите явные выражения для фазовой
и групповой скорости через wp, k и c,
разрешив дисперсионное соотношение
как уравнение относительно ω(k) с
последующим дифференцированием. В
качестве второго задания получите
выражение для групповой скорости,
использую прием дифференцирования
неявно заданных функций.

2.2. Частные производные.

Среда Maple позволяет
вычислять частные производные любого
порядка функций нескольких переменных.
Рассмотрим для примера функцию двух
переменных
.
Вычислим частные производные первого
порядка по обоим аргументам и смешанную
производную второго порядка в варианте
дифференцирования выражений.

>
restart;
f:=cos(x*y)/y;

>
diff(f,x);diff(f,y);diff(f,x,y);

Сделаем тоже самое в
варианте дифференцирования функций.

>
restart;
f:=(x,y)->cos(x*y)/y;

>
D[1](f);D[2](f);D[1,2](f);

Проектное задание
2.2.1

Вычислите частные
производные первого порядка по обоим
аргументам (x,y) и все три
частные производные
второго порядка, включая смешанную,
функции
,
здесь К(k)-полный эллиптический интеграл
первого рода. (В среде Maple для него
используется обозначение EllipticK).
Проведите расчет производных в варианте
дифференцирования выражений, используя
команду diff.
Упростите
полученные выражения, используя команды
expand
(раскрыть скобки) и
simplify.

Тест рубежного контроля
№2

Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и вычисляет производную
выражения

?
1. >diff(x,sin^3(x)/x^3);
2. >diff(sin(x)^3/x^3,x);
3. >Diff(sin(x)^3/x^3,x);
4. >Diff(x,sin(x)^3/x^3);
Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и вычисляет производную
выражения

?
1. >diff(x,exp^x-1/x^2);
2. >diff((exp(x)-1)/x^2,x);
3. >Diff(x,exp^x-1/x^2);
4. >Diff((exp(x)-1)/x^2,x);
Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и вычисляет производную
функции

?
1. >
  diff(x^1/2*((x+1)^1/2-x^1/2),x);
2. >
  D(x^1/2*((x+1)^1/2-x^1/2),x);
3. >
  D(x->x^(1/2)*((x+1)^(1/2)-x^(1/2)),x);
4. >
  D(x->x^(1/2)*((x+1)^(1/2)-x^(1/2)));
Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и вычисляет вторую
смешанную частную производную функции

?
1. >
  D((x,y)->(1+tan^2(x)^2)*(1+3*tan^2(y)),x,y);
2. >
  D((x,y)->(1+tan(x)^2)*(1+3*tan(y)^2),x,y);
3. >
  D[1,2]((x,y)->(1+tan(x)^2)*(1+3*tan(y)^2));
4. >
  D(D((x,y)->(1+tan(x)^2)*(1+3*tan(y)^2)));

Бланк ответов

№	1	2	3	4
1)
2)
3)
4)

МОДУЛЬ 3

Комплексная цель:
изучение команды
интегрирования функций и выражений в
среде Maple.

Краткое изложение
программного материала: в
модуле рассмотрены конкретные примеры
вычисления определенных и
неопределенных интегралов в двух
возможных формах синтаксиса
подынтегрального выражения:

– однократные интегралы
от элементарных функций;

– однократные интегралы
от специальных функций;

– кратные (двойные и
тройные) интегралы.

В каждый подраздел модуля
включен ряд проектных заданий
для самостоятельной работы.

Содержание модуля 3

Вычисление
интегралов.

В курсе математического
анализа вы изучали способы нахождения
интегралов в аналитическом виде,
основанные, как правило, на удачной
замене переменной интегрирования.
Математики давно облегчили этот процесс,
опубликовав в виде отдельных справочников
и таблиц результаты интегрирования как
элементарных, так и специальных функций.
По-видимому, наилучшим справочником
является “Таблицы интегралов, сумм,
рядов и произведений” И.С.Градштейна
и И.М.Рыжика [5], который можно найти в
библиотеке.

3.1.
Интегрирование элементарных функций.

Для аналитического
интегрирования в среде Maple используется
команда int.
Проинтегрируем
для примера функцию sin(x).

>
int(sin(x),x);

В следующем примере под
интегралом стоит выражение f=sin(x)*x.

>
f:=sin(x)*x;
int(f,x);

(Отметим, что запись f(x) в
случае выражений недопустима.)

Проинтегрируем функцию
двух переменных g(x,y)=sin(x*y)*x
по переменной x. Для задания функции и
интегрирования введем две команды.

>
g:=(x,y)->sin(x*y)*x;

>
int(g(x,y),x);

Кроме команды
интегрирования int
в среде
Maple имеется также инертная, или отложенная
команда Int,
предназначенная
только для отображения на дисплее самого
интеграла без его вычисления.

>
s1:=Int(exp(x),x);

Вы можете спросить, а
зачем нужна эта команда, если она ничего
не делает? Дело в том, что Int
команда, предназначенная
в первую очередь для проверки правильности
набора подынтегрального выражения. При
наборе длинных выражений зачастую
совершаются ошибки в расстановке скобок
или в учете приоритета операций. Если
вы допустили такую ошибку, то сразу ее
обнаружите. Если подынтегральное
выражение набрано правильно, то выполнить
отложенное интегрирование можно с
помощью команды value.

> s1:=Int(exp(x),x);

>
s1:=value(s1);

Я предлагаю вам всегда
вычислять интегралы таким способом,
объединяя команды Int
и value,
поскольку вы потратите
меньше времени на исправление досадных
ошибок.

На следующем примере рассмотрим
вычисление определенных интегралов.

> s2:=Int(tan(x),x=0..1);

>
s2:=value(s2);

Для получения численного
значение интеграла используйте команду
evalf.

>
evalf(s2);

Если вы хотите
получить только численное значение
результата интегрирования, можно
обойтись и баз команды evalf,
просто задав пределы интегрирования в
форме числа с плавающей точкой.

> s2:=Int(tan(x),x=0..1.);

>
value(s2);

Среда Maple
позволяет вычислять интегралы и в
бесконечных пределах, но при этом вам,
возможно, придется ввести некоторые
указания, используя команду assume.
Это примерно
все, что вам нужно знать для проведения
интегрирования. Внимательно изучите
справку о работе с командой интегрирования,
введя >?int,
и познакомьтесь
с рядом полезных дополнительных опций
команды интегрирования. Далее выполним
ряд упражнений.

Проектное задание
3.1.1

Вычислите следующие
интегралы, используя для записи
подынтегрального выражения синтаксис
выражений в примерах (а)-(г), и синтаксис
функций в примерах (д)-(ж). Получите
численные значения результата
интегрирования для (д) и (е). Проблема
возникнет с интегралом (ж). Попробуйте
ее обойти, указав, что коэффициент a
в показателе экспоненты положителен.
Упростите ответ c
использованием команды simplify.

(а)

(б)

(в)

(г)

(д)

(е)

(ж)

Справка. Бесконечность
в среде Maple
обозначается как infinity.

Проектное задание
3.1.2

Рассмотрим
поверхность полусферы, заданную
сферическими координатами r=R
и θ=0..π/2.
На ее поверхности находится заряд с
поверхностной плотностью σ.
Найдем
электростатический потенциал V(z)
в точках, расположенных на оси z.
Радиус-вектор точки наблюдения,
расположенной на оси z,
запишем как r₁=zk,
где k–единичный
вектор в направлении оси z.
Радиус-вектор бесконечно-малого участка
поверхности с зарядом

запишем как r₂=Rn,
где n–единичный
вектор в направлении элемента заряда.
Выразив расстояние |r₁–r₂|
через
cos(θ),
получим:

Интегрирование проводится
по обоим переменным θ (в пределах от 0
до π/2) и φ (в пределах от 0 до 2π). Результат
интегрирования по переменной φ дает:

Определим потенциал V(z),
как функцию от аргумента z,
как мы это делали ранее. Например,
экспоненциальную функцию можно задать
таким образом:

>
V:=z->exp(-z);

В нашем же случае, так как
потенциал задан интегралом, мы используем
для определения функции V(z)
команду int,
а именно >V:=z->int(…).
Обозначим диэлектрическую
постоянную ε₀
как e0. Присвоим всем константам
определенные численные значения для
того чтобы построить график V(z).

>restart:
e0:=8.854e-12; sigma:=1e-10; R:=0.5;

>V:=z->int(sigma*R^2*sin(theta)/sqrt(R^2+z^2

–2*R*z*cos(theta)),theta=0..Pi/2)/(2*e0);

Вы заметили, что Maple
не возвращает результат в явном виде.
Я не разработчик этой среды, поэтому
для меня это осталось загадкой. Тем не
менее, вы можете пользоваться V(z)
как функцией, для вычисления потенциала
в определенной заданной точке, или для
построения графика.

(a)
Вычислите значение потенциала в точках
z=1.1
и z=
-1.1

(б) Построите график V(z)
в диапазоне значений z
от -5 до 5.

(в) Вычислите общий заряд
на полусфере и наложите на график функции
V(z)
потенциал точечного заряда, помещенного
в начало координат, равному заряду
полусферы. Оба графика на участках с
|z|>>R
должны быть близки друг к другу. Попробуйте
изменить место расположения точечного
заряда, чтоб добиться как можно лучшего
совпадения обеих кривых. Напомню, что
потенциал точечного заряда

Проектное задание
3.1.3

Рассмотрим пример
использования интегралов в классической
задаче механики о колебании маятника.
Уравнение движения
маятника
имеет
вид:

Здесь
Ω
– частота
малых
колебаний.
Если мы умножим обе части
этого уравнения на dθ/dt
и проинтегрируем по времени, мы получим
интеграл движения в форме закона
сохранения полной энергии.

Здесь θ₀
– амплитуда колебаний. Пусть в момент
времени t=0
маятник был отклонен на угол θ₀
и покоился, а затем был отпущен. Мы хотим
вычислить время, за которое маятник
достигает положения устойчивого
равновесия (θ=0), т.е. четверть периода
колебаний. (а) Представим интеграл
движения, полученный выше, в виде:

Очевидно, что четверть
периода колебаний задается интегралом:

(б) Попробуйте вычислить
этот интеграл, обозначив θ через theta,
и θ₀ через
theta0.
В ответ Maple
поместит на дисплей сообщение об ошибке.

Error,
(in
limit)
numeric
exception:
division
by
zero

Дело в том, что Maple
ничего не знает о типе и величине theta0.
В принципе допустимо использовать эту
величину как комплексную переменную.
Постараемся ему немного помочь, указав
вещественный тип и интервал значений
величины theta0
с помощью команды assume.

>
assume(theta0,real,0<theta0,theta0<Pi);

(Отметим, что все переменные,
на которые наложены ограничения,
отображаются с дополнительным значком
~). Выполните интегрирование снова.
Теперь попытка увенчается успехом, но
ответ выглядит несколько необычно, для
тех, кто знаком с формулой для периода
колебаний маятника. Выполним интегрирование
снова, заменив
.

>
subs({cos(theta)=1-2*sin(theta/2)^2,cos(theta0)=1-

2*sin(theta0/2)^2},Int(…));

> value(4*%);

В итоге получилась знаменитая
формула из курса классической механики.

(в) Постройте график
периода колебаний, как функцию начального
угла θ₀
в диапазоне от 0 до π. Придайте физический
смысл поведению кривой на участке малых
значений θ₀
и в окрестности π.

Проектное задание
3.1.4

Известно, что
момент инерции твердого тела относительно
мгновенной оси вращения выражается
через интеграл
где s-
длина перпендикуляра, опущенного из
точки интегрирования на ось вращения,
ρ- плотность массы тела, dV-
элемент объема. (dV=dxdydz
в декартовых координатах).

(а) Используя
Maple,
вычислите момент инерции шара относительно
оси, проходящей через его центр.
Воспользуйтесь сферическими координатами,
в которых
.
Направим координатную ось z
по направлению оси вращения шара, тогда

.
Считаем, что плотность массы всюду
одинакова и равна отношению массы шара
M
к его объему. Вы должны получить величину
момента инерции
.

(б) Найдите с
использованием Maple
момент инерции конуса относительно
оси, проходящей через его ось симметрии.
Используйте цилиндрические координаты,
в которых
.
Считаем, что плотность массы всюду
одинакова и равна отношению массы конуса
M
к его объему, т.е.
.

3.2.
Интегрирование
специальных
функций.

Среда Maple
позволяет вычислять как определенные,
так и неопределенные интегралы от
практически всех, встречающихся в
физических приложениях специальных
функций, например функций Бесселя,
Лежандра, гипергеометрических функций
и т.д. Общее число специальных функций,
встроенных в Maple,
превышает сотню. Ввод команды

> ?inifunction

отображает на экране
дисплея перечень всех специальных
функций с их стандартными определениями.
Результаты интегрирования специальных
функций, как правило, так же выражаются
через специальные функции. Но если вам
необходимо получить только численное
значение результата, используйте для
этого команды Int
и evalf.
Вычислим,
например
определенный
интеграл
от
функции
Бесселя
J₀(x).

Попробуем вычислить интеграл в
аналитическом виде

> s1:=Int(BesselJ(0,x),x=0..1);

>
value(s1);

Результат интегрирования
выразился через функцию Струве, с которой
редко кто знаком, и вряд ли вы найдете
таблицы ее значений. А как найти численное
значение результата интегрирования?
Можно просто задать пределы интегрирования
в виде числа с плавающей точкой.

> s1:=Int(BesselJ(0,x),x=0..1.);

>
value(s1);

Проектное задание
3.2.1

Вычислите следующие
интегралы от функций Бесселя как
неопределенные, а затем как определенные
в интервале [1.0..2.0].

(а)

(б)

(в)

(г)

Приведем для справки их
обозначение в среде Maple:
BesselJ(0,x),
BesselK(0,x),
BesselI(1,x).

Проектное задание
3.2.2

Вычислите следующие
интегралы от функций (полиномов) Лежандра
как неопределенные, а затем как
определенные в интервале [-1.0..1.0].

(а)

(б)

Справка. Для начала работы
с ортогональными полиномами, к которым
относится полином Лежандра, необходимо
ввести команду

>
with(orthopoly);

Полиномы
Лежандра в среде Maple обозначаются как
P(n,x).

Проектное задание
3.2.3

Возможно, вы были удивлены
результатом, полученным при вычислении
определенного интеграла (б) предыдущего
задания. Этот результат отражает просто
общее свойство ортогональных полиномов
– определенные интегралы в интервале
[-1..1] от произведения двух разных полиномов
Лежандра равны нулю. Это свойство очень
важно, так как позволяет раскладывать
заданные функции одного переменного
по набору ортогональных полиномов. Этим
приемом пользуются в квантовой механике
при разложении волновой функции по
базисному набору стационарных состояний.
Оказывается, что существует множество
функций со свойствами ортогональности.
В данном задании мы познакомимся с
некоторыми из них.

(а) Проверим ортогональность
функций

и
на
интервале [0..2π]. Вычислите для этого
значения интегралов с m
и n
с равными и неравными друг другу.

Подсказка. Так как в нашем
случае величины m
и n
целые, то необходимо указать это, введя
команду >
assume(m,integer,n,integer);

(б) Проверьте взаимную
ортогональность полиномов Лежандра c
неравными друг другу значениями индекса
n
на интервале [-1..1]. Кроме этого вычислите
интеграл нормировки
.
Не забудьте о команде >with(orthopoly);

Найдите значение этого
интеграла для нескольких значений
индекса n
и попытайтесь, на основе найденного,
получить аналитическое выражение для
интеграла нормировки. (Оно очень простое
и приведено во всех справочниках по
специальным функциям.)

(в) Показать, что функции
Бесселя

взаимно ортогональны с весом x
на отрезке [0..1]. Для этого следует
вычислить значение интеграла
,
где α_p
и α_q
– нули функции
.
Их можно найти, используя функцию Maple
BesselJZeros(n,m),
здесь n-
порядок функции Бесселя (в рассматриваемом
случае n=0),
m-порядковый
номер искомого нуля. Например, введя
команду >BesselJZeros(0.,1);
мы
найдем значение α₁=
2.404825558.
(Отметим, что порядок функции Бесселя
необходимо вводить в форме числа с
плавающей точкой, а не как целое!). Далее,
найдите аналитическое выражение для
этого интеграла при p=q.
Значение величины α_p
при этом следует вводить аналитически,
т.е. как BesselJZeros(0,p)
(порядок функции Бесселя
вводится без десятичной точки). Результатом
интегрирования будет простое аналитическое
выражение:

Проектное задание
3.2.4

Вычислите интегралы (а,б,в) как
неопределенные и определенные в пределах
от 0.5 до 1.0, а интеграл (г) как определенный.

(а)

(Гамма функция Эйлера обозначается
как GAMMA)

(б)

(Функция ошибок обозначается как
erf)

(в)

(Полный эллиптический интеграл
обозначается как EllipticK)

(г)

(В качестве верхнего предела
используйте 1 как целое число, и как
число с плавающей точкой 1.0).

3.3.
Двойные интегралы

Кратные интегралы (двойные,
тройные, и т.д.) достаточно часто
встречаются в физических теориях.
Рассмотрим, например двойной интеграл

.
Для его вычисления в среде Maple
следует просто использовать команду
интегрирования Int
как повторную:

> restart;

>
s1:=Int(Int(erf(x*sin(y)),x=0..1),y=0..1);

> s1:=value(s1);

Как обычно, если Maple
отображает на дисплей результат в виде
интеграла, это означает, что получение
аналитического выражения зачастую
невозможно, но можно получить результат
численно, если использовать далее
команду evalf.

>
evalf(s1);

Если вам необходим только
результат численного интегрирования,
то соответствующие команды вычисления
интеграла следует ввести внутри скобок
команды evalf:

>
evalf(Int(Int(erf(x*sin(y)),x=0..1.),y=0..1.));

Кроме того, если вам не
нужна большая точность вычисления,
можно задать нужное количество значащих
цифр результата (6 как в данном примере)
внутри команды интегрирования
вслед за заданием пределов,
что резко сократит время вычисления.

>
evalf(Int(Int(erf(x*sin(y)),x=0..1.,6),y=0..1.,6));

Проектное задание
3.3.1

Найдите
численное значение
двойного интеграла.

3.4.
Тройные
интегралы.

Достаточно часто вы
встречаетесь с необходимостью вычисления
тройных интегралов, например следующего
вида
.

В среде Maple
для этого следует использовать команду

>
s1:=int(int(int(cos(x)*erf(x*sin(y*z)),x=0..1),

y=0..1),z=0..1);

Как видите, результатом
является символическая запись данного
тройного интеграла, т.к. Maple
не находит его значение в аналитическом
виде. Вычислим интеграл численно,
используя для этого команду >evalf(s1).
После ее ввода может
показаться, что компьютер завис, но это
не так. Просто для вычисления тройных
интегралов требуется большое количество
операций, которые среда Maple
выполняет слишком медленно. Давайте
прекратим дальнейшее вычисление
интеграла, нажав на кнопку “stop”,
расположенную на панели инструментов,
и заново вычислим его численное значение,
уменьшив требуемую точность до четырех
значащих цифр.

>
evalf(Int(Int(Int(cos(x)*erf(x*sin(y*z)),

x=0..1.,4),y=0..1.,4),z=0..1.,4));

Как
видите, вычисление интеграла занимает
всего несколько секунд.

Проектное задание
3.4.1

Вычислите
численное значение тройного интеграла
с точностью до четырех значащих цифр
по внутреннему объему сферы радиуса
r=2
с использованием сферической системы
координат.

Даже вычисление с
относительно невысокой точностью в
случае тройных интегралов занимает
продолжительное время. Попытайтесь
найти способ уменьшить время его
вычисления, например, попробовав
вычислить один из внутренних интегралов
аналитически. В этом случае задача
сведется к дальнейшему двойному
интегрированию, которое проводится
значительно быстрее. В среде Maple
есть еще один способ вычисления двойных
и тройных интегралов. Для этого следует
использовать команды пакета расширения
student.
Для получения доступа к
этому пакета наберем в строке приглашения
ввода команду:

> with(student);

На дисплее отобразиться
полный список команд данного пакета.
Для того, чтобы узнать назначение всех
этих команд с примерами их использования,
войдите в раздел справки по работе с
пакетом расширения student.

>
?student

Тест рубежного контроля №3

Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и вычисляет
неопределённый интеграл

?
1. >int(x,1/x/(1+x^2)^5);
2. >int(x,(1/x)/(1+x^2)^5);
3. >int(1/x*(1+x^2)^(-5),x);
4. >value(Int((1/x*(1+x^2)^5),x));
Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и вычисляет определённый
интеграл

?
1. >int(x=0..infinity,sin^3(x)/x^3);
2. >int(x=0..infinity,sin(x)^3/x^3);
3. >int(sin(x)^3/x^3,x=0..infinity);
4. >value(Int(sin(x)^3/x^3,x=0..infinity));
Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и вычисляет двойной
определённый интеграл

?
1. >int(int((1+xy)^(-1),x=0..y),y=0..1);
2. >int(int(1/(1+xy),y=0..1),x=0..y);
3. >int(int(1/(1+x*y),x=0..y),y=0..1);
4. >value(Int(Int(1/(1+x*y),x=0..y),y=0..1));
Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и вычисляет численное
значение тройного интеграла

с точностью до пяти значащих цифр ?
1. >
  evalf(int(int(int(1/(1+x*y*z),x=0..y,5),y=0..z,5),z=0..1,5));
2. >
  evalf(int(int(int(1/(1+x*y*z),x=0..y),y=0..z),z=0..1),5);
3. >
  evalf(Int(Int(Int(1/(1+x*y*z),x=0..y,5),y=0..z,5),z=0..1,5));
4. >
  evalf(Int(Int(Int(1/(1+x*y*z),x=0..y),y=0..z),z=0..1),5);

Бланк ответов

№	1	2	3	4
1)
2)
3)
4)

МОДУЛЬ 4

Комплексная цель:
изучение команды разложения
в степенной ряд функций и выражений в
среде Maple.

Краткое изложение
программного материала: в
модуле на конкретном примере разложения
функции гиперболического
секанса в ряд Тейлора показано назначение
всех опций команды taylor.
Модуль содержит ряд
проектных заданий для
самостоятельной работы, в которых даны
дополнительные сведения о командах
разложения функций в степенные ряды в
окрестности точек сингулярности (команда
series)
и в асимптотические ряды (команда
asympt).

Содержание модуля 4

Разложение в ряды

Одной из наиболее важных
математических идей во многих физических
теориях является идея представления
решения той или иной задачи в виде
разложения в ряд. В физике это важно,
потому что обычно невозможно получение
точного аналитического решения
поставленной задачи, и представление
решения в виде ряда дает нам общее
представление о качественном поведении
ее решения. Рассмотрим, например функцию
sech(x).
Это функция гиперболического
секанса. И что это говорит нам о ее
поведении? В окрестности нулевого
значения аргумента гиперболический
секанс аппроксимируется простой
функцией
.

Теперь вы можете видеть,
что при нулевом значении аргумента она
принимает значение, равное единице, и
ведет себя как перевернутая парабола
вдоль обоих направлений, отложенных от
точки x=0.
Но таково поведение гиперболического
секанса в сравнительно малой окрестности
нуля ее аргумента (|x|<1).
При большом значении аргумента (|x|>>1)
данная функция аппроксимируется
функцией
.
Отсюда видно, что с увеличением модуля
аргумента гиперболический секанс
начинает вести себя как экспоненциально
затухающая функция, так что ее общее
поведение на всем интервале по форме
напоминает стог сена.

Среда Maple
позволяет находить аппроксимации
большинства элементарных и специальных
(высших трансцендентных) функций с
помощью команд: taylor,
series
и asympt.
Для вызова
справочной информации об указанных
командах достаточно ввести имя
соответствующей команды, поместить
курсор на ее имя и нажать функциональную
клавишу F1.
В данном разделе мы рассмотрим первую
из этих команд, т.е. команду разложения
функций в ряд Тейлора.

Согласно
теореме Тейлора функция f(x),
имеющая определенное значение вместе
со всеми своими производными в точке
x=a,
в окрестности этой точки может быть
аппроксимирована рядом:

+ . . .

Найдем
разложение гиперболического секанса
в ряд Тейлора в окрестности точки x=0,
используя для этого команду taylor.

> taylor(sech(x),x=0,20);

Опция x=0
задает окрестность разложения, т.е. a=0
для рассматриваемого случая. Следующая
опция 20 задает количество членов ряда,
включая член погрешности разложения
O(x²⁰).

Проектное задание
4.1

Найдите разложение в рад
Тейлора для следующих функций в
окрестности точки x=0,
включая член
погрешности разложения O(x¹⁰).

(а) sin(x)
, (б)
cos(x)
, (в)
arctan(x),
(г) e^x
, (д)
ln(1+x)
, (е)
(1+x)^p

Результат
будет выглядеть очень впечатляюще, но
в большинстве проблем физики, где
разложение в ряды являются важными,
обычно сохраняют только два или три
первых члена разложения, поэтому зачастую
достаточно использование команды
разложения taylor(f(x),x=0,3).

Проектное задание
4.2

Среда Maple
позволяет находить разложение практически
всех, использующихся в физических
приложениях, специальных функций в ряд
Тейлора. Найдите соответствующие
разложения для следующих функций,
включая член
погрешности разложения O(x¹⁰):

(а) J₀(x)
, (б) I₂(x)
, (в) K(x)
(полный эллиптический
интеграл EllipticK),

(г) Г(x)
. Ответ для варианта (г)
будет мало пригоден для его дальнейшего
применения, так как найденные величины
коэффициентов разложения еще не
представлены в численном виде. Последнее
легко сделать, используя команду
>evalf(%);
или c
самого начала задать точку окрестности
разложения в форме числа с плавающей
точкой, т.е. x=1.0

Проектное задание
4.3

Попытайтесь найти
разложение в ряд Тейлора функции
из
семейства функций Бесселя в окрестности
точки x=0.
Данная функция в среде Maple
обозначается как
BesselK(0,x).
Ответа вы не получите, но на дисплей
отобразится сообщение, которое оказывается
весьма полезным.

Error,
does not have a taylor expansion, try series()

Дело в том, что рассматриваемая
функция имеет логарифмическую
сингулярность в окрестности точки x=0,
так что все ее производные в данной
точке обращаются в бесконечность.
Поэтому ее разложение в ряд Тейлора в
окрестности точки сингулярности попросту
невозможно.

Но в математическом
анализе существуют и иные виды рядов
для аппроксимации функций. В среде
Maple
для этой цели следует
использовать команду series,
полностью аналогичную команде taylor,
но более общую, позволяющую находить
разложение функций в ряды в окрестности
положений точек сингулярностей. Введите
команду >series(BesselK(0,x),x=0,3);

и
посмотрите на полученный результат.

Сосредоточим наше внимание
только на ведущем члене разложения.
Ясно видно, что функция K₀(x)
действительно имеет логарифмическую
сингулярность. Заметим также, что в
разложении в ряд появляется постоянная
Эйлера, обозначенная как γ. Определение
этой постоянной содержится в справочной
информации, которую можно вывести на
дисплей, введя команду >?gamma.
Выполнив
указанные пункты, найдите разложение
в ряд для следующих функций (в окрестности
нулевого значения аргумента):

(а)

, (б)

, (в)

.

Попробуйте использовать значение
третий опции команды разложения в ряд,
не только равное 3, как в предыдущем
примере, но и большие величины, и
проанализируйте полученные в этом
случае члены оценки ошибки разложения.

Проектное задание
4.4

Существует
иной вид разложения, часто используемый
в математической физике: асимптотическое
разложение. Формально это разложение
в окрестности бесконечности, которое
на первый взгляд покажется странным,
но дает представление о поведении
функции, когда ее аргумент принимает
достаточно большие значения. В среде
Maple
для нахождения асимптотического
разложения имеются две равнозначных
команды:

>asympt(f(x),x,2);
или

>series(f(x),x=infinity,2);

Найдите
асимптотические разложения следующих
функций:

(а)
J₀(x)
, (б) I₁(x)
, (в)
K₀(x)
, (г)
Г(x)

Используйте
команду series
для примеров (а), (б) и команду asympt
для примеров (в), (г). В каждом случае
сохраните только два члена в асимптотическом
выражении, как выше указано в примерах
использования обеих команд.

Я предложил использовать
число 2 в качестве третьей опции,
поскольку, как правило, нас интересует
ведущий член асимптотического разложения,
поскольку именно он дает ответ на важный
вопрос о поведении функции на бесконечности:
является ли функция затухающей, или
неограниченно возрастающей, и по какому
порядку степени аргумента это происходит?

Проектное задание
4.5

В специальной
теории относительности Эйнштейна
энергия объекта с массой m,
движущегося со скоростью v,
дается знаменитой формулой
.
Поставим вопрос, каким образом из этой
формулы получается известное всем
первокурсникам выражение для кинетической
энергии массивных объектов
.
Ответ на этот вопрос легко получить из
разложения в ряд Тейлора эйнштейновского
выражения для энергии. Будем считать,
что массивный объект движется со
скоростью намного меньшей скорости
света. Разложите указанную выше формулу
в ряд Тейлора по переменной v
и сохраните два первых члена разложения.
Один из этих членов будет являться
знакомым нам выражением для кинетической
энергии тел в классической механике, а
второй совпадет со знаменитой формулой
Эйнштейна для энергии массы покоя. Какое
численное значение третьей опции команды
разложения в ряд Тейлора следует
использовать для получения явных
выражений для двух членов этого
разложения?

Проектное задание
4.6

Из курса теории электричества
и магнетизма нам известна формула,
определяющая величину потенциала (в
вольтах) точечного заряда
.
В качестве задания предлагается найти
аналогичную формулу для потенциала
электрического диполя, используя
выражение для потенциала точечного
заряда. Среда Maple
поможет нам легко справиться с этим
заданием. Электрический диполь
представляет собой два заряда с величинами
q и
–q,
разделенных расстоянием d.
Дипольный момент таких зарядов обозначим
символом p,
а его величина p=qd.
Давайте поместим положительный заряд
в точку на оси Z
декартовой системы координат на
расстоянии

от начала координат, а отрицательный
заряд также на ось Z,
но со значением координаты z=.
Переходя далее к сферической системе
координат, запишем потенциал
рассматриваемого диполя как функцию
расстояния от начала координат r
и полярного угла θ.

Найдите разложение в ряд
данной функции по величине расстояния
между зарядами d
и сохраните только ведущий член разложения
с целью вывода формулы для потенциала
диполя в сферической системе координат.
Дополнительно следует “подсказать”
среде Maple,
что величина расстояния r>0,
введя соответствующую команду

>assume(r>0);

Поэкспериментируйте с
порядком разложения потенциала в ряд
и убедитесь, что задание величины порядка
разложения, равной 1, не дает никакого
полезного результата. Так как же найти
только ведущий член разложения? Для
этого в команде разложения в ряд следует
указать еще одну дополнительную опцию
‘leadterm’.
Изучите самостоятельно встроенную в
среду Maple
справочную информацию о данной опции.
Для вывода на дисплей соответствующей
справки введите команду

>?series[leadterm].

Тест рубежного контроля
№4

Тест содержит 3 задания;
даны четыре варианта ответа
на каждый вопрос, из которых необходимо
выбрать один верный. На
выполнение каждого задания отводится
3 минуты. Выберите наиболее правильный,
по Вашему мнению, вариант ответа и
отметьте его любым значком в бланке
ответов. Тест оценивается по 5-балльной
системе: отлично – 3 правильных ответа;
хорошо – 2 правильных ответа;
удовлетворительно – 1 правильный ответ;
неудовлетворительно – не одного
правильного ответа.

Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и находит для функции

разложение в ряд Тейлора в окрестности
точки x=0,
включая член
погрешности разложения
O(x¹⁰)
?
1. >taylor(sin(x)^3/x^3,x=0,10);
2. >taylor(x->sin(x)^3/x^3,x=0,10);
3. >taylor(sin(x)^3/x^3,x=0,12);
4. >taylor(x->sin(x)^3/x^3,x=0,12);
Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и находит для функции

разложение в ряд в окрестности точки
сингулярности x=0,
включая член
погрешности разложения
O(x¹⁰)
?
1. >series((exp(x)-1)/x^2,x=0,10);
2. >series((exp(1)^x-1)/x^2,x=0,10);
3. >series((exp(x)-1)/x^2,x=0,12);
4. >series((exp(1)^x-1)/x^2,x=0,12);
Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и находит асимптотическое
разложение функции
,
включая член погрешности разложения
O(x¹⁰)
?
1. >asympt(x->x^(1/2)*((x+1)^(1/2)-x^(1/2)),x,10);
2. >asympt(x^(1/2)*((x+1)^(1/2)-x^(1/2)),x=infinity,10);
3. >asympt(x^(1/2)*((x+1)^(1/2)-x^(1/2)),x,10);
4. >series(x^(1/2)*((x+1)^(1/2)-x^(1/2)),x=infinity,10);

Бланк ответов

№	1	2	3	4
1)
2)
3)

МОДУЛЬ 5

Комплексная цель:
изучение команды суммирования
конечных и бесконечных рядов в среде
Maple.

Краткое изложение
программного материала: в
модуле рассмотрен конкретный пример
нахождения суммы бесконечного ряда,
встречающегося в курсе статистической
физики, в двух возможных вариантах
синтаксической записи членов ряда:

– в виде выражения;

– в виде функции индекса
суммирования.

Указан способ доступа к встроенной
справочной информации о команде
суммирования, содержащей ряд примеров
ее использования.

Содержание модуля 5

Суммирование рядов

Среда Maple позволяет
производить суммирование рядов, как
конечных, так и бесконечных (в случае
если бесконечный ряд суммируем). Для
этого следует использовать команду
суммирования sum,
синтаксис которой полностью аналогичен
синтаксису изученной нами ранее команды
интегрирования int.
Отметим, что аналогично команде
интегрирования, команда суммирования
рядов также имеет инертную форму: Sum.

Просуммируем для примера
ряд, встречающейся в курсе статистической
физики
.

>
restart;

>
sum(1/’n’^2,’n’=1..infinity);

и получим
красивый и нетривиальный результат.
Вы заметили, что индекс суммирования
n, как в первом аргументе команды sum,
задающем выражение для общего члена
ряда, так и во втором аргументе, задающем
пределы суммирования, записан в одиночных
кавычках? Опыт работы в среде Maple
показывает, что использование одиночных
кавычек не всегда обязательно. Если вы,
как в данном примере, начали сеанс работы
после ввода команды restart,
данный ряд можно просуммировать командой

> sum(1/n^2,n=1..infinity);

Однако если вы перед
суммированием данного ряда уже
использовали переменную n в качестве
индекса для нумерации элементов
последовательности или массива, и
присвоили этой переменной конкретное
значение, использование команды
суммирования ряда, без использования
одиночных кавычек приведет к ошибке.
Запись индекса суммирования в одиночных
кавычках среда Maple воспринимает как
фиктивную переменную, и игнорирует все
её предыдущие присвоения.

Команда sum,
а также ее инертная форма Sum
позволяет
вычислять суммы рядов, члены которого
заданы как функции индекса суммирования.

>
fn:=n->1/n^2;

>
s1:=Sum(fn(n),n=1..infinity);

>
value(s1);

Не пренебрегайте
встроенной в среду Maple справочной
системой. Изучите примеры использования
команды суммирования рядов. Для этого
выведем их на дисплей с помощью команды
> ?sum

Проектное задание
5.1

Вычислить перечисленные ниже
суммы рядов, используя для записи общего
члена ряда форму выражения в примерах
(а,б,в) и форму функции в примерах (г,д,е).

(а)

(б)

(в)

(г)

(д)

(е)

Примечание: в примере
(г) предполагается, что переменная N
стремится к бесконечности в обоих
слагаемых, а не только в записи верхнего
предела суммирования. Вы должны получить
в результате очень компактный ответ,
содержащий единственный символ γ. Это
не является ошибкой, так как этим символом
обозначается постоянная Эйлера. Вычислите
ее
численное
значение,
используя
команду
>evalf(%);

Тест рубежного контроля
№5

Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и может быть
использована для получения результата
суммирования бесконечного ряда

в аналитическом виде?
1. >value(sum(k/(k+1)^4,k=0..infinity));
2. >value(Sum(k/(k+1)^4,k=0..infinity));
3. >sum(‘k/(k+1)^4’,’k’=0..infinity);
4. >sum(‘k’/(‘k’+1)^4,’k’=0..infinity);
Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и может быть
использована для получения численного
значения суммы бесконечного ряда

?
1. >evalf(sum(1/k^4,k=1..infinity));
2. >evalf(Sum(1/k^4,k=1..infinity));
3. >evalf(sum(‘1/k^4’,’k’=1..infinity));
4. >evalf(sum(1/’k’^4,’k’=1..infinity));
Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и может быть
использована для получения результата
суммирования конечного ряда

в аналитическом виде?
1. >value(sum(k^2/(k+1)^4,k=0..N));
2. >value(Sum(k^2/(k+1)^4,k=0..N));
3. >sum(‘k^2/(k+1)^4’,’k’=0..N);
4. >sum(‘k’^2/(‘k’+1)^4,’k’=0..N);
Какая из перечисленных
команд имеет в среде Maple синтаксически
правильную запись и может быть
использована для получения численного
значения суммы конечного ряда

?
1. >evalf(sum(1/k^4,k=1..1000));
2. >evalf(Sum(1/k^4,k=1..1000));
3. >evalf(sum(‘1/k^4’,’k’=1..1000));
4. >evalf(sum(1/’k’^4,’k’=1..1000));

Бланк ответов

№	1	2	3	4
1)
2)
3)
4)

Литература

Прохоров,Г.В, Леденев,М.А,
Колбеев,В.В. Пакет символьных вычислений
Maple V. Москва: Компания “Петит”, 1997. –
198c.
Говорухин,В.Н, Цибулин,В.Г.
Ведение в Maple.
Математический пакет для всех. Москва:
Издательство “Мир”,
1997. – 205c.
Васильев,А.Н, Самоучитель
Maple
8. Москва: Издательство
“Диалектика”, 2003.
– 351c.
Дьяконов,В.П, Maple
9.5/10 в математике, физике и образовании.
Москва: Солон-пресс,
2006. – 719c.
Градштейн,И.С, Рыжик,И.М,
Таблицы интегралов, сумм, рядов и
произведений. Москва:
Издательство “Наука”,
1997.
– 1108 c.

Источник

уметь применять указанные команды для решения математических задач.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

Дифференцирование выражений

Команды diff ( ) и Diff ( ) предназначены для вычисления обыкновенных и частных производных аналитического выражения по одной или нескольким переменным. Вторая команда является отложенной командой, которая не вычисляет производную от выражения, а просто отображает математическую запись взятия производной. Результат действия отложенной команды можно присвоить переменной Maple, а в дальнейшем при помощи команды value ( ) вычислить результат этой отложенной команды. Отложенная форма команды удобна, когда необходимо видеть, какие операции были сделаны для получе-ния нужного выражения. Кроме этой команды еще целый ряд команд имеют отложенную форму, информацию о которых можно получить в Справке.

Синтаксис команды дифференцирования следующий:

diff (выражение, переменная_1, переменная_2, . переменная_n);

diff (выражение, [переменная_1, переменная_2, . переменная_n]);

В результате выполнения любой из приведенных команд будет вычислена частная производная n-гo порядка от заданного первым параметром выражения по заданным n переменным.

При вычислении производных высокого порядка можно использовать оператор последовательности $, который позволяет проще и нагляднее задать производную. Например, для вычисления третьей производной функции f (х) по переменной х можно использовать команду diff (f (х) , х, х, х), в которой три раза указано дифференцирование по переменной х, или применить в команде дифференцирования оператор последовательности х$3, что упрощает и делает более наглядным задание третьей производной: diff (f (х) , х$3).

Пример 1. Вычисление производных.

Последние три команды показывают использование отложенной формы команды дифференцирования.

2. Интегрирование выражений

Команда int( ) имеет отложенную форму Int( ) и осуществляет интегрирование выражений по заданной переменной. Эта команда вычисляет неопределенный интеграл от выражения (при этом, правда, в ответе не будет никакой постоянной интегрирования) используя следующий синтаксис:

int (выражение, переменная);

Определенный интеграл вычисляется при следующем синтаксисе команды:

int (выражение, переменная = a..b);

где a и b являются пределами интегрирования, причем эти пределы могут быть и аналитическими выражениями.

Пример 2. Интегрирование функций.

Для символьного вычисления определенного интеграла существуют две опции, управляющие обработкой разрывов подынтегральной функции. Эти опции задаются третьим параметром в командах int( ) и Int( ).

По умолчанию команда интегрирования проверяет выражение на не-прерывность в области интегрирования и вычисляет интеграл как сумму от-дельных определенных интегралов на промежутках непрерывности функции. Опция `continuous` отключает этот режим и вычисляет интеграл как разность значений первообразной подынтегральной функции в точке начала и конца промежутка интегрирования. Еще одна опция `CauchyPrincipalValue` вычисляет несобственные интегралы первого и второго рода в смысле главного значения Коши.

Если Maple не находит замкнутую форму выражения для определенно-го интеграла, то команда интегрирования возвращает вызов самой себя (в области вывода печатается математическая запись вычисления интеграла, как при обращении к отложенной команде интегрирования). В таких случаях можно вычислить значение определенного интеграла численным способом с помощью команды evalf ( ). Синтаксис при этом следующий:

evalf( int (f,x=a. .b) ) ;

evalf ( Int (f,x=a. .b) ) ;

evalf (Int (f ,x=a. .b), digits, flag);

Параметр digits позволяет задать число значащих цифр при вычислени-ях приближенного значения интеграла (по умолчанию это число равно числу значащих цифр, определенных значением системной константы Digits).

При численном интегрировании по умолчанию используется квадра-турная формула Кленшо-Куртиса (Clenshaw-Curtis). Если в подынтегральном выражении встречается сингулярность, то применяется специальная методи-ка символьного анализа для ее разрешения. Для задач с неустранимыми сингулярностями используется адаптивный метод двойных экспоненциаль-ных квадратур. Параметр flag позволяет явно задать метод численного интегрирования. Он может принимать значения, представленные в табл. 1.

Таблица 1. Значения параметра flag при численном интегрировании.

Применяется только квадратура Кленшо-Куртиса без вызова процедуры обработки сингулярности

Применяется адаптивный метод двойных экспоненциальных квадратур

Применяется метод квадратурной формулы Ньютона-Котеса, являющийся методом фиксированного порядка, и не эффективен для высоких точностей (Digits > 15)

Пример 3 помогает освоиться с использованием вышеприведенной методики.

Пример 3. Численное интегрирование функций.

Первый интеграл примера 3 вычисляется в аналитическом виде, но представляется через значение специальной функции интегральный косинус. Для получения ответа в виде десятичного числа применяется алгоритм чис-ленного интегрирования. Здесь же показано использование отложенной формы команды интегрирования для более удобного представления ответа.

Численное интегрирование даже функций, внешний вид которых представляется не достаточно сложным, может потребовать значительного времени. Если будет казаться, что Maple завис (а такое случается), то надо следить за изменением времени в правой части строки состояния. Если оно изменяется, то просто следует дождаться завершения интегрирования.

В системе Maple имеется набор команд для полного исследования функций: limit ( ) — для отыскания предела функции, sum ( ) — для нахождения всевозможных конечных сумм, series ( ) — для разложения функций в ряды Тейлора, Маклорена и Лорана, extrema ( ) — для исследования экстремумов функций как одной, так многих переменных, minimize ( ) и maximize ( ) — для поиска минимума и максимума функции на заданном промежутке. Описание всех этих и других команд можно, естественно, найти в Справке Maple.

Для нахождения предела выражения или функции в Maple используется команда limit (параметр 1, параметр 2). Первый параметр — выражение, второй параметр — имя переменной, приравненное значению переменной в точке предела. Необязательный третий параметр — направление предела. Если направление не задано, вычисляется стандартный двусторонний предел. Если предел не существует, в качестве ответа возвращается сообщение «undefined». Если Maple не способен вычислить предел (однако он может существовать), возвращается невыполненная команда.

В большом количестве случаев выражение, которое не имеет двустороннего предела, имеет односторонний предел:

В команде limit ( ) может присутствовать также необязательная опция complex или real в качестве третьего параметра аргумента. Эта опция определяет, в комплексной или действительной области вычисляется предел.

Задачи для самостоятельного решения.

1. Найти производную:

2. Найти интеграл:

3. Найти следующие пределы:

. 1.1; 2.1; 3.1; . 1.9; 2.9; 3.9;

. 1.2; 2.2; 3.2; . 1.10; 2.10; 3.10;

. 1.3; 2.3; 3.3; . 1.11; 2.11; 3.11;

. 1.4; 2.4; 3.4; . 1.12; 2.12; 3.12;

. 1.5; 2.5; 3.5; . 1.13; 2.13; 3.13;

. 1.6; 2.6; 3.6; . 1.1; 2.2; 3.3;

. 1.7; 2.7; 3.7; . 1.13; 2.12; 3.11.

1. Говорухин В.Н., Цибулин В.Г. Введение в Maple. Математический пакет для всех. — М.: Мир, 1997. — 208 с.

2. Дьяконов В.П. Математическая система Maple V. — М.: Издательство “Солон”,1998.

3. Двайт Г.Б. Таблицы интегралов и другие математические формулы. — М.: Наука. Главная редакция физико-математической литературы, 1983. — 176 с.

4. Матросов А.В. Maple 6. Решение задач высшей математики и механики. — СПб.:БХВ — Петербург, 2001.- 528 с.

5. Манзон Б.М. Maple V Power Edition — М.: Информационно-издательский дом “Филинъ”,1998г.

Интегрирование

такие же, как и в команде прямого исполнения int. Команда Int выдает на экран интеграл в аналитическом виде математической формулы.

Для вычисления определенного интеграла в командах int и Int добавляются пределы интегрирования, например,

Если в команде интегрирования добавить опцию continuous:

int(f, x, continuous), то Maple будет игнорировать любые возможные разрывы подынтегральной функции в диапазоне интегрирования. Это позволяет вычислять несобственные интегралы от неограниченных функций. Несобственные интегралы с бесконечными пределами интегрирования вычисляются, если в параметрах команды int указывать, например, x=0..+infinity.

Численное интегрирование выполняется командой

evalf(int(f, x=x1..x2), e), где e — точность вычислений (число знаков после запятой).

Как посчитать интеграл в maple

Библиографическая ссылка на статью:
Рабчук А.В., Самигуллина Р.Г. Лабораторные работы и индивидуальные задания в среде Maple (часть 1 — производные и интегралы) // Современная педагогика. 2015. № 11 [Электронный ресурс]. URL: https://pedagogika.snauka.ru/2015/11/5084 (дата обращения: 24.01.2022).

Для начала дадим некоторые основные процедуры и функции:
Restart — начинать с каждой новой задачи. ^ — возведение в степень, / – деление, * – умножить, <shift+enter>- переход на другую строку без вычислений,< enter>- переход на другую строку с вычислением, := – оператор присваивания, floor(x)- целая часть х, Рlot (%) – печать графика последней функции , если (%%)-предпоследней и т.д. Другие варианты, более сложные, покажем далее; sqrt(X) — , sec(X) –секанс, sin(X)-синус, exp(x) -e , csc(X)- косеканс, cos(X)-косинус, ln(x) – натуральный логарифм, tan(X)-тангенс, log[d](X)-логарифм по основанию d, log10x – десятичный логарифм, arctan(x)-арктангенс , arctcot(x)-арккотангенс, cot(X) –котангенс.
Лабораторная работа N 1.
Вычисление производных.
Оператор diff (), -параметры процедуры: функция от которой берут производную, и переменная по которой берут производную.
ПРИМЕР1 . diff (sin(x),x); < enter> ответ: cos(x)
Plot (%);< enter> график косинуса
ПРИМЕР2. Найти производную
Y= (xsina+cosa) (xcosa-sina),
Можно сначала определить функцию следующим образом
Y:=x->(x*sin(a)+cos(a)*(x*cos(a)-sin(a)) ; < enter>
diff(Y(x),x) ); < enter>
Plot (%) ;< enter>
ПРИМЕР 3. y=[x] cos(10 x)
Y: =x->floor(x)*cos(10*pi*x); < enter>
diff( Y(x),x ); < enter>
Plot (%) ;< enter>
Можно использовать оператор D.
D (SIN); ОТВЕТ COS или D (sin(x)); ответ cos(x).
ПРИМЕР 4.

Y=
Производная от кусочно-гладкой функции с помощью процедуры
PIECEWISE ( …) в ней последний интервал не указывается
Y: =X-> PIECEWISE(X<1, 1-X, X<=2, (1-X)*(2-X),-2+X); < enter>
F: =X->diff(Y(X),X) ; < enter>
F(X); < enter>
plot ([Y(X),F(X)]) ;< enter> графики функции и производной.

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
1. 11. ;
2. 12. ;
3. 13. ;
4. 14. ;
5. 15. ;
6. ; 16. ;
7. ; 17. ;
8. ; 18. ;
9. ; 19. ;
10. ; 20. .

21.	26.
22.	27.
23.	28.
24.	29.
25.	30.

Лабораторная работа N 2.

Процедура двумерной графики
Для двумерной графики используются процедуры plot(), если функции заданы явно или параметрически и implicitplot() — для неявно заданных функций . В таблице (Табл.1) даны некоторые параметры, которые могут использоваться для построения графиков.

Табл.1 Параметры процедуры plot()

Параметр	Описание
title	Заголовок рисунка – строка символов, переход на новую строку обозначается n
titlefont	ШРИФТ заголовка. Тип- TIMES,COURIER, HELVETICA,SYMBOL. Стиль – ROMAN –прямой, BOLD – жирный, ITALIC-курсив. Размер шрифта в пунктах, пункт=1/72 дюйма.
thickness	Толщина линии. По умолчанию 10 пунктов.
labers	Надпись на осях. Это список из двух строк. Первая – надпись для оси абсцисс, вторая – для оси ординат.
color	Цвет линии графика. Black- Черный, blue- синий, navy-темно-синий, coral-красный , cyan-голубой, green-зеленый, gray-серый,
linestyle	Стиль линии. От1 до 4, что одно и то же из названий: SOLID- Сплошная, DOT-пунктир, DASH- штрихованная, DASHDOT-штрихпунктир.
legend	Легенда графика.Если графиков много , тогда задается список – строки легенды этих графиков
simbol	Тип символа для отображения графика. BOX- Квадрат, CROSS- крест, CIRCLE- круг, POINT-точка, DIAMOND- ромб.

Пример 1 . Найти производную и построить графики функции и ее производной

y:=x – >piecewise(abs(x)<1,x^2*exp(-x^2),1>abs(x),1/exp(1));
f:=diff(y(x),x);
plot([y(x),f],x=-2 . .2,color[GREEN,NAVY], linestyle=[SOLID,DASHDOT],title=”кусочно-гладкая функция”,
titlefont=[COURIER,BOLD,15],legend=[“y(x)”,”производная”]);

Пример 2 . Найти производную и построить график функции и ее производной, если функция задана параметрически x=2cos2t, y=5sin2t,
x:=2*cos(t);
y:=5*sin(t);
f:=diff(y,t)/diff(x,t);
plot([x,y,t=0 . . 2*pi],[x,f,t=0. .2*pi],-2 . .2,-8 . .+8,
color=[RED,BLUE],style=[POINT,LINE],symbol=DIAMOND,
title=”параметрическая функция n и ее производная”,
titlefont=[COURIER,BOLD,15]);
Списки в операторе plot в [ ] содержат три элемента: две переменные, зависящие от t и область изменения t . Наличие трех элементов уже говорит о параметрической зависимости.
Пример 3 . Нарисовать график функции
implicitplot(x^2/16+y^2/9=1, x=-4. .4, y=-3. .3, thickness=2,
title=”неявно заданная функция”,
titlefont=[COURIER,BOLD,15] );

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ

N – НОМЕР ПО СПИСКУ.
1. Кардиоида или
2.Циклоида или
3.Эвольвента круга
4.Астроида или .
5.Четырехлепестковая роза , или .
6. Улитка Паскаля
или
7. Строфоида или
8.Циссоида
9. Лемниската или
10.Овал Кассини

Лабораторная работа N 3.
Вычисление производных от функций заданных неявно.
Для вычисления производных от функций заданных неявно предусмотрена процедура implicitdiff () . Первый параметр – заданное выражение, второй – функция, от которой берется производная, третий – переменная по которой производная берется.
Пример 1 . Найти производную
implicitdiff(x^2+2*x*y-y^2=2*x,y,x) ;
===============================================на экране

Можно построить график с помощью процедуры implicitplot () . Но иногда нужно подключить процедуру plots с помощью команды with().

with(plots);
implicitplot ( x^2+2*x*y-y^2=2*x,x=-5. .5,y=-5. .5 );
Пример 2 . Найти производную функции в точке
x=2, y=4.
Зададим уравнение
F:=x^2/a^2+y^2/b^2=1;
Далее вычисляем производную
FX:= implicitdiff(F,y,x);
Присваиваем переменным заданные значения
x:=2;
y:=4;
%%%- выполнение пред-предпоследней команды (третья снизу)
‘производная в точке’=%%%;
===============================================на экране
производная в точке =

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
ЗАДАНИЕ 1. Вычислить программно и проверить аналитически
1. , 2.
3. 4.
5. 6.
7. , 8.
9. 10.
ЗАДАНИЕ 2. Найти производную функций в заданной точке и проверить аналитически.
1. , 2.
3. 4.
5. 6.
7. , 8.
9. 10.

Лабораторная работа N4.
Интегралы.
Int(…)- неактивная форма для вывода информации в символьном виде;
int(…) – активная форма для вычисления интеграла.
ПРИМЕР 1. Вычисление может быть таким – в операторах описан интеграл и переменная интегрирования.
Int(exp(alpha*x)*(cos(b*x),x)=int(exp(alpha*x)*cos(b*x),x); < enter>
Ответ. =
Определенный интеграл вычисляется так
ПРИМЕР 2.
Int(x^2*cos(x),x=0..2*pi)=int(x^2*cos(x),x=0..2*pi); < enter>
Ответ . =4
ПРИМЕР 3.
Int(x*ln(x)/((1+x^2)^2),x=0..infinity)=int(x*ln(x)/((1+x^2)^2),x=0..infinity);
< enter>
Ответ. =0
ПРИМЕР 4. Найти интеграл и построить графики функции и интеграла

f:=x- >piecewise(x<0,1,x<=1,x+1,2*x);
f(x); проверка записи
F: =x->int(f(x),x);
F(x); проверка записи
Печать графиков
plot ([f(x),F(x)], x=-1. .2,
color=[RED,NAVY], linestyle=[DOT,SOLID],
thickness=2, title=”кусочно-гладкая функция n и ее интеграл”,
titlefont=[TIMES,BOLD,15],legend=[“функция”,”интеграл”]);

ИНДИВИДУАЛЬНЫЕ ЗАДАНИЯ
1. 10. 19.
2 11. 20.
3. dx 12.
4. 13.
5. 14.
6. 15.
7. 16.
8. 17.
9. 18.

Источник

Предел функции

Нахождение пределов.

Дифференцирование выражений и функций.

Вычисление интегралов.

3.1. Интегрирование элементарных функций.

3.3. Двойные интегралы

3.4. Тройные интегралы.

Разложение в ряды

Суммирование рядов

Интегрирование

Как посчитать интеграл в maple

Вам также может понравиться

Как найти игру в реборне

Как найти частоту колебаний маятника через период

Как найти прописку человека по инн

Добавить комментарий Отменить ответ

Дифференцирование
выражений и функций.

Вычисление
интегралов.

3.1.
Интегрирование элементарных функций.

3.3.
Двойные интегралы

3.4.
Тройные
интегралы.