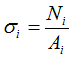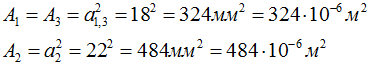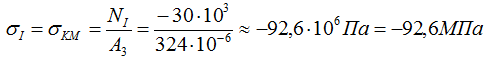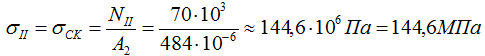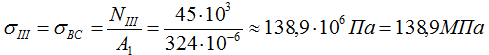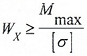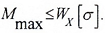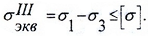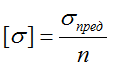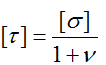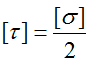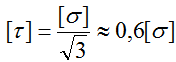Как найти предельное напряжение стержня

Предельные и допустимые напряжения

Предельным
напряжением считают напряжение, при
котором

в материале
возникает опасное состояние (разрушение
или опасная дефомация).

Для пластичных
материалов предельным напряжением
считают предел текучести, т. к. возникающие
пластические деформации не исчезают
после снятия нагрузки: σ_пред
=σ_т

Для хрупких
материалов, где пластические деформации
отсутствуют, а разрушение возникает по
хрупкому типу (шейки не образуется), за
предельное напряжение принимают предел
прочности: σ_пред
=σ_т

Для пластично-хрупких
материалов предельным напряжением
считают напряжение, соответствующее
максимальной деформации 0,2% (σ_0,2):

σ_пред
=σ_0,2

Допускаемое
напряжение — максимальное напряжение,
при котором материал должен нормально
работать.

Допускаемые
напряжения получают по предельным с
учетом запаса прочности: [σ]= σ_пред
/[s]

где [σ] — допускаемое
напряжение; в — коэффициент запаса
прочности; [s]
— допускаемый коэффициент запаса
прочности.

Примечание.
В квадратных скобках принято обозначать
допускаемое значение величины.

Допускаемый
коэффициент запаса прочности зависит
от качества материала, условий работы
детали, назначения детали, точности
обработки и расчета и т. д.

Он может колебаться
от 1,25 для простых деталей до 12,5 для
сложных деталей, работающих при переменных
нагрузках в условиях ударов и вибраций.

Расчеты
на прочность при растяжении и сжатии

Расчеты
на прочность ведутся по условиям
прочности — нера­венствам,
выполнение которых гарантирует прочность
детали при данных
условиях.

Для
обеспечения прочности расчетное
напряжение не должно превышать
допускаемого напряжения:
Расчетное
напряжение σ
зависит
от
нагрузки и размеров попе­речного
сечения, допускаемое только от
материала детали и
усло­вий
работы.

Существуют
три вида расчета на прочность.

Проектировочный
расчет
—
задана расчетная схема и нагрузки;
материал
или размеры детали подбираются:

определение
размеров поперечного сечения:
подбор
материала
по
величине σ_пред
можно
подобрать марку материала.

Проверочный
расчет
—
известны нагрузки, материал, размеры
детали; необходимо проверить,
обеспечена ли прочность.

Проверяется
неравенство

Определение
нагрузочной способности
(максимальной
нагрузки):

Тема 2.3 практические расчеты на срез и смятие

Понятие
о срезе и смятии. Условия прочности

Срезом
или сдвигом
называется деформация, возникающая под
действием двух близко расположенных
противоположно напра­вленных равных
сил. При этом возникают касательные
напря­жения.

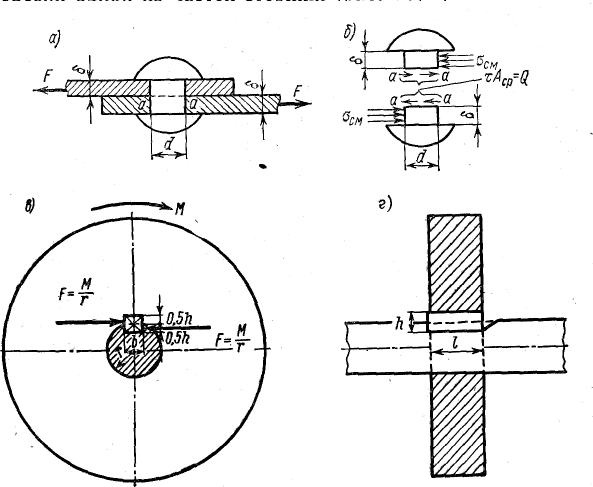
Примером
элемента металлических конструкций,
работающего на срез, может служить
заклепка . При некоторой величине
действующих сил F
стержень заклепки может быть сре­зан
по сечению аа.
Силы
F
передаются путем давления стенок
отверстия на стержень заклепки.

Деформация
среза возникает также в шпоночном
соединении, схематично изображенном
на рис.
Вращающий
момент М
от
шкива передается на вал радиуса г с
помощью сил F
=М/r.
Эти
силы вызывают срез или сдвиг шпонки по
ее среднему сече­нию. Частный случай
среза — скалывание волокнистых
матери­алов, в частности древесины,
по плоскостям, параллельным волокнам.
При большом давлении может произойти
значительное смятие стенок отверстия
или стержня заклепки по поверхности их
соприкосновения. В шпоночном соединении
смятие может про­изойти по площади
контакта вала или шкива со шпонкой.

Смятием
называется
местная деформация сжатия по площад­кам
передачи давления. Возникающие нормальные
напряжения смятия
являются местными; величина их быстро
убывает при уда­лении
от площадки соприкосновения элементов.

Чтобы
найти напряжения, возникающие в сечении
аа
стержня
заклепки
под действием сил
F
,
применим
метод сечений. Рассечем мысленно стержень
заклепки на две части и рассмотрим
условия равновесия
одной из частей стержня (рис. б).

Со
стороны листа на нее передается внешняя
сила F,
а
по сечению
аа
действуют
внутренние силы. Поперечная сила Q,
возникающая
в сечении аа,
уравновешивает
внешнюю силу F
и
численно равна ей
Q
= F.

Приближенно
можно принять, что касательные напряжения
распределяются
по сечению равномерно

τ=
Q
/A_СР.

Условие
прочности элементов, работающих на
срез, имеет вид
τ
= Q
/A_ср≤[
τ
_СР],

где
A_гр
—площадь среза; [τ
_ср]
—допускаемое касательное на­пряжение.

Величину
допускаемого напряжения назначают па
основании испытаний
на срез. Обычно принимают [τ
_ср]
=(0,70…
0,80) [σ]

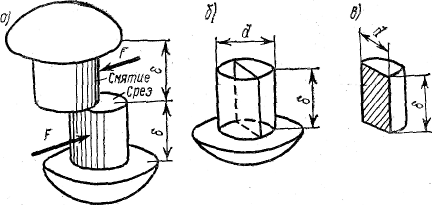
На
стержень заклепки давление со стороны
отверстия в листе передается по боковой
поверхности полуцилиндра высотой,
рав­ной
толщине листа б.

Напряжения
смятия распределены по поверхности
неравно­мерно.
Так как закон их распределения точно
неизвестен, расчет ведут упрощенно,
считая их постоянными по расчетной
площади смятия.

Проверку
элементов конструкции на смятие
производят по формуле
σ_см
= Q/А_см
≤
[σ_см]

где
А_см
— площадь смятия; [σ_см]
— допускаемое напряжение на
смятие. Обычно принимают [σ_см]
=
(1,74…2,2) [σ].
Расчет­ные
площади среза и смятия, входящие в
формулы, вычисляются
в каждом конкретном случае в зависимости
от вида соединения и характера передачи
усилий. Так, для заклепочного соединения,
изображенного на рис,
площадь
среза одной
заклепки
соответствует ее поперечному
сечению А_ор=πd²/4
.

За
площадь смятия заклепки условно принимают
ее диаметраль­ное
сечение под одним листом, т. е. прямоугольник
A_см⁼dδ.

Для
шпоночного соединения, площади
среза и смятия также нетрудно опре­делить

A_ср
= lb,

A_cм
= l0,5h.

Расчет
сварных соединений

Сварка
является наиболее механизированным и
совершенным способом соединения
элементов стальных конструкций.
Соедине­ние
сваркой элементов конструкций
осуществляется внахлестку и
встык. Соединение внахлестку производится
при помощи валиковых
(угловых) швов.

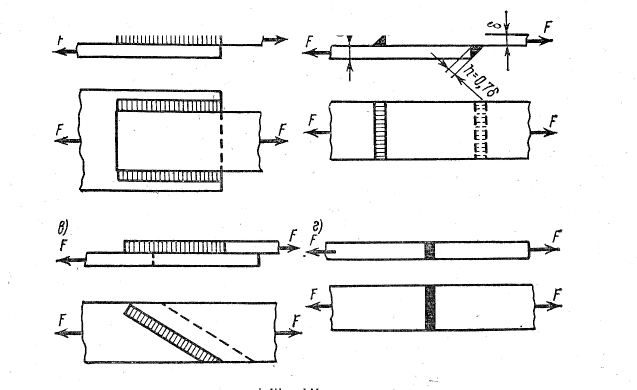
Валиковые
швы называются фланговыми, если они
расположены
параллельно
направлению силы (рис.а),
лобовыми,
если они
расположены
перпендикулярно направлению силы
(рис.б),
и
косыми, если они идут под углом к
направлению действующей
силы
(рис. в). ^!

Валиковые
швы рассчитывают на срез. Расчетное
сечение среза
— площадь А
=
lh,
где
l
—длина валикового шва; h
—
расчетная
высота шва, связанная с толщиной
свариваемых листов соотношением
(рис. б)

Н
=
δ соs45°
≈ 0,76.

Когда
сваривают листы различной толщины, то
при вычисле­нии
высоты шва в расчет вводится минимальная
толщина. Условие прочности сварного
шва имеет вид

τ=
F/
lh
= F/
l
δ ≤
[τ_ср
]

где
[τ_ср
] —допускаемое напряжение на срез для
сварного шва.

Чаще
всего применяют сварное соединение
листов встык (рис.,
г), когда зазор между соединяемыми
листами заполняется расплавленным
металлом. При сравнительно большой
толщине соединяемых
элементов их кромки перед сваркой
специально обра­батывают.
Высоту шва обычно принимают равной
толщине листов.

Прочность
стыкового сварного шва, как правило, не
уступает прочности
свариваемого металла. Сварной шов в
соединении

встык
работает на тот же вид деформации, что
и соединяемые элементы,
наиболее часто — на растяжение или на
сжатие. Условие
прочности шва в этом случае имеет вид

σ=
F/
lh
= F/
l
δ ≤[σ’]

где
[σ’]
—допускаемое напряжение на растяжение
или сжатие сварного
шва.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #

  08.03.201514.37 Mб15Конспект лекций по ИУРЭ ДВОРСОН.doc

• #
• #
• #
• #
• #
• #
• #
• #

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Устойчивость сжатых стержней

Продольный изгиб

При расчетах на прочность подразумевалось, что равновесие конструкции под действием внешних сил является устойчивым. Однако выход конструкции из строя может произойти из-за того, что равновесие конструкций в силу тех или иных причин окажется неустойчивым. Во многих случаях, кроме проверки прочности, необходимо производить еще проверку устойчивости элементов конструкций.

Состояние равновесия считается устойчивым, если при любом возможном отклонении системы от положения равновесия возникают силы, стремящиеся вернуть её в первоначальное положение.

Рассмотрим известные виды равновесия.

Неустойчивое равновесное состояние будет в том случае, когда хотя бы при одном из возможных отклонений системы от положения равновесия возникнут силы, стремящиеся удалить её от начального положения.

Состояние равновесия будет безразличным, если при разных отклонениях системы от положения равновесия возникают силы, стремящиеся вернуть её в начальное положение, но хотя бы при одном из возможных отклонений система продолжает оставаться в равновесии при отсутствии сил, стремящихся вернуть её в начальное положение или удалить от этого положения.

При потере устойчивости характер работы конструкции меняется, так как этот вид деформации переходит в другой, более опасный, способный привести её к разрушению при нагрузке значительно меньшей, чем это следовало из расчета на прочность. Очень существенно, что потеря устойчивости сопровождается нарастанием больших деформаций, поэтому явление это носит характер катастрофичности.

При переходе от устойчивого равновесного состояния к неустойчивому конструкция проходит через состояние безразличного равновесия. Если находящейся в этом состоянии конструкции сообщить некоторое небольшое отклонение от начального положения, то по прекращении действия причины, вызвавшей это отклонение, конструкция в исходное положение уже не вернется, но будет способна сохранить приданное ей, благодаря отклонению, новое положение.

Состояние безразличного равновесия, представляющее как бы границу между двумя основными состояниями – устойчивым и неустойчивым, называется критическим состоянием. Нагрузка, при которой конструкция сохраняет состояние безразличного равновесия, называется критической нагрузкой.

Эксперименты показывают, что обычно достаточно немного увеличить нагрузку по сравнению с её критическим значением, чтобы конструкция из-за больших деформаций потеряла свою несущую способность, вышла из строя. В строительной технике потеря устойчивости даже одним элементом конструкции вызывает перераспределение усилий во всей конструкции и нередко влечет к аварии.

Изгиб стержня,связанный с потерей устойчивости, называется продольным изгибом.

Критическая сила. Критическое напряжение

Наименьшая величина сжимающей силы, при которой первоначальная форма равновесия стержня – прямолинейная становится неустойчивой – искривленной, называется критической.

При исследовании устойчивости форм равновесия упругих систем первые шаги были сделаны Эйлером.

В упругой стадии деформирования стержня при напряжениях, не превышающих предел пропорциональности, критическая сила вычисляется по формуле Эйлера:

где I_min – минимальный момент инерции сечения стержня (обусловлено тем, что изгиб стержня происходит в плоскости с наименьшей жесткостью), однако исключения могут быть только в случаях, когда условия закрепления концов стержня различны в разных плоскостях, ℓ — геометрическая длина стержня, μ – коэффициент приведенной длины или коэффициент приведения (зависит от способов закрепления концов стержня), Значения μ приведены под соответствующей схемой закрепления стержней

Критическое напряжение вычисляется следующим образом

, где гибкость стержня ,

а радиус инерции сечения.

Введем понятие предельной гибкости.

Величина λ_пред зависит только от вида материала:

Если у стали 3 Е=2∙10 11 Па, а σ_пц=200МПа, то предельная гибкость

Для дерева (сосна, ель) предельная гибкость λпред=70, для чугуна λпред=80

Таким образом, для стержней большой гибкости λ≥λ_пред критическая сила определяется по формуле Эйлера.

В упругопластической стадии деформирования стержня, когда значение гибкости находится в диапазоне λ₀≤λ≤λ_пр, (стержни средней гибкости) расчет проводится по эмпирическим формулам, например, можно использовать формулу Ясинского Ф.С. Значения введенных в нее параметров определены эмпирически для каждого материала.

где a и b – постоянные, определяемые экспериментальным путем (эмпирические коэффициенты).Так, для стали3 а=310МПа, b=1,14МПа.

При значениях гибкости стержня 0≤λ≤λ₀ (стержни малой гибкости) потеря устойчивости не наблюдается.

Таким образом, пределы применимости формулы Эйлера — применяется только в зоне упругих деформаций.

Условие устойчивости. Типы задач при расчете на устойчивость. Коэффициент продольного изгиба

Условием устойчивости сжатого стержня является неравенство:

Здесь допускаемое напряжение по устойчивости [σуст] — не постоянная величина, как это было в условиях прочности, а зависящая от следующих факторов:

1) от длины стержня, от размеров и даже от формы поперечных сечений,

2) от способа закрепления концов стержня,

Как и всякая допускаемая величина, [σуст] определяется отношением опасного для сжатого стержня напряжения к коэффициенту запаса. Для сжатого стержня опасным является так называемое критическое напряжение σкр, при котором стержень теряет устойчивость первоначальной формы равновесия.

Величину коэффициента запаса в задачах устойчивости принимают несколько большей, чем значение коэффициента запаса прочности, то есть если k=1÷2, то kуст=2÷5.

Допускаемое напряжение по устойчивости можно связать с допускаемым напряжением по прочности:

где σт – опасное с точки зрения прочности напряжение (для пластичных материалов это предел текучести, а для хрупких – предел прочности на сжатие σвс).

Коэффициент φ Запись опубликована 24.09.2014 автором admin в рубрике Устойчивость.

Источник

iSopromat.ru

Пример решения задачи на расчет нормальных напряжений в сечениях прямого ступенчатого стержня при продольном нагружении.

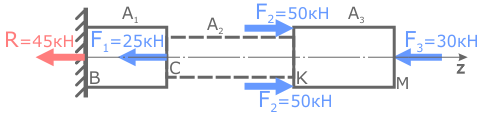
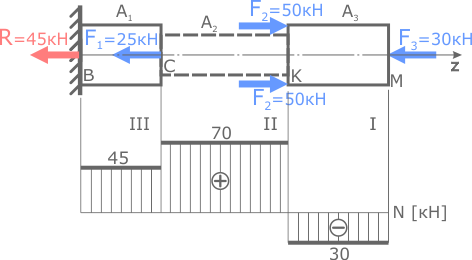
Задача

Рассчитать величину напряжений в стержне заданной формы, нагруженном продольными силами и построить их эпюру.

Пример решения

Предыдущие пункты решения задачи:

т.е. напряжения определяются отношением соответствующей величины внутренней силы к площади поперечного сечения на рассматриваемом участке стержня.

Площади поперечного сечения стержня:

В пределах участка стержня, где внутренняя сила и площадь постоянны, напряжения тоже будут одинаковы, при этом положительные (растягивающие) внутренние силы в сечениях вызывают действие положительных напряжений, и наоборот.

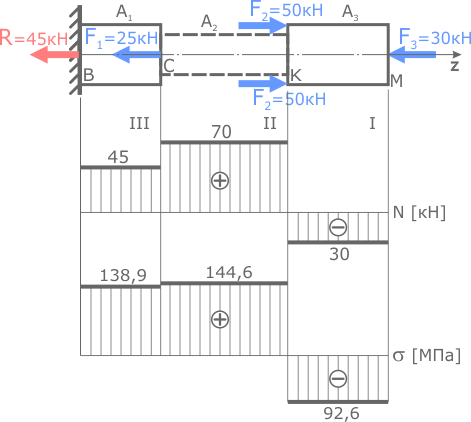
Величину и знаки внутренних сил примем с построенной эпюры N.

Расчет напряжений

По этим данным строим эпюру нормальных напряжений σ .

По эпюре видно, что все напряжения лежат в пределах допустимых значений, следовательно, поперечные размеры стержня были рассчитаны правильно и необходимая прочность обеспечена.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник

iSopromat.ru

Важнейшим критерием оценки прочности балок при изгибе являются напряжения.

Рассмотрим способы расчета напряжений при плоском поперечном изгибе балки

Расчет напряжений

Возникающий в поперечных сечениях при чистом прямом изгибе изгибающий момент M_x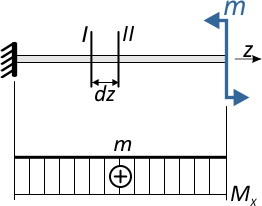

представляет собой равнодействующий момент внутренних нормальных сил, распределенных по сечению и вызывающих нормальные напряжения в точках сечения.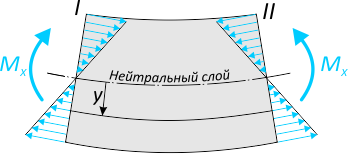

Закон распределения нормальных напряжений по высоте сечения выражается формулой: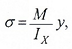

где:
M — изгибающий момент, действующий в рассматриваемом сечении относительно его нейтральной линии X;
I_x — осевой момент инерции поперечного сечения балки относительно нейтральной оси;
y – расстояние от нейтральной оси до точки, в которой определяется напряжение.

Нейтральная ось при изгибе проходит через центр тяжести поперечного сечения.

По вышеуказанной формуле, нормальные напряжения по высоте сечения изменяются по линейному закону.

Наибольшие значения имеют напряжения у верхнего и нижнего краев сечения.

Например, для симметричного относительно нейтральной оси сечения, где y₁=y₂=h/2: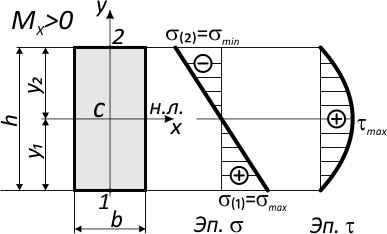

Напряжения в крайних точках по вертикали (точки 1 и 2) равны по величине, но противоположны по знаку.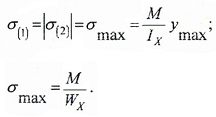

Для несимметричного сечения

напряжения определяются отдельно для нижней точки 1 и верхней точки 2: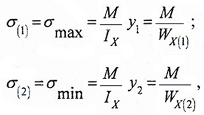

где: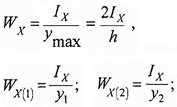

W_X — осевой момент сопротивления симметричного сечения;
W_X(1) и W_X(2) — осевые моменты сопротивления несимметричного сечения для нижних и верхних слоев балки.

Знаки нормальных напряжений при их расчете, рекомендуется определять по физическому смыслу в зависимости от того, растянуты или сжаты рассматриваемые слои балки.

Условия прочности при изгибе

Прочность по нормальным напряжениям

Условие прочности по нормальным напряжениям для балок из пластичного материала записывается в одной крайней точке.

В случае балки из хрупких материалов, которые, как известно, по-разному сопротивляются растяжению и сжатию – в двух крайних точках сечения.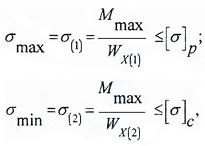

Здесь:
M_max — максимальное значение изгибающего момента, определяемого по эпюре M_x;
[ σ], [ σ]_р, [ σ]_с — допустимые значения напряжений для материала балки (для хрупких материалов – на растяжение (р) и сжатие (с)).

Для балки из хрупкого материала обычно применяют сечения, несимметричные относительно нейтральной оси. При этом сечения располагают таким образом, чтобы наиболее удаленная точка сечения размещалась в зоне сжатия, так как [ σ]_с>[ σ]_р.

В таких случаях, проверку прочности следует обязательно проводить в двух сечениях: с наибольшим положительным изгибающим моментом и с наибольшим по абсолютной величине (модулю) отрицательным значением изгибающего момента.

При расчете элементов конструкций, работающих на изгиб, с использованием вышеуказанных условий прочности решаются три типа задач:

1. Проверка прочности
   
2. Подбор сечений
   
3. Определение максимально допустимой нагрузки
   

Прочность по касательным напряжениям

В случае прямого поперечного изгиба в сечениях балки, кроме нормальных напряжений σ от изгибающего момента, возникают касательные напряжения τ от поперечной силы Q.

Закон распределения касательных напряжений по высоте сечения выражается формулой Д.И. Журавского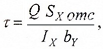

где
S_{x отс} — статический момент относительно нейтральной оси отсеченной части площади поперечного сечения балки, расположенной выше или ниже точки, в которой определяются касательные напряжения;
b_y — ширина поперечного сечения балки на уровне рассматриваемой точки, в которой рассчитывается величина касательных напряжений τ.

Условие прочности по касательным напряжениям записывается для сечения с максимальным значением поперечной силы Q_max: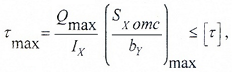

где [ τ] – допустимое значение касательных напряжений для материала балки.

Полная проверка прочности

Полную проверку прочности балки производят в следующей последовательности:

1. По максимальным нормальным напряжениям для сечения, в котором возникает наибольший по абсолютному значению изгибающий момент M.
2. По максимальным касательным напряжениям для сечения, в котором возникает наибольшая по абсолютному значению поперечная сила Q.
3. По главным напряжениям для сечения, в котором изгибающий момент и поперечная сила одновременно достигают значительных величин (или когда M_max и Q_max действуют в одном и том же сечении балки).

При анализе плоского напряженного состояния главные напряжения при изгибе, примут вид: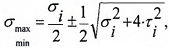

так как нормальные напряжения в поперечном направлении к оси балки принимаются равными нулю.

Проверка прочности осуществляется с помощью соответствующих гипотез прочности, например, гипотезы наибольших касательных напряжений:

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Источник