Как найти предельную норму замены товара

Задача № 1 Расчёт дохода потребителя

Индивид покупает 8 единиц товара Х и 4 единицы товара Y. Найти его доход, если известно, что цена товара Х равна 2 ден. ед., а предельная норма замены равна 0,5.

Решение:

В точке оптимума выполняется равенство:

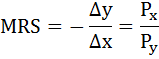
По условию MRS = 0,5 и Р_х = 2. Следовательно, Р_у = Р_х / MRS = 2/0,5=4.
Найдём доход индивида, используя бюджетное ограничение:

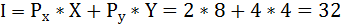
где I – доход,
Р_х и Р_у – цены двух рассматриваемых благ,
Х и Y – их количества.

Задача № 2. Расчёт общей и предельной полезности

Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.

Решение:

Найдём общую полезность товара А.

Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара

TU(1)=MU(1)=20

TU(2)=MU(2) + TU(1)=15 + 20=35

TU(3)=MU(3) + TU(2)=12 + 35=47

TU(4)=MU(4) + TU(3)=8 + 47=55

TU(5)=MU(5) + TU(4)=6 + 55=61

Найдём предельную полезность товара В.

Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара — Общая полезность N-1-й единицы товара

MU(1)=TU(1)=19

MU(2)= TU(2) — TU(1)=30 – 19 = 11

MU(3)= TU(3) — TU(2)=38 – 30 = 8

MU(4)= TU(4) — TU(3)=43 – 38=5

MU(5)= TU(5) — TU(4)=45 – 43=2

Найдём общую и предельную полезности товара С.

MU(1)=TU(1)=22

TU(2)=MU(2) + TU(1)=10 + 22=32

MU(3)= TU(3) — TU(2)=39 – 32=7

MU(4)= TU(4) — TU(3)=44 – 39=5

TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:

Задача № 3. Расчёт общей полезности

Предельная полезность первой единицы блага равна 420. При потреблении первых трёх единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 4 раза. Найти общую полезность блага при условии, что его потребление составляет 8 единиц.

Решение:

Распишем условие задачи следующим образом:

MU(1) = 420,

MU(2) = 420/2=210,

MU(3) = 210/2=105,

MU(4) = 105/4=26,25,

MU(5) = 26,25/4=6,5625,

MU(6) = 6,5625/4=1,640625,

MU(7) = 1,640625/4=0,410156,

MU(8) = 0,410156/4=0,102539.

Найдём общую полезность блага при условии, что его потребление составляет 8 единиц.

TU(8) = MU(8) + TU(7) = MU(8) + MU(7) + TU(6) =…=

= MU(8) + MU(7) + MU(6) + MU(5) + MU(4) + MU(3) + MU(2) + MU(1) =

= 420 + 210 + 105 + 26,25 + 6,5625 + 1,640625 + 0,410156 + 0,102539 = 769,96582

Задача № 4. Расчёт оптимального объёма потребления двух благ

В таблице представлены следующие данные о предельной полезности двух благ.

Количество, кг	Конфеты	Виноград
1	60	150
2	40	120
3	20	90

Цена 1 кг конфет 80 ден. ед., а цена 1 кг винограда 160 ден. ед.
Бюджет потребителя составляет 400 ден. ед.

Определить оптимальный объём потребления конфет и винограда.

Решение:

Оптимальный объём потребления конфет и винограда достигается тогда, когда отношение предельных полезностей равно отношению цен этих благ.

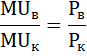
Среди перечисленных вариантов таким свойством обладает комбинация 2 кг винограда (MUв=120) и 1 кг конфет (MUк=60).

Предельная полезность винограда, разделённая на предельную полезность конфет равна отношению их цен:

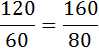
Проверим соответствие этой комбинации бюджетному ограничению:

80*1 + 160*2 = 400

Бюджет полностью израсходован.

Задача № 5. Расчёт цен товаров Х и Y

Потребитель покупает 4 единицы блага Х и 9 единиц блага Y, имея доход 100 ден. ед. Найти цены товаров X и Y, если известно, что предельная норма замены товара Y товаром X (MRSxy) равна 4.

Решение:

Предельную норму замены товара Y товаром X(MRS_xy) можно определить как отношение цены товара Х к цене товара Y:

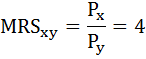
Запишем бюджетное ограничение:

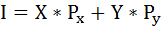
100 = 4*P_x + 9*P_y,

где

Px, Py – цены благ Х и Y соответственно.

Составим и решим систему уравнений:

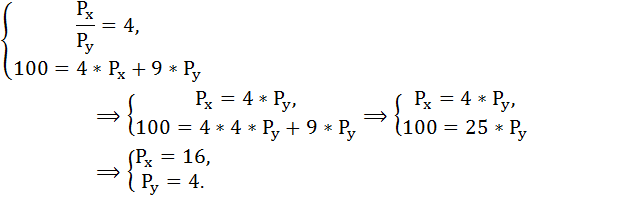
Задача № 6. Расчёт оптимального объёма потребления

У студента Иванова в холодильнике сыр и колбаса нарезаны для удобства кусочками по 100 г. Общая полезность их потребления представлена в таблице. Определите количество съеденного им в день, если известно, что он в целом употребляет 700 г названных продуктов и при этом добивается максимума полезности.

Количество, г	Колбаса (общая польза)	Сыр (общая польза)
100	2000	1900
200	3900	3750
300	5700	5550
400	7400	7300
500	8000	9000
600	9500	10650

Решение:

Рассчитаем предельную полезность от потребления этих двух продуктов.

Предельная полезность в дискретном случае определяется по формуле:

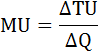
где

ΔTU – приращение общей полезности (TU₁ – TU₀),

ΔQ – приращение количества потребляемого блага (Q₁ – Q₀).

Вычисления занесём в таблицу.

Количество, г	Колбаса (общая польза)	Сыр (общая польза)	Предельная полезность колбасы	Предельная полезность сыра
100	2000	1900	2000	1900
200	3900	3750	1900	1850
300	5700	5550	1800	1800
400	7400	7300	1700	1750
500	9000	9000	1600	1700
600	10500	10650	1500	1650

Известно, что в целом студент употребляет 700 г колбасы и сыра, то есть всего 7 кусочков, и при этом добивается максимума полезности.

Решение об оптимальном объёме потребления можно представить в виде таблицы, где на каждом шаге будем сравнивать предельную полезность каждого кусочка колбасы и сыра и выбирать наибольшую величину предельной полезности, что в сумме даст их максимум.

Итак, на первом шаге наибольшая предельная полезность, равная 2000 будет получена от потребления 1 кусочка/100 грамм колбасы. Дальше студенту без разницы, что употребить, так как первый кусочек сыра и второй кусочек колбасы приносят одинаковую полезность – 1900. Пусть, например, это будет сначала сыр, а затем колбаса. Но вот на четвёртом шаге наибольшую полезность принесёт  второй кусочек сыра. Предельная полезность, полученная от его потребления 1850 больше, чем 1800 – предельная полезность третьего куска колбасы или  третьего кусочка сыра. На пятом шаге студенту опять всё равно, что съесть первым, третий кусочек сыра или третий кусочек колбасы, так  как полезность от дополнительного потребления этих продуктов одинакова. И наконец, седьмым кусочком должен стать сыр, поскольку предельная полезность четвёртого кусочка сыра (1750), больше чем предельная полезность четвёртого кусочка колбасы (1700).

Общая полезность от потребления 3 кусочков колбасы и 4 кусочков сыра  будет максимальной и составит:

TU = 2000 + 1900 + 1900 + 1850 + 1800 + 1800 + 1750 = 13 000

Таким образом, студент Иванов получит максимум полезности при употреблении 3 кусочков (300 грамм) колбасы и 4 кусочков (400 грамм) сыра.

Задача № 7. Расчёт отимального объёма потребления

Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:

1) U(Q)= 1 – 5 × Q²

2) U(Q)= 5 + Q – Q²

3) U(Q) = Q² – 5 × Q³

Как будут выглядеть функции предельной полезности? Проиллюстрируйте ответ.

Решение:

Оптимальный для потребителя объем блага Q будет определяться в точке, где потребитель получит максимум удовлетворения полезности. Задача сводится к нахождению экстремума функции полезности. Найдём производную функции полезности (предельную полезность MU) и приравняем её к нулю.

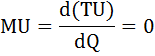
1) MU = –10 × Q = 0, следовательно, Q = 0;

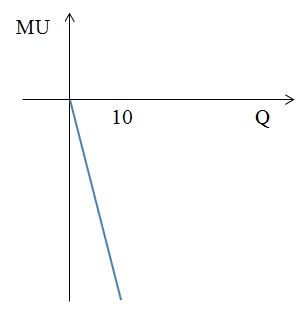
2) MU = 1 – 2 × Q = 0, следовательно, Q = 1/2;

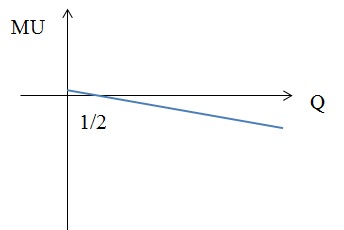
3) MU = 2 × Q – 15 × Q² = 0, следовательно, Q = 0; Q = 2/15.

Задача № 8. Расчёт цен товаров X и Y

Индивид покупает 4 единицы блага X и 9 единиц блага Y, имея доход равный 100 денежным единицам. Найти цены товаров X и Y, если известно, что предельная норма замены X на Y равна 4.

Решение:

По условию задачи предельная норма замены благом Y блага X () равно 4. Это значит, что количество блага Х должно быть сокращено на 4 единицы в обмен на увеличение количества блага Y на единицу, при неизменном уровне удовлетворения потребителя.

Равновесие потребителя может быть представлено математически как:

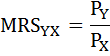
— это предельная норма замещения, равная отношению цен благ Y и X. Данное условие оптимума потребителя следует понимать так. Соотношение, в котором потребитель при данных ценах способен замещать один товар другим, равно соотношению, в котором потребитель согласен замещать один товар другим, не изменяя уровень своего удовлетворения.

Отсюда

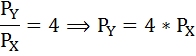
Далее воспользуемся формулой бюджетного ограничения:

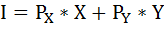
где I – доход или бюджет потребителя.

100 = 4 × P_X + 9 × P_Y

100 = 4 × P_X + 9 × 4 × P_X

100 = 40 × P_X

P_X = 2,5

P_Y = 4 × 2,5 = 10.

Ответ: P_X = 2,5; P_Y = 10.

Задача № 9. Определение рационального выбора потребителя

Потребитель имеет функцию полезности:

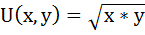
и может на свой доход равный 100 единицам приобретать только эти два товара по ценам:

P_x = 2

P_y = 5

Определить рациональный выбор потребителя. Какой максимальный уровень полезности достижим?

Решение:

Рациональный выбор потребителя осуществляется в соответствии со вторым законом Госсена:

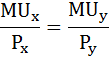
Предельная полезность товара х будет равна производной функции общей полезности по аргументу х:

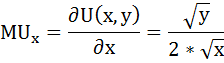
Аналогично находим предельную полезность товара y:

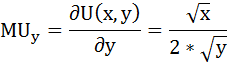
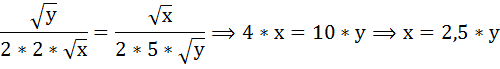
Далее воспользуемся бюджетным ограничением:

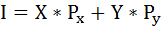
Из условия задачи известно, что:

I = 100

P_x = 2

P_y = 5

Составим и решим систему уравнений:

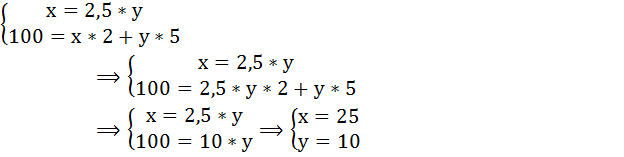
При х = 25 и у = 10 общая полезность достигнет максимума:

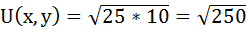
Задача № 10. Расчёт оптимального объёма потребления

У Оксаны есть 30 рублей. Она хочет купить шоколадки «Шок» ценой 3 р. Полезность от этой покупки она оценивает функцией:

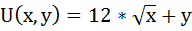
х – приобретённое количество шоколадок,

y – оставшаяся часть дохода.

Сколько купит шоколадок «Шок» рациональная Оксана?

Решение:

Рациональное поведение потребителя можно определить, как стремление максимизировать излишек потребителя. Потребитель будет покупать дополнительные единицы до тех пор, пока они приносят дополнительный избыток, т.е. пока цена, которую потребитель готов уплатить за единицу блага, превосходит реальную цену:

MU > P

Однако каждая последующая единица потребления обычно приносит уменьшающийся прирост полезности, т.е. при покупке благ «одно за другим» рано или поздно предельная полезность какого-то блага сравняется с его ценой:

MU = P

После того как предельная полезность сравняется с ценой, потребитель прекратит дальнейшие покупки: оптимальный объём потребления достигнут.

Найдём предельную полезность MU, как производную функции общей полезности по аргументу х:

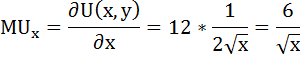
Оптимальный объём потребления будет достигнут при МU = P:

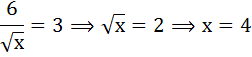
Таким образом, рациональная Оксана купит 4 шоколадки, потратив на эту покупку 12 рублей.

$MRS$ (предельная норма замещения) – это мера, которая позволяет оценить максимальный объем продукции, от которой покупатель в состоянии отказаться ради приобретения других товаров.

Понятие предельной нормы замещения

Повышение полезности от покупки одних товаров должно уравновесить уменьшение потребления других. В конечном счете данные замещения обеспечивают одинаковую полезность на одинаковые денежные затраты личного бюджета потребителей. Повышая полезность своих расходов, рациональные покупатели стремятся уравновесить и взаимно замещаемые товары, и цены данных товаров. Именно цены позволяют достичь равновесия в пропорциях взаимного замещения продукции. Предельная норма замены (замещения) одной продукции другой должна равняться соотношению цен взаимозаменяемых товаров. К примеру, если представить, что $X$ и $Y$ – это товары, замещаемые потребителем с целью максимизации полезности своих денежных затрат на их покупку, то он будет руководствоваться нормой замещения для данных товаров, которая выражается следующим равенством:

$MRS х,у = MUx / MUy = Px / Py$.

Для рационального потребителя максимизация полезности достигается при распределении его бюджета таким образом, что предельная полезность денежной единицы затрат будет одинаковой для каждого приобретаемого товара. Если же полезность от расхода дополнительных единиц денежных затрат на товар $X$ будет выше, чем от единицы денежных затрат на товар $Y$ то покупатель будет стараться максимизировать общую полезность путем приращения покупок товаров $X$, и наоборот.

Со временем предельная полезность приобретаемых товаров снизится, а потребитель уменьшит приращение затрат денежных средств на его покупку, перераспределяя их на иные товары, имеющие для покупателя предельную полезность несколько выше.

Распределяя постоянно денежные затраты из фиксированного бюджета, потребители обеспечивают равновесие и доступное им максимальное благосостояние в том случае, когда предельная полезность каждых дополнительных денежных единиц затрат одинакова для всех приобретаемых товаров.

«MRS – предельная норма замещения в экономике» 👇

Очевидно, что нарушается принцип равной предельной полезности затрат денежных средств, когда предельная полезность товаров $X$ и $Y$ вдвое или втрое выше их стоимости.

Особенности предельной нормы замещения

Как правило все стандартные кривые безразличия характеризуются не только отрицательным наклоном, но и вогнуты к началу координат. Степень вогнутости прямо зависит от степени замещения одних товаров другими.

Предельная норма замены товаром $Q_1$ товара $Q_2$ показывает то число товара $Q_2$, которым покупатель готов пожертвовать для покупки дополнительной единицы $Q_1$, с неизменным уровнем общего удовлетворения

$MRS = ∆ Q_2 / ∆ Q_1$

Данное соотношение будет всегда отрицательным из-за убывающего характера кривой безразличия. Для удобства иногда в правой части ставится минус, что делает значение $MRS$ положительным. Если описать зависимость количества $Q_1, Q_2$ и уровня полезности $U$ в виде функции $Q_2 = f(Q_1)$, то предельная норма замены будет равняться производной функции полезности: $MRS = f(Q_1)$.

Анализируя предельную норму замены необходимо учитывать некоторые особенности:

• Максимизация полезности продукции для покупателя при распределении его бюджета достигается в том случае, когда идентична предельная полезность какого-либо объекта затрат;
• Если уровень полезности дополнительного товара выше, то покупатель имеет право свести к минимуму полезность путем приращения покупок интересующих товаров;
• Предельную полезность на приобретаемые товары можно снизить при условии, что потребитель уменьшит приращение своих финансовых расходов на покупку товаров, распределяя при этом свои средства на приобретение другой продукции с большей полезностью;
• Постоянное перераспределение финансовых расходов из личного бюджета позволяет потребителям обеспечивать максимальное равновесие и благосостояние в то время, когда идентична наибольшая полезность для дополнительных товаров;
• Будет нарушен принцип предельной полезности тогда, когда полезность одних товаров в несколько раз выше их цены. В такой ситуации предпочтение будет отдано объектам с большей полезностью. Уменьшая объемы закупок товаров с меньшей полезностью, потребитель будет оптимизировать свои расходы и приближать их к условной равновесной точке.

Свойства $MRS$

При движении по кривой безразличия степень замещения товара $Q_2$ товаров $Q_1$ не будет оставаться постоянной (Рисунок 1).

При перемещении по кривой предельная норма замены будет уменьшаться, поскольку оставшиеся единицы товара $Q_2$ будут приобретать в глазах покупателя большую ценность, а дополнительные товары $Q_1$ будут приносить все меньшее дополнительное удовлетворение.

Перечислим важнейшие свойства $MRS$:

1. Предельная норма замены товара $Q_2$ товаром $Q_1$ равняется отношению их предельной полезности, т.е. $MU_1$ к $MU_2$. – $∆ Q_2 / ∆ Q_1 = MU_1 / MU_2$. Отрицательный знак означает, что чем больше товаров $Q_1$, то тем меньше должно быть товаров $Q_2$ в потребительском наборе, для того, чтобы совокупная полезность оставалась неизменной.
2. Если две любые точки на кривой безразличия сливаются воедино, то $MRS$ будет равняться тангенсу угла наклона прямой к кривой безразличия;
3. Предельная норма замены обладает значением только лишь при движении по кривой, но не имеет значения при перемещении между рассматриваемыми кривыми;
4. Не является универсальным принцип убывания $MRS$, он выполняется только при кривых безразличия, имеющих стандартный вид.

Преде́льная но́рма замеще́ния в микроэкономике — величина, определяющая количество товара, от которого потребитель готов отказаться ради увеличения другого товара на единицу. При этом происходит замещение одного товара другим, а интенсивность замещения как раз показывает предельная норма замещения.
Предельную норму замещения обозначают через MRS (от англ. marginal rate of substitution) и вычисляют по формуле:

где  — количество одного блага,  — количество другого блага, соответственно и изменение соответствующих благ.
Также предельная норма замещения может быть определена (при количественном (кардиналистском) подходе к теории полезности) через отношения предельных полезностей товаров и :

Если опираться на понятие кривой безразличия (линия, показывающая все комбинации двух благ в выборе между которыми потребитель безразличен, то есть все эти комбинации приносят ему один и тот же уровень полезности), то предельную норму замещения можно рассматривать как наклон кривой безразличия. То есть считается, что для сохранения достигнутого уровня полезности потребитель может отказаться от какого-то одного блага для получения того же количества общей полезности путём потребления какого-то количества другого блага. Геометрически MRS равна тангенсу угла наклона касательной кривой безразличия в данной точке, взятому с обратным знаком.

Пример[править | править код]

Например, потребителю безразличен выбор между следующими наборами: три яблока и один апельсин — первый набор, и два яблока и два апельсина — второй набор. Хотя через эти две точки нельзя однозначно провести кривую безразличия, предельную норму замещения апельсинов яблоками можно посчитать следующим образом:

где  — количество яблок,  — количество апельсинов, соответственно  — изменение потребления яблок во втором наборе относительно первого,  — изменение потребления апельсинов во втором наборе относительно первого. То есть в данном примере предельная норма замещения апельсинов яблоками равна единице и потребитель готов сократить потребление яблок на единицу и увеличить потребление апельсинов на единицу, чтобы его удовлетворённость от потребления этих фруктов не изменилась.

А вот при переходе от набора 10:2 к набору 8:3 каких-то двух благ при условии, что эти точки лежат на одной кривой безразличия, предельная норма замещения первого блага вторым будет равна двум, .

Примечания[править | править код]

Ссылки[править | править код]

• Экономико-математический словарь (недоступная ссылка с 14-06-2016 [2512 дней])

См. также[править | править код]

• Функция полезности
• Предельная полезность
• Ординалистская теория полезности
• Кривая безразличия
• Бюджетная прямая
• Предельная норма технического замещения

Но в какой мере может потребитель отказаться, например, от апельсинов, чтобы приобрести дополнительно еще одно яблоко? Это помогает определить т.н. предельная норма замещения.

Предельная норма замещения Y на Х (МRSху) – количество товара Y, от которого потребитель отказался бы, чтобы получить еще одну единицу товара X, при этом оставаясь на данной кривой безразличия. Кривизна изображенных ранее кривых безразличия означает, что количество Y, от которого потребитель хочет отказаться ради еще одной единицы X, уменьшается по мере увеличения количества X, замещающего Y в наборе.

Чтобы увидеть это начнем двигаться вдоль кривой безразличия, изображенной на рис. 6.4. Q_у – недельное потребление товара Y, от которого потребитель отказался бы, чтобы получить еще одну единицу товара X. Выигрыш в недельном потреблении единицы товара Х составляет Q_х = 1.

Количество товара Y, которое будет обменено на единицу товара X, между любыми двумя точками на кривой может быть записано как Q_у/Q_х. Это наклон кривой безразличия, вдоль которой движется потребитель, отказываясь от единиц товара Y, для получения единиц товара X. Однако наклон кривых безразличия отрицателен.

Такое рассмотрение MRSху приводит к получению отрицательного числа. Предельная же норма замещения определяется как положительное количество товара Y, от которого потребитель желает отказаться ради дополнительной единицы X. Поэтому он есть произведение наклона кривых безразличия на -1.

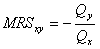
Кривизна кривой безразличия, изображенная на рис. 6.4. подразумевает уменьшение предельной нормы замещения Y на X. Обратите внимание, как их наклон изменяется по мере того, как потребитель, следуя по данной кривой, замещает Y на X. По мере того, как Х замещает Y вдоль кривой, она становится менее крутой.

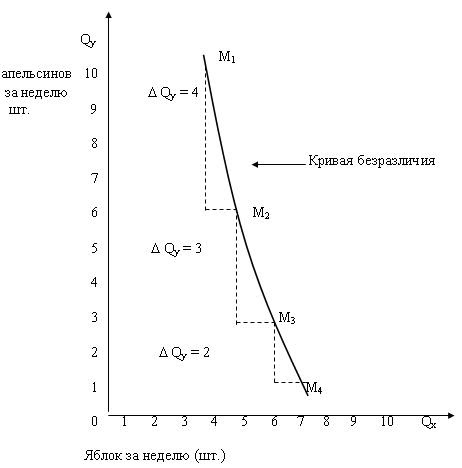
Рис. 6.4 – Уменьшение MRSху вдоль кривой безразличия

Таблица 6.2 – Предельная норма замещения Y на X

Набор	Qу	Qх	MRSху
М1 М2 М3 М4	10 6 3 1	4 5 6 7	4 ед. Y за 1 ед. Х 3 ед. Y за 1 ед. Х 2 ед. Y за 1 ед. Х

Анализ кривых безразличия не требует, чтобы полезность была количественно измерима, достаточно только предположить, что потребители способны ранжировать альтернативы, то есть, что полезность порядково измерима (позиция ординалистов).

Если бы полезность была количественно измерима (позиция кардиналистов), была бы возможность вычислить, сколько полезности при добавлении в набор еще одной единицы товара или услуги. То есть предельную норму замещения вдоль кривой безразличия можно связать с предельными полезностями благ на каждой из осей.

Изъятие Q_у единиц товара Y из набора наносит потребителю ущерб. Потеря полезности составляет Q_у MU_у, где МU_у – предельная полезность Y для потребителя. При замене потерянного количества Y тем количеством X, которое необходимо для возвращения потребителя в состояние прежней удовлетворенности, приобретенная полезность составила бы

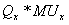
(где МU_х – предельная полезность X). Если потребителю необходимо вернуться на ту же самую кривую безразличия, прирост полезности от добавления Х равен потери полезности от изъятия Y. Таким образом:

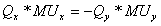
Следовательно,

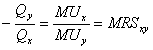
Предельная норма замещения Y на Х поэтому может рассматриваться как отношение предельной полезности Х к предельной полезности Y.

В нашем примере предельная полезность яблок (товар Х) уменьшается, когда его количество растет, и, соответственно она увеличивается у апельсинов (товар Y), когда их количество уменьшается. Поскольку МUх уменьшается, когда товар Х (яблоки) замещает товар Y (апельсины), в то время как МU_у увеличивается, отношение МU_х/МU_у равное МRSху уменьшается.

Отсюда вытекает, что предельная норма замещения Y на Х тоже должна падать при замене Y на X, если предельные полезности Х и Y находятся в обратном отношении к количествам этих товаров, покупаемых за период.

Уменьшение предельной полезности товаров, при предположении количественной измеримости полезности, объяснило бы выпуклую форму кривых безразличия.

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете заказать решение задач, написание учебных работ и онлайн помощь

Подробнее

Предельная норма замещения 
(MRS)
показывает, от какого количества единиц
одного блага потребитель должен
отказаться, чтобы приобрести дополнительную
единицу другого блага. Иными словами,
это соотношениепредельной
полезности двух
благ.

MRS =
ΔY /
ΔX

Предельная норма замещения
представляет собой норму, в соответствии
с которой одно благо может быть замещено
другим без выигрыша или потери для
удовлетворения потребителя.

Значения предельной нормы
замещения всегда отрицательны, так как
увеличение количества приобретенных
единиц одного блага предполагает
уменьшение потребления другого, т.е.
имеются разные знаки. Поскольку кривая
безразличия выпукла
вниз, к началу координат, то предельная
норма замещения чаще всего уменьшается
по мере увеличения потребления одного
блага вместо другого. Это явление
называют уменьшающейся предельной
нормой замещения.

Предельная норма замещения

На графике показано, что по
мере увеличения потребления товара X на
каждую дополнительную единицу (ΔX)
(движение от точки К к
точке N)
количество товара Y,
от которого потребитель готов отказаться
(ΔY),
сокращается, т.е. предельная норма
замещения убывает.

Таким образом, чем менее
дефицитным становится товар X,
тем меньшим количеством товара Y мы
готовы пожертвовать.

19. Бюджетная линия и равновесие потребителя.

Бюджетная
линия (budget
line)
— это прямая, точки которой показывают
наборы благ, при покупке которых
выделенный доход тратится полностью.
Бюджетная линия пересекает оси координат
в точках, показывающих максимально
возможные количества благ, которые
можно приобрести на данный доход при
определенных ценах. Для каждой бюджетной
линии можно построитькривую
безразличия,
которая будет иметь с бюджетной линией
точку касания.

Если I —
доход потребителя, Р_х —
цена блага Х, Р_y –
цена блага Y,
а Х и Y составляют
купленные количества благ, то уравнение
бюджетного ограничения можно записать
следующим образом:
I = Р_х × Х + Р_y × Y

Равновесие потребителя (consumer
equilibrium) — точка, в
которой потребитель максимизирует
свою общую
полезность или
удовлетворение от расходования
фиксированного дохода.

Равновесие потребителя
может быть выражено следующим образом:

где MU —
предельная полезность отдельных
товаров;
P —
их цена.

Если кривая
безразличия показывает,
что потребитель хотел бы купить,
а бюджетная
линия —
что потребитель может купить, то в своем
единстве они могут ответить на вопрос,
как обеспечить максимальное удовлетворение
от покупки при ограниченном бюджете.
Кривые безразличия и бюджетная линия
используются для графической интерпретации
ситуации, когда потребитель
максимизирует полезность,
получаемую им от покупки двух разных
благ при имеющемся бюджете.

Оптимальный набор
потребительских благ должен отвечать
двум требованиям:

• находиться
  на бюджетной линии;

• предоставить
  потребителю наиболее предпочтительное
  сочетание.

Данные условия и их реализация
обеспечивают оптимальный выбор точки
на бюджетной линии. Для этого необходимо
наложить бюджетную линию на карту
кривых безразличия,
как это показано на графике.

Равновесие потребителя

В данном случае прямая KL —
это бюджетная линия, а кривые U₁, U₂, U₃, U₄ —
это кривые безразличия. При имеющемся
доходе потребитель, свободно перемещаясь
по прямой KL,
будет стремиться к точке М (бюджетная
линия KL касается
кривой безразличия U₂),
где он получит наибольшую
полезность. U₂ является
наивысшей кривой которую может достичь
потребитель при имеющемся доходе.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #