Как найти предельную норму замещения в точке

Делая выбор между двумя, тремя и большим
числом товаров, люди идут на компромиссы.
Потребитель готов отказаться от
нескольких единиц товара X,
чтобы получить одну единицу товара Y.
Для количественного определения объ­ема
одного товара, которым потребитель
готов пожертвовать ради другого,
ис­пользуется мера, названная предельной
нормой замещения (MRS).
Предель­ная норма замещения товара
X товаром Y
представляет собой максимальное
ко­личество товара Y ,
от которого готов отказаться человек,
чтобы получить одну дополнительную
единицу товара X.

Рис.8.6. Предельная норма замещения

Например, предельная норма замещения
в точке С (рис.8.6) выражается как – (ΔYC:
ΔХС)и равна абсолютному значению тангенса
угла наклона каса­тельной к кривой
безразличия в этой точке. При движении
вдоль кривой безраз­личия от набора
А к точке Е отмечаем снижение предельной
нормы замещения (поскольку, чтобы
получить одну единицу товара X,
потребитель готов отка­заться от ΔY
b
единиц товара Y в точке
В, от ΔYC единиц товара У
– в точке С, от ΔYD единиц
товара У – в точке D и при
этом ΔYB > ΔYC,
a ΔYC > ΔYD)
и уменьшение угла наклона касательной
к кривой безразличия.

Семейство кривых безразличия дает
описание личных предпочтений в отношении
различных сочетаний товаров и услуг,
однако предпочтения не объ­ясняют
полностью поведение потребителя,
поскольку на индивидуальный вы­бор
влияют также бюджетные ограничения.

8.4. Бюджетная линия

Рассмотрим случай, когда покупатель
имеет доход I, не делает
никаких сбережений и хочет его потратить
на два вида товаров – товары X
и товары Y. Если обозначить
через QX количество товаров
X, через QY
количество товаров Y,
через РХ и PY цены этих
товаров, то все сочетания X
и Y , при которых об­щая
сумма равна доходу, подчиняются равенству
РХ * QX + PY*
QY = I.

Графически это выражение представляется
прямой, которая называется бюджетной
линией (рис.16).

Рис.8.7. Бюджетная линия

Длина отрезков ОА и ОЕ, отсекаемых этой
линией на осях, составляет: ОА= I
: PY и ОЕ = I
: РХ , а тангенс угла ее наклона равен tg
λ ~ – (ОА/ОЕ)= = – ( РХ: PY),
т.е. является отрицательным отношением
цен двух товаров. Вели­чина этого
отношения указывает норму замещения
товаров при неизменной общей сумме
затрачиваемых денег.

Положение и наклон бюджетной линии
зависят от уровня дохода потре­бителя
и цен на товары. При изменении дохода
(рис.8.8) меняется длина отрезка ОА = I:
PY , а угол наклона при
условии, что цена ни одного из товаров
не из­менилась, остается неизменным.

Рис.8.8. Влияние величины дохода на
бюджетную линию

Следовательно, при увеличении дохода
бюджетная линия сдвигается вправо, а
при уменьшении – влево.

Рассмотрим, что происходит с бюджетной
линией, если цена одного това­ра
изменится, а другого останется прежней
(рис.8.9). Предположим, что в два раза
увеличилась цена товара X,
тогда отрезок, отсекаемый на вертикальной
оси (ОА = I: PY),
остается прежним, а тангенс угла наклона
линии изменится с – РХ / PY
до – 2 РХ / PY . То есть новую
бюджетную линию L2 получаем
путем вращения первоначальной линии
L1 по часовой стрелке
относительно точки ее пересечения с
вертикальной осью.

В этом случае покупательская способность
человека, закупающего значи­тельное
количество товара X,
существенно снижается. В другом случае,
когда цена товара X
снижается наполовину, угловой коэффициент
бюджетной линии изменится с – РХ / PY
до – 1/2 РХ / PY и новую
бюджетную линию L3 получа­ем
путем вращения первоначальной линии
L1 против часовой стрелки,
а поку­пательная способность человека,
приобретающего значительный объем
товара X, увеличивается.

Рис.8.9. Влияние изменения цен на
бюджетную линию

Если же цены товаров X и
Y меняются так, что их
соотношение остается неизменным, то
угол наклона бюджетной линии сохраняется
прежним (по­скольку тангенс угла
наклона бюджетной линии равен отношению
цен), а сама бюджетная линия займет новое
положение параллельно старой. При этом
если цены обоих товаров увеличиваются,
то бюджетная линия перемещается влево,
поскольку отрезки, отсекаемые ею на
осях координат, уменьшаются. В против­ном
случае, когда цены обоих товаров
уменьшаются, бюджетная линия переме­щается
вправо.

В экономике, сильно подверженной
инфляции, возможна ситуация, при которой
и доход потребителя, и цены на оба товара
возрастут одинаково. В этом случае
наклон бюджетной линии, определяемый
соотношением цен, остается прежним.
Также прежними остаются отсекаемые на
осях длины отрезков, соот­ветствующие
максимальному количеству товаров,
которое может быть куплено, поскольку
цены на оба товара увеличились так же,
как и доход.

Далее, учитывая предпочтения и бюджетные
ограничения потребителей, определим,
какие сочетания товаров потребители
выберут для покупки. Для этого рассмотрим
совместно кривые безразличия и бюджетную
линию (рис.8.10).

Рис.8.10. Максимизация удовлетворения
потребностей потребителя

При этом будем предполагать, что
потребители выбирают товары так, чтобы
достичь максимального удовлетворения
своих потребностей.

Оптимальный набор потребительских
товаров и услуг должен отвечать
одновременно двум требованиям: находиться
на бюджетной линии и представ­лять
для потребителя наиболее предпочтительное
сочетание товаров. Это озна­чает, что
набор, который обеспечивает максимальное
удовлетворение потребно­стей, должен
соответствовать точке К — точке касания
бюджетной линии с са­мой высокой
кривой безразличия. В этой точке угол
наклона бюджетной линии равен углу
наклона касательной для кривой
безразличия. Тангенс этого угла ра­вен
– (РХ / PY). А поскольку
предельная норма замещения в любой
точке равна

по абсолютному значению тангенсу угла
наклона касательной к кривой безраз­личия
в этой точке, то для точки К имеем MRS
= РХ / PY . Следовательно,
по­требитель получает максимальное
удовлетворение своих потребностей,
прини­мая такой порядок их выбора,
при котором предельная норма замещения
одного товара другим равняется отношению
цен.

Наряду с использованием ординалистского
подхода и кривых безразличия потребительские
предпочтения можно также объяснить на
основе кардиналист-ского подхода к
анализу полезности и предельной
полезности. Теория предель­ной
полезности предполагает, что полезность
количественно измерима. При этом под
полезностью понимается степень
удовлетворения, получаемого субъ­ектом
от потребления товара. Полезность
используется для того, чтобы описать
предпочтение при ранжировании наборов
потребительских товаров. Функция
полезности сопоставляет каждому набору
потребительских товаров некоторое
число, и для нее могут быть построены
соответствующие кривые безразличия.

Как функции полезности, так и карты
безразличия упорядочивают выби­раемые
потребителем наборы по уровням
удовлетворения потребностей. При
использовании функции полезности, как
правило, обращается внимание не на
абсолютные числовые значения, а на их
ранжирование. Однако в случаях, когда
осуществляется выбор, сопряженный с
риском, или проводится сравнение
про­ектов, целесообразно использовать
количественные измерения функции
полез­ности. Тогда анализ потребительского
выбора проводится с использованием
концепции предельной полезности. Под
предельной полезностью имеется в ви­ду
добавочная полезность или удовлетворение,
которое получает потребитель от одной
дополнительной единицы конкретного
товара (продукта). Предельная полезность
каждой последующей единицы этого товара
будет падать, поскольку потребность в
данном товаре будет постепенно
удовлетворяться. Такое падение предельной
полезности по мере приобретения
потребителем дополнительных единиц
определенного товара известно под
названием закона убывающей по­лезности.

Для установления связи предельной
полезности с ранее полученными
ха­рактеристиками рассмотрим небольшое
смещение вниз по кривой безразличия.
Это снижение означает дополнительное
потребление ΔХ товара X,
дает допол­нительную, предельную
полезность Vx для каждой
единицы товара X и приво­дит
к росту полезности на величину Vx*ΔX.
Одновременно потеря потребления ΔY
товара Y снизит предельную
полезность на единицу товара на Vy
и приве­дет к общей потере Vy*ΔY.
Величины Vx*ΔX
и Vy*ΔY должны
уравновеши­вать друг друга, поскольку
все точки на кривой безразличия
обеспечивают оди­наковый уровень
полезности, то есть Vx*ΔX
+ Vy*ΔY=0.

Преобразовывая это уравнение, получаем
итоговое соотношение

ΔY: ΔX=Vx:Vy

Так как левая часть равенства представляет
собой MRS – предельную норму
замещения X на У, то из
итогового соотношения следует, что
предельная норма замещения является
отношением предельной полезности X
к предельной полезности У. В то же время
ранее было получено, что предельная
норма замещения равна

MRS-PX:PY

Приравнивая правые части этих уравнений,
получаем:

VX: VY=PX:PY
или VX:PX
=VY:PY

Полученное уравнение показывает, что
максимум полезности достигается при
таком принципе распределения бюджета,
при котором предельная полез­ность
одной денежной единицы расходов одинакова
для каждого товара.

Это подтверждается и логическими
рассуждениями. Если добавочная по­лезность
от расходов дополнительной денежной
единицы на товар X выше,
чем добавочная полезность от расхода
такой же денежной единицы на товар Y,
то потребитель может увеличить полезность
набора за счет увеличения расходов на
товар X. Увеличение покупок
товара X за счет товара Y
будет происходить до тех пор, пока
предельная полезность расходов на товар
X выше, чем расходов на
товар Y. Постепенно
предельная полезность товара X
снизится, а предельная полезность товара
Y возрастет.

Когда же в результате такого процесса
предельная полезность товара X
станет равной предельной полезности
товара Y, то будет достигнут
максимум полезности товарного набора
X и Y.

Итак, на основании изложенного можно
сделать следующие выводы:

1. Теория потребительского поведения
основана на предположении о том, что
покупатель делает свой выбор рационально
и при заданных ценах так стре­мится
распределить свои средства на приобретение
товаров и услуг, чтобы мак­симизировать
ожидаемую полезность от их приобретения.

2. Свой выбор потребитель осуществляет
путем сравнения наборов това­ров и
услуг. При этом предполагается, что
потребитель способен упорядочить
альтернативные наборы товаров и услуг
при помощи отношений предпочтения или
безразличия, что его предпочтения
транзитивны (если товарный набор А с
точки зрения потребителя предпочтительнее
набора В, а последний – набора С, то набор
А предпочтительнее набора С) и он всегда
предпочитает большее ко­личество
товаров и услуг меньшему.

3. В настоящее время в экономической
науке используются два подхода к решению
проблемы соизмеримости полезности благ
и их наборов – ординали-стский (порядковый),
когда используются лишь порядковые
свойства полезно­сти, и кардиналистский
(количественный), когда важны количественные
свой­ства полезности.

4. Ординалистский подход позволяет
выразить предпочтения потребителя
графически путем анализа кривой
безразличия, представляющей собой
сово­купность потребительских наборов
товаров, которые обеспечивают одинаковый
уровень полезности. Предпочтения
человека по всем наборам товаров
описыва­ет карта безразличия –
ранжированное по порядку множество
кривых безразли­чия, соответствующих
всем возможным уровням удовлетворения
для данного индивида.

5. Предельная норма замещения товаром
X товара Y
(количество товара У, от которого
потребитель отказался бы, чтобы получить
еще одну единицу това­ра X,
оставаясь на той же кривой безразличия)
снижается по мере движения вниз по
кривой безразличия.

6. Потребитель, предпочитая определенные
количества каждого из двух товаров X
и Y, получает максимум
удовлетворения тогда, когда предельная
норма замещения товаров равна отношению
цен этих товаров.

7. При кардиналистском (количественном)
подходе для выражения удов­летворения,
получаемого индивидом от потребления
разных объемов благ, ис­пользуются
функции полезности, позволяющие
сопоставить каждому набору потребительских
товаров некоторое число.

8. Функции полезности применяются в тех
случаях, когда могут быть важны
количественные свойства полезности,
например, когда анализируется выбор в
условиях риска или проводится анализ
при трех и большем числе това­ров.
Функции полезности удовлетворяют
принципу убывающей предельной по­лезности:
чем больше потребляется товара, тем
меньше приращение полезно­сти.

9. Потребитель с фиксированным доходом
и при заданных рыночных це­нах достигает
максимальной общей полезности тогда,
когда предельная полез­ность одной
денежной единицы, потраченной на тот
или иной товар, является такой же, как
и предельная полезность одной денежной
единицы, потраченной на любой другой
товар.

Темы рефератов

1. Теория предельной полезности:
возникновение, сущность, развитие.

2. Структура потребностей и степень их
удовлетворения.

3. Динамика цен потребительской корзины
90-х гг. в России.

4. Анализ факторов, определяющих спрос
потребителя.

5. Принцип убывающей предельной полезности.

6. Как изменения в доходах и ценах
на товар влияют на выбор потребителя.

Задачи

Задача №1

В какой точке на рисунке наклоны
бюджетной линии и кривой безразличия
равны?

Решение:

Точка В.

Задача №2

Потребитель «Х» потреблял 5 шт. товара
А, приносящего ему 8 ед. полезности, и

12 шт. товара Б, дающего 18 ед. полезности.
Он решил, что ничего не произойдет, если
он будет потреблять 7 шт. товара А и 10
шт. товара Б, которые принесут ему,
соответственно 10 и 16 ед. полезности.
Определить величины предельной полезности
для каждого товара и предельную норму
замещения товаров.

Решение:

1. Определим предельную полезность
каждого из товаров по формуле:

2. Определим предельную норму замещения
одного товара другим по формуле:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Но в какой мере может потребитель отказаться, например, от апельсинов, чтобы приобрести дополнительно еще одно яблоко? Это помогает определить т.н. предельная норма замещения.

Предельная норма замещения Y на Х (МRSху) – количество товара Y, от которого потребитель отказался бы, чтобы получить еще одну единицу товара X, при этом оставаясь на данной кривой безразличия. Кривизна изображенных ранее кривых безразличия означает, что количество Y, от которого потребитель хочет отказаться ради еще одной единицы X, уменьшается по мере увеличения количества X, замещающего Y в наборе.

Чтобы увидеть это начнем двигаться вдоль кривой безразличия, изображенной на рис. 6.4. Q_у – недельное потребление товара Y, от которого потребитель отказался бы, чтобы получить еще одну единицу товара X. Выигрыш в недельном потреблении единицы товара Х составляет Q_х = 1.

Количество товара Y, которое будет обменено на единицу товара X, между любыми двумя точками на кривой может быть записано как Q_у/Q_х. Это наклон кривой безразличия, вдоль которой движется потребитель, отказываясь от единиц товара Y, для получения единиц товара X. Однако наклон кривых безразличия отрицателен.

Такое рассмотрение MRSху приводит к получению отрицательного числа. Предельная же норма замещения определяется как положительное количество товара Y, от которого потребитель желает отказаться ради дополнительной единицы X. Поэтому он есть произведение наклона кривых безразличия на -1.

Кривизна кривой безразличия, изображенная на рис. 6.4. подразумевает уменьшение предельной нормы замещения Y на X. Обратите внимание, как их наклон изменяется по мере того, как потребитель, следуя по данной кривой, замещает Y на X. По мере того, как Х замещает Y вдоль кривой, она становится менее крутой.

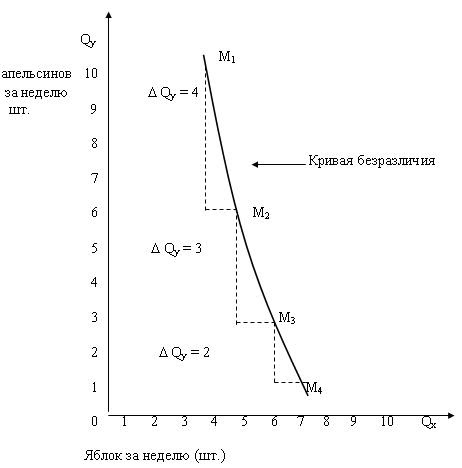
Рис. 6.4 – Уменьшение MRSху вдоль кривой безразличия

Таблица 6.2 – Предельная норма замещения Y на X

Набор	Qу	Qх	MRSху
М1 М2 М3 М4	10 6 3 1	4 5 6 7	4 ед. Y за 1 ед. Х 3 ед. Y за 1 ед. Х 2 ед. Y за 1 ед. Х

Анализ кривых безразличия не требует, чтобы полезность была количественно измерима, достаточно только предположить, что потребители способны ранжировать альтернативы, то есть, что полезность порядково измерима (позиция ординалистов).

Если бы полезность была количественно измерима (позиция кардиналистов), была бы возможность вычислить, сколько полезности при добавлении в набор еще одной единицы товара или услуги. То есть предельную норму замещения вдоль кривой безразличия можно связать с предельными полезностями благ на каждой из осей.

Изъятие Q_у единиц товара Y из набора наносит потребителю ущерб. Потеря полезности составляет Q_у MU_у, где МU_у – предельная полезность Y для потребителя. При замене потерянного количества Y тем количеством X, которое необходимо для возвращения потребителя в состояние прежней удовлетворенности, приобретенная полезность составила бы

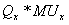
(где МU_х – предельная полезность X). Если потребителю необходимо вернуться на ту же самую кривую безразличия, прирост полезности от добавления Х равен потери полезности от изъятия Y. Таким образом:

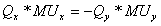
Следовательно,

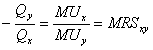
Предельная норма замещения Y на Х поэтому может рассматриваться как отношение предельной полезности Х к предельной полезности Y.

В нашем примере предельная полезность яблок (товар Х) уменьшается, когда его количество растет, и, соответственно она увеличивается у апельсинов (товар Y), когда их количество уменьшается. Поскольку МUх уменьшается, когда товар Х (яблоки) замещает товар Y (апельсины), в то время как МU_у увеличивается, отношение МU_х/МU_у равное МRSху уменьшается.

Отсюда вытекает, что предельная норма замещения Y на Х тоже должна падать при замене Y на X, если предельные полезности Х и Y находятся в обратном отношении к количествам этих товаров, покупаемых за период.

Уменьшение предельной полезности товаров, при предположении количественной измеримости полезности, объяснило бы выпуклую форму кривых безразличия.

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете заказать решение задач, написание учебных работ и онлайн помощь

Подробнее

Преде́льная но́рма замеще́ния в микроэкономике — величина, определяющая количество товара, от которого потребитель готов отказаться ради увеличения другого товара на единицу. При этом происходит замещение одного товара другим, а интенсивность замещения как раз показывает предельная норма замещения.
Предельную норму замещения обозначают через MRS (от англ. marginal rate of substitution) и вычисляют по формуле:

где  — количество одного блага,  — количество другого блага, соответственно и изменение соответствующих благ.
Также предельная норма замещения может быть определена (при количественном (кардиналистском) подходе к теории полезности) через отношения предельных полезностей товаров и :

Если опираться на понятие кривой безразличия (линия, показывающая все комбинации двух благ в выборе между которыми потребитель безразличен, то есть все эти комбинации приносят ему один и тот же уровень полезности), то предельную норму замещения можно рассматривать как наклон кривой безразличия. То есть считается, что для сохранения достигнутого уровня полезности потребитель может отказаться от какого-то одного блага для получения того же количества общей полезности путём потребления какого-то количества другого блага. Геометрически MRS равна тангенсу угла наклона касательной кривой безразличия в данной точке, взятому с обратным знаком.

Пример[править | править код]

Например, потребителю безразличен выбор между следующими наборами: три яблока и один апельсин — первый набор, и два яблока и два апельсина — второй набор. Хотя через эти две точки нельзя однозначно провести кривую безразличия, предельную норму замещения апельсинов яблоками можно посчитать следующим образом:

где  — количество яблок,  — количество апельсинов, соответственно  — изменение потребления яблок во втором наборе относительно первого,  — изменение потребления апельсинов во втором наборе относительно первого. То есть в данном примере предельная норма замещения апельсинов яблоками равна единице и потребитель готов сократить потребление яблок на единицу и увеличить потребление апельсинов на единицу, чтобы его удовлетворённость от потребления этих фруктов не изменилась.

А вот при переходе от набора 10:2 к набору 8:3 каких-то двух благ при условии, что эти точки лежат на одной кривой безразличия, предельная норма замещения первого блага вторым будет равна двум, .

Примечания[править | править код]

Ссылки[править | править код]

• Экономико-математический словарь (недоступная ссылка с 14-06-2016 [2512 дней])

См. также[править | править код]

• Функция полезности
• Предельная полезность
• Ординалистская теория полезности
• Кривая безразличия
• Бюджетная прямая
• Предельная норма технического замещения

Предельная норма замещения – это норма, при которой потребитель готов заменить один товар другим. При малых изменениях предельная скорость замещения равна наклону кривой безразличия.

Кривая безразличия – это график различных комбинаций двух товаров, к которым потребитель безразличен, то есть он не отдает предпочтения одному товару над другим.

Для сохранения состояния безразличия при уменьшении объемов потребления одного товара придется увеличивать объемы потребления другого товара.

Предельная норма замещения – это норма, при которой уменьшение одного блага должно быть компенсировано увеличением другого.

Рассмотрим потребителя, чье безразличие к двум товарам – кинофильмам и обедам – выглядит следующим образом:

Набор	Фильмы	Обеды
A	1	10.00
B	2	5.00
C	3	3.33
D	4	2.50
E	5	2.00
F	6	1.67

Построенная на основании этих данных кривая безразличия будет иметь следующий вид:

Если потребитель перемещается из точки B в точку D, то есть смотрит 4 фильма вместо 2, он должен сократить свои обеды. Предельная норма замещения – это норма, которая диктует, от какой части обедов он должен отказаться, чтобы насладиться большим количеством фильмов.

Формула

Закон убывающей предельной полезности гласит, что предельная полезность, то есть дополнительная полезность каждой новой единицы товара, ниже предельной полезности предшествующей единицы, то есть первая единица товара имеет наибольшую полезность, вторая единица имеет вторую наибольшую полезность и так далее.

Теперь, если потребитель заменяет один товар, скажем X, другим товаром, скажем Y, он должен компенсировать потребление самыми высокими единицами Y для первой единицы X, вторыми самыми высокими единицами Y для второй единицы X и так далее.

Предельная норма замещения непрерывно изменяется по мере того, как мы движемся по кривой безразличия.

Для очень малых изменений в одном товаре предельная скорость замещения приближается к наклону кривой безразличия, которая равна изменению Y, деленному на изменение X.

Предельная норма замещения X (то есть фильмов) на Y (то есть обедов) определяется следующим образом:

MRS_XY = – (Y₁ – Y₀) ÷ (X₁ – X₀)

MRS_XY и MRS_YX не одно и то же, на самом деле они взаимны друг другу, то есть:

MRS_XY = 1 / MRS_YX

Предельная норма замещения зависит от относительных предпочтений потребителей, то есть от их относительных предельных полезностей и исходных точек.

Можно показать, что предельная норма замещения Y на X равна цене X, деленной на Y, которая, в свою очередь, равна предельной полезности X, деленной на предельную полезность Y:

MRS_XY = P_X / P_Y = MU_X / MU_Y

Кривые безразличия становятся более плоскими по мере того, как мы перемещаемся от оси Y к оси X.

Это происходит потому, что по мере того, как Y становится дефицитным, а X – изобильным, предельная норма замещения X на Y снижается. Это явление называется снижающейся предельной нормой замещения.

From Wikipedia, the free encyclopedia

In economics, the marginal rate of substitution (MRS) is the rate at which a consumer can give up some amount of one good in exchange for another good while maintaining the same level of utility. At equilibrium consumption levels (assuming no externalities), marginal rates of substitution are identical. The marginal rate of substitution is one of the three factors from marginal productivity, the others being marginal rates of transformation and marginal productivity of a factor.^[1]

As the slope of indifference curve[edit]

Under the standard assumption of neoclassical economics that goods and services are continuously divisible, the marginal rates of substitution will be the same regardless of the direction of exchange, and will correspond to the slope of an indifference curve (more precisely, to the slope multiplied by −1) passing through the consumption bundle in question, at that point: mathematically, it is the implicit derivative. MRS of X for Y is the amount of Y which a consumer can exchange for one unit of X locally. The MRS is different at each point along the indifference curve thus it is important to keep locus in the definition. Further on this assumption, or otherwise on the assumption that utility is quantified, the marginal rate of substitution of good or service X for good or service Y (MRS_xy) is also equivalent to the marginal utility of X over the marginal utility of Y. Formally,

It is important to note that when comparing bundles of goods X and Y that give a constant utility (points along an indifference curve), the marginal utility of X is measured in terms of units of Y that is being given up.

For example, if the MRS_xy = 2, the consumer will give up 2 units of Y to obtain 1 additional unit of X.

As one moves down a (standardly convex) indifference curve, the marginal rate of substitution decreases (as measured by the absolute value of the slope of the indifference curve, which decreases). This is known as the law of diminishing marginal rate of substitution.

Since the indifference curve is convex with respect to the origin and we have defined the MRS as the negative slope of the indifference curve,

Simple mathematical analysis[edit]

Assume the consumer utility function is defined by , where U is consumer utility, x and y are goods. Then the marginal rate of substitution can be computed via partial differentiation, as follows.

Also, note that:

where is the marginal utility with respect to good x and is the marginal utility with respect to good y.

By taking the total differential of the utility function equation, we obtain the following results:

, or substituting from above,

, or, without loss of generality, the total derivative of the utility function with respect to good x,

, that is,

.

Through any point on the indifference curve, dU/dx = 0, because U = c, where c is a constant. It follows from the above equation that:

, or rearranging

The marginal rate of substitution is defined as the absolute value of the slope of the indifference curve at whichever commodity bundle quantities are of interest. That turns out to equal the ratio of the marginal utilities:

.

---

When consumers maximize utility with respect to a budget constraint, the indifference curve is tangent to the budget line, therefore, with m representing slope:

Therefore, when the consumer is choosing his utility maximized market basket on his budget line,

This important result tells us that utility is maximized when the consumer’s budget is allocated so that the marginal utility per unit of money spent is equal for each good. If this equality did not hold, the consumer could increase his/her utility by cutting spending on the good with lower marginal utility per unit of money and increase spending on the other good. To decrease the marginal rate of substitution, the consumer must buy more of the good for which he/she wishes the marginal utility to fall for (due to the law of diminishing marginal utility).

Diminishing Marginal rate of Substitution[edit]

An important principle of economic theory is that marginal rate of substitution of X for Y diminishes as more and more of good X is substituted for good Y. In other words, as the consumer has more and more of good X, he is prepared to forego less and less of good Y.

It means that as the consumer’s stock of X increases and his stock of Y decreases, he is willing to forego less and less of Y for a given increment in X. In other words, the marginal rate of substitution of X for Y falls as the consumer has more of X and less of Y. That the marginal rate of substitution of X for Y diminishes can also be known from drawing tangents at different points on an indifference curve.

Using MRS to determine Convexity[edit]

When analyzing the utility function of consumer’s in terms of determining if they are convex or not. For the horizon of two goods we can apply a quick derivative test (take the derivative of MRS) to determine if our consumer’s preferences are convex. If the derivative of MRS is negative the utility curve would be concave down meaning that it has a maximum and then decreases on either side of the maximum. This utility curve may have an appearance similar to that of a lower case n. If the derivative of MRS is equal to 0 the utility curve would be linear, the slope would stay constant throughout the utility curve. If the derivative of MRS is positive the utility curve would be convex up meaning that it has a minimum and then increases on either side of the minimum. This utility curve may have an appearance similar to that of a u. These statements are shown mathematically below.

For more than two variables, the use of the Hessian matrix is required.

See also[edit]

• Marginal concepts
• Marginal rate of technical substitution (the same concept on production side)
• Indifference curves
• Consumer theory
• Convex preferences
• Implicit differentiation
• Labour economics

References[edit]

Adam Hayes. (2021, March 31). Inside the marginal rate of substitution. Investopedia.
Jerelin, R. (2017, May 30). Diminishing marginal rate of substitution | Indifference curve | Economics. Economics Discussion

• Krugman, Paul; Wells, Robin (2008). Microeconomics (2nd ed.). Palgrave. ISBN 978-0-7167-7159-3.
• Pindyck, Robert S.; Rubinfeld, Daniel L. (2005). Microeconomics (6th ed.). Pearson Prentice Hall. ISBN 0-13-008461-1.
• Dorfman, R. (2008). “Marginal Productivity Theory”. In Palgrave Macmillan (ed.). The New Palgrave Dictionary of Economics. London: Palgrave Macmillan. pp. 1–5. doi:10.1057/978-1-349-95121-5_988-2. ISBN 978-1-349-95121-5 – via SpringerLink.