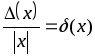-
Погрешности значения функции
При
вычислении значения функции
![]() в точке
в точке![]() (считаем
(считаем![]() приближенным значением точного числа
приближенным значением точного числа![]() )
)
возникают погрешности – предельная
абсолютная![]() и предельная относительная
и предельная относительная![]() .
.
Выразим эти погрешности через погрешности
числа![]() (будем полагать, что функция
(будем полагать, что функция![]() дифференцируема в точке
дифференцируема в точке![]() ).
).
Так
как функция
![]() дифференцируема в точке
дифференцируема в точке![]() ,
,
то
![]() ,
,
(4.1)
где
![]() мало при малом
мало при малом![]() (иными словами, слагаемым
(иными словами, слагаемым![]() в формуле (4.1) можно пренебречь, если
в формуле (4.1) можно пренебречь, если![]() мало).
мало).
Учитывая
равенство (4.1), истинная абсолютная
погрешность
![]() будет оцениваться неравенством
будет оцениваться неравенством
(приближенным)
![]() ,
,
откуда по определению
предельной абсолютной погрешности
![]() . (4.2)
. (4.2)
Итак,
предельная
абсолютная погрешность значения функции
в точке
![]() (
(![]() – приближенное число) равна произведению
– приближенное число) равна произведению
модуля производной этой функции в точке![]() на предельную абсолютную погрешность
на предельную абсолютную погрешность
числа![]() .
.
Соответственно
предельная относительная погрешность
![]() вычисляется следующим образом
вычисляется следующим образом
![]() =
= . (4.3)
. (4.3)
Найдем
с помощью формул (4.2), (4.3) погрешности
значений основных элементарных функций.
Пусть
![]() (
(![]() – действительное число). Тогда
– действительное число). Тогда
![]() ,
,
![]() .
.
В
частности при
![]() :
:![]() .
.
Пусть
![]() .
.
Тогда
![]() ,
,
![]() .
.
Пусть
![]() .
.
Тогда
![]() ,
,
![]() .
.
В
частности, если
![]() ,
,
то![]() .
.
Аналогично
определяются погрешности значений
других основных элементарных функций
(см. таблицу 4.1).
Таблица 4.1.
|
№ |
|
|
|
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
Пример
4.1. Дана
функция
![]() .
.
Протабулировать ее на отрезке![]() (считать
(считать![]() ),
),
разбив его на![]() равных частей (все расчеты проводить с
равных частей (все расчеты проводить с
4 знаками после запятой). Вычислить
предельные абсолютные, относительные
погрешности значений функции в узлах
табулирования.
Решение:
Протабулировать функцию
![]() на отрезке
на отрезке![]() с постоянным шагом
с постоянным шагом![]() означает составить таблицу значений
означает составить таблицу значений![]() ,
,![]() (точки
(точки![]() называются узлами табулирования), где
называются узлами табулирования), где
![]() . (4.4)
. (4.4)
В
нашем случае
![]() ,
,![]() ,
,![]() ;
;
узлы определяются следующим образом:
![]() . (4.5)
. (4.5)
Вычислим значения
функции в узлах табулирования (4.5):
![]() .
.
Имеем
![]() ,
,![]() ;
;
![]() ,
,
![]() 3,3261,
3,3261,
![]() ,
,
![]()
и так далее.
Все
вычисления значения функции в узлах
табулирования заполняем в таблицу 4.2.
Учитывая
формулы (4.2), (4.3), находим погрешности в
узлах (4.5) (при этом число
![]() можно считать точным, а тогда
можно считать точным, а тогда![]() ;
;
в остальных же узлах (4.5)![]() ,00005)
,00005)
![]() ,
,
 .
.
Таблица 4.2.
|
i |
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
3 |
0 |
0 |
|
1 |
0,6284 |
0,7927 |
0,5334 |
3,3261 |
4,8678 |
1,46 |
|
2 |
1,2568 |
1,2111 |
0,2846 |
3,4057 |
8,0695 |
2,37 |
|
3 |
1,8852 |
1,3730 |
0,1518 |
3,5248 |
1,0618 |
0,3 |
|
4 |
2,5136 |
1,5854 |
0,0809 |
3,6663 |
1,1724 |
0,32 |
|
5 |
3,1420 |
1,7726 |
0,0432 |
3,8158 |
1,1944 |
0,31 |
-
Полиномиальные интерполяции
Весьма
редко удается решить задачу прямыми
аналитическими методами, тем более
реализовать решение в виде вычислительного
алгоритма. Основными требованиями к
алгоритму являются:
–
изменяемость в зависимости от начальных
(исходных) условий, т.е. путь решения
должен быть по возможности универсальным;
–
схематизированность (однозначно должна
быть определена последовательность
действий),
–
рекурсированность – рекурсированный
алгоритм состоит из небольших частей,
которые неоднократно реализуются для
различных наборов значений;
–
решение, реализуемое алгоритмом должно
быть конечным, т.е. должно приводить к
конечному результату за конечное число
шагов. Другими словами, не должно
существовать различного рода расходимостей
(например, часто встречаются т.н.
логарифмические расходимости вида
![]() ,
,
разрывы первого и второго родов, скачки
значений производных и т.д.), которые
могут оказать существенное влияние на
конечный результат. Поэтому реализации
алгоритма непосредственно на ЭВМ должен
предшествовать тщательный анализ задачи
с целью выявления различных особенностей
в поведении исследуемого процесса.
Последнее требование
представляется авторам наиболее важным
с точки зрения достоверности получаемых
результатов вычисления.
Часто
при обработке статистических данных
возникает задача замены аналитического
описания некоторого реального процесса
на другое, более удобное с точки зрения
дальнейших математических преобразований.
Т.е. мы заменяем некоторую функцию f(x)
(известную, неизвестную, частично
известную), другой ψ(x),
полученной в результате некоторых
преобразований. В зависимости от цели
исследования выбирается метод
интерполяции1
или экстраполяции – процесс построения
приближенного или аппроксимирующего
многочлена соответственно внутри и вне
промежутка исследования. Так как методики
интерполяции и экстраполяции практически
не отличаются друг от друга, то в
дальнейшем будем ограничиваться
примерами интерполяции. В связи с этим
вышеупомянутую процедуру должен
предварять анализ исходной зависимости
f(x),
а именно:
-
Способ
и интервал задания функции (аналитический
или табличный); -
Оценка степени
гладкости функции, имеется ли возможность
определения производных; -
Требования
к интерполирующей функции ψ(x)
(определение ее класса); -
Определение
критерия качества интерполяции, иначе
говоря, задание способа оценки погрешности
интерполяции. Необходимо в первую
очередь определить источники погрешностей.
Чаще всего наиболее существенное
влияние оказывают следующие:
— погрешность
исходных данных;
— погрешность
метода;
— погрешность
округления;
Погрешность
исходных данных, как правило, легче
всего поддается оценке и соответствующей
корректировке. Более того, часто удается
получить точную аналитическую формулу
ошибок, исходя из выводов теории
вероятностей и математической статистики.
Так
как вычислительный алгоритм является
рекурсивным, состоящим из целого ряда
операций, то происходит т.н. накопление
погрешностей: погрешности результата
каждого шага оказываются исходными для
следующей операции, поэтому точный
анализ погрешностей оказывается
трудновыполнимым и приходится
ограничиваться доверительными оценками.
Сформулируем
основные положения.
Первое.
Будем рассматривать как таблично, так
и аналитически заданные функции.
Второе.
В основном будем использовать
полиномиальную или кусочно-полиномиальную
интерполяцию, т.е. рассматривать в
качестве аппроксимирующих функций ψ(x)
только многочлены. Данная форма ψ(x)
выглядит в большинстве случаев более
предпочтительной с точки зрения упрощения
дальнейших математических действий
(дифференцирования, интегрирования).
Другие виды приближений (тригонометрическое,
экспоненциальное и пр.) будут применены
в следующих разделах.
Третье.
Построение аппроксимирующего многочлена
и оценку погрешности будем производить
с помощью функционалов
 (1)
(1)
 (2)
(2)
соответственно
для непрерывных и дискретных функций.
Оценка погрешности (степени близости
функций f(x)
и ψ(x))
по формулам (1) и (2) смысл среднеквадратичной
погрешности.
Будем
называть вычислительный метод устойчивым,
если для любого
![]() существует такое
существует такое![]() ,
,
что максимальная погрешность результата
вычислений меньше![]() при максимальной погрешности исходных
при максимальной погрешности исходных
данных меньше![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вычисление погрешности функций. Определение допустимой погрешности аргументов по допустимой погрешности функций
Страницы работы
Фрагмент текста работы
б) 0,096835; ![]() . б)
. б)
0,66385; ![]() .
.
3) а)12,688 ; б)
4,636. 3) а) 6,743; б) 0,543 .
18.4.
ВЫЧИСЛЕНИЕ ПОГРЕШНОСТИ ФУНКЦИЙ
18.4.1. Функции одной переменной. Абсолютная погрешность дифференцируемой
функции ![]() , вызываемая достаточно малой погрешностью
, вызываемая достаточно малой погрешностью
аргумента ![]() , оценивается величиной
, оценивается величиной
![]() ,
,
(18.12)
Если значения функции ![]() положительны, то для относительной погрешности
положительны, то для относительной погрешности
имеет место оценка
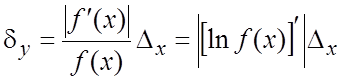 . (18.13)
. (18.13)
Например, для
тригонометрических функций абсолютные погрешности синуса и косинуса не
превосходят абсолютных погрешностей аргумента:
![]() ,
, ![]() . (18.14)
. (18.14)
18.4.2. Функции нескольких
переменных. Пусть
задана некоторая функция ![]() , от п аргументов
, от п аргументов
![]() и пусть значения каждого из аргументов
и пусть значения каждого из аргументов ![]() , определены с некоторыми погрешностями
, определены с некоторыми погрешностями ![]() , i = 1, 2,…, п.
, i = 1, 2,…, п.
Требуется найти погрешность данной функции.
Для
решения этой задачи будем предполагать, что функция ![]() является
является
дифференцируемой в некоторой области D. Абсолютная погрешность ![]() функции
функции
y при заданных абсолютных погрешностях
![]() аргументов
аргументов ![]() равна
равна
![]() . (18.15)
. (18.15)
Предполагая, что величины ![]() , i = 1, 2,…, п достаточно
, i = 1, 2,…, п достаточно
малы, можно записать приближенные равенства ![]()
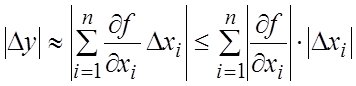 (18.16)
(18.16)
Следовательно, предельная абсолютная
погрешность ![]() функции y равна
функции y равна
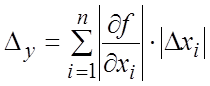 ,
,
(18.17)
где ![]() предельная
предельная
абсолютная погрешность аргумента ![]() .
.
Оценка для относительной
погрешности функции получается путем деления обеих частей неравенства (18.15)
на ![]()
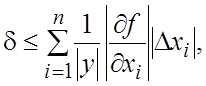 (18.18)
(18.18)
Из формулы (18.18) получаем выражение
для предельной относительной погрешности функции у
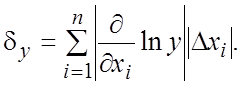 (18.19)
(18.19)
Рассмотрим
отдельные примеры на вычисление погрешностей различных функциональных
соотношений. Будем предполагать, что в каждом примере заданы те или иные
погрешности аргументов.
1. Пусть ![]() .
.
По формуле (18.17) предельная абсолютная погрешность суммы п слагаемых
равна
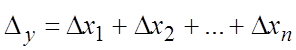 . (18.20)
. (18.20)
2. Пусть ![]() . По
. По
формуле (18.17) предельная абсолютная погрешность разности двух чисел равна
![]() .
.
3. Пусть ![]() , причем xi (i=1, 2, …, п) положительны. В соответствии с формулой (18.19)
, причем xi (i=1, 2, …, п) положительны. В соответствии с формулой (18.19)
проведем преобразования с целью получения выражения для предельной
относительной погрешности произведения п сомножителей
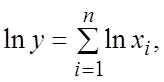
![]() .
.
4. Пусть 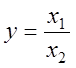 . По
. По
формуле (18.19) предельная относительная погрешность частного равна
![]() .
.
5. Пусть ![]() . Тогда
. Тогда ![]() .
.
![]() .
.
6. Пусть ![]() .
.
Следовательно, 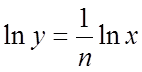 .
.
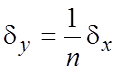 .
.
18.5. Определение допустимой погрешности аргументов по допустимой
погрешности функций
Задача определения какими должны быть
погрешности исходных приближений, чтобы полученный результат имел заданную
степень точности, имеет однозначное решение только для функции одной переменной
![]() : если эта функция дифференцируема и
: если эта функция дифференцируема и ![]() , то
, то
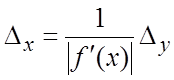 .
.
(18.21)
Для функций
нескольких переменных ![]() эта задача решается
эта задача решается
неоднозначно. Для ее решения необходимо наложить какие-либо условия на
погрешность исходных данных. Если использовать принцип равных влияний, считая что в формуле (18.17) все
слагаемые 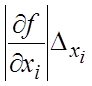 равны между собой, получим
равны между собой, получим
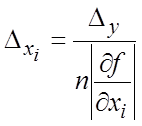
![]() .
.
(18.22)
Пример
8. Даны числа ![]() ;
; ![]() . Тогда
. Тогда
![]() . Причем последняя цифра сомнительная.
. Причем последняя цифра сомнительная.
Пример
9. Найти сумму ![]() , где
, где ![]() ;
; ![]() ;
; ![]() . Причем
. Причем
все цифры верные.
![]()
Имеем ![]() . Предельная абсолютная погрешность суммы
. Предельная абсолютная погрешность суммы ![]() . Стало быть, 7.84 < y< 7.87. В результате верными будут
. Стало быть, 7.84 < y< 7.87. В результате верными будут
цифры 7.8. Последняя цифра 4 сомнительная. #
Похожие материалы
- Вычисление приближенных значений
- Вычисление тройного интеграла в декартовых координатах
- Действительные функции одного переменного
Информация о работе
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
Основная задача теории погрешности заключается в следующем: с какой точностью можно найти значение функции Y=f(X1*, x2*,…, xn*), если аргументы XI* Известны с некоторой точностью. И обратная задача: с какой точностью надо задать значения аргументов функции, чтобы погрешность функции не превосходила заданной величины? Решение таких задач опираются на теорему Лагранжа, согласно которой предельная абсолютная погрешность функции равна произведению абсолютной величины ее производной на предельную абсолютную погрешность аргумента D(F*)=|F ’|D(X*). Если задана дифференцируемая функция Y= f(X1, x2,…, xn) и ее приближенное значение Y*= f(X1*, x2*,…, xn*), где Xi – Точные значения аргументов функции, а Xi* – приближенные к ним, и пусть D(Xi*) (I=1,2,…,n) абсолютные погрешности аргументов функции.
Определение. Предельной абсолютной погрешностью функции А(Y*) называют наилучшую при имеющейся информации оценку погрешности величины Y*= f(X1*+D(X1*), x2+D(X2*) , …, xn+D(Xn*) ),
Т. е. А(Y*)=Sup| F(X1, X2,…, Xn)- F(X1*, X2*,…, Xn*)|.
Линейная оценка погрешности функции записывается в виде:
 .
.
Разделив обе части неравенства на y*, будем иметь оценку для Предельной относительной погрешности функции D (Y*):
 =D(Y*).
=D(Y*).
| < Предыдущая | Следующая > |
|---|