Задача № 1 Расчёт дохода потребителя
Индивид покупает 8 единиц товара Х и 4 единицы товара Y. Найти его доход, если известно, что цена товара Х равна 2 ден. ед., а предельная норма замены равна 0,5.
Решение:
В точке оптимума выполняется равенство:
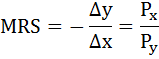
По условию MRS = 0,5 и Рх = 2. Следовательно, Ру = Рх / MRS = 2/0,5=4.
Найдём доход индивида, используя бюджетное ограничение:
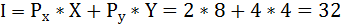
где I – доход,
Рх и Ру – цены двух рассматриваемых благ,
Х и Y – их количества.
Задача № 2. Расчёт общей и предельной полезности
Общая TU и предельная MU полезности товаров А, В, С представлены в таблице. Заполнить пропуски в таблице.

Решение:
Найдём общую полезность товара А.
Общая полезность N-й единицы товара = Предельная полезность N-й единицы товара + Общая полезность N-1-й единицы товара
TU(1)=MU(1)=20
TU(2)=MU(2) + TU(1)=15 + 20=35
TU(3)=MU(3) + TU(2)=12 + 35=47
TU(4)=MU(4) + TU(3)=8 + 47=55
TU(5)=MU(5) + TU(4)=6 + 55=61
Найдём предельную полезность товара В.
Предельная полезность N-й единицы товара=Общая полезность N-й единицы товара — Общая полезность N-1-й единицы товара
MU(1)=TU(1)=19
MU(2)= TU(2) — TU(1)=30 – 19 = 11
MU(3)= TU(3) — TU(2)=38 – 30 = 8
MU(4)= TU(4) — TU(3)=43 – 38=5
MU(5)= TU(5) — TU(4)=45 – 43=2
Найдём общую и предельную полезности товара С.
MU(1)=TU(1)=22
TU(2)=MU(2) + TU(1)=10 + 22=32
MU(3)= TU(3) — TU(2)=39 – 32=7
MU(4)= TU(4) — TU(3)=44 – 39=5
TU(5)=MU(5) + TU(4)=3 + 44=47
Заполним пропуски в таблице:

Задача № 3. Расчёт общей полезности
Предельная полезность первой единицы блага равна 420. При потреблении первых трёх единиц блага предельная полезность каждой последующей единицы уменьшается в 2 раза; предельная полезность каждой последующей единицы блага при дальнейшем потреблении падает в 4 раза. Найти общую полезность блага при условии, что его потребление составляет 8 единиц.
Решение:
Распишем условие задачи следующим образом:
MU(1) = 420,
MU(2) = 420/2=210,
MU(3) = 210/2=105,
MU(4) = 105/4=26,25,
MU(5) = 26,25/4=6,5625,
MU(6) = 6,5625/4=1,640625,
MU(7) = 1,640625/4=0,410156,
MU(8) = 0,410156/4=0,102539.
Найдём общую полезность блага при условии, что его потребление составляет 8 единиц.
TU(8) = MU(8) + TU(7) = MU(8) + MU(7) + TU(6) =…=
= MU(8) + MU(7) + MU(6) + MU(5) + MU(4) + MU(3) + MU(2) + MU(1) =
= 420 + 210 + 105 + 26,25 + 6,5625 + 1,640625 + 0,410156 + 0,102539 = 769,96582
Задача № 4. Расчёт оптимального объёма потребления двух благ
В таблице представлены следующие данные о предельной полезности двух благ.
| Количество, кг | Конфеты | Виноград |
|---|---|---|
| 1 | 60 | 150 |
| 2 | 40 | 120 |
| 3 | 20 | 90 |
Цена 1 кг конфет 80 ден. ед., а цена 1 кг винограда 160 ден. ед.
Бюджет потребителя составляет 400 ден. ед.
Определить оптимальный объём потребления конфет и винограда.
Решение:
Оптимальный объём потребления конфет и винограда достигается тогда, когда отношение предельных полезностей равно отношению цен этих благ.
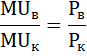
Среди перечисленных вариантов таким свойством обладает комбинация 2 кг винограда (MUв=120) и 1 кг конфет (MUк=60).
Предельная полезность винограда, разделённая на предельную полезность конфет равна отношению их цен:
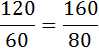
Проверим соответствие этой комбинации бюджетному ограничению:
80*1 + 160*2 = 400
Бюджет полностью израсходован.
Задача № 5. Расчёт цен товаров Х и Y
Потребитель покупает 4 единицы блага Х и 9 единиц блага Y, имея доход 100 ден. ед. Найти цены товаров X и Y, если известно, что предельная норма замены товара Y товаром X (MRSxy) равна 4.
Решение:
Предельную норму замены товара Y товаром X(MRSxy) можно определить как отношение цены товара Х к цене товара Y:
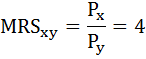
Запишем бюджетное ограничение:
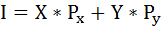
100 = 4*Px + 9*Py,
где
Px, Py – цены благ Х и Y соответственно.
Составим и решим систему уравнений:
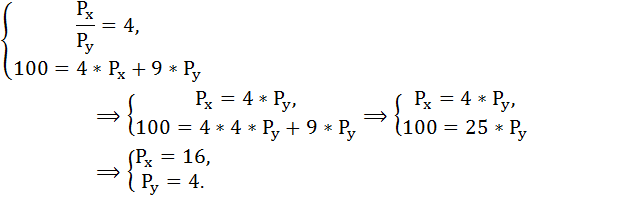
Задача № 6. Расчёт оптимального объёма потребления
У студента Иванова в холодильнике сыр и колбаса нарезаны для удобства кусочками по 100 г. Общая полезность их потребления представлена в таблице. Определите количество съеденного им в день, если известно, что он в целом употребляет 700 г названных продуктов и при этом добивается максимума полезности.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) |
| 100 | 2000 | 1900 |
| 200 | 3900 | 3750 |
| 300 | 5700 | 5550 |
| 400 | 7400 | 7300 |
| 500 | 8000 | 9000 |
| 600 | 9500 | 10650 |
Решение:
Рассчитаем предельную полезность от потребления этих двух продуктов.
Предельная полезность в дискретном случае определяется по формуле:
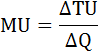
где
ΔTU – приращение общей полезности (TU1 – TU0),
ΔQ – приращение количества потребляемого блага (Q1 – Q0).
Вычисления занесём в таблицу.
| Количество, г | Колбаса (общая польза) | Сыр (общая польза) | Предельная полезность колбасы | Предельная полезность сыра |
| 100 | 2000 | 1900 | 2000 | 1900 |
| 200 | 3900 | 3750 | 1900 | 1850 |
| 300 | 5700 | 5550 | 1800 | 1800 |
| 400 | 7400 | 7300 | 1700 | 1750 |
| 500 | 9000 | 9000 | 1600 | 1700 |
| 600 | 10500 | 10650 | 1500 | 1650 |
Известно, что в целом студент употребляет 700 г колбасы и сыра, то есть всего 7 кусочков, и при этом добивается максимума полезности.
Решение об оптимальном объёме потребления можно представить в виде таблицы, где на каждом шаге будем сравнивать предельную полезность каждого кусочка колбасы и сыра и выбирать наибольшую величину предельной полезности, что в сумме даст их максимум.

Итак, на первом шаге наибольшая предельная полезность, равная 2000 будет получена от потребления 1 кусочка/100 грамм колбасы. Дальше студенту без разницы, что употребить, так как первый кусочек сыра и второй кусочек колбасы приносят одинаковую полезность – 1900. Пусть, например, это будет сначала сыр, а затем колбаса. Но вот на четвёртом шаге наибольшую полезность принесёт второй кусочек сыра. Предельная полезность, полученная от его потребления 1850 больше, чем 1800 – предельная полезность третьего куска колбасы или третьего кусочка сыра. На пятом шаге студенту опять всё равно, что съесть первым, третий кусочек сыра или третий кусочек колбасы, так как полезность от дополнительного потребления этих продуктов одинакова. И наконец, седьмым кусочком должен стать сыр, поскольку предельная полезность четвёртого кусочка сыра (1750), больше чем предельная полезность четвёртого кусочка колбасы (1700).
Общая полезность от потребления 3 кусочков колбасы и 4 кусочков сыра будет максимальной и составит:
TU = 2000 + 1900 + 1900 + 1850 + 1800 + 1800 + 1750 = 13 000
Таким образом, студент Иванов получит максимум полезности при употреблении 3 кусочков (300 грамм) колбасы и 4 кусочков (400 грамм) сыра.
Задача № 7. Расчёт отимального объёма потребления
Определите оптимальный для потребителя объем блага Q, если известно, что функция полезности индивида от обладания этим благом имеет вид:
1) U(Q)= 1 – 5 × Q2
2) U(Q)= 5 + Q – Q2
3) U(Q) = Q2 – 5 × Q3
Как будут выглядеть функции предельной полезности? Проиллюстрируйте ответ.
Решение:
Оптимальный для потребителя объем блага Q будет определяться в точке, где потребитель получит максимум удовлетворения полезности. Задача сводится к нахождению экстремума функции полезности. Найдём производную функции полезности (предельную полезность MU) и приравняем её к нулю.
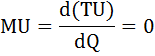
1) MU = –10 × Q = 0, следовательно, Q = 0;
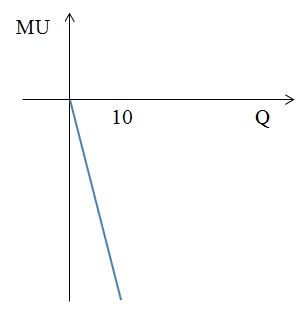
2) MU = 1 – 2 × Q = 0, следовательно, Q = 1/2;
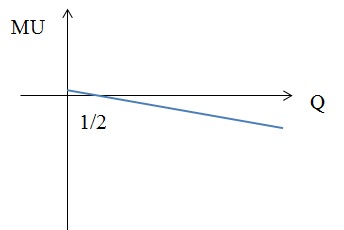
3) MU = 2 × Q – 15 × Q2 = 0, следовательно, Q = 0; Q = 2/15.
Задача № 8. Расчёт цен товаров X и Y
Индивид покупает 4 единицы блага X и 9 единиц блага Y, имея доход равный 100 денежным единицам. Найти цены товаров X и Y, если известно, что предельная норма замены X на Y равна 4.
Решение:
По условию задачи предельная норма замены благом Y блага X () равно 4. Это значит, что количество блага Х должно быть сокращено на 4 единицы в обмен на увеличение количества блага Y на единицу, при неизменном уровне удовлетворения потребителя.
Равновесие потребителя может быть представлено математически как:
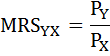
— это предельная норма замещения, равная отношению цен благ Y и X. Данное условие оптимума потребителя следует понимать так. Соотношение, в котором потребитель при данных ценах способен замещать один товар другим, равно соотношению, в котором потребитель согласен замещать один товар другим, не изменяя уровень своего удовлетворения.
Отсюда
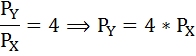
Далее воспользуемся формулой бюджетного ограничения:
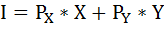
где I – доход или бюджет потребителя.
100 = 4 × PX + 9 × PY
100 = 4 × PX + 9 × 4 × PX
100 = 40 × PX
PX = 2,5
PY = 4 × 2,5 = 10.
Ответ: PX = 2,5; PY = 10.
Задача № 9. Определение рационального выбора потребителя
Потребитель имеет функцию полезности:
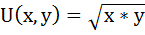
и может на свой доход равный 100 единицам приобретать только эти два товара по ценам:
Px = 2
Py = 5
Определить рациональный выбор потребителя. Какой максимальный уровень полезности достижим?
Решение:
Рациональный выбор потребителя осуществляется в соответствии со вторым законом Госсена:
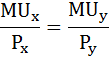
Предельная полезность товара х будет равна производной функции общей полезности по аргументу х:
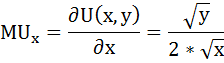
Аналогично находим предельную полезность товара y:
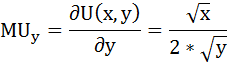
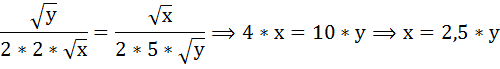
Далее воспользуемся бюджетным ограничением:
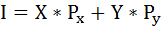
Из условия задачи известно, что:
I = 100
Px = 2
Py = 5
Составим и решим систему уравнений:
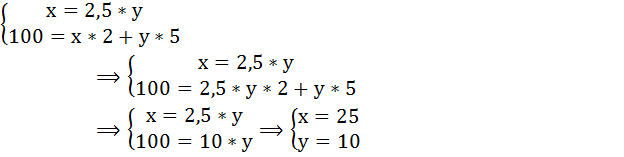
При х = 25 и у = 10 общая полезность достигнет максимума:
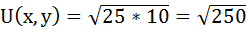
Задача № 10. Расчёт оптимального объёма потребления
У Оксаны есть 30 рублей. Она хочет купить шоколадки «Шок» ценой 3 р. Полезность от этой покупки она оценивает функцией:
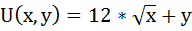
х – приобретённое количество шоколадок,
y – оставшаяся часть дохода.
Сколько купит шоколадок «Шок» рациональная Оксана?
Решение:
Рациональное поведение потребителя можно определить, как стремление максимизировать излишек потребителя. Потребитель будет покупать дополнительные единицы до тех пор, пока они приносят дополнительный избыток, т.е. пока цена, которую потребитель готов уплатить за единицу блага, превосходит реальную цену:
MU > P
Однако каждая последующая единица потребления обычно приносит уменьшающийся прирост полезности, т.е. при покупке благ «одно за другим» рано или поздно предельная полезность какого-то блага сравняется с его ценой:
MU = P
После того как предельная полезность сравняется с ценой, потребитель прекратит дальнейшие покупки: оптимальный объём потребления достигнут.
Найдём предельную полезность MU, как производную функции общей полезности по аргументу х:
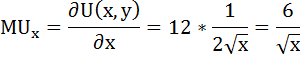
Оптимальный объём потребления будет достигнут при МU = P:
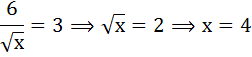
Таким образом, рациональная Оксана купит 4 шоколадки, потратив на эту покупку 12 рублей.
Предельная полезность помогает как экономистам, так и отдельным людям придать товарам количественную ценность. Предприятия используют предельную полезность для определения успешности продукта или услуги и корректировки производства по мере необходимости. Крупные корпорации используют сложные расчеты, но предельную полезность можно найти с помощью простой формулы. В этой статье мы обсудим, что такое предельная полезность и как ее рассчитать на примере.
Что такое предельная полезность?
Предельная полезность оценивает удовлетворенность клиентов, заказчиков и потребителей после получения большего количества единиц товара или услуги. Экономисты используют предельную полезность для оценки того, сколько товара или услуги хотят купить покупатели. Когда потребляется больше одной и той же единицы товара и общая полезность возрастает, возникает положительная предельная полезность. Когда происходит обратное, продукт получает отрицательную предельную полезность.
Третий распространенный тип предельной полезности известен как нулевая предельная полезность. Это происходит, когда наличие более чем одного предмета не приносит дальнейшего удовлетворения потребителю. Например, нулевая предельная полезность возникает, если потребитель покупает два одинаковых выпуска комикса, и второй экземпляр не дает никакой дополнительной ценности.
Откуда взялась идея предельной полезности?
В 19 веке экономисты собрались вместе, чтобы проанализировать концепцию цены. Преобладающей идеей было то, что цена влияет на полезность. Однако они столкнулись с парадоксом, когда заметили, что цены на некоторые товары не первой необходимости намного выше, чем на товары первой необходимости. Например, бриллианты имеют большую ценность, чем хлеб, несмотря на то, что хлеб имеет большую полезность. Это явление стало известно как парадокс стоимости, который позже был решен с помощью предельной полезности. Поскольку алмазы редки, потребители готовы платить больше, чтобы получить их, что делает их предельную полезность выше, чем у хлеба, который менее дефицитен.
Почему важна предельная полезность?
Общая удовлетворенность продуктом или услугой позволяет оценить будущие решения потребителей.
Например, производитель закусок создает новое сэндвич-печенье со вкусом, который никогда ранее не использовался. Сэндвич-печенье распространяется только на тестовых рынках. По прошествии некоторого времени в Интернете появляются отзывы о продукте, показывающие, что людям он нравится. Остатки продукта быстро уходят с полок, так как потребители покупают сразу несколько единиц товара. Это доказывает производителю, что положительная предельная полезность имеет место, и он может расширить свой рыночный ассортимент.
Закон убывающей предельной полезности
Благодаря своему успеху производитель заключает сделки с большим количеством поставщиков, что позволяет продавать товар по всей стране. Однако этот успех сглаживается законом убывающей предельной полезности. Этот закон, разработанный экономистами, гласит, что со временем предельная полезность уменьшается с каждой единицей, полученной потребителем. Если предположить, что все остальные переменные, связанные с продуктом, остаются неизменными, потребители в конечном итоге переходят от одного продукта к другому, подобно причуде.
Как рассчитать предельную полезность
Полезность можно рассматривать как ценность, которую клиент придает определенному товару или услуге. Проще говоря, его можно определить как то, сколько человек готов заплатить за товар.
Например, коллекционер произведений искусства замечает в социальных сетях, что работа одного из его любимых художников выставлена на аукцион. Инкассатор мчится на аукцион, готовый выписать чек. Хотя стартовая цена составляет $800, он сразу же делает ставку в $5 000, чтобы обеспечить себе приобретение этого предмета. Поскольку вещь доставляет ему большое удовлетворение, он придает ей большую ценность или стоимость.
В экономике стандартное правило гласит, что предельная полезность равна изменению общей полезности, деленному на изменение количества товара. Формула выглядит следующим образом:
Предельная полезность = разность общей полезности и количества товаров
-
Найдите общую полезность первого события.
-
Найдите общую полезность второго события.
-
Найдите разницу между обоими (или всеми) событиями.
-
Найти разницу между количеством товаров между обоими (или всеми) событиями.
-
Примените формулу.
1. Найдите общую полезность первого события
Нахождение предельной полезности предполагает сравнение двух или более событий для нахождения среднего значения. Если эти события связаны с оценкой цены покупки, сложите каждую цену вместе, чтобы найти общую полезность первого события.
2. Найдите общую полезность второго события
Рассмотрим информацию, полученную во время второго события. Определите количество измененных товаров, а также предложенную цену покупки. Сложите все покупки вместе, чтобы найти общую полезность второго события.
3. Найдите разницу между обоими (или всеми) событиями
Соберите итоговые суммы по обоим или всем событиям и найдите их разность. Полученный ответ становится общей разницей полезности для формулы.
4. Найдите разницу между количеством товаров между обоими (или всеми) событиями
Сложите все купленные товары с первого мероприятия и найдите общую сумму. Затем соберите вместе все купленные товары из второго (и всех последующих) событий. Вычтите итоговые значения друг из друга и найдите решение.
5. Примените формулу
Найдя обе конечные разницы, примените полученную информацию к формуле. Разделите обе разницы и установите их равными предельной полезности.
Пример расчета предельной полезности
Во время своего обеденного перерыва доктор. Авасарала направляется к ближайшей тележке, продающей тако. Каждое тако стоит всего $2, но Dr. Авасарала так голодна, что готова заплатить по $5 за каждую порцию. Несмотря на то, что тако стоят всего два доллара каждый, она оценивает полезность в $5.
Во время пребывания в грузовике она хочет съесть два тако. Зная, что после первого тако она будет почти сыта, она готова заплатить только $3 за второе тако, что снижает ее полезность. Чтобы найти общую полезность, она складывает оба итога вместе:
Общая полезность = 5 + 3
Общая полезность = 8
Dr. Авасарала кладет $8 общей полезности на два тако.
Во время отдельного посещения продуктового фургона, Др. Авасарала решает, что она готова съесть 5 тако. Заплатив $5 за первое тако, она решает, что второе тако стоит всего $4, потому что она наелась до отвала. После второго тако она заплатит по $1 за оставшиеся 3 тако. Чтобы найти общую полезность второго посещения, она складывает все покупки вместе:
Общая полезность = 5 + 4 + 1 + 1 + 1
Общая полезность = 12
Доктор. Авасарала оценивает общую полезность пяти тако в $12.
Чтобы найти предельную полезность, она находит разницу между обоими посещениями.
Разница в общей полезности = 12 – 8
Общая разница в полезности = 4
Далее, Dr. Авасарала вычитает количество тако из каждого посещения друг из друга:
Разница в количестве товаров = 5 – 2
Разница в количестве товаров = 3
Доктор. У Авасаралы есть разница в 3 тако.
Имея на руках эту информацию, Др. Авасарала применяет формулу:
Предельная полезность = 4 3
Предельная полезность = ~1.3 = 1.4
Доктор. Авасарала обнаруживает, что ее предельная полезность составляет около $1.40 на каждое тако.
Download Article
Download Article
In economics, marginal utility (MU) is a way to measure how much value or satisfaction a consumer gets out of consuming something. As a general rule, MU is equal to the change in total utility divided by the change in the quantity of goods consumed.[1]
A common way of thinking of this is that MU is the utility someone gets from each additional unit of goods consumed.
-

1
Understand the economic concept of utility. Utility is the “value” or “satisfaction” that a consumer gets from consuming a certain number of goods. A good way of thinking of it is that utility is how much money a consumer would hypothetically pay for the satisfaction provided by a good.[2]
- For example, let’s say that you are hungry and are buying fish to eat for supper. Let’s also say that one fish costs $2. If you’re so hungry that you would pay $8 for the fish, the fish is said to provide $8 worth of utility. In other words, you’re willing to pay $8 to get the satisfaction from the fish no matter what it actually costs.
-

2
Find the total utility from consuming a certain number of goods. Total utility is just the concept of utility applied to more than one good. If consuming one good gives you a certain amount of utility, consuming more than one of the same good will give you an amount that is higher, lower, or the same.[3]
- For example, let’s say that you plan to eat two fish. However, after eating the first fish, you’re not quite as hungry as before. Now, you’d only pay $6 for the extra satisfaction of the second fish. It’s not worth as much to you now that you’re somewhat full. This means the two fish provide $6 + $8 (first fish) = $14 of “total utility” together.
- Note that it doesn’t matter whether or not you actually buy the second fish. MU is only concerned with what you would pay for it. In real life, economists use complex mathematical models to predict what consumers hypothetically would pay for something.
Advertisement
-

3
Find the total utility from consuming a different number of goods. To find MU, you need two different total utility measurements. You’ll use the difference between them to make your MU calculation.[4]
- Let’s say that, in the example situation in Step 2, you decide that you’re hungry enough to eat four whole fish. After the second fish, you’re feeling a little full, so you would only pay about $3 for the next fish. After the third fish, you’re almost completely full, so you would only pay $1 for the final fish.
- The satisfaction you would get from it is almost cancelled out by the feeling of being uncomfortably full. You can say that the four fish provide a total utility of $8 + $6 + $3 + $1 = $18.
-

4
Calculate MU. Divide the difference in total utility over the difference in units. The answer you get will be the marginal utility, or the utility given by each additional unit consumed.[5]
In the example situation, you would calculate your MU as follows:- $18 – $14 (example from Step 2) = $4
- 4 (fish) – 2 (fish) = 2
- $4/2 = $2
- This means that, between the second and the fourth fish, each extra fish is only worth $2 of utility to you. This is an average value; the third fish is actually worth $3 and the fourth is actually worth $1, of course.
Advertisement
-

1
Use the equation to find the MU for each additional unit. In the example above, we found the average MU for several goods being consumed. This is one valid way to use MU. However, it’s actually more often applied to individual units of goods consumed. This gives us the precise MU for each additional good (not an average value).[6]
- Finding this is easier than it sounds. Just use the normal equation to find the MU when the change in quantity of goods consumed is one.
- In the example situation, you already know the MUs for each individual unit. When you haven’t had any fish, the MU of the first fish is $8 ($8 of total utility – the $0 you had before/change of 1 unit), the MU of the second fish is $6 ($14 of total utility – the $8 you had before/change of 1 unit), and so on.
-

2
Use the equation to maximize your utility. In economic theory, consumers make decisions about how to spend their money in an effort to maximize their utility. In other words, consumers want to get as much satisfaction as possible for their money. This means that consumers will tend to buy products or goods until the marginal utility of buying one more good is smaller than the marginal cost (the price of one more unit).[7]
-

3
Determine lost utility. Let’s look at the example situation one more time. First we said that each fish costs $2. Then we determined that the first fish has an MU of $8, the second has an MU of $6, the third has an MU of $3, and the fourth has an MU of $1.[8]
- Given this information, you wouldn’t actually end up buying the fourth fish. Its marginal utility ($1) is less than its marginal cost ($2). Basically, you’re losing utility on this transaction, so it’s not in your favor.)
Advertisement
| Tickets Bought | Total utility | Marginal utility |
|---|---|---|
| 1 | 10 | 10 |
| 2 | 18 | 8 |
| 3 | 24 | 6 |
| 4 | 28 | 4 |
| 5 | 30 | 2 |
| 6 | 30 | 0 |
| 7 | 28 | -2 |
| 8 | 18 | -10 |
-

1
Assign columns for quantity, total utility, and marginal utility. Most MU charts have at least these three columns. There may sometimes be more, but these display the most crucial information. Typically, these are arranged from left to right.[9]
- Note that the column headers will not always match these exactly. For example, the “Quantity” column may be labeled “Items bought,” “Units purchased,” or something similar. The important thing is the information in the column.
-

2
Look for a trend of diminishing returns. A “classic” MU chart is often used to demonstrate that, as a consumer buys more of a certain good, the desire to purchase even more goods will drop. In other words, after a point, the marginal utility of each additional good purchased will start to decrease. Eventually, the consumer will start to be less satisfied overall than before buying the additional goods.[10]
- In the example chart above, this trend of diminishing returns starts almost immediately. The first ticket to the film festival provides lots of marginal utility, but each ticket after the first gives a little less. After six tickets, each extra ticket actually has a negative MU, which decreases the total satisfaction. An explanation for this might be that, after six visits, the consumer starts to get tired of seeing the same movies again and again.
-

3
Determine Maximum Utility. This is the point where marginal price exceeds MU. A marginal utility chart makes it easy to predict how many units of goods a consumer will buy. As a reminder, consumers tend to buy goods until the marginal price (the cost of one more unit of the goods) is greater than the MU. If you know how much the goods being analyzed in the chart cost, the point where utility is maximized is the last row where MU is higher than the marginal cost.[11]
- Let’s say that the tickets in the example chart cost $3 each. In this case, utility is maximized when the consumer buys 4 tickets. The next ticket after this has an MU of $2, which is less than the marginal cost of $3.
- Note that utility isn’t necessarily maximized when the MU starts to become negative. It’s possible for goods to give some benefit to the consumer without being “worth it.” For instance, the fifth ticket in the chart above still gives $2 worth of MU. This isn’t a negative MU but it still decreases the total utility because it’s not worth the cost.
-

4
Use the chart data to find additional information. Once you have the three “core” columns above, it becomes easy to get more numerical data about the model situation the chart is analyzing. This is especially true if you’re using a spreadsheet program such as Microsoft Excel that can do the math for you. Here are two types of data you may want to put in extra columns to the right of the three used above:[12]
- Average Utility: The total utility in each row divided by the quantity of goods purchased.[13]
- Consumer Surplus: The marginal utility in each row minus the product’s marginal cost. It represents the “profit” in terms of utility the consumer gets from buying each product. It is also called “economic surplus.”[14]
- Average Utility: The total utility in each row divided by the quantity of goods purchased.[13]
Advertisement
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
It’s important to understand that the situations in the examples are model situations. That is, they represent hypothetical consumers (rather than real ones). In real life, consumers aren’t perfectly rational; they may, for instance, not buy exactly as many goods as are needed to maximize utility. Good economic models are great tools for predicting consumer behavior on a broad scale, but they often don’t “match” real life exactly.[15]
-
If you add a consumer surplus column to your chart (as discussed above), the point at which utility is maximized will be the last row before consumer surplus becomes negative.
Advertisement
References
About This Article
Article SummaryX
Marginal utility is used to measure how satisfying or valuable something is to a consumer. To calculate the marginal utility of something, just divide the change in total utility by the change in the number of goods consumed. In other words, divide the difference in total utility by the difference in units to find marginal utility. To learn more from our Entrepreneur co-author, like how to use a marginal utility chart, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 659,385 times.
Reader Success Stories
-

Mujammil Islam
Apr 19, 2017
“Thank you for this article. At first I could not understand the total and marginal utility. Then I found this…” more
Did this article help you?
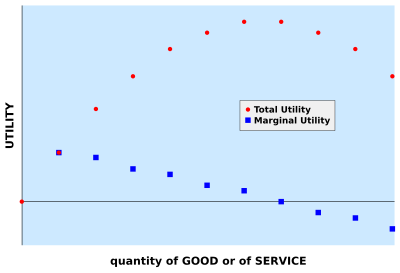
Сравнение общей и предельной полезности
Предельная полезность — это полезность, которую потребитель получает от использования ещё одной дополнительной единицы блага.
Другими словами, предельная полезность — это увеличение общей полезности при потреблении одной дополнительной единицы блага (производная):
где 

Принцип предельной полезности сводится к следующему: ценность блага данного рода определяется полезностью предельного экземпляра, удовлетворяющего наименее настоятельную потребность[1]. Предельная полезность определяет спрос на товар.
История[править | править код]
Теория предельной полезности возникла как альтернатива трудовой теории стоимости для пояснения наблюдаемых закономерностей в ценах на товары. Основные положения теории предельной полезности были сформулированы Германом Генрихом Госсеном в надолго всеми забытой работе 1854 года. Массированное проникновение маржиналистских идей в экономическую литературу, получившее название «маржиналистская революция», началось в середине 1880-х годов. Принцип предельной полезности был изложен почти одновременно тремя учёными-экономистами Стенли Джевонсом, Карлом Менгером и Леоном Вальрасом. Хотя Джевонс изложил свои идеи в лекции, опубликованной в 1866, Менгер в «Основаниях политической экономии» в 1871, а Леон Вальрас в 1874, все трое писали независимо друг от друга. Термин «предельная полезность» (нем. Grenznutzen) был введён в экономическую науку Фридрихом фон Визером[2].
Согласно данной концепции, ценность товаров определяется их предельной полезностью на базе субъективных оценок. Даже в отношении одной и той же потребности благо может иметь различную предельную полезность (например, полезность хлеба для сытого и для голодного). Предельная полезность какого-либо блага обозначает ту пользу, которую приносит последняя единица этого блага, причём последнее благо обычно удовлетворяет самые маловажные нужды. При этом фактором ценности считается и редкость товара. Предельная полезность повышается при недостатке блага и понижается при его избытке.
Субъективная ценность — это личная оценка товара как потребителем, так и продавцом; объективная же ценность — это меновые пропорции, цены, которые формируются в ходе конкуренции на рынке. По мере постепенного насыщения потребностей субъекта, полезность вещи для него падает. Теория предельной полезности пытается дать совет, как наилучшим образом распределить средства для удовлетворения потребностей при ограниченности ресурсов.
В 1890 году английский экономист Альфред Маршалл опубликовал монографию «Принципы экономической науки», ставшую основным учебником по микроэкономике. Он предложил компромиссный вариант определения рыночной стоимости предельной полезностью, определяющей спрос на товар, и затратами производства, сформулировал закон спроса и предложения.
Современные экономисты продолжают использовать теорию предельной полезности, акцентируя внимание на изучении закономерностей потребительского спроса, анализе предложения, исследовании рынков и ценообразования на микроэкономическом уровне.
Закон убывающей предельной полезности[править | править код]
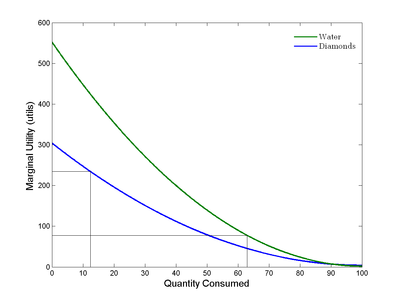
График показывает предельную полезность (измеряется в единицах полезности) алмазов и воды как функцию объёма потребления
Закон убывающей предельной полезности заключается в том, что с ростом потребления блага (при неизменном объёме потребления всех остальных благ) общая полезность, получаемая потребителем, возрастает, но скорость роста замедляется.
Математически это означает, что первая производная функции общей полезности в зависимости от потребления данного блага положительна, но уменьшается, а вторая — отрицательна. Иначе говоря, закон убывающей предельной полезности гласит, что функция общей полезности возрастает и выпукла вверх.
Предельная полезность (производная) убывает с ростом потребления, обращается в ноль при максимальной общей полезности и затем становится отрицательной, а общая полезность, достигнув максимального значения, начинает уменьшаться.
Например, для голодного человека предельная полезность первой тарелки супа выше, чем второй, второй — выше, чем третьей. Так и с другим благом.
Из этого закона следует необходимость понижения цены для того, чтобы побудить потребителя к увеличению покупок конкретного продукта.
Однако закон убывающей предельной полезности не всегда действует при малых количествах товара. Например, если человек принимает одну таблетку — он излечивается не полностью. Если две — то он излечивается полностью, и предельная полезность возрастает по сравнению с одной таблеткой. Однако дальнейшее потребление таблеток может только вредить организму, и предельная полезность станет отрицательной.
Ограниченность применимости закона[править | править код]
- Однородные единицы. Сравнивать можно товар с однородными единицами и потребляемые одним потребителем. Например, нельзя рассматривать яблоки и бананы. Точно так же нельзя рассматривать зелёные и красные яблоки вместе. Все единицы товара должны быть одного веса и качества. Например, если первое яблоко кислое, а второе — сладкое, то второе яблоко даст больше удовлетворения потребителю, чем первое.
- Рассматривается потребитель с неизменными вкусами. Не должно быть никаких изменений во вкусах, привычках, обычаях, предпочтениях и доходах потребителя. Изменение в одном из перечисленных факторов изменит полезность продукта и закон становится неприменимым.
- Непрерывность потребления. Формулировка закона исходит из того, что процесс потребления какого-либо продукта потребителем непрерывен. В противном случае его предельная полезность не обязательно пойдёт на спад. Если после потребления одной единицы продукта есть пауза, то вполне возможно, что потребность в нём возобновится и потребление последующей единицы продукта даст такое же удовлетворение, как от предыдущей .
- Постоянные цены. Цены на продукт или на его заместителей предполагаются неизменными. Потребитель может отказаться от покупки товара или увеличить покупки лишь в силу изменения цены, а не потому, что произошло изменение оценки полезности товара.
На практике одновременное выполнение всех этих условий встречается крайне редко.
Ограниченность законов предельной полезности обсуждалась многократно, однако показать их в микроэкономической модели пока удается только в виртуализированной экономике[источник не указан 1242 дня].
Предельная полезность и спрос[править | править код]
Теория субъективной полезности выводит закон убывания объёма спроса с ростом цены из аксиомы снижения предельной полезности[3].
См. также[править | править код]
- Ординалистская теория полезности
- Функция полезности
- Законы Госсена
- Предельная норма замещения
- Предельные издержки
- Маржинализм
Примечания[править | править код]
- ↑ Курс экономической теории: учебник — 6-е исправленное, дополненное и переработанное издание. — Киров: «АСА», 2009. — 848 с.
- ↑ Хайек Ф. А. Глава 2. Карл Менгер (1840-1921) // Судьбы либерализма в XX веке. — М.: ИРИСЭН, 2009. — С. 79—118. — 337 с. — 1000 экз. — ISBN 978-5-91066-028-5.
- ↑ Лекция 2. Спрос Архивная копия от 12 июня 2020 на Wayback Machine // 50 лекций по микроэкономике. — СПб.: Экономическая школа. 2004. Т. 1.
Литература[править | править код]
- Блюмин, И. Г. Эволюция теории «предельной полезности» // Критика буржуазной политической экономии: В 3 томах. — М.: Изд-во АН СССР, 1962. — Т. III. Кризис современной буржуазной политической экономии. — С. 97-113. — 379 с. — 3200 экз.
- Веблен, Торстейн. Ограниченность теории предельной полезности Архивная копия от 20 января 2022 на Wayback Machine.
Предельная полезность товара
Полезность-это «ценность» или «удовлетворение», которое потребитель получает от потребления определенного количества товаров. Хороший способ понять полезность заключается в том, что это то, сколько денег потребитель гипотетически заплатит за удовлетворение, которое обеспечит товар.
Например, предположим, что вы голодны и покупаете рыбу, чтобы поесть на ужин. Допустим также, что одна рыба стоит 2000. Если вы так голодны, что заплатили бы 8000 за рыбу, говорят, что рыба обеспечивает полезность на 8000. Другими словами, вы готовы заплатить 8000, чтобы получить удовлетворение от рыбы, независимо от того, что она на самом деле стоит.
Предельная полезность измеряет увеличение удовлетворенности потребителей от потребления дополнительной единицы товара или услуги. Предельная полезность рассчитывается путем разницы в общей стоимости и деления на изменение потребляемого количества.
Предельная полезность = (TUf – TUi)/(Qf – Qi)
Где,
TUi — Общая полезность в единицах Q i
TUf — Общая полезность в единицах Q f
Qi — количество единиц потребления изначально
Qf — количество единиц потребления в конечном итоге
Полезность-это удовлетворение, которое человек получает от потребления товара или услуги. Общая полезность-это общее удовлетворение, полученное от потребления данного общего количества товара или услуги, в то время как предельная полезность-это удовлетворение, полученное от потребления дополнительного количества этого товара.
Пример: Таблица полезности
| Количество потребляемого | Общая полезность (сумма полезности от потребления) | Предельная полезность (изменение общей полезности, деленное на изменение потребленного количества) | Средняя полезность (общая полезность, деленная на общее количество потребленного) |
|---|---|---|---|
| 1 | 50 | 50 | = 50/1 = 50 |
| 2 | 90 | 40 | = 90/2 = 45 |
| 3 | 120 | 30 | = 120/3 = 40 |

