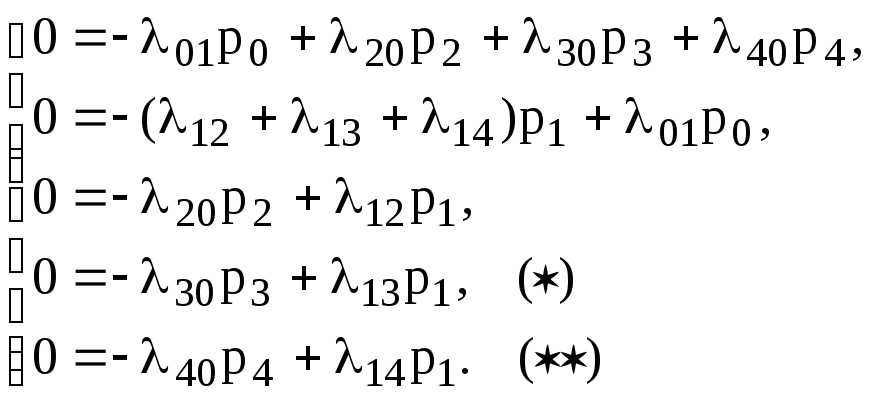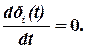Как найти предельные вероятности состояния системы

Уравнения Колмогорова.
Предельные вероятности состояний

Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока “окончаний ремонтов” первого узла и т.п.

Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния: .

Вероятностью i-го состояния называется вероятность того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма вероятностей всех состояний равна единице:

Рассмотрим систему в момент и, задав малый промежуток , найдем вероятность того, что система в момент будет находиться в состоянии . Это достигается разными способами.

1. Система в момент с вероятностью находилась в состоянии , а за время не вышла из него.

Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной . А вероятность того, что система не выйдет из состояния , равна . Вероятность того, что система будет находиться в состоянии по первому способу (т.е. того, что находилась в состоянии и не выйдет из него за время ), равна по теореме умножения вероятностей:

2. Система в момент с вероятностями (или ) находилась в состоянии или и за время перешла в состояние .

Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).

Применяя теорему сложения вероятностей, получим

откуда

Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):

Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.

Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:

Сформулируем правило составления уравнений Колмогорова. В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).

В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).

Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии , т.е. при начальных условиях .

Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени. Особый интерес представляют вероятности системы в предельном стационарном режиме, т.е. при , которые называются предельными (или финальными) вероятностями состояний.

В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.

Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии. Например, если предельная вероятность состояния , т.е. , то это означает, что в среднем половину времени система находится в состоянии .

Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:

Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом, согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.

---

Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при

Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или

(Здесь мы вместо одного “лишнего” уравнения системы (10) записали нормировочное условие (8)).

Решив систему (11), получим , т.е. в предельном, стационарном режиме система в среднем 40% времени будет находиться в состоянии (оба узла исправны), 20% — в состоянии (первый узел ремонтируется, второй работает), 27% — в состоянии (второй узел ремонтируется, первый работает) и 13% времени — в состоянии (оба узла ремонтируются)

---

Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).

Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел — . В то же время первый узел находится в ремонте в среднем долю времени, равную , а второй узел — . Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен

ден. ед.

Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока “окончаний ремонтов” каждого узла, т.е. теперь и система линейных алгебраических уравнений (10), описывающая стационарный режим системы , вместе с нормировочным условием (8) примет вид:

Решив систему, получим .

Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход в единицу времени:

ден.ед.

Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.

---

Процесс гибели и размножения

В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения. Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.

Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.

Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния возможны переходы только либо в состояние , либо в состояние .

Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или .

По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).

В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния

для состояния имеем , которое с учетом (12) приводится к виду

Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:

к которой добавляется нормировочное условие

При анализе численности популяций считают, что состояние соответствует численности популяции, равной , и переход системы из состояния в состояние происходит при рождении одного члена популяции, а переход в состояние – при гибели одного члена популяции.

Решая систему (14), (15), можно получить

Легко заметить, что в формулах (17) для коэффициенты при есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния , а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния .

---

Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.

Решение. По формуле (16) найдем

по (17)

т.е. в установившемся, стационарном режиме в среднем 70,6% времени система будет находиться в состоянии , 17,6% — в состоянии и 11,8% — в состоянии .

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Предельные вероятности состояний

При выполнении
определенных условий при t
в системе наступает стационарный
режим. При этом вероятности состояний
перестают зависеть от времени, то есть
становятся постоянными величинами.
Эти вероятности называются предельными
(финальными, стационарными) [3]. В
отличие от вероятностей p_k(t)
эти вероятности будем обозначать p_k
(без переменной t в скобках т.е.
p_k=lim_t→∞p_k(t)).

Если число состояний
системы конечно и из каждого состояния
можно перейти (за конечное число шагов
) в каждое другое, то предельные вероятности
существуют и не зависят от начальных
условий. Случайный процесс, протекающий
в такой системе, называют эргодическим
[11].

Для вычисления
предельных вероятностей в уравнениях
Колмогорова нужно положить все левые
части (производные) равными нулю, так
как в стационарном режиме вероятности
состояний – постоянные величины. Тогда
система дифференциальных уравнений
превращается в систему линейных,
однородных алгебраических уравнений.
Совместно с нормировочным уравнением
p_i=1 эти
уравнения позволяют вычислить предельные
вероятности. Во многих прикладных
задачах интерес представляют именно
предельные вероятности.

Уравнения Колмогорова
тесно связаны с известными уравнениями
Кирхгофа. Для установившегося режима
уравнения Колмогорова по аналогии с
уравнениями Кирхгофа можно сформулировать
так: суммарная интенсивность потоков
событий, проходящих через любое возможное
состояние системы, равна нулю [14].

Пример

Среднее
время между отказами некоторого
устройства равно t₀
часов. Отказу соответствует переходу
S₀S₁
на
графе состояний (рис. 3.4). После отказа
проводится предварительный осмотр
устройства, на который требуется в
среднем
t₁
часов. В результате предварительного
осмотра может быть принято одно из трех
решений:

–
Требуется замена отказавшего элемента,
на что тратится в среднем t₂
часов.
Вероятность этого решения q₁₂,
ему соответствует переход S₁S₂.

–
Требуется замена ряда узлов с последующей
регулировкой, на что тратится в среднем
t₃
часов.
Вероятность этого решения q₁₃,
ему
соответствует переход S₁S₃.

–
Требуется сложный ремонт, регулировка
и проведение цикла испытаний, на что
тратится в среднем t₄
часов. Вероятность этого решения q₁₄
, ему соответствует переход S₁S₄.

Сумма
q₁₂+
q₁₃+
q₁₄=1.
Плотность распределения времени
проведения операции t_i
(i=0…4) – экспоненциальная.

Требуется
определить среднее время пребывания
системы в работоспособном состоянии
(S₀).

Решение.
Определим интенсивности
переходов:

– Из
состояния S₀
возможен переход только в состояние
S₁,
следовательно, ₀₁=₀=1/t₀.

–
Интенсивность перехода из состояния
S₁ ₁=1/t₁,
а относительные вероятности переходов
– q₁₂,
q₁₃,
q₁₄.
Следовательно,

.

– Из
состояний S₂,
S₃,
S₄
возможны переходы только в состояние
S₀,
следовательно, ₂₀=1/t₂,
₃₀=1/t₃,
₄₀=1/t₄.

Система
алгебраических уравнений для определения
предельных вероятностей:

Нормировочное
уравнение
.

Для
нахождения предельных вероятностей
все вероятности, начиная с первой,
последовательно выражаются через p₀,
после чего, воспользовавшись нормировочным
уравнением, находится p₀.
Из второго уравнения сразу определяется
p₁=h₁p₀.
Подстановкой p₁
в уравнения ()
и ()
находятся p_i=h_ip₀
для i =2, 3, 4. Коэффициенты h_i
зависят от интенсивностей переходов.
Из равенства

находим
.

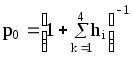
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Уравнения Колмогорова.
Предельные вероятности состояний

Рассмотрим математическое описание марковского процесса с дискретными состояниями и непрерывным временем* на примере случайного процесса из примера 1, граф которого изображен на рис. 1. Будем полагать, что все переходы системы из состояния в происходят под воздействием простейших потоков событий с интенсивностями ; так, переход системы из состояния в будет происходить под воздействием потока отказов первого узла, а обратный переход из состояния в — под воздействием потока “окончаний ремонтов” первого узла и т.п.

Граф состояний системы с проставленными у стрелок интенсивностями будем называть размеченным (см. рис. 1). Рассматриваемая система имеет четыре возможных состояния: .

Вероятностью i-го состояния называется вероятность того, что в момент система будет находиться в состоянии . Очевидно, что для любого момента сумма вероятностей всех состояний равна единице:

Рассмотрим систему в момент и, задав малый промежуток , найдем вероятность того, что система в момент будет находиться в состоянии . Это достигается разными способами.

1. Система в момент с вероятностью находилась в состоянии , а за время не вышла из него.

Вывести систему из этого состояния (см. граф на рис. 1) можно суммарным простейшим потоком с интенсивностью , т.е. в соответствии с формулой (7), с вероятностью, приближенно равной . А вероятность того, что система не выйдет из состояния , равна . Вероятность того, что система будет находиться в состоянии по первому способу (т.е. того, что находилась в состоянии и не выйдет из него за время ), равна по теореме умножения вероятностей:

2. Система в момент с вероятностями (или ) находилась в состоянии или и за время перешла в состояние .

Потоком интенсивностью (или — с- рис. 1) система перейдет в состояние с вероятностью, приближенно равной (или ). Вероятность того, что система будет находиться в состоянии по этому способу, равна (или ).

Применяя теорему сложения вероятностей, получим

Переходя к пределу при (приближенные равенства, связанные с применением формулы (7), перейдут в точные), получим в левой части уравнения производную (обозначим ее для простоты ):

Получили дифференциальное уравнение первого порядка, т.е. уравнение, содержащее как саму неизвестную функцию, так и ее производную первого порядка.

Рассуждая аналогично для других состояний системы , можно получить систему дифференциальных уравнений Колмогорова для вероятностей состояний:

Сформулируем правило составления уравнений Колмогорова . В левой части каждого из них стоит производная вероятности i-го состояния. В правой части — сумма произведений вероятностей всех состояний (из которых идут стрелки в данное состояние) на интенсивности соответствующих потоков событий, минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного (i-го состояния).

В системе (9) независимых уравнений на единицу меньше общего числа уравнений. Поэтому для решения системы необходимо добавить уравнение (8).

Особенность решения дифференциальных уравнений вообще состоит в том, что требуется задать так называемые начальные условия, т.е. в данном случае вероятности состояний системы в начальный момент . Так, например, систему уравнений (9) естественно решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии , т.е. при начальных условиях .

Уравнения Колмогорова дают возможность найти все вероятности состояний как функции времени . Особый интерес представляют вероятности системы в предельном стационарном режиме , т.е. при , которые называются предельными (или финальными) вероятностями состояний.

В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют.

Предельная вероятность состояния имеет четкий смысл: она показывает среднее относительное время пребывания системы в этом состоянии . Например, если предельная вероятность состояния , т.е. , то это означает, что в среднем половину времени система находится в состоянии .

Так как предельные вероятности постоянны, то, заменяя в уравнениях Колмогорова их производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим. Для системы с графом состояний, изображенном на рис. 1), такая система уравнений имеет вид:

Систему (10) можно составить непосредственно по размеченному графу состояний, если руководствоваться правилом , согласно которому слева в уравнениях стоит предельная вероятность данного состояния , умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в i-е состояние, на вероятности тех состояний, из которых эти потоки исходят.

Пример 2. Найти предельные вероятности для системы из примера 1, граф состояний которой приведен на рис. 1, при

Решение. Система алгебраических уравнений, описывающих стационарный режим для данной системы, имеет вид (10) или

(Здесь мы вместо одного “лишнего” уравнения системы (10) записали нормировочное условие (8)).

Решив систему (11), получим , т.е. в предельном, стационарном режиме система в среднем 40% времени будет находиться в состоянии (оба узла исправны), 20% — в состоянии (первый узел ремонтируется, второй работает), 27% — в состоянии (второй узел ремонтируется, первый работает) и 13% времени — в состоянии (оба узла ремонтируются)

Пример 3. Найти средний чистый доход от эксплуатации в стационарном режиме системы в условиях примеров 1 и 2, если известно, что в единицу времени исправная работа первого и второго узлов приносит доход соответственно в 10 и 6 ден.ед., а их ремонт требует затрат соответственно в 4 и 2 ден.ед. Оценить экономическую эффективность имеющейся возможности уменьшения вдвое среднего времени ремонта каждого из двух узлов, если при этом придется вдвое увеличить затраты на ремонт каждого узла (в единицу времени).

Решение. Из примера 2 следует, что в среднем первый узел исправно работает долю времени, равную , а второй узел — . В то же время первый узел находится в ремонте в среднем долю времени, равную , а второй узел — . Поэтому средний чистый доход в единицу времени от эксплуатации системы, т.е. разность между доходами и затратами, равен

Уменьшение вдвое среднего времени ремонта каждого из узлов в соответствии с (6) будет означать увеличение вдвое интенсивностей потока “окончаний ремонтов” каждого узла, т.е. теперь и система линейных алгебраических уравнений (10), описывающая стационарный режим системы , вместе с нормировочным условием (8) примет вид:

Решив систему, получим .

Учитывая, что , а затраты на ремонт первого и второго узла составляют теперь соответственно 8 и 4 ден.ед., вычислим средний чистый доход в единицу времени:

Так как больше (примерно на 20%), то экономическая целесообразность ускорения ремонтов узлов очевидна.

Процесс гибели и размножения

В теории массового обслуживания широкое распространение имеет специальный класс случайных процессов — так называемый процесс гибели и размножения . Название этого процесса связано с рядом биологических задач, где он является математической моделью изменения численности биологических популяций.

Граф состояний процесса гибели и размножения имеет вид, показанный на рис. 4.

Рассмотрим упорядоченное множество состояний системы . Переходы могут осуществляться из любого состояния только в состояния с соседними номерами, т.е. из состояния возможны переходы только либо в состояние , либо в состояние .

Предположим, что все потоки событий, переводящие систему по стрелкам графа, простейшие с соответствующими интенсивностями или .

По графу, представленному на рис. 4, составим и решим алгебраические уравнения для предельных вероятностей состояний (их существование вытекает из возможности перехода из каждого состояния в каждое другое и конечности числа состояний).

В соответствии с правилом составления таких уравнений (см. 13) получим: для состояния

для состояния имеем , которое с учетом (12) приводится к виду

Аналогично, записывая уравнения для предельных вероятностей других состояний, можно получить следующую систему уравнений:

к которой добавляется нормировочное условие

При анализе численности популяций считают, что состояние соответствует численности популяции, равной , и переход системы из состояния в состояние происходит при рождении одного члена популяции, а переход в состояние – при гибели одного члена популяции.

Решая систему (14), (15), можно получить

Легко заметить, что в формулах (17) для коэффициенты при есть слагаемые, стоящие после единицы в формуле (16). Числители этих коэффициентов представляют произведение всех интенсивностей, стоящих у стрелок, ведущих слева направо до данного состояния , а знаменатели — произведение всех интенсивностей, стоящих у стрелок, ведущих справа налево до состояния .

Пример 4. Процесс гибели и размножения представлен графом (рис. 5). Найти предельные вероятности состояний.

Потоки событий. Уравнения Колмогорова

Теория систем массового обслуживания

Основные понятия и классификация систем массового

Обслуживания

При решении задач рациональной организации торговли, бытового обслуживания, складского хозяйства и т.д. весьма полезной бывает интерпретация деятельности производственной структуры как системы массового обслуживания (СМО), т.е. системы в которой, с одной стороны, постоянно возникают запросы на выполнение каких-либо работ, а с другой – происходит посто­янное удовлетворение этих запросов. Главной особенностью процессов массового обслуживания является случайность.

Всякая СМО включает четыре элемента: входящий поток требований, их очередь на обслуживание, обслуживающее устройство, выходящий поток обслуженных требований.

Требованием (клиентом, заявкой) в СМО называется каж­дый отдельный запрос на выполнение какой-либо работы. Обслуживание — это выполнение работы по удовлетворе­нию поступившего требования. Объект, выполняющий обслужи­вание требований, называется обслуживающим устройством (прибором) или каналом обслуживания.

Временем обслуживания называется период, в течение ко­торого удовлетворяется требование на обслуживание, т.е. пери­од от начала обслуживания и до его завершения. Период от мо­мента поступления требования в систему и до начала обслужи­вания называется временем ожидания обслуживания. Время ожидания обслуживания в совокупности с временем обслужива­ния составляет время пребывания требования в системе.

СМО классифицируются по разным признакам.

1. По числу каналов обслуживания СМО делятся на одноканальные и многоканальные.

2. В зависимости от условий ожидания требованием нача­ла обслуживания различают СМО с потерями (отказами) и СМО с ожиданием.

В СМО с потерями требования, поступившие в момент, когда все приборы заняты обслуживанием, получают отказ, они теряются для данной системы и никакого влияния на дальней­ший процесс обслуживания не оказывают. Классическим приме­ром системы с отказами является телефонная станция – требо­вание на соединение получает отказ, если вызываемый абонент занят. Для системы с отказами основной характеристикой эффек­тивности функционирования является вероятность отказа или средняя доля заявок, оставшихся необслуженными.

В СМО с ожиданием требование, поступившее в момент, когда все приборы заняты обслуживанием, не покидает систему, а становится в очередь и ожидает пока не освободится один из каналов. При освобождении очередного прибора одна из заявок, стоящих в очереди, немедленно принимается на обслуживание.

Для СМО с ожиданием основными характеристиками яв­ляются математические ожидания длины очереди и времени ожидания. Примером системы с ожиданием может служить процесс восстановления телевизоров в ремонтной мастерской.

Встречаются системы, лежащие между указанными двумя группами (смешанные СМО). Для них характерно наличие не­которых промежуточных условий: ограничениями могут быть ограничения по времени ожидания начала обслуживания, по длине очереди и т.п.

В качестве характеристик эффективности может приме­няться вероятность отказа как в системах с потерями (или харак­теристики времени ожидания) и в системах с ожиданием.

3. По дисциплине обслуживания СМО делятся на систе­мы с приоритетом в обслуживании и на системы без приоритета в обслуживании.

Требования могут обслуживаться в порядке их поступле­ния либо случайным образом, либо в зависимости от установлен­ных приоритетов.

4. СМО могут быть однофазными и многофазными. В однофазных системах требования обслуживаются кана­лами одного типа (например, рабочими одной профессии) без передачи их от одного канала к другому, в многофазных систе­мах такие передачи возможны.

5. По месту нахождения источника требований СМО де­лятся на разомкнутые (когда источник требования находится вне системы) и замкнутые (когда источник находится в самой сис­теме).

К замкнутым относятся системы, в которых поступающий поток требований ограничен. Например, мастер, задачей кото­рого является наладка станков в цехе, должен периодически их обслуживать. Каждый налаженный станок становится в будущем потенциальным источником требований на наладку. В подобных системах общее число циркулирующих требований конечно и чаще всего постоянно.

Если питающий источник обладает бесконечным числом требований, то системы называются разомкнутыми. Примерами подобных систем могут служить магазины, кассы вокзалов, пор­тов и т.п. Для этих систем поступающий поток требований можно считать неограниченным.

Методы и модели исследования СМО можно условно раз­бить на аналитические и статистические (имитационного моде­лирования процессов массового обслуживания).

Аналитические методы позволяют получить характеристи­ки системы как некоторые функции от параметров ее функционирования. Благодаря этому появляется возможность проводить качественный анализ влияния отдельных факторов на эффектив­ность работы СМО.

К сожалению, аналитическому решению поддается лишь довольно ограниченный круг задач теории массового обслужи­вания. Несмотря на постоянно ведущуюся разработку аналити­ческих методов, во многих реальных случаях аналитическое ре­шение либо невозможно получить, либо итоговые зависимости оказываются настолько сложными, что их анализ становится са­мостоятельной трудной задачей. Поэтому ради возможности при­менения аналитических методов решения приходится прибегать к различным упрощающим предположениям, что в некоторой степени компенсируется возможностью применения качествен­ного анализа итоговых зависимостей (при этом, разумеется, не­обходимо, чтобы принятые допущения не искажали реальной картины процесса).

Потоки событий. Уравнения Колмогорова

В настоящее время теоретически наиболее разработаны и удобны в практических приложениях методы решения таких за­дач массового обслуживания, в которых поток требований явля­ется простейшим (пуассоновским).

Для простейшего потока частота поступления требований в систему подчиняется закону Пуассона, то есть вероятность поступления за время t, ровно kтребований задается форму­лой:

P_k= e – λt

где λ – параметр потока (интенсивность – среднее число требований, поступивших в систему за единицу времени).

Простейший поток обладает тремя основными свойствами: ординарностью, стационарностью и отсутствием последействия.

Ординарность потока означает практическую невозмож­ность одновременного поступления двух и более требований. Например, достаточно малой является вероятность того, что из группы станков, обслуживаемых бригадой ремонтников, одно­временно выйдут из строя несколько станков.

Стационарным называется поток, вероятные характеристики которого не зависят от времени. Например, математи­ческое ожидание числа требований, поступающих в систему в единицу времени, является величиной постоянной и называется интенсивностью потока. Таким образом, вероятность поступления в систему определен­ного количества требований в течение заданного промежутка времени t зависит от его величины и не зависит от начала его отсчета на оси времени.

Отсутствие последействия означает, что число требований, поступивших в систему до момента t, не определяет того, сколько требований поступит в систему за время t + t.

Например, если на ткацком станке в данный момент про­изошел обрыв нити, и он устранен ткачихой, то это не опреде­ляет того, произойдет новый обрыв на данном станке в следую­щий момент или нет, тем более это не влияет на вероятность возникновения обрыва на других станках.

Вероятность того, что на временном интервале t = τ не поступит ни одного требования p₀ определяется как:

Тогда вероятность того, что на этом же временном интервале появится хотя бы одно требование определяется соотношением

p(t) = 1– p₀ = 1– e – λτ .

Вероятность попадания на элементарный временной интервал, т.е. когда τ = Δt, хотя бы одного события (требования) потока, можно определить, заменив функцию e – λτ двумя первыми числами её разложения в ряд Маклорена по степеням Δt. Действительно:

p(Δt) = 1–e – λΔt ≈ λ Δt.

Важной характеристикой СМО является время обслужива­ния требований в системе. Время обслуживания является, как правило, случайной величиной и, следовательно, может быть описано законом распределения. Наибольшее распространение в теории и, особенно в практических приложениях, получил экс­поненциальный закон. Для этого закона функция распределения вероятностей имеет вид:

р (t – t ,

т.е. вероятность того, что время обслуживания не превосходит некоторой величины t, где μ – интенсивность потока обслуживания тре­бований в системе (среднее число требований, обслуженных в единицу времени).

Очевидно, что вероятность обслуживания хотя бы одного требования за элементарный временной отрезок будет определяться как:

p(Δt) = 1–e -Δ t ≈ μλ Δt.

При анализе случайных процессов с дискретными состояниями пользуются графиком состояний, где прямоугольником изображаются состояния, а переходы из состояния в состояние – стрелками. У стрелок обычно проставляются значения интенсивностей λ_ij (μ_ij) перехода системы из состояния S_i в состояние S_j, которые происходят под воздействием простейших потоков событий.

Рассмотрим систему, которая может находиться в двух состояниях: S₀– система исправна; S₁ – система находится в состоянии отказа и ремонтируется (рис. 8.1).

Рис. 8.1. Граф системы

Будем характеризовать состояние системы (S₀,S₁) вероятностями состояния р₀ (t) и р₁ (t). Очевидно, что

Найдем вероятность того, что система в момент (t+Δt) будет находиться в состоянии S₀.

Это возможно, во-первых, в том случае, если система в момент времени t с вероятностью р₀(t)находилась в состоянии S₀ и за время Δtиз него не вышла. Вероятность выхода системы за время Δt из состояния S₀ в состояние S₁ определяется как λ· Δt. Противоположная вероятность (что система не выйдет из S₀) определяется как (1 – λΔt). Вероятность того, что система, находившаяся в состоянии S₀ с вероятностью р₀(t), за время Δt не выйдет из него, равна по теореме умножения вероятностей

Во-вторых, система в момент времени t находилась с вероятностью р₁(t)в состоянии S₁ и за интервал времени Δt с вероятностью μ·Δt перешла в состояние S₀, т.е.

Вероятность р₀(t + Δt) нахождения системы в состоянии S₀ момент времени (t + Δt)по какому-либо из двух рассмотренных способов равна сумме рассмотренных вероятностей

Преобразуем соотношение к виду

Переходя к пределу при Δt→0, получим

По аналогии составляется уравнение, описывающее вероятность того, что система в момент (t + Δt)будет находиться в состоянии S₁, но проще это найти из условия нормирования

С учетом этого условия система уравнений для двух состояний графа имеет вид

Задав начальные условия, можно решить систему уравнений и найти систему функций времени р_i(t), где i – номер состояния.

Для достаточно большого значения tраспределение вероятностей стабилизируется и практически не зависит от времени, т.е.

Тогда система уравнений упрощается (стационарный режим)

Откуда вероятности состояний установившегося процесса определяются как

В частности, если μ=2; λ=1, то Р₀=0,67; Р₁=0,33. Таким образом, в среднем система будет находиться в рабочем состоянии 67%, а в состоянии ремонта 33% времени.

В общем случае система уравнений Колмогорова может быть составлена по следующему алгоритму.

1. В левой части каждого уравнения стоит производная вероятности i-го состояния.

2. В правой части каждого уравнения стоит:

2.1. Сумма произведений вероятностей всех состояний, из которых идут стрелки в i-е состояние, на интенсивности соответствующих потоков событий.

2.2. Минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность i-го состояния.

Система Колмогорова состоит из независимых уравнений и условия нормирования.

СМО с ожиданием

Рассмотрим аналитические модели СМО с ожиданием (наиболее распространенные СМО, в которых требования, по­ступившие в момент, когда все обслуживающие единицы заня­ты, становятся в очередь и обслуживаются по мере освобожде­ния обслуживающих единиц).

Задачи с очередями являются типичными в производствен­ных условиях, например при организации наладочных и ремон­тных работ, при многостаночном обслуживании и т.д.

Постановка задачи в общем виде выглядит следующим образом.

Система состоит из nобслуживающих каналов. Каждый из них может одновременно обслуживать только одно требование. В систему поступает простейший (пуассоновский) поток требо­ваний с параметром . Если в момент поступления очередного требования в системе на обслуживании уже находится не мень­ше n требований (т.е. все каналы заняты), то это требование ста­новится в очередь и ждет начала обслуживания. Время обслуживания каждого требования t_об является слу­чайной величиной, которая подчиняется экспоненциальному закону распределения с параметром .

Как отмечалось выше, СМО с ожиданием можно разбить на две большие группы: замкнутые и разомкнутые. Особенности функционирования каждой из этих двух ви­дов систем накладывают свой оттенок на используемый матема­тический аппарат. Расчет характеристик работы СМО различного вида может быть проведен на основе расчета вероятностей со­стояний СМО (формулы Эрланга).

Замкнутая СМО с ожиданием

Поскольку система замкнутая, то к постановке задачи сле­дует добавить условие: поток поступающих требований ограни­чен, т.е. в системе обслуживания одновременно не может нахо­диться больше m требований (m – число обслуживаемых объек­тов).

Такую систему можно классифицировать как многоканальную СМО (n – каналов) и ограниченной данной очереди l, причем n +l = m.

Граф состояний такой системы изображен на рис. 8.2.

Рис. 8.2. Граф состояний многоканальной СМО с ограниченной очередью

Состояния данной системы означают:

S₀ – отсутствие требований в системе;

S₁ – одно требование обслуживается, очереди нет;

S₂ – два требования обслуживаются, очереди нет;

S_n– n требований обслуживаются, очереди нет;

S_n+1 – n требований обслуживаются, одно требование стоит в очереди;

S_n+l– n требований обслуживаются, l требований стоят в очереди.

Система уравнений вероятностей состояний в стационарном режиме для цепочки S₀ – S_n будет:

Для цепочки состояний S_n+1 – S_n+lсистема уравнений стационарного режима будет:

В качестве основных критериев, характеризующих качество функционирования рассматриваемой системы, выберем: 1) от­ношение средней длины очереди к наибольшему числу требова­ний, находящихся одновременно в обслуживающей системе – коэффициент простоя обслуживаемого объекта; 2) отношение среднего числа незанятых обслуживающих каналов к их общему числу – коэффициент простоя обслуживаемого канала.

Рассмотрим расчет необходимых вероятностных характе­ристик (показателей качества функционирования) замкнутой СМО.

1. Вероятность того, что в системе находится k требований при условии, когда их число не превышает числа обслуживаю­щих аппаратов п:

P_k=α_kP₀, (1 k n),

где α_k= или α_k= ;

;

– интенсивность поступления требований в си­стему от одного источника;

_об – средняя продолжительность обслуживания одного требования;

т – наибольшее возможное число требований, находящих­ся в обслуживающей системе одновременно (m=n+l);

п– число обслуживающих аппаратов;

Р₀ – вероятность того, что все обслуживающие аппараты свободны.

2. Вероятность того, что в системе находится k требований при условии, когда их число больше числа обслуживающих ап­паратов:

P_k= 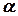_kP₀, (n k m),

где 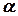_k= ( _об) k или α_k= .

3. Вероятность того, что все обслуживающие аппараты сво­бодны, определяется из условия

4. Среднее число требований, ожидающих начала обслужи­вания (средняя длина очереди):

.

5. Коэффициент простоя требования в ожидании обслужи­вания:

a₁= .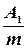

6. Вероятность того, что все обслуживающие аппараты заняты:

P_отк= .

7. Среднее число требований, находящихся в обслуживающей системе (обслуживаемых и ожидающих обслуживания):

A₂= = .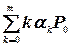

8. Коэффициент полного простоя требований на обслуживании и в ожидании обслуживания:

a₂= .

9. Среднее время простоя требования в очереди на обслуживание:

T_ож=a₁/ .

10. Среднее число свободных обслуживающих аппаратов:

A₃= .

11 . Коэффициент простоя обслуживающих аппаратов:

a₃ = .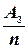

12. Вероятность того, что число требований, ожидаю­щих обслуживания, больше некоторого числа В (вероятность того, что в очереди на обслуживание находится более В тре­бований):

P_–B = = .

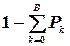
Рассмотрим пример расчета характеристик замкнутой СМО.

Пример 8.1. Оптовый склад строительных материалов обслу­живает шесть предприятий-потребителей материалов. Каждый из потребителей направляет на склад автомашину за мате­риалами в среднем один раз в смену (продолжительность сме­ны 8 ч). На складе имеется один автопогрузчик, который исполь­зуется только для погрузки материалов на прибывающие авто­машины. Прибывшая на склад автомашина становится в оче­редь, если автопогрузчик занят погрузкой другой автомашины. Обработка статистических данных о продолжительности погруз­ки одной автомашины и проверка соответствующей гипотезы по­казали, что продолжительность погрузки одной автомашины подчиняется показательному закону распределения и составля­ет в среднем 48 мин (0,1 смены). Статистическое исследование потока автомашин показа­ло, что число автомашин, поступающих на склад в единицу вре­мени, подчиняется пуассоновскому закону распределения. Требуется провести расчет характеристик функционирова­ния приведенной производственной системы как СМО.

Решение. Рассчитаем основные параметры системы для условий задачи.

Вероятность того, что все обслуживающие ап­параты свободны (на складе нет автомашин) определяется как P₀, λ=1, μ=0,1.

Вероятность того, что на складе одна автомашина:

P₁= 0,1P₀=0,6P₀,

а вероятность того, что на складе две автомашины (одна под погрузкой, а другая в очереди):

P₂= 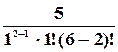0,1 2 P₀=0,3P₀.

Рассчитывая аналогично, получим: Р₃=0,12Р₀; Р₄=0,036Р₀;Р₅= 0,0072Р₀; Р₆= 0,0007Р₀. Так как сумма вероятнос­тей нахождения системы в любом из состояний равна 1, т.е.

=1,

то P₀(1 + 0,6 + 0,3 + 0,12 + 0,036 + 0,0072 + 0,0007) = 2,0639; Р₀ = 1.

Отсюда находим Р₀ = 0,4845.

Дальнейшие расчеты затруднений не вызывают. Напри­мер, средняя длина очереди равна

Теория случайных процессов и теория массового обслуживания

Теорией случайных процессов называют раздел математики, изучающий закономерности случайных явлений в динамике их развития. Теория случайных процессов — это сравнительно новый раздел теории вероятностей, особенно интенсивно развивающийся в настоящее время в связи с широким кругом его практических приложений.

Содержание:

Элементы теории случайных процессов и теории массового обслуживания

Теория случайных процессов – это раздел математической науки, который изучает закономерности случайных явлений в динамике их развития.

Определение случайного процесса и его характеристики

Случайным процессом называется процесс, значение которого при любом значении аргумента является случайной величиной.

Реализацией случайного процесса называется детерминированная функция в которую преобразуется случайный процесс вследствие испытания, то есть его траектория.

Количество реализаций определенного случайного процесса изображено на рис. 4.1. Пусть сечение процесса при данном является непрерывной случайной величиной. Тогда случайный процесс при данном определяется плотностью вероятности

Очевидно, что плотность вероятности не является исчерпывающей задачей случайного процесса поскольку она не выражает зависимости между его сечениями в разные моменты времени.

Случайный процесс представляет собой совокупность всех сечений при всех возможных значениях поэтому для его задания необходимо рассматривать многомерную случайную величину образованную из всех сечений этого процесса.

Таких сечений бесконечно много, но для задания случайного процесса удается ограничиться сравнительно небольшим количеством сечений.

Случайный процесс имеет порядок если он полностью определяется плотностью общего распределения произвольных сечений процесса, то есть плотностью -мерной случайной величины где – сечение случайного процесса в момент времени

Случайный процесс может быть задан числовыми характеристиками.

Математическим ожиданием случайного процесса называется детерминированная функция которая при любом значении переменной равна математическому ожиданию соответствующего сечения случайного процесса то есть

Дисперсией случайного процесса называется детерминированная функция которая при любом значении переменной равна дисперсии соответствующего сечения случайного процесса то есть

Средним квадратическим отклонением случайного процесса называется арифметическое значение квадратного корня из его дисперсии, то есть

Математическое ожидание случайного процесса характеризует среднюю траекторию всех возможных его реализаций, а его дисперсия или среднее квадратическое отклонение – разброс реализаций относительно средней траектории.

Корреляционной функцией случайного процесса называется детерминированная функция

двух переменных и которая для каждой пары переменных и равна ковариации соответствующих сечений и случайного процесса.

Корреляционная функция характеризует не только степень близости линейной зависимости между двумя сечениями, а и разброс этих сечений относительно математического ожидания

Поэтому рассматривается также нормированная корреляционная функция случайного процесса.

Нормированной корреляционной функцией случайного процесса называется функция

Пример. Случайный процесс определяется формулой где – случайная величина. Найти основные характеристики этого процесса, если

Решение. Согласно свойствам математического ожидания и дисперсии получим:

Находим далее корреляционную функцию

а также нормированную корреляционную функцию

Случайные процессы можно классифицировать в зависимости от того, плавно или скачкообразно изменяются состояния системы, в которой они происходят, конечное или бесконечное множество этих состояний. Среди случайных процессов особое место занимают марковские случайные процессы, которые составляют основу теории массового обслуживания.

Основные понятия теории массового обслуживания

На практике часто приходится сталкиваться с системами, предназначенными для многоразового использования во время решения однотипных задач. Процессы, которые при этом происходят, называются процессами обслуживания, а соответствующие системы – системами массового обслуживания (СМО).

Примерами таких систем являются телефонные системы, ремонтные мастерские, вычислительные комплексы, кассы, где продаются железнодорожные или авиабилеты, магазины, парикмахерские и т.п.

Каждая МСО состоит из определенного количества обслуживаемых единиц (приборов, пунктов, станций), которые будем называть каналами обслуживания. Каналами могут быть линии связи, рабочие точки, вычислительные машины, продавцы и т.п. По количеству каналов СМО делятся на одно- и многоканальные.

Заявки поступают в СМО конечно нерегулярно, а случайно, образуя так называемый случайный поток заявок (ссылок). Обслуживание заявок также длится в течение определенного случайного времени. Учитывая случайность потока заявок и время обслуживания, СМО загружаются неравномерно: в определенные периоды накапливается очень много заявок (они или стают в очередь, или оставляют СМО не обслуженными), в другие периоды СМО работает с малой загрузкой или простаивает.

Предметом теории массового обслуживания является построение математических моделей, которые связывают заданные условия работы СМО с показателями ее эффективности, которые описывают способность этой системы обрабатывать потоки заявок.

Показателями эффективности СМО являются:

• – среднее количество заявок, которые она обслуживает за единицу времени;
• – среднее количество заявок в очереди;
• – среднее время ожидания обслуживания;
• – вероятность отказа в обслуживании без ожидания;
• – вероятность того, что количество заявок в очереди превышает определенное значение и т.д.

СМО делятся на два основных класса: СМО с отказами и СМО с ожиданием (очередью).

В СМО с отказами заявка, которая поступила в момент, когда все каналы были заняты, получив отказ, оставляет СМО и в дальнейшем процессе обслуживания не участвует.

В СМО с ожиданием заявка, которая поступает в момент, когда все каналы заняты, не оставляет систему, а становится в очередь на обслуживание.

Процесс работы СМО представляет собой случайный процесс.

Процесс называется процессом с дискретными состояниями, если его возможные состояния можно заранее пересчитать, а переход системы от одного к другому происходит мгновенно (скачкообразно). Процесс называется процессом с непрерывным временем, если моменты возможных переходов системы из одного состояния в другое не фиксированы заранее, а случайные.

Процесс функционирования СМО представляет собой случайный процесс с дискретными состояниями и непрерывным временем.

Математический анализ работы СМО существенно упрощается, если процесс этой работы – марковский.

Понятие марковского процесса

Случайный процесс называется марковским, если для любого момента времени вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент и не зависят от того, когда и как система приняла это состояние.

Пример. Система – счетчик в такси. Состояние системы в момент характеризуется количеством километров, пройденных автомобилем до данного момента. Пусть в момент счетчик показывает Вероятность того, что в момент счетчик будет показывать то или иное количество километров зависит от но не зависит от того, в какие моменты времени изменялись показатели счетчика до момента

Некоторые процессы можно приблизительно считать марковскими.

Пример. Система – группа шахматистов. Состояние системы характеризуется количеством фигур противника, которые остались на доске до момента Вероятность того, что в момент материальное преимущество будет на стороне одного из противников, зависит, прежде всего от того, в каком состоянии находится система в данный момент а не от того, когда и в какой последовательности исчезали фигуры с доски до момента

Анализируя случайный процессы с дискретными состояниями, удобно пользоваться геометрической схемой – так называемым графом состояний Обычно состояния системы изображают прямоугольниками (кругами), а возможные переходы от одного состояния к другому – стрелками, которые соединяют состояния.

Пример. Построить граф состояний такого случайного процесса: прибор состоит из двух узлов, каждый из которых в случайный момент времени может выйти из строя, после чего немедленно начинается ремонт узла, который длится в течение заранее неизвестного случайного времени.

Решение. Возможные состояния системы: – оба узла исправны; – первый узел ремонтируется, а второй исправный; второй узел ремонтируется, а первый исправный; – оба узла ремонтируются.

Граф системы приведен на рис. 4.2.

Стрелка, направленная из до означает переход системы в момент отказа первого узла; стрелка из до – переход в момент окончания ремонта этого узла. Стрелки из до нет, поскольку допускается, что узлы выходят из строя независимо друг от друга.

Для математического описания марковского случайного процесса с дискретными состояниями и непрерывным временем, которое происходит в СМО, рассмотрим одно из важных понятий теории вероятностей – понятие потока событий.

Простейший поток событий

Потоком событий называется последовательность событий, которые происходят один за другим в случайный момент времени Например, поток заявок, поступающий на предприятие бытового обслуживания, поток вызовов на телефонной станции, поток отказов (сбоев) во время работы на ЭВМ и т.д. Среднее количество событий, которые происходят за единицу времени, называется интенсивностью потока.

Поток называется простейшим, если он имеет такие свойства:

1) стационарность – вероятность того, что за некоторый промежуток времени произойдет то или иное количество событий, зависит только от длины промежутка и не зависит от начала его отсчета, то есть интенсивность потока постоянная;

2) отсутствие последействия – вероятность наступления некоторого количества событий в произвольном промежутке времени не зависит от того, какое количество событий произошло до начала этого промежутка;

3) ординарность – вероятность наступления двух и более событий за малый промежуток времени существенно меньше, чем вероятность того, что произойдет одно событие.

Если поток событий простейший, то вероятность того, что за промежуток времени событие наступит раз, определяется формулой: где – интенсивность потока. Эта формула отражает все свойства простейшего потока, а следовательно, является его математической моделью.

Пример. Среднее количество заявок, поступающих на комбинат бытового обслуживания за 1 час равно 4. Найти вероятность того, что за 3 часа поступит: 1) 6 заявок; 2) менее 6 заявок; 3) не менее 6 заявок.

Решение. Пусть событие – “поступление одной заявки”. Поток заявок простейший. Поэтому для решения задачи используем приведенную только что формулу, в которой Вычислим соответствующие вероятности:

Уравнения Колмогорова. Предельные вероятности состояний

Вероятностью состояния называется вероятность того, что в момент система будет находиться в состоянии

Очевидно, что для любого момента сумма вероятностей состояний равна 1:

Правило построений уравнений Колмогорова. В левой части каждого из уравнений должна быть производная вероятности состояния. В правой части = сумма произведений вероятностей всех состояний (из которых происходим переход в данное состояние) на интенсивности соответствующих потоков событий минус суммарная интенсивность всех потоков, которые выводят систему из данного состояния, умноженная на вероятность этого состояния.

Например, для системы которая имеет четыре состояния система дифференцированных уравнений Колмогорова для вероятностей состояний принимает такой вид:

В системе (2) независимых уравнений на одно меньше от общего количества уравнений. Поэтому для решения системы необходимо прибавит уравнений (1) при

Особенность решения дифференциальных уравнений вообще состоит в том, что нужно задавать так называемые начальные условия, в данном случае – вероятности состояний системы в начальный момент Так, систему (2) должны решать при условии, что в начальный момент оба узла исправны и система находилась в состоянии то есть при начальных условиях

Уравнения Колмогорова дают возможность находить все вероятности состояний как функции времени. Особый интерес представляет вероятности системы в предельном стационарном режиме, то есть при которые называются предельными вероятностями состояний.

В теории случайных процессов доказано, что количество состояний системы конечное и из каждого из них можно перейти к любому другому состоянию, то предельные вероятности существуют.

Предельная вероятность состояния имеет такое содержание: она показывает среднюю относительную продолжительность пребывания системы в этом состоянии. Например, если предельная вероятность состояния составляет то это означает, что в среднем половину времен системы находится в состоянии

Пример 1. Найти предельные вероятности для системы из последнего примера, граф состояний которой приведен на рис. 4.2. При

Решение. Система алгебраических уравнений, которая описывает стационарный режим для данной системы, принадлежит к виду (1):

Решая эту систему уравнений, получаем Следовательно, в предельном стационарном режиме система в среднем 40% времени находится в состоянии 20% – в состоянии 27% – в состоянии 13% – в состоянии

Пример 2. Найти прибыль от эксплуатации в стационаром режиме системы когда известно, что за единицу времени исправная работа первого и второго узлов приносит доход, который составляет соответственно 10 и 6 ус. ед., а их ремонт требует расходов, которые составляют соответственно 4 и 2 ус. ед.

Оценить экономическую эффективность уменьшения вдвое средней продолжительности ремонта каждого из этих узлов, если в этом случае придется вдвое увеличить расходы на ремонт.

Решение. Из примера 1 следует, что в среднем первый узел исправен в течение части времени, которая составляет а второй узел – в течение части В этом случае первый узел находится в ремонте в среднем часть времени, равной а второй – Поэтому средняя прибыль за единицу времени от эксплуатации системы (разница между доходом и расходами) будет такой:

Прибыль = (ус. ед.).

Уменьшение вдвое среднего времени ремонта каждого из узлов согласно с будет означать увеличение вдвое интенсивности потока “окончания ремонта” каждого узла. Следовательно, в этом случае и система линейных алгебраических уравнений (1) принимает вид:

Решая эту системы, получаем

Поскольку то расходы на ремонт первого и второго узла будут составлять соответственно 8 и 4 ус. ед. Отсюда получим среднюю прибыль за единицу времени:

(Прибыль) (ус. ед.)

(Прибыль) больше, чем Прибыль (приблизительно – на 2%), поэтому экономическая целесообразность сокращения срока ремонта узлов очевидна.

Лекции:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

[spoiler title=”источники:”]

http://lektsii.org/7-1858.html

http://natalibrilenova.ru/teoriya-sluchajnyih-protsessov-i-teoriya-massovogo-obsluzhivaniya/

[/spoiler]

1