Функция общих издержек имеет вид:
TC = 3Q2 + 5Q + 20
Определить функции:
а) постоянных и переменных издержек;
б) средних постоянных, переменных и общих (совокупных) издержек;
в) предельных издержек;
Решение:
а) Общие издержки TC состоят из постоянных FC, которые не зависят от объёма выпускаемой продукции, и переменных издержек VC, которые связаны с объёмом производства Q.
Рассмотрим функцию общих издержек:
TC = 3Q2 + 5Q + 20
В этой функции, слагаемые содержащие переменную Q и есть переменные издержки, то есть функция переменных издержек имеет вид:
VC = 3Q2 + 5Q
, а постоянные издержки соответственно равны:
FC = 20.
б) Функция средних постоянных издержек AFC будет равна отношению постоянных издержек FC к объёму выпущенной продукции Q:
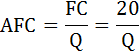
Функция средних переменных издержек AVC будет равна отношению переменных издержек VC к объёму выпущенной продукции Q:
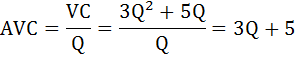
Функция средних общих издержек ATC (или АС) будет равна отношению общих издержек TC к объёму выпущенной продукции Q:
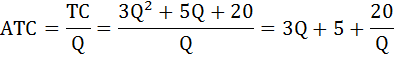
в) Функция предельных издержек MC получается путём дифференцирования функции совокупных издержек:
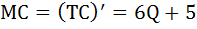
Не трудно заметить, что тот же результат получится, если вместо функции общих издержек TC взять функцию переменных затрат VC:
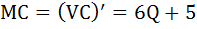
6.2.4. Средние и предельные издержки. Технологический оптимум краткосрочного периода
Мощным инструментом экономического анализа является изучение средних издержек, или издержек в расчете на единицу продукции.
Средние постоянные издержки
Средние постоянные издержки (AFC) характеризуются затратами постоянного ресурса, с которыми в среднем производится единица продукции. AFC определяются отношением постоянных издержек TFC и величиной выработки Q:

Между средними постоянными издержками AFC и средним продуктом по постоянному ресурсу 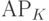 имеется обратная зависимость:
имеется обратная зависимость:
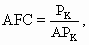
где 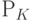 – цена единицы постоянного ресурса.
– цена единицы постоянного ресурса.
Действительно,

где K – количество постоянного ресурса.
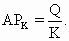
Таким образом,
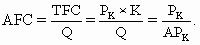
График AFC представляет собой гиперболу, асимптотически приближающуюся к осям абсцисс и ординат (
рис.
6.9). Действительно

При увеличении объема производства AFC снижаются. Это явление называют распределением накладных расходов. По понятным соображениям для фирмы оно служит мощным стимулом увеличения производства.
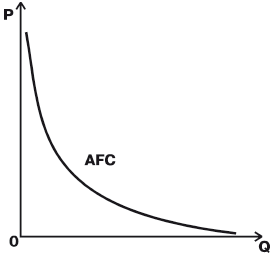
Рис.
6.9.
Средние постоянные издержки
Средние переменные издержки (AVC) характеризуют затраты переменного ресурса, с которыми в среднем производится единица продукции. AVC определяются отношением переменных издержек TVC и величины выработки Q.
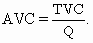
Между средними переменными издержками AVC и средним продуктом по переменному ресурсу 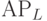 также имеется обратная зависимость.
также имеется обратная зависимость.

где  – цена единицы переменного ресурса.
– цена единицы переменного ресурса.
Действительно

где L – количество переменного ресурса.
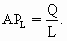
Таким образом,
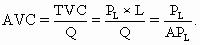
Динамика средних переменных издержек обусловлена изменением отдачи от переменного ресурса. Обратная взаимосвязь средних переменных издержек AVC и среднего продукта по переменному ресурсу 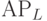 позволяет утверждать следующее. Если
позволяет утверждать следующее. Если 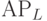 растет, AVC должны падать; если
растет, AVC должны падать; если 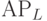 снижается, AVC увеличиваются. Таким образом, в случае непосредственной смены возрастающей отдачи убывающей график функции AVC сначала убывает, а затем, достигая минимума в точке, соответствующей максимуму
снижается, AVC увеличиваются. Таким образом, в случае непосредственной смены возрастающей отдачи убывающей график функции AVC сначала убывает, а затем, достигая минимума в точке, соответствующей максимуму 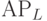 , начинает возрастать.
, начинает возрастать.
Если для производства свойственна зона постоянной отдачи, то в этой зоне график AVC горизонтален (
рис.
6.10).
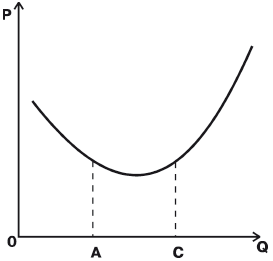
Рис.
6.10.
Средние переменные издержки
Средние общие (суммарные) издержки
Средние общие (суммарные) издержки (АТС) характеризуют затраты переменного и постоянного ресурсов, с которыми в среднем производится единица продукции. АТС определяется отношением валовых издержек ТС и величины выработки Q:

Так как ТС = TFC + TVC,

Величина средних общих издержек представляет большой интерес для предпринимателя. Ведь, сравнивая его с ценой единицы выпускаемой продукции, он может оценить свою прибыль от каждого выпущенного товара.
В динамике средних валовых издержек АТС проявляются особенности поведения как средних постоянных, так и средних переменных издержек. Это не случайно, ведь АТС = AFC + AVC. График АТС, подобно графику АVC, сначала убывает, а затем возрастает, т.е. кривая АТС имеет U-образную форму. Причем по мере роста выработки кривая АТС сближается с кривой AVC. Действительно, AFC падают с ростом объема производства, расстояние между АТС и AVC становится все меньше (
рис.
6.11). Заметим, что минимальное значение АТС приходится на точку с бо2льшим объемом производства, нежели для минимального значения AVC. Это обусловлено следующими обстоятельствами: вначале рост AVC компенсируется падением AFC, в результате АТС продолжают убывать. Однако при дальнейшем росте производства увеличение AVC уже перекрывает снижение AFC, поэтому АТС начинает возрастать.
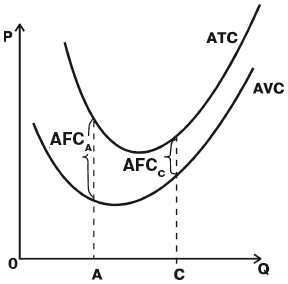
Рис.
6.11.
Средние общие издержки
Предельные издержки
Предельные издержки (МС) представляют собой изменение валовых издержек, связанное с производством дополнительной единицы продукции.
Различают дискретные предельные издержки и непрерывные предельные издержки. Дискретные предельные издержки определяют как разность между суммарными издержками при производстве n единиц продукта и суммарными издержками при производстве n – 1 единиц продукта. Непрерывные переменные издержки определяются как производная функции суммарных издержек.
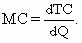
Так как ТС = ТFC + TVC, а TFC = const, то


То есть предельные издержки можно определить и как производную функции переменных издержек.
Таким образом, предельные издержки характеризуют скорость роста суммарных (переменных) издержек при увеличении объема производства.
Между переменными издержками МС и предельным продуктом МР имеется обратная зависимость:

Для предпринимателя значение предельных издержек служит очень важным индикатором при выборе наиболее выгодного объема производства. Ведь они показывают величину затрат, которые фирма понесет, если увеличит выработку на единицу, или, наоборот, от которых будет избавлена, если откажется от выпуска этой единицы.
Поведение предельных издержек МС обусловлено изменением отдачи от переменного ресурса. На участке повышающейся отдачи и роста предельного продукта МС убывают, на участке убывающей отдачи и снижения МР предельные издержки растут. Таким образом, график функции МС сначала убывает, а затем, достигая минимума в точке, соответствующей максимуму МР, начинает возрастать.
Если для производства свойственна зона постоянной отдачи, то на графике МС в этой зоне (так же как и на графике МР) имеется более или менее выраженный горизонтальный участок (
рис.
6.12).
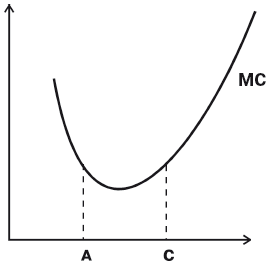
Рис.
6.12.
Предельные издержки
Связь средних и предельных издержек
Взаимное расположение графиков МС и AVC имеет такую закономерность: кривая МС пересекает кривую AVC в точке, соответствующей минимальному значению величины средних переменных издержек. Действительно, пока издержки производства дополнительной единицы продукции меньше средних переменных издержек предыдущей единицы, рост выпуска продукции будет снижать значения AVC. Если издержки дополнительной единицы выше средних переменных издержек производства предыдущей единицы, новые значения AVC будут увеличиваться. Таким образом, приближаясь к точке пересечения с МС, кривая АVC падает, а после ее прохождения – растет. Легко понять, что минимум AVC достигается в точке пересечения.
Подобные рассуждения, если их повторить применительно к средним общим издержкам, позволяют также утверждать, что кривая МС пересекает кривую АТС также в точке, соответствующей минимальному значению средних совокупных издержек (
рис.
6.13).
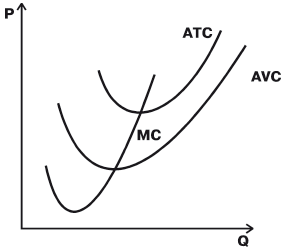
Рис.
6.13.
Связь предельных, средних переменных и средних общих издержек
Точка технологического оптимума
Объем производства, соответствующий минимальным средним совокупным издержкам, называется точкой технологического оптимума. Он достигается, когда пропорция переменного и постоянного ресурса оптимальна с технической стороны.
Заметим, что это не обязательно оптимальный размер выпуска с точки зрения экономических интересов фирмы. Позже мы убедимся, что очень часто максимальная прибыль достигается при совсем других объемах. Но одно несомненно: экономика тем более эффективна, чем ближе реальный выпуск продукции фирмами к точкам их технологического оптимума.

Содержание
- Формулы и функции
- Изменение затрат
- Изменение количества
- Как рассчитывается предельная стоимость?
- Расчет
- Решенные упражнения
- Пример 1
- Пример 2
- Ссылки
В предельная стоимость – это изменение общей стоимости производства, вызванное производством дополнительной позиции. То есть это стоимость производства еще одной единицы продукта. Цель анализа предельных затрат – определить, в какой момент организация может достичь экономии за счет масштаба.
На каждом уровне и периоде времени, который считается производственным, предельные затраты включают все затраты, которые меняются в зависимости от уровня производства, в то время как другие затраты, которые не меняются с производством, являются фиксированными и, следовательно, не имеют предельных затрат.

В экономической теории предельные издержки становятся важным фактором, потому что компания, стремящаяся максимизировать свою прибыль, будет производить до тех пор, пока предельные издержки не будут равны предельному доходу.
Типичные переменные затраты, включенные в расчет, включают оплату труда и материалов. Формула предельной стоимости может использоваться в финансовых моделях для оптимизации генерирования денежных потоков.
Формулы и функции
Если функция затрат (C) является непрерывной и дифференцируемой, предельные затраты (CM) являются первой производной этой функции затрат по отношению к произведенному количеству (Q):
CM (Q) = dC / dQ = изменение затрат / изменение количества.
Изменение затрат
На каждом уровне производства издержки производства могут увеличиваться или уменьшаться, особенно когда возникает необходимость произвести больший или меньший объем продукции.
Если изготовление дополнительных единиц требует найма одного или двух дополнительных рабочих и увеличивает стоимость закупки сырья, то общие затраты на производство изменятся.
Предельные издержки производства включают в себя все затраты, которые зависят от уровня производства. Например, если компании необходимо построить новый завод, чтобы производить больше товаров, стоимость строительства завода является предельной стоимостью.
Затраты на производство состоят из постоянных и переменных затрат. Переменные затраты относятся к затратам, необходимым для производства каждой единицы. С другой стороны, постоянные затраты относятся к общим затратам, которые распределяются между произведенными единицами.
Чтобы определить изменение затрат, производственные затраты, понесенные во время первого производственного цикла, вычитаются из производственных затрат, понесенных в следующей партии, когда производство увеличилось.
Изменение количества
Поскольку объем производства неизбежно будет увеличиваться или уменьшаться с каждым уровнем производства, задействованные количества достаточно значительны, чтобы оценить внесенные изменения.
Увеличение или уменьшение объема произведенных товаров приводит к стоимости произведенных товаров. Поэтому важно знать разницу.
Чтобы определить изменения в количестве, количество продуктов, произведенных в первом производственном цикле, вычитается из объема производства, произведенного в следующем производственном цикле.
Как рассчитывается предельная стоимость?
Расчет предельных затрат чаще используется производителями как средство достижения оптимального уровня производства. Производители изучают стоимость добавления еще одной единицы в свои производственные графики.
Расчет предельных затрат помогает бизнесу определить момент, когда увеличение количества произведенных товаров также приведет к увеличению средней стоимости.
По мере увеличения объема предельные затраты также могут увеличиваться, если бизнесу необходимо добавить оборудование, переехать на более крупный объект или если у него возникнут трудности с поиском поставщика, который может предоставить достаточно материалов.
Расчет
Если компания может произвести 200 единиц продукции общей стоимостью 2000 долларов США, а производство 201 единиц стоит 2020 долларов США, то средняя стоимость единицы будет составлять прибл. 10 долларов США (2020 долларов США / 201 = 10,05 доллара США), а предельная стоимость единицы 201 составит 20 долларов США.
Вот формула для расчета предельных затрат: разделите изменение общих затрат на изменение количества произведенных товаров. В приведенном выше примере изменение стоимости составляет 20 долларов США (2 020–2 000 долларов США), а изменение количества составляет 1 (201–200 долларов США). 20, разделенное на 1, равно 20.
На графике предельные издержки представляют собой кривую, имеющую тенденцию повторять U-образную форму. Издержки начинаются высокими до тех пор, пока производство не прекращается, даже когда фиксированные издержки покрываются.
Он остается на этом низком уровне в течение некоторого времени, а затем начинает расти, поскольку увеличение производства требует затрат денег на большее количество сотрудников, оборудование и т. Д.
Понимание предельной стоимости продукта помогает компании оценивать свою прибыльность и принимать решения, связанные с продуктом, включая ценообразование.
Решенные упражнения
Пример 1
Давайте рассмотрим производителя шляп. На каждую изготовленную шляпу нужно заплатить 0,75 доллара за пластик и ткань. Фабрика головных уборов несет постоянные расходы в размере 100 долларов в месяц.
Если в месяц производится 50 головных уборов, то на каждую шляпу приходится 2 доллара (100/50 долларов) постоянных затрат. В этом простом примере общая стоимость шляпы, включая пластик и ткань, составит 2,75 доллара (2,75 доллара = 0,75 доллара + (100/50)).
Однако, если объем производства увеличится и теперь будет производиться 100 головных уборов в месяц, то каждая шляпа будет нести 1 доллар фиксированных затрат, потому что постоянные затраты распределяются по произведенным единицам.
Общая стоимость шляпы упадет до 1,75 доллара (1,75 доллара = 0,75 доллара + (100/100)). В этой ситуации увеличение объема производства снижает предельные издержки.
Пример 2
Компания-производитель X занимается производством систем отопления. Существующее оборудование устарело и не соответствует вашим производственным потребностям, не укладывается в производственный график.
Дополнительное оборудование необходимо покупать или арендовать, чтобы поддерживать производство на прежнем уровне.
Следовательно, необходимо рассчитать предельную стоимость систем отопления, которые будут производиться с новым оборудованием, включая стоимость его приобретения.
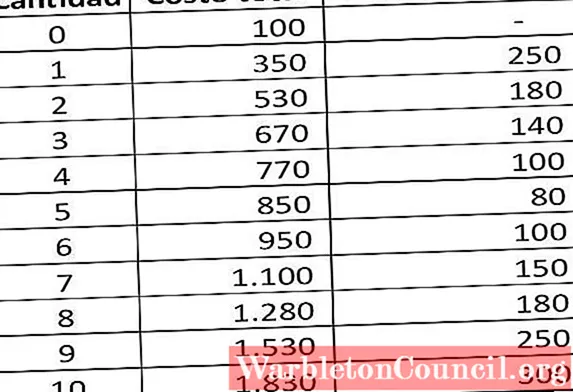
График, представляющий значения предельных затрат, указанных в таблице, выглядит следующим образом:
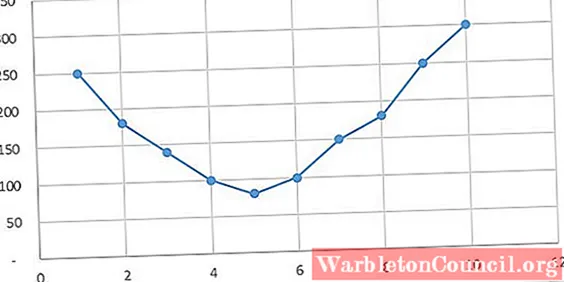
Можно видеть, что общие затраты увеличиваются с увеличением количества продукта, потому что требуется большее количество факторов производства.
Предельные издержки снижаются до определенного уровня производства (Количество = 5). Затем он продолжает расти вместе с производством.
В предельных затратах на изготовление дополнительной единицы систем отопления на каждом уровне производства необходимо учитывать внезапное увеличение количества сырья.
Если необходимо найти других поставщиков, предельные затраты могут увеличиться из-за более длинных расстояний и более высоких цен на сырье.
Ссылки
- Уилл Кентон (2018). Предельная себестоимость продукции. Взято с: investopedia.com
- Википедия, бесплатная энциклопедия (2019). Предельная стоимость. Взято с: en.wikipedia.org.
- CFI (2019). Формула предельной стоимости. Взято с: enterprisefinanceinstitute.com.
- Shopify (2019). Предельная стоимость. Взято с: shopify.com.
- Мой бухгалтерский курс (2019). Что такое предельная стоимость? Взято с: myaccountingcourse.com.
Задача №1. Расчёт экономической прибыли конкурентной фирмы
Фирма, находясь в условиях совершенной конкуренции, имеет следующую функцию общих затрат:
ТС = 140 + 10 × Q + 40 × Q2.
При каком выпуске прибыль фирмы достигнет максимума, если цена установилась на уровне 250 ден. ед.? Определить размер прибыли фирмы.
Будут ли в длительном периоде в эту отрасль стремиться войти новые фирмы?
Решение:
Наличие в составе общих затрат фиксированных (постоянных) затрат (FC = 140) свидетельствует о том, что речь идёт о краткосрочном периоде.
Найдём объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде имеет вид:
Р = МС = МR = AR.
Определим функцию предельных издержек фирмы: найдём производную общих издержек.
МС = (ТС)’ = 10 + 80 × Q.
Приравняем эту функцию к цене равной 250.
10 + 80 × Q = 250
80 × Q = 240
Q = 3
Вычислим прибыль фирмы при объёме выпуска равном 3 по формуле:
П = TR — TC = P × Q — TC = 250 × 3 — (140 + 10 × 3 + 40 × 32) = 220 ден. ед.
В долгосрочном периоде наличие неотрицательной экономической прибыли будет привлекать в отрасль новые фирмы.
Задача № 2. Определение рыночной цены и отраслевого выпуска продукции
В отрасли действуют 130 одинаковых фирм. Издержки производства каждой фирмы описываются функциями
ТС =Q3 — 36*Q2 + 384*Q,
где
Q — объём производства в тысячах штук. Найти рыночную цену и отраслевой выпуск продукции, при которых на конкурентном рынке устанавливается долгосрочное равновесие.
Решение:
В долгосрочном периоде на рынке совершенной конкуренции соблюдается равенство:
P = MC = MR = AR = minAC.
Найдём функцию средних издержек каждой фирмы по следующей формуле:
АС = ТС / Q = Q2 — 36*Q + 384
Далее необходимо найти минимум данной функции. Для этого определим производную функции АС и приравняем её к нулю.
2*Q — 36 = 0
Q = 18
AC(18) = 182 — 36*18 + 384 = 60
Так как Р = minAC в долгосрочном периоде, следовательно, рыночная цена равна Р = 60.
Найдём отраслевой выпуск. Так как каждая из фирм отрасли производит 18 тысяч штук продукции, значит 130 фирм произведут:
Qотр. = 18*130 = 2340 тысяч штук
Задача № 3. Определение рыночной цены в долгосрочном периоде
Конкурентная фирма находится в состоянии равновесия в долгосрочном периоде и имеет следующие затраты: TC = Q3 — 38*Q2 + 418*Q. Определите цену на этом рынке в долгосрочном периоде.
Решение:
В долгосрочном периоде цена в условиях соверешенной конкуренции устанавливается на уровне минимума средних затрат. При этом фирма совершенный конкурент получает нулевую экономическую прибыль.
Условие равновесия на рынке будет иметь вид:
Р = МС = МR = AR = min AC
Найдём средние затраты фирмы по формуле:
АС = ТС / Q = Q2 — 38*Q + 418
Определим минимум функции средних затрат. Для нахождения экстремума функции приравняем к нулю её производную:
АС’ = 2*Q — 38
2*Q — 38 = 0
Q = 19
При выпуске Q = 19 средние затраты будут равны:
АС = 192 — 38*19 + 418 = 57.
Таким образом, цена в долгосрочном периоде будет равна 57.
Задача № 4. Расчёт рыночной цены, при которой фирма уйдёт с рынка
Общие затраты фирмы, действующей на рынке совершенной конкуренции, составляют
0,5*Q3 — 15*Q2 + 300*Q + 250 000.
При какой цене фирме становится невыгодным работать на этом рынке в краткосрочном периоде?
Решение:
В краткосрочном периоде фирма совершенный конкурент уйдёт с рынка, если цена окажется меньше минимума её средних переменных издержек: Р < min AVC.
Найдём переменные издержки фирмы, а точнее запишем функцию переменных издержек:
VC = 0,5*Q3 — 15*Q2 + 300*Q
Теперь определим функцию средних переменных издержек по формуле:
АVC = VC / Q = 0,5*Q2 — 15*Q + 300
Найдём экстремум этой функции, приравняв к нулю её производную.
Q — 15 = 0
Q = 15.
При объёме производства Q = 15 средние переменные издержки будут минимальными.
АVC(15) = 0,5*152 — 15*15 + 300 = 187,5
Это так называемая точка закрытия фирмы. Фирма совершенный конкурент уйдёт с рынка, если цена упадёт ниже этой точки в краткосрочном периоде.
При Р < 187,5 фирме становится невыгодным работать на этом рынке в краткосрочном периоде.
Задача № 5. Расчёт объёма выпуска, максимизирующего прибыль фирмы
Функция издержек фирмы ТС = Q2 — Q + 3, где Q — объём производства. Рыночная цена на продукцию фирмы составляет 7 и не зависит от объёма продаж этой фирмы. Найти объём выпуска продукции, максимизирующий прибыль фирмы.
Решение:
По условию рыночная цена не зависит от объёма продаж этой фирмы, это говорит о том, что фирма функционирует в условиях совершенной конкуренции.
Максимум прибыли фирмы действующей в условиях совершенной конкуренции определяется тождеством: Р = МС.
Найдём предельные издержки фирмы по формуле:
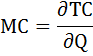
МС =(TC)’= 2Q — 1
Найдём объём выпуска продукции, максимизирующий прибыль фирмы.
Цена по условию равна Р = 7.
Р = МС
7 = 2Q — 1
Q = 4
Задача №6. Расчёт объёма производства в краткосрочном периоде
В отрасли совершенной конкуренции установилась цена Р = 30. В эту отрасль входит фирма с общими издержками ТС = 1/2 * Q2 + 10 * Q + 100. Найти её объём производства в краткосрочном периоде.
Решение:
Фирма выберет такой объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли: МС = MR.
На рынке совершенной конкуренции предельный доход равен цене: MR = P.
Отсюда следует, что цена равна предельным издержкам: P = MC.
Найдём предельные издержки. Предельные издержки в непрерывном случае (т.е. когда общие издержки заданы функцией) равны производной от функции общих издержек:
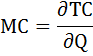
Функция предельных издержек будет иметь вид:
МС = Q + 10
P = MC
30 = Q + 10
Q = 20 — оптимальный объём производства фирмы.
Задача № 7. Расчёт рыночной цены и объёма выпуска на конкурентном рынке
Конкурентная фирма имеет общие затраты
ТС = 800 + 40*Q + 2*Q2
Она получает в краткосрочном периоде максимально возможную прибыль, равную 1000.
Определить цену на рынке и объём выпуска данной фирмы.
Решение:
Формула прибыли фирмы имеет вид:
П = TR — TC = P*Q — TC
По условию максимально возможная прибыль равна 1000.
P*Q — (800 + 40*Q + 2*Q2) = 1000
Найдём цену.
Условие максимизации прибыли на рынке совершенной конкуренции имеет вид:
Р = МС = MR = AR
Так как Р = МС, а МС = ТС’ = 40 + 4*Q, следовательно, Р = 40 + 4*Q. Подставим это выражение в формулу прибыли и получим:
(40 + 4*Q)*Q — (800 + 40*Q + 2*Q2) = 1000
40*Q + 4*Q2 — 800 — 40*Q — 2*Q2 — 1000 = 0
2*Q2 = 1800
Q2 = 900
Q1,2 = ±30
Так как отрицательный корень экономического содержания не имеет, берём Q = 30.
Тогда цена будет равна:
Р = 40 + 4*30 = 160
Задача № 8. Расчёт рыночной цены на конкурентном рынке в долгосрочном периоде
Допустим, общие затраты фирмы на выпуск Q единиц продукции составляют:
Q3 – 16*Q2 + 400*Q.
а) При каком значении Q средние затраты достигают минимума?
б) При какой цене этой фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде?
Решение:
а) Найдём функцию средних затрат по формуле:
АС = ТС / Q = (Q3 – 16*Q2 + 400*Q) / Q = Q2 – 16*Q + 400
Определим минимум функции. Для нахождения экстремума функции необходимо найти её производную и приравнять её к нулю.
AC’ =(Q2 – 16*Q + 400)’ = 2*Q – 16
2*Q – 16 = 0
Q = 8
При Q = 8 средние затраты достигают минимума.
б) В долгосрочном периоде фирме становится выгодным участвовать в совершенной конкуренции, если Р ≥ АС. При этом фирма имеет нулевую прибыль. И выполняется условие:
Р = МС = MR = minАС
Рассчитаем minAC. Подставим Q = 8 в функцию средних затрат:
minAC(Q=8) = 82 – 16*8 + 400 = 336
Итак, при цене Р ≥ 336 фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде.
Задача № 9. Расчёт цены и объёма производства, максимизирующих прибыль
Спрос на продукцию конкурентной отрасли:
Qd = 55 – P
Предложение:
Qs = 2P – 5
Если у одной из фирм отрасли восходящий участок кривой предельных издержек:
МС = 3Q + 5
При каких цене и объёме производства фирма максимизирует прибыль?
Решение:
Найдём цену равновесия. Приравняем функцию спроса и предложения:
Qd = Qs
55 – P = 2P – 5
3 * Р = 60
Р = 20 – цена рыночного равновесия, то есть цена по которой фирмы будут продавать свою продукцию.
Фирма в условиях совершенной конкуренции получает максимум прибыли при условии равенства цены и предельных затрат.
МС = Р
3Q + 5 = 20
Q = 5 – объём производства, при котором прибыль фирмы будет максимальной.
Задача №10. Расчёт рыночной цены и объёма выпуска на конкурентном рынке
Конкурентная фирма имеет предельные затраты:
МС = 30 + 2 × Q
при фиксированных затратах, равных 500 денежным единицам.
Она получает в краткосрочном периоде максимально возможную прибыль, равную 1100 денежным единицам.
Определить цену на рынке и объём выпуска данной фирмы.
Решение:
Формула прибыли имеет вид:
П = TR – TC = P*Q – TC
Определим функцию общих затрат. Так как функция предельных затрат это производная функции общих затрат, следовательно, функцию общих затрат можно определить как первообразную от функции предельных затрат.
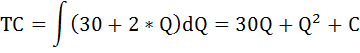
где
С – константа, равная величине фиксированных затрат, которые по условию равны 500.
Таким образом функция общих затрат имеет вид:
ТС = Q2 +30*Q + 500
Теперь запишем условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде:
Р = МС = MR = AR
Воспользуемся тем, что:
Р = МС
По условию задачи:
МС = 30 + 2 × Q, то есть Р = 30 + 2 * Q
Подставим это выражение, а так же функцию общих затрат в формулу прибыли и получим уравнение с одной неизвестной.
(30 + 2 * Q) * Q – (Q2 +30*Q + 500) = 1100
Q2 = 1600
Q = ± 40
Так как отрицательное значение Q экономического смысла не имеет, следовательно, объём выпуска данной фирмы Q = 40.
Тогда рыночная цена будет равна:
Р = 30 + 2 * 40 = 110.
