Двойные интегралы используют в математике, механике, физике. С его помощью можно решить огромное количество непростых задач. Ниже приведено 10 примеров на двойные и тройные интегралы, которые в значительной степени облегчат подготовку к контрольной работе или экзамену. Примеры взяты из индивидуальной работы по высшей математики.
ВАРИАНТ – 12
Двойной интеграл
ЗАДАНИЕ 1.18 Изменить порядок интегрирования в двойном интеграле:
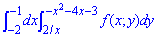
Решение: Сначала записываем область интегрирования, которая ограничена границами
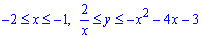
где y=2/x – гипербола.
y=-x2-4x-3 – парабола с вершиной в точке S (-2;1), ветками вниз.
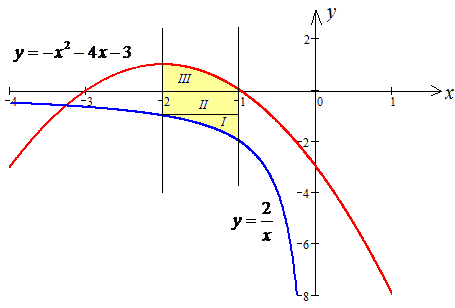
Чтобы знать, как расставить пределы интегрирования при изменении порядка интегрирования изобразим область интегрирования на плоскости
 Выражаем полученные функции через переменную y:
Выражаем полученные функции через переменную y:
y=2/x, отсюда x=2/y; y=-x2-4x-3, отсюда 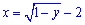 , перед радикалом стоит знак “+” поскольку часть параболы находится в правой (положительной по x=-2) части полуплоскости.
, перед радикалом стоит знак “+” поскольку часть параболы находится в правой (положительной по x=-2) части полуплоскости.
Из рисунка видим, что при изменении порядка интегрирования область необходимо разделить на три части: D=D1+D2+D3.
Расставим пределы интегрирования в каждой области:
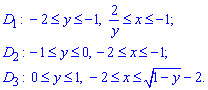
Изменяем порядок интегрирования функции
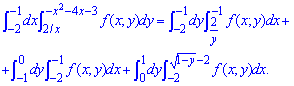 Как видите ничего сложного нет, главное представлять график функции и иметь точки их пересечения – пределы интегрирования.
Как видите ничего сложного нет, главное представлять график функции и иметь точки их пересечения – пределы интегрирования.
ЗАДАНИЕ 2.19 Найти площадь плоской фигуры, заданной следующими условиями, : y=2x, y=5, 2x-2y+3=0.
Решение: Прежде всего выполняем построение всех кривых, чтобы видеть как будут изменяться пределы интегрирования
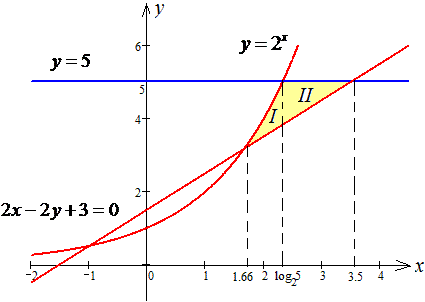 Дальше найдем точки пересечения графиков заданных функций :
Дальше найдем точки пересечения графиков заданных функций :
1 и 2
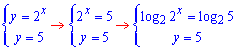
отсюда 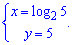
Дальше точки пересечения 2 и 3 функций
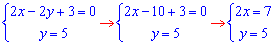
отсюда 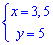
Напоследок пересечение 1 и 3 ф-й
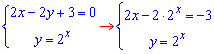
отсюда 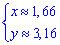
Заданную область будем разбивать на две области: D=D1+D2.
Расставим пределы для каждой из областей:
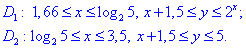
Через двойной интеграл находим площадь фигуры которая ограничена заданными кривыми, :
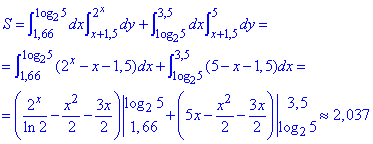 Функции не тяжелые для интегрирования, поэтому в предпоследнем выражении подставьте пределы самостоятельно.
Функции не тяжелые для интегрирования, поэтому в предпоследнем выражении подставьте пределы самостоятельно.
При округлении площадь криволинейной трапеции равна 2,037 единиц квадратных.
ЗАДАНИЕ 3.20 Найти двойной интеграл 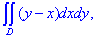 по области D, ограниченной указанными линиями: D: y=x2-1, y=3.
по области D, ограниченной указанными линиями: D: y=x2-1, y=3.
Решение: Найдем точки пересечения графиков заданных функций: y=x2-1 и y=3:
3=x2-1, x2-4=0, (x-2)(x+2)=0, x=-2; x=2.
Параболу и прямую изобразим графически
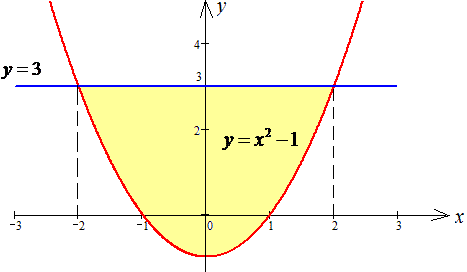 Расставим пределы интегрирования в заданной области D:
Расставим пределы интегрирования в заданной области D:
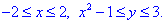
Вычислим двойной интеграл по области которая ограничена параболой и прямой:
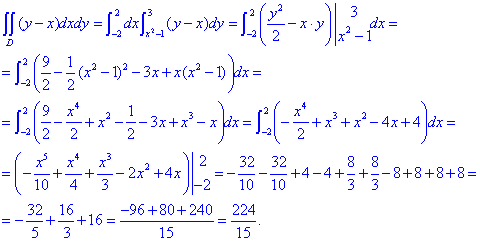 Определенный интеграл равен I=224/15=14,9 (3).
Определенный интеграл равен I=224/15=14,9 (3).
ЗАДАНИЕ 4.21 Найти двойной интеграл, используя полярные координаты:
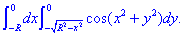
Решение: Построим область интегрирования, которая ограничена кривыми
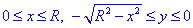
где 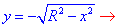 y=R2– x2, x2+y2=R2
y=R2– x2, x2+y2=R2
Получили круг с центром в точке O (0;0) и радиусом R (нижняя половина).
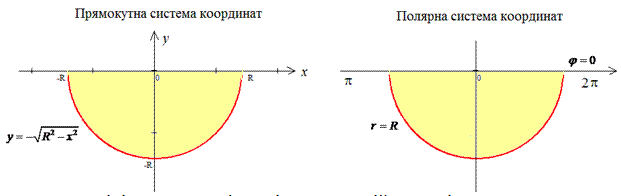 Используя замену переменных
Используя замену переменных
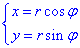
перейдем к полярной системе координат (СК).
При этом подынтегральную функцию следует умножить на якобиан перехода, который находим через определитель из производных:
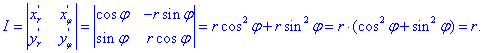
Перепишем подинтегральную функцию в полярной СК :
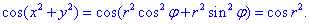
Пределы интегрирования при переходе к полярной системе координат изменятся на следующие:
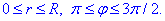
Вычислим двойной интеграл:
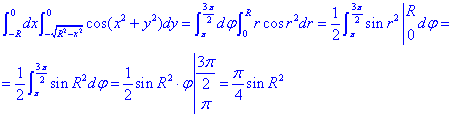 Он равен I=Pi/4*sin (R2).
Он равен I=Pi/4*sin (R2).
ЗАДАНИЕ 5.22 Вычислить площадь области D, ограниченной указанными линиями: D: x3=3y, y2=3x.
Решение: Найдем точку пересечения двух графиков 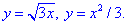 :
: 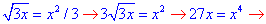 x1=0, y1=0; x2=3, y2=3.
x1=0, y1=0; x2=3, y2=3.
Графики кривой в декартовой системе координат имеет вид
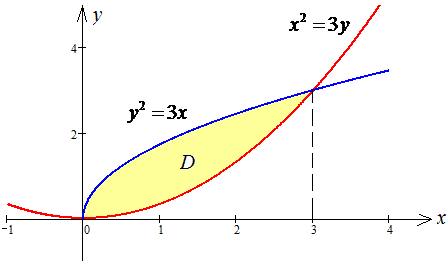 Расставим пределы интегрирования в области D:
Расставим пределы интегрирования в области D:
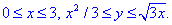
Найдем площадь криволинейной трапеции которая ограничена указанными линиями:
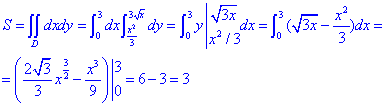 Площадь равна 3 единицы квадратные.
Площадь равна 3 единицы квадратные.
ЗАДАНИЕ 6.23 Используя двойной интеграл, вычислить, перейдя к полярным координатам, площадь плоской фигуры : (x2+y2)3=4a2xy (x2-y2).
Решение: Сначала построим чотирёх лепесток
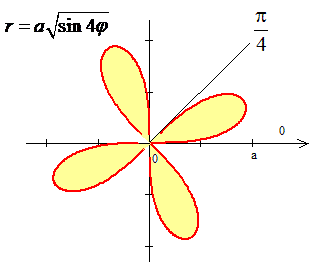
Перейдем к полярной системе координат:
Якобиан перехода из предыдущих примеров равен I=r.
Найдем пределы интегрирования в новой системе координат
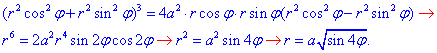
Переменные приобретают значение:
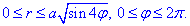
Расставляем пределы интегрирования в двойном интеграле, таким образом найдем четверть площади плоской фигуры.
Дальше результат умножим на 4:
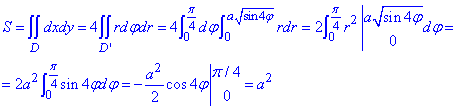 Площадь равна S=a2 единиц квадратных.
Площадь равна S=a2 единиц квадратных.
Внимательно проанализируйте как определять пределы интегрирования. Это тяжелее всего, что может быть в подобных задачах.
Как вычислить определенный интеграл, как правило, должны знать все студенты. Здесь лишь расширяется его приложение.
Тройной интеграл
ЗАДАНИЕ 8.25 Расставить пределы интегрирования в тройном интеграле 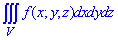 , если область V ограничена указанными поверхностями: V: x=2
, если область V ограничена указанными поверхностями: V: x=2 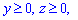 y=3x, z=4 (x2+y2).
y=3x, z=4 (x2+y2).
Нарисовать область интегрирования.
Решение: Уравнение поверхности в пространстве z=4 (x2+y2) – эллиптический параболоид.
График параболоида и проекция в декартовую плоскость тела имеют вид
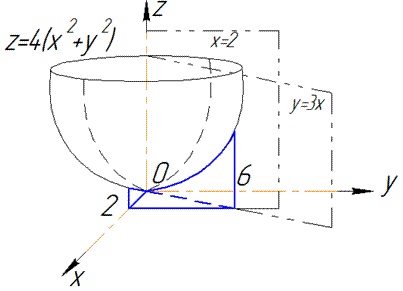
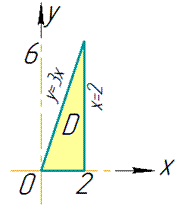 Пределы интегрирования расставим следующим образом:
Пределы интегрирования расставим следующим образом:
V: 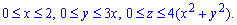
Расставляем пределы интегрирования в соответствии с областью
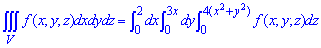
ЗАДАНИЕ 9.6 Вычислить тройные интегралы:
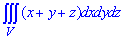
где V: 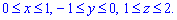
Решение: Выполним построение области интегрирования
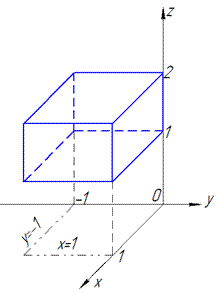 Заданная область V является параллелепипедом, поэтому без трудностей расставляем пределы интегрирования и от внутреннего к внешнему находим интеграл
Заданная область V является параллелепипедом, поэтому без трудностей расставляем пределы интегрирования и от внутреннего к внешнему находим интеграл
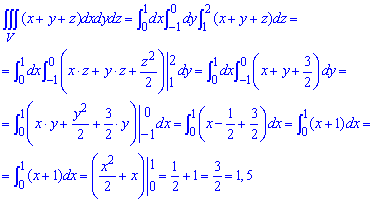
Вычисления не сложны, поэтому превращение в формуле проанализируйте самостоятельно.
Вычисление двойных интегралов с помощью повторного интегрирования
Пусть
функция
определена в области
![]()
,
где![]()
и
![]()
–
непрерывные функции на отрезке
![]()
.
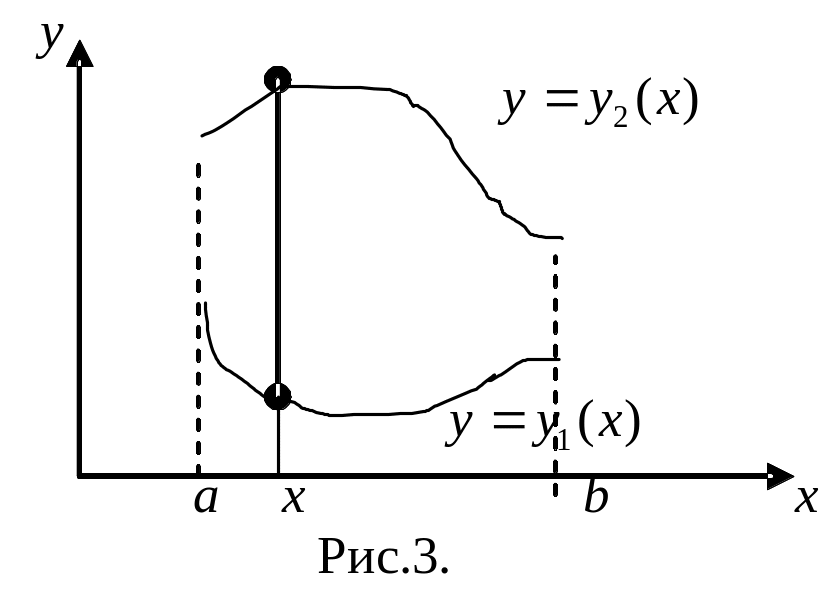
Область, в которой
всякая прямая параллельная оси![]()
,
проходящая через внутреннюю точку
области, пересекает ее границы в двух
точках, называется правильной
относительно
оси
(рис.3).
Аналогично
определяется о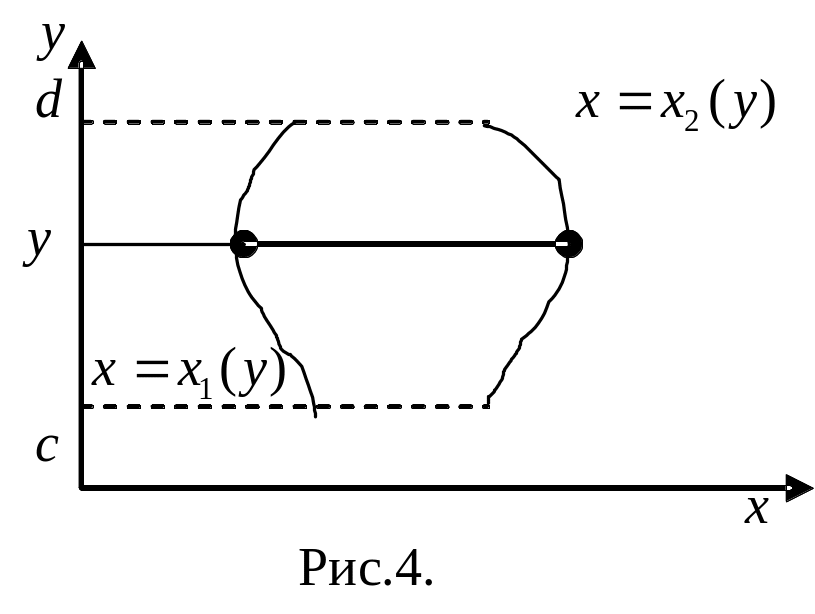
бласть
правильная
относительно оси![]()
:
![]()
где
функции
![]()
и
![]()
–
непрерывные функции на отрезке
![]()
(рис.4).
Выражения
вида
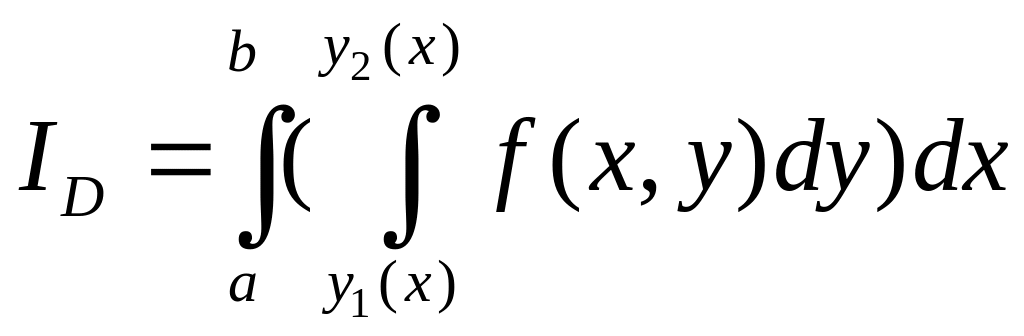
,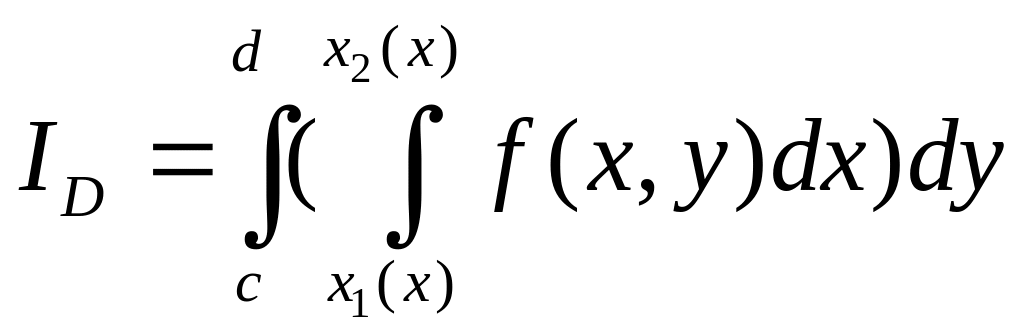
называются
повторными
интегралами
от функции
по
области
.
Теорема.
Двойной интеграл от непрерывной функции
по
правильной области
равен повторному интегралу от этой
функции по области
.
![]()
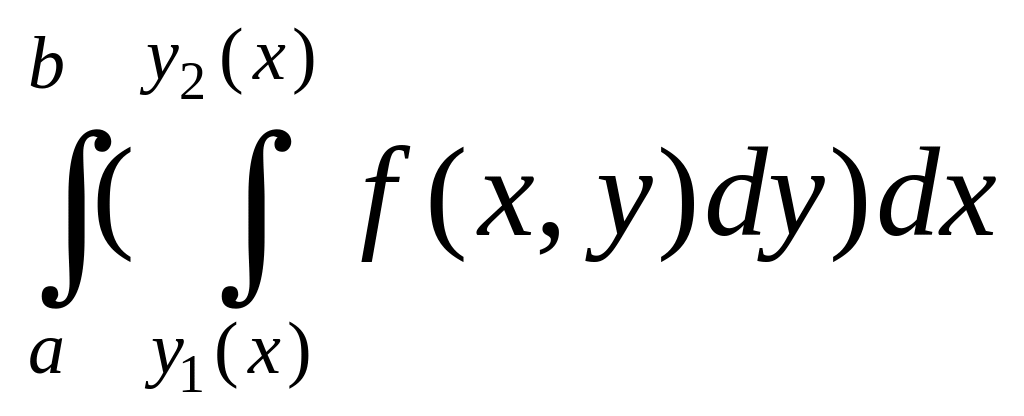
=
.
Если
область правильная относительно оси
,
то двойной интеграл вычисляется как
повторный вида
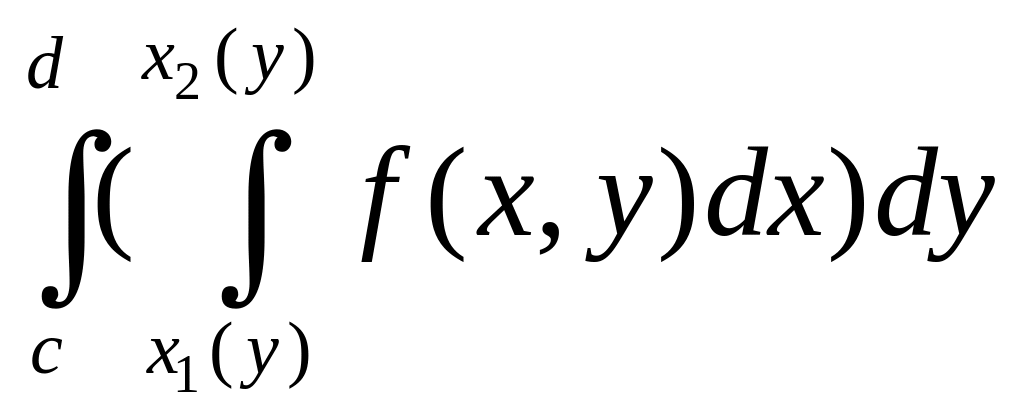
=
В
случае, когда область
не является правильной, ее разбивают
на части, каждая из которых является
правильной.
Частный
случай. Если
область интегрирования есть прямоугольник,
ограниченный прямыми
![]()
![]()
то
формула преобразования двойного
интеграла в повторный имеет вид
![]()
.
Если
кроме того, в подынтегральной функции
переменные разделены, то есть![]()
,
то двойной интеграл превращается в
произведение двух определенных
интегралов:
![]()
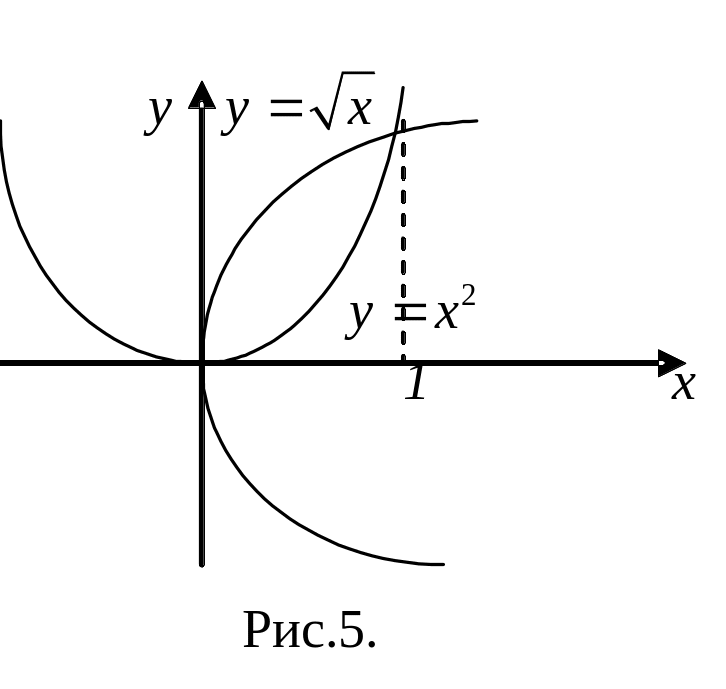
![]()
.
Пример.
Найти![]()
,
где
–
область, ограниченная линиями
![]()
(рис.5).
Решение.
=
=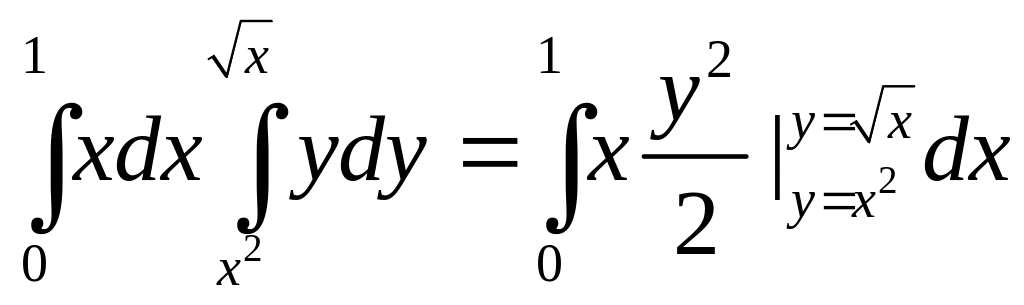
![]()
Пример.
Найти![]()
,
где
–
квадрат
![]()
(рис.6).

Решение.
=
=
![]()
![]()
Представление
двойного интеграла в виде повторного
=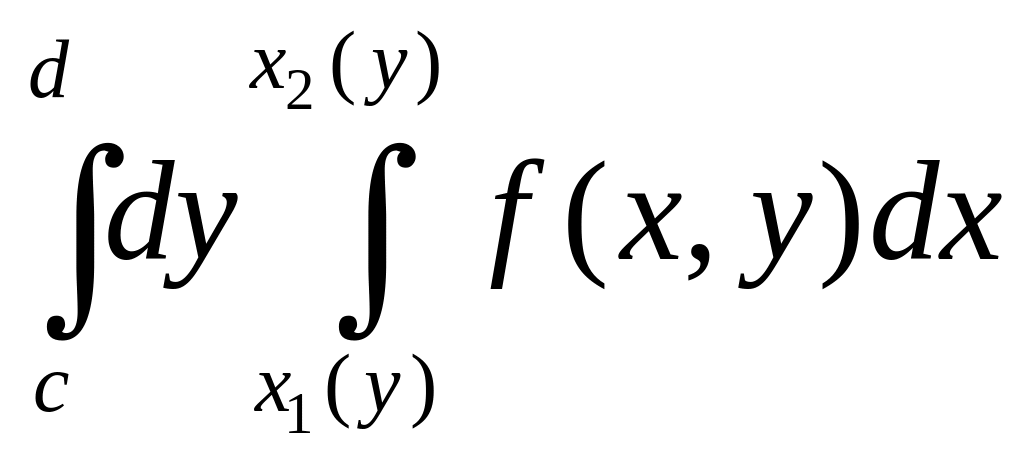
называют
расстановкой пределов интегрирования
в определенном порядке. Задача расстановки
пределов интегрирования допускает
несколько вариантов.
1.
Задан двойной интеграл по области
.
Расставить пределы интегрирования в
том и другом порядке.
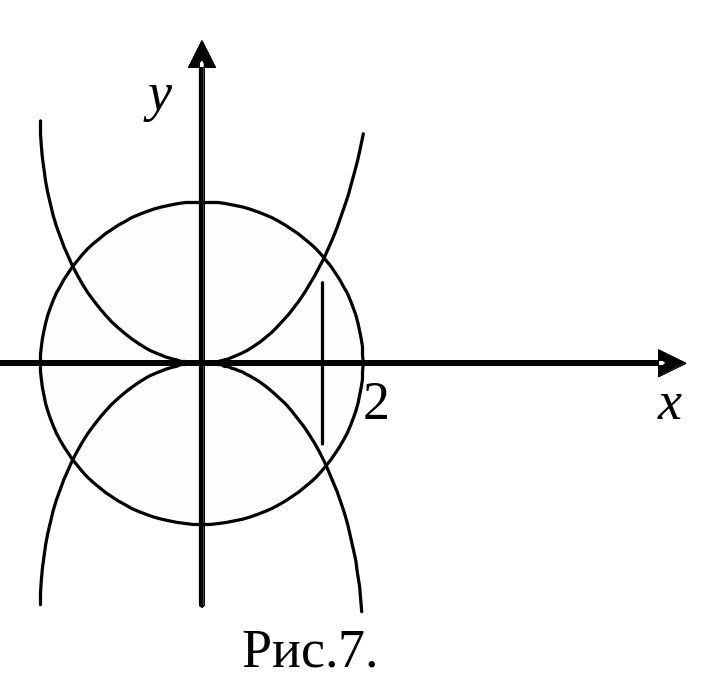
Пример. Область
лежит в правой полуплоскости (т.е.
![]()
и
ограничена
кривыми:
![]()
(рис.7). В двойном интеграле
расставить пределы интегрирования в
одном и другом порядке.
Решение.
Запишем неравенства, которым должны
удовлетворять координаты точек области
:
![]()
![]()
или
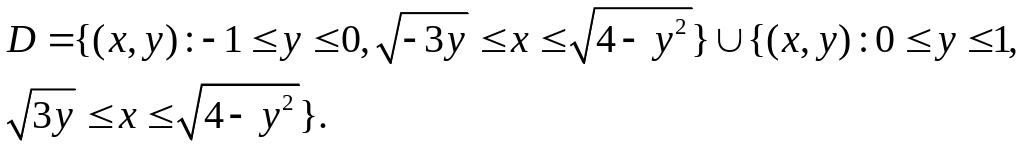
Расставим
пределы интегрирования
=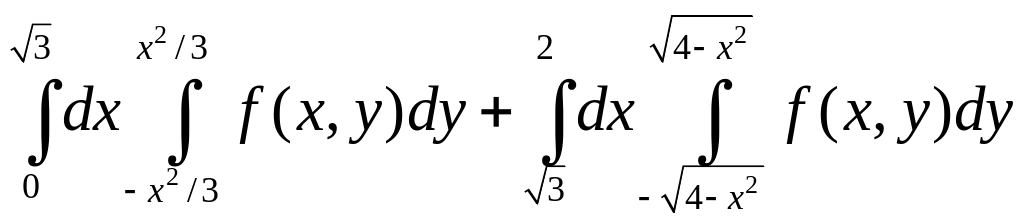
=

2.
Задан двойной интеграл по области
.
Расставить пределы интегрирования в
каком-либо порядке.
В
этом случае выбирают порядок
интегрирования, при котором интеграл
имеет наиболее простое представление.
Выбор может определяться как видом
области интегрирования, так и свойствами
подынтегральной функции. Например,
расстановка пределов в одном порядке
требует разбиения множества
на меньшее число составляющих, чем
расстановка в другом порядке.

Пример. Расставить
пределы интегрирования в интеграле
,
где
–
область ограниченная линиями:![]()
,
![]()
,![]()
(рис.8).
Решение.
Для расстановки пределов интегрирования
в порядке
![]()
можно не разбивать
на составляющие области, а для другого
порядка расстановки пределов такое
разбиение необходимо. Исходя из этого
выбираем порядок
.
Решая систему
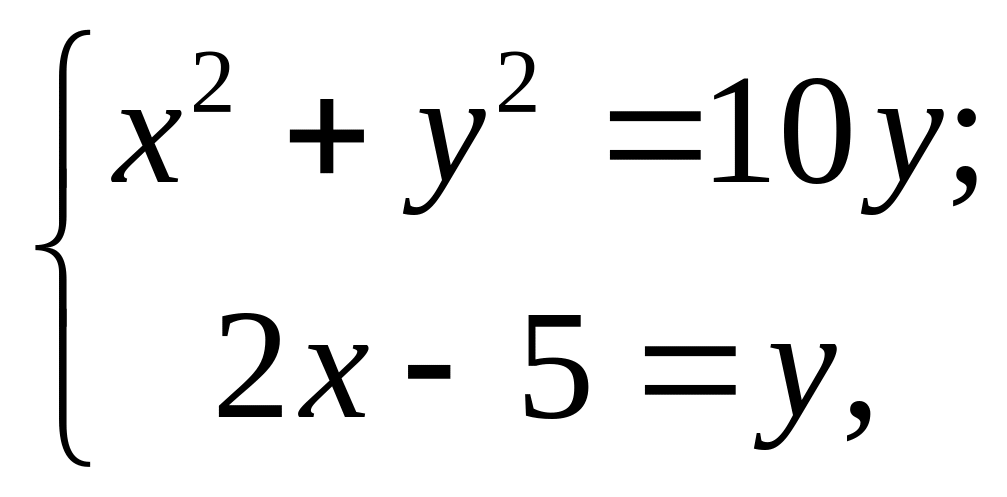
получаем координаты точек пересечения:![]()
.
Следовательно,
![]()
и
=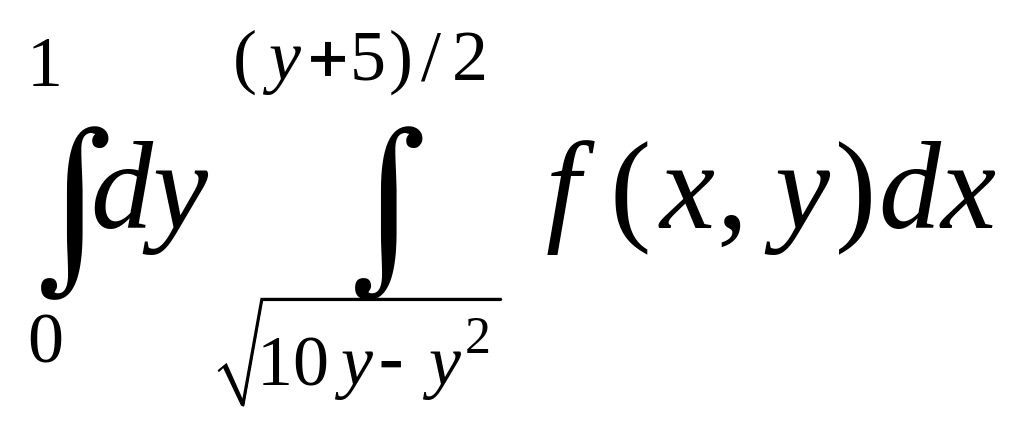
.
3.Задан
повторный интеграл
.
Поменять порядок интегрирования.
Для
решения такой задачи сначала делают
переход от заданного повторного интеграла
к двойному, то есть восстанавливают по
данным пределам область интегрирования
:
=
.
Условия на координаты точек (![]()
множества
получаем исходя из заданного повторного
интеграла
![]()
![]()
.
В полученном двойном интеграле проведем
расстановку пределов интегрирования
в требуемом порядке. Таким образом,
считая область
правильной относительно обеих осей
и
,
получаем цепочку равенств
=
=
.

Пример. Изменить
порядок интегрирования в повторном
интеграле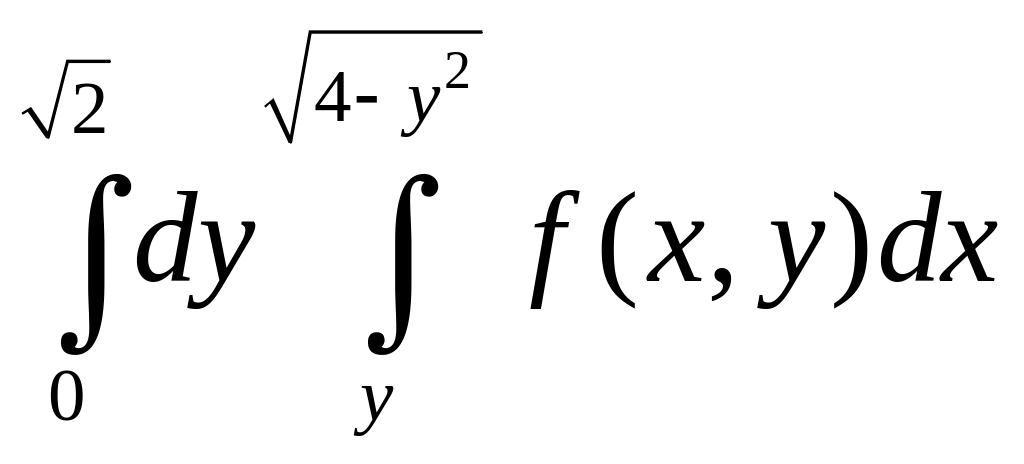
.
Решение.
Запишем условие на координаты точек
![]()
из множества
,
по которому берется
интеграл:
![]()
(рис.9).
Область
правильная как относительно оси
,
так и относительно оси
.
Так как при интегрировании в порядке
![]()
верхняя граница области
задается двумя различными функциями,
представим множество
в виде![]()
,
где

Итак,
=
.
Двойной
интеграл в полярной системе координат
Выведем
формулу перехода от декартовых координат
к полярным в двойном интеграле.
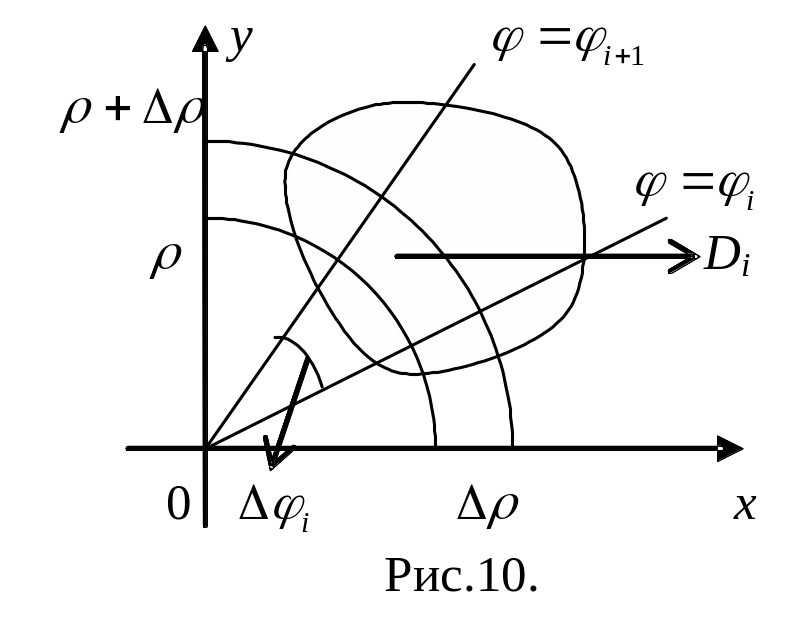
Пусть
– непрерывная функция на ограниченной
замкнутой области
.
Так как при определении двойного
интеграла предел последовательности
интегральных сумм не зависел от способа
разбиения области
на
части
,
то разобьем область
на
концентрическими окружностями
![]()
и лучами
![]()
(рис.10). Тогда площадь
![]()
с
точностью до бесконечно малых более
высокого порядка малости чем
![]()
.
Таким образом, двумерный элемент
площади в полярных координатах
запишется в виде
![]()
.

Пусть теперь
область
правильная относительно![]()
,
то есть любой луч, исходящий из полюса
и проходящий через внутреннюю точку
области пересекает границу области
только в двух точках. В этом случае
область
можно задать множеством
![]()
(рис.11).
Тогда повторный интеграл по области
представим в виде

Е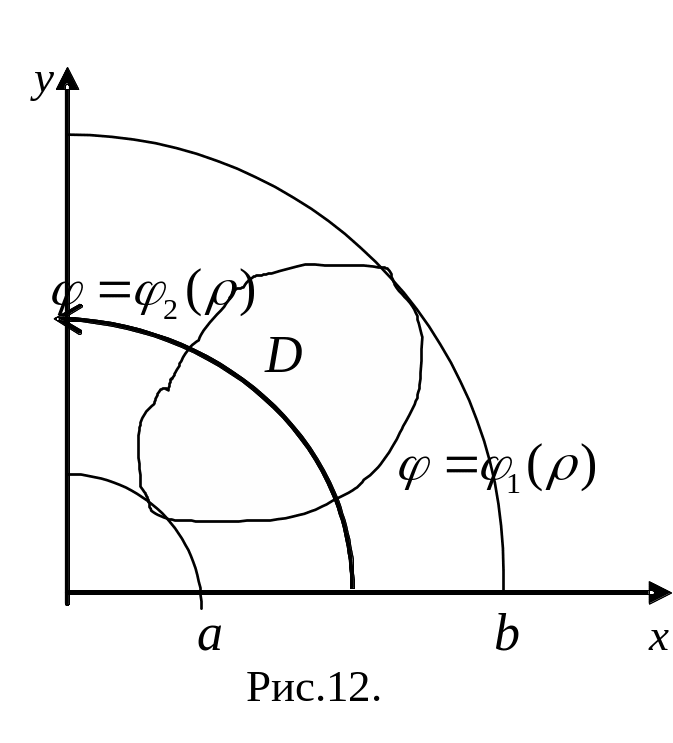
сли
любая окружность с центром в начале
координат, проходящая через внутреннюю
точку области пересекает линию границы
в двух точках, то есть область
есть множество:
![]()

,
(рис.12), то повторный интеграл примет
вид
![]()
=
В
случае, когда полюс лежит внутри области
и любой луч пересекает границу не более
чем в одной точке (рис.13), для вычисления
удобно использовать формулу

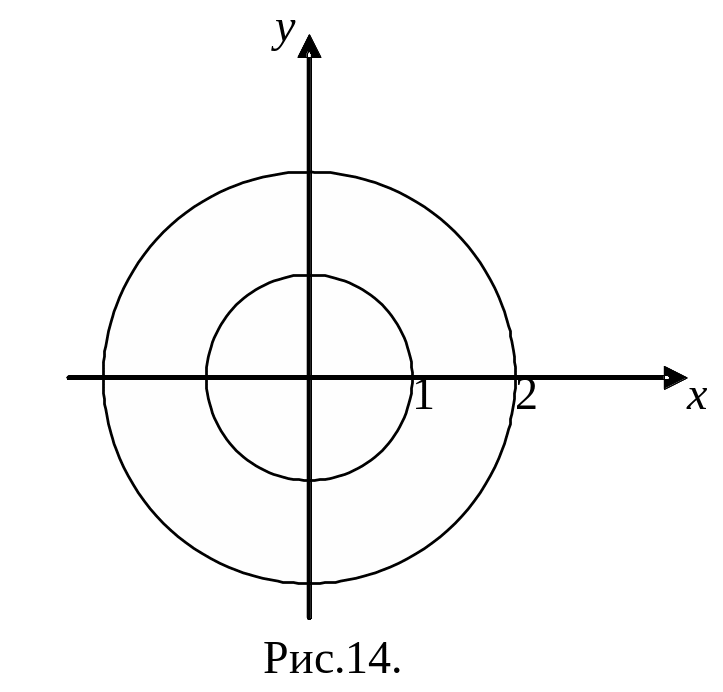
Пример.
Вычислить двойной интеграл
![]()
в
полярной
системе координат по области
,
ограниченной линиями![]()
,
расположенной в I
квадранте (рис.14).
Решение.
![]()
![]()
![]()
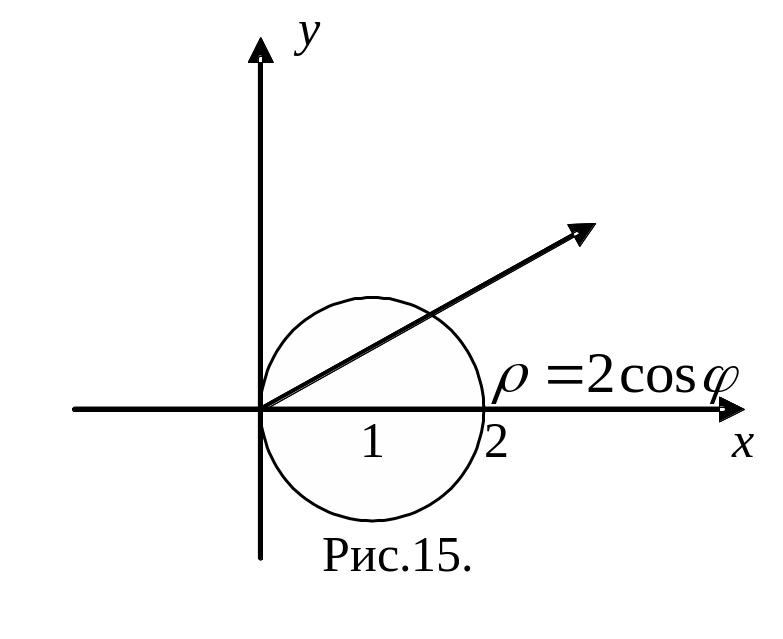
Пример. Вычислить
двойной интеграл
![]()
в полярной системе координат по области
,
ограниченной окружностью![]()
(рис.15).
Решение.
Перейдем к полярным координатам c
полюсом в точке
![]()
:![]()
Угол
![]()
изменяется от
![]()
до
![]()
Подставляя полярные
координаты
в уравнение окружности, получим![]()
,
откуда
![]()
или
![]()
– уравнение окружности в полярных
координатах. Двойной интеграл по области
сводится повторному
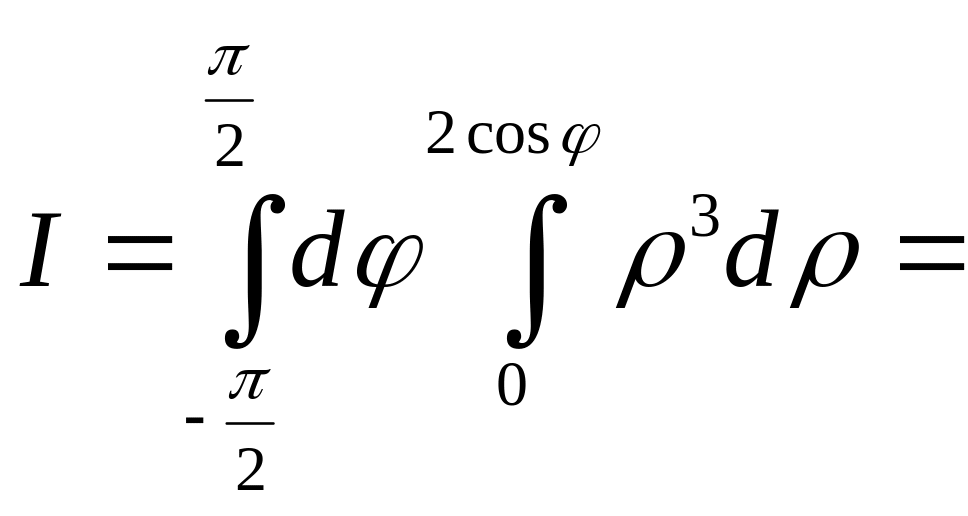

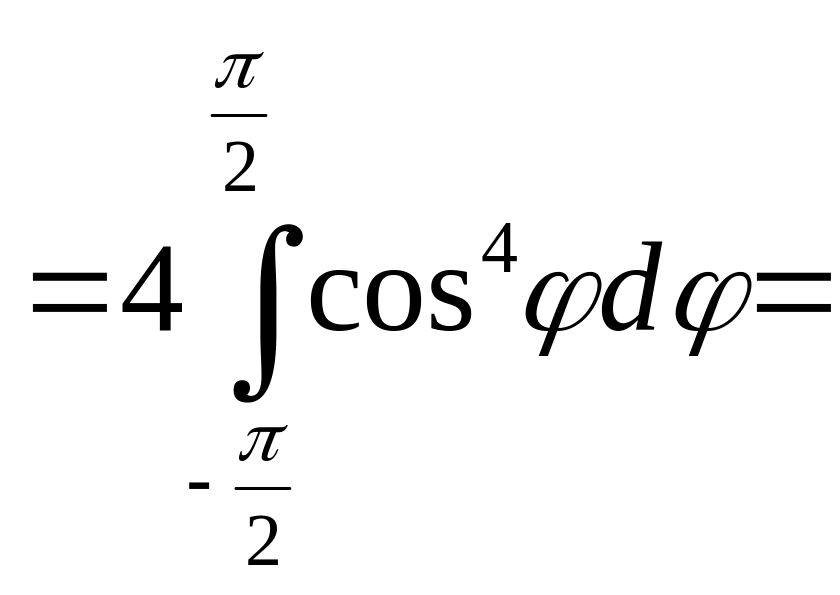
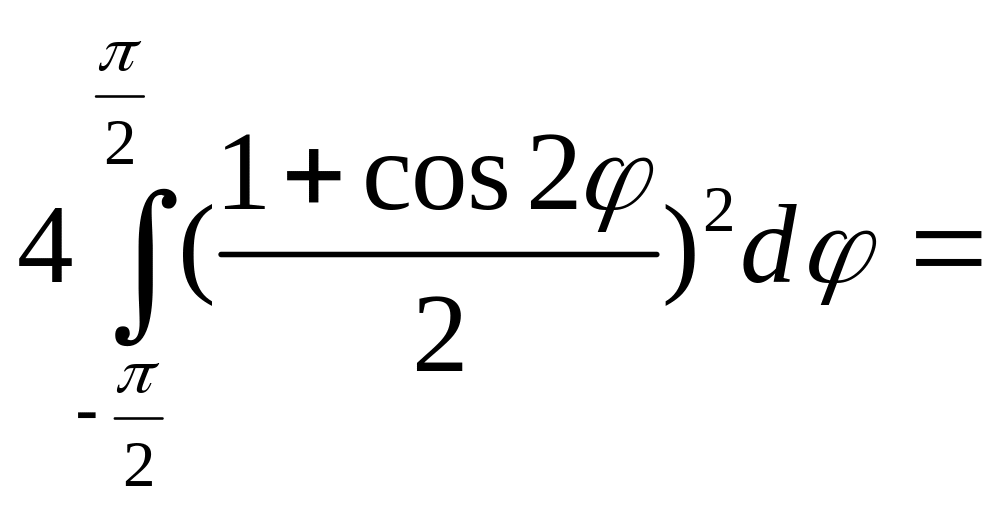

=![]()
![]()
![]()
Замена
переменных в двойном интеграле.
Рассмотрим
двойной интеграл вида
.
Замена переменных в двойном интеграле
состоит в переходе от
переменных
![]()
и
![]()
к новым переменным
![]()
и
![]()
по формулам
![]()
,![]()
.
При этом каждая точка
области
соответствует некоторой точке
![]()
области![]()
,
а каждая точка
области
переходит в некоторую точку
области
![]()
Функции
называют также отображением области
плоскости
на область
плоскости
.
Пусть отображение удовлетворяет
следующим условиям:
1.
Отображение взаимно однозначно, то есть
различным точкам
![]()
области
соответствуют различные точки
![]()
области
.
2.Функции
имеют
в области
непрерывные частные производные первого
порядка.
3.
Якобиан отображения![]()
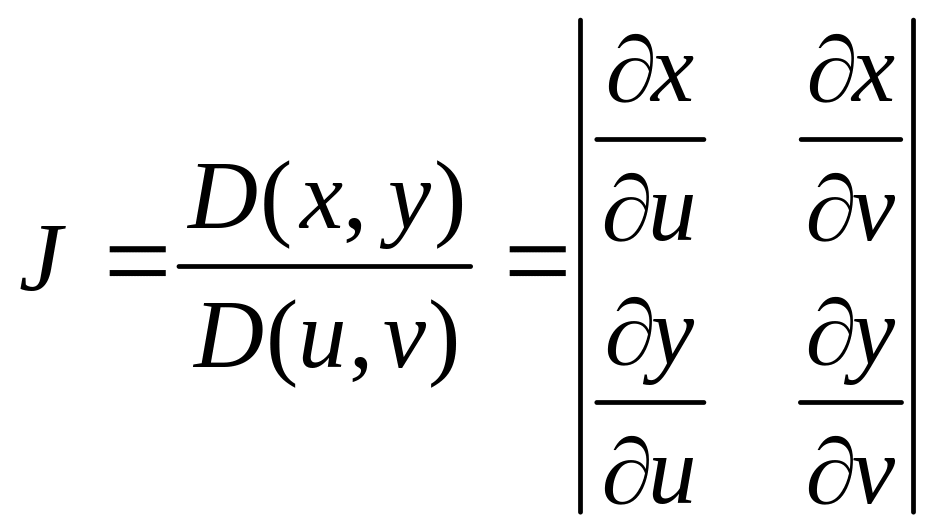
отличен от нуля во всех точках области
.
Тогда
справедливо равенство
=![]()
Эта
формула называется формулой замены
переменных в
двойном
интеграле.
Замечание.
При переходе к полярной системе координат
якобиан перехода имеет вид
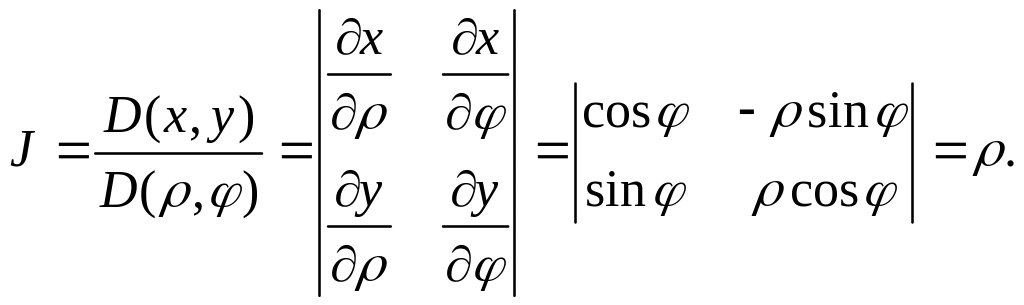
Приложения
двойных интегралов.
Двойные
интегралы применяются для вычисления
площадей плоских фигур и поверхностей,
объемов пространственных тел, механических
величин связанных с непрерывным
распределением массы в плоской области,
а также для решения многих других задач.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Кратные интегралы разбиваются на соответствующее количество обычных определенных.
Пределы внутреннего интеграла определяются “как бы лучом”, проходящим область насквозь: линия, на которой луч “входит” в фигуру – нижний предел, на которой “выходит” – верхний.
Пределы внешнего интеграла – просто по границам области по соответствующей оси, как в обычном определенном интеграле.
Важно отметить то, что раскрывать кратные интегралы можно в любой последовательности (можно менять порядок интегрирования): внешним может являться интеграл как по dx, так и по dy (а внутренний, соответственно, наоборот).
Если раскрывать, начиная с dx, то луч “проходит” снизу вверх; если с dy – слева-направо.
Иногда область может быть необходимо разделить на несколько частей (по аналогии с подсчетом площадей с помощью обычного определенного интеграла). Твой пример – как раз такой случай.
Ну и само собой, непосредственное вычисление начинается с внутреннего интеграла, в результате получается некоторая функция, которую мы потом еще раз интегрируем (внешним интегралом) и в ответе получаем просто число.
Содержание:
В теории определенного интеграла для нахождения площади криволинейной трапеции вводится понятие интегральной суммы, пределом которой является определенный интеграл. Определенный интеграл существует для трех типов функций: непрерывных, кусочно-непрерывных и монотонных. Задача интегрирования может быть также сформулирована и для функции n переменных, заданной в ограниченной области 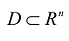
Интегрирование функций многих переменных
Понятие двумерной интегральной суммы, пределом которой является двойной интеграл, можно ввести на основе задачи об объеме тела.
Задача: Найти объем тела, ограниченного сверху непрерывной поверхностью 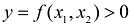
Для этого разобьем основание S на конечное число элементарных ячеек 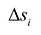 и в каждой из этих ячеек выберем точку
и в каждой из этих ячеек выберем точку 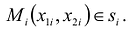 Объем такого элемента равен
Объем такого элемента равен 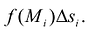 Объем всей фигуры можно приближенно найти как сумму
Объем всей фигуры можно приближенно найти как сумму 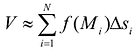 с любой степенью точности в зависимости от числа ячеек
с любой степенью точности в зависимости от числа ячеек  и, соответственно, их размера. Если предположить, что число элементарных ячеек
и, соответственно, их размера. Если предположить, что число элементарных ячеек  бесконечно возрастает, а их диаметр при этом является величиной бесконечно малой, то можно получить точное выражение для объема всей фигуры:
бесконечно возрастает, а их диаметр при этом является величиной бесконечно малой, то можно получить точное выражение для объема всей фигуры: 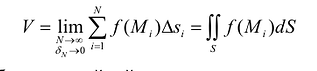
Таким образом, двойной интеграл имеет простой геометрический смысл, он выражает объем криволинейного цилиндрического бруса, ограниченного сверху непрерывной поверхностью 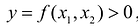 , снизу – конечной замкнутой областью S плоскости
, снизу – конечной замкнутой областью S плоскости  и с боков – прямой цилиндрической поверхностью, построенной на границе объекта S и имеющей образующие, перпендикулярные плоскости
и с боков – прямой цилиндрической поверхностью, построенной на границе объекта S и имеющей образующие, перпендикулярные плоскости  .
.
Двумерной интегральной суммой от данной функции 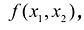 определенной на области S называется сумма парных произведений площадей элементарных ячеек
определенной на области S называется сумма парных произведений площадей элементарных ячеек 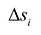 области S на значения функции
области S на значения функции 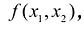 в точке
в точке 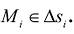
Двойным интегралом от функции 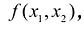 определенной на области S называется предел соответствующей двумерной интегральной суммы при неограниченном возрастании числа N элементарных ячеек
определенной на области S называется предел соответствующей двумерной интегральной суммы при неограниченном возрастании числа N элементарных ячеек 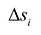 и стремлении к нулю их наибольшего диаметра
и стремлении к нулю их наибольшего диаметра 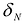 при условии, что этот предел существует и не зависит от способа разбиения области S на элементарные ячейки
при условии, что этот предел существует и не зависит от способа разбиения области S на элементарные ячейки 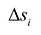 и выбора точек
и выбора точек 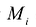 в них.
в них.
Теорема. Если область S с кусочно-непрерывной границей I ограничена и замкнута, а функция 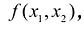 непрерывна в области S, то двойной интеграл
непрерывна в области S, то двойной интеграл
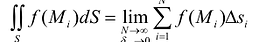 , т.е. предел соответствующей двумерной интегральной суммы существует и не зависит от способа разбиения области S на элементарные ячейки
, т.е. предел соответствующей двумерной интегральной суммы существует и не зависит от способа разбиения области S на элементарные ячейки 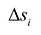 и выбора точек
и выбора точек 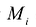 в них.
в них.
Так как значение двойного интеграла не зависит от вида элементарных ячеек, то в дальнейшем целесообразно пользоваться наиболее удобным для декартовой системы координат разбиением на прямоугольную сетку, образованную пересечением двух систем прямых, параллельных соответственно координатным осям Ох и Оу. В этом случае элементарными ячейками являются прямоугольники, со сторонами 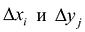 . Таким образом, в обозначении интеграла можно учесть что
. Таким образом, в обозначении интеграла можно учесть что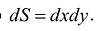 Тогда:
Тогда: 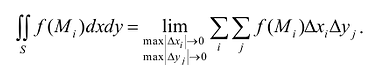
Для вычисления двойного интеграла применяется процедура повторного интегрирования.
Предположим для определенности, что область интегрирования S представляет собой криволинейную трапецию: 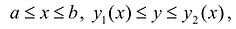 где
где 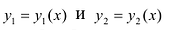 – однозначные непрерывные функции на отрезке [а,b]. Важно отметить, что вертикаль, проходящая через любую точку х па отрезке [а,b) оси Ох, пересекает границу области интегрирования S только в двух точках: в точке входа
– однозначные непрерывные функции на отрезке [а,b]. Важно отметить, что вертикаль, проходящая через любую точку х па отрезке [а,b) оси Ох, пересекает границу области интегрирования S только в двух точках: в точке входа 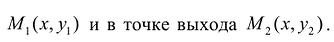 Такая область называется стандартной относительно оси Оу.
Такая область называется стандартной относительно оси Оу.
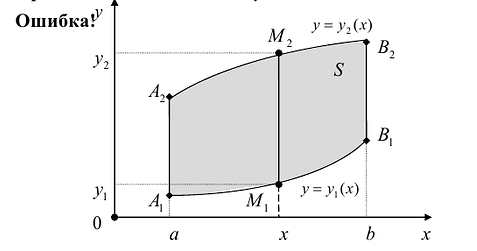
Теорема. Если для функции f(x,y) определенной в области S (стандартной относительно оси Оу), существует двойной интеграл 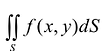 и существует интеграл
и существует интеграл 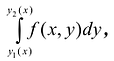 то
то 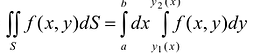 .
.
При этом, интеграл 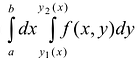 называется повторным.
называется повторным.
Таким образом, вычисление двойного интеграла сводится к вычислению двух интегралов: вначале находится внутренний интеграл по переменной у (при этом переменная х рассматривается как постоянная величина); после этого полученное выражение повторно интегрируется по переменной х.
Задача вычисления кратного интеграла может быть обобщена на n-мерный случай и аналогично решена путем сведения кратного интеграла к повторному. Пусть функция у = f(M) определена и ограничена в замкнутой области 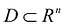 . Область D разбивается на N элементарных частей
. Область D разбивается на N элементарных частей 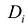
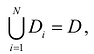 пересечением любой пары элементарных частей будет множество точек, размерность которого не превышает n -1.
пересечением любой пары элементарных частей будет множество точек, размерность которого не превышает n -1.
В каждой элементарной части выбирается точка 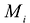 и составляется интегральная сумма:
и составляется интегральная сумма: 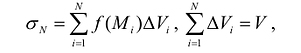 где
где 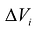 – объемная мера области
– объемная мера области 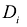 ; V-объемная мера области D.
; V-объемная мера области D.
Для того чтобы вычислить интегральную сумму, необходимо, чтобы элементарные части 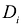 допускали исчисление объемной меры в достаточно простой и редуктируемой форме.
допускали исчисление объемной меры в достаточно простой и редуктируемой форме.
n-кратным интегралом функции у = f(M) по области D называется предел интегральной суммы 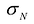 при
при 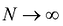 и, соответственно,
и, соответственно, 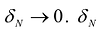 – наибольшая протяженность элементарной области
– наибольшая протяженность элементарной области 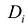 для данного разбиения.
для данного разбиения.
Этот предел не должен зависеть от способов разбиения D на части и от выбора точек 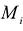 в каждой из них. Указанный интеграл можно представить в следующим образом:
в каждой из них. Указанный интеграл можно представить в следующим образом:
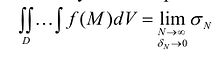
По форме этот интеграл сходен с определенным интегралом 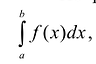 , который также является пределом интегральной суммы:
, который также является пределом интегральной суммы:
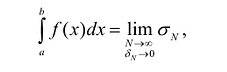
где 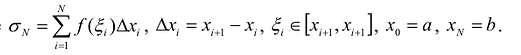
Очевидно, что в n-кратном интеграле, как и в случае определенного интеграла, интегральные суммы ограничены снизу и сверху значениями сумм Дарбу 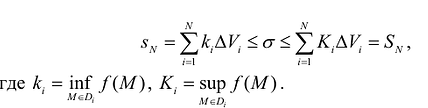
Свойствами одномерных сумм Дарбу обладают и n -мерные суммы. При этом для любой ограниченной функции: 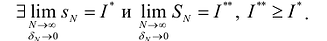
Необходимым и достаточным условием интегрируемости функции является условие 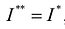 , что эквивалентно выражению:
, что эквивалентно выражению:
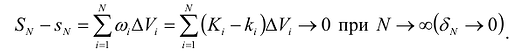
Величина 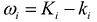 , называется колебанием функции в элементарной области
, называется колебанием функции в элементарной области 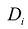 и является величиной положительной при любом i.
и является величиной положительной при любом i.
В результате можно установить, что к числу интегрируемых функций будут относиться функции, непрерывные на замкнутой области D. При вычислении n-кратный интеграл сводится к повторному интегралу, т.е. вычислению обычного интеграла от внутреннего интеграла кратности n -1.
Свойства n-кратного интеграла
- Интеграл по области, имеющей нулевую «объемную» меру в
 , равен нулю. При этом к областям с нулевой «объемной» мерой в
, равен нулю. При этом к областям с нулевой «объемной» мерой в 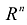 , относятся разнообразные множества, которые заданы в пространстве
, относятся разнообразные множества, которые заданы в пространстве 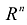 , (m
, (m
- Если две функции f(M) и g(M) интегрируемы в D, то сумма этих функций также интегрируема в D и
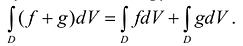
- Если функция f(M) интегрируема в D, а С – постоянная величина, то функция С f(M) также интегрируема в D и
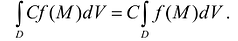
- Пусть область D является объединением областей
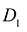 и
и 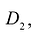 , а пересечение этих областей есть множество S, размерность которого меньше N. Если функция f(M) интегрируема в D, то она интегрируема в
, а пересечение этих областей есть множество S, размерность которого меньше N. Если функция f(M) интегрируема в D, то она интегрируема в 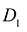 и
и 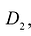 и при этом
и при этом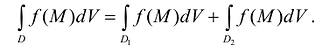
- Если функция f(M) определена и интегрируема в D, и при этом
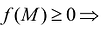 (за исключением, быть может, некоторой части D с размерностью меньше n), то
(за исключением, быть может, некоторой части D с размерностью меньше n), то 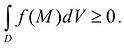
- Если две функции /fМ) и g(M) определены и интегрируемы в D, причем
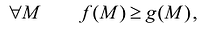 то
то 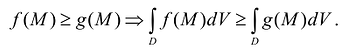
- Если функция f(M) определена и интегрируема в D, то
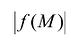 также интегрируема в D, причем
также интегрируема в D, причем 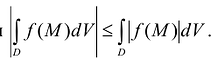
- Если функция f(M) = С является постоянной
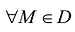 , то
, то 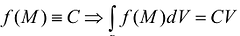 .
. - Если функция f(M) определена и интегрируема в D и ограничена снизу и сверху значениями к к К, соответственно
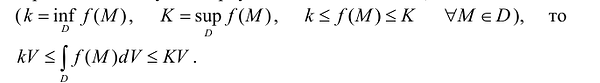
Понятие о двойном интеграле
Мы рассматривали определенный интеграл, как предел суммы для случая, когда функция f(x) определена на отрезке  , который называется отрезком интегрирования. В настоящем параграфе мы обобщим понятие интеграла на случай, когда областью интегрирования является некоторая область на плоскости, или некоторая область в пространстве, при этом мы будем пользоваться интуитивным представлением площади и объема.
, который называется отрезком интегрирования. В настоящем параграфе мы обобщим понятие интеграла на случай, когда областью интегрирования является некоторая область на плоскости, или некоторая область в пространстве, при этом мы будем пользоваться интуитивным представлением площади и объема.
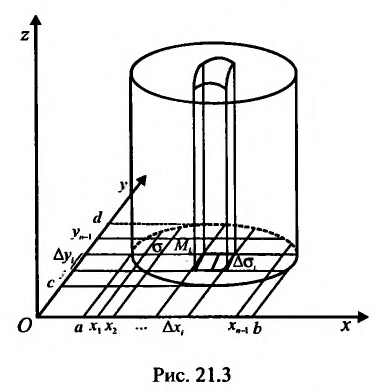
Пусть 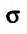 – ограниченная плоская область (см. рис. 21.3). Рассмотрим функцию z = f{x,y), определенную и непрерывную в области
– ограниченная плоская область (см. рис. 21.3). Рассмотрим функцию z = f{x,y), определенную и непрерывную в области 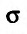 , ограниченной замкнутой линией L. Разобьем область о на элементарные области
, ограниченной замкнутой линией L. Разобьем область о на элементарные области 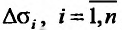 , произвольной формы, при-чем через
, произвольной формы, при-чем через 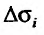 , обозначим сами элементарные области и их площади. В каждой из элементарных областей
, обозначим сами элементарные области и их площади. В каждой из элементарных областей 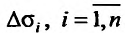 произвольно выберем точки
произвольно выберем точки 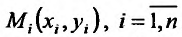 , и вычислим значения функции в этих точках:
, и вычислим значения функции в этих точках: 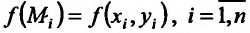 . Составим сумму произведений значений функции
. Составим сумму произведений значений функции 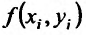 на площади
на площади 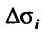 :
:
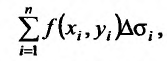 которая называется интегральной суммой.
которая называется интегральной суммой.
Предел этой интегральной суммы при неограниченном увеличении числа делений и неограниченном уменьшении каждой из элементарных областей 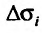 , если он существует, называется двукратным (двойным) интегралом от функции f(x,y) и обозначается
, если он существует, называется двукратным (двойным) интегралом от функции f(x,y) и обозначается 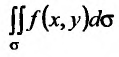
Если 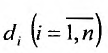 – максимальное расстояние между двумя точками элементарной области
– максимальное расстояние между двумя точками элементарной области 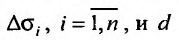 – наибольшее из этих чисел:
– наибольшее из этих чисел: 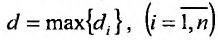 то неограниченное уменьшение каждой из элементарных областей равносильно тому, что
то неограниченное уменьшение каждой из элементарных областей равносильно тому, что 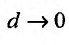 . Тогда можно записать:
. Тогда можно записать:
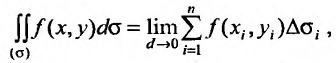
где f(х,у) – подынтегральная функция, а 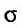 – область интегрирования.
– область интегрирования.
Если отнести область 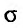 к прямоугольной системе координат (см. рис. 21.3), то
к прямоугольной системе координат (см. рис. 21.3), то 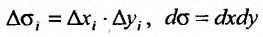 (элемент площади) и тогда справедливо равенство:
(элемент площади) и тогда справедливо равенство:
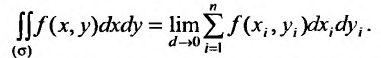
Геометрический смысл двойного интеграла состоит в том, что он равен объему цилиндра с основанием о и ограниченного сверху поверхностью 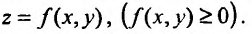
Вычисление двойного интеграла сводится к вычислению двух определенных интегралов; при вычислении “внутреннего интеграла” (записанного в скобках) х (у) считается постоянным (рис. 21.4):
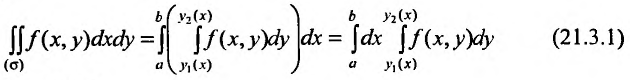
или (рис. 21.5)
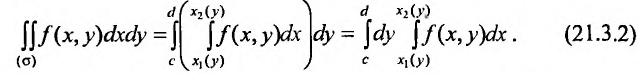
Если область интегрирования о отлична от областей, указанных на рисунках 21.4 и 21.5, то ее разбиваем на части прямыми, параллельными оси Ох и оси Оу, чтобы каждая из полученных частей имела соответствующий вид. 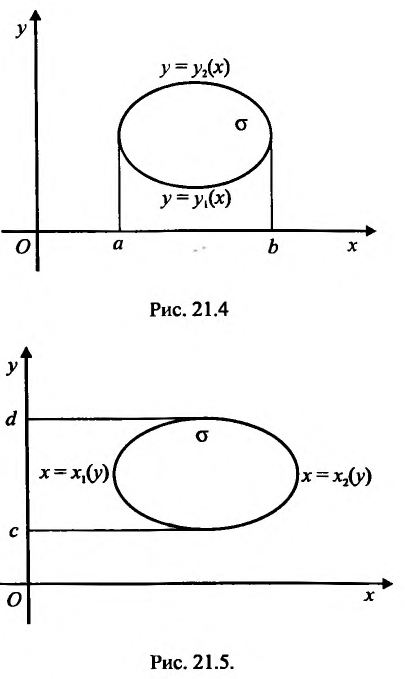
Пример №1
Вычислить двойной интеграл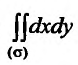 по области
по области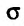 , ограниченной линиями:
, ограниченной линиями: 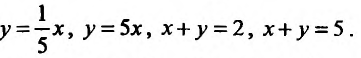
Решение:
Построим на плоскости хОу область а (см. рис. 21.6).
Из рисунка 21.6 мы видим, что область 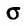 отлична от областей, указанных на рисунках 21.5 и 21.6, так как ни одну из границ в направлении оси Ох или оси Оу нельзя записать одним уравнением
отлична от областей, указанных на рисунках 21.5 и 21.6, так как ни одну из границ в направлении оси Ох или оси Оу нельзя записать одним уравнением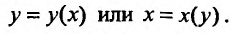
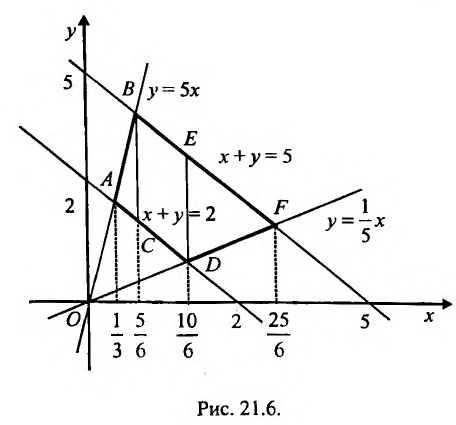
Поэтому разобьем заданную область на части прямыми 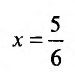
(абсцисса точки пересечения прямых _у = 5х и х + у = 5) и 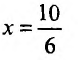
(абсцисса точки пересечения прямых 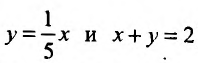 ). Тогда заданный интеграл будет равен сумме трех интегралов по областям: ABC, CBED, DEF:
). Тогда заданный интеграл будет равен сумме трех интегралов по областям: ABC, CBED, DEF: 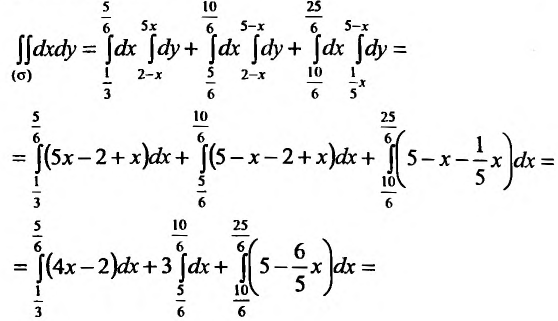
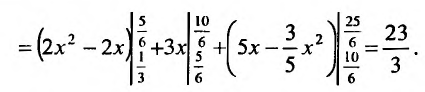
- Заказать решение задач по высшей математике
Понятие о тройном интеграле
По аналогии с двойным интегралом вводится понятие тройного интеграла. Пусть задана замкнутая пространственная область V, в которой задана непрерывная функция 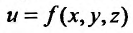 . Разобьем область V на и элементарных пространственных областей
. Разобьем область V на и элементарных пространственных областей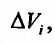
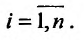 . Составим сумму произведений значений функции на объемы элементарных областей:
. Составим сумму произведений значений функции на объемы элементарных областей:
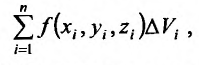
которая называется интегральной суммой.
Обозначим 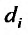 – максимальное расстояние между двумя точками элементарной пространственной области
– максимальное расстояние между двумя точками элементарной пространственной области 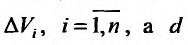 -наибольшее из этих чисел:
-наибольшее из этих чисел: 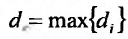 . Предел этой интегральной суммы, при неограниченном увеличении числа делений n и неограниченном уменьшении (при
. Предел этой интегральной суммы, при неограниченном увеличении числа делений n и неограниченном уменьшении (при 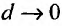 ) каждой из элементарных областей
) каждой из элементарных областей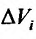 , если он существует, называется трехкратным (тройным) интегралом от функции f (х, у, z) и обозначается
, если он существует, называется трехкратным (тройным) интегралом от функции f (х, у, z) и обозначается
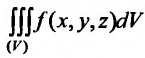 . Итак, по определению:
. Итак, по определению:
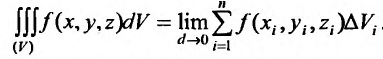
Если ввести в пространстве прямоугольные координаты, то будет справедливо равенство:
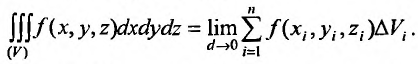
При вычислении тройного интеграла, он сводится к двойному интегралу, путем проектирования поверхности, ограничивающий объем V , на плоскость хОу в виде области 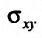 и определение координат
и определение координат 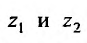 точек входа и выхода прямой, параллельной оси Oz и проведенной через точку (х, у) области
точек входа и выхода прямой, параллельной оси Oz и проведенной через точку (х, у) области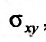 и вычисления интеграла
и вычисления интеграла 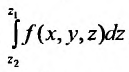 , считая х и у постоянными, а затем вычисляется двойной интеграл:
, считая х и у постоянными, а затем вычисляется двойной интеграл:
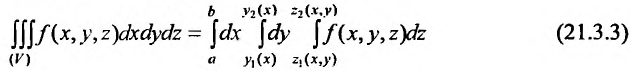
или
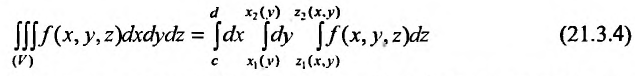
Кратные интегралы (двойные и тройные) удовлетворяют следующим основным свойствам:
- Постоянный множитель можно выносить за знак кратного интеграла.
- Кратный интеграл от алгебраической суммы интегрируемых функций равен алгебраической сумме кратных интегралов от отдельных слагаемых.
- Если подынтегральная функция интегрируема в области, а эта область разбита на две непересекающиеся части, то кратный интеграл по области равен сумме кратных интегралов по непересекающимся частям.
Пример №2
Вычислить тройной интеграл 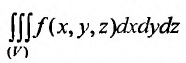 по пространственной области V, ограниченной плоскостями:
по пространственной области V, ограниченной плоскостями: 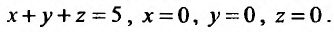
Решение:
Область V является треугольной пирамидой (см. рис. 21.7), ограниченной плоскостью х + у + z = 5 . Спроектируем поверхность, ограничивающую объем V, на плоскость хОу, получим греугольник ЛОВ, при этом z будет изменяться от 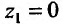 до
до 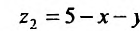 . Двойной интеграл
. Двойной интеграл 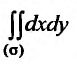 вычислим, используя формулу (21.3.1).
вычислим, используя формулу (21.3.1). 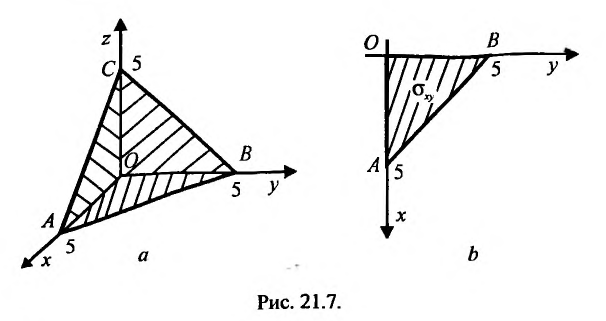
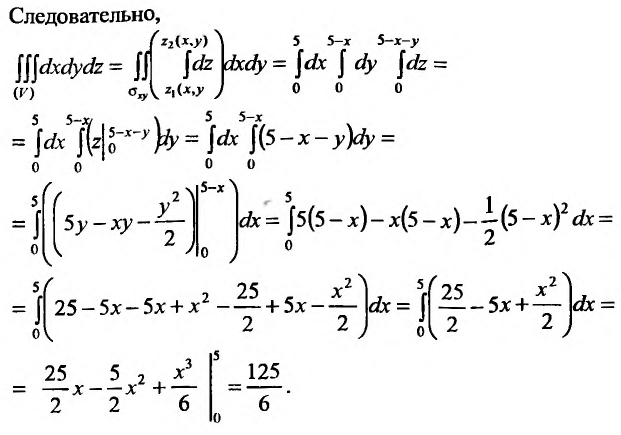
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица – определение и нахождение
- Ранг матрицы – определение и вычисление
- Пространство R”
- Неопределённый интеграл
- Методы интегрирования неопределенного интеграла
- Определённый интеграл
