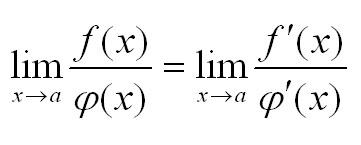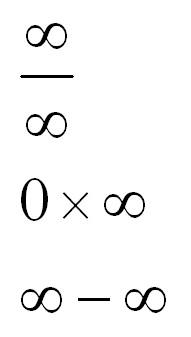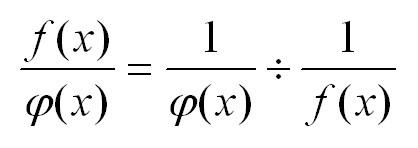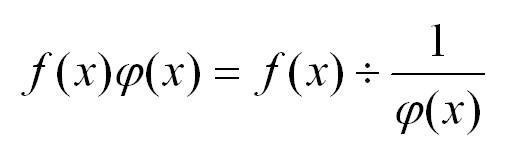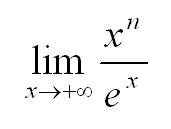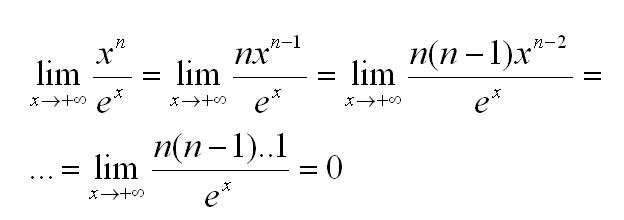Мы уже начали разбираться с пределами и их решением. Продолжим по горячим следам и разберемся с решением пределов по правилу Лопиталя. Этому простому правилу по силам помочь Вам выбраться из коварных и сложных ловушек, которые преподаватели так любят использовать в примерах на контрольных по высшей математике и матанализу. Решение правилом Лопиталя – простое и быстрое. Главное – уметь дифференцировать.
Правило Лопиталя: история и определение
На самом деле это не совсем правило Лопиталя, а правило Лопиталя-Бернулли. Сформулировал его швейцарский математик Иоганн Бернулли, а француз Гийом Лопиталь впервые опубликовал в своем учебнике бесконечно малых в славном 1696 году. Представляете, как людям приходилось решать пределы с раскрытием неопределенностей до того, как это случилось? Мы – нет.
Кстати, о том, какой вклад внес в науку сын Иоганна Бернулли, читайте в статье про течение жидкостей и уравнение Бернулли.
Прежде чем приступать к разбору правила Лопиталя, рекомендуем прочитать вводную статью про пределы в математике и методы их решений. Часто в заданиях встречается формулировка: найти предел, не используя правило Лопиталя. О приемах, которые помогут Вам в этом, также читайте в нашей статье.
Если имеешь дело с пределами дроби двух функций, будь готов: скоро встретишься с неопределенностью вида 0/0 или бесконечность/бесконечность. Как это понимать? В числителе и знаменателе выражения стремятся к нулю или бесконечности. Что делать с таким пределом, на первый взгляд – совершенно непонятно. Однако если применить правило Лопиталя и немного подумать, все становится на свои места.
Но сформулируем правило Лопиталя-Бернулли. Если быть совершенно точными, оно выражается теоремой. Правило Лопиталя, определение:
Если две функции дифференцируемы в окрестности точки x=a обращаются в нуль в этой точке, и существует предел отношения производных этих функций, то при х стремящемся к а существует предел отношения самих функций, равный пределу отношения производных.
Запишем формулу, и все сразу станет проще. Правило Лопиталя, формула:
Так как нас интересует практическая сторона вопроса, не будем приводить здесь доказательство этой теоремы. Вам придется или поверить нам на слово, или найти его в любом учебнике по математическому анализу и убедится, что теорема верна.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Раскрытие неопределенностей по правилу Лопиталя
В раскрытии каких неопределенностей может помочь правило Лопиталя? Ранее мы говорили в основном о неопределенности 0/0. Однако это далеко не единственная неопределенность, с которой можно встретиться. Вот другие виды неопределенностей:
Рассмотрим преобразования, с помощью которых можно привести эти неопределенности к виду 0/0 или бесконечность/бесконечность. После преобразования можно будет применять правило Лопиталя-Бернулли и щелкать примеры как орешки.
Неопределенность вида бесконечность/бесконечность сводится к неопределенность вида 0/0 простым преобразованием:
Пусть есть произведение двух функций, одна из которых первая стремиться к нулю, а вторая – к бесконечности. Применяем преобразование, и произведение нуля и бесконечности превращается в неопределенность 0/0:
Для нахождения пределов с неопределенностями типа бесконечность минус бесконечность используем следующее преобразование, приводящее к неопределенности 0/0:
Для того чтобы пользоваться правилом Лопиталя, нужно уметь брать производные. Приведем ниже таблицу производных элементарных функций, которой Вы сможете пользоваться при решении примеров, а также правила вычисления производных сложных функций:
Теперь перейдем к примерам.
Пример 1
Найти предел по правилу Лопиталя:
Пример 2
Вычислить с использованием правила Лопиталя:
Важный момент! Если предел вторых и последующих производных функций существует при х стремящемся к а, то правило Лопиталя можно применять несколько раз.
Найдем предел (n – натуральное число). Для этого применим правило Лопиталя n раз:
Желаем удачи в освоении математического анализа. А если Вам понадобится найти предел используя правило Лопиталя, написать реферат по правилу Лопиталя, вычислить корни дифференциального уравнения или даже рассчитать тензор инерции тела, обращайтесь к нашим авторам. Они с радостью помогут разобраться в тонкостях решения.
В задачах на пределы можно столкнуться с ситуациями, разрешить которые достаточно просто, используя правило Лопиталя. Относительно простая закономерность является очень полезной, когда требуется найти ответ к заданию по математике или математическому анализу. При этом важно владеть навыками дифференцирования.
Правило Лопиталя — в чем суть, понятие
Название этой закономерности не совсем соответствует действительности. Было бы правильнее говорить «правило Лопиталя — Бернулли». Первая подробная формулировка была представлена швейцарским математиком Иоганном Бернулли. Французский ученый Гийом Лопиталь впервые опубликовал это правило в издании собственного учебника в 1696 году.
Правило Лопиталя позволяет существенно упростить некоторые расчеты предела отношения (displaystyle frac{f(x)}{g(x)}) при (xrightarrow a) в том случае, когда (f) и (g) одновременно представляют собой бесконечно малые, либо бесконечно большие величины. С помощью выведенной закономерности допустимо осуществлять замену предела отношения функции, используя предел отношения их производных.
Доказательство 1 и 2 правила Лопиталя, вывод теоремы
Теорема 1
Допустим, что функции (f(x)) и (g(x)) дифференцируются на промежутке ((a,b)):
(lim_{xrightarrow a+0}f(x)=0)
(lim_{xrightarrow a+0}g(x)=0)
(g'(x)neq 0 ) для всех ( xin(a,b))
Тогда имеет место конечный и бесконечный:
(lim_{xrightarrow a+0}frac{f'(x)}{g'(x)}=A)
Таким образом, также существует и равен A:
(displaystylelim_{xrightarrow a+0}frac{f(x)}{g(x)})
Можно сделать вывод:
(lim_{xrightarrow a+0}frac{f(x)}{g(x)}=lim_{xrightarrow a+0}frac{f'(x)}{g'(x)})(lim_{xrightarrow a+0}frac{f(x)}{g(x)}=lim_{xrightarrow a+0}frac{f'(x)}{g'(x)})
Докажем данную теорию.
Допустим, что (xin(a,b))
Следует доопределить функции (f(x)) и (g(x)) в точке a, имея в виду, что:
(f(a)=g(a)=0)
Таким образом, из условий функций следует, что (f) и (g) непрерывны на отрезке [a,x]. По теореме Коши имеется точка (xiin (a,x)), такая, что:
(frac{f(x)}{g(x)}=frac{f(x)-f(a)}{g(x)-g(a)}=frac{f'(xi)}{g'(xi)})
В том случае, когда (xrightarrow a+0), можно определить, что (xirightarrow a+0). Зная, что существует (displaystyle lim_{xrightarrow a+0}frac{f'(xi)}{g'(xi)}=A), можно сделать вывод о справедливости утверждения (eqref).
Теорема, доказательства которой представлены путем соответствующих изменений ее условий, работает, когда (xrightarrow a-0) и (xrightarrow a). Точка a в данном случае является конечной.
Теорема 1 остается справедливой в таких ситуациях, когда (a=+infty) или (a=-infty), а также:
(displaystyle lim_{xrightarrow +infty}f(x)=lim_{xrightarrow +infty} g(x)=0)
( g'(x)neq 0) при (x > x_0)и существует (displaystyle lim_{xrightarrow +infty}frac{f'(x)}{g'(x)}=A)
В этом случае (displaystyle lim_{xrightarrow +infty}frac{f(x)}{g(x)}=A)
Доказательство данного утверждения выполнено с помощью замены переменного (displaystyle x=frac{1}{t}) и Теоремы 1.
Теорема 2
Допустим, что функции (f(x)) и (g(x)) дифференцируются при (x > alpha) и (g'(x)neq 0) при (x > alpha)
(lim_{xrightarrow+infty}f(x)=infty,quad lim_{xrightarrow +infty}g(x)=infty)
и существует конечный:
(lim_{xrightarrow +infty}frac{f'(x)}{g'(x)}=A)
В таком случае, существует (displaystyle lim_{xrightarrow +infty}frac{f(x)}{g(x)}), равный A.
Таким образом:
(lim_{xrightarrow +infty}frac{f(x)}{g(x)}=lim_{xrightarrow +infty}frac{f'(x)}{g'(x)} )
Доказательство
Зная, что:
(existsalpha_{1} > alpha: forall x > alpha_{1}rightarrow |f(x)| > 1)
( |g(x)| > 1)
Исходя из записанного выражения, получим, что (f(x)neq 0) и ( g(x)neq 0) при (x > alpha_1).
Согласно определению, для заданного числа (varepsilon > 0) можно вычислить (delta=delta_1(varepsilon)geq alpha_1) такое, что для всех (t > delta_{1}) выполняется неравенство:
(A-frac{varepsilon}{2} < frac{f'(t)}{g'(t)} < A+frac{varepsilon}{2})
Определив (x_{0} > delta_{1}) на рисунке, выберем число (delta_{2} > x_{0}) такое, чтобы при всех (x > delta_{2}) выполнялись неравенства:
(left|frac{f(x_{0})}{f(x)}right| < frac{1}{2},quad left|frac{g(x_{0})}{g(x)}right| < frac{1}{2})
В качестве доказательства выражения нужно определить, что существует (delta) такое, при котором, если все (x > delta), выполняется неравенство:
(A-varepsilon < frac{f(x)}{g(x)} < A+varepsilon)
Число (delta) будет выбрано ниже. Учитывая, что (x > delta), можно применить к функциям (f) и (g) на интервале ([x_0,x]) теорему Коши о среднем. Согласно данному утверждению, должна существовать точка (xiin [x_{0},x]) такая, при которой:
(frac{f(x)-f(x_{0})}{g(x)-g(x_{0})}=frac{f'(xi)}{g'(xi)})
Преобразуем левую часть равенства:
(frac{f(x)-f(x_{0})}{g(x)-g(x_{0})}=frac{f(x)}{g(x)}(varphi(x))^{-1})
где (varphi(x)=frac{1-g(x_0)/g(x)}{1-f(x_0)/f(x)}=1+beta(x)).
Можно заметить, что (beta(x)rightarrow 0) при (xrightarrow +infty).
Таким образом:
(forall varepsilon > 0 existsdeltageqdelta_{2}: forall x > deltarightarrow|beta(x)| < frac{varepsilon/2}{|A|+varepsilon/2})
Исходя из того, что (xi > x_{0} > delta_{1}) и вышеуказанных выражений, следует, что для всех (x > delta_{2}) выполняется неравенство:
(A-frac{varepsilon}{2} < frac{f(x)}{g(x)}(varphi(x))^{-1} < A+frac{varepsilon}{2})
Когда (x > delta), получаем (phi(x) > 0.)
Таким образом, выведенное неравенство равносильно следующему:
((A-frac{varepsilon}{2})(1+beta(x)) < frac{f(x)}{g(x)} < (A+frac{varepsilon}{2})(1+beta(x)))
Исходя из этого утверждения, можно записать:
((A-frac{varepsilon}{2})(1+beta(x))=A-frac{varepsilon}{2}+left(A-frac{varepsilon}{2}right)beta(x)geq A-frac{varepsilon}{2}-left(|A|+frac{varepsilon}{2}right)|beta(x)| > A-frac{varepsilon}{2}-frac{varepsilon}{2}=A-varepsilon)
Аналогичным способом можно определить:
(left(A+frac{varepsilon}{2}right)(1+beta(x)) leq A+frac{varepsilon}{2}+left(|A|+frac{varepsilon}{2}right)|beta(x)| < A+varepsilon)
Получим, что для всех (x > delta) справедливо выведенное в теореме неравенство.
Теорема 2 работает при условии, что (A=+infty) или (A=-infty).
Теорема справедлива и в тех случаях, когда (xrightarrow a (xrightarrow a-0, xrightarrow a+0)), где a является конечной точкой.
Исходя из теорем 1 и 2, правило Лопиталя можно применять для раскрытия неопределенностей вида (displaystyle frac{0}{0}) или (displaystyle frac{infty}{infty}).
Неопределенности видов (0cdot infty, infty-infty, 0^{0}, infty^{0}, 1^{infty}) нередко удается преобразить в неопределенности типа (displaystyle frac{0}{0}) или (displaystyle frac{infty}{infty}), используя при этом различные преобразования.
Правило Лопиталя для вычисления пределов
Решить пределы можно различными методами и формулами. Наиболее быстрый и простой способ, а также универсальный — это правило Лопиталя. Умение искать производные разных функций позволит использовать данную закономерность наиболее эффективно. Можно сформулировать правило Лопиталя при следующих условиях:
- (lim limits_{x to a} f(x) = lim limits_{x to a} g(x) = 0 text{ или } infty)
- имеются (f'(a) text{ и } g'(a))
- (g'(x)neq0)
- присутствует (lim limits_{x to a} frac{f(x)}{g(x)})
В таком случае:
(lim limits_{x to a} frac{f(x)}{g(x)} = lim limits_{x to a} frac{f'(x)}{g'(x)})
Последовательность решения:
- нужно подставить точку x в предел;
- в том случае, когда получается (frac{0}{0} text{ или } frac{infty}{infty}), можно определить производную числителя и знаменателя;
- далее следует подставить точку x в записанный предел и рассчитать его. При получении неопределенности следует повторить пункты 2 и 3.
Раскрытие неопределенностей по правилу Лопиталя
В том случае, когда функции (f(x)) и (g(x)) дифференцируются в точке a, при этом (f(a)=g(a)=0) и (g'(a)neq 0), то, применяя к функциям (f) и (g) локальную формулу Тейлора при (n=1), получаем:
(f(x)=f'(a)(x-a)+o((x-a)))
(g(x)=g'(a)(x-a)+o((x-a)))
Таким образом:
(lim_{xrightarrow a}frac{f(x)}{g(x)}=frac{f'(a)}{g'(a)})
Аналогичным методом можно определить, что, при условии (f^{(n)}a) и (g^{(n)}a), получим:
(f(a)=f'(a)=ldots =f^{(n-1)}(a)=0)
(g(a)=g'(a)=ldots =g^{(n-1)}(a)=0)
Учитывая, что (g^{(n)}(a)neq 0), можно записать выражение:
(lim_{xrightarrow a}frac{f(x)}{g(x)}=displaystylelim_{xrightarrow a}frac{displaystyle frac{f^{(n)}(a)}{n!}(x-a)^{n}+o((x-a)^n)}{displaystyle frac{g^{(n)}(a)}{n!}(x-a)^{n}+o((x-a)^n)}=frac{f^{(n)}(a)}{g^{(n)}(a)})
Правило Лопиталя применимо в случае неопределенностей типа (0 cdot infty, infty – infty, 0^0, 1^{infty}, infty^0.)
Первую и вторую неопределенности (0 cdot infty) и (infty – infty) достаточно просто преобразовать в (largefrac{0}{0}normalsize) или (largefrac{infty}{infty}normalsize) по средствам алгебраических операций. А неопределенности (0^0, 1^{infty}) и (infty^0) можно свести к типу (0 cdot infty), используя соотношение:
(f{left( x right)^{gleft( x right)}} = {e^{gleft( x right)ln fleft( x right)}})
Формула и примеры решений
Правило Лопиталя: в том случае, когда две функции дифференцируемы в окрестности точки x=a, обращаются в нуль в этой точке, и существует предел отношения производных этих функций, то при х, которое стремится к а, существует предел отношения самих функций, который соотвесттвует пределу отношения производных.
Формула имеет следующий вид:
(lim_{xrightarrow a}frac{f(x)}{varphi (x)}=lim_{xrightarrow a}frac{f^{,}(x)}{varphi^{,} (x)})
Задача 1
Требуется найти предел:
(limlimits_{x to -1} frac{x^2-1}{x^3+x+2})
Решение
(lim limits_{x to -1} frac{x^2-1}{x^3+x+2} = frac{0}{0})
В полученной неопределенности (frac{0}{0}) можно заменить (х) точкой (x = -1). Данный вывод говорит о необходимости применения формулы расчета предела. Получим:
(lim limits_{x to -1} frac{(x^2-1)’}{(x^3+x+2)’} =lim limits_{x to -1} frac{2x}{3x^2+1})
Далее необходимо вновь рассчитать предел с помощью подстановки (x=-1) в последний предел. Таким образом:
(frac{2 cdot (-1)}{3 cdot (-1)^2+1} = frac{-2}{4} = -frac{1}{2})
Ответ: (limlimits_{x to -1} frac{x^2-1}{x^3+x+2} = -frac{1}{2})
Задача 2
Требуется вычислить предел, используя правило Лопиталя:
(lim limits_{x to infty} frac{ln x}{x})
Решение
Алгоритм вычислений стандартный:
(lim limits_{x to infty} frac{ln x}{x} = frac{infty}{infty} = lim limits_{x to infty} frac{(ln x)’}{(x)’}=lim limits_{x to infty} frac{frac{1}{x}}{1}=lim limits_{x to infty} frac{1}{x} = frac{1}{infty} = 0)
Ответ: (lim limits_{x to infty} frac{ln x}{x} = 0)
Задача 3
Необходимо предоставить решение предела с помощью формулы Лопиталя:
(lim limits_{x to 0} frac{cos x – 1}{x^2})
Решение
(lim limits_{xto 0} frac{cos x-1}{x^2} = frac{0}{0} = lim limits_{x to 0} frac{(cos x-1)’}{(x^2)’} =lim limits_{x to 0} frac{-sin x}{2x} = frac{0}{0}=lim limits_{x to 0} frac{(-sin x)’}{(2x)’} =lim limits_{x to 0} frac{-cos x}{2}=)
( = frac{-cos 0}{2} = -frac{1}{2})
Ответ: (lim limits_{x to 0} frac{cos x – 1}{x^2} = -frac{1}{2})
Задача 4
Нужно решить предел:
(lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1})
Решение
(lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1} = frac{0}{0}=lim limits_{xto 0} frac{(sin 2x-e^{5x}+1)’}{(x-cos x+1)’} =lim limits_{xto 0} frac{(sin 2x)’-(e^{5x})’+(1)’}{(x)’-(cos x)’+(1)’}=lim limits_{xto 0} frac{2cos 2x-5e^{5x}}{1+sin x} =)
(=frac{2cos0-5e^0}{1+sin 0}=frac{2cdot 1-5cdot 1}{1+0} = frac{-3}{1} = -3)
Ответ: (lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1} = -3)
Правилом Лопиталя допустимо пользоваться при решении задач с односторонними пределами. Можно сказать, что эта методика является наиболее эффективной для раскрытия неопределенностей вида (frac{0}{0}) и (frac{infty}{infty}) в том случае, когда необходимо вычислить предел. Смысл правила заключается в том, что предел отношения функций равен пределу отношений производных от этих функций. Если в процессе освоения этой и других подобных тем возникли сложности, всегда можно обратиться за помощью к сервису Феникс.Хелп.
Назначение сервиса. Данный сервис предназначен для решения пределов, используя правило Лопиталя. Результаты вычисления оформляются в формате Word (см. пример).
Это поле предназначено для ввода числителя дроби.
Правила ввода функций:
Например, x2+3x, записываем как x^2+3*x; ln(1+sin2x) ≡ ln(1+sin(x)^2)
Это поле предназначено для ввода знаменателя дроби. Если знаменатель отсутствует, можно оставить это поле пустым или указать 1.
Правила ввода функций:
Пример. Найти 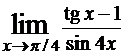
Решение.Сначала убедимся, что правило Лопиталя применить можно. Действительно, величины, стоящие в числителе и знаменателе при x → π/4 являются бесконечно малыми, то есть имеем неопределенность вида 0/0, следовательно можно воспользоваться правилом Лопиталя:
Теорема Лопита́ля (также правило Бернулли — Лопиталя[1]) — метод нахождения пределов функций, раскрывающий неопределённости вида 

Точная формулировка[править | править код]
Основной источник: [2]
Теорема Лопиталя:
Если: 




или
;
в
;
- существует
;
тогда существует 
Пределы также могут быть односторонними.
История[править | править код]
Способ раскрытия такого рода неопределённостей был опубликован в учебнике «Analyse des Infiniment Petits» 1696 года за авторством Гийома Лопиталя. Метод был сообщён Лопиталю в письме его первооткрывателем Иоганном Бернулли.[3]
Примеры[править | править код]
Следствие[править | править код]
Простое, но полезное следствие правила Лопиталя — признак дифференцируемости функций, состоит в следующем:
Пусть функция 







Для доказательства достаточно применить правило Лопиталя к отношению 
См. также[править | править код]
Аналогом правила Лопиталя для последовательностей вещественных чисел является Теорема Штольца.
Примечания[править | править код]
- ↑ Архивированная копия. Дата обращения: 14 декабря 2010. Архивировано 6 февраля 2009 года.
- ↑ Фихтенгольц, 1966, с. 314—316.
- ↑ Paul J. Nahin, An Imaginary Tale: The Story of
, p.216
Литература[править | править код]
- Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — Т. I. — 680 с. — ISBN 5-9221-0156-0.
Правило Лопиталя
Формула
Для решения пределов существуют различные методы решений и формулы. Но самым быстрым и легким способом, а также универсальным является метод Лопиталя. Для того, чтобы успешно пользоваться этим замечательным простым способом вычисления пределов достаточно хорошо уметь находить производные различных функций. Начнём с теории.
Сформулируем правило Лопиталя. Если:
- $ lim limits_{x to a} f(x) = lim limits_{x to a} g(x) = 0 text{ или } infty $
- Существуют $ f'(a) text{ и } g'(a) $
- $ g'(x)neq0 $
- Существует $ lim limits_{x to a} frac{f(x)}{g(x)} $
тогда существует $ lim limits_{x to a} frac{f(x)}{g(x)} = lim limits_{x to a} frac{f'(x)}{g'(x)} $
- Подставляем точку $ x $ в предел
- Если получается $ frac{0}{0} text{ или } frac{infty}{infty} $, тогда находим производную числителя и знаменателя
- Подставляем точку $ x $ в получившийся предел и вычисляем его. Если получается неопределенность, то повторяем пункты 2 и 3
Примеры решения
| Пример 1 |
| Решить предел по правилу Лопиталя: $ limlimits_{x to -1} frac{x^2-1}{x^3+x+2} $ |
| Решение |
|
$$ lim limits_{x to -1} frac{x^2-1}{x^3+x+2} = frac{0}{0} = $$ Видим, что получилась неопределенность $ frac{0}{0} $, если подставить вместо иксов точку $ x = -1 $, а это первый сигнал о том, что необходимо применить формулу для вычисления предела. Используем её: $$ = lim limits_{x to -1} frac{(x^2-1)’}{(x^3+x+2)’} = $$ $$ =lim limits_{x to -1} frac{2x}{3x^2+1} = $$ Снова попробуем вычислить предел подставив $ x=-1 $ в последний предел, получаем: $$ =frac{2 cdot (-1)}{3 cdot (-1)^2+1} = frac{-2}{4} = -frac{1}{2} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ limlimits_{x to -1} frac{x^2-1}{x^3+x+2} = -frac{1}{2} $$ |
| Пример 2 |
| Вычислить пределы правилом Лопиталя: $ lim limits_{x to infty} frac{ln x}{x} $ |
| Решение |
|
Решение проводим стандартно, подставляя икс. $$ lim limits_{x to infty} frac{ln x}{x} = frac{infty}{infty} = lim limits_{x to infty} frac{(ln x)’}{(x)’}= $$ $$ =lim limits_{x to infty} frac{frac{1}{x}}{1}=lim limits_{x to infty} frac{1}{x} = frac{1}{infty} = 0 $$ |
| Ответ |
| $$ lim limits_{x to infty} frac{ln x}{x} = 0 $$ |
| Пример 3 |
| Воспользовавшись формулой Лопиталя решить предел: $ lim limits_{x to 0} frac{cos x – 1}{x^2} $ |
| Решение |
|
$$ lim limits_{xto 0} frac{cos x-1}{x^2} = frac{0}{0} = lim limits_{x to 0} frac{(cos x-1)’}{(x^2)’}= $$ $$ =lim limits_{x to 0} frac{-sin x}{2x} = frac{0}{0}=lim limits_{x to 0} frac{(-sin x)’}{(2x)’}= $$ $$ =lim limits_{x to 0} frac{-cos x}{2} = frac{-cos 0}{2} = -frac{1}{2} $$ |
| Ответ |
| $$ lim limits_{x to 0} frac{cos x – 1}{x^2} = -frac{1}{2} $$ |
| Пример 4 |
| Вычислить предел используя правило Лопиталя: $ lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1} $ |
| Решение |
|
$$ lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1} = frac{0}{0}= $$ $$ =lim limits_{xto 0} frac{(sin 2x-e^{5x}+1)’}{(x-cos x+1)’} = $$ $$ =lim limits_{xto 0} frac{(sin 2x)’-(e^{5x})’+(1)’}{(x)’-(cos x)’+(1)’}= $$ $$ =lim limits_{xto 0} frac{2cos 2x-5e^{5x}}{1+sin x} =frac{2cos0-5e^0}{1+sin 0}= $$ $$ =frac{2cdot 1-5cdot 1}{1+0} = frac{-3}{1} = -3 $$ |
| Ответ |
| $$ lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1} = -3 $$ |
Подведем итог: Правило Лопиталя – это способ и метод благодаря которому можно раскрывать неопределенности вида $ frac{0}{0} $ и $ frac{infty}{infty} $ при вычислении пределов. Суть его состоит в том, что предел отношения функций равен пределу отношений производных от этих функций.