Как найти пределы с помощью правила лопиталя

Мы уже начали разбираться с пределами и их решением. Продолжим по горячим следам и разберемся с решением пределов по правилу Лопиталя. Этому простому правилу по силам помочь Вам выбраться из коварных и сложных ловушек, которые преподаватели так любят использовать в примерах на контрольных по высшей математике и матанализу. Решение правилом Лопиталя – простое и быстрое. Главное – уметь дифференцировать.

Правило Лопиталя: история и определение

На самом деле это не совсем правило Лопиталя, а правило Лопиталя-Бернулли. Сформулировал его швейцарский математик Иоганн Бернулли, а француз Гийом Лопиталь впервые опубликовал в своем учебнике бесконечно малых в славном 1696 году. Представляете, как людям приходилось решать пределы с раскрытием неопределенностей до того, как это случилось? Мы – нет.

Кстати, о том, какой вклад внес в науку сын Иоганна Бернулли, читайте в статье про течение жидкостей и уравнение Бернулли.

Прежде чем приступать к разбору правила Лопиталя, рекомендуем прочитать вводную статью про пределы в математике и методы их решений. Часто в заданиях встречается формулировка: найти предел, не используя правило Лопиталя. О приемах, которые помогут Вам в этом, также читайте в нашей статье.

Если имеешь дело с пределами дроби двух функций, будь готов: скоро встретишься с неопределенностью вида 0/0 или бесконечность/бесконечность. Как это понимать? В числителе и знаменателе выражения стремятся к нулю или бесконечности. Что делать с таким пределом, на первый взгляд – совершенно непонятно. Однако если применить правило Лопиталя и немного подумать, все становится на свои места.

Но сформулируем правило Лопиталя-Бернулли. Если быть совершенно точными, оно выражается теоремой. Правило Лопиталя, определение:

Если две функции дифференцируемы в окрестности точки x=a обращаются в нуль в этой точке, и существует предел отношения производных этих функций, то при х стремящемся к а существует предел отношения самих функций, равный пределу отношения производных.

Запишем формулу, и все сразу станет проще. Правило Лопиталя, формула:

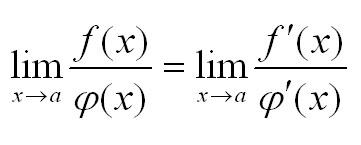
Так как нас интересует практическая сторона вопроса, не будем приводить здесь доказательство этой теоремы. Вам придется или поверить нам на слово, или найти его в любом учебнике по математическому анализу и убедится, что теорема верна.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Раскрытие неопределенностей по правилу Лопиталя

В раскрытии каких неопределенностей может помочь правило Лопиталя? Ранее мы говорили в основном о неопределенности 0/0. Однако это далеко не единственная неопределенность, с которой можно встретиться. Вот другие виды неопределенностей:

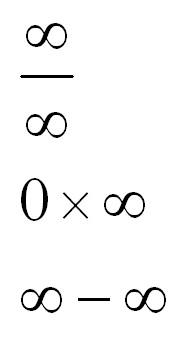
Рассмотрим преобразования, с помощью которых можно привести эти неопределенности к виду 0/0 или бесконечность/бесконечность. После преобразования можно будет применять правило Лопиталя-Бернулли и щелкать примеры как орешки.

Неопределенность вида бесконечность/бесконечность сводится к неопределенность вида 0/0 простым преобразованием:

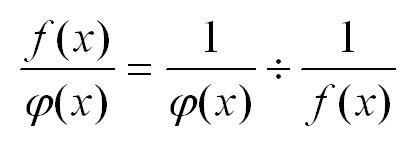
Пусть есть произведение двух функций, одна из которых первая стремиться к нулю, а вторая – к бесконечности. Применяем преобразование, и произведение нуля и бесконечности превращается в неопределенность 0/0:

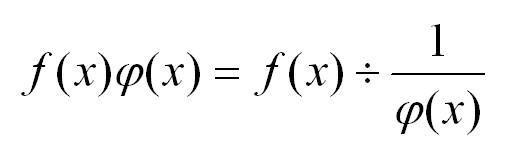
Для нахождения пределов с неопределенностями типа бесконечность минус бесконечность используем следующее преобразование,  приводящее к неопределенности 0/0:

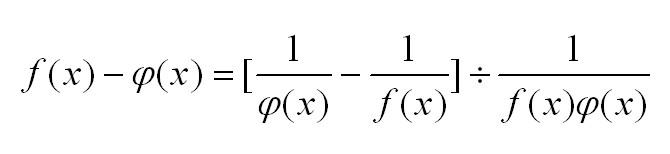
Для того чтобы пользоваться правилом Лопиталя, нужно уметь брать производные. Приведем ниже таблицу производных элементарных функций, которой Вы сможете пользоваться при решении примеров, а также правила вычисления производных сложных функций:

Теперь перейдем к примерам.

Пример 1

Найти предел по правилу Лопиталя:

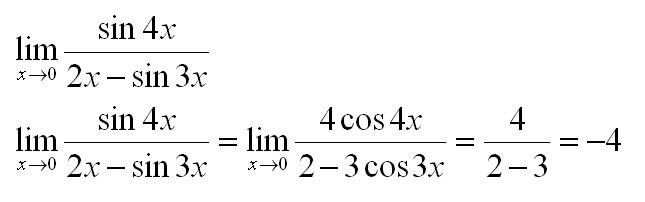
Пример 2

Вычислить с использованием правила Лопиталя:

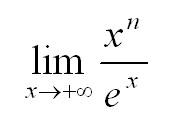
Важный момент! Если предел вторых и последующих производных функций существует при х стремящемся к а, то правило Лопиталя можно применять несколько раз.

Найдем предел (n – натуральное число). Для этого применим правило Лопиталя n раз:

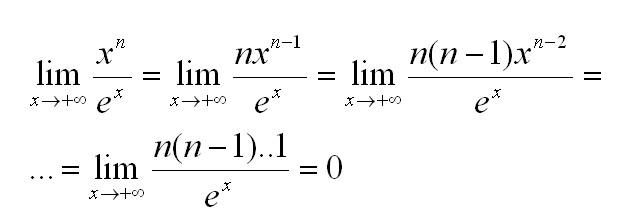
Желаем удачи в освоении математического анализа. А если Вам понадобится найти предел используя правило Лопиталя, написать реферат по правилу Лопиталя, вычислить корни дифференциального уравнения или даже рассчитать тензор инерции тела, обращайтесь к нашим авторам. Они с радостью помогут разобраться в тонкостях решения.

Теорема Лопита́ля (также правило Бернулли — Лопиталя^[1]) — метод нахождения пределов функций, раскрывающий неопределённости вида и . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.

Точная формулировка[править | править код]

Основной источник: ^[2]

Теорема Лопиталя:

Если:  — действительнозначные функции, дифференцируемые в проколотой окрестности точки , где  — действительное число или один из символов , причём

1. или ;
2. в ;
3. существует ;

тогда существует .

Пределы также могут быть односторонними.

История[править | править код]

Способ раскрытия такого рода неопределённостей был опубликован в учебнике «Analyse des Infiniment Petits» 1696 года за авторством Гийома Лопиталя. Метод был сообщён Лопиталю в письме его первооткрывателем Иоганном Бернулли.^[3]

Примеры[править | править код]

• 

Следствие[править | править код]

Простое, но полезное следствие правила Лопиталя — признак дифференцируемости функций, состоит в следующем:

Пусть функция дифференцируема в проколотой окрестности точки , а в самой этой точке она непрерывна и имеет предел производной . Тогда функция дифференцируема и в самой точке , и (то есть, производная непрерывна в точке ).

Для доказательства достаточно применить правило Лопиталя к отношению .

См. также[править | править код]

Аналогом правила Лопиталя для последовательностей вещественных чисел является Теорема Штольца.

Примечания[править | править код]

Литература[править | править код]

• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — изд. 6-е. — М.: Наука, 1966. — Т. I. — 680 с. — ISBN 5-9221-0156-0.

В задачах на пределы можно столкнуться с ситуациями, разрешить которые достаточно просто, используя правило Лопиталя. Относительно простая закономерность является очень полезной, когда требуется найти ответ к заданию по математике или математическому анализу. При этом важно владеть навыками дифференцирования.

Правило Лопиталя — в чем суть, понятие

Название этой закономерности не совсем соответствует действительности. Было бы правильнее говорить «правило Лопиталя — Бернулли». Первая подробная формулировка была представлена швейцарским математиком Иоганном Бернулли. Французский ученый Гийом Лопиталь впервые опубликовал это правило в издании собственного учебника в 1696 году.

Правило Лопиталя позволяет существенно упростить некоторые расчеты предела отношения (displaystyle frac{f(x)}{g(x)}) при (xrightarrow a) в том случае, когда (f) и (g) одновременно представляют собой бесконечно малые, либо бесконечно большие величины. С помощью выведенной закономерности допустимо осуществлять замену предела отношения функции, используя предел отношения их производных.

Доказательство 1 и 2 правила Лопиталя, вывод теоремы

Теорема 1

Допустим, что функции (f(x)) и (g(x)) дифференцируются на промежутке ((a,b)):

(lim_{xrightarrow a+0}f(x)=0)

(lim_{xrightarrow a+0}g(x)=0)

(g'(x)neq 0 ) для всех ( xin(a,b))

Тогда имеет место конечный и бесконечный:

(lim_{xrightarrow a+0}frac{f'(x)}{g'(x)}=A)

Таким образом, также существует и равен A:

(displaystylelim_{xrightarrow a+0}frac{f(x)}{g(x)})

Можно сделать вывод:

(lim_{xrightarrow a+0}frac{f(x)}{g(x)}=lim_{xrightarrow a+0}frac{f'(x)}{g'(x)})(lim_{xrightarrow a+0}frac{f(x)}{g(x)}=lim_{xrightarrow a+0}frac{f'(x)}{g'(x)})

Докажем данную теорию.

Допустим, что (xin(a,b))

Следует доопределить функции (f(x)) и (g(x)) в точке a, имея в виду, что:

(f(a)=g(a)=0)

Таким образом, из условий функций следует, что (f) и (g) непрерывны на отрезке [a,x]. По теореме Коши имеется точка (xiin (a,x)), такая, что:

(frac{f(x)}{g(x)}=frac{f(x)-f(a)}{g(x)-g(a)}=frac{f'(xi)}{g'(xi)})

В том случае, когда (xrightarrow a+0), можно определить, что (xirightarrow a+0). Зная, что  существует (displaystyle lim_{xrightarrow a+0}frac{f'(xi)}{g'(xi)}=A), можно сделать вывод о справедливости утверждения (eqref).

Теорема, доказательства которой представлены путем соответствующих изменений ее условий, работает, когда (xrightarrow a-0) и (xrightarrow a). Точка a в данном случае является конечной.

Теорема 1 остается справедливой в таких ситуациях, когда (a=+infty) или (a=-infty), а также:

(displaystyle lim_{xrightarrow +infty}f(x)=lim_{xrightarrow +infty} g(x)=0)

( g'(x)neq 0) при (x > x_0)и существует (displaystyle lim_{xrightarrow +infty}frac{f'(x)}{g'(x)}=A)

В этом случае (displaystyle lim_{xrightarrow +infty}frac{f(x)}{g(x)}=A)

Доказательство данного утверждения выполнено с помощью замены переменного (displaystyle x=frac{1}{t}) и Теоремы 1.

Теорема 2

Допустим, что функции (f(x)) и (g(x)) дифференцируются при (x > alpha) и (g'(x)neq 0) при (x > alpha)

(lim_{xrightarrow+infty}f(x)=infty,quad lim_{xrightarrow +infty}g(x)=infty)

и существует конечный:

(lim_{xrightarrow +infty}frac{f'(x)}{g'(x)}=A)

В таком случае, существует (displaystyle lim_{xrightarrow +infty}frac{f(x)}{g(x)}), равный A.

Таким образом:

(lim_{xrightarrow +infty}frac{f(x)}{g(x)}=lim_{xrightarrow +infty}frac{f'(x)}{g'(x)} )

Доказательство

Зная, что:

(existsalpha_{1} > alpha: forall x > alpha_{1}rightarrow |f(x)| > 1)

( |g(x)| > 1)

Исходя из записанного выражения, получим, что (f(x)neq 0) и ( g(x)neq 0) при (x > alpha_1).

Согласно определению, для заданного числа (varepsilon > 0) можно вычислить (delta=delta_1(varepsilon)geq alpha_1) такое, что для всех (t > delta_{1}) выполняется неравенство:

(A-frac{varepsilon}{2} < frac{f'(t)}{g'(t)} < A+frac{varepsilon}{2})

Определив (x_{0} > delta_{1}) на рисунке, выберем число (delta_{2} > x_{0}) такое, чтобы при всех (x > delta_{2}) выполнялись неравенства:

(left|frac{f(x_{0})}{f(x)}right| < frac{1}{2},quad left|frac{g(x_{0})}{g(x)}right| < frac{1}{2})

В качестве доказательства выражения нужно определить, что существует (delta) такое, при котором, если все (x > delta), выполняется неравенство:

(A-varepsilon < frac{f(x)}{g(x)} < A+varepsilon)

Число (delta) будет выбрано ниже. Учитывая, что (x > delta), можно применить к функциям (f) и (g) на интервале ([x_0,x]) теорему Коши о среднем. Согласно данному утверждению, должна существовать точка (xiin [x_{0},x]) такая, при которой:

(frac{f(x)-f(x_{0})}{g(x)-g(x_{0})}=frac{f'(xi)}{g'(xi)})

Преобразуем левую часть равенства:

(frac{f(x)-f(x_{0})}{g(x)-g(x_{0})}=frac{f(x)}{g(x)}(varphi(x))^{-1})

где (varphi(x)=frac{1-g(x_0)/g(x)}{1-f(x_0)/f(x)}=1+beta(x)).

Можно заметить, что (beta(x)rightarrow 0) при (xrightarrow +infty).

Таким образом:

(forall varepsilon > 0 existsdeltageqdelta_{2}: forall x > deltarightarrow|beta(x)| < frac{varepsilon/2}{|A|+varepsilon/2})

Исходя из того, что (xi > x_{0} > delta_{1}) и вышеуказанных выражений, следует, что для всех (x > delta_{2}) выполняется неравенство:

(A-frac{varepsilon}{2} < frac{f(x)}{g(x)}(varphi(x))^{-1} < A+frac{varepsilon}{2})

Когда (x > delta), получаем (phi(x) > 0.)

Таким образом, выведенное неравенство равносильно следующему:

((A-frac{varepsilon}{2})(1+beta(x)) < frac{f(x)}{g(x)} < (A+frac{varepsilon}{2})(1+beta(x)))

Исходя из этого утверждения, можно записать:

((A-frac{varepsilon}{2})(1+beta(x))=A-frac{varepsilon}{2}+left(A-frac{varepsilon}{2}right)beta(x)geq A-frac{varepsilon}{2}-left(|A|+frac{varepsilon}{2}right)|beta(x)| > A-frac{varepsilon}{2}-frac{varepsilon}{2}=A-varepsilon)

Аналогичным способом можно определить:

(left(A+frac{varepsilon}{2}right)(1+beta(x)) leq A+frac{varepsilon}{2}+left(|A|+frac{varepsilon}{2}right)|beta(x)| < A+varepsilon)

Получим, что для всех (x > delta) справедливо выведенное в теореме неравенство.

Теорема 2 работает при условии, что (A=+infty) или (A=-infty).

Теорема справедлива и в тех случаях, когда (xrightarrow a (xrightarrow a-0, xrightarrow a+0)), где a является конечной точкой.

Исходя из теорем 1 и 2, правило Лопиталя можно применять для раскрытия неопределенностей вида (displaystyle frac{0}{0}) или (displaystyle frac{infty}{infty}).

Неопределенности видов (0cdot infty, infty-infty, 0^{0}, infty^{0}, 1^{infty}) нередко удается преобразить в неопределенности типа (displaystyle frac{0}{0}) или (displaystyle frac{infty}{infty}), используя при этом различные преобразования.

Правило Лопиталя для вычисления пределов

Решить пределы можно различными методами и формулами. Наиболее быстрый и простой способ, а также универсальный — это правило Лопиталя. Умение искать производные разных функций позволит использовать данную закономерность наиболее эффективно. Можно сформулировать правило Лопиталя при следующих условиях:

• (lim limits_{x to a} f(x) = lim limits_{x to a} g(x) = 0 text{ или } infty)
• имеются (f'(a) text{ и } g'(a))
• (g'(x)neq0)
• присутствует (lim limits_{x to a} frac{f(x)}{g(x)})

В таком случае:

(lim limits_{x to a} frac{f(x)}{g(x)} = lim limits_{x to a} frac{f'(x)}{g'(x)})

Последовательность решения:

• нужно подставить точку x в предел;
• в том случае, когда получается (frac{0}{0} text{ или } frac{infty}{infty}), можно определить производную числителя и знаменателя;
• далее следует подставить точку x в записанный предел и рассчитать его. При получении неопределенности следует повторить пункты 2 и 3.

Раскрытие неопределенностей по правилу Лопиталя

В том случае, когда функции (f(x)) и (g(x)) дифференцируются в точке a, при этом (f(a)=g(a)=0) и (g'(a)neq 0), то, применяя к функциям (f) и (g) локальную формулу Тейлора при (n=1), получаем:

(f(x)=f'(a)(x-a)+o((x-a)))

(g(x)=g'(a)(x-a)+o((x-a)))

Таким образом:

(lim_{xrightarrow a}frac{f(x)}{g(x)}=frac{f'(a)}{g'(a)})

Аналогичным методом можно определить, что, при условии (f^{(n)}a) и (g^{(n)}a), получим:

(f(a)=f'(a)=ldots =f^{(n-1)}(a)=0)

(g(a)=g'(a)=ldots =g^{(n-1)}(a)=0)

Учитывая, что (g^{(n)}(a)neq 0), можно записать выражение:

(lim_{xrightarrow a}frac{f(x)}{g(x)}=displaystylelim_{xrightarrow a}frac{displaystyle frac{f^{(n)}(a)}{n!}(x-a)^{n}+o((x-a)^n)}{displaystyle frac{g^{(n)}(a)}{n!}(x-a)^{n}+o((x-a)^n)}=frac{f^{(n)}(a)}{g^{(n)}(a)})

Правило Лопиталя применимо в случае неопределенностей типа (0 cdot infty, infty – infty, 0^0, 1^{infty}, infty^0.)

Первую и вторую неопределенности (0 cdot infty)  и (infty – infty) достаточно просто преобразовать в (largefrac{0}{0}normalsize) или (largefrac{infty}{infty}normalsize) по средствам алгебраических операций. А неопределенности (0^0, 1^{infty}) и (infty^0) можно свести к типу (0 cdot infty), используя соотношение:

(f{left( x right)^{gleft( x right)}} = {e^{gleft( x right)ln fleft( x right)}})

Формула и примеры решений

Правило Лопиталя: в том случае, когда две функции дифференцируемы в окрестности точки x=a, обращаются в нуль в этой точке, и существует предел отношения производных этих функций, то при х, которое стремится к а, существует предел отношения самих функций, который соотвесттвует пределу отношения производных.

Формула имеет следующий вид:

(lim_{xrightarrow a}frac{f(x)}{varphi (x)}=lim_{xrightarrow a}frac{f^{,}(x)}{varphi^{,} (x)})

Задача 1

Требуется найти предел:

(limlimits_{x to -1} frac{x^2-1}{x^3+x+2})

Решение

(lim limits_{x to -1} frac{x^2-1}{x^3+x+2} = frac{0}{0})

В полученной неопределенности (frac{0}{0}) можно заменить (х) точкой (x = -1). Данный вывод говорит о необходимости применения формулы расчета предела. Получим:

(lim limits_{x to -1} frac{(x^2-1)’}{(x^3+x+2)’} =lim limits_{x to -1} frac{2x}{3x^2+1})

Далее необходимо вновь рассчитать предел с помощью подстановки (x=-1) в последний предел. Таким образом:

(frac{2 cdot (-1)}{3 cdot (-1)^2+1} = frac{-2}{4} = -frac{1}{2})

Ответ: (limlimits_{x to -1} frac{x^2-1}{x^3+x+2} = -frac{1}{2})

Задача 2

Требуется вычислить предел, используя правило Лопиталя:

(lim limits_{x to infty} frac{ln x}{x})

Решение

Алгоритм вычислений стандартный:

(lim limits_{x to infty} frac{ln x}{x} = frac{infty}{infty} = lim limits_{x to infty} frac{(ln x)’}{(x)’}=lim limits_{x to infty} frac{frac{1}{x}}{1}=lim limits_{x to infty} frac{1}{x} = frac{1}{infty} = 0)

Ответ: (lim limits_{x to infty} frac{ln x}{x} = 0)

Задача 3

Необходимо предоставить решение предела с помощью формулы Лопиталя:

(lim limits_{x to 0} frac{cos x – 1}{x^2})

Решение
(lim limits_{xto 0} frac{cos x-1}{x^2} = frac{0}{0} = lim limits_{x to 0} frac{(cos x-1)’}{(x^2)’} =lim limits_{x to 0} frac{-sin x}{2x} = frac{0}{0}=lim limits_{x to 0} frac{(-sin x)’}{(2x)’} =lim limits_{x to 0} frac{-cos x}{2}=)

( = frac{-cos 0}{2} = -frac{1}{2})

Ответ: (lim limits_{x to 0} frac{cos x – 1}{x^2} = -frac{1}{2})

Задача 4

Нужно решить предел:

(lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1})

Решение

(lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1} = frac{0}{0}=lim limits_{xto 0} frac{(sin 2x-e^{5x}+1)’}{(x-cos x+1)’} =lim limits_{xto 0} frac{(sin 2x)’-(e^{5x})’+(1)’}{(x)’-(cos x)’+(1)’}=lim limits_{xto 0} frac{2cos 2x-5e^{5x}}{1+sin x} =)

(=frac{2cos0-5e^0}{1+sin 0}=frac{2cdot 1-5cdot 1}{1+0} = frac{-3}{1} = -3)

Ответ: (lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1} = -3)

Правилом Лопиталя допустимо пользоваться при решении задач с односторонними пределами. Можно сказать, что эта методика является наиболее эффективной для раскрытия неопределенностей вида (frac{0}{0}) и (frac{infty}{infty}) в том случае, когда необходимо вычислить предел. Смысл правила заключается в том, что предел отношения функций равен пределу отношений производных от этих функций. Если в процессе освоения этой и других подобных тем возникли сложности, всегда можно обратиться за помощью к сервису Феникс.Хелп.

Уважаемые студенты!
Заказать решение задач можно у нас всего за 10 минут.

Правило Лопиталя

Формула

Для решения пределов существуют различные методы решений и формулы. Но самым быстрым и легким способом, а также универсальным является метод Лопиталя. Для того, чтобы успешно пользоваться этим замечательным простым способом вычисления пределов достаточно хорошо уметь находить производные различных функций. Начнём с теории.

Сформулируем правило Лопиталя. Если:

• $ lim limits_{x to a} f(x) = lim limits_{x to a} g(x) = 0 text{ или } infty $
• Существуют $ f'(a) text{ и } g'(a) $
• $ g'(x)neq0 $
• Существует $ lim limits_{x to a} frac{f(x)}{g(x)} $

тогда существует $ lim limits_{x to a} frac{f(x)}{g(x)} = lim limits_{x to a} frac{f'(x)}{g'(x)} $

Примеры решения

Пример 1

Решить предел по правилу Лопиталя: $ limlimits_{x to -1} frac{x^2-1}{x^3+x+2} $

Решение

$$ lim limits_{x to -1} frac{x^2-1}{x^3+x+2} = frac{0}{0} = $$ Видим, что получилась неопределенность $ frac{0}{0} $, если подставить вместо иксов точку $ x = -1 $, а это первый сигнал о том, что необходимо применить формулу для вычисления предела. Используем её: $$ = lim limits_{x to -1} frac{(x^2-1)’}{(x^3+x+2)’} = $$ $$ =lim limits_{x to -1} frac{2x}{3x^2+1} = $$ Снова попробуем вычислить предел подставив $ x=-1 $ в последний предел, получаем: $$ =frac{2 cdot (-1)}{3 cdot (-1)^2+1} = frac{-2}{4} = -frac{1}{2} $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ limlimits_{x to -1} frac{x^2-1}{x^3+x+2} = -frac{1}{2} $$

Пример 2

Вычислить пределы правилом Лопиталя: $ lim limits_{x to infty} frac{ln x}{x} $

Решение

Решение проводим стандартно, подставляя икс. $$ lim limits_{x to infty} frac{ln x}{x} = frac{infty}{infty} = lim limits_{x to infty} frac{(ln x)’}{(x)’}= $$ $$ =lim limits_{x to infty} frac{frac{1}{x}}{1}=lim limits_{x to infty} frac{1}{x} = frac{1}{infty} = 0 $$

Ответ

$$ lim limits_{x to infty} frac{ln x}{x} = 0 $$

Пример 3

Воспользовавшись формулой Лопиталя решить предел: $ lim limits_{x to 0} frac{cos x – 1}{x^2} $

Решение

$$ lim limits_{xto 0} frac{cos x-1}{x^2} = frac{0}{0} = lim limits_{x to 0} frac{(cos x-1)’}{(x^2)’}= $$ $$ =lim limits_{x to 0} frac{-sin x}{2x} = frac{0}{0}=lim limits_{x to 0} frac{(-sin x)’}{(2x)’}= $$ $$ =lim limits_{x to 0} frac{-cos x}{2} = frac{-cos 0}{2} = -frac{1}{2} $$

Ответ

$$ lim limits_{x to 0} frac{cos x – 1}{x^2} = -frac{1}{2} $$

Пример 4

Вычислить предел используя правило Лопиталя: $ lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1} $

Решение

$$ lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1} = frac{0}{0}= $$ $$ =lim limits_{xto 0} frac{(sin 2x-e^{5x}+1)’}{(x-cos x+1)’} = $$ $$ =lim limits_{xto 0} frac{(sin 2x)’-(e^{5x})’+(1)’}{(x)’-(cos x)’+(1)’}= $$ $$ =lim limits_{xto 0} frac{2cos 2x-5e^{5x}}{1+sin x} =frac{2cos0-5e^0}{1+sin 0}= $$ $$ =frac{2cdot 1-5cdot 1}{1+0} = frac{-3}{1} = -3 $$

Ответ

$$ lim limits_{xto 0} frac{sin 2x-e^{5x}+1}{x-cos x+1} = -3 $$

Подведем итог: Правило Лопиталя – это способ и метод благодаря которому можно раскрывать неопределенности вида $ frac{0}{0} $ и $ frac{infty}{infty} $ при вычислении пределов. Суть его состоит в том, что предел отношения функций равен пределу отношений производных от этих функций.

Правило Лопиталя

Правило Лопиталя было открыто шведским математиком Иоганном Бернулли, который затем рассказал в письме о нём Лопиталю. Лопиталь же опубликовал это правило в первом учебнике по дифференциальному исчислению в 1696 году со своим авторством.

Правило Лопиталя применяется для выражений, сводимых к неопределенностям следующего вида:

$frac{0}{0} begin{array}{ccc} {} & {} & {frac{infty }{infty } } end{array}$

Вместо нуля в первом выражении может быть какая-либо бесконечно малая величина.

В общем случае правилом Лопиталя можно воспользоваться, если и в числителе, и в знаменателе одновременно нуль или бесконечность.

Условия, при которых можно применять правило Лопиталя:

• Соблюдается условие, при котором пределы функций $f(x)$ и $g(x)$ при $x$ стремящемся к $a$ равны между собой и стремятся к нулю или бесконечности: $mathop{lim }limits_{xto a} f(x)=mathop{lim }limits_{xto a} g(x)=0$ или $mathop{lim }limits_{xto a} f(x)=mathop{lim }limits_{xto a} g(x)=infty $;
• Возможно получить производные $f(x)$ и $g(x)$ в окрестности $a$;
• Производная функции $g(x)$ не нулевая $g'(x)ne 0$ в окрестности $a$;
• Предел отношения производных функций $f(x)$ и $g(x)$, в записи выглядящий как $mathop{lim }limits_{xto a} frac{f'(x)}{g'(x)} $ существует.

Доказательство правила Лопиталя:

1. Пусть даны функции $f(x)$ и $g(x)$, причём наблюдается равенство пределов:
2. $mathop{lim }limits_{xto a+0} f(x)=mathop{lim }limits_{xto a+0} g(x)=0 $.
3. Доопределим функции в точке $a$. Для этой точки будет справедливым условие:
4. $frac{f(x)}{g(x)} =frac{f(x)-f(a)}{g(x)-g(a)} =frac{f'(c)}{g'(c)}$.
5. Величина $c$ зависит от $x$, но если $xto a+0$, то $cto a$.
6. $mathop{lim }limits_{xto a+0} frac{f(x)}{g(x)} =mathop{lim }limits_{cto a+0} frac{f'(c)}{g'(c)} =mathop{lim }limits_{xto a+0} frac{f'(c)}{g'(c)} $.

«Правило Лопиталя» 👇

Алгоритм вычисления решения с использованием правила Лопиталя

1. Проверка всего выражения на неопределенность.
2. Проверка всех условий, изложенных выше перед дальнейшим использованием правила Лопиталя.
3. Проверка стремления производной функции к $0$.
4. Повторная проверка на неопределенность.

Пример № 1:

Найти предел:

$mathop{lim }limits_{xto 0} frac{x^{2} +5x}{3x} $

Решение:

Проверим условия применимости правила Лопиталя:

• Предел функции $f(x)$ равен пределу $g(x)$ и оба они равны нулю: $mathop{lim }limits_{xto a} f(x)=mathop{lim }limits_{xto 0} (x^{2} +5x)=0$; $mathop{lim }limits_{xto a} g(x)=mathop{lim }limits_{xto 0} (3x)=0$
• $f(x)$ и $g(x)$ дифференцируемы в окрестности $a$
• $g'(x)=3ne 0$ в окрестности $a$
• $mathop{lim }limits_{xto a} frac{f'(x)}{g'(x)} =mathop{lim }limits_{xto 0} frac{2x+5}{3} $

Запишем производную и найдем предел функции:

$mathop{lim }limits_{xto 0} frac{x^{2} +5x}{3x} =leftlangle frac{0}{0} rightrangle =mathop{lim }limits_{xto 0} frac{left(x^{2} +5xright)’}{left(3xright)’} =mathop{lim }limits_{xto 0} frac{2x+5}{3} =frac{0+5}{3} =frac{5}{3} $

Пример № 2:

Найти предел:

$mathop{lim }limits_{xto infty } frac{x^{3} -3x^{2} +2x}{x^{3} -x} $

Решение:

Проверим условия применимости правила Лопиталя:

• $mathop{lim }limits_{xto a} f(x)=mathop{lim }limits_{xto infty } (x^{3} -3x^{2} +2x)=infty $; $mathop{lim }limits_{xto a} g(x)=mathop{lim }limits_{xto infty } (x^{3} -x)=infty $
• $f(x)$ и $g(x)$ дифференцируемы в окрестности $a$
• $g'(x)=6ne 0$ в окрестности $a$
• $mathop{lim }limits_{xto a} frac{f'(x)}{g'(x)} =mathop{lim }limits_{xto infty } frac{3x^{2} -6x+2}{3x^{2} -1} $

Запишем производную и найдем предел функции:

$mathop{lim }limits_{xto infty } frac{x^{3} -3x^{2} +2x}{x^{3} -x} =leftlangle frac{infty }{infty } rightrangle =mathop{lim }limits_{xto infty } frac{left(x^{3} -3x^{2} +2xright)’}{left(x^{3} -xright)’} =mathop{lim }limits_{xto infty } frac{3x^{2} -6x+2}{3x^{2} -1} =leftlangle frac{infty }{infty } rightrangle $

Повторяем вычисление производной пока не избавимся от неопределенности:

$mathop{lim }limits_{xto infty } frac{left(3x^{2} -6x+2right)’}{left(3x^{2} -1right)’} =mathop{lim }limits_{xto infty } frac{6x-6}{6x} =leftlangle frac{infty }{infty } rightrangle =mathop{lim }limits_{xto infty } frac{left(6x-6right)’}{left(6xright)’} =frac{6}{6} =1$

Пример № 3:

Найти предел:

$mathop{lim }limits_{xto 0} frac{sin 5x}{x} $

Решение:

$mathop{lim }limits_{xto 0} frac{sin 5x}{x} =leftlangle frac{0}{0} rightrangle =mathop{lim }limits_{xto 0} frac{left(sin 5xright)’}{left(xright)’} =mathop{lim }limits_{xto 0} frac{5cos 5x}{1} =5mathop{lim }limits_{xto 0} cos 5x=5$

Пример № 4:

Найти предел:

$mathop{lim }limits_{xto infty } (1+x^{2} )^{1/x} $

Решение:

Прологарифмируем функцию:

$ln y=frac{1}{x} ln (1+x^{2} )=frac{ln (1+x^{2} )}{x} $

$mathop{lim }limits_{xto infty } frac{ln (1+x^{2} )}{x} =mathop{lim }limits_{xto infty } frac{left[ln (1+x^{2} )right]’}{x’} =mathop{lim }limits_{xto infty } frac{frac{2x}{1+x^{2} } }{1} =0$

Поскольку функция $ln(y)$ — непрерывная, получим:

$mathop{lim }limits_{xto infty } (ln y)=ln (mathop{lim }limits_{xto infty } y)$

Следовательно,

$ln (mathop{lim }limits_{xto infty } y)=0$

$mathop{lim }limits_{xto infty } y=1$

Значит,

$mathop{lim }limits_{xto infty } (1+x^{2} )^{1/x} =1$