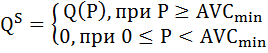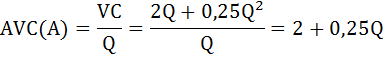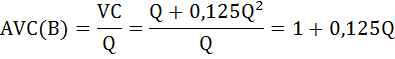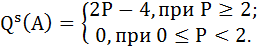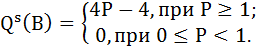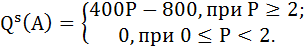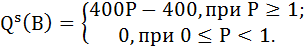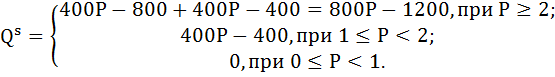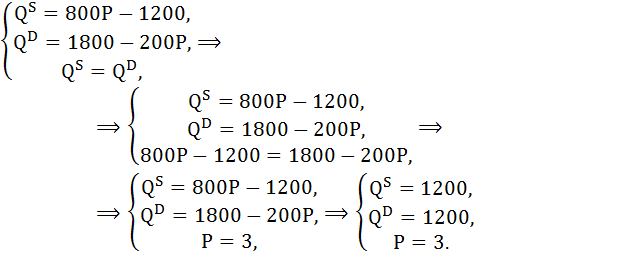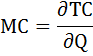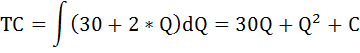Как найти предложение зная издержки

На некотором рынке совершенной конкуренции действуют фирмы двух типов:

200 фирм типа А, каждая из которых имеет общие затраты:

TC (A) = 200 + 2 × Q + 0,25 × Q²

100 фирм типа В, каждая из которых несёт общие затраты в размере:

TC (В) = 200 + Q + 0,125 × Q².

Требуется:

а) Вывести формулу рыночного предложения.

б) Найти равновесную цену и рыночный объём производства при условии, что рыночный спрос задан функцией:

Q_d = 1800 – 200 × P.

в) Сколько при этом будут производить фирма типа А и типа В?

Решение:

а) Чтобы вывести формулу предложения отрасли, необходимо определить функцию предложения одного предприятия.

Функция предложения совпадает с функцией предельных издержек, начиная с точки пересечения с кривой средних переменных издержек, включая эту точку. Кривая предельных издержек пересекается с кривой средних переменных издержек в точке их минимума.

То есть функция предложения в краткосрочном периоде (как определить период смотрите в задаче №102) должна удовлетворять следующим условиям:

Согласно условию максимизации прибыли на рынке совершенной конкуренции:

МС = Р.

Тогда это условие для каждого типа фирм будет иметь вид:

МС(А) = Р и МС(В) = Р

2 + 0,5 × Q_A = Р и 1 + 0,25 × Q_B = Р

Q_A = 2Р – 4 и Q_B = 4Р – 4

Определим функции средних переменных издержек:

Их минимальные значения равны:

min AVC(A) = 2,

min AVC(B) = 1.

Таким образом, функция предложения фирм типа А имеет вид:

Функция предложения фирм типа В имеет вид:

Так как на рынке действует 200 фирм типа А, их совокупное предложение равно:

Совокупное предложение 100 фирм типа В равно:

Совокупное предложение на рынке найдём суммированием по горизонтали индивидуальных предложений:

б) Найдём равновесие на рынке.

Q_S = Q_D

Так как Q_S(при Р=2) = 400 < Q_D(при Р=2) = 1200 и так как функция спроса имеет падающий вид, а функция предложения растущая, кривая спроса должна пересечься с кривой предложения при цене выше 2; значит рыночное равновесие имеет место при 800Р – 1200.

в) Объём производства каждой фирмы типа А при Р = 3 составит:

Q(A) = 2 × 3 – 4 = 2.

А объём производства каждой фирмы типа В составит:

Q(В) = 4 × 3 – 4 = 8.

Функция издержек и функция предложения

Задача №169. Нахождение уравнений кривых спроса и предложения

Спрос и предложение на рынке на товар задаются линейными уравнениями. Известно, что равновесная цена равна 200 руб. за упаковку товара, а равновесное количество – 100 упаковок в день. В точке равновесия однопроцентное повышение цены на данный товар влечет снижение величины спроса на 1,5% и повышение величины предложения на 0,5%.

Определите уравнения кривых спроса и предложения, считая их линейными.

Решение:

Общая точка двух прямых спроса и предложения имеет координаты:

Общий вид линейной функции спроса:

Так как однопроцентное повышение цены на данный товар влечет снижение величины спроса на 1,5%, следовательно, коэффициент эластичности спроса равен:

Запишем формулу точечной эластичности спроса по цене:

Подставим имеющиеся по условию данные:

Тогда функция спроса на данный товар имеет вид:

Общий вид линейной функции предложения:

Так как однопроцентное повышение цены на данный товар влечет повышение величины предложения на 0,5%., следовательно, коэффициент эластичности предложения равен:

Формула эластичности предложения будет иметь вид:

Подставим имеющиеся по условию данные:

Тогда функция предложения на данный товар имеет вид:

Определение функции предложения

Предположим, что зависимость совокупных издержек от объема производство конкретной фирмы задана уравнением:

ТС = 500 + 20Q – Q 2 , где TFC = 500 у.е.

Необходимо подсчитать, какой объем производства будет предло­жен компанией на рынок при сложившейся цене Р — 10 у.е.

Для начала определим функцию предложения фирмы в краткосроч­ном периоде.

1) Выведем уравнение предельных издержек (МС):

2) Приравняем придельные издержки к рыночной цене и получим ис­комую функцию предложения:

20 – 2Q = P; 2Q= 20 – Р; Q_s = 10 – 0,5Р.

3) Определим объем выпуска при Р = 10 у.е., подставив соответст­вующее значение в функцию предложения:

До сих пор мы рассматривали краткосрочный период, кото­рый предполагает существование неизменного числа фирм в отрасли и наличие у предприятий определенного объема постоянных ре­сурсов.

В долгосрочном периоде все факторы производства являются переменными. Для действующих на рынке фирм это предпола­гает возможность изменения размеров производства, внедрения новой технологии и модификации продукции, а для отрасли в целом — изменение числа фирм-производителей. Поскольку мы рассматриваем конкурентную отрасль, то допускаем отсут­ствие каких-либо ограничений на вход или выход из отрасли.

Если уровень сложившихся в отрасли издержек позволяет отдельным производителям получать положительную кратко­срочную экономическую прибыль, то действующие на рынке фирмы стремятся расширить свое производство и получить максимальную выгоду от благоприятной рыночной конъюнк­туры.

Одновременно с этим возрастает инвестиционная привлекательность отрасли и все большее количество внешних фирм начинает проявлять заинтересованность в проникновении на данный рынок. Очевидно, что скорость протекания данных процессов будет в значительной степени зависеть от ожидае­мой нормы отраслевой прибыли.

Появление в отрасли новых фирм и расширение деятельно­сти старых неизбежно увеличат рыночное предложение, вызо­вут тенденцию к сокращению рыночной цены и, как следст­вие, к уменьшению прибылей.

Если по каким-либо причинам (например, крайне высокая привлекательность рынка) рыночное предложение увеличится до уровня, при котором фирмы не смогут извлекать даже нормальную прибыль, начнется постепенный отток компаний в более прибыльные сферы деятельности и сокращение масшта­бов деятельности на оставшихся производствах.

Сокращение отраслевого предложения вызывает обратный процесс. Цены постепенно начинают возрастать, убытки со­кращаться, и отток фирм приостанавливается.

Следует отметить, что на практике регулирующие силы рынка лучше работают на расширение, чем на сжатие. Эконо­мическая прибыль и свобода входа на рынок активно стимули­руют увеличение объемов отраслевого производства. Напро­тив, процесс выдавливания фирм из чрезмерно расширенной и убыточной отрасли требует времени и является крайне болез­ненным для фирм-участниц.

Процесс входа-выхода фирм будет продолжаться до тех пор, пока не установится долгосрочное рыночное равновесие.

Таким образом, конкурентное долгосрочное равновесие предполагает выполнение трех условий:

во-первых, все действующие фирмы отрасли наилучшим образом используют имеющиеся в их распоряжении ресурсы и максимизируют свою прибыль

Р = МС;

во-вторых, ни у одной из фирм не существует побудительных мотивов для входа или выхода из отрасли, поскольку все фир­мы отрасли получают нулевую экономическую прибыль

в-третьих, цена на рынке такова, что совокупное предложение рынка соответствует совокупному спросу потребителей

Лекция предложение. Величина предложения. Функция предложения

ПРЕДЛОЖЕНИЕ. ВЕЛИЧИНА ПРЕДЛОЖЕНИЯ. ФУНКЦИЯ ПРЕДЛОЖЕНИЯ

Предложение (от англ. supplu, S) – зависимость между ценой и количеством экономического блага, которое производитель желает и готов предложить к продаже в течение некоторого промежутка времени.

В данном определении не дается ни качественной ни количественной оценки упомянутой зависимости. Подчеркивается лишь необходимость наличия у производителей желания продать на рынке некоторое благо и готовности это сделать. Конкретизировать количественную сторону рассматриваемой зависимости можно, если задать производителям один из следующих вопросов:

Ø «Какое максимальное количество блага вы готовы продать при данном значении цены?»

Ø «При каком минимальном значении цены вы готовы продать данное количество блага?»

В качестве ответов на данные вопросы мы получим то, что в экономической теории называется величиной прёдложения и ценой предложения соответственно.

Величина предложения – максимальное количество экономического блага, которое производители желают и готовы продать при данном значении цены.

Цена предложения – минимальное значение цены, при котором производители желают и готовы продать данное количество экономического блага.

Если предположить, что подобные вопросы заданы относительно всех возможных значений цен или объемов, а ответы нанесены в соответствующих координатах (Q – количество, Р – цена), то кривая. соединяющая полученные точки, называется кривой предложения.

Закон предложения: при повышении цены экономического блага величина предложения растет, то есть существует положительная зависимость между ценой товара и величиной предложения.

Математически закон предложения можно выразить функцией предложения.

Зависимость предложения от определяющих его факторов называется функцией предложения.

Функцию предложения можно представить следующим образом:

где QSA – объем предложения товара А в определенный период времени

РА – цена товара А,

Рв. PZ – цены других товаров,

L– величина, характеризующая технический прогресс,

Т – величина, характеризующая налоги и дотации /

N – величина, характеризующая природно-климатические условия,

. – прочие факторы, влияющие на предложение.

Если представить, что все факторы, определяющие пред­ложение товара, кроме цены самого товара, не изменяются, то функция предложения примет вид функции предложения това­ра от его цены.

Функцию предложения от цены, как и функцию спроса от цены, можно представить следующими способами.

Табличный способ.

С помощью шкалы предложения.

Шкала предложения – таблица, которая показывает какое количество товара будет предложено к продаже по различным ценам в течение определенного периода времени.

Аналитический способ.

Если между ценой и величиной предложения Qs существует взаимно-однозначное соответствие, то имеется как прямая, так и обратная функции предложения.

Прямая функция предложения Q=Q(P) показывает минимальное количество товара, которое продавец согласен продать по определенной цене.

Обратная функция предложения P=P(Q) показывает минимальную цену, по которой продавец готов продать определенное количество товара.

Если существует линейная зависимость между QS и Р, то формула предложения от цены будет иметь вид QS = а + bР., где b>0.

Например, математическая формула функции, описываю­щей зависимость QS и Р, приведенных в шкале предложения, имеет вид:

QS = 3Р-2, где (QS – объем предложения товара; Р – цена этого товара.

Если функция предложения задана в виде

Графический способ

Кривая предложения – кривая, каждая точка которой показывает значение:

Ø величины предложения при соответствующем значении цены экономического блага;

Ø цены предложения при соответствующем значении количества экономического блага.

Наклон линии предложения отражает закон предложения: с ростом цены увеличивается объем предложения. Поэтому, для большинства товаров и услуг линия предложения имеет поло­жительный наклон.

График предложения может быть полу­чен при помощи данных шкалы предложения или путем построения графика функции предложения от цены.

В данном случае, линия предложения демонстрирует, что при цене Р = 6 денежных единиц объем предложения товара : составит QS = 16 тысяч единиц в месяц; такому состоянию рын­ка соответствует точка А линии S.

Если цена на рынке пони­зится до Р=3 денежных единиц, объем предложения сократится до QS = 7 тысяч единиц в месяц. Эту ситуацию на рынке отражает точка В линии предложения.

Примеры кривой предложения

При изучении данной темы очень важно не путать такие понятия, как «предложение» и «величина предложения». Предложение отражает объем планируемых продаж при всех возможных уровнях цены товара или услуги, то есть графически представляет собой весь график кривой предложения. Величина предложения – это количество блага, которое продавцы готовы продать при конкретном уровне цены, представляет собой одну точку на графике кривой предложения.

Увеличение предложения означает, что при каждом уровне цены производители готовы продать больший объем товара, чем прежде. При увеличении предложения кривая предложения сдвигается вправо – вниз.

Снижение предложения означает, что при каждом уровне цены производители готовы продать меньший объем товара, чем прежде. При снижении предложения кривая предложения сдвигается влево – вверх.

Зная уравнение или график кривой предложения, можно определить объем предложения при любой цене. Таким образом:

Ø изменение предложения – это сдвиг всей кривой предложения, то есть изменение величины предложения при всех возможных значениях цены экономического блага;

Ø изменение величины предложения – это сдвиг вдоль кривой предложения, связанный с изменением цены экономического блага.

При снижении цены товара производители будут склонны предлагать на продажу меньшее его количество. При повышении цены товара последствия прямо противоположные (рис. 2).

Рис.2 Последствия изменения цены экономического блага

Рассмотрим теперь неценовые факторы предложения, то есть параметры, влияющие на планируемый объем продаж производителей и вызывающие сдвиг кривой предложения.

Неценовые факторы предложения:

Производителю, для того чтобы произвести какой-либо товар, необходимо использовать экономические ресурсы. Как мы уже знаем, предложение отражает минимальную цену, за которую производитель готов поставить данный объем товара на рынок. Изменение цены экономических ресурсов при прочих равных условиях приведет к тому, что себестоимость производства данного товара вырастет.

Следовательно, при данном уровне цены производитель не получит ожидаемой прибыли или же вообще не покроет затраты на его производство. Таким образом, при повышении цен ресурсов производитель будет вынужден либо увеличить цену предложения при каждом из уровней количества товара, либо сократить объем предложения при каждом из возможных уровней цены. В любом случае переложение данного товара на рынке сокращается и кривая предложения сдвигается влево – вверх. Падение цен ресурсов сопровождается обратными последствиями.

Увеличение цен ресурсов Снижение цен ресурсов

Рис. 3 Последствия изменения цен ресурсов

Под технологией можно понимать определенный способ организации процесса использования экономических ресурсов для получения определенного товара или услуги. Таким образом, улучшением технологии можно считать создание нового способа производства, который даст возможность при тех же количествах ресурсов произвести больший объем продукции или, соответственно, возможность произвести тот же объем продукции при меньших количествах ресурсов. При этом производитель, естественно, сможет предложить больший объем товара на рынок при любом из возможных уровней цены. Таким образом, при улучшении технологии производства товара предложение товара растет, а график кривой предложения сдвигается вправо – вниз.

Рис. 4. Последствия изменения цен ресурсов

Может показаться, что в современном мире, в обстановке постоянного научно-технического прогресса невозможны ситуации ухудшения технологий. Это не так. Можно привести довольно простые примеры:

Ø стихийное бедствие серьезно повреждает линии электропередач и сами электростанции, тем самым вынуждая значительную часть производств вернуться к использованию ручного труда вместо станков;

Ø одна компания возбуждает и выигрывает судебное дело против другой, обвинив ее в незаконном использовании запатентованных современных технологий, что приводит виновную фирму к необходимости возврата к устаревшим технологиям до момента покупки лицензии или разработки собственных решений.

При ухудшении технологии производства товара предложение товара снижается.

Налоги на производителей

Цена, получаемая производителем за товар, является для него доходом. Налоги снижают величину этого дохода производителя, поскольку теперь он обязан некоторую часть цены товара отдавать государству. Таким образом, введение налога равносильно для производителя тому, что он должен будет получать за каждую продаваемую единицу товара меньшую цену. Введение или увеличение налога приводит к снижению предложения товара. Снижение же или отмена налога приводит к росту предложения товара.

Рис. 5 Последствия изменения действия налогов

Субсидии (трансферты) производителям

Трансферты увеличивают величину дохода производителя, поскольку теперь государство доплачивает ему некоторую сумму за каждую единицу товара. Таким образом, введение или увеличение трансферта приводит к росту предложения товара, а снижение или отмена – к падению предложения товара.

Рис. 6. Последствия изменения действия трансфертов

Очевидно, что двадцать фирм способны предложить на рынок больше продукции, чем одна при одном и том же уровне цены. Таким образом, чем больше число производителей, тем выше рыночное предложение (при снижении числа производителей предложение товара сокращается).

Рис. 7. Последствия изменения количества производителей

Ожидания производителей относительно будущих изменений на рынках влияют на их предложение товара в настоящий момент времени. Если, например, салон связи ожидает, что цена на мобильные телефоны данной модели в будущем вырастет, то каким образом он изменит их предложение в текущий момент времени? Скорее всего, продавец предпочтет продать больше товара в будущем, получив за него боле высокую цену. Таким образом, предложение данного товара сегодня снизится.

Рис. 8. Последствия ожидания изменения цены товара в будущем

Если же производитель предполагает, что в скором времени будет выпущена новая, улучшенная модель мобильного телефона, то, скорее всего, предложение старой модели в текущий момент увеличится, безусловно, вы сталкивались с таким явлением, как сезонные распродажи, когда фирмы активно стараются сбыть, пусть и по сниженным ценам, остатки старых партий продукции. Таким образом, различные ожидания производителей оказывают разное влияние на предложение/

Существует множество других причин, оказывающих влияние на предложение. Это могут быть смена руководства фирмы, открытие новых месторождений полезных ископаемых, погодные условия, политические события и т. д. Перечислить и рассмотреть влияние всех возможных факторов изменения предложения невозможно, но попробуем обобщить все, что мы узнали о факторах предложения.

РЫНОЧНАЯ КРИВАЯ ПРЕДЛОЖЕНИЯ

СЛОЖЕНИЕ ИНДИВИДУАЛЬНЫХ КРИВЫХ ПРЕДЛОЖЕНИЯ

Количество производителей положительно влияет на рыночное предложение. При увеличении количества производителей на рынке может быть предложен больший объем экономического блага при каждом уровне цены. В соответствии с этим утверждением и производится сложение отдельных индивидуальных кривых предложения для получения общей рыночной кривой предложения: при каждом возможном уровне цены необходимо сложить величины индивидуальных предложений отдельных производителей. Сложению подвергаются именно величины индивидуальных предложений, то есть кривые предложения «складываются по горизонтали».

Для того чтобы сложить кривые предложения, можно воспользоваться следующей схемой:

1. Определяем минимальное значение цены, при котором на рынке присутствует хотя бы один продавец.

2. Отмечаем, какой объем товара предлагается на рынке при данной цене.

3. Определяем, при какой цене к продавцам, действовавшим на рынке при цене пункта 1, присоединится следующий продавец (или продавцы).

4. Отмечаем, какой объем товара предлагается на рынке всеми продавцами при данной цене.

5. Повторяем шаги З и 4 пока на рынок не вступят все продавцы.

Рассмотрим пример сложения двух кривых предложения, когда производители готовы начать предлагать товар по одинаковой минимальной цене Рмин. Предложение первого производителя представлено на рис. 9 линией 8. Предложение второго производителя представлено линией В данных условиях минимальная цена, при которой производители готовы предлагать товар, одинакова и равна Рмин. Следовательно, минимальная цена на суммарной кривой предложения – Рмин. При некотором уровне цены Р2> Рмин на рынке действуют два производителя, готовые предложить, соответственно, объем товара, равный: 1 02 =

Рис. 9 Индивидуальные и суммар-

ная рыночная кривые предложения

Рис.9. Индивидуальные и суммарная кривая предложения

Рассмотрим пример сложения двух кривых предложения, когда производители готовы вступить на рынок при разных минимальных ценах: Рмин1 и Рмин2. Предложение первого производителя представлено на рис. 10 линией S1, предложение второго производителя – линией S2.

В данных условиях минимальной ценой, при которой хотя бы один производитель готов предлагать товар на рынке, является цена первого производителя Рмин1 (так как Рмин1 Рмин2 на рынке действуют оба производителя, готовые предложить, соответственно, объем товара, равный: Q2+Q3=Qрын.

Рис. 10 Индивидуальные и суммарная рыночная кривые предложения

Уравнение суммарной рыночной кривой предложения можно получить аналитически на основе уравнений индивидуальных кривых предложения. Для этого можно воспользоваться следующей схемой:

1. Записать уравнения индивидуальных кривых предложения в виде функций: Q = Q(Р).

2. Сложить правые части полученных уравнений в соответствии с областями определения.

3. Записать аналитически кривую рыночного предложения.

ПРАКТИКУМ ДЛЯ ЗАКРЕПЛЕНИЯ ТЕМЫ «ПРЕДЛОЖЕНИЕ»

1. В таблице приведена индивидуальная шкала предложения растительного масла. Выведите аналитически функцию предложения, если известно, что она является непрерывной линейной функцией.

[spoiler title=”источники:”]

http://helpiks.org/8-99439.html

http://pandia.ru/text/80/079/49717.php

[/spoiler]

Пусть исходные
данные имеют следующие числовые значения:

a₀
= 31 a₁
= 6 a₂
= 5 P₀
= 216 Q^–
= 5 Q⁺
= 37

3.1. Исследование
функции прибыли

Нам известна
функция общих издержек, которые несет
фирма при производстве Q
ед. продукции:

TC(Q)
= 31 + 6∙Q
+ 5∙Q²

По условию задачи
любой объем выпускаемой продукции фирма
может продать по действующей цене. Это
позволяет нам определить функцию валовой
выручки фирмы от продажи Q
ед.
продукции:

TR(Q)
= P₀∙Q
= 216∙Q

Прибыль, по
определению, есть разница между валовой
выручкой фирмы и общими издержками:

π(Q)
= TR(Q)
– TC(Q)
= 216∙Q
– (31 + 6∙Q
+ 5∙Q²)
= 210∙Q
– 31 – 5∙Q²

Исследуем данную
функцию на экстремум. Для этого найдем
первую и вторую производные:

Точкой глобального
экстремума функции прибыли является
Q*
= 21, а вогнутость функции указывает на
то, что эта точка – глобальный максимум.

Таким образом,
максимизирующий прибыль объем производства
составляет 21 ед.

Максимальная
прибыль при действующей рыночной цене
составит:

π*(21)
= 210∙21 – 31 – 5∙21²
= 2174

Определим теперь
интервал безубыточности, то есть такие
объемы выпуска продукции, при которых
фирма не будет нести убыток. Для этого
требуется решить следующую задачу

Найти все значения
Q
: π(Q)
= 210∙Q
– 31 – 5∙Q²
≥ 0

Для начала нам
необходимо определить объемы производства,
при которых прибыль фирмы равняется
нулю (точки безубыточности). Для этого
решим уравнение:

π(Q)
= 210∙Q
– 31 – 5∙Q²
= 0

Откуда получаем:
Q₁
= 0.15; Q₂
= 41.85

Так как функция
прибыли непрерывна и вогнута, то найденные
объемы производства определяют интервал
безубыточности:

Получаем

Q^без
[0.15;
41.85]

3.2. Графический
анализ модели производителя

3.2А. Построение
графиков общих издержек (TC(Q))
и валовой выручки (TR(Q))

Определим необходимые
для построения графиков функции.

Общие издержки
фирмы описываются квадратичной
зависимостью от объема производства:

TC(Q)
= 31 + 6∙Q
+ 5∙Q²

На графике данная
функция имеет вид параболы с минимумом
в точке Q
= -0.6:

Валовая выручка
фирмы есть произведение цены реализации
на объем реализации продукции:

TR(Q)
= P₀∙Q
= 216∙Q

Валовая выручка
фирмы линейно зависит от объема
производства.

Если валовая
выручка производителя превышает его
общие издержки, то он получает прибыль,
которая на рисунке представляет собой
расстояние между линией TR(Q)
и линией TC(Q).
Чем больше это расстояние, тем большую
прибыль получает производитель. Как
видно из Рис. 2.1, при найденных в п. 1
объемах безубыточности (0.15 и 41.85 ед.)
линии валовой выручки и общих издержек
пересекаются. Это означает, что
производитель при данных объемах
производства получает нулевую прибыль.

Валовая выручка
растет быстрее чем общие издержки вплоть
до достижения объема производства в 21
ед. Это означает, что увеличивая объем
выпуска вплоть до 21 ед. производитель
будет увеличивать получаемую прибыль.
При производстве 21 ед. продукции валовая
выручка (TR(Q))
будет максимально превышать общие
издержки (TC(Q)),
что и означает, что производитель получит
максимальную прибыль. Если производитель
продолжит увеличивать объем производства
сверх оптимального уровня, то общие
издержки станут расти быстрее валовой
выручки, что приведет к сокращению
прибыли.

Из рис. 3.1 видно,
что при объеме производства в 21 ед.,
фирма получит максимальную прибыль
2174, при этом валовая выручка фирмы
составит 4536, а общие издержки 2362.

3.2Б. Построение
графиков средних (AC(Q))
и предельных издержек (MC(Q))
и предельной выручки (MR
= P₀).

Если в п. 3.2А мы
имели дело с валовыми показателями, то
здесь мы будем иметь дело с удельными.

Средние издержки
(AC(Q))
представляют собой затраты, которые
фирма в среднем несет на производство
единицы продукции:

В данном случае
средние издержки вначале убывают с
ростом производства продукции, достигая
своего минимума, а потом начинают
возрастать. Минимальное значение средних
издержек определяется из условия
глобального минимума и равно 31 руб. при
объеме производства в 2.5 ед.:

Предельные издержки
(MC(Q))
есть издержки, необходимые для производства
дополнительной единицы продукции:

Как видим, в данном
случае предельные издержки на производство
продукции линейно возрастают с
возрастанием объема производства, это
означает, что производство каждой новой
единицы продукции будет обходиться на
10 руб. дороже, чем предыдущей.

Предельная выручка
представляет собой доход фирмы от
продажи дополнительной единицы продукции.
Так как действующая рыночная цена не
зависит от объема продаж фирмы, то
предельная выручка совпадает с действующей
ценой:

Изобразим данные
функции на графике и решим графически
задачу максимизации прибыли.

AC,
MC, MR

AC(Q) MC(Q)

216
MR = P₀
= 216

π*

112.5

31

Q

0.15 2.5 21
41.85

Рисунок
3.2.
Максимизация
прибыли производителя

Средние издержки
два раза пересекаются с линией рыночной
цены, точки их пересечения определяют
объемы безубыточности (0.15; 41.85).

Превышение рыночной
цены над средними издержками показывает,
какую прибыль получает фирма от продажи
каждой единицы продукции. Наибольшую
прибыль в расчете на единицу продукции
фирма (185 руб.) получает в случае минимума
средних издержек, то есть при объеме
производства 2.5 ед.

Однако фирма
заинтересована в максимизации общей
прибыли, равной произведению объема
производства на разницу между рыночной
ценой и средними издержками.

Для того чтобы
найти максимизирующий прибыль объем
производства, нам необходимо посмотреть
на линию предельных издержек и предельной
выручки.

По определению
предельные издержки показывают издержки,
требующиеся на производство дополнительной
единицы продукции, а предельная выручка
– насколько увеличится доход при продаже
дополнительной единицы продукции.
Значит, пока дополнительная единица
продукции будет приносить доход больший,
чем издержки на ее производство, будет
выгодно увеличивать выпуск продукции.

Таким образом,
фирма будет увеличивать производство
продукции до тех пор, пока предельные
издержки не сравняются с предельной
выручкой (в данном случае с рыночной
ценой, равной 216 руб.), это произойдет
при объеме производства 21 ед. Из рис.
2.2 также видно, что производить продукцию
в объеме более чем 21 ед. фирме не выгодно,
так как прирост дохода от ее продажи
будет меньше, чем издержки на ее
производство, а значит производство
каждой дополнительной единицы продукции
сверх 21 ед. будет вести к снижению
прибыли.

Максимальный объем
прибыли на Рис. 3.2 определяется как
площадь прямоугольника π*
(см. заштрихованную площадь), которая
равна 2174 руб., при этом объем производства
равен 21ед., а средние издержки составляют
112.5 руб.

3.3. Построение
функции предложения фирмы (S(P))
при условии ограниченных мощностей

Функция предложения
фирмы показывает, какой объем производства
фирма может и готова предложить на рынок
в зависимости от рыночной цены. Для
построения функции предложения мы
должны учесть ряд важных условий:

1. Максимизация
прибыли.

2. Неотрицательность
прибыли.

3. Ограниченность
производственных мощностей.

1. Максимизация
прибыли.
Фирма должна быть заинтересована в
предложении соответствующего объема
производства при данной рыночной цене.
Это условие выполняется, если фирма при
данном объеме производства и рыночной
цене будет максимизировать свою прибыль.

Данное условие
дает нам зависимость между рыночной
ценой и максимизирующим прибыль объемом
производства (Q*(P)).
Заметим, что этот объем будет определяться
исходя из равенства рыночной цены
предельным издержкам:

2. Неотрицательность
прибыли.
Фирма может отказаться от производства
продукции в случае, если она заведомо
получит убыток при любом допустимом
объеме производства. Это означает, что
прибыль фирмы должна быть неотрицательна
или, другими словами, что средние издержки
не превышают рыночной цены.

Условие 1 задает
зависимость между оптимальным выпуском
продукции и рыночной ценой. Следовательно,
условие неотрицательности прибыли
можно записать следующим образом:

Таким образом,
минимальный оптимальный объем
производства, дающий неотрицательную
прибыль, равен 2.5 ед., соответствующим
рыночной цене в 31 руб. Если рыночная
цена окажется меньше чем 31 руб., то фирма
при любом объеме производства получит
отрицательную прибыль. С другой стороны,
фирма всегда получит прибыль, если цена
будет превышать 31 руб. Неудивительно,
что минимальный объем производства
соответствует минимуму средних издержек.

Итак, если бы у
фирмы не было бы ограничений по мощностям,
то ее функция предложения выглядела бы
следующим образом:

Другими словами,
при отсутствии ограничений по мощностям
функцией предложения фирмы является
часть функции предельных издержек,
превышающая средние издержки.

3. Ограниченность
производственных мощностей.
Производственные возможности фирмы
ограничены мощностями. Это означает,
что фирма не может производить меньше
чем Q^–
= 5 и больше чем
Q⁺
= 37, либо фирме не выгодно начинать
производство вообще.

Сначала рассмотрим
ограничение по минимальному выпуску
продукции. По первым двум условиям,
фирма выбрала бы объем производства
только при цене 56 руб. (P=6+10∙5=56,
см. условие 1), при этом фирма получила
бы прибыль в объеме 94 руб. (π=56∙5-31-6∙5-5∙5²,
см. условие 1). Однако фирма согласилась
бы производить 5 ед. продукции и при
меньшей цене, которая обеспечила бы ей
хоть какую-то прибыль, так как в ином
случае прибыль фирмы составила бы 0 руб.
Для этого достаточно, чтобы цена превышала
средние издержки производства 5 ед.
продукции:

Таким образом,
если рыночная цена продукции фирмы
будет в диапазоне [37.2; 56], то фирма будет
производить 5 ед. продукции. Если рыночная
цена окажется меньше чем 37.2 руб., то
фирме не выгодно организовывать
производство, а если превысит 56 руб., то
фирме выгоднее будет увеличить выпуск
продукции, в соответствии с условием
максимизации прибыли.

Рассмотрим теперь
ограничение по максимальному объему
производства (Q≥37).
Фирма выбрала бы этот объем производства
при рыночной цене равной 376 руб.
(P(37)=6+10∙37=376,
см. условие 1). Если бы цена превысила
376 руб., то фирме, согласно условию
максимизации прибыли было бы выгодно
увеличить выпуск продукции, однако
сделать этого в силу ограниченных
производственных мощностей она не
может, а потому при цене продукции
большей или равной 376 руб. фирма выберет
объем производства 37 ед.

Мы получили функцию
предложения, учитывающую все условия.

Представим данную
функцию на рисунке 3.3.

Ответ.

1. Q*
=21 ; π*
= 2174 ; Q^без
[0.15;
41.85]

Соседние файлы в папке Все ИДЗ 2 курс(Задания)

• #

  20.06.201554.27 Кб100ГРАФИЧЕСКИ.XLS

• #

  20.06.201557.34 Кб98ДВОЙСТВЕННАЯ.XLS

• #

  20.06.201540.45 Кб196Задача 1.xls

• #

  20.06.201539.42 Кб132Задача 2.xls

• #

  20.06.2015155.65 Кб108Задача 4.xls

• #
• #
• #
• #
• #

  20.06.201552.74 Кб61Назначение_напарников.xls

• #

Задача №1. Расчёт экономической прибыли конкурентной фирмы

Фирма, находясь в условиях совершенной конкуренции, имеет следующую функцию общих затрат:

ТС = 140 + 10 × Q + 40 × Q².

При каком выпуске прибыль фирмы достигнет максимума, если цена установилась на уровне 250 ден. ед.? Определить размер прибыли фирмы.

Будут ли в длительном периоде в эту отрасль стремиться войти новые фирмы?

Решение:

Наличие  в составе общих затрат фиксированных (постоянных) затрат (FC = 140) свидетельствует о том, что речь идёт о краткосрочном периоде.

Найдём объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде имеет вид:

Р = МС = МR = AR.

Определим функцию предельных издержек фирмы: найдём производную общих издержек.

МС = (ТС)’ = 10 + 80 × Q.

Приравняем эту функцию к цене равной 250.

10 + 80 × Q = 250

80 × Q = 240

Q = 3

Вычислим прибыль фирмы при объёме выпуска равном 3 по формуле:

П = TR — TC = P × Q — TC = 250 × 3 — (140 + 10 × 3 + 40 × 3²) = 220 ден. ед.

В долгосрочном периоде наличие неотрицательной экономической прибыли будет привлекать в отрасль новые фирмы.

Задача № 2. Определение рыночной цены и отраслевого выпуска продукции

В отрасли действуют 130 одинаковых фирм. Издержки производства каждой фирмы описываются функциями

ТС =Q³ — 36*Q² + 384*Q,

где

Q — объём производства в тысячах штук. Найти рыночную цену и отраслевой выпуск продукции, при которых на конкурентном рынке устанавливается долгосрочное равновесие.

Решение:

В долгосрочном периоде на рынке совершенной конкуренции соблюдается равенство:

P = MC = MR = AR = minAC.

Найдём функцию средних издержек каждой фирмы по следующей формуле:

АС = ТС / Q = Q² — 36*Q + 384

Далее необходимо найти минимум данной функции. Для этого определим производную функции АС и приравняем её к нулю.

2*Q — 36 = 0

Q = 18

AC(18) = 18² — 36*18 + 384 = 60

Так как Р = minAC в долгосрочном периоде, следовательно, рыночная цена равна Р = 60.

Найдём отраслевой выпуск. Так как каждая из фирм отрасли производит 18 тысяч штук продукции, значит 130 фирм произведут:

Q_отр. = 18*130 = 2340 тысяч штук

Задача № 3. Определение рыночной цены в долгосрочном периоде

Конкурентная фирма находится в состоянии равновесия в долгосрочном периоде и имеет следующие затраты: TC = Q³ — 38*Q² + 418*Q. Определите цену на этом рынке в долгосрочном периоде.

Решение:

В долгосрочном периоде цена в условиях соверешенной конкуренции устанавливается на уровне минимума средних затрат. При этом фирма совершенный конкурент получает нулевую экономическую прибыль.

Условие равновесия на рынке будет иметь вид:

Р = МС = МR = AR = min AC

Найдём средние затраты фирмы по формуле:

АС = ТС / Q = Q² — 38*Q + 418

Определим минимум функции средних затрат. Для нахождения экстремума функции  приравняем к нулю её производную:

АС’ = 2*Q — 38

2*Q — 38 = 0

Q = 19

При выпуске Q = 19 средние затраты будут равны:

АС = 19² — 38*19 + 418 = 57.

Таким образом, цена в долгосрочном периоде будет равна 57.

Задача № 4. Расчёт рыночной цены, при которой фирма уйдёт с рынка

Общие затраты фирмы, действующей на рынке совершенной конкуренции, составляют

0,5*Q³ — 15*Q² + 300*Q + 250 000.

При какой цене фирме становится невыгодным работать на этом рынке в краткосрочном периоде?

Решение:

В краткосрочном периоде фирма совершенный конкурент уйдёт с рынка, если цена окажется меньше  минимума её средних переменных издержек: Р < min AVC.

Найдём переменные издержки фирмы, а точнее запишем функцию переменных издержек:

VC = 0,5*Q³ — 15*Q² + 300*Q

Теперь определим функцию средних переменных издержек  по формуле:

АVC = VC / Q = 0,5*Q² — 15*Q + 300

Найдём экстремум этой функции, приравняв к нулю её производную.

Q — 15 = 0

Q = 15.

При объёме производства Q = 15 средние переменные издержки будут минимальными.

АVC(15) = 0,5*15² — 15*15 + 300 = 187,5

Это так называемая точка закрытия фирмы. Фирма совершенный конкурент уйдёт с рынка, если цена упадёт ниже этой точки в краткосрочном периоде.

При Р < 187,5 фирме становится невыгодным работать на этом рынке в краткосрочном периоде.

Задача № 5. Расчёт объёма выпуска, максимизирующего прибыль фирмы

Функция издержек фирмы ТС = Q² — Q + 3, где Q — объём производства. Рыночная цена на продукцию фирмы составляет 7 и не зависит от объёма продаж этой фирмы. Найти объём выпуска продукции, максимизирующий прибыль фирмы.

Решение:

По условию рыночная цена не зависит от объёма продаж этой фирмы, это говорит о том, что фирма функционирует в условиях совершенной конкуренции.

Максимум прибыли фирмы действующей в условиях совершенной конкуренции определяется тождеством: Р = МС.

Найдём предельные издержки фирмы по формуле:

МС =(TC)’= 2Q — 1

Найдём объём выпуска продукции, максимизирующий прибыль фирмы.

Цена по условию равна Р = 7.

Р = МС

7 = 2Q — 1

Q = 4

Задача №6. Расчёт объёма производства в краткосрочном периоде

В отрасли совершенной конкуренции установилась цена Р = 30. В эту отрасль входит фирма с общими издержками ТС = 1/2 * Q² + 10 * Q + 100. Найти её объём производства в краткосрочном периоде.

Решение:

Фирма выберет такой объём производства, при котором прибыль будет максимальна. Условие максимизации прибыли: МС = MR.

На рынке совершенной конкуренции предельный доход равен цене: MR = P.

Отсюда следует, что цена равна предельным издержкам: P = MC.

Найдём предельные издержки. Предельные издержки в непрерывном случае (т.е. когда общие издержки заданы функцией) равны производной от функции общих издержек:

Функция предельных издержек будет иметь вид:

МС = Q + 10
P = MC
30 = Q + 10
Q = 20 — оптимальный объём производства фирмы.

Задача № 7. Расчёт рыночной цены и объёма выпуска на конкурентном рынке

Конкурентная фирма имеет общие затраты

ТС = 800 + 40*Q + 2*Q²

Она получает в краткосрочном периоде максимально возможную прибыль, равную 1000.

Определить цену на рынке и объём выпуска данной фирмы.

Решение:

Формула прибыли фирмы имеет вид:

П = TR — TC = P*Q — TC

По условию максимально возможная прибыль равна 1000.

P*Q — (800 + 40*Q + 2*Q²) = 1000

Найдём цену.

Условие максимизации прибыли на рынке совершенной конкуренции имеет вид:

Р = МС = MR = AR

Так как Р = МС, а МС = ТС’ = 40 + 4*Q, следовательно, Р = 40 + 4*Q. Подставим это выражение в формулу прибыли и получим:

(40 + 4*Q)*Q — (800 + 40*Q + 2*Q²) = 1000

40*Q + 4*Q² — 800 — 40*Q — 2*Q² — 1000 = 0

2*Q² = 1800

Q² = 900

Q_1,2 = ±30

Так как отрицательный корень экономического содержания не имеет, берём Q = 30.

Тогда цена будет равна:

Р = 40 + 4*30 = 160

Задача № 8. Расчёт рыночной цены на конкурентном рынке в долгосрочном периоде

Допустим, общие затраты фирмы на выпуск Q единиц продукции составляют:

Q³ – 16*Q² + 400*Q.

а) При каком значении Q средние затраты достигают минимума?

б) При какой цене этой фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде?

Решение:

а) Найдём функцию средних затрат по формуле:

АС = ТС / Q = (Q³ – 16*Q² + 400*Q) / Q = Q² – 16*Q + 400

Определим минимум функции. Для нахождения экстремума функции необходимо найти её производную и приравнять её к нулю.

AC’ =(Q2 – 16*Q + 400)’ = 2*Q – 16
2*Q – 16 = 0
Q = 8

При Q = 8 средние затраты достигают минимума.

б) В долгосрочном периоде фирме становится выгодным участвовать в совершенной конкуренции, если Р ≥ АС. При этом фирма имеет нулевую прибыль. И выполняется условие:

Р = МС = MR = minАС

Рассчитаем minAC. Подставим Q = 8 в функцию средних затрат:

minAC(Q=8) = 82 – 16*8 + 400 = 336

Итак, при цене Р ≥ 336 фирме становится выгодным участвовать в совершенной конкуренции в долгосрочном периоде.

Задача № 9. Расчёт цены и объёма производства, максимизирующих прибыль

Спрос на продукцию конкурентной отрасли:

Q_d = 55 – P

Предложение:

Q_s = 2P – 5

Если у одной из фирм отрасли восходящий участок кривой предельных издержек:

МС = 3Q + 5

При каких цене и объёме производства фирма максимизирует прибыль?

Решение:

Найдём цену равновесия. Приравняем функцию спроса и предложения:

Qd = Qs
55 – P = 2P – 5
3 * Р = 60
Р = 20 – цена рыночного равновесия, то есть цена по которой фирмы будут продавать свою продукцию.

Фирма в условиях совершенной конкуренции получает максимум прибыли при условии равенства цены и предельных затрат.

МС = Р
3Q + 5 = 20
Q = 5 – объём производства, при котором прибыль фирмы будет максимальной.

Задача №10. Расчёт рыночной цены и объёма выпуска на конкурентном рынке

Конкурентная фирма имеет предельные затраты:

МС = 30 + 2 × Q

при фиксированных затратах, равных 500 денежным единицам.

Она получает в краткосрочном периоде максимально возможную прибыль, равную 1100 денежным единицам.

Определить цену на рынке и объём выпуска данной фирмы.

Решение:

Формула прибыли имеет вид:

П = TR – TC = P*Q – TC

Определим функцию общих затрат. Так как функция предельных затрат это производная функции общих затрат, следовательно, функцию общих затрат можно определить как первообразную от функции предельных затрат.

где

С – константа, равная величине фиксированных затрат, которые по условию равны 500.

Таким образом функция общих затрат имеет вид:

ТС = Q² +30*Q + 500

Теперь запишем условие максимизации прибыли на рынке совершенной конкуренции в краткосрочном периоде:
Р = МС = MR = AR

Воспользуемся тем, что:

Р = МС

По условию задачи:

МС = 30 + 2 × Q, то есть Р = 30 + 2 * Q

Подставим это выражение, а так же функцию общих затрат в формулу прибыли и получим уравнение с одной неизвестной.

(30 + 2 * Q) * Q – (Q² +30*Q + 500) = 1100
Q2 = 1600
Q = ± 40

Так как отрицательное значение Q экономического смысла не имеет, следовательно, объём выпуска данной фирмы Q = 40.

Тогда рыночная цена будет равна:

Р = 30 + 2 * 40 = 110.