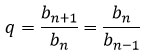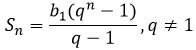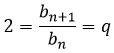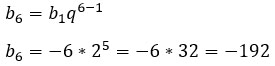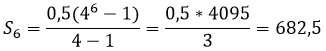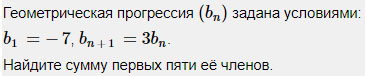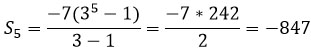Как найти предыдущий член геометрической прогрессии

Геометрическая прогрессия

Геометрическая прогрессия — это числовая последовательность b₁, b₂, . , b_n, . , для которой для каждого натурального n выполняется равенство:

где q – это знаменатель геометрической прогрессии, q ≠ 0 и b_n ≠ 0.

Пример: последовательность чисел 3, 12, 48, 192, 768, . является геометрической прогрессией со знаменателем q = 4.

Знаменатель определяет вид геометрической прогрессии:

1. Если q > 0, тогда все члены геометрической прогрессии имеют один и тот же знак, равный знаку b₁ Пример: последовательность чисел 1, 2, 4, 8, 16, . со знаменателем q = 2.
2. Если q Пример: последовательность чисел 2, –6, 18, –54, 162, . со знаменателем q = –3.
3. Если –1 Пример: последовательность чисел 400, 200, 100, 50, 25, . со знаменателем q = 0.5.

Основные формулы геометрической прогрессии

Знаменатель геометрической прогрессии

Знаменатель геометрической прогрессии можно вычислить с помощью текущего и следующего членов геометрической прогрессии по формуле:

Члены геометрической прогрессии

Общая формула для вычисления n-ого члена геометрической прогрессии по первому члену и знаменателю:

Следующий член геометрической прогрессии можно найти по предыдущему члену и знаменателю:

Предыдущий член геометрической прогрессии можно найти по следующему члену и знаменателю:

Также член геометрической прогрессии можно найти, если известны следующий и предыдущий члены:

Сумма геометрической прогрессии

Сумма первых n членов геометрической прогрессии равна

S_n = b₁ ⋅ (1 — q n ) / (1 — q), где q ≠ 1

Также сумму можно вычислить, используя другую формулу:

Решение задач на геометрическую прогрессию

Рассмотрим несколько типичных задач, посвященных геометрической прогрессии.

Дана геометрическая прогрессия 3, 6, 12, . . Найти 8-ой член геометрической прогрессии и сумму первых 10 членов.

b₈ = b₁ ⋅ q 7 = 3 ⋅ 2 7 = 3 ⋅ 128 = 384

S₁₀ = b₁ ⋅ (1 — q 10 ) / (1 — q) = 3 ⋅ (1 — 2 10 ) / (1 — 2) = 3 ⋅ (1 — 1024) / (–1) = 3069

Ответ: 384 и 3069

Число 486 является членом геометрической прогрессии 2, 6, 18, . . Найдите его номер.

Применив формулу для вычисления n-ого члена геометрической прогрессии, можно получить n:

Сумма n первых членов геометрической прогрессии равна –93. b₁ = –3, q = 2. Найти n.

Чтобы вычислить число членов геометрической прогрессии, можно воспользоваться формулой ее суммы:

Геометрическая прогрессия

Геометрической прогрессией называют числовую последовательность, каждый следующий член которой получается из предыдущего умножением его на постоянное число, не равное нулю.

Это число называют знаменателем геометрической прогрессии и обозначают буквой (q).

Например, последовательность (3); (6); (12); (24); (48)… является геометрической прогрессией, потому что каждый следующий элемент отличается от предыдущего в два раза (иначе говоря, может быть получен из предыдущего умножением его на два):

Как и любую последовательность, геометрическую прогрессию обозначают маленькой латинской буквой. Числа, образующие прогрессию, называют ее членами (или элементами). Их обозначают той же буквой, что и геометрическую прогрессию, но с числовым индексом, равным номеру элемента по порядку.

Например, геометрическая прогрессия (b_n = <3; 6; 12; 24; 48…>) состоит из элементов (b_1=3); (b_2=6); (b_3=12) и так далее. Иными словами:

порядковый номер элемента

Если вы поняли вышеизложенную информацию, то уже сможете решить большинство задач на эту тему.

Пример (ОГЭ): Геометрическая прогрессия задана условиями (b_1=-2); (q=7). Найдите (b_4).
Решение:

Зная первый член и знаменатель, последовательно вычисляем элементы, пока не дойдем до нужного.

Можно писать ответ.

Пример (ОГЭ): Даны первые три члена прогрессии (324); (-108); (36)…. Найдите (b_5).
Решение:

Чтобы продолжить последовательность, нам нужно знать знаменатель. Найдем его из двух соседних элементов: на что нужно умножить (324), чтоб получилось (-108)?

Отсюда без проблем вычисляем знаменатель.

Теперь мы легко находим нужный нам элемент.

Пример: Прогрессия задана условием (b_n=0,8·5^n). Какое из чисел является членом этой прогрессии:

Решение: Из формулировки задания очевидно, что одно из этих чисел точно есть в нашей прогрессии. Поэтому мы можем просто вычислять ее члены по очереди, пока не найдем нужное нам значение. Так как у нас прогрессия задана формулой n-го члена , то вычисляем значения элементов, подставляя разные (n):
(n=1); (b_1=0,8·5^1=0,8·5=4) – такого числа в списке нет. Продолжаем.
(n=2); (b_2=0,8·5^2=0,8·25=20) – и этого тоже нет.
(n=3); (b_3=0,8·5^3=0,8·125=100) – а вот и наш чемпион!

Пример (ОГЭ): Даны несколько идущих последовательно друг за другом членов геометрической прогрессии …(8); (x); (50); (-125)…. Найдите значение элемента, обозначенного буквой (x).

Найти (x), можно, например, умножив (8) на знаменатель прогрессии. Однако мы его не знаем, поэтому сначала найдем знаменатель из двух известных соседних членов.

Теперь вычисляем икс, умножая (8) на (-2,5).

Пример (ОГЭ): Прогрессия задана условиями (b_1=7), (b_=2b_n). Найдите сумму первых (4) членов этой прогрессии.

Мы знаем первый элемент и имеем рекуррентное соотношение – формулу для вычисления следующего элемента по предыдущему.
Вот и найдем необходимые нам первые (4) элемента, подставляя разные (n).

Теперь найдем сумму.

Пример (ОГЭ): Известно, что в геометрической прогрессии (b_6=-11), (b_9=704). Найдите знаменатель (q).

Из схемы слева видно, что чтобы «попасть» из (b_6) в (b_9) – мы делаем три «шага», то есть три раза умножаем (b_6) на знаменатель прогрессии. Иными словами (b_9=b_6·q·q·q=b_6·q^3).

Подставим известные нам значения.

«Перевернем» уравнение и разделим его на ((-11)).

Какое число в кубе даст (-64)?
Конечно, (-4)!

Ответ найден. Его можно проверить, восстановив цепочку чисел от (-11) до (704).

Все сошлось – ответ верен.

Важнейшие формулы

Как видите, большинство задач на геометрическую прогрессию можно решать чистой логикой, просто понимая суть (это вообще характерно для математики). Но иногда знание некоторых формул и закономерностей ускоряет и существенно облегчает решение. Мы изучим две такие формулы.

Формула (n)-го члена: (b_n=b_1·q^), где (b_1) – первый член прогрессии; (n) – номер искомого элемента; (q) – знаменатель прогрессии; (b_n) – член прогрессии с номером (n).

С помощью этой формулы можно, например, решить задачу из самого первого примера буквально в одно действие.

Пример (ОГЭ): Геометрическая прогрессия задана условиями (b_1=-2); (q=7). Найдите (b_4).
Решение:

Нам нужен четвертый член, вот и вычисляем его сразу, напрямую, не находя всех промежуточных.

Этот пример был простым, поэтому формула нам облегчила вычисления не слишком сильно. Давайте разберем задачку чуть посложнее.

Пример: Геометрическая прогрессия задана условиями (b_1=20480); (q=frac<1><2>). Найдите (b_<12>).
Решение:

Действуем как в предыдущей задаче.

Конечно, возводить (frac<1><2>) в (11)-ую степень не слишком радостно, но всё же проще чем (11) раз делить (20480) на два.

Сумма (n) первых членов: (S_n=) ( frac) , где (b_1) – первый член прогрессии; (n) – количество суммируемых элементов; (q) – знаменатель прогрессии; (S_n) – сумма (n) первых членов прогрессии.

Пример (ОГЭ): Дана геометрическая прогрессия (b_n), знаменатель которой равен (5), а первый член (b_1=frac<2><5>). Найдите сумму первых шести членов этой прогрессии.
Решение:

Все данные есть, сразу вычисляем ответ.

И вновь мы могли решить задачу «в лоб» – найти по очереди все шесть элементов, а затем сложить результаты. Однако количество вычислений, а значит и шанс случайной ошибки, резко возросли бы.

Для геометрической прогрессии есть еще несколько формул, которые мы не стали рассматривать тут из-за их низкой практической пользы. Вы можете найти эти формулы здесь .

Возрастающие и убывающие геометрические прогрессии

У рассмотренной в самом начале статьи прогрессии (b_n = <3; 6; 12; 24; 48…>) знаменатель (q) больше единицы и поэтому каждый следующий член больше предыдущего. Такие прогрессии называются возрастающими.

Если же (q) меньше единицы, но при этом положителен (то есть, лежит в пределах от нуля до единицы), то каждый следующий элемент будет меньше чем предыдущий. Например, в прогрессии (4); (2); (1); (0,5); (0,25)… знаменатель (q) равен (frac<1><2>).

Эти прогрессии называются убывающими. Обратите внимание, что ни один из элементов такой прогрессии не будет отрицателен, они просто становятся всё меньше и меньше с каждым шагом. То есть, мы будем постепенно приближаться к нулю, но никогда его не достигнем и за него не перейдем. Математики в таких случаях говорят «стремиться к нулю».

Отметим, что при отрицательном знаменателе элементы геометрической прогрессии будут обязательно менять знак. Например, у прогрессии (5); (-15); (45); (-135); (675)… знаменатель (q) равен (-3), и из-за этого знаки элементов «мигают».

Как решать уравнения геометрической прогрессии

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

[spoiler title=”источники:”]

http://cos-cos.ru/math/244/

http://yukhym.com/ru/matematika/geometricheskaya-progressiya.html

[/spoiler]

Геометрическая прогрессия — это числовая последовательность b₁, b₂, … , b_n, …, для которой для каждого натурального n выполняется равенство:

b_n+1 = b_n ⋅ q

где q – это знаменатель геометрической прогрессии, q ≠ 0 и b_n ≠ 0.

Пример: последовательность чисел 3, 12, 48, 192, 768, … является геометрической прогрессией со знаменателем q = 4.

Знаменатель определяет вид геометрической прогрессии:

1. Если q > 0, тогда все члены геометрической прогрессии имеют один и тот же знак, равный знаку b₁
   

   ---

   Пример: последовательность чисел 1, 2, 4, 8, 16, … со знаменателем q = 2.

2. Если q < 0, тогда знаки членов геометрической прогрессии чередуются
   
   

   ---

   Пример: последовательность чисел 2, –6, 18, –54, 162, … со знаменателем q = –3.

3. Если –1 < q < 1, тогда геометрическая прогрессия является бесконечно убывающей
   

   ---

   Пример: последовательность чисел 400, 200, 100, 50, 25, … со знаменателем q = 0.5.

Основные формулы геометрической прогрессии

Знаменатель геометрической прогрессии

Знаменатель геометрической прогрессии можно вычислить с помощью текущего и следующего членов геометрической прогрессии по формуле:

q = b_n+1 / b_n

Члены геометрической прогрессии

Общая формула для вычисления n-ого члена геометрической прогрессии по первому члену и знаменателю:

b_n = b₁ ⋅ q^{n – 1}

Следующий член геометрической прогрессии можно найти по предыдущему члену и знаменателю:

b_n+1 = b_n ⋅ q

Предыдущий член геометрической прогрессии можно найти по следующему члену и знаменателю:

b_n-1 = b_n / q

Также член геометрической прогрессии можно найти, если известны следующий и предыдущий члены:

b_n = √b_n-1 ⋅ b_n+1, где n > 1

Сумма геометрической прогрессии

Сумма первых n членов геометрической прогрессии равна

S_n = b₁ ⋅ (1 — qⁿ) / (1 — q), где q ≠ 1

Также сумму можно вычислить, используя другую формулу:

S_n = (b₁ — b_n ⋅ q) / (1 — q), где q ≠ 1

Решение задач на геометрическую прогрессию

Рассмотрим несколько типичных задач, посвященных геометрической прогрессии.

Решение.

Достаточно очевидно, что (0,(8)=0,8+0,08+0,008+…)  Слагаемые в правой части равенства образуют бесконечно убывающую геометрическую прогрессию, первый член которой равен (0,8), знаменатель равен (0,1). Найдём сумму по  формуле:

Осталось выполнить нужные действия с десятичными дробями:

Таким образом, бесконечная периодическая десятичная дробь (0,(8)) обращается в обыкновенную дробь (8/9).

Ответ: (0,(8)=8/9).

Геометрическая прогрессия

Кусочек теории.

Геометрическая прогрессия – это последовательность чисел, не равных нулю, в которой каждый следующий член, начиная со второго, в одно и то же количество раз больше (или меньше) предыдущего.

Последовательность чисел 2; 4; 8; 16; 32; 64; … будет являться геометрической прогрессией, причем возрастающей, т.к. каждое следующее число больше предыдущего в 2 раза. В данном случае число 2 является знаменателем этой прогрессии.

Также геометрической прогрессией будет являться последовательность чисел 12; 6; 3; 1,5; 0,75; 0,375; … , причем убывающей, т.к. в ней числа уменьшаются в 2 раза. Но геометрическую прогрессию прежде всего связывают с умножением, поэтому правильнее сказать, что в последовательности числа увеличиваются в 0,5 раз. Здесь знаменателем будет число 0,5.

Знаменатель геометрической прогрессии обозначают буквой q. Если знаменатель не дан, то найти его можно делением текущего члена прогрессии на предыдущий:

Найти любой по счету член геометрической прогрессии можно, зная ее первый член и знаменатель. Запишем формулу n-ого члена:

Но необязательно знать именно первый член прогрессии. Пригодится может любое по счету число. Только тогда формула чутка изменится:

И держи третью формулу для нахождения n-ого члена геометрической прогрессии через предыдущий и последующий члены (правда по модулю)!

Помимо этих трех формул пригодится еще формула суммы:

Практика.

Задание 1.

Это задание можно решить без формул. Но если уж так хочется, то можно и по формулам, но мне вот не хочется)

Откинем пока минусы…

Если разделить 125 на 100, то мы увидим во сколько раз следующее число меньше предыдущего: в 1,25 раз. То же самое число получится, если 100 разделить на 80.

Найдем 4-ое число в этой последовательности: 80 : 1,25 = 64.

И 5-ое: 64 : 1,25 = 51,2.

Но не забываем, что знаки у чисел чередуются: четвертое число будет отрицательным, а пятое – положительным.

Ответ: 51,2.

Задание 2.

Опять знаки у чисел чередуются, значит число, спрятанное под иксом, будет отрицательным.

Не будем морочить голову формулами, пойдем задом наперед: разделим 4-ое число на 3-ое (найдем знаменатель прогрессии):

96 : 24 = 4 (знаки у чисел мы откинули временно).

Значит, чтобы найти икс надо 24 разделить на знаменатель 4 и взять результат с минусом.

Ответ: -6.

Задание 3.

По данной нам в условии задаче формуле можно сразу понять, что 2 – знаменатель прогрессии. Если это не понятно – вот доказательство:

Здесь схитрить не получится, поэтому используем формулу и находим b₆.

Ответ: -192.

Задание 4.

Каждое следующее число в 4 раза больше предыдущего, значит знаменатель q равен 4.

Зная первый член прогрессии и знаменатель можно найти сумму первых шести членов (n = 6).

Ответ: 682,5.

Задание 5.

Похожее условие уже встречалось в задании 3. Из данной формулы делаем вывод, что знаменатель q = 3.

Находим сумму:

Ответ: -847.

Вот и всё!

С наилучшими пожеланиями, твой персональный препод)

Формулы n-го члена арифметической и геометрической прогрессий

Вспомним, что в арифметической прогрессии каждый следующий член получается прибавлением к предыдущему некоторого числа , которое называется разностью арифметической прогрессии:

В геометрической прогрессии, чтобы получить следующий член,  предыдущий необходимо умножить на некоторое число , называемое знаменателем геометрической прогрессии:

Такие соотношения называются рекуррентными, поскольку они выражают следующий член последовательности через предыдущие. Но для вычислений это не всегда удобно.

Задача 1. Тяжелоатлет Вася при подготовке к соревнованиям решил каждую неделю увеличивать массу штанги на  кг. Начал он со  кг. Штангу какой массы он будет поднимать к -й неделе тренировок?

Решение.

Отметим, что значения массы штанги в разные недели – это арифметическая прогрессия. Первый ее член , разность прогрессии . Нужно найти -й член этой прогрессии, т. е. . С помощью рекуррентной формулы это делать долго:

Можно ли как-то ускорить процесс подсчета?

Вспомним, что последовательность еще можно задать с помощью формулы n-го члена (аналитически). Попробуем это сделать для произвольной арифметической прогрессии. Выпишем первые члены:

Прибавляем еще  к :

Далее аналогично:

Видим, что для получения, например, -го члена нам нужно к первому члену прибавить   раза. Соответственно, чтобы получить -й член прогрессии, мы должны  прибавить  раз. Получаем формулу n-гочлена арифметической прогрессии:

С ее помощью мы легко решим задачу:

Тогда:

Ответ:  кг.

Аналогично можно получить и формулу -го члена геометрической прогрессии. Снова выпишем первые несколько членов:

Умножаем  еще на :

Аналогично:

Как и в случае с арифметической прогрессией, обобщим результат. Для получения n-го члена нужно умножить первый член на знаменатель прогрессии  раз. Получим формулу n-го члена геометрической прогрессии:

Итак, арифметическую и геометрическую прогрессию можно задать с помощью формулы n-го члена. В этих формулах присутствует два параметра – числа, которые определяют прогрессию: первый член () и разность  или знаменатель  в арифметической и геометрической прогрессии соответственно. Эти формулы можно преобразовать и получить в несколько другом виде. Подробнее об этом ниже.

---

Формулы -го члена прогрессий

Рассмотрим формулу n-го члена арифметической прогрессии:

Раскроем скобки около  и отдельно сгруппируем член с переменной  и отдельно – без него:

Обозначим:

Тогда:

Видим, что арифметическая прогрессия является линейной функцией натурального аргумента (см. рис. 1).

Рис. 1. Арифметическая прогрессия является линейной функцией натурального аргумента

Сравните со следующей функцией:

Аналогичным образом можно преобразовать и выражение для геометрической прогрессии – умножим и разделим правую часть формулы на :

Обозначим:

Тогда:

Если посмотреть на эту запись как на функцию натурального аргумента, то такая зависимость будет называться «показательной». Она имеет такое название, поскольку аргумент функции  является показателем степени. В старших классах вы еще будете изучать показательные функции, имеющие общий вид:

Сравните:

Т. е. геометрическую прогрессию еще можно назвать показательной функцией натурального аргумента (см. рис. 2).

Рис. 2. Геометрическая прогрессия является показательной функцией натурального аргумента

---

Сведение задачи с n-м членом к решению системы уравнений

В целом формулы n-го члена прогрессии достаточно для работы с прогрессиями. Какие бы ни были условия, мы всегда можем записать каждый член прогрессии в общем виде. Затем получится система уравнений, неизвестными в которой могут быть номер члена прогрессии, первый член ( или ), разность  или знаменатель . Решаем систему, получаем ответ.

Задание 1. Определить знаменатель геометрической прогрессии , если:

Решение.

Записываем формулу n-го члена геометрической прогрессии:

Соответственно:

С учетом условия получаем систему:

Осталось решить систему и найти .

Разделим почленно первое уравнение системы на второе:

Т. к. , то:

Ответ:.

Свойства арифметической и геометрической прогрессий

Описанный метод сведения задачи к решению системы уравнений сработает всегда. Но иногда полученная система будет достаточно сложной или ее решение будет занимать много времени. Для облегчения задачи удобно использовать некоторые свойства, присущие членам арифметической или геометрической прогрессий.

Мы уже знаем, почему прогрессия называется арифметической: каждый ее член является средним арифметическим своих соседей:

Попробуем обобщить это свойство.

Рассмотрим члены прогрессии, равноудаленные от n-го, и преобразуем их сумму, используя формулу -го члена:

Обычно это свойство переписывают в виде:

и  формулируют так: любой член арифметической прогрессии равен среднему арифметическому членов прогрессии, равноудаленных от него.

Аналогичное свойство можно получить и для геометрической прогрессии. Мы обсуждали, что любой член геометрической прогрессии равен среднему геометрическому своих соседей:

Рассмотрим некоторый член прогрессии  и равноудаленные от него:

И для любых равноудаленных от n-го членов прогрессии:

Если извлечь квадратный корень из обеих частей равенства, получим:

Это свойство формулируют так: любой член геометрической прогрессии равен по модулю среднему геометрическому членов прогрессии, равноудаленных от него.

Интересно, что эти свойства прогрессий также являются и признаками этих прогрессий. Т. е. если указанные соотношения выполняются для всех членов последовательности, то она является, соответственно, арифметической или геометрической прогрессией.

---

Доказательство свойств

Рассмотренные свойства прогрессий можно еще обобщить. В арифметической прогрессии если сумма индексов двух членов прогрессии равна сумме индексов двух других, то суммы этих членов прогрессии также равны:

В геометрической прогрессии если сумма индексов двух членов прогрессии равна сумме индексов двух других, то произведения этих членов прогрессии также равны:

Докажем свойство для арифметической прогрессии:

Запишем в общем виде формулы каждого из членов:

Распишем суммы:

Поскольку , то:

Значит:

Аналогичным образом доказывается свойство и для геометрической прогрессии.

Доказано.

---

Задание 2. Найти четыре числа, образующих геометрическую прогрессию , в которой сумма крайних членов равна , а произведение средних – .

Решение.

Имеем геометрическую прогрессию : , в которой:

Задачу можно решить «в лоб», записав общий вид для каждого члена прогрессии и решив полученную систему:

Но проще воспользоваться свойством геометрической прогрессии. Сумма индексов , значит:

Получим систему, которую легче решить, чем предыдущую:

Решая систему, получаем два ответа:

Ответ: или .

---

Решение системы

Будем решать систему методом подстановки:

Из первого уравнения получаем:

Раскрываем скобки. Получили квадратное уравнение:

Решим полученное квадратное уравнение, используя формулу дискриминанта:

Найдем корни квадратного уравнения:

Тогда:

---

Имеем две прогрессии:

1. ;
2. .

Найдем  и  в каждом случае.

1. Используя формулу -го члена геометрической прогрессии , получим:

Тогда:

Имеем прогрессию:

2. Аналогично:

Тогда:

Имеем прогрессию:

Ответ:  или .

Формулы суммы первых  членов арифметической и геометрической прогрессий

Иногда вам могут встретиться задачи, в которых фигурирует сумма членов прогрессии. Например, в магазине канцтоваров действует акция: первая ручка стоит  рублей, а каждая следующая стоит на  рубль дешевле предыдущей. Сколько вы потратите при покупке  ручек?

Тут нужно считать: . Можно ли как-то быстро вычислить эту сумму? И вообще научиться вычислять сумму членов арифметической прогрессии, зная первый член и ее разность?

Сумму первых  членов арифметической прогрессии  можно найти по формуле:

А сумму первых  членов геометрической прогрессии  можно найти по формуле:

Если же , то все члены геометрической прогрессии равны и сумма будет равна:

С доказательством этих формул вы можете ознакомиться ниже.

---

Доказательство формул суммы прогрессий

Докажем, что сумму первых n членов арифметической прогрессии  можно найти по формуле:

Запишем два раза сумму, в прямом и обратном порядке:

Складывая, получаем:

Суммы индексов слагаемых в скобках одинаковы (равны ), значит, по свойству арифметической прогрессии, будут равны и суммы самих членов:

Т. е.:

Таких скобок всего  штук. Получаем:

Или окончательно:

Теперь докажем формулу для суммы геометрической прогрессии при :

Рассмотрим сумму:

Умножим обе части равенства на знаменатель прогрессии :

По определению геометрической прогрессии:

Тогда:

Вычтем из этого равенства предыдущее:

При раскрытии скобок в правой части сократится множество слагаемых. Останется:

Выражая , получаем:

---

Полученные формулы не очень удобны: в них для вычисления нужно знать n-й или -й член. Мы говорили, что прогрессия однозначно задается первым членом и разностью (знаменателем). Попробуем преобразовать формулы, чтобы можно было вычислять сумму, зная только эти характеристики прогрессии.

Формулы для суммы прогрессий можно преобразовать, используя формулу общего члена прогрессии:

С помощью полученных формул легко решить рассмотренную ранее задачу. Первая ручка стоит  рублей:

Каждая следующая – на  рубль дешевле предыдущей:

Общая стоимость  ручек:

Сведение задачи с суммой первых членов к решению системы уравнений

Обратите внимание, что полученные формулы для сумм содержат номер члена прогрессии , первый член (или ), разность  или знаменатель :

Соответственно, мы снова можем свести задачу к системе уравнений относительно этих неизвестных величин.

Задание 3. Шесть чисел образуют арифметическую прогрессию (). Сумма первых трех ее членов равна , а сумма трех последних равна . Найти эти числа.

Решение.

По условию сумма первых трех , а сумму первых шести  мы можем найти:

Воспользуемся формулой суммы первых  членов арифметической прогрессии:

Тогда:

Составим систему, состоящую из двух уравнений:

Отсюда:

Ответ: .

---

Решение системы

Вынесем за скобки общий множитель в первом уравнении системы:

Сократим дроби в каждом уравнении системы:

Разделим каждое уравнение системы на :

Решим систему уравнений методом сложения. Умножим левую и правую части первого уравнения системы на :

Складываем уравнения и получаем:

Тогда:

---

Найдем остальные члены прогрессии, используя формулу -го члена:

Тогда:

Ответ:.

Задание 4. Чтобы заасфальтировать участок длиной  м, используют два катка. Первый каток установили на одном из концов участка, второй – на противоположном. Работать они начали одновременно. За первую минуту первый каток прошел  м, за каждую следующую минуту он проходил на  м больше, чем за предыдущую. Второй каток за каждую минуту проходил  м. Через сколько минут оба катка встретятся?

Решение.

Составим математическую модель задачи. Пусть два катка встретятся через  минут, тогда второй каток проедет до встречи путь, равный  м, а первый проедет путь, который можно выразить с помощью суммы арифметической прогрессии, где :

Тогда, с учетом вышесказанного:

Весь путь равен  м, следовательно:

Решая данное уравнение, получаем корни:

 – это количество минут, поэтому  не удовлетворяет условию задачи. Значит, оба катка встретятся через  минут.

Ответ:  минут.

---

Решение уравнения

Преобразуем второе слагаемое в левой части уравнения:

Получим квадратное уравнение:

Решим полученное квадратное уравнение, используя формулу дискриминанта:

---

Формула суммы бесконечной геометрической прогрессии

Вернемся к формуле суммы геометрической прогрессии:

Рассмотрим случай, когда:

Если мы будем возводить такое число во все большую и большую степень, то оно будет становиться все меньше и меньше. Например:

И если мы возьмем очень большое , то  уменьшится практически до нуля:

Более строго в математике это записывают так:

Если мы возьмем бесконечное большое значение , то  будем считать равным нулю.

Что это значит для нашей формулы суммы геометрической прогрессии? Это значит, что сумма бесконечного количества членов геометрической прогрессии при  будет равна:

Например, при  получим:

Но как так? Мы складываем бесконечно количество положительных чисел, а получаем ? Посмотрим, что это за числа в нашем примере:

Представьте: у вас есть торт. Вы разрезали его пополам, съели половину  (см. рис. 3).

Рис. 3. Торт разрезали пополам и съели половину

Оставшуюся половинку разрезали еще пополам и съели одну часть  (см. рис. 4).

Рис. 4. Оставшуюся половину торта  разрезали пополам и съели одну часть

Теперь вы съели  торта. Оставшуюся половинку делите еще пополам и берете одну часть .

Рис. 5. Оставшуюся половину торта  разрезали пополам и съели одну часть

Итого:

И так вы можете делить до бесконечности! В итоге, если это действительно происходило бесконечное количество раз, то вы бы съели весь торт.

Но бесконечность – это все же математическая абстракция. Мы не можем есть торт бесконечно. И за очень большое, но все же конечное число таких операций мы бы съели почти весь торт:

Решение задачи с использованием формулы суммы бесконечно убывающей геометрической прогрессии вы можете посмотреть ниже.

---

Задача с бесконечной геометрической прогрессией

Задача 1. Найти третий член бесконечной геометрической прогрессии , сумма которой равна , а второй член равен .

Решение.

Для решения задачи будем использовать формулы суммы бесконечной геометрической прогрессии и n-го члена геометрической прогрессии:

Учитывая, что , составим и решим систему:

Разделим почленно второе уравнение системы на первое:

Воспользуемся теоремой Виета для поиска корней уравнения:

Откуда:

Значение  не удовлетворяет условию . Следовательно:

Тогда:

Ответ:

---

Список литературы

1. Никольский С.М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра, 9 класс. Учебник. – М.: ФГОС, «Просвещение», 2018.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Алгебра, 9 класс. Учебник. – М.: «Просвещение», 2018.
3. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра, 9 класс. Учебник. – М.: «Просвещение», 2018.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал yaklass.ru (Источник)
2. Интернет-портал math10.com (Источник)
3. Интернет-портал bymath.net (Источник)

Домашнее задание

1. Сумма второго и шестого членов убывающей арифметической прогрессии равна . Произведение третьего и пятого ее членов равно . Найти первый член этой прогрессии.
2. Найти сумму первых восьми членов геометрической прогрессии, если , .
3. Сумма трех чисел, составляющих возрастающую арифметическую прогрессию, равна . Если к первому числу прибавить , ко второму прибавить , а третье оставить без изменения, то полученные числа составят геометрическую прогрессию. Найти эти числа.