Свойства тонкой линзы определяются главным образом расположением ее главных фокусов. Поэтому, зная расстояние от источника света до линзы, а также ее фокусное расстояние (положение фокусов), мы можем определить расстояние до изображения, опустив описание хода лучей внутри самой линзы. Поэтому в изображении на чертеже точного вида сферических поверхностей линзы необходимость отсутствует.
Схематически тонкие линзы обозначают отрезком со стрелками на конце. Они смотрят от центра в противоположные стороны, если линза собирающая, и они направлены к центру отрезка, если линза рассеивающая.
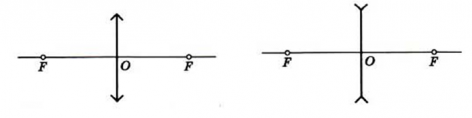
Внимание!
Напомним, что линзы могут давать действительные и мнительные изображения. Причем, собирающая линза может давать как действительные, так и мнимые изображения. Рассеивающая линза всегда дает только мнимые изображения.
Способ построения изображений, а также вид самих изображений в линзе зависит от того, где расположен изображаемый предмет. Он может располагаться за двойным фокусным расстоянием, в фокальной плоскости второго фокуса, между вторым и первым фокусом, в фокальной плоскости главного фокуса и на расстоянии меньше фокусного расстояния линзы.
Определение
Вторым фокусом называют точку, которая расположена на главной оптической оси от главного фокуса на расстоянии, равном фокусному расстоянию линзы. Относительно линзы он располагается на расстоянии, равном двойному фокусному расстоянию линзы.
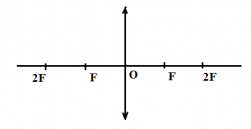
Построение изображения в собирающей линзе
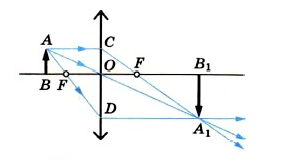
Предметы схематично изображаются в виде стрелки. Чтобы построить изображение предмета в собирающей линзе, нужно найти положение верхней и нижней точки этого изображения. Сначала находят положение точки изображения, соответствующей верхней точки предмета (точки А). Для этого из этой точки нужно пустить два луча:
Два вида лучей при построении изображений в линзе
Первый луч проходит из верхней точки предмета (точки А) параллельно главной оптической оси. На линзе (в точке С) луч преломляется и проходит через точку фокуса (точку F).
Второй луч необходимо направить из верхней точки предмета (точки А) через оптический центр линзы (точку О). Он пройдет, не преломившись.
На пересечении двух лучей обозначаем точку А1. Это и будет изображение верхней точки предмета. Таким же образом нужно поступить с нижней точкой предмета. Но на пересечении вышедших из линзы лучей нужно поставить точку В1. Изображение предмета при этом — А1 В1.
В зависимости от того, где расположен предмет, изображение может получиться действительным или мнимым, увеличенным или уменьшенным, перевернутым или прямым. Построим изображения для каждого из таких случаев.
| Схема построения изображения | Расположение предмета относительно линзы + характеристика изображение |
 |
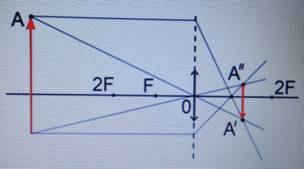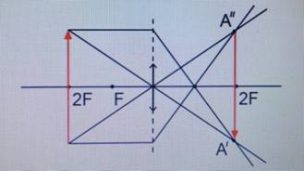
Предмет располагается за двойным фокусом.
Изображение:
|
 |
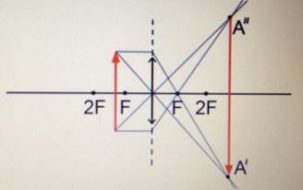
Предмет располагается в фокальной плоскости второго фокуса.
Изображение:
|
 |
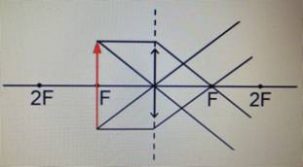
Предмет располагается в пространстве между фокусом и двойным фокусом.
Изображение:
|
 |
Предмет находится в фокальной плоскости.
Изображения нет, поскольку лучи идут параллельно друг другу и не пересекаются. |
 |
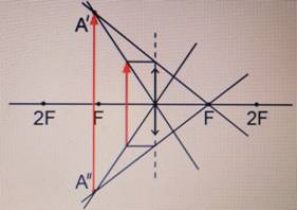Предмет располагается между линзой и фокусом.
Изображение:
|
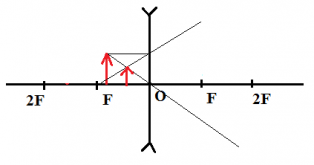
Пример №1. Построить изображение предмета, изображенного на рисунке. Определить тип изображения.
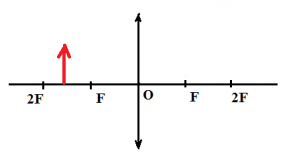
Чтобы построить изображение предмета, достаточно определить его положение одной точки — верхней. Поскольку предмет расположен параллельно линзе, для построения изображения, достаточно будет соединить найденную точку изображения для верхней точки предмета перпендикуляром, проведенным к главной оптической оси.
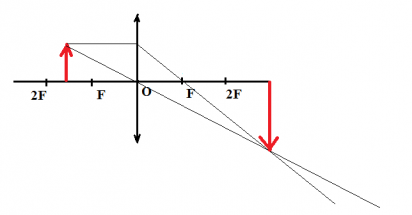
Чтобы построить изображение верхней точки, пустим от нее два луча — побочную оптическую ось через оптический центр и перпендикуляр к линзе. Затем найдем пересечение побочной оптической оси с преломленным лучом. Теперь пустим перпендикуляр к главной оптической оси и получим изображение. Оно является действительным, увеличенным и перевернутым.
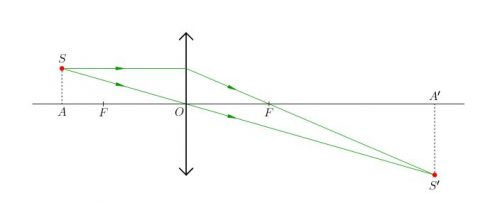
Частный случай — построение изображения точки
Положение изображения точки можно найти тем же способом, описанным выше. Нужно лишь построить два луча и найти их пересечение после выхода из линзы (см. рисунок ниже). Так, изображению точки S соответствует точка S´.
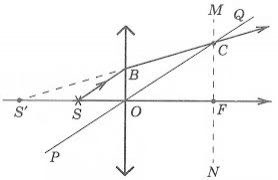
Особую сложность составляет случай, когда точка расположена на главной оптической оси. Сложность заключается в том, что все лучи, которые можно построить, будут совпадать с главной оптической осью. Поэтому возникает необходимость в определении хода произвольного луча. Направим луч от точки S (луч SB) к собирающей линзе. Затем построим побочную оптическую ось PQ такую, которая будет параллельна лучу SB. После этого построим фокальную плоскость и найдем точку пересечения (точка С) фокальной плоскости с побочной оптической осью. Теперь соединим полученную точку С с точкой В. Это будет преломленный луч. Продолжим его до пересечения с главной оптической осью. Точка пересечения с ней и будет изображением точки S. В данном случае оно является мнимым.
Пример №2. Построить изображение точки, расположенной на главной оптической оси.
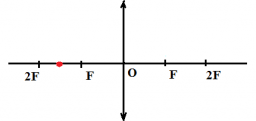
Чтобы построить изображение, пустим произвольный луч к линзе. Затем построим параллельную ему побочную оптическую ось и фокальную плоскость. Из места пересечения этой оси с фокальной плоскостью пустим луч, также проходящий через точку пересечения линзы с произвольным лучом. Построим продолжение луча до получения точки пересечения с главной оптической осью. Отметим точку пересечения — она является действительным изображением точки.
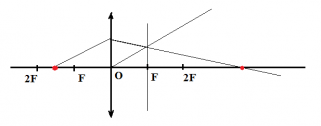
Построение изображения в рассеивающей линзе
Чтобы построить изображение предмета в рассеивающей линзе, нужно определить положения точек изображения, соответствующих верхней и нижней точкам предмета. Вот как определить положение точки изображения для верхней точки предмета:
- Нужно пустить луч, перпендикулярный главной оптической оси. Этот луч после преломления отклонится. Но его продолжение обязательно пересечет главный фокус линзы.
- Нужно пустить луч от верхней точки предмета через оптический центр линзы (построить побочную оптическую ось).
- Точку пересечения продолжения луча, полученного в шаге 1, с побочной оптической осью, нужно обозначить за изображение верхней точки предмета (на рисунке это точка А´).
Точно такие же действия нужно выполнить для нижней точки предмета. В результате получится точка пересечения, соответствующая изображению нижней точки предмета (на рисунке это точка А´´).
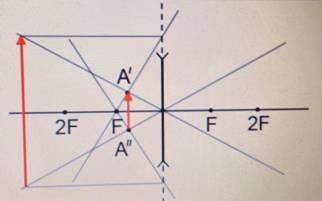
Внимание! Независимо от расположения предмета относительно рассеивающей линзы, изображение всегда получается прямым, уменьшенным, мнимым.
Пример №3. Построить изображение предмета в рассеивающей линзе.
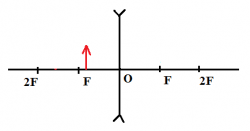
Чтобы построить изображение, пустим от верхней точки предмета побочную оптическую ось через оптический центр и проведем перпендикуляр к линзе. Затем из точки главного фокуса проведем луч через точку пересечения линзы с перпендикуляром. Пересечение этого луча с побочной оптической осью есть изображение верхней точки предмета. Теперь проведем от нее перпендикуляр к главной оптической оси. Это и будет являться изображением предмета. Оно является мнимым, уменьшенным и прямым.
Построение изображений в плоском зеркале
Определение
Плоское зеркало — это плоская поверхность, зеркально отражающая свет.
Построение изображения в зеркалах основывается на законах прямолинейного распространения и отражения света. Продемонстрируем это с помощью рисунка ниже.
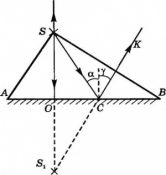
Построим изображение точечного источника S. От точечного источника света лучи распространяются во все стороны. На зеркало падает пучок света ASB, и изображение создается всем пучком сразу. Но для построения изображения достаточно взять любые два луча из этого пучка. Пусть это будут лучи SO и SC. Луч SO падает перпендикулярно поверхности зеркала АВ. Поскольку угол между ним и перпендикуляром, восстановленным в точке падения, равен 0, то угол падения принимаем равным за 0. поэтому отраженный пойдет в обратном направлении OS. Луч SC отразится под углом γ=α. Отраженные лучи OS и СК расходятся и не пересекаются, но если они попадают в глаз человека, то человек увидит изображение S1, которое представляет собой точку пересечения продолжения отраженных лучей.
Таким образом, чтобы получить изображение в плоском зеркале, нужно:
- Пустить от источника света луч, перпендикулярный к плоскости зеркала (падающий луч совпадает с отраженным лучом).
- Пустить от источника света к плоскости зеркала еще один луч под произвольным углом.
- Построить отраженный луч от падающего луча, построенного в шаге 2, используя закон отражения света.
- Найти пересечение продолжений отраженных от зеркала лучей (пущенного под прямым углом и произвольным углом).
Внимание!
Изображение в зеркале всегда является мнимым. Это связано с тем, что изображение строится на пересечении продолжении лучей, а не на самих лучах.
Изображение в плоском зеркале находится от зеркала на таком же расстоянии, как предмет от этого зеркала. Это легко доказать тем, что треугольники SOC и S1OC равны по стороне и двум углам. Следовательно SO = S1O. Отсюда делаем вывод, что для построения изображения точечного источника света достаточно знать расстояние, на котором он находится от зеркала. Останется только провести к зеркалу перпендикулярную прямую и отложить на ней точку на нужном расстоянии.
При построении изображения какого-либо предмета последний представляют как совокупность точечных источников света. Поэтому достаточно найти изображение крайних точек предмета. Так, изображение А1В1 соответствует предмету АВ.
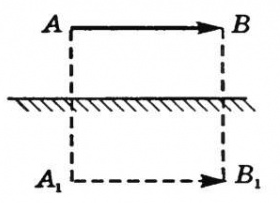
Изображение и сам предмет всегда симметричны относительно зеркала.
Пример №4. Построить изображение треугольника ABC в плоском зеркале.
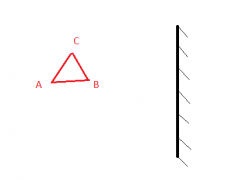
Чтобы построить изображение, пустим к плоскому зеркалу перпендикулярные прямые. Затем измерим расстояние от каждой точки до зеркала и отложим их по перпендикуляру от зеркала в обратную сторону. Так для точки А мы находим точку А´, для В — В´, для С — С´.
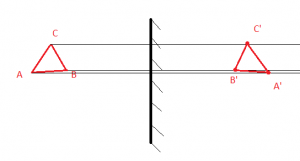
Видно, что треугольник отразился зеркально (изображение и предмет симметричны друг другу). Так и должно быть в случае с зеркалом.
Задание EF17760
Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет AC лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла C лежит ближе к центру линзы, чем вершина острого угла A. Расстояние от центра линзы до точки A равно удвоенному фокусному расстоянию линзы, AC = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Сделать рисунок — построить изображение в линзе.
3.Записать формулу для нахождения площади полученной фигуры.
4.Выполнить решение в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Оптическая сила линзы: D = 2,5 дптр.
• Сторона треугольника AC = 4 см.
4 см = 0,04 м
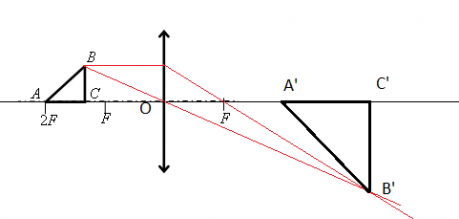
Построим изображение в линзе. Для этого достаточно построить изображение точки В. Сначала пустим луч, параллельный главной оптической оси, к плоскости линзы. Он будет преломляться, после чего пройдет через фокус. Затем пустим луч через оптический центр. На месте пересечения двух лучей поставим точку и обозначим ее за B´.
Так как точки B и C предмета лежат на одной прямой, перпендикулярной главной оптической оси, для нахождения точки изображения C´ достаточно пустить перпендикуляр от B´ этой оси. На месте пересечения поставим точку и обозначим ее C´.
Рассматривать ход лучей для построения точки A´ тоже не будем. Точка A лежит в плоскости второго фокуса. Значит, она будет находиться в этой же точке и с противоположной стороны линзы. Это легко доказать с помощью формулы тонкой линзы:
1d+1f=1F
Если расстояние от предмета до линзы равно 2F, то и расстояние от линзы до его изображения будет 2F:
12F+1f=1F
1f=1F−12F=2−12F=12F
f=2F
Теперь соединим все найденные точки и получим треугольник A´ B´ C´. Найдем его площадь. Поскольку это прямоугольный треугольник, его площадь будет равна половине произведения двух катетов — B´ C´и A´ C´:
S=A´C´·B´C´2
Из формулы оптической силы линзы найдем фокусное расстояние:
F=1D=12,5=0,4 (м)
Известно, что точка A находится в точке двойного фокусного расстояния. И ее изображение тоже находится на таком же расстоянии от линзы. Следовательно, чтобы найти длину катета A´ C´, нужно найти расстояние от точки C до ее изображения. Расстояние от этой точки до линзы равно разности двойного фокусного расстояния и длины отрезка AC:
dC=2F−AC=2·0,4−0,04=0,76 (м)
Используя формулу тонкой линзы, вычислим расстояние от линзы до изображения этой точки:
10,76+1f=1F
1fC=1F−10,76=0,76−F0,76F=0,76−0,40,76·0,4
fC=0,76·0,40,76−0,4=0,844 (м)
Тогда длина катета A´ C´ будет равна:
A´C´=fC−fA=fC−2F=0,844−0,4·2=0,044 (м)
Треугольники BCO и B´ C´O подобны по 3 углам. Углы O равны как вертикальные. Углы C и C´ как прямые, а B и B´ как накрест лежащие (полученные при пересечении секущей в виде луча через оптический центр и параллельных фокальных плоскостей). Следовательно BC относится к B´ C´ так же, как OC относится к C´O:
BCB´C´=ACA´C´
Треугольник ABC равнобедренный, поэтому BC = AС. Тогда:
ACB´C´=ACA´C´
Следовательно:
B´C´=A´C´
Отсюда площадь треугольника равна:
S=A´C´·A´C´2=(0,044)22=0,000968 (м2)=9,68 (см2)
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18181
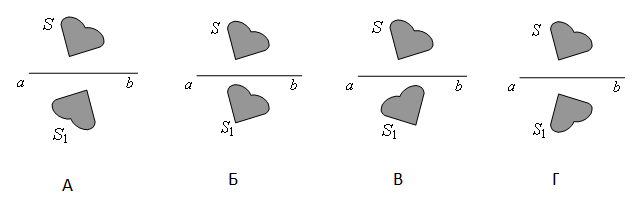
Предмет S отражается в плоском зеркале ab. На каком рисунке верно показано изображение S1 этого предмета?
Ответ:
Алгоритм решения
- Записать, какое изображение дает плоское зеркало.
- Выбрать изображение, которое соответствует типу описанного изображения.
Решение
Зеркало дает мнимое изображение предмета без увеличения в зеркальном отражении. Это значит, что предмет и его изображение должны быть симметричны относительно плоскости зеркала. Симметричными являются только предмет и его изображение на последнем рисунке — Г.
Ответ: Г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18876
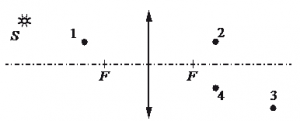Какая точка является изображением точки S (см. рисунок), создаваемым тонкой собирающей линзой с фокусным расстоянием F?
Алгоритм решения
1.Построить изображение точки.
Решение
Построим изображение точки с учетом того, что линза собирающая. Для этого пустим из этой точки луч света, параллельный главной оптической оси. После прохождения через линзу луч преломится и пройдет через фокус. Затем пустим луч от этой точки через оптический центр линзы. Точка, в которой оба луча пересекутся, будет искомой. В данном случае это точка 4.
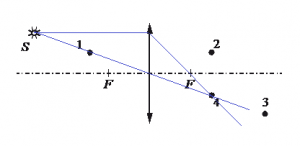
Ответ: 4
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 31.9k
Предмет находится на главной оптической оси (точка В). В этом примере построение изображения точки А строится следующим образом: луч, параллельный главной оптической оси после линзы идет так, как если бы выходил из точки F; другой луч идёт через оптический центр без преломления; мнимое пересечение этих лучей даст изображение точки А. Для построения изображения точки В необходимо воспользоваться побочной осью, роль которой может сыграть луч, выходящий из точки А.
Смотрите данное построение в видеоролике.
Вы уже знаете, что линзы — это прозрачные тела, которые фокусируют (собирают) или рассеивают свет. Но каковы характеристики изображений, создаваемых линзами, и, как и в случае с зеркалами, можно ли их построить?
Оптические характеристики линз
Основная функция линзы в оптической системе заключается в фокусировке или рассеивании падающих световых лучей симметрично относительно оптической оси (см. рисунок 1). В случае двояковыпуклой или двояковогнутой линзы оптическая ось — это линия, соединяющая центры сфер, ограничивающих линзу. Эта ось также является осью симметрии линзы.
На оптической оси находится центр линзы — его можно определить графически, как показано на рисунке 2 ниже.
При прохождении через линзу свет преломляется дважды: один раз, когда он входит в линзу, и второй раз, когда он выходит из нее.
Когда лучи света, идущие параллельно оптической оси, проходят через собирающую линзу, они пересекаются в точке на оптической оси. Эта точка называется фокусом линзы и обозначается буквой F. Расстояние этой точки от центра S линзы называется фокусным расстоянием f (см. рисунок 3).
Помните! Фокусная точка (F) собирающей линзы — это точка пересечения всех лучей светового пучка после его прохождения через линзу, которые до попадания в линзу шли параллельно ее оптической оси.
Фокусное расстояние (f) линзы — это расстояние от фокусной точки (F) до центра линзы (S).
В случае рассеивающей линзы падающий пучок света расходится — лучи света, входящие в линзу, рассеиваются таким образом, что их продолжения пересекаются в одной точке. Это называется мнимым (кажущимся) фокусом рассеивающей линзы (см. рисунок 4). Он расположен на той же стороне линзы, откуда исходили лучи.
Как формируется изображение с помощью собирающей линзы?
Чтобы увидеть, какие изображения мы получаем с помощью собирающей линзы, давайте проведем эксперимент.
Опыт 1. Наблюдение изображений, создаваемых линзой.
Что вам понадобится?
- фонарик;
- кусок черного картона размером больше стекла фонарика;
- ножницы;
- скотч (липкая лента);
- большая лупа;
- белая картонная коробка (экран).
Инструкция.
- Вырежьте стрелку в черной картонной коробке.
- С помощью скотча приклейте черный картон к экрану фонарика.
- Расположите лупу, фонарь и экран на оптической оси лупы.
- Измените положение фонаря и экрана для получения четкого изображения.
Какой вывод получится?
Изменяя положение экрана и фонарика относительно лупы, вы получите различные изображения — однократно увеличенное, однократно уменьшенное, перевернутое и прямое. Как вы заметите, собирающая линза не обязательно увеличивает наблюдаемый объект. Почему это происходит?
Как и в случае с зеркалами, геометрические построения изображений с использованием лучей (см. рисунок 5), характерных для линз, окажутся полезными для ответа на вопрос, поставленный в резюме эксперимента.
Когда нам нужно построить изображение с помощью собирающей линзы, мы обычно выбираем два из трех перечисленных ниже лучей:
- луч, параллельный оптической оси — после прохождения через линзу он проходит через фокус;
- луч, проходящий через центр линзы — после прохождения через линзу его направление (путь) не меняется;
- луч, проходящий через фокусную точку — после прохождения через линзу выходит параллельно оптической оси.
Последнее предложение справедливо для тонких линз, которые мы и будем использовать в наших экспериментах. Затем мы проигнорируем толщину линзы и нарисуем ее в виде отрезка, заканчивающегося стрелками.
Изображение точки образуется при пересечении как минимум двух лучей или их продолжений.
Сводная информация о положении изображения в зависимости от положения объекта и характеристиках получаемых изображений приведена в таблице 1 ниже.
| Положение объекта, x | Положение изображения, y | Особенности изображения |
| x > 2f | f < y < 2f | Перевернутое, действительное, уменьшенное |
| x = 2f | y = 2f | Перевернутое, действительное, имеет те же размеры, что и объект |
| 2f > x > f | y > 2f | Перевернутое, действительное, увеличенное |
| x = f | лучи проходят через линзу и параллельны друг другу | Без изображения |
| x < f | изображение появляется на той же стороне, что и объект | Прямое, мнимое, увеличенное |
Из таблицы 1 можно сделать вывод, что характеристики изображения, формируемого в собирающей линзе, зависят от расстояния объекта от линзы.
Помните! Реальное изображение точки формируется там, где пересекаются лучи, преломленные через линзу. Однако часто бывает так, что преломленные лучи расходятся. Тогда их продолжения всегда пересекаются, и получается мнимое (иллюзорное) изображение. Если преломленные лучи параллельны друг другу, изображение вообще не образуется.
Как создается изображение при использовании рассеивающей линзы?
В случае с рассеивающей линзой построение изображения несколько иное. Пучок лучей, падающих параллельно линзе после ее выхода, является расходящимся. Как уже говорилось, пересекаются только продолжения лучей, преломленных в так называемой мнимой фокусной точке (см. рисунок 6).
Для построения изображения в рассеивающей линзе (как и в собирающей) достаточно двух лучей:
- падающий луч, параллельный оптической оси — после прохождения через линзу падающий луч движется таким образом, что его продолжение проходит через мнимую фокусную точку;
- луч, проходящий через центр линзы — при прохождении через линзу он не меняет направления.
Помните! В рассеивающей линзе результирующее изображение всегда прямое, уменьшенное и мнимое.
В уроках «Изображение светящейся точки, даваемое линзой» и «Изображение предмета, даваемое линзой», мы уже рассматривали построение различных изображений. Также в этих уроках находятся памятки для построения изображения точки или предмета, которые могут вам пригодиться.
В данном уроке представлены дополнительные интересные задачи на построение изображений. И, конечно, вы можете ознакомиться с их решением, разбором построения и итоговым чертежом.
Задача №1
На рисунке 1 показан ход светового луча, падающего на рассеивающую линзу. Выполнив необходимые построения, найдите положения фокусов линзы и положение изображения светящейся точки $S$.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Если луч падает параллельно оптической оси на рассеивающую линзу и преломляется, то продолжение этого преломленного луча пересечет оптическую ось в мнимом фокусе рассеивающей линзы.
Поэтому мы продолжим преломленный луч (отмечен синим цветом) до пересечения с оптической осью. Точка пересечения — это мнимый фокус $F$. Отметим его на чертеже (рисунок 2, а).
С другой стороны от линзы отмерим точно такое же фокусное расстояние и отметим второй фокус линзы.
Теперь нужно построить изображение светящейся точки (рисунок 2, б). Один преломленный луч у нас на чертеже уже есть (использовать мы будем его продолжение). Значит, нужно провести второй луч.
Выберем и проведем на чертеже луч, проходящий через оптический центр линзы $O$. После прохождения через линзу он не изменит направления своего распространения. Поэтому его продолжение совпадет с падающим лучом $SO$.
В итоге, на пересечении двух продолжений преломленных лучей мы получаем мнимое изображение светящейся точки $S_1$.
Задача №2
На рисунке 3 изображены положения главной оптической оси линзы, источника света $S$ и его изображения $S_1$. С помощью этих данных постройте оптический центр, отметьте на чертеже саму линзу и ее фокусы.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
В этой задаче у нас уже есть изображение светящейся точки. Обычно, когда мы занимаемся его построением, мы используем два световых луча. Один из них — это луч, проходящий через оптический центр $O$, который лежит на оптической оси линзы. После прохождения через линзу (ее оптический центр) он не изменяет своего направления.
А изображение $S_1$ лежит на пересечении этого луча с другим. Значит, мы можем соединить точки $S$ и $S_1$ друг с другом (рисунок 4, а).
Полученная прямая $SS_1$ пересекает оптическую ось в точке — это и есть оптический центр $O$. Отметим его на рисунке.
Зная положение оптического центра, мы можем отметить на чертеже и саму линзу. Какая это будет линза: собирающая или рассеивающая? Изображение $S_1$ является действительным, так как оно находится по другую сторону от линзы и явно будет на пересечении двух преломленных лучей. Действительное изображение мы можем получить только с помощью собирающей линзы (рисунок 4, б).
Теперь у нас на чертеже есть: оптическая линза, оптическая ось, оптический центр $O$, точка $S$, ее изображение $S_1$, падающий луч $SO$ и преломленный луч $OS_1$. Построим ход второго луча.
Луч $SC$ падает на линзу параллельно ее оптической оси. По определению, после преломления он должен пройти через фокус линзы и пересечься с другим преломленным лучом.
Этот преломленный луч будет выходить из точки $C$ и пересекаться с другим преломленным лучом в точке $S_1$. Отметим на чертеже этот луч $CS_1$ (рисунок 4, в).
Он пересек оптическую ось в точке — это и есть фокус линзы $F$. Чтобы отметить второй фокус, нужно отложить такое же фокусное расстояние с другой стороны линзы.
Задача №3
Постройте оптический центр, отметьте линзу и ее фокусы на чертеже, используя данные рисунка 5.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
По аналогии с построением в предыдущей задаче соединим прямой точку $S$ и ее изображение $S_1$. Но в этом случае прямая $SS_1$ не пересекла оптическую ось. Продолжим ее до пересечения, чтобы получить положение оптического центра $O$ (рисунок 6, а).
Мы видим, что точка и ее изображение находятся по одну сторону от линзы (ее оптического центра). Значит, изображение $S_1$ — мнимое. В точке $S_1$ должны пересечься продолжения преломленных лучей. Это возможно, если мы будем использовать рассеивающую линзу. Отметим ее на чертеже (рисунок 6, б).
Луч $SO$ после прохождения сквозь линзу не изменит своего направления. Продолжение преломленного луча совпадает с самим падающим лучом $SO$.
Проведем второй луч, идущий параллельно оптическое оси — луч $SС$. После прохождения сквозь линзу продолжение преломленного луча пересекается с продолжением другого преломленного луча $SO$ в точке $S_1$. Продолжим его до пересечения с оптической осью.
Так мы получили положение мнимого фокуса $F$ (рисунок 6, в). Чтобы отметить второй фокус, нужно отложить такое же фокусное расстояние с другой стороны линзы.
Задача №4
Постройте изображение предмета, расположение которого показано на рисунке 7. Охарактеризуйте его.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
На исходном рисунке 7 изображена выпуклая линза — собирающая. Отметим саму линзу и ее оптический центр $O$ на чертеже. Обозначим крайние точки предмета точками $A$ и $B$ (рисунок 8, а).
Начнем построение изображения предмета. Так как обе его точки не лежат на оптической оси, то и изображение нужно будет строить сначала для одной точки, а потом — для второй.
Займемся построением изображения точки $A$ (рисунок 8, б). Проведем два падающих луча $AC$ и $AO$. Луч $AO$ после преломления не изменит своего направления, а луч $AC$ преломится в линзе и после пройдет через фокус $F$.
Продолжим эти два преломленных луча до пересечения друг с другом. Получим изображение $A_1$.
Теперь построим изображение точки $B$ (рисунок 8, в). На линзу падают лучи $BO$ и $BD$. После преломления они пересекутся в точке $B_1$.
Соединим точки $A_1$ и $B_1$. Так мы получили изображение предмета $A_1B_1$. Охарактеризуем его.
Полученное изображение предмета:
1. Действительное
2. Увеличенное
3. Перевернутое
4. $f > 2F$
Описывая положение изображения в последнем пункте, под величиной $f$ мы принимаем расстояние от изображения предмета до линзы.
Задача №5
Постройте изображение предмета, находящегося в фокусе собирающей и рассеивающей линз (рисунок 9). Сравните полученные изображения.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Предмет располагается перпендикулярно оптической оси. При этом одна его крайняя точка ($B$) лежит на оптической оси. Поэтому, для построения изображения достаточно будет построить изображение крайней точки $A$ и опустить перпендикуляр на оптическую ось, чтобы получить изображение точки $B$.
Начнем с построения изображения предмета, даваемого собирающей линзой (рисунок 10, а). Из точки выходят два луча $AC$ и $AO$. Как видно из чертежа после прохождения сквозь линзу преломленные лучи параллельны друг другу — они никогда не пересекутся. Значит, изображения мы не получим.
Теперь построим изображение предмета в рассеивающей линзе (рисунок 10, б). Из крайней точки $A$ выходят два луча $AC$ и $AO$. Так как линза рассеивающая, изображение точки $A_1$ мы получим на пересечении продолжений преломленных лучей. Опустим перпендикуляр на оптическую ось и получим точку $B_1$. Соединим полученные точки друг с другом — получим изображение предмета $A_1B_1$.
Если предмет находится в фокусе собирающей линзы, то мы не получим его изображения.
Если предмет находится в фокусе рассеивающей линзы, то изображение предмета:
1. Мнимое
2. Уменьшенное
3. Прямое
4. $f < F$
Описывая положение изображения в последнем пункте, под величиной $f$ мы принимаем расстояние от изображения предмета до линзы.
Задача №6
Постройте изображение предмета, расположенного от собирающей линзы на расстоянии $3F$ (рисунок 11).
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Предмет располагается перпендикулярно оптической оси. При этом одна его крайняя точка ($B$) лежит на оптической оси. Поэтому, для построения изображения достаточно будет построить изображение крайней точки $A$ и опустить перпендикуляр на оптическую ось, чтобы получить изображение точки $B$.
Из точка $A$ на линзу падают лучи $AC$ и $AO$ (рисунок 12). После прохождения сквозь линзу они преломляются и пересекаются друг с другом в точке $A_1$ — изображении точки $A$.
Опустим перпендикуляр на оптическую ось и получим точку $B_1$ — изображение точки $B$. Соединим точки $A_1$ и $B_1$ между собой и получим изображение предмета $A_1B_1$.
Охарактеризуем полученное изображение. При этом $d$ — это расстояние от предмета до линзы, а $f$ — расстояние от изображения предмета до линзы.
Если $d = 3F$, то изображение предмета, даваемое собирающей линзой:
1. Действительное
2. Уменьшенное
3. Перевернутое
2. $2F > f >F$
Задача №7
Постройте изображение предмета, расположенного от собирающей линзы на расстоянии $4F$ (рисунок 13). Сравните его с изображением предмета, полученным в задаче №6.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Предмет располагается перпендикулярно оптической оси. При этом одна его крайняя точка ($B$) лежит на оптической оси. Поэтому, для построения изображения достаточно будет построить изображение крайней точки $A$ и опустить перпендикуляр на оптическую ось, чтобы получить изображение точки $B$.
Построим изображение точки $A$ (рисунок 14). Из нее выходят два луча: $AC$ и $AO$. После преломления они пересекаются в точке $A_1$. Опустим перпендикуляр на оптическую ось, чтобы получить изображение точки $B$ — $B_1$.
Соединим точки $A_1$ и $B_1$ между собой и получим изображение предмета $A_1B_1$.
Охарактеризуем полученное изображение. При этом $d$ — это расстояние от предмета до линзы, а $f$ — расстояние от изображения предмета до линзы.
Если $d = 4F$, то изображение предмета, даваемое собирающей линзой:
1. Действительное
2. Уменьшенное
3. Перевернутое
2. $2F > f >F$
Сравнивая полученное изображение предмета с изображением, полученным в предыдущей задаче, мы уже можем сделать определенные выводы. Для полной картины используем полученное изображение в задаче, рассмотренной в уроке «Изображение предмета, даваемое линзой». Там предмет находился в двойном фокусе линзы, а его полученное изображение было действительным, перевернутым, равным по размеру предмету и находилось в двойном фокусе с другой стороны линзы.
Тогда мы можем сделать вывод:
по мере отдаления предмета от линзы на двойное фокусное расстояние и дальше, действительное и перевернутое изображение предмета уменьшается и приближается к фокусу линзы, но никогда не окажется в нем.
Постройте изображение предмета, расположение которого показано на рисунке 15, и охарактеризуйте его.
Показать готовый чертеж и пояснения
Скрыть
Построение изображения:
Хоть одна из крайних точек предмета и находится на оптической оси, сам предмет расположен под углом к ней. Поэтому, при построении изображения необходимо будет отдельно строить изображения крайних точек $A$ и $B$.
Начнем с более сложного построения. Построим изображение точки, лежащей на оптической оси линзы — точки $B$ (рисунок 16).
Луч $BO$ проходит через оптический центр и после преломления не изменит своего направления. Эти лучи лежат оптической оси линзы.
Произвольный луч $BC$ падает на линзу. Теперь нам нужно построить ход этого луча после преломления в линзе. Для этого проведем побочную оптическую ось $MN$, параллельную этому лучу.
Далее отметим на чертеже фокальную плоскость, перпендикулярную оптической оси и проходящую через фокус $F$ (обозначена на рисунке пунктирной линией-перпендикуляром, опущенным в точку $F$).
Побочная оптическая ось $MN$ пересечет фокальную плоскость в точке $F’$ — побочном фокусе.
Преломленный луч будет проходить через этот побочный фокус. Соединим точки $C$ и $F’$ — получим преломленный луч $CF’$. Продолжим его до пересечения с первым преломленным лучом (который совпадает с оптической осью). На этом пересечении мы получаем точку $B_1$ — изображение точки $B$.
Теперь привычным для нас способом построим изображение точки $A$ (рисунок 17).
Лучи $AD$ и $AO$ после преломления в линзе пересекаются в точке $A_1$. Соединим точки $A_1$ и $B_1$ и получим изображение предмета $A_1B_1$.
Полученное изображение предмета, находящегося от линзы на расстоянии $2F > d >F$:
1. Действительное
2. Увеличенное
3. Перевернутое
4. $f > 3F$
Видеоурок 1: Изображение в собирающей линзе – Физика в опытах и экспериментах
Видеоурок 2: Построение изображений с помощью линз
Лекция: Ход луча, прошедшего линзу под произвольным углом к её главной оптической оси. Построение изображений точки и отрезка прямой в собирающих и рассеивающих линзах и их системах
Итак, вспомним предыдущие вопросы о собирающей и рассеивающей линзах. Первая названа так, потому что все лучи, что попадают на неё, собираются за ней в одной точке; вторая же, наоборот, рассеивает эти лучи.
Собирающая линза
Если параллельные лучи будут падать на собирающуюся линзу, то они встретятся в фокусе, если же они будут выходить из мнимого фокуса и попадать на линзу, то после нее они пройдут параллельно друг другу.
Если же параллельные лучи пойдут под некоторым углом к основной оси, то они так же соберутся в одной точке, однако она будет назваться побочным фокусом, который находится в фокальной плоскости.
Правила хода лучей:
1. Лучи, попавшие в оптический центр, не изменяют траектории движения.
2. Параллельный к главной оси луч собирается в фокусе.
3. Чтобы понять, куда пойдет луч, падающий под некоторым углом на линзу, следует построить побочную ось, что будет ему параллельна.
Вести её следует до точки пересечения с фокально плоскостью. Это позволит определить побочный фокус.
Рассеивающая линза
Итак, в рассеивающейся линзе пучок собирается во мнимом фокусе и расходится за пределами линзы.
Если же лучи будут падать под некоторым углом к линзе, то они в любом случае будут расходиться, однако перед линзой соберутся в мнимом побочном фокусе.
Правила хода лучей:
1. Данное правило справедливо для всех линз – лучи, проходящие через оптический центр, не меняют траектории.
2. Если луч, параллельный главной оптической оси, попадает на линзу, то он рассеивается, но пересекает мнимый фокус.
3. Для определения побочного мнимого фокуса для луча, который падает на линзу под углом, следует провести побочную ось, параллельную ходу лучей.
Построение изображений
Без всех предыдущих правил построить изображение, полученное в результате преломления линзой лучей, невозможно. Все они позволяют обобщить правила в теорему:
Если перед линзой находится некоторая точка, излучающая свет, то изображение от данной точки можно получить в случае пересечения лучей в фокусе.
В случае, когда лучи пересекаются в некоторой точке после того, как преломились, то говорят, что полученное изображение является действительным. Если же мы получили изображение из-за пересечения лучей вблизи мнимого фокуса, то оно называется мнимым. Как уже говорилось ранее – мнимое изображение получается в результате обманных процессов в нашем мозге, когда нам кажется, что предмет находится где-то в зеркале.
Построение изображения в собирающей линзе
Рассмотрим несколько возможных вариантов расположения светящейся точки перед линзой.
1. Расстояние от предмета до линзы больше, чем фокусное расстояние: d>F.
Для получения изображения направим один луч SO через центр линзы, а второй SX произвольный. Параллельно к произвольному расположим побочную оптическую ось OP до пересечения с фокальной плоскостью. Проведем луч через точку пересечения фокальной плоскости и побочной оси. Будем вести луч до тех пор, пока он не пересечется с лучом SO. В данной точке и покажем изображение.
Если светящаяся точка находится в некотором месте на оси, то поступаем таким же образом – ведем произвольный луч до линзы, параллельно ему побочную ось, после линзы пропускаем луч через точку пересечения фокальной плоскости и побочной оси. Место, где данный луч пересечет главную оптическую ось, и будет местом расположения изображения.
Существует так же более простой способ построения изображения. Однако, он используется только в том случае, когда светящаяся точка находится вне главной оси.
От предмета проводим два луча – один через оптический центр, а другой параллельно главной оси до пересечения с линзой. Когда второй луч пересек линзу, направляем его через фокус. Место, где пересекутся два луча – это и есть место для расположения изображения.
Полученные изображения от предметов после собирающей линзы
1. Предмет находится между первым и вторым фокусом, то есть 2F > d >F.
Если один край предмета находится на главной оси, то следует находить расположение за линзой только конечной его точки. Как проецировать точку, мы уже знаем.
Стоит отметить тот факт, что если тело находится между первым и вторым фокусами, то благодаря собирающей линзе его изображение получается перевернутым, увеличенным и действительным.
Чтобы определить, насколько изображение получится больше, чем предмет, следует воспользоваться формулой:
2. Изображение за вторым фокусом d > 2F.
Если местонахождение предмета сместилось левее относительно линзы, то в ту же сторону сместится и полученное изображение.
Изображение получается уменьшенное, перевернутое и действительное.
Представьте себе ситуацию – вы смотрите на некоторый предмет через бинокль, чем сильнее вы отдаляетесь от него, тем меньше он становится – в этом и суть изображения от предмета, который находится за вторым фокусом.
3. Расстояние до предмета меньше расстояния до фокуса: F > d.
В данном случае, если мы воспользуемся известными правилами и проведем один луч через центр линзы, а второй параллельно, а потом через фокус, то увидим, что они будут расходиться. Соединятся они только в том случае, если их продолжить перед линзой.
Данное изображение получится мнимое, увеличенное и прямое.
4. Расстояние до предмета равно расстоянию до фокуса: d = F.
Если использовать те же правила, что и ранее, то можно заметить, что лучи после линзы идут параллельно – это значит, что изображения не будет.
Рассеивающая линза
Для данной линзы используем все те же правила, что и раньше. В результате построения аналогичных изображений, получим:
Где бы не находился предмет относительно рассеивающей линзы: изображение мнимое, прямое, увеличенное.
