Как найти преобразование в каноническую форму

Приведение квадратичной формы к каноническому виду.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Метод собственных векторов:

Рассмотрим квадратичную форму $A(x,x) =sumlimits_{i,j=1}^na_{i,j}x_ix_j$ в евклидовом пространстве $R^n.$ Так как ее матрица $A=(a_ij)$ симметрична, то она может быть представлена в виде $A=UDU^{T},$ где $D -$ диагональная матрица, на диагонали которой стоят собственные числа матрицы, а $U -$ ортогональная матрица. Столбцы матрицы $U$ являются координатами некоторого ортонормированного базиса $B’=(e_1, …, e_n),$ в котором матрица $A$ имеет диагональный вид $D,$ и, следовательно, квадратичная форма – искомый канонический вид. Соответствующие преобразования координат определяются соотношением $$begin{pmatrix}x_1\vdots\x_nend{pmatrix}=Ubegin{pmatrix}x_1’\vdots\x_n’end{pmatrix}.$$

Пример.

Найти ортогональное преобразование, приводящее следующие формы к каноническому виду, и написать этот канонический вид:

4.213. $11x_1^2+5x_2^2+2x_3^2+16x_1x_2+4x_1x_3-20x_2x_3.$

Решение.

Матрица квадратичной формы имеет вид $$begin{pmatrix}11&8&2\8&5&-10\2&-10&2end{pmatrix}.$$

Найдем собственные числа этой матрицы. Для этого запишем характеристическое уравнение:

$$A-lambda E=begin{pmatrix}11&8&2\8&5&-10\2&-10&2end{pmatrix}-lambdabegin{pmatrix}1&0&0\0&1&0\0&0&1end{pmatrix}=$$ $$=begin{pmatrix}11-lambda&8&2\8&5-lambda&-10\2&-10&2-lambdaend{pmatrix}.$$

$$det(A-lambda E)=begin{vmatrix}11-lambda&8&2\8&5-lambda&-10\2&-10&2-lambdaend{vmatrix}=$$  $$=(11-lambda)(5-lambda)(2-lambda)+2cdot 8cdot (-10)+2cdot 8cdot (-10)-$$ $$-2cdot(5-lambda)cdot 2-(11-lambda)cdot(-10)cdot(-10)-8cdot 8cdot(2-lambda)=$$ $$=-lambda^3+lambda^2(2+5+11)-lambda(10+22+55)+110-160-160-20+$$ $$+4lambda-1100+100lambda-128+64lambda=$$ $$=-lambda^3+18lambda^2+81lambda-1458=-lambda(lambda^2-81)+18(lambda^2-81)=$$ $$=(lambda-9)(lambda+9)(-lambda+18)=0.$$

Отсюда находим собственные числа:

$$lambda_1=9,quad lambda_2=-9, quadlambda_3=18.$$

Далее находим собственные вектора:

 {jumi[*5]}

Собственный вектор для собственного числа $lambda_1=9$ найдем из системы $$(A-lambda E)X=0, Xneq 0, Rightarrow (A-9E)X=0, Xneq 0$$

$$(A-9E)X=begin{pmatrix}11-9&8&2\8&5-9&-10\2&-10&2-9end{pmatrix}begin{pmatrix}x_1\x_2\x_3end{pmatrix}=$$ $$=begin{pmatrix}2x_1+8x_2+2x_3\8x_1-4x_2-10x_3\2x_1-10x_2-7x_3end{pmatrix}=0.$$

Решим однородную систему уравнений:

$$left{begin{array}{lcl}2x_1+8x_2+2x_3=0\ 8x_1-4x_2-10x_3=0\2x_1-10x_2-7x_3=0end{array}right.$$ 

Вычислим ранг матрицы коэффициентов $A=begin{pmatrix}2&8&2\8&-4&-10\2&-10&-7end{pmatrix}$ методом окаймляющих миноров:    

Фиксируем минор отличный от нуля второго порядка $M_2=begin{vmatrix}2&8\8&-4end{vmatrix}=-8-64=-72neq 0.$

Рассмотрим окаймляющий минор третьего порядка:  $begin{vmatrix}2&8&2\8&-4&-10\2&-10&-7end{vmatrix}=56-160-160+16-200+448=0;$

Таким образом ранг матрицы $A$ равен двум.

Выберем в качестве базисного минор $M=begin{vmatrix}2&8\8&-4end{vmatrix}=-72neq 0.$ Тогда, полагая $x_3=c,$ получаем: $$left{begin{array}{lcl}2x_1+8x_2+2c=0\ 8x_1-4x_2-10c=0end{array}right.Rightarrowleft{begin{array}{lcl}2x_1+8x_2=-2c\8x_1-4x_2=10cend{array}right.$$ 

 По правилу Крамера находим $x_1$ и $x_2:$

 $Delta=begin{vmatrix}2&8\8&-4end{vmatrix}=-8-64=-72;$

 $Delta_1=begin{vmatrix}-2c&8\10c&-4end{vmatrix}=8c-80c=-72c;$

 $Delta_2=begin{vmatrix}2&-2c\8&10cend{vmatrix}=20c+16c=36c;$

 $x_1=frac{Delta_1}{Delta}=frac{-72c}{-72}=c;$ $x_2=frac{Delta_2}{Delta}=frac{36c}{-72}=-c/2.$

 Таким образом, общее решение системы $X(c)=begin{pmatrix}c\-c/2\cend{pmatrix}.$

 Из общего решения находим фундаментальную систему решений: $E=X(1)=begin{pmatrix}1\-1/2\1end{pmatrix}.$ 

Соответсвующий ортонормированный собственный вектор: $$e_1’=left(frac{2}{sqrt{4+1+4}},frac{-1}{sqrt{4+1+4}},frac{2}{sqrt{4+1+4}}right)=left(frac{2}{3},frac{-1}{3},frac{2}{3}right).$$

Собственный вектор для собственного числа $lambda_2=-9$ найдем из системы $$(A-lambda E)X=0, Xneq 0, Rightarrow (A+9E)X=0, Xneq 0$$

$$(A+9E)X=begin{pmatrix}11+9&8&2\8&5+9&-10\2&-10&2+9end{pmatrix}begin{pmatrix}x_1\x_2\x_3end{pmatrix}=$$ $$=begin{pmatrix}20x_1+8x_2+2x_3\8x_1+14x_2-10x_3\2x_1-10x_2+11x_3end{pmatrix}=0.$$

Решим однородную систему уравнений:

$$left{begin{array}{lcl}20x_1+8x_2+2x_3=0\ 8x_1+14x_2-10x_3=0\2x_1-10x_2+11x_3=0end{array}right.$$ 

Вычислим ранг матрицы коэффициентов $A=begin{pmatrix}20&8&2\8&14&-10\2&-10&11end{pmatrix}$ методом окаймляющих миноров:    

Фиксируем минор отличный от нуля второго порядка $M_2=begin{vmatrix}20&8\8&14end{vmatrix}=280-64=216neq 0.$

Рассмотрим окаймляющий минор третьего порядка:  $begin{vmatrix}20&8&2\8&14&-10\2&-10&11end{vmatrix}=3080-160-160-56-2000-704=0;$

Таким образом ранг матрицы $A$ равен двум.

Выберем в качестве базисного минор $M=begin{vmatrix}20&8\8&14end{vmatrix}=216neq 0.$ Тогда, полагая $x_3=c,$ получаем: $$left{begin{array}{lcl}20x_1+8x_2+2c=0\ 8x_1+14x_2-10c=0end{array}right.Rightarrowleft{begin{array}{lcl}20x_1+8x_2=-2c\8x_1+14x_2=10cend{array}right.$$ 

 По правилу Крамера находим $x_1$ и $x_2:$

 $Delta=begin{vmatrix}20&8\8&14end{vmatrix}=280-64=216;$

 $Delta_1=begin{vmatrix}-2c&8\10c&14end{vmatrix}=-28c-80c=-108c;$

 $Delta_2=begin{vmatrix}20&-2c\8&10cend{vmatrix}=200c+16c=216c;$

 $x_1=frac{Delta_1}{Delta}=frac{-108c}{216}=-c/2;$ $x_2=frac{Delta_2}{Delta}=frac{216c}{216}=c.$

 Таким образом, общее решение системы $X(c)=begin{pmatrix}-c/2\c\cend{pmatrix}.$

 Из общего решения находим фундаментальную систему решений: $E=X(1)=begin{pmatrix}-1/2\1\1end{pmatrix}.$ 

Соответсвующий ортонормированный собственный вектор: $$e’_2=left(frac{-1}{sqrt{4+1+4}},frac{2}{sqrt{4+1+4}},frac{2}{sqrt{4+1+4}}right)=left(frac{-1}{3},frac{2}{3},frac{2}{3}right).$$

Собственный вектор для собственного числа $lambda=18$ найдем из системы $$(A-lambda E)X=0, Xneq 0, Rightarrow (A-18E)X=0, Xneq 0$$

$$(A-18E)X=begin{pmatrix}11-18&8&2\8&5-18&-10\2&-10&2-18end{pmatrix}begin{pmatrix}x_1\x_2\x_3end{pmatrix}=$$ $$=begin{pmatrix}-7x_1+8x_2+2x_3\8x_1-13x_2-10x_3\2x_1-10x_2-16x_3end{pmatrix}=0.$$

Решим однородную систему уравнений:

$$left{begin{array}{lcl}-7x_1+8x_2+2x_3=0\ 8x_1-13x_2-10x_3=0\2x_1-10x_2-16x_3=0end{array}right.$$ 

Вычислим ранг матрицы коэффициентов $A=begin{pmatrix}-7&8&2\8&-13&-10\2&-10&-16end{pmatrix}$ методом окаймляющих миноров:    

Фиксируем минор отличный от нуля второго порядка $M_2=begin{vmatrix}-7&8\8&-13end{vmatrix}=91-64=27neq 0.$

Рассмотрим окаймляющий минор третьего порядка:  $begin{vmatrix}-7&8&2\8&-13&-10\2&-10&-16end{vmatrix}=-1456-160-160+52+700+1024=0;$

Таким образом ранг матрицы $A$ равен двум.

Выберем в качестве базисного минор $M=begin{vmatrix}-7&8\8&-13end{vmatrix}=27neq 0.$ Тогда, полагая $x_3=c,$ получаем: $$left{begin{array}{lcl}-7x_1+8x_2+2c=0\ 8x_1-13x_2-10c=0end{array}right.Rightarrowleft{begin{array}{lcl}-7x_1+8x_2=-2c\8x_1-13x_2=10cend{array}right.$$ 

 {jumi[*4]}

По правилу Крамера находим $x_1$ и $x_2:$

$Delta=begin{vmatrix}-7&8\8&-13end{vmatrix}=91-64=27;$

$Delta_1=begin{vmatrix}-2c&8\10c&-13end{vmatrix}=26c-80c=-54c;$

$Delta_2=begin{vmatrix}-7&-2c\8&10cend{vmatrix}=-70c+16c=-54c;$

$x_1=frac{Delta_1}{Delta}=frac{-54c}{27}=-2c;$ $x_2=frac{Delta_2}{Delta}=frac{-54c}{27}=-2c.$

Таким образом, общее решение системы $X(c)=begin{pmatrix}-2c\-2c\cend{pmatrix}.$

Из общего решения находим фундаментальную систему решений: $E=X(1)=begin{pmatrix}-2\-2\1end{pmatrix}.$ 

Соответсвующий ортонормированный собственный вектор: $$e’_3=left(frac{-2}{sqrt{4+4+1}},frac{-2}{sqrt{4+4+1}},frac{1}{sqrt{4+4+1}}right)=left(frac{-2}{3},frac{-2}{3},frac{1}{3}right).$$

Таким образом, мы нашли вектора 

$$e_1’=left(frac{2}{3},frac{-1}{3},frac{2}{3}right);$$

$$e_2’=left(frac{-1}{3},frac{2}{3},frac{2}{3}right);$$

$$e_3’=left(frac{-2}{3},frac{-2}{3},frac{1}{3}right).$$ И следовательно, 

$$U=frac{1}{3}begin{pmatrix}2&-1&-2\-1&2&-2\2&2&1end{pmatrix}, quad U^T=frac{1}{3}begin{pmatrix}2&-1&2\-1&2&2\-2&-2&1end{pmatrix}.$$

В базисе $B’=(e_1′, e_2′, e_3′)$ заданная квадратичная форма имеет вид $$A(x, x)=9x_1^2-9x_2^2+18x_3^2,$$ а соответствующее преобразование координат: 

$$x_1=2x_1 ‘-x_2’-2x_3’$$

$$x_2=-x_1 ‘+2x_2’-2x_3’$$

$$x_3=2x_1 ‘+2x_2’+x_3’$$

Ответ: $A(x, x)=9x_1^2-9x_2^2+18x_3^2;$

$$x_1=2x_1 ‘-x_2′-2x_3’;$$

$$x_2=-x_1 ‘+2x_2′-2x_3’;$$

$$x_3=2x_1 ‘+2x_2’+x_3’.$$

1. Методы приведения квадратичной формы к каноническому виду.

   1. Метод Лагранжа

Данный метод
состоит в последовательном выделении
в квадратичной форме полных квадратов.

Пусть дана
квадратичная форма

Напомним, что,
ввиду симметричности матрицы

,

Возможны два
случая:

1.Хотя бы один
из коэффициентовпри
квадратах отличен от нуля. Не нарушая
общности, будем считать(этого
всегда можно добиться соответствующей
перенумерацией переменных);

2.Все
коэффициенты,

но есть коэффициент ,
отличный от нуля (для определённости
пусть будет).

В первом случаепреобразуем квадратичную форму следующим
образом:

,

где
,

а через
обозначены все остальные слагаемые.

представляет собой
квадратичную форму от (n—1) переменных .

С ней поступают
аналогичным образом и так далее.

Заметим, что

Второй случайзаменой переменных

сводится к первому.

Пример 1:Квадратичную форму привести к каноническому виду посредством невырожденного линейного преобразования.

Решение.
Соберём все слагаемые, содержащие
неизвестное
,
и дополним их до полного квадрата

.

(Так
как
.)

Положим

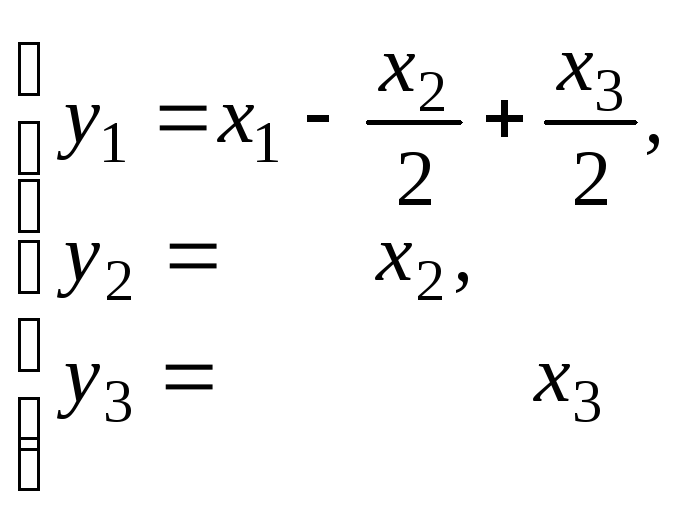или

(3)

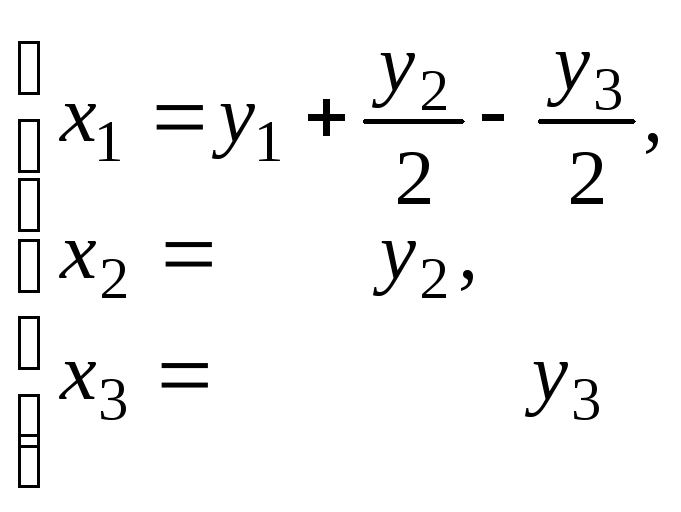или

(4)

и
от неизвестных
формапримет вид.
Далее полагаем

или

и
от неизвестных
формапримет уже канонический вид

.
(4)

Разрешим
равенства (3) относительно
:

или

Последовательное
выполнение линейных преобразований
и,
где

,

имеет матрицей

.

Линейное
преобразование неизвестных
приводит
квадратичную форму

к каноническому виду (4). Переменные
связаны с новыми переменнымисоотношениями

См
также ссылку
http://mathhelpplanet.com/static.php?p=privedenie-kvadratichnoi-formy-k-kanonicheskomu-vidu

С
LU
– разложением мы познакомились в
практикуме 2_1

Вспомним
утверждения из практикума 2_1

Утверждения(см.Л.5, стр. 176)

1. Пусть
   A
   – квадратная матрица порядка n
   и все главные миноры матрицы A
   отличны от нуля.
   Тогда существуют единственная нижняя
   треугольная матрица L=(l_ij),
   где l_ii
   =1 для всех i,
   j
   =1,2,…,n
   (т.е. с единицами на главной диагонали)
   и единственная верхняя треугольная
   матрица U=(u_ij),
   такие что A=LU
   и
   .

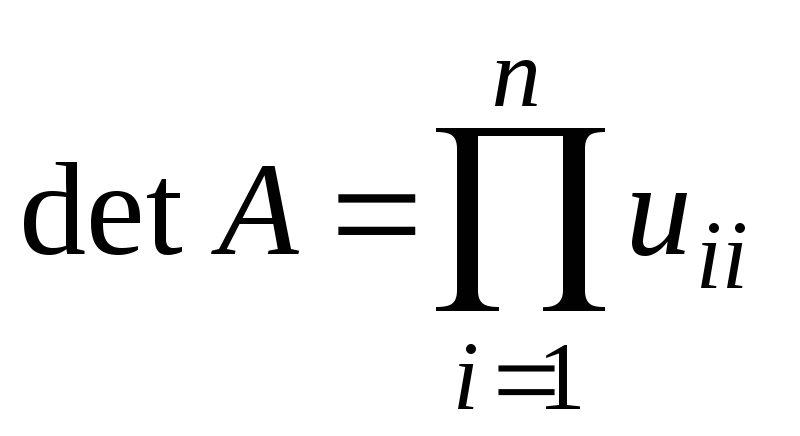2. В тех
   же предположениях можно доказать
   единственность разложения матрицы A
   в произведение
   ,
   гдеL
   – нижняя, S
   – верхняя треугольные матрицы с единицами
   на главной диагонали, а D
   – диагональная матрица.

3. Если
   A-
   симметричная матрица, то из
   следует, что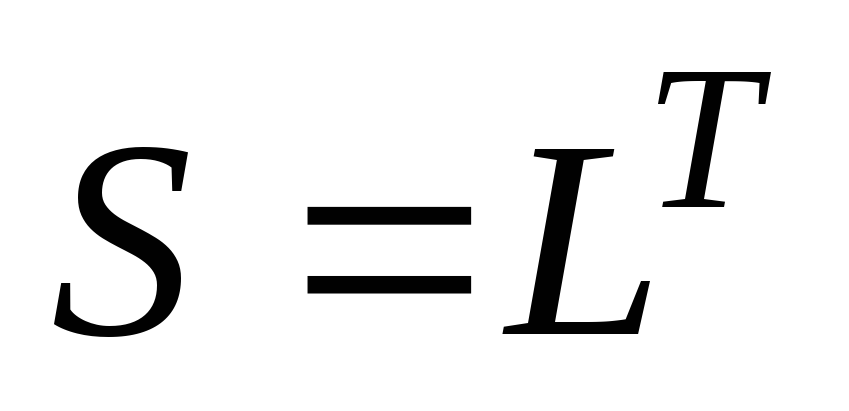

Данный
скрипт призван понять роль LU
в методе Лагранжа, с ним нужно работать
в блокноте EDITOR
с помощью кнопки F9.

А в
прилагаемых ниже заданиях лучше создать
свои М-функции, помогающие вычислению
и осознанию задач линейной алгебры (в
рамках данной работы)

syms
x1x2x3

X=[x1;x2;x3]

A=[4
-2 2;-2 1 -3/2;2 -3/2 1]

Ax=X.’*A*X
% получаем квадратичную
форму

Ax=simple(Ax)
% упрощаем
ее

Ax =

4*x1^2 – 4*x1*x2 + 4*x1*x3 +
x2^2 – 3*x2*x3 + x3^2

%
найдем LU
разложение без перестановки строк
матрицы A

%
При преобразовании матрицы к ступенчатому
виду

%без
перестановок строк, мы получим матрицу
M1 и U3

%
U получается из A
U3=M1*A,

M1=[1
0 0;0.5 1 0;-0.5 0 1]

%
вот такой матрицей элементарных
преобразований

M1
=

1.0000
0 0

0.5000
1.0000 0

-0.5000
0 1.0000

%мы
получим U3=M1*A, где

U=M1*A

U
=

4.0000
-2.0000 2.0000

0
0 -0.5000

0
-0.5000 0

%
из M1
легко получить L1,
поменяв знаки

%
в первом столбце во всех строках кроме
первой.

L1=[1
0 0;-0.5 1 0;0.5 0 1]

L1 =

1.0000 0 0

-0.5000 1.0000 0

0.5000
0 1.0000

%
L1 такое, что

A_=L1*U
% вот это и
есть нужное нам LU
разложение

isequal(A,A_)
% должно совпасть с исходной
A

%
Элементы, стоящие на главной диагонали
U
–

%
это коэффициенты при квадратах y_i^2

%
в преобразованной квадратичной форме

%
в нашем случае, есть один только
коэффициент

%
значит, в новых координатах будет только
4y₁²
в квадрате ,

%
при остальных 0y₂²
и 0y₃²

коэффициенты равны нулю

%
столбцы матрицы L1 – это разложение Y по
X

%
по первому столбцу видим y1=x1-0.5×2+0.5×3

%
по второму видим y2=x2; по третьему y3=x3.

%
если
транспонировать
L1,

%
то есть T=L1.’

%
T
– матрица перехода от {X}
к {Y}:
Y=TX

T=L1.’

L1 =

1.0000 0 0

-0.5000 1.0000 0

0.5000 0 1.0000

T =

1.0000 -0.5000 0.5000

0 1.0000 0

0 0 1.0000

%
A2
– матрица преобразованной квадратичной
формы

%
Заметим
U=A2*L1.’ и
A=L1* A2*L1.’

A2=[4
0 0;0 0 -0.5;0 -0.5 0]

A2=

4.0000 0 0

0 0 -0.5000

0 -0.5000 0

U=A2*L1.’

U =

4.0000 -2.0000 2.0000

0 0 -0.5000

0
-0.5000 0

A2= 4.0000 0 0 0 0 -0.5000 0 -0.5000 0

T = 1.0000 -0.5000 0.5000 0 1.0000 0 0 0 1.0000

%
Итак, мы получили разложение A_=L1*
A2*L1.’ или
A_=T.’* A2*T

%
показывающее замену переменных

%
y1=x1-0.5×2+0.5×3

%
y2=x2;

%
y3=x3.

%
и представление квадратичной формы в
новых координатах

A_=T.’*A2*T
% T=L1.’
матрица перехода от {X}
к {Y}:
Y=TX

isequal(A,A_)
% должно совпасть с исходной
A

A_=T.’*U*T

A_
=

4.0000
-2.0000 2.0000

-2.0000
1.0000 -1.5000

2.0000
-1.5000 1.0000

Q1=inv(T)
% находим
матрицу перехода от {Y}
к {X}

%
X=Q1Y

%
Найдем
преобразование,

%
приводящее квадратичную форму Ax=X.’*A*X

%
к новому виду Ay=(Q1Y).’*A*Q1Y=Y.’ (Q1.’*A*Q1)*Y=Y.’
(U)*Y

A2=Q1.’*A*Q1

syms
y1y2y3

Y=[y1;y2;y3]

Ay=Y.’*A2*Y

Ay
=4*y1^2 – y2*y3

Yx=
T*X

Yx
=

x1
– x2/2 + x3/2

x2

x3

Ax_=Yx.’*A2*Yx

Ax_=simple(Ax_)

Ax_=factor(Ax_)

%
Y=Q2Z

Q2=[1
0 0;0 1 -1;0 1 1]

%
матрица второго преобразования,

%
которая составляется значительно проще.

Q2 =

1 0 0

0 1 -1

0 1 1

syms
z1z2z3

Z=[z1;z2;z3]

Zy=Q2*Z

Zy
=

z1

z2
– z3

z2
+ z3

Az=Zy.’*U*Zy

Az=simple(Az)

Az
=

4*z1^2
– z2^2 + z3^2

Uz=[4
0 0;0 -1 0;0 0 1]

Az_=Z.’*Uz*Z

isequal(Az,Az_)

%
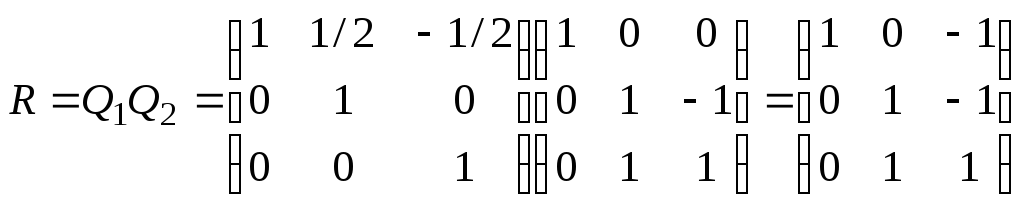
R=Q1*Q2, X=R*Z

R=Q1*Q2
% невырожденное
линейное преобразование

%
приводящее матрицу оператора к
каноническому виду.

R
=

1
0 -1

0
1 -1

0
1 1

R.’*A*R

ans
=

4
0 0

0
-1 0

0
0 1

det(R)
% определитель
не равен нулю – преобразование
невырожденное

ans
=

2

Xz=R*Z

Xz
=

z1
– z3

z2
– z3

z2
+ z3

Ax=X.’*A*X

Ax=simple(Ax)

x1=
z1 – z3

x2=
z2 – z3

x3=z2
+ z3

ans
=

4*z1^2
– z2^2 + z3^2 ok

Uz=[4
0 0;0 -1 0;0 0 1]

Az_=Xz.’*A*Xz

Az_=simple(Az_)

Az_=factor(Az_)

Az_
=

4*z1^2
– z2^2 + z3^2

1. Алгоритм приведения
   квадратичной формы к каноническому
   виду ортогональным преобразованием

   Определение:
   Будем называть линейное преобразование
   переменных
   ортогональным,
   если матрица
   ортогональная,
   т.е.
   

Сформулируем
алгоритм приведения квадратичной
формы к
каноническому виду ортогональным
преобразованием:

1. Находим собственные
   значения линейного оператора, решая
   характеристическое уравнение
   

2. Для каждого
   собственного значения находим собственные
   векторы, решая систему линейных уравнений
   (У этой системы мы должны найти
   фундаментальную систему решений).

3. Если собственное
   значение
   имеет кратность, большую 1 (в
   характеристическом уравнении), то
   векторы из ф.с.р. могут оказаться не
   ортогональными друг другу – в этом
   случае к ним надо применитьпроцесс
   ортогонализации Шмидта
   (изучите самостоятельно, читайте:
   Ржавинская Е. В., Олейник Т. А., Соколова
   Т. В. Лекции по линейной алгебре и
   аналитической геометрии, М., МИЭТ.
   2007. )

4. Нормируем найденные
   собственные векторы, т.е. каждый вектор
   делим на его длину.

5. Записываем
   канонический вид квадратичной формы
   и преобразование координат, приводящее
   её к этому виду.

Соседние файлы в папке МатЛаб – Алгебра

• #
• #
• #
• #
• #
• #
• #

Приведение квадратичной формы к каноническому виду

Говорят, что квадратичная форма имеет канонический вид, если ее матрица диагональная, другими словами, в квадратичной форме имеются только члены с квадратами переменных, а все попарные произведения различных переменных отсутствуют (соответствующие коэффициенты равны нулю):

где — диагональная матрица, для которой условие симметричности матрицы квадратичной формы, разумеется, выполняется.

Задача приведения квадратичной формы к каноническому виду формулируется следующим образом. Для данной квадратичной формы (6.5) требуется найти такую линейную невырожденную замену переменных (6.8), при которой квадратичная форма принимает канонический вид (6.11). Как показывает следующая теорема, эта задача всегда разрешима. Заметим, что на практике нередко бывает достаточно определить только канонический вид квадратичной формы, не указывая замены переменных.

Теорема 6.1 о приведении квадратичной формы к каноническому виду. Любая квадратичная форма может быть приведена к каноническому виду при помощи некоторой линейной невырожденной замены переменных.

Конструктивное доказательство этой теоремы составляет содержание метода Лагранжа приведения квадратичной формы к каноническому виду.

---

Метод Лагранжа приведения квадратичной формы к каноническому виду

Для приведения квадратичной формы переменных

к каноническому виду нужно выполнить следующие действия.

1. Выбрать такую переменную (ведущую), которая входит в квадратичную форму во второй и в первой степени одновременно (если в квадратичной форме есть член с квадратом переменной и с произведением этой переменной на другую переменную), и перейти к пункту 2.

Если в квадратичной форме нет ведущих переменных, то выбрать пару переменных, произведение которых входит в квадратичную форму с отличным от нуля коэффициентом, и перейти к п.3.

Если в квадратичной форме отсутствуют произведения различных переменных, то никаких преобразований делать не надо, так как она уже имеет канонический вид.

2. По ведущей переменной выделить полный квадрат: собрать в квадратичной форме все члены с ведущей переменной, дополнить сумму этих членов до полного квадрата (разумеется, добавленные члены нужно также и вычесть, чтобы не изменилась сумма). Получим сумму полного квадрата некоторой линейной формы (в которую входит ведущая переменная) и квадратичной формы, в которую ведущая переменная не входит. Сделать замену переменных: линейную форму, содержащую ведущую переменную, принять за одну из новых переменных, а все старые переменные, за исключением ведущей, принять за соответствующие новые. Продолжить преобразования с пункта 1.

3. Выбранную пару переменных заменить на разность и сумму двух новых переменных, а остальные старые переменные принять за соответствующие новые переменные. При этом произведение пары выбранных переменных преобразуется к разности квадратов двух новых переменных, т.е. в новой квадратичной форме будут квадраты переменных с отличными от нуля коэффициентами. Продолжить преобразования новой квадратичной формы с пункта 1.

Идея метода Лагранжа состоит в том, что прием, используемый в п.2 (выделение полного квадрата), исключает одну переменную из числа ведущих. Например, если переменная — ведущая (т.е. и хотя бы один из коэффициентов отличен от нуля), то выделяем полный квадрат по переменной (собираем все члены с и дополняем их сумму до полного квадрата):

Выражение, стоящее в квадратных скобках, есть полный квадрат. Поэтому

где — квадратичная форма, в которую не входит ведущая переменная — линейная форма, содержащая ведущую переменную . Обозначим , или, что то же самое, сделаем линейную замену переменных:

Тогда данная квадратичная форма преобразуется к виду .

Заметим, что в результате этого преобразования все члены, содержащие ведущую переменную в первой и второй степени, заменены квадратом одной новой переменной . В дальнейших преобразованиях переменная ух уже никогда не будет ведущей.

Многократно применяя этот прием, исключаем одну за другой все ведущие переменные, получая тем самым канонический вид квадратичной формы. Однако выделение полного квадрата невозможно, если в квадратичной форме вообще отсутствуют члены с квадратами переменных. В этом случае применяется способ, описанный в п.3, который порождает члены с квадратами переменных.

Например, в п. 1 выделена пара переменных и , произведение которых входит в квадратичную форму с отличным от нуля коэффициентом . Тогда нужно сделать замену переменных

При этом получим новую квадратичную форму , в которой появятся квадраты новых переменных с отличными от нуля коэффициентами, так как в результате замены член преобразуется к виду

а других членов с в новой квадратичной форме не будет.

Заметим, что при помощи метода Лагранжа не только находится канонический вид, но и определяется искомая невырожденная замена переменных. В самом деле, замены переменных (6.12), (6.13), которые производятся в п.2, 3 алгоритма, это линейные замены с матрицами

Определители матриц отличны от нуля . Следовательно, эти замены переменных невырожденные. Выполняя п.2, 3 алгоритма, можно определить матрицы используемых замен переменных. В результате их перемножения (в порядке нахождения) получается матрица искомой замены (согласно свойству 2 линейных замен переменных).

Пример 6.8. Привести квадратичную форму к каноническому виду.

Решение

Замечания 6.4

1. Канонический вид квадратичной формы определен неоднозначно, так как зависит от последовательности выбора ведущих переменных. Сделав, например, замену переменных в (6.11), получим другую квадратичную форму, которая тоже имеет канонический вид.

2. Элементы матрицы невырожденной линейной замены переменных, приводящей квадратичную форму к каноническому виду, вычисляются при помощи арифметических операций по коэффициентам квадратичной формы. Поэтому, если коэффициенты квадратичной формы рациональные, действительные, комплексные, то и коэффициенты линейной замены рациональные, действительные, комплексные соответственно.

---

Метод Якоби приведения квадратичной формы к каноническому виду

Рассмотрим еще один метод приведения квадратичной формы к каноническому виду, который учитывает особенности преобразования (6.10) матрицы квадратичной формы при линейной замене переменных.

Две квадратные матрицы и одного и того же порядка называются конгруэнтными, если существует такая невырожденная матрица , что . Конгруэнтными, например, являются матрицы квадратичных форм, получающиеся при невырожденной замене переменных (6.8), так как они связаны равенством (6.10).

Напомним, что главными минорами квадратной матрицы называются миноры, составленные из ее элементов, стоящих на пересечении строк и столбцов с одинаковыми номерами. Например, — главный минор k-го порядка квадратной матрицы n-го порядка. Угловыми минорами квадратной матрицы (n-го порядка) называются следующие главные миноры

где угловой минор k-го порядка составлен из элементов матрицы , стоящих на пересечении первых строк и первых столбцов матрицы , т.е.

---

Свойства конгруэнтных матриц

1. Конгруэнтные матрицы имеют равные ранги. В самом деле, ранг произведения матрицы на невырожденную матрицу и равен рангу матрицы (см. следствие теоремы 3.5).

2. Матрица, конгруэнтная симметрической матрице, также является симметрической. Действительно, если и , то

3. Определители действительных конгруэнтных матриц имеют одинаковые знаки. В частности, если и , то . В самом деле, из равенства и свойства 1 определителя следует, что , т.е. знаки величин и совпадают. Если же , тo .

4. Если квадратные матрицы и связаны соотношением , где матрица — верхняя треугольная с единицами на главной диагонали

то все угловые миноры матриц и равны, где в (6.15) звездочкой обозначаются любые числа.

Действительно, разобьем квадратные матрицы и на блоки, выделив в каждой квадратный блок в первых строках и первых столбцах:

Здесь — нулевые матрицы соответствующих размеров, а звездочкой обозначаются блоки соответствующих размеров, значения элементов которых для доказательства не существенны и могут быть любыми. Получили, что . Учитывая, что для любого , по свойству 3 имеем

т.е. угловые миноры и матриц и равны для любого .

Замечания 6.5

1. Линейная невырожденная замена переменных не изменяет ранга квадратичной формы. Это следует из свойства 1 конгруэнтных матриц.

2. Ранг квадратичной формы равен количеству отличных от нуля коэффициентов в ее каноническом виде (6.11). Действительно, согласно предыдущему пункту , но ранг диагональной матрицы равен количеству ненулевых ее элементов.

---

Теорема 6.2 Якоби о каноническом виде квадратичной формы. Если квадратичная форма имеет ранг и ее угловые миноры отличны от нуля:

то ее можно привести к каноническому виду

при помощи линейной замены переменных с верхней треугольной матрицей вида (6.15).

Действительно, применяя метод Лагранжа, выбираем первую переменную в качестве ведущей и выделяем по ней полный квадрат. Другими словами, делаем линейную замену переменных (6.12). Этой замене соответствует матрица в (6.14), которая является верхней треугольной вида (6.15). Получим квадратичную форму с матрицей

где звездочкой обозначены некоторые элементы матрицы . Заметим, что матрица — верхняя треугольная с единицами на главной диагонали. Тогда по свойству 4 конгруэнтных матриц, получаем , следовательно . Отсюда . Значит, вторую переменную можно взять в качестве ведущей и выделить по ней полный квадрат. Для этого делаем линейную замену переменных с матрицей вида (6.15) и т.д. Условия (6.16) обеспечивают возможность применения пункта 2 метода Лагранжа раз. В результате описанных действий получается канонический вид (6.17). Формулы (6.17) для вычисления следуют из свойства 4 конгруэнтных матриц. Так как угловые миноры матриц и соответственно равны (по свойству 4 конгруэнтных матриц), то

. Отсюда .

Остальные угловые миноры равны нулю , так как .

Таким образом, для нахождения канонического вида квадратичной формы методом Якоби необходимо выполнить следующие действия.

1. Составить матрицу (n-го порядка) квадратичной формы.

2. Найти первые отличных от нуля угловых миноров матрицы квадратичной формы. Если , то перейти к пункту 3, положив . Если , то процесс закончить, так как метод Якоби неприменим. Если и , где , то найти отличный от нуля минор (r+l)-порядка, окаймляющий минор . Если такого минора нет, то перейти к пункту 3, иначе процесс закончить, так как метод Якоби неприменим.

3. Записать искомый канонический вид (6.17) квадратичной формы

---

Замечания 6.6

1. Алгоритм метода Якоби можно модифицировать, дополнив его перенумерацией переменных. Например, замена на и, одновременно, на (короче, перенумерация ) приводит к перестановке i-й и j-й строк, а также i-го и j-го столбцов матрицы квадратичной формы. Такая замена является линейной невырожденной и не нарушает симметричности матрицы квадратичной формы. При помощи таких двойных перестановок можно любой главный минор симметрической матрицы переместить в левый верхний угол, т.е. сделать его угловым. Например, для матрицы квадратичной формы метод Якоби неприменим, так как . Перенумеровав переменные , получаем матрицу , для которой условия (6.16) применимости метода Якоби выполняются.

2. При выполнении условий теоремы 6.2 метод Лагранжа (последовательного выделения полных квадратов) соответствует методу Гаусса приведения матрицы к ступенчатому виду.

3. При выполнении условий теоремы 6.2 для нахождения матрицы линейной замены переменных, приводящей квадратичную форму к каноническому виду, нужно выполнить следующие действия:

1) Составить блочную матрицу , приписав к матрице квадратичной формы единичную матрицу тех же размеров.

2) Привести левый блок к ступенчатому виду при помощи элементарных преобразований III типа строк блочной матрицы . В результате получить блочную матрицу , где — искомая матрица замены переменных. Элементы главной диагонали матрицы равны коэффициентам в квадратичной форме (6.17):

Пример 6.9. Привести квадратичную форму к каноническому виду методом Якоби

Решение

Пример 6.10. Найти матрицу линейной замены переменных, приводящей квадратичную форму к каноническому виду

Решение

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

В гамильтоновой механике каноническое преобразование (также контактное преобразование) — это преобразование канонических переменных, не меняющее общий вид уравнений Гамильтона для любого гамильтониана. Канонические преобразования могут быть введены и в квантовом случае как не меняющие вид уравнений Гейзенберга. Они позволяют свести задачу с определённым гамильтонианом к задаче с более простым гамильтонианом как в классическом, так и в квантовом случае. Канонические преобразования образуют группу.

Определение[править | править код]

Преобразования

, где  — число степеней свободы,

называются каноническими, если это преобразование переводит уравнения Гамильтона с функцией Гамильтона :

в уравнения Гамильтона с функцией Гамильтона :

Переменные и называются новыми координатами и импульсами, соответственно, а и  — старыми координатами и импульсами.

Производящие функции[править | править код]

Из инвариантности интеграла Пуанкаре — Картана и теоремы Ли Хуа-чжуна о его единственности можно получить:

где постоянную называют валентностью канонического преобразования,  — полный дифференциал некоторой функции (предполагается, что и также выражены через старые переменные). Она называется производящей функцией канонического преобразования. Канонические преобразования взаимнооднозначно определяются производящей функцией и валентностью.

Канонические преобразования для которых называется унивалентными. Так как при заданной производящей функции различные изменяют выражения для новых координат через старые, а также для гамильтониана только на константу, то часто рассматривают только унивалентные канонические преобразования.

Производящая функция часто может быть выражена не через старые координаты и импульсы, а через любые две из четырёх переменных , причём выбор независим для каждого . Удобным оказывается выразить её так, чтобы для каждого одна переменная была новой, а другая старой. Существует лемма, утверждающая, что это можно сделать всегда. Дифференциал функции имеет явный вид полного дифференциала в том случае, когда она выражена через старые и новые координаты . При использовании других пар координат удобно перейти к функциям, дифференциал которых будет иметь явный вид полного дифференциала для соответствующих переменных. Для этого нужно сделать преобразования Лежандра исходной функции . Полученные функции называют производящими функциями канонического преобразования в соответствующих координатах. В случае когда выбор координат одинаков для всех возможны четыре варианта выбора переменных, соответствующие функции принято обозначать номерами:

где для простоты введены векторы старых координат и импульсов , , аналогично и для новых координат и импульсов. О таких производящих функциях говорят как о производящих функциях 1-го, 2-го, 3-го или 4-го типа соответственно.

Производящая функция 1-го типа[править | править код]

Пусть  — произвольная невырожденная функция старых координат, новых координат и времени:

кроме того, задано некоторое число , тогда пара задаёт каноническое преобразование по правилу

Связь с исходной производящей функцией:

Каноническое преобразование может быть получено с помощью такой функции, если не равен нулю якобиан:

Канонические преобразования, дополненные этим условием называют свободными.

Производящая функция 2-го типа[править | править код]

Пусть  — произвольная невырожденная функция старых координат, новых импульсов и времени:

кроме того, задано некоторое число , тогда пара задаёт каноническое преобразование по правилу

Связь с исходной производящей функцией:

Каноническое преобразование может быть получено с помощью такой функции, если не равен нулю якобиан:

Производящая функция 3-го типа[править | править код]

Пусть  — произвольная невырожденная функция старых импульсов, новых координат и времени:

кроме того, задано некоторое число , тогда пара задаёт каноническое преобразование по правилу

Связь с исходной производящей функцией:

Каноническое преобразование может быть получено с помощью такой функции, если не равен нулю якобиан:

Производящая функция 4-го типа[править | править код]

Пусть  — произвольная невырожденная функция старых импульсов, новых импульсов и времени:

кроме того, задано некоторое число , тогда пара задаёт каноническое преобразование по правилу

Связь с исходной производящей функцией:

Каноническое преобразование может быть получено с помощью такой функции, если не равен нулю якобиан:

Примеры[править | править код]

1. Тождественное преобразование

может быть получено при:

2. Если задать

то полученное преобразование будет иметь вид:

Таким образом, разделение канонических переменных на координаты и импульсы с математической точки зрения является условным.

3. Преобразование инверсии

может быть получено при:

4. Точечные преобразования (преобразования при которых новые координаты выражаются только через старые координаты и время, но не старые импульсы.)

Они всегда могут быть заданы с помощью:

тогда

В частности, если

где  — ортогональная матрица:

то

К точечным преобразования приводит и функция:

тогда

В частности функция

задаёт переход от декартовых координат к цилиндрическим.

5. Линейные преобразования переменных системы с одной степенью свободы:

является унивалентным каноническим преобразованием при

производящая функция:

Такие преобразования образуют специальную линейную группу .

Действие как производящая функция[править | править код]

Действие, выраженное как функция координат и импульсов конечной точки

задаёт каноническое преобразование гамильтоновой системы.

Скобки Пуассона и Лагранжа[править | править код]

Необходимое и достаточное условие каноничности преобразований может быть записано с помощью скобок Пуассона:

Кроме того, необходимым и достаточным условием каноничности преобразования является выполнение для произвольных функций и условия:

где под и понимаются скобки Пуассона по старым и новым координатам соответственно.

В случае унивалентных канонических преобразований:

и говорят, что скобки Пуассона инвариантны относительно таких преобразований. Иногда канонические преобразования так определяют (при этом каноническими преобразованиями считают только унивалентные).

Аналогично, необходимое и достаточное условие каноничности преобразований может быть записано с помощью скобок Лагранжа:

Литература[править | править код]

• Арнольд В. И. Математические методы классической механики. — 5-е изд., стереотипное. — М.: Едиториал УРСС, 2003. — 416 с. — 1500 экз. — ISBN 5-354-00341-5.
  Книга в электронной библиотеке мехмата МГУ
• Ландау Л. Д., Лифшиц E. M. §46. Канонические преобразования. Глава VII. Канонические уравнения. // Механика. — 5-е изд., стереотипное. — М.: ФИЗМАТЛИТ, 2004. — 224 с. — 3000 экз. — ISBN 5-9221-0055-6. Книга в электронной библиотеке мехмата МГУ
• Гантмахер Ф. Р.  Лекции по аналитической механике. 3-е изд. — М.: Физматлит, 2005. — 264 с. — ISBN 5-9221-0067-X..
• Ольховский И. И.  Курс теоретической механики для физиков. 4-е изд. — СПб.: Лань, 2009. — 576 с. — ISBN 978-5-8114-0857-3..

Уравнение	Канонический вид	Тип	Измерение
9x^2+12xy+4y^2-24x-16y+3=0	x^2=1	Две параллельные прямые	Линия
x^2-2xy+y^2-10x-6y+25=0	y^2=4*sqrt(2)*x	Парабола	Линия
5x^2+4xy+y^2-6x-2y+2=0	x^2/(1/sqrt(2*sqrt(2)+3))^2 + y^2/(1/sqrt(-2*sqrt(2)+3))^2=0	Вырожденный эллипс	Линия
5*x^2+4*x*y+8*y^2+8*x+14*y+5=0	x^2/(3/4)^2+y^2/(1/2)^2=1	Эллипс	Линия
2*x^2+4*y^2+z^2-4*x*y-4*y-2*z+5=0	z^2/(2/sqrt(2)/sqrt(3-sqrt(5)))^2+x^2/(2/sqrt(2)/sqrt(3+sqrt(5)))^2+y^2/(2/sqrt(2))^2=-1	Мнимый эллипсоид	Поверхность
x^2+y^2-z^2-2*x-2*y+2*z+2=0	x^2/1^2+y^2-z^2=-1	Двухсторонний гиперболоид	Поверхность
x^2+y^2-6*x+6*y-4*z+18=0	x^2/2+y^2-2*z=0 или x^2/2+y^2+2*z=0	Эллиптический параболоид	Поверхность
x^2+4*y^2+9*z^2+4*x*y+12*y*z+6*x*z-4*x-8*y-12*z+3=0	x^2/=1/14	Две параллельные плоскости	Поверхность