Как найти приближенное решение уравнения

8

Приближённое решение алгебраических и трансцендентных уравнений

1.
Общая постановка задачи.

Найти
действительные корни уравнения

,
где

–
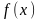
алгебраическая или трансцендентная
функция.

Точные
методы решения уравнений подходят
только к узкому классу уравнений
(квадратные, биквадратные, некоторые
тригонометрические, показательные,
логарифмические).

В
общем случае решение данного уравнения
находится приближённо в следующей
последовательности:

1)
отделение (локализация) корня;

2)
приближённое вычисление корня до
заданной точности.

2.
Отделение корня.

Отделение
действительного корня уравнения

–
это нахождение отрезка

,
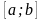
в котором лежит только один корень
данного уравнения. Такой отрезок
называется отрезком изоляции (локализации)
корня.

Наиболее
удобным и наглядным является графический
метод отделения корней:

1)
строится график функции

,
и определяются абсциссы точек пересечения
этого графика с осью

,
которые и являются корнями уравнения

;

2)
если

–
сложная функция, то её надо представить
в виде

так, чтобы легко строились графики
функций

и

.
Так как

,
то

.
Тогда абсциссы точек пересечения этих
графиков и будут корнями уравнения

.

Пример.
Графически
отделить корень уравнения

.

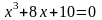
Р
ешение.
Представим левую часть уравнения в виде

.
Получим: Построим графики функций

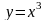
и

.

Абсцисса
точки пересечения графиков находится
на отрезке

,
значит корень уравнения

.

3. Уточнение корня.

Если
искомый корень уравнения

отделён, т.е. определён отрезок

,
на котором существует только один
действительный корень уравнения, то
далее необходимо найти приближённое
значение корня с заданной точностью.

Такая
задача называется задачей уточнения
корня.

Уточнение
корня можно производить различными
методами:

1)
метод половинного деления (бисекции);

2)
метод итераций;

3)
метод хорд (секущих);

4)
метод касательных (Ньютона);

5)
комбинированные методы.

4. Метод половинного деления (бисекции).

Отрезок
изоляции корня можно уменьшить путём
деления его пополам.

Такой
метод можно применять, если функция

непрерывна на отрезке

и на его концах принимает значения
разных знаков, т.е. выполняется условие

(1).

Разделим
отрезок

пополам точкой

,
которая будет приближённым значением
корня

.

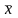
Для
уменьшения погрешности приближения
корня уточняют отрезок изоляции корня.
В этом случае продолжают делить отрезки,
содержащие корень, пополам.

Из
отрезков

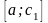
и

выбирают тот, для которого выполняется
неравенство (1).

В
нашем случае это отрезок

,
где

.

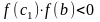
Далее
повторяем операцию деления отрезка
пополам, т.е. находим

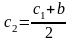
и так далее до тех пор, пока не будет
достигнута заданная точность

.
Т.е. до тех пор, пока не перестанут
изменяться сохраняемые в ответе
десятичные знаки или до выполнения
неравенства

.

Достоинство
метода: простота (достаточно выполнения
неравенства (1)).

Недостаток
метода: медленная сходимость результата
к заданной точности.

Пример.
Решить
уравнение

методом половинного деления с точностью
до 0,001.

Решение.
Известен
отрезок изоляции корня

и заданная точность

.
По уравнению составим функцию

.

Найдём
значения функции на концах отрезка:

,


.

Проверим
выполнение неравенства (1):

–
условие выполняется, значит можно
применить метод половинного деления.

Найдём
середину отрезка

и вычислим значение функции в полученной
точке:

,

.

Среди
значений

и

выберем два значения разных знаков, но
близких друг к другу. Это

и

.
Следовательно, из отрезков

и

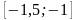
выбираем тот, на концах которого значения
функции разных знаков. В нашем случае
это отрезок

и опять находим середину отрезка и
вычисляем значение функции в этой точке:

,

,

,

–
заданная точность результата не
достигнута, продолжим вычисления.

,

,

,

.

,

,

,

.

,

,

,

.

,

,

,

.

,

,

,

.

,

,

,

.

,

,

,

.

,

,

,

.

,

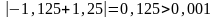
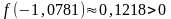
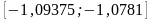
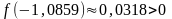
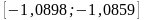
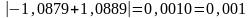
– заданная точность результата достигнута,
значит, нашли приближённое значение
корня

.

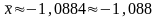
Ответ:
корень уравнения

с точностью до 0,001.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #

  16.03.2016121.34 Кб1414.doc

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Приближенное решение алгебраических и трансцендентных уравнений

Введение

Каждый уважающий себя инженер или IT-шник должен быть на «ты» с вычислительной математикой и ее численными методами для решений различных задач, возможно даже тривиальных, которые «голову в порядок приводят». В процессе изучения хотелось обратить более тщательное внимание на методы приближенного решения алгебраических и трансцендентных уравнений, а так же их анализ.

Методы численного решения нелинейных уравнений

Задачу решения я разделил на 3 части:

• Аналитический способ отделения корней
• Численные методы уточнения корней
• Программная реализация вычислительного процесса

Целью статьи, как я уже называл является разбор и анализ численных методов, по этому в этой статье аналитический способ отделения корней я рассматривать не буду.

Метод дихотомии или половинного деления.

Метод дихотомии заключается в последовательном делении отрезка. Выберется промежуток функции — необходимо отделить корни, на пример графическим способом. Получив интервал функции вычисляется его середина и определяется какой отрезок функции, разделенный серединой, больше или меньше нуля, это необходимо для выбора дальнейшего сужения интервала. Процесс сужения продолжается до определенной погрешности, которая задается.
К плюсам данного метода конечно стоит отнести его простоту. Им легко вычислять как аналитически, так и программно. К минусам нужно отнести затраты на приведенные итерации, по сравнению с методом хорд и касательных на пример.

Комбинированный метод или метод хорд и касательных

Методы хорд и метод касательных дают приближения к корню с разных сторон. Совместное использование методов позволяет на каждой итерации находить приближенные значения с недостатком и с избытком, что ускоряет процесс сходимости.
Идея метода хорд состоит в том чтобы заменить функцию на отрезке хордой, а идея метода касательных или метода Ньютона является замена дуги кривой функции ее касательной. Стоит отметить, что начальное приближение метода хорд определяется тот конец промежутка для которого производная в данной точке умноженная на двойную производную этой же точки меньше нуля, а для метода касательных больше нуля. Процесс сужения так же производится до указанной точности. К плюсам, как уже отмечалось относится быстрота нахождения и меньшая затратность на приведенные итерации

Метод итераций

Предварительно необходимо преобразовать уравнение f(x) = 0 к виду x = φ(x).
В качестве начального приближения x0 выбирается любая точка интервала [a,b].
Выделяют 2 итерационных метода: лестница и спираль. Если знак производной φ(x) положителен, то используют метод лестницы и наоборот спирали.

Главным и достаточным условием сходимости итерационного процесса является |φ'(x)|<1.
Достоинство метода. Надежность (обладает самокоррекцией): ошибка в вычислениях, при которой х остается в пределах [a,b ], не влияет на конечный результат, т.к. ошибочное значение можно рассматривать как новое х0.

Практика. Применение методов.

Возьмем для примера задачу из области автоматизированного управления — нахождения нулей характеристического уравнения передаточной функции замкнутой системы автоматического управления высокого порядка для оценки ее устойчивости по методу Ляпунова. Сам метод выходит за рамки данного поста, но в прямом методе Ляпунова используется нахождение нулевых корней для выявления устойчивости системы. А для нахождения корней вполне подходят перечисленные методы. Какой метод эффективнее? На этот вопрос сложно ответить не зная конкретной системы к которой это будет применяться. Следует учитывать не только скорость операций, но так же и занимаемые ресурсы.

Вывод:

1. Рассмотренные методы уточнения корней одинаково применимы как к алгебраическим, так и к трансцендентным уравнениям.
2. Операция отделения корней значительно сложнее для трансцендентных уравнений, чем для алгебраических.
3. Наиболее производительным из рассмотренных является комбинированный метод.

Мат.часть описанных методов.

PS: Первый пост и еще не совсем освоился. Помещаю пост в алгоритмы, т.к. блога по выч.мату не нашел.

ПРИБЛИЖЕННОЕ РЕШЕНИЕ УРАВНЕНИЙ

Действительные корни уравнения f(x)=0 (как алгебраического, так и трансцендентного) можно приближенно найти графически или посредством отделения корней. Для графического решения уравнения f(x)=0 строят график функции у=f(x); абсциссы точек пересечения и точек касания графика с осью абсцисс являются корнями уравнения. Метод отделения корней состоит в том, что находят таких два числа a и b, при которых функция f(x), предполагаемая непрерывной, имеет различные знаки – в этом случае между а и b заключен, по крайней мере, один корень; если производная f'(x) сохраняет знак в интервале от а до b, значит, f(x) – монотонная функция, то этот корень единственный (рис. 1).

Рисунок 1.

Более совершенными приемами, позволяющими найти корень с любой точностью, являются следующие. Пусть найдены такие два значения аргумента х=а, x=b (а

По способу хорд: значение корня х₁ уравнения f(х) = 0 в интервале [а, b] в первом приближении находится по формуле

Затем выбирается тот из интервалов [a, х₁], [x₁, b], на концах которого значения f(x) имеют различные знаки и находится корень х₂ во втором приближении по той же формуле, но с заменой числа х₁ на х₂, а числа b или а на x₁ (в зависимости от того, взят ли интервал [a, x₁] или [х₁, b]). Аналогично находятся последующие приближения (рис. 2).

Рисунок 2.

По способу касательных (или способу Ньютона) рассматривают тот из концов интервала [а, b], где f(x) и f”(х) имеют одинаковые знаки (рис. 3).

Рисунок 3.

В зависимости от того, выполняется ли это условие на конце х=а или на конце х=b, значение корня x₁ в первом приближении определяется по одной из формул

Затем рассматривается интервал [x₁, b] (если была использована первая из указанных формул) или [a, x₁] (если была использована вторая формула) и аналогичным путем находится значение корня x₂ по второму приближению и т. д.

Совместное применение способа хорд и способа касательных заключается в следующем. Устанавливают, на каком конце интервала [а, b] величины f(x) и f”(x) имеют одинаковые знаки. Для этого конца интервала применяют соответственно одну из формул способа касательных, получая значение x₁. Применяя для одного из интервалов [a, x₁], [x₁, b] формулу по способу хорд, получают значение x₂. Затем таким же образом проводят вычисления для интервала [x₁, x₂] и т. д.

Пример 1: y=f(х)=х³+2х-6=0. Путем проб находим 1,4<х< 1,5. Определяем корень по способу хорд: a=1,4; f(a)=-0,456; b=1,5; f(b)=0,375.
Первое приближение:

Повторяем операцию, заменяя значения а, f(a) на x₁=1,455; f(x₁)=-0,010.

Второе приближение:

Пример 2: x-1,5 cos x=0. Первое приближение находим с помощью табл. 1.35: если задаться x₁=0,92, то cos x₁=0,60582 и 0,92≈1,5?0,61. Уточняем корень по способу касательных: y’=1+1,5 sin x; y”=1,5 cos x. По той же таблице имеем:

Окончательно

К приближенным приемам решения уравнений относится также способ итераций. Он состоит в том, что каким-либо способом уравнение приводится к виду x=φ(x). Найдя приближенно х₁, подставляют найденное значение в правую часть уравнения и находят уточненные приближенные значения x₂=φ(x₁), x₃=φ(x₂) и т.д.; числа х₂, х₃, … приближаются к искомому корню (процесс сходится), если ?φ?(х)?<1.

Пример 3: найти корни уравнения x=tg x по способу итераций.

Для нахождения первых приближений к корням построим графики двух линий – y=x и y=tg x (рис. 4); точки пересечения этих линий дадут значения х, удовлетворяющие заданному уравнению.

Рисунок 4.

Как видим грубо приближенные значения корней будут

Учтя, что (tg x)? = sec²x>1, перепишем уравнение в следующем виде: x=arctg x. Положим x₀= тогда

Нетрудно убедиться, что подстановка значения x=4,4935 в заданное уравнение x=tg x обращает его в тождество (в пределах заданной точности).

Лекция 3

Раздел 2. Численные методы

2.1.

2.1.1. Приближенные решения алгебраических и трансцендентных
уравнений

План лекции

1.       Алгебраические и трансцендентные уравнения

2.       Графический метод решения уравнений

3.       Отделение корней

1. Алгебраические и трансцендентные уравнения

При решении практических задач часто приходится сталкиваться
с решением уравнений. Всякое уравнение с одним неизвестным можно представить в
виде

(x)=g(x),                   (1)

где (х) и g (х) —
данные функции, определенные на некотором числовом множестве X, называемом областью допустимых значений
уравнения.

В
общем случае нелинейное уравнение можно записать в виде:

где
функция F(x) определена и непрерывна
на конечном или бесконечном интервале .

? Совокупность значений переменной х, при которых
уравнение (1) превращается в тождество, называется решением этого
уравнения, а каждое значение х: из этой совокупности называется корнем
уравнения.

?Всякое число , обращающее функцию F(x) в нуль, т.е. такое, при котором F()=0, называется корнем
уравнения (1).

?Число называется корнем k-той кратности, если при x=вместе с функцией F(x) равны нулю ее производные до (k-1)
порядка включительно:

F() = F^/() = … = F^(k-1)( ) = 0.

Однократный
корень называется простым.

?Решить уравнение – значит найти множество всех
корней этого уравнения.

Оно может быть конечным или бесконечным.

?Два уравнения F(x)=0 и G(x=0) называются равносильными (эквивалентными), если всякое решение
каждого из них является решением и для другого, то есть множества решений этих
уравнений совпадают.

В зависимости от того, какие функции входят в уравнения (1)
или (2), уравнения разделяются на два больших класса: линейные и нелинейные.

Нелинейные
уравнения делятся, в свою очередь на: алгебраические
и трансцендентные.

Уравнение
(2) называется алгебраическим, если функция является алгебраической функцией.
Путем алгебраических преобразований из всякого алгебраического уравнения можно
получить уравнение в канонической форме:

P_n(x)=a₀xⁿ+a₁x^n-1+…+a_n=0,

где a₀,a₁, … ,a_n – коэффициенты уравнения, а x-неизвестное. Показатель n называется степенью алгебраического
уравнения.

Если
функция F(x) не является
алгебраической, то уравнение (1) называется трансцендентным.

В
некоторых случаях решение трансцендентных уравнений можно свести к решению алгебраических
уравнений.

Уравнения

линейные
                                          нелинейные

 

алгебраические                                трансцендентные

Решение
уравнения с одним неизвестным заключается в отыскании корней, т. е. тех
значений х, которые обращают уравнение в тождество. Корни уравнения могут быть
вещественными и невещественными (комплексными).

Найти
точные значения корней уравнения можно только в исключительных случаях, обычно,
когда есть какая-либо простая формула для вычисления значения корней, выражающая
их через известные величины.

Поскольку
подавляющее большинство нелинейных уравнений с одной переменой не решаются
путем аналитических преобразований (точными методами), на практике их решают
только численными методами.

При
решении многих практических задач точное решение уравнения не всегда является
необходимым. Задача нахождения корней считается решенной, если корни вычислены
с заданной степенью точности.

?Решить уравнение – это значит

·   установить,
имеет ли оно корни,

·   сколько
корней,

·   и
найти значение корней с заданной точностью.

?Задача численного нахождения действительных и комплексных корней
уравнения (2) обычно состоит из двух этапов:

1.  отделение корней, т.е. нахождение достаточно
малых окрестностей рассматриваемой области, в которых находится одно значение
корня,

2.  и уточнение корней, т.е. вычисление корней с заданной степенью
точности в некоторой окрестности.

Наиболее
распространенными на практике численными методами решения уравнения (2)
являются: метод половинного деления, метод хорд, метод касательных (Ньютона),
комбинированный метод, метод простой итерации. Применение того или иного метода
для решения уравнения (2) зависит от числа корней, задания исходного
приближения и поведения функции F(x).

2. Графические методы решения уравнений

Одним
из методов решения уравнений является графический. Точность такого решения
невелика, однако с помощью графика можно разумно выбрать первое приближение, с
которого начнется дальнейшее решение уравнения. Существуют два способа
графического решения уравнений.

Первый способ. Все члены уравнения переносят в левую часть, т. е.
представляют его в виде f(х) = 0. После этого строят график функции у = f(x), где f(х) – левая часть уравнения. Абсциссы точек пересечения графика функции у = f(х) с осью Ох и
являются корнями уравнения, так как в этих точках у = 0 (рис. 1).

 Рисунок 1

Второй способ. Все члены уравнения разбивают
на две группы, одну из них записывают в левой части уравнения, а другую в
правой, т. е. представляют его в виде f(х) = g(х).

После
этого строят графики двух функций у = f(х) и у = g(х). Абсциссы точек пересечения графиков этих двух функций и служат
корнями данного уравнения. Пусть точка пересечения графиков имеет абсциссу х₀,
ординаты обоих графиков в этой точке равны между собой, т. е. f(х₀) = g(х₀).
Из этого равенства следует, что х₀ – корень уравнения (рис. 2).

 Рисунок 2

Подводя
итог вышеизложенному, можно рекомендовать для графического решения уравнения f(х) = 0, все корни которого лежат в промежутке
[а, b], следующую простую схему.

1.
Представить указанное уравнение в виде (х) = g(х) с таким расчетом, чтобы функции у=(х) и у
=g (х) были просты и удобны для исследования и построения.

2.
На бумаге вычертить графики функций у =(х) и у
= g(х) в промежутке [а, b].

3.
Если графики не пересекаются, то корней в данном промежутке нет. Если же
графики пересекаются, то нужно определить точки их пересечения, найти абсциссы
этих точек, которые и будут приближенными значениями корней рассматриваемого
уравнения.

3. Отделение корней

Первый
этап численного решения уравнения (2) состоит в отделении корней, т.е. в установлении
“тесных” промежутков, содержащих только один корень.

?Корень  уравнения f(х) = 0 считается отделенным на
отрезке [a,b], если на этом отрезке уравнение f(х) = 0 не имеет других корней.

?Отделить корни – это значит разбить всю область допустимых значений на
отрезки, в каждом из которых содержится один корень.

Отделение
корней можно произвести двумя способами – графическим и аналитическим.

Графический метод отделения корней. При
графическом методе отделения корней поступают так же, как и при графическом
методе решения уравнений.

Графический
метод отделения корней не обладает большой точностью. Он дает возможность грубо
определить интервалы изоляции корня. Далее корни уточняются одним из способов, указанных ниже.

Аналитический метод отделения корней.
Аналитически корни уравнения f(х) =0 можно отделить, используя некоторые
свойства функций, изучаемые в курсе математического анализа.

Сформулируем
без доказательства теоремы, знание которых необходимо при отделении корней.

1)
Если непрерывная на отрезке  функция F(x) принимает на его концах значения разных
знаков, то уравнение (2) имеет на этом отрезке, по меньшей мере, один корень

2)
Если функция F(x) к тому же еще и
строго монотонна, то корень на отрезке  единственный.

Рассмотрим
примеры поведения некоторых функций:

       Рисунок 7

Для
отделения корней можно эффективно использовать ЭВМ.

Пусть имеется уравнение F(x)=0, причем можно считать, что все корни
находятся на отрезке , в которой функция F(x) отделена, непрерывна и F(A)*F(B)<0. Требуется
отделить корни уравнения, т.е. указать все отрезки< , содержат не по одному корню.

Будем вычислять значения F(x), начиная с точки X=A, двигаясь
вправо с некоторым шагом h.

Как только обнаружится пара соседних значений F(x), имеющих разные знаки, и функция F(x) монотонна на этом отрезке, так соответствующие
значения аргумента X (предыдущее и последующее) можно
считать концами отрезка, содержащего корень.

Схема соответствующего алгоритма изображена ниже. Результатом
решения поставленной задачи будут выводимые на дисплей в цикле значения
параметров X₁ и X₂ (Концов выделенных отрезков).

1) Графический метод. Отделение корней. Действительные корни уравнения являются абсциссами точек пересечения кривой с осью , а если это уравнение преобразуется к виду , то его действительные корни будут абсциссами точек пересечения кривых и .
Пользуясь этим, как было показано в решении задачи 2 (урок 7), можно находить приближенные значения действительных корней алгебраических и трансцендентных уравнений путем построения соответствующих кривых.
Однако этим графическим методом можно получить лишь грубо приближенные значения корней уравнения, но нельзя их вычислить с наперед заданной большой точностью.
Поэтому графический метод обычно применяется лишь как вспомогательное средство для определения числа действительных корней уравнения и для их отделения, т. е. для нахождения таких отрезков оси , внутри которых содержится только по одному корню. Затем, после такого отделения корней, каждый из них может быть вычислен с любой желаемой точностью посредством аналитических методов.
2) Уточнение корней уравнения методом хорд и касательных. Если на отрезке функция непрерывна, а ее производная сохраняет знак и если , то внутри этого отрезка содержится только один действительный корень функции или уравнения .
Если, кроме того, на этом отрезке также сохраняет знак, то можно найти границы и более узкого отрезка, содержащего тот же корень, по формулам

где – тот конец отрезка , в котором имеет тот же знак, что и .
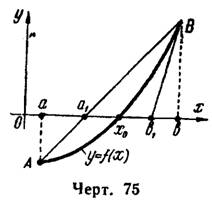
Геометрически (рис. 75) границы нового отрезка и представляют абсциссы точек пересечения с осью хорды и касательной , которые будут ближе к искомому корню , чем границы исходного отрезка .
Далее, исходя из полученного суженного отрезка, по тем же формулам (*) можно найти границы и еще более узкого отрезка, содержащего в себе корень .
Повторяя этот процесс последовательного сужения отрезка, содержащего корень т. е. повторяя применение формул (*), можно найти приближенное значение корня с любой заданной точностью.
Чтобы найти с точностью до , следует вести вычисление и до тех пор, когда впервые окажется

или

Тогда, с точностью до , в первом случае (или ), а во втором случае .
Пример 1. Отделить действительные корни следующих уравнений:
1) ; 2) ; 3) .

Решение. Чтобы отделить действительные корни данного уравнения, т. е. чтобы каждый из них заключить внутри особого небольшого отрезка, воспользуемся графическим методом.
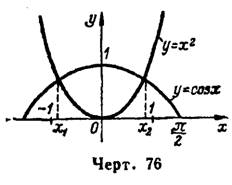
1) Преобразуем данное уравнение к виду и построим кривые и , в одних и тех же координатных осях и при одной и той же единице масштаба (рис. 76).
Число точек пересечения этих кривых равно числу действительных корней данного уравнения, а их абсциссы являются этими корнями.
Согласно этому положению из чертежа находим: данное трансцендентное уравнение имеет два действительных корня, один из которых содержится на отрезке [- 1;- 0,8], а другой на отрезке [0,8; 1].

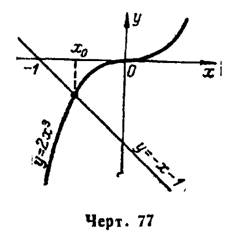
2) Преобразуя уравнение к виду и построив кривые и в одних координатных осях (рис. 77), заключаем: данное алгебраическое уравнение имеет только один действительный корень, содержащийся на отрезке [- 0,6; -0,5].
3) Приводим уравнение к виду и построим кривые и (рис. 78).

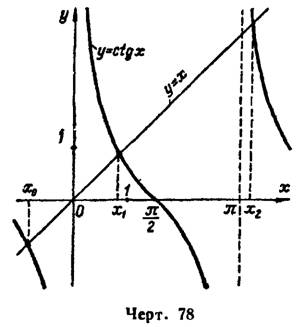
Котангенсоида имеет бесчисленное множество бесконечных ветвей, каждая из которых пересекает прямую . Поэтому данное уравнение имеет бесчисленное множество действительных корней. Наименьший положительный корень этого уравнения содержится на отрезке [0,8; 0,9].