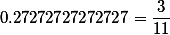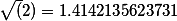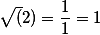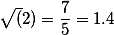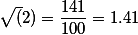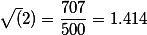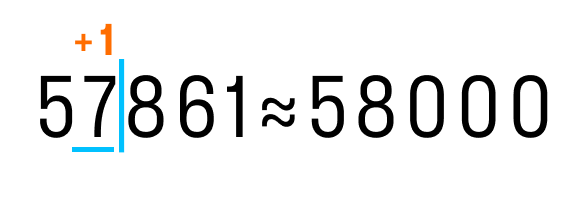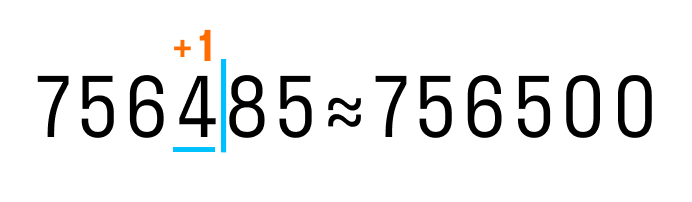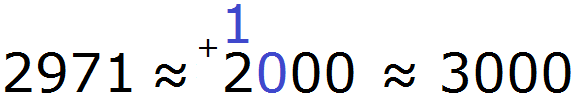Математика
6 класс
Урок № 68
Приближение десятичных дробей
Перечень рассматриваемых вопросов:
- Десятичная дробь, приближённое значение, округление.
- Значащая цифра десятичной дроби.
Тезаурус
Округление десятичной дроби – нахождение приближённого значения.
Десятичная дробь – дробь, записанная в десятичной форме.
Значащая цифра десятичной дроби – это первая слева направо отличная от нуля цифра, а также все следующие за ней цифры.
Основная литература
Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95с.
Теоретический материал для самостоятельного изучения
Не всегда возможно и нужно найти точные ответы на некоторые вопросы. Например, сколько кубических метров воды содержит Каспийское море? Сколько тонн снега выпало зимой? Сколько волос на голове человека? Поэтому, вместо точных берут другие значения, близкие к искомым, приближённые.
Рассмотрим несколько чисел. 1,3; 1,5; 1,8
Все эти числа имеют целую часть – единицу, значит, находятся между соседними натуральными числами 1 и 2.
При этом 1,3 находится ближе к 1, а 1,8 ближе к 2.
Поэтому можно сказать, что 1,3 приближённо равно 1,
а 1,8 приближённо равно 2.
Число 1,5 находится точно в середине, его можно приблизить и к единице, и к двум.
1,3 ≈ 1
1,8 ≈ 2
1,5≈1; 1,5≈2
Но если следовать правилам округления чисел, то 1,5 приближённо равно 2.
Приближение десятичных дробей, которое мы выполнили, называется округлением десятичной дроби до единиц.
Округление десятичной дроби – нахождение приближённого значения.
Если число А мало отличается от числа Б, то говорят, что число А приближённо равно числу Б. А ≈ Б; ≈ – знак приближённого равенства.
Если при этом Б меньше, чем А, то Б называют приближением А с недостатком.
Если Б больше, чем А, то его называют приближением А с избытком.
Рассмотрим на примере произвольной десятичной дроби.
А = 3,42845
Оборвём эту дробь на цифре второго разряда после запятой.
3,42845
Получим число, меньшее, чем А. 3,42 < А
Если увеличить число сотых на единицу, получим число, большее, чем А. 3,43 > А
Таким образом, первоначальное число А находится между данными числами. 3,42 < А < 3,43
Поэтому получаем, что 3,42 – приближение числа А с точностью до одной сотой с недостатком.
А ≈ 3,42 с точностью до 0,01 с недостатком.
3,43 – приближение числа А с точностью до одной сотой с избытком.
А ≈ 3,43 с точностью до 0,01 с избытком.
Так как третья цифра после запятой у числа А больше пяти, то оно ближе к 3,43, чем к 3,42. Поэтому говорят, что 3,43 есть приближение А с точностью до одной сотой с округлением.
Введём понятие значащей цифры десятичной дроби. Это первая слева направо отличная от нуля цифра, а также все следующие за ней цифры.
Например,
0,403 – все цифры после запятой значащие.
0,00256 – все цифры, начиная с двойки – значащие.
Округлим некоторые числа до третьей значащей цифры. Это означает, что округляем до того разряда, где находится третья значащая цифра, заменив следующие цифры нулями.
3,14159 ≈ 3,14000 = 3,14
0,046052 ≈ 0,046100 = 0,0461
– 0,023039 ≈ – 0,023000 = – 0,0230
Разбор заданий тренировочного модуля
Тип 1. Зачеркивания элементов.
Зачеркните неверный ответ.
Задание. Округлите число 1037,9301 до четырёх значащих цифр.
Варианты ответов: 1037,9; 1038
Решение. Значащие цифры – это первая отличная от нуля цифра, а также все следующие за ней. Значащими цифрами в данном числе являются все цифры, начиная с первой. Четыре значащие – это вся целая часть дроби. После запятой в разряде десятых стоит цифра 9, значит, при округлении к цифре разряда единиц мы прибавим 1. Получим 1038.
Ответ: 1038
Тип 2. Ввод с клавиатуры в пропуски в тексте.
Задание. Впишите в пропуски цифры, чтобы получилось верное округление
А) 383,_75 ≈ 383,6
Б) 2_9,746 ≈ 210
В) 548,_77 ≈ 548,18
Решение.
А) Дробь округлена до десятых. Следующая цифра после разряда десятых – 7. Значит, при округлении к цифре десятых прибавили единицу. Получилось 6. Значит, исходная цифра — 5.
Ответ: 383,575 ≈ 383,6
Б) Дробь округлена до десятков. Следующая цифра после разряда десятков – 9. Значит, при округлении к цифре десятков прибавили единицу. Получилось 1. Значит, исходная цифра десятков – 0.
Ответ: 209,746 ≈ 210
В) Дробь округлена до сотых. При этом количество десятых не менялось, и в конечном числе равно 1. Значит. И в исходном числе количество десятых – 1.
Ответ: 548,177 ≈ 548,18
Вычисление приближенной правильной дроби
| Выражение или значениеm для которого рассчитываются приближенные значения |
| Рассчитываем элементы непрерывной дроби для числа |
| Приближение дроби а также его абсолютное отклонение от точного значения |
Вычисление приближенной правильной дроби
Надеюсь всем, кто читает данную статью известно различие между рациональной и иррациональной числом?
Если нет, то напомним что рациональное число всегда можно выразить точным(!) отношением двух целых чисел
Например
Иррациональное же число никогда нельзя выразить точно через отношение двух целых чисел.
Но зато, мы иррациональное число можем представить в виде приближений двух чисел и с той точностью которая нам необходима.
Например
Нарисуем ряд дробей которые будут нам давать все более приближенные значения иррационального числа
Первое приближение понятно это
Второе приближение это
Третье приближение
Четвертое приближение
и так далее
Таким образом мы можем определять дроби которые могут представить нам с нужной точностью любое иррациональное число.
Бот этого сайта выдает список всех возможных приближений через рациональную дробь, до той точности которая возможна в языке PHP
Содержание
- Приближение по недостатку и по избытку
- Округление десятичных дробей
- Правила округления десятичной дроби
- Примеры округления десятичной дроби
- Математика. 6 класс
- Приближённые значения. Округление чисел.
- Содержание
- Приближённые значения
- Правила округления натуральных чисел
- Как правильно округлить натуральное число
- Округление десятичных дробей до целых
- Как правильно округлить десятичную дробь
- Округление дробных чисел при переводе обыкновенных дробей в десятичные
- Правильное округление чисел
- Приближенные значения
- Примерчики
- Округление натуральных чисел
- Округление десятичных дробей
- Пример 1
- Пример 2
Приближение по недостатку и по избытку
Проводя различные измерения, решая уравнения графическим способом, выполняя арифметические вычисления, часто получают приближенные значения, а не точные. Например, при вычислении корня числа может получиться бесконечная непериодическая дробь (т. е. иррациональное число). Кроме того, существуют бесконечные периодические дроби, использовать которые в вычислениях также неудобно.
Поэтому числа, являющиеся бесконечными десятичными дробями или конечными, но имеющими множество знаков после запятой, принято округлять.
Когда округление выполняется в большую сторону, то говорят о приближении по избытку. Когда округление выполняется в меньшую сторону, то говорят о приближении по недостатку.
Полученное при округлении число называют приближенным по недостатку или избытку с определенной точностью. Рассмотрим несколько примеров приближения.
Число π является бесконечной дробью 3,1415926535. Обычно его округляют с точностью до 0,01. Это значит, что после запятой оставляют только два знака. При приближении по избытку получится 3,15. При приближении по недостатку получится 3,14.
Для числа π обычно используют приближение по недостатку, так как согласно правилу округления положительные числа округляются в большую сторону, если первая отбрасываемая цифра 5 или больше пяти. Так как у числа π третья цифра после запятой — это 1, то округление выполняется в меньшую сторону, то есть для расчетов выполняется приближение по недостатку.
Однако, несмотря на правила округления, имеют право быть приближения как по недостатку, так и по избытку.
Если выполнять приближение числа π с точностью до 0,0001, то по избытку получим π ≈ 3,1416, а по недостатку π ≈ 3,1415.
Рассмотрим иррациональное число √2, которое равно 1,414213. . Вычислим его приближение по недостатку и по избытку с точностью до 0,001. Поскольку приближение выполняется до тысячных долей, то у числа надо оставить три знака после запятой. При приближении по недостатку просто отбрасываются все цифры после третьей после запятой. При приближении по избытку цифры после третьей после запятой отбрасываются, а третья цифра увеличивается на 1. Таким образом, приближение по недостатку будет √2 ≈ 1,414, а по избытку √2 ≈ 1,415.
Но примеры, рассмотренные выше, это положительные числа. А так ли обстоит дело при приближении отрицательных чисел. Если взять число –√2 = –1,414213. то его приближением по избытку до тысячных долей будет –1,414, так как это число больше, чем –√2. А вот приближением по недостатку будет –1,415, так как это число меньше, чем –√2.
Источник
Округление десятичных дробей
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Правила округления десятичной дроби
Точность — это вежливость королей. А математика, как известно, царица наук, поэтому, чем меньше приближенных значений в ваших решениях, тем лучше.
В повседневной жизни редко можно услышать приближенное значение в ответ на вопросы:
Вряд ли кто-то из нас слышал в ответ 17 часов 27 минут 16 секунд, 1 килограмм 952 грамма или 543 рубля (ладно, с последним бывает).
Округление — это то, с чем мы сталкиваемся каждый день. Поэтому лучше как можно раньше овладеть искусством доводить до приближенного значения. Чтобы без запинки отвечать: половина седьмого; 2 килограмма; 550 рублей.
Число, полученное при округлении, называют приближенным значением данного числа.
Десятичную дробь можно округлить как до целых, так и до разрядов дробной части: десятых, сотых, тысячных и т.д. Чтобы без труда округлить любую десятичную дробь, нужно знать названия всех разрядов.
Если число c
Еще одно правило округления, которое нужно запомнить
Если при округлении десятичной дроби последней из оставшихся цифр в дробной части оказывается ноль, то его не нужно отбрасывать. Оставшийся ноль показывает, до какого разряда округлено число.
Если десятичную дробь округляем до разряда выше единиц (десятков, сотен и т.д.), то дробная часть отбрасывается, а целая часть округляется по правилам округления натуральных чисел.
Примеры округления десятичной дроби
Давайте разберем несколько примеров округления дробной части десятичных дробей.
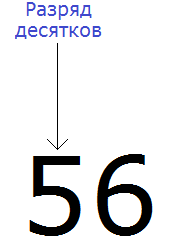
Пример 1. Округлите дробь 56,786 до сотых.
Цифра, которую нужно округлить, — 8. Обращайтесь к таблице с подсказками названия разрядов, чтобы верно определять нужную цифру.
Справа от цифры округляемого разряда цифра 6.
Смотрим на пункт 4. Прибавляем: 8 + 1 = 9.
Ответ. 56,786 ≈ 56,79.
Пример 2. Округлите дробь 0,647 до десятых.
Округляемая цифра — 6.
Смотрим пункт 3. Значит, цифра 6 остается неизменной.
Пример 3. Округлите дробь 23,98 до разряда единиц в целой части.
Цифра, которую нужно округлить, — 3.
Первая цифра после запятой — 9. Значит, нужно прибавить: 3 + 1.
Затем отбрасываем все остальные цифры, стоящие справа.
Пример 4. Округлите дробь 3,286 до десятых.
Цифра, которую нужно округлить, — 2.
Согласно правилу, прибавляем: 2 + 1.
Затем отбрасываем все остальные цифры, стоящие справа.
Пример 5. Округлите дробь 45,387 до сотых.
Прибавляем: 8 + 1.
Затем отбрасываем все остальные цифры, стоящие справа.
Источник
Математика. 6 класс
Конспект урока
Приближение десятичных дробей
Перечень рассматриваемых вопросов:
- Десятичная дробь, приближённое значение, округление.
- Значащая цифра десятичной дроби.
Округление десятичной дроби – нахождение приближённого значения.
Десятичная дробь – дробь, записанная в десятичной форме.
Значащая цифра десятичной дроби – это первая слева направо отличная от нуля цифра, а также все следующие за ней цифры.
Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
1. Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. — М.: Просвещение, 2009. — 142с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин. — М.: Просвещение, 2014. — 95с.
Теоретический материал для самостоятельного изучения
Не всегда возможно и нужно найти точные ответы на некоторые вопросы. Например, сколько кубических метров воды содержит Каспийское море? Сколько тонн снега выпало зимой? Сколько волос на голове человека? Поэтому, вместо точных берут другие значения, близкие к искомым, приближённые.
Рассмотрим несколько чисел. 1,3; 1,5; 1,8
Все эти числа имеют целую часть – единицу, значит, находятся между соседними натуральными числами 1 и 2.
При этом 1,3 находится ближе к 1, а 1,8 ближе к 2.
Поэтому можно сказать, что 1,3 приближённо равно 1,
а 1,8 приближённо равно 2.
Число 1,5 находится точно в середине, его можно приблизить и к единице, и к двум.
Но если следовать правилам округления чисел, то 1,5 приближённо равно 2.
Приближение десятичных дробей, которое мы выполнили, называется округлением десятичной дроби до единиц.
Округление десятичной дроби – нахождение приближённого значения.
Если число А мало отличается от числа Б, то говорят, что число А приближённо равно числу Б. А ≈ Б; ≈ – знак приближённого равенства.
Если при этом Б меньше, чем А, то Б называют приближением А с недостатком.
Если Б больше, чем А, то его называют приближением А с избытком.
Рассмотрим на примере произвольной десятичной дроби.
Оборвём эту дробь на цифре второго разряда после запятой.
Источник
Приближённые значения. Округление чисел.
Содержание
Приближённые значения применяются в случаях, если невозможно вычислить точное значение или если точное значение не требуется.
Приближённые значения
Представьте, что вы смотрите на часы в комнате и они показывают два часа и две минуты. Но когда вы переходите в другую комнату, там на часах $13.59$. Какие-то из этих часов отстают или спешат… Но если вам не нужно совершенно точно указать время, то можно смело сказать, что часы показывают приблизительно два часа.
Другой пример. В интернете можно встретить информацию, что размер африканского слона около $300$ сантиметров. На самом деле есть слоны покрупнее и помельче, кто-то из них достигает почти четырёх метров, а слонихи обычно ростом $270-280$ см. И, конечно, никому не приходит в голову перемерить всех имеющихся слонов, чтобы указать их точные размеры. Вместо этого называют приблизительное или, говоря математическим языком, приближённое значение. Размеры слона округляют до $300$ сантиметров.
Правила округления натуральных чисел
Округлением натурального числа называют замену этого числа таким ближайшим по значению, у которого одна или несколько последних цифр в записи заменяется нулями.
Поэтому такой процесс и называется округление – число заканчивается на круглые нули.
Как правильно округлить натуральное число
- Выбрать в записи числа разряд, до которого производится округление (можно подчеркнуть его для удобства)
- Выделить число справа от выбранного разряда
- Если это число справа от подчёркнутой цифры $0, 1, 2, 3$ или $4$, то все цифры, включая данное число, заменить нулями, а цифру разряда, до которой округляли, оставить без изменений
- Если число справа от подчёркнутой цифры $5, 6, 7, 8$ или $9$, то также все цифры справа от подчёркнутой заменяем нулями, а к цифре разряда, до которой округляли, увеличиваем на $1$
При округлении используется вот такой знак:
Давайте рассмотрим принцип округления на примере слона Гектора. Его рост $320$ см, нужно округлить до сотен.
Подчёркиваем число в разряде сотен и смотрим на следующее число (разряд десятков). Это $2$, следовательно, заменяем все цифры после разряда сотен нулями, а число сотен оставляем без изменений.
А рост слонихи Офелии $275$ см. Давайте округлим его до десятков.
Подчёркиваем число десятков, смотрим на разряд справа (единицы). Это $5$. Заменяем число единиц нулями, а цифру в разряде десятков увеличиваем на $1$.
Обратите внимание, что когда мы округляли массу слона, у нас получилось меньшее число, а когда массу слонихи – большее.
Можно сказать, что $300$ – это приближение числа $320$ с недостатком, а $280$ – это приближение числа $275$ с избытком.
Округление десятичных дробей до целых
Образавру подарили арбуз. Он решил его взвесить, но у него не было хороших весов. На тех, которые были, оказались только килограммовые деления. Вот что показали весы:
Арбуз весит больше $4$ кг, но немного меньше $5$ кг. Если обозначить массу арбуза буквой n, получается, что $4 
Можете ли сказать, чему приближённо равен отрезок АВ?
Отрезок АВ приближённо равен $8.5$ см.
Как правильно округлить десятичную дробь
- Выбрать в записи числа разряд, до которого производится округление (можно подчеркнуть его для удобства)
- Выделить число справа от выбранного разряда
- Если это число справа от подчёркнутой цифры $0, 1, 2, 3$ или $4$, то все цифры, включая данное число, заменить нулями, а цифру разряда, до которой округляли, оставить без изменений
- Если число справа от подчёркнутой цифры $5, 6, 7, 8$ или $9$, то также все цифры справа от подчёркнутой заменяем нулями, а к цифре разряда, до которой округляли, увеличиваем на $1$
- Если цифры, заменяемые нулями, находятся в дробной части (справа от запятой), то нули не записываются, а просто отбрасываются
Давайте потренируемся. Длина карандаша равна $17.72$ см. Округлите это значение до десятых.
Чтобы округлить число $17.textcolor <7>textcolor<2>$ до десятых, нам нужно заменить все цифры после разряда десятых нулями. В нашем случае это одна цифра. Сравним эту цифру с $5. $
$$2 
Округление дробных чисел при переводе обыкновенных дробей в десятичные
При переводе обыкновенных дробей в десятичные иногда мы сталкиваемся с ситуацией, когда дробь не может быть представлена в виде десятичной.
Например, $frac<1><6>$. Если мы разделим $1$ на $6$, калькулятор покажет вот такое число:
Известно, что дробь может быть переведена в десятичную только в том случае, если её знаменатель раскладывается на простые множители $2$ и $5. $
Получается, мы не можем представить дробь $frac<1><6>$ в виде десятичной. Мы можем только найти приближённое значение.
Например, мы можем округлить число на рисунке 5 до тысячных.
Как это можно сделать?
Выделим число, до которого нужно округлить (тысячные) и то, которое следует за ним (десятитысячные).
Посмотрим на число десятитысячных. Это $6. $
Следовательно, мы берём число тысячных и увеличиваем его на $1. $
У нас получается $0.167$
Приближённые значения приходят к нам на помощь, когда вычислить точное значение не представляется возможным. Но всё-таки в рамках школьного курса математики мы чаще имеем дело с точными цифрами, и, если есть возможность получить точный ответ, следует стараться это сделать.
Источник
Правильное округление чисел
О чем эта статья:
Приближенные значения
В обычной жизни мы часто встречаем два вида чисел: точные и приближенные. И если точные до сих пор были понятны, то с приближенными предстоит познакомиться в 5 классе.
У квадрата четыре стороны — число 4 невозможно оспорить, оно точное. У каждого окна есть своя ширина, и его параметры однозначно точные. А вот арбуз весит примерно 5 кг, и никакие весы не покажут абсолютно точный вес. И градусник показывает температуру с небольшой погрешностью. Поэтому вместо точных значений величин иногда можно использовать приближенные значения.
Примерчики
Весы показывают, что арбуз весит 5,160 кг. Можно сказать, что арбуз весит примерно 5 кг. Это приближенное значение с недостатком.
Часы показывают время: два часа дня и пятьдесят пять минут. В разговоре про время можно сказать: «почти три» или «время около трех». Это значение времени с избытком.
Если длина платья 1 м 30 см, то 1 м — это приближенное значение длины с недостатком, а 1,5 м — это приближенное значение длины с избытком.
Приближенное значение — число, которое получилось после округления.
Для записи результата округления используют знак «приблизительно равно» — ≈.
Округлить можно любое число — для всех чисел работают одни и те же правила.
Округлить число значит сократить его значение до нужного разряда, например, до сотых, десятков или тысячных, остальные значения откидываются. Это нужно в случаях, когда полная точность не нужна или невозможна.
Округление натуральных чисел
Натуральные числа — это числа, которые мы используем, чтобы посчитать что-то конкретное, осязаемое. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и так далее.
Особенности натуральных чисел:
- Наименьшее натуральное число: единица (1).
- Наибольшего натурального числа не существует. Натуральный ряд бесконечен.
- У натурального ряда каждое следующее число больше предыдущего на единицу: 1, 2, 3, 4, 5, 6, 7.
Округление натурального числа — это замена его таким ближайшим по значению числом, у которого одна или несколько последних цифр в его записи заменены нулями.
Чтобы округлить натуральное число, нужно в записи числа выбрать разряд, до которого производится округление.
Правила округления чисел:
- Подчеркнуть цифру разряда, до которого надо округлить число.
- Отделить все цифры справа от этого разряда вертикальной чертой.
- Если справа от подчеркнутой цифры стоит 0,1, 2, 3 или 4 — все цифры, которые отделены справа, заменяем нулями. Цифру разряда, до которой округляли, оставляем без изменений.
- Если справа от подчеркнутой цифры стоит 5, 6, 7, 8 или 9 — все цифры, которые отделены справа, заменяем нулями. К цифре разряда, до которой округляли, прибавляем 1.
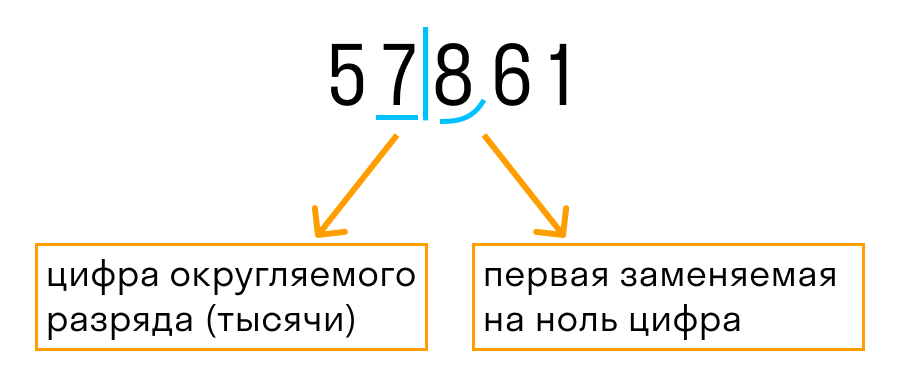
Давайте рассмотрим, как округлить число 57 861 до тысяч. Выполним первые два пункта из правил округления.
После подчеркнутой цифры стоит 8, значит к цифре разряда тысяч (в данном случае 7) прибавим 1. На месте цифр, отделенных вертикальной чертой, ставим нули.
Теперь округлим 756 485 до сотен:
Округлим число 123 до десятков: 123 ≈ 120.
Округлим число 3581 до сотен: 3581 ≈ 3580.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу — в этом разряде записывается цифра 0, а цифра слева в соседнем старшем разряде увеличивается на 1.
- как округлить число 697 до десятков — 697 ≈ 700;
- как округлить число 980 до сотен — 980 ≈ 1000.
Иногда уместно записать округленный результат с сокращениями «тыс.» (тысяча), «млн.» (миллион) и «млрд.» (миллиард). Вот так:
- 7 882 000 = 7 882 тыс.
- 1 000 000 = 1 млн.
Округление десятичных дробей
Дробь — одна из форм записи частного чисел a и b, представленная в виде a/b. Есть два формата записи:
- обыкновенный вид — 1/2 или a/b,
- десятичный вид — 0,5.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10 000 и т. д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Такую дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
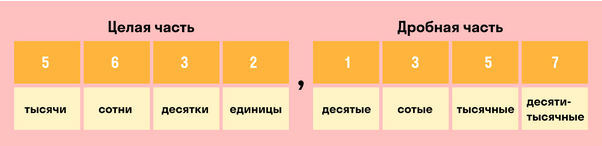
При округлении десятичных дробей следует быть особенно внимательным, потому что десятичная дробь состоит из целой и дробной части. И у каждой из этих частей есть свои разряды:
Разряды целой части:
- разряд единиц;
- разряд десятков;
- разряд сотен;
- разряд тысяч.
Разряды дробной части:
- разряд десятых;
- разряд сотых;
- разряд тысячных.
Разряд — это позиция, место расположения цифры в записи натурального числа. У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие.
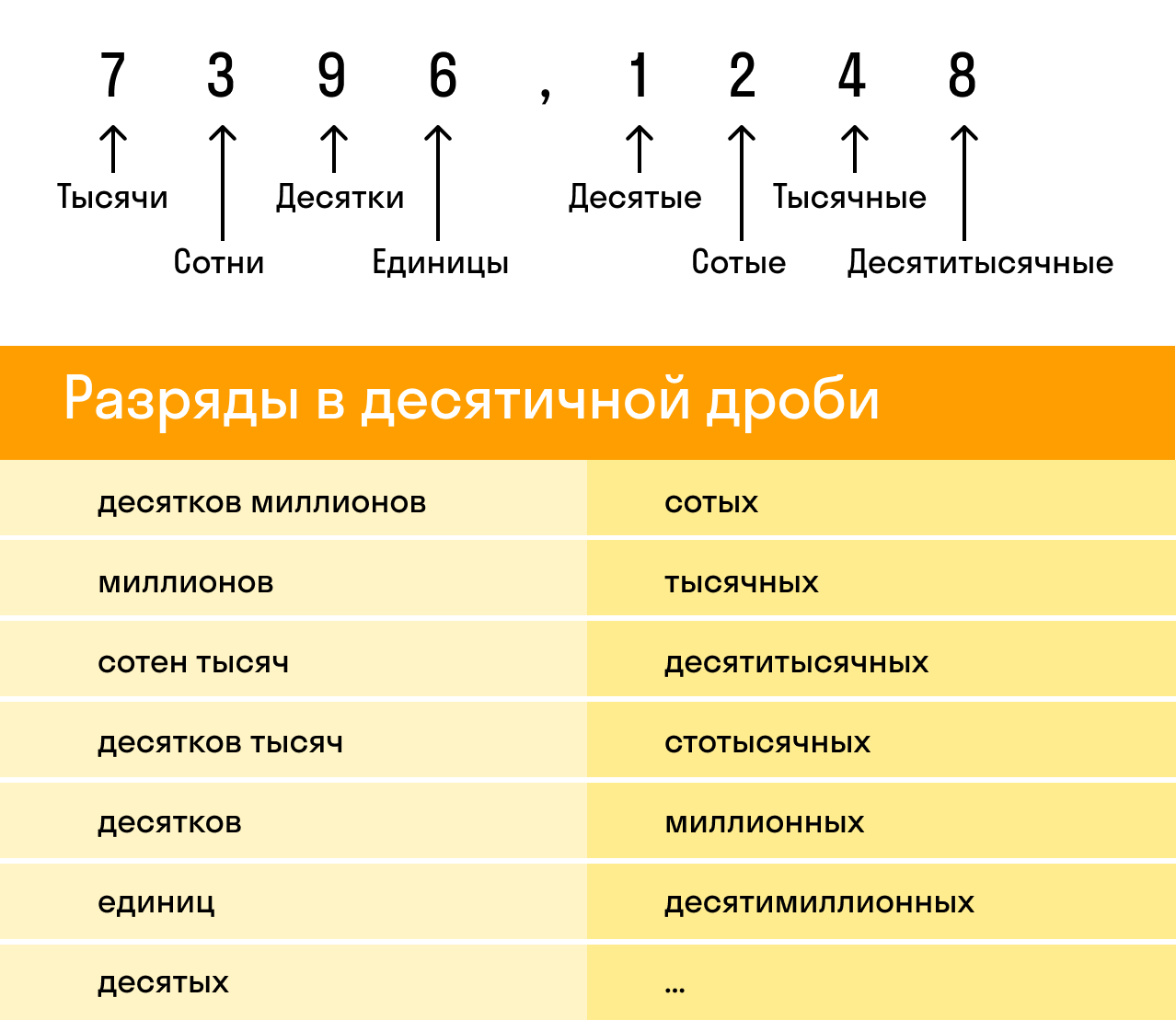
Рассмотрим десятичную дробь 7396,1248. Здесь целая часть — 7396, а дробная — 1248. При этом у каждой из них есть свои разряды, которые важно не перепутать:
Чтобы округлить десятичную дробь, нужно в записи числа выбрать разряд, до которого производится округление.
То число, к которому дробь ближе, называют округленным значением числа.
Цифра, которая записана в данном разряде:
- не меняется, если следующая за ней справа цифра — 0,1, 2, 3 или 4;
- увеличивается на единицу, если за ней справа следует цифра — 5, 6, 7, 8 или 9.
Как округлить до десятых. Оставить одну цифру после запятой, остальные отбросить. Согласно правилу выше, если первая отбрасываемая цифра — 0, 1, 2, 3 или 4, то цифра после запятой остается той же. Если мы отбрасываем цифру 5, 6, 7, 8 или 9 — цифра после запятой увеличивается на единицу.
Как округлить до сотых. Оставить две цифры после запятой, остальные отбросить. И снова не забываем про правило: если следующая цифра 0, 1, 2, 4 — цифра в разряде сотых остается неизменной. Если же это 5, 6, 7, 8 или 9, то цифра в разряде сотых увеличится на 1.
Как округлить до целых. Заменить десятичную дробь ближайшим к ней целым числом. Ближайшим будет наименьшее расстояние. При этом если расстояние до приближенного значения числа с недостатком и расстояние до приближенного значения числа с избытком равны, то округляют в большую сторону.
Все цифры, которые стоят справа от данного разряда, заменяются нулями. Если эти нули стоят в дробной части числа, то их можно не писать.
Пример 1
256,43 ≈ 256,4 — округление до десятых;
4,578 ≈ 4,58 — округление до сотых;
17,935 ≈ 18 — округление до целых.
Если в разряде, до которого производится округление, стоит цифра 9 и необходимо ее увеличить на единицу, то в этом разряде записывается цифра 0, а цифра слева в предыдущем разряде увеличивается на 1.
Пример 2
79,7 ≈ 80 — округление до десятков;
0,099 ≈ 0,10 — округление до сотых.
Математическое округление и его правила быстро запомнится, если не лениться решать примеры и задачки из учебников 5 класса.
Источник
Adblock
detector
Сегодня мы рассмотрим довольно скучную тему, без понимания которой двигаться дальше не представляется возможным. Эта тема называется «округление чисел» или по-другому «приближённые значения чисел».
Приближённые значения
Приближённые (или приблизительные) значения применяются тогда, когда точное значение чего-то найти невозможно, или же не важно чтобы это значение было точным для исследуемого предмета.
Например, на словах можно сказать, что в городе проживает полмиллиона человек, но это высказывание не будет истинным, поскольку количество человек в городе меняется — люди приезжают и уезжают, рождаются и умирают. Поэтому правильнее будет сказать, что в городе проживает приблизительно полмиллиона человек.
Ещё пример. В девять утра начинаются занятия. Мы вышли из дома в 8:30. Через некоторое время по дороге мы встретили своего товарища, который спросил у нас сколько сейчас времени. Когда мы выходили из дома было 8:30, на дорогу мы потратили какое-то неизвестное время. Мы не знаем сколько сейчас времени, поэтому отвечаем товарищу: «сейчас приблизительно около девяти часов».
В математике приближенные значения указываются с помощью специального знака. Выглядит он следующим образом:
Читается как «приближённо (приблизительно) равно».
Чтобы указать приближённое (приблизительное) значение, прибегают к такому действию как округление чисел.
Округление чисел
Для нахождения приближенного значения применяется такое действие как округление чисел.
Слово «округление» говорит само за себя. Округлить число значит сделать его круглым. Круглым называется число, которое оканчивается нулём. Например, следующие числа являются круглыми:
10, 20, 30, 100, 300, 700, 1000
Любое число можно сделать круглым. Процедуру, при которой число делают круглым, называют округлением числá.
Мы уже занимались «округлением» чисел, когда делили большие числа. Напомним, что для этого мы оставляли без изменения цифру, образующую старший разряд, а остальные цифры заменяли нулями. Но это были лишь наброски, которые мы делали для облегчения деления. Своего рода лайфхак. По факту, это даже не являлось округлением чисел. Именно поэтому в начале данного абзаца мы взяли слово округление в кавычки.
На самом деле, суть округления заключается в том, чтобы найти ближайшее значение от исходного. При этом, число может быть округлено до определённого разряда — до разряда десятков, разряда сотен, разряда тысяч.
Рассмотрим простой пример на округление. Дано число 17. Требуется округлить его до разряда десятков.
Не забегая вперёд попробуем понять, что означает «округлить до разряда десятков». Когда говорят округлить число 17, то надо понимать, что от нас требуют найти ближайшее круглое число от числá 17. Причём в ходе этого поиска возможно изменения коснутся и той цифры, которая располагается в разряде десятков числá 17 (т.е цифры 1).
Предстáвим числа от 10 до 20 с помощью следующего рисунка:
На рисунке видно, что для числá 17 ближайшее круглое число это число 20. Значит ответ к задаче таким и будет: «17 приближённо равно 20″
17 ≈ 20
Мы нашли приближённое значение для 17, то есть округлили его до разряда десятков. Видно, что после округления в разряде десятков появилась новая цифра 2.
Попробуем найти приближённое число для числа 12. Для этого снова предстáвим числа от 10 до 20 с помощью рисунка:
На рисунке видно, что ближайшее круглое число для 12 это число 10. Значит ответ к задаче таким и будет: 12 приближённо равно 10
12 ≈ 10
Мы нашли приближённое значение для 12, то есть округлили его до разряда десятков. В этот раз цифра 1, которая стояла в разряде десятков в числе 12, не пострадала от округления. Почему так получилось мы расскажем позже.
Попробуем найти ближайшее число для числá 15. Снова предстáвим числа от 10 до 20 с помощью рисунка:
На рисунке видно, что число 15 одинаково удалено от круглых чисел 10 и 20. Возникает вопрос: которое из этих круглых чисел будет приближённым значением для числа 15? Для таких случаев условились принимать бóльшее число за приближённое. 20 больше чем 10, поэтому приближённое значение для 15 будет число 20
15 ≈ 20
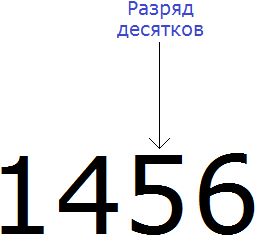
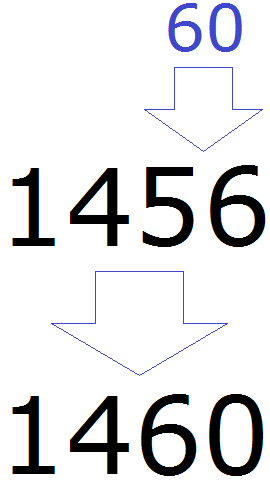
Округлять можно и большие числа. Естественно, для них делать рисунки и изображать числа не представляется возможным. Для них существует свой способ. Например, округлим число 1456 до разряда десятков.
Итак, мы должны округлить 1456 до разряда десятков. Разряд десятков начинается на пятёрке:
Теперь о существовании первых цифр 1 и 4 временно забываем. Остается число 56
Теперь смотрим, какое круглое число находится ближе к числу 56. Очевидно, что ближайшее круглое число для 56 это число 60. Значит заменяем число 56 на число 60
Значит при округлении числа 1456 до разряда десятков полýчим 1460
1456 ≈ 1460
Видно, что после округления числа 1456 до разряда десятков, изменения коснулись и самогó разряда десятков. В новом полученном числе в разряде десятков теперь располагается цифра 6, а не 5.
Округлять числа можно не только до разряда десятков. Округлять число можно до разряда сотен, тысяч, десятков тысяч и так далее.
После того, как станóвится ясно, что округление это ни что иное как поиск ближáйшего числá, можно применять готовые правила, которые значительно облегчают округление чисел.
Первое правило округления
В предыдущих примерах мы видели, что округляя число до определенного разряда, младшие разряды заменяются нулями. Цифры, которые заменяются нулями, называют отбрасываемыми цифрами.
Первое правило округления выглядит следующим образом:
Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
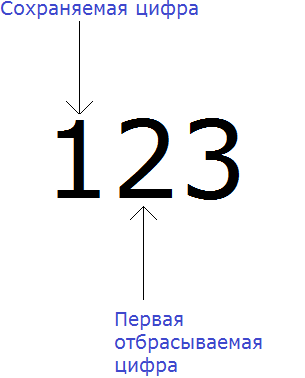
Например, округлим число 123 до разряда десятков.
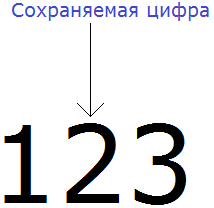
В первую очередь находим сохраняемую цифру. Для этого надо прочитать самó задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 123 до разряда десятков.
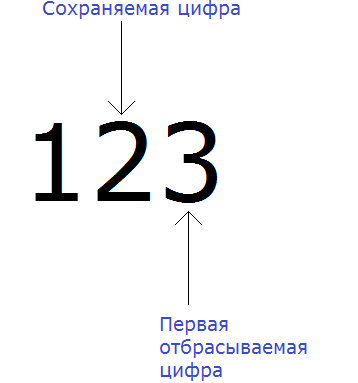
Видим, что в разряде десятков нахóдится двойка. Значит сохраняемой цифрой является цифра 2
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после двойки это цифра 3. Значит цифра 3 является первой отбрасываемой цифрой.
Теперь применяем правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Так и делаем. Оставляем без изменения сохраняемую цифру, а все младшие разряды заменяем нулями. Другими словами, всё что следует после цифры 2 заменяем нулями (точнее нулём):
123 ≈ 120
Значит при округлении числа 123 до разряда десятков, получаем приближённое ему число 120.
Теперь попробуем округлить то же самое число 123, но уже до разряда сотен.
Нам требуется округлить число 123 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 1, поскольку мы округляем число до разряда сотен.
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после единицы это цифра 2. Значит цифра 2 является первой отбрасываемой цифрой:
Теперь применим правило. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Так и делаем. Оставляем без изменения сохраняемую цифру, а все младшие разряды заменяем нулями. Другими словами, всё что следует после цифры 1 заменяем нулями:
123 ≈ 100
Значит при округлении числа 123 до разряда сотен, получаем приближённое ему число 100.
Пример 3. Округлить число 1234 до разряда десятков.
Здесь сохраняемая цифра это 3. А первая отбрасываемая цифра это 4. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит оставляем сохраняемую цифру 3 без изменений, а всё что располагается после неё заменяем нулём:
1234 ≈ 1230
Пример 4. Округлить число 1234 до разряда сотен.
Здесь сохраняемая цифра это 2. А первая отбрасываемая цифра это 3. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит оставляем сохраняемую цифру 2 без изменений, а всё что располагается после неё заменяем нулями:
1234 ≈ 1200
Пример 3. Округлить число 1234 до разряда тысяч.
Здесь сохраняемая цифра это 1. А первая отбрасываемая цифра это 2. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит оставляем сохраняемую цифру 1 без изменений, а всё что располагается после неё заменяем нулями:
1234 ≈ 1000
Второе правило округления
Второе правило округления выглядит следующим образом:
Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
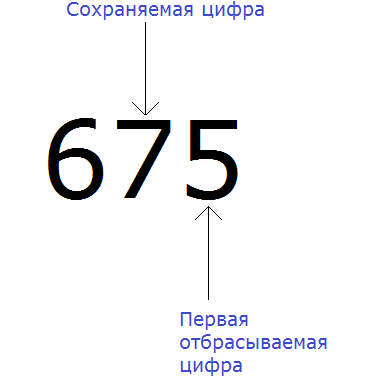
Например, округлим число 675 до разряда десятков.
В первую очередь находим сохраняемую цифру. Для этого надо прочитать само задание. В разряде, о котором говорится в задании и находится сохраняемая цифра. В задании сказано: округлить число 675 до разряда десятков.
Видим, что в разряде десятков находится семёрка. Значит сохраняемой цифрой является цифра 7
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после семёрки это цифра 5. Значит цифра 5 является первой отбрасываемой цифрой.
Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
У нас первая из отбрасываемых цифр это 5. Значит мы должны увеличить на единицу сохраняемую цифру 7, а всё что следует после неё заменить нулём:
675 ≈ 680
Значит при округлении числа 675 до разряда десятков, получаем приближённое ему число 680.
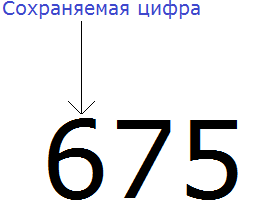
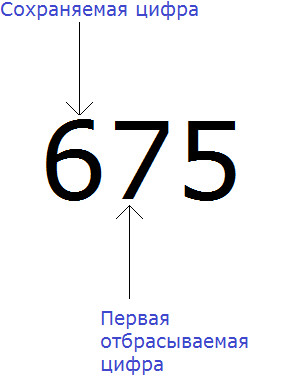
Теперь попробуем округлить то же самое число 675, но уже до разряда сотен.
Нам требуется округлить число 675 до разряда сотен. Снова ищем сохраняемую цифру. В этот раз сохраняемой цифрой является 6, поскольку мы округляем число до разряда сотен:
Теперь находим первую из отбрасываемых цифр. Первой из отбрасываемых цифр является та цифра, которая следует после сохраняемой цифрой. Видим, что первая цифра после шестёрки это цифра 7. Значит цифра 7 является первой отбрасываемой цифрой:
Теперь применяем второе правило округления. Оно говорит, что если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
У нас первая из отбрасываемых цифр это 7. Значит мы должны увеличить на единицу сохраняемую цифру 6, а всё что следует после неё заменить нулями:
675 ≈ 700
Значит при округлении числа 675 до разряда сотен, получаем приближённое ему число 700.
Пример 3. Округлить число 9876 до разряда десятков.
Здесь сохраняемая цифра это 7. А первая отбрасываемая цифра это 6. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 7, а всё что располагается после неё заменяем нулём:
9876 ≈ 9880
Пример 4. Округлить число 9876 до разряда сотен.
Здесь сохраняемая цифра это 8. А первая отбрасываемая цифра это 7. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 8, а всё что располагается после неё заменяем нулями:
9876 ≈ 9900
Пример 5. Округлить число 9876 до разряда тысяч.
Здесь сохраняемая цифра это 9. А первая отбрасываемая цифра это 8. Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит увеличиваем на единицу сохраняемую цифру 9, а всё что располагается после неё заменяем нулями:
9876 ≈ 10000
Пример 6. Округлить число 2971 до сотен.
При округлении этого числа до сотен следует быть внимательным, поскольку сохраняемая цифра здесь 9, а первая отбрасываемая цифра это 7. Значит цифра 9 должна увеличиться на единицу. Но дело в том, что после увеличения девятки на единицу получится 10, а это цифра не вместится в разряд сотен нового числа.
В этом случае, в разряде сотен нового числа надо записать 0, а единицу перенести на следующий разряд и сложить с цифрой, которая там находится. Далее заменить все цифры после сохраняемой нулями:
2971 ≈ 3000
Округление десятичных дробей
При округлении десятичных дробей следует быть особенно внимательным, поскольку десятичная дробь состоит из целой и дробной части. И каждая из этих двух частей имеет свои разряды:
Разряды целой части:
- разряд единиц;
- разряд десятков;
- разряд сотен;
- разряд тысяч.
Разряды дробной части:
- разряд десятых;
- разряд сотых;
- разряд тысячных
Рассмотрим десятичную дробь 123,456 — сто двадцать три целых четыреста пятьдесят шесть тысячных. Здесь целая часть это 123, а дробная часть 456. При этом у каждой из этих частей есть свои разряды. Очень важно не путать их:
Для целой части применяются те же правила округления, что и для обычных чисел. Отличие в том, что после округления целой части и замены нулями всех цифр после сохраняемой цифры, дробная часть полностью отбрасывается.
Например, округлим дробь 123,456 до разряда десятков. Именно до разряда десятков, а не разряда десятых. Очень важно не перепутать эти разряды. Разряд десятков располагается в целой части, а разряд десятых в дробной.
Итак, мы должны округлить 123,456 до разряда десятков. Сохраняемая цифра здесь это 2, а первая из отбрасываемых цифр это 3
Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. А что делать с дробной частью? Её просто отбрасывают (убирают):
123,456 ≈ 120
Теперь попробуем округлить ту же самую дробь 123,456 до разряда единиц. Сохраняемая цифра здесь будет 3, а первая из отбрасываемых цифр это 4, которая находится в дробной части:
Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.
Значит сохраняемая цифра останется без изменений, а всё остальное заменится нулём. Оставшаяся дробная часть будет отброшена:
123,456 ≈ 123,0
Ноль, который остался после запятой тоже можно отбросить. Значит окончательный ответ будет выглядеть следующим образом:
123,456 ≈ 123,0 ≈ 123
Теперь займёмся округлением дробных частей. Для округления дробных частей справедливы те же правила, что и для округления целых частей. Попробуем округлить дробь 123,456 до разряда десятых. В разряде десятых располагается цифра 4, значит она является сохраняемой цифрой, а первая отбрасываемая цифра это 5, которая находится в разряде сотых:
Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит сохраняемая цифра 4 увеличится на единицу, а остальная часть заменится нулями
123,456 ≈ 123,500
Попробуем округлить ту же самую дробь 123,456 до разряда сотых. Сохраняемая цифра здесь это 5, а первая из отбрасываемых цифр это 6, которая находится в разряде тысячных:
Согласно правилу, если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.
Значит сохраняемая цифра 5 увеличится на единицу, а остальная часть заменится нулями
123,456 ≈ 123,460
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже

Приближенное вычисление десятичных дробей
Десятичную дробь можно рассматривать как частное от деления двух натуральных чисел. Десятичные дроби в частном и процессе деления натуральных чисел получаются, если делимое меньше делителя или не кратно ему.
При делении двух натуральных чисел дробь будет конечной, если делимое кратно делителю, и бесконечной (периодической или непериодической), если делимое не кратно делителю.
Определение. Конечной десятичной дробью называется такая дробь, у которой при делении в каком-то из разрядов поэтапного деления остаток отсутствует. Такое деление возможно, если делимое кратно делителю.
Делимое кратно делителю, если при разложении на множители в его составе как множитель присутствует делитель.
Например:
3 : 15 = 0,2
Т. к. 3 * 10 = 30; 30 = 2 * 15, следовательно, делитель 15 присутствует как множитель в числе 30.
446,5 : 19 = 23,5
Т. к. 4 465 = 19 * 235, следовательно, делитель 19 присутствует как множитель в числе 446,5
Определение. Бесконечной десятичной дробью называется дробь с неограниченным числом знаков после занятой (в каждом поэтапном частном получается остаток). Такое деление можно продолжать до бесконечности, так как результат не является конечной десятичной дробью.
Бесконечная десятичная дробь получается, например, если делимое 1 или разрядная единица, а в делителе есть множители 3 или 7.
1 : 3 = 0,333333…
1 : 21 = 0,047619… (21 = 3 * 7)
1 000 : 224 = 4,4642… (224 = 7 * 32)
1 : 56 = 0,017857142… (56 = 7 * 8)
Бесконечные десятичные дроби могут иметь в определенной закономерности повторяющиеся цифры в дробной части при делении. Это может быть одна цифра или группа цифр, которые или стоят сразу после запятой, или через несколько цифр после запятой начинается повторение цифры или группы цифр.
Определение. Повторяющиеся цифры в дробной части бесконечной десятичной дроби образуют период десятичной дроби. Период в частном помещают в скобки и запись бесконечной дроби ограничивают одним периодом.
Например:
1:3 = 1,3333… можно записать как бесконечную десятичную дробь с периодом 3: 1,33333… = 1,(3)
172,3 : 3 = 57,43333… можно записать как бесконечную десятичную дробь с периодом 3: 172,3:3 = 57,4 (3)
Чтобы убедиться, что дробь периодическая, достаточно получить в частном два-три периода дроби.
Определение. Приближенное вычисление десятичных дробей состоит в том, что полученный результат округляют до определенного разряда. Для этого вычисляется одни «лишний» разряд, а затем проводится округление по обычным правилам.
Если «лишний» разряд содержит цифры 0, 1, 2, 3, 4, то разряд, до которого округляют, не изменяют, а «лишний» разряд отбрасывают; если «лишний» разряд содержит цифры 5, 6, 7, 8, 9, то его отбрасывают, а разряд, до которого округляют, увеличивают на 1.
Например, если частное равно дроби 1,23 (75), то мы можем при округлении до сотых взять число 1,23, отбросив период. Тогда в частном мы приблизились к точному ответу с недостатком (отбросили период, что составит 0,008). Если мы запишем в ответе число сотых с учетом периода и округлим до сотых, то в ответе получим 1,24 (получили приближенный ответ с избытком).