Алгебра
7 класс
Урок № 10
Приближения числа
Перечень вопросов, рассматриваемых в теме:
- Приближённое значение числа.
- Приближение с недостатком, приближение с избытком.
- Округление действительных чисел.
- Арифметические действия с приближёнными значениями действительных чисел.
Тезаурус:
- Если a < x < b, то a называют приближённым значением числа x с недостатком, b приближённым значением с избытком.
- Приближение по недостатку и приближение по избытку называют округлением числа.
- Округлить число с точностью до какого-то разряда – это значит, округлить число до того разряда, где находится значащая цифра, заменив следующие цифры нулями.
- При округлении числа до какого-нибудь разряда цифры во всех следующих разрядах заменяют нулями, а стоящие после запятой ‑ отбрасывают.
- Если следующая за разрядом, до которого округляем, цифра равна 5, 6, 7, 8, 9, то остающийся разряд увеличивают на 1. Если цифра равна 0, 1, 2, 3 или 4, то остающийся разряд оставляют без изменения.
Основная литература:
1. Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
1. Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
2. Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
3. Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
При решении практических задач иногда невозможно указать точный результат. Если число a1 мало отличается от числа a, то пишут: a ≈ a1.
Говорят, что число a приближённо равно числу a1 или a1 –это приближение числа a.
Если a1 < a, то a1 называют приближением с недостатком.
Если a1 > a, то a1 называют приближением с избытком.
Действительные числа, задаваемые бесконечными десятичными дробями, заменяют конечными десятичными дробями.
Пример: пусть a = 2,3(28) или a = 2,32828… Отбросим все цифры, начиная со второй после запятой, получим 2,32. Увеличим дробь на 0,01, получим 2,33. Число a находится между ними: 2,32 < a < 2,33
Таким образом, a ≈ 2,32 или a ≈ 2,33.
2,32 – приближение числа с недостатком;
2,33 – приближение числа с избытком, с точностью до 0,01.
Более точное приближение числа a получим при приближении с точностью до 0,001. Тогда, 2,328 < a < 2,329
Если число отрицательное:
пусть b = –2,3(28) = -2,32828…, отбросим все цифры, начиная со второй после запятой, тогда –2,33 < b < -2,32.
-2,33 – приближение числа с недостатком;
-2,32 – приближение числа с избытком, с точностью до 0,01 или до единицы второго разряда.
Значащей цифрой десятичной дроби называют её первую (слева направо), отличную от нуля, цифру, а также все следующие за ней цифры. В числе 235000 все цифры значащие, в числе 0,302 значащие – три цифры после запятой.
Значащими цифрами являются:
– все ненулевые цифры;
– нули, содержащиеся между ненулевыми цифрами;
– нули, являющиеся представителями сохраненных десятичных разрядов при округлении.
Округление.
Округлить число с точностью до значащей цифры – это значит, округлить число до того разряда, где находится значащая цифра, заменив следующие цифры нулями.
Пример: 3,7523… округлите с точностью до 0,01.
3,75|23 ≈ 3,7500 ≈ 3,75.
Незначащие цифры, нули, нужно отбросить. При этом помним правило округления:
Если правее разряда, до которого округляем, стоит цифра 5, 6, 7, 8, 9, то цифру в разряде увеличиваем на 1.
Если правее разряда, до которого округляем, стоит цифра 0, 1, 2, 3, 4, то цифру в разряде не изменяем.
Разбор решения заданий тренировочного модуля
Задача 1.
Пусть: а = 23,1834567 и b = -4,2375.
Найдите сумму и разность с точностью до одной сотой.
Решение:
Чтобы вычислить приближённую сумму, разность двух чисел, надо округлить эти числа с одинаковой точностью, затем выполнить сложение или вычитание.
Решение: округляем до 0,01.
а =23,18|34567 ≈ 23,18 и b = -4,23|75 ≈ -4,24.
Находим:
а + b ≈ 23,18 + (-4,24) = 18,94.
а – b ≈ 23,18 – (-4,24) = 23,18 + 4,24 = 27,42..
Ответ: 18,94; 27,42.
Задача 2.
Пусть: а = 135,78665 и b = 0,0068751. Найдите произведение и частное чисел, округлите результат до третьей значащей цифры.
Решение.
Чтобы вычислить приближённо произведение, частное двух чисел, надо округлить эти числа с одинаковой точностью, затем выполнить умножение или деление, затем округлить результат до той же значащей цифры.
Округляем до третьей значащей цифры, получим:
а ≈ 136 и b ≈ 0,00688.
Находим:
а · b ≈ 136 · 0,00688 = 0,93568 ≈ 0,936.
а : b ≈ 136 : 0,00688 = 197|67,4 ≈ 19800.
Ответ: 0,936; 19800.
В математике используют приближённые значения действительных чисел для графического решения уравнений и для выполнения практических вычислений с действительными числами.
Действительные числа — бесконечные десятичные дроби.
Пример:
найди площадь круга с радиусом (2) см.
Решение:
найдём площадь круга по формуле S=πR2=4⋅3,14159265359…=12,5663706144….
В ответ мы можем написать приближённое значение:
1) S≈ (12,56) — приближённое значение этого числа с недостатком с точностью до сотых,
или
2) S≈(12,57) — приближённое значение этого числа с избытком с точностью до сотых.
Таким образом, используют округление с недостатком и округление с избытком.
Абсолютная погрешность приближения показывает точность приближённого значения и находится по формуле (h=) x−a, где (x) — точное значение величины, (a) — её приближённое значение.
Погрешность приближённого равенства
S≈
(12,56) или
S≈
(12,57) выражается как
S−12,56
или соответственно как
S−12,57
.
Правило округления.
Если первая отбрасываемая цифра меньше (5), то нужно брать приближение с недостатком; если первая отбрасываемая цифра больше или равна (5), то нужно брать приближение с избытком.
(S=12,5663706144…) С точностью до (0,01) имеем
S≈
(12,57); выбрали приближение с избытком, т. к. на третьем месте после запятой стоит цифра (6) — её и отбросим.
Пример:
при точности до (0,0001) получим S≈(12,5664) — тоже выбрали приближение с избытком, т. к. на пятом месте после запятой стоит цифра (7) (мы её отбрасываем).
При точности до (0,001) нужно выбрать приближение с недостатком: S≈(12,566).
Если (a) — приближённое значение числа (x) и x−a≤h, то говорят, что абсолютная погрешность приближения не превосходит (h) или что число (x) равно числу (a) с точностью до (h).
☰
Приближение по недостатку и по избытку
Проводя различные измерения, решая уравнения графическим способом, выполняя арифметические вычисления, часто получают приближенные значения, а не точные. Например, при вычислении корня числа может получиться бесконечная непериодическая дробь (т. е. иррациональное число). Кроме того, существуют бесконечные периодические дроби, использовать которые в вычислениях также неудобно.
Поэтому числа, являющиеся бесконечными десятичными дробями или конечными, но имеющими множество знаков после запятой, принято округлять.
Когда округление выполняется в большую сторону, то говорят о приближении по избытку. Когда округление выполняется в меньшую сторону, то говорят о приближении по недостатку.
Полученное при округлении число называют приближенным по недостатку или избытку с определенной точностью. Рассмотрим несколько примеров приближения.
Число π является бесконечной дробью 3,1415926535… Обычно его округляют с точностью до 0,01. Это значит, что после запятой оставляют только два знака. При приближении по избытку получится 3,15. При приближении по недостатку получится 3,14.
Для числа π обычно используют приближение по недостатку, так как согласно правилу округления положительные числа округляются в большую сторону, если первая отбрасываемая цифра 5 или больше пяти. Так как у числа π третья цифра после запятой — это 1, то округление выполняется в меньшую сторону, то есть для расчетов выполняется приближение по недостатку.
Однако, несмотря на правила округления, имеют право быть приближения как по недостатку, так и по избытку.
Если выполнять приближение числа π с точностью до 0,0001, то по избытку получим π ≈ 3,1416, а по недостатку π ≈ 3,1415.
Рассмотрим иррациональное число √2, которое равно 1,414213… . Вычислим его приближение по недостатку и по избытку с точностью до 0,001. Поскольку приближение выполняется до тысячных долей, то у числа надо оставить три знака после запятой. При приближении по недостатку просто отбрасываются все цифры после третьей после запятой. При приближении по избытку цифры после третьей после запятой отбрасываются, а третья цифра увеличивается на 1. Таким образом, приближение по недостатку будет √2 ≈ 1,414, а по избытку √2 ≈ 1,415.
Но примеры, рассмотренные выше, это положительные числа. А так ли обстоит дело при приближении отрицательных чисел. Если взять число –√2 = –1,414213…, то его приближением по избытку до тысячных долей будет –1,414, так как это число больше, чем –√2. А вот приближением по недостатку будет –1,415, так как это число меньше, чем –√2.
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Приближенные значения действительных чисел
Приближенные значения действительных чисел
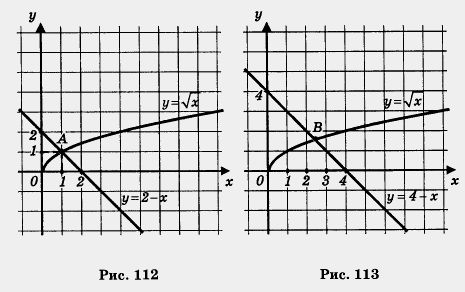
И в 7-м и в 8-м классе мы часто решали уравнения графически. Заметили ли вы, что практически во всех таких примерах уравнения имели «хорошие» корни? Это были целые числа, которые без труда отыскивались с помощью графиков, особенно на клетчатой бумаге. Но так бывает далеко не всегда, просто мы до сих пор подбирали «хорошие» примеры.
Рассмотрим два уравнения: = 2 – х и
= 4 – х. Первое уравнение имеет единственный корень х = 1, поскольку графики функций у =
и у = 2 – х пересекаются в одной точке А (1; 1) (рис. 112). Во втором случае графики функций
— фс и у = 4 – х также пересекаются в одной точке В (рис. 113), но с «плохими» координатами. Пользуясь чертежом, можно сделать вывод, что абсцисса точки В примерно равна 2,5. В подобных случаях говорят не о точном, а о приближенном решении уравнения и пишут так:
Это одна из причин, по которым математики решили ввести понятие приближенного значения действительного числа. Есть и вторая причина, причем, может быть, даже более важная.Что такое действительное число? Это бесконечная десятичная дробь. Но производить вычисления с бесконечными десятичными дробями неудобно, поэтому на практике пользуются приближенными значениями действительных чисел. Например, для числа пользуются приближенным равенством
3,141 или
3,142. Первое называют приближенным значением (или приближением) числа п по недостатку с точностью до 0,001; второе называют приближенным значением (приближением) числа к по избытку с точностью до 0,001. Можно взять более точные приближения: например,
3,1415 — приближение по недостатку с точностью до 0,0001;
3,1416 — приближение по избытку с точностью до 0,0001. Можно взять менее точные приближения, скажем, с точностью до 0,01: по недостатку
3,14, по избытку
3,15.
Знак приближенного равенства » вы использовали и в курсе математики 5—6-го классов и, вероятно, в курсе физики, да и мы пользовались им раньше, например в § 27.
Пример 1. Найти приближенные значения по недостатку и по избытку с точностью до 0,01 для чисел:
Решение,
а) Мы знаем, что = 2,236… (см. § 27), следовательно,
2,23 — это приближение по недостатку с точностью до 0,01;
2,24 — это приближение по избытку с точностью до 0,01.
б) 2 + = 2,000… + 2,236… = 4,236… . Значит, 2 +
4,23 — это приближение по недостатку с точностью до 0,01; 2 +
4,24 — это приближение по избытку с точностью до 0,01.
в) Имеем
0,31818… (см. § 26). Таким образом,
0,31 — это приближение по недостатку с точностью до 0,01;
0,32 — это приближение по избытку с точностью до 0,01.
Приближение по недостатку и приближение по избытку называют иногда округлением натуральные числа.
Определение.Погрешностью приближения (абсолютной погрешностью) называют модуль разности между точным значением величины х и ее приближенным значением а: погрешность приближения — это | х – а |.
Например, погрешность приближенного равенства выражается как
или соответственно как
,
Возникает чисто практический вопрос: какое приближение лучше, по недостатку или по избытку, т. е. в каком случае погрешность меньше? Это, конечно, зависит от конкретного числа, для которого составляются приближения. Обычно при округлении положительных чисел пользуются следующим правилом:
Применим это правило ко всем рассмотренным в этом параграфе числам; выберем для рассмотренных чисел те приближения, для которых погрешность окажется наименьшей.
1) = 3,141592… . С точностью до 0,001 имеем
3,142; здесь первая отбрасываемая цифра равна 5 (на четвертом месте после запятой), поэтому взяли приближение по избытку.
С точностью до 0,0001 имеем 3,1416 — и здесь взяли приближение по избытку, поскольку первая отбрасываемая цифра (на пятом месте после запятой) равна 9. А вот с точностью до 0,01 надо взять приближение по недостатку:
3,14.
2) = 2,236… . С точностью до 0,01 имеем
2,24 (приближение по избытку).
3) 2 + = 4,236… . С точностью до 0,01 имеем 2 +
4,24 (приближение по избытку).
4) = 0,31818… . С точностью до 0,001 имеем
0,318 (приближение по недостатку).
Рассмотрим последний пример подробнее. Возьмем укрупненный фрагмент координатной прямой (рис. 114).
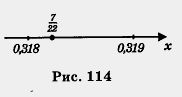
Точка принадлежит отрезку [0,318, 0,319], значит, ее расстояния от концов отрезка не превосходят длины отрезка. Расстояния точки
от концов отрезка равны соответственно
отрезка [0,318, 0,319] равна 0,001. Значит,
и
Итак, в обоих случаях (и для приближения числа по недостатку, и для приближения его по избытку) погрешность не превосходит 0,001.
До сих пор мы говорили: приближения с точностью до 0,01, до 0,001 и т. д. Теперь мы можем навести порядок в использовании терминологии.
Если а — приближенное значение числа х и , тo говорят, что погрешность приближения не превосходит h или что число х равно числу а с точностью до h.
Почему же важно уметь находить приближенные значения чисел? Дело в том, что практически невозможно оперировать с бесконечными десятичными дробями и использовать их для измерения величин. На практике во многих случаях вместо точных значений берут приближения с заранее заданной точностью (погрешностью). Эта идея заложена и в калькуляторах, на дисплеях которых высвечивается конечная десятичная дробь, т. е. приближение выводимого на экран числа (за редким исключением, когда выводимое число представляет собой конечную десятичную дробь, умещающуюся на экране).
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Сборник конспектов уроков по математике скачать, календарно-тематическое планирование, учебники по всем предметам онлайн
Содержание урокаконспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний – Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.
Разработка – Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
Округление чисел
- Правила округления
Числа, с которыми нам приходится иметь дело в реальной жизни, бывают двух типов. Одни в точности передают истинную величину, другие — только приблизительную. Первые называют точными, вторые — приближёнными.
В реальной жизни чаще всего пользуются приближёнными числами вместо точных, так как последние обычно не требуются. Например, приближённые значения используются при указании таких величин как длина или вес. Во многих же случаях точное число найти невозможно.
Правила округления
Для получения приближённого значения, полученное в результате каких-либо действий число нужно округлить, то есть заменить его ближайшим круглым
числом.
Числа всегда округляют до определённого разряда. Натуральные числа округляются до десятков, сотен, тысяч и т. д. При округлении чисел до десятков, их заменяют круглыми
числами, состоящими только из целых десятков, у таких чисел в разряде единиц стоят нули. При округлении до сотен, числа заменяются на более круглые
, состоящие только из целых сотен, то есть нули стоят уже и в разряде единиц, и в разряде десятков. И так далее.
Десятичные дроби можно округлять так же как и натуральные числа, то есть до десятков, сотен и т. д. Но также их можно округлять и до десятых, сотых, тысячных частей и т. д. При округлении десятичных знаков разряды не заполняются нулями, а просто отбрасываются. В обоих случаях округление производится по определённому правилу:
Если отбрасываемая цифра больше или равна 5, то предыдущую нужно увеличить на единицу, а если меньше 5, то предыдущая цифра не меняется.
Рассмотрим несколько примеров округления чисел:
- Округлить 43152 до тысяч. Здесь надо отбросить 152 единицы, так как справа от разряда тысяч стоит цифра 1, то предыдущую цифру отставляем без изменений. Приближённое значение числа 43152, округлённое до тысяч будет равно 43000.
- Округлить 43152 до сотен. Первая из отбрасываемых чисел 5, значит предыдущую цифру увеличиваем на единицу:
43152 ≈ 43200.
- Округлить 43152 до десятков:
43152 ≈ 43150.
- Округлить 17,7438 до единиц:
17,7438 ≈ 18.
- Округлить 17,7438 до десятых:
17,7438 ≈ 17,7.
- Округлить 17,7438 до сотых:
17,7438 ≈ 17,74.
- Округлить 17,7438 до тысячных:
17,7438 ≈ 17,744.
Знак ≈
называют знаком приближённого равенства, он читается — приближённо равно
.
Если при округлении числа результат получился больше начального значения, то полученное значение называется приближённым значением с избытком, если меньше — приближённым значением с недостатком:
7928 ≈ 8000,
число 8000 — приближённое значением с избытком,
5102 ≈ 5000,
число 5000 — приближённое значением с недостатком.