Как найти приближенное значение функции калькулятор - Сайт, где вы сможете решить свои вопросы

Данный онлайн калькулятор находит корень уравнения приближённо. В основе алгоритма его работы лежит метод Ньютона. Чтобы начать работу, необходимо ввести исходные данные своей задачи.

Метод Ньютона является численным, т.е. корень уравнения находится приближенно. При этом можно заранее задать точность его нахождения.

Пусть нам дано уравнение

Формула для поиска корня уравнения выглядит следующим образом:

и

– приближённые значения корня уравнения

на
-ой и
()-ой итерациях соответственно,

– значение функции

в точке
,

– значение производной функции

в точке
.

Как видно, для того чтобы начать работу необходимо задать точку

– начальное приближение для корня уравнения
. От выбора точки

зависит сойдётся ли алгоритм к решению или нет. Сходимость метода квадратичная, но она резко ухудшается если мы ищем кратный корень уравнения, т.е. если

и одновременно
, где

– кратный корень уравнения
.

Вычисления по приведённой выше формуле можно продолжать до бесконечности, соответственно на практике необходим некоторый критерий, который будет определять нужно ли нам продолжать вычисления или нет. Как правило, используется критерий останова вычислений на основе приращения или же на основе близости функции

к нулю в некоторой точке
.

Критерий останова вычислений на основе приращения задаётся следующей формулой:

т.е. различие (по модулю) между двумя последовательными приближениями к корню уравнения (

и

) должны быть меньше, некоторой наперёд заданной величины
.

Критерий останова вычислений на основе близости функции к нулю определяется следующей формулой:

т.е. отличие (по модулю) между функцией

в некоторой точке

и нулём меньше
.

В тоже время, если последовательность

к корню не сходится, то критерии останова не сработают и процесс поиска корня будет продолжаться бесконечно. Чтобы предотвратить такую ситуацию, на практике вычисления прекращают после некоторого, заданного количества итераций.

На рисунке ниже приведена геометрическая интерпретация процесса поиска корня уравнения

методом Ньютона.

В точке

мы строим
касательную к графику функции
. Уравнение касательной в этой точке имеет вид:

Находим точку пересечения полученной касательной с осью абсцисс, т.е. рассматриваем точку с координатами
. Подставляя координаты указанной точки в уравнение касательной, получаем следующее соотношение:

Из данного уравнения находим
:

Продолжая данный процесс, получим формулу метода Ньютона, приведенную выше. Из-за того, что на каждой итерации фактически происходит построение касательной, метод Ньютона также иногда называют методом касательных.

Источник

Описание метода вычисления значения производной можно найти под калькулятором.

Вычисление производной по ее определению

Начальное приращение аргумента

Параметр изменения приращения

Точность вычисления

Знаков после запятой: 4

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Вычисление производной по ее определению

Задача численного дифференцирования возникает когда функция задана таблично, или когда прямое дифференцирование затруднено (например, при сложном аналитическом виде функции). Если функция задана аналитически, то можно применить вычисление значения производной по ее определению.

В этом случае у нас есть некоторая функция y=f(x) , для которой нам надо вычислить значение производной в точке x₀. Мы предполагаем, что эта функция определена в окрестности точки x₀ и имеет производную в этой точке. Исходя из определения производной
$y'(x_0) = f'(x_0)=lim_{Delta x rightarrow 0} frac{Delta y}{Delta x}$
существует предел отношения приращения функции Δy к приращению аргумента Δx при Δx→0, где
$Delta x = x - x_0 \ Delta y = f(x_0 + Delta x) - f(x_0)$

Значение производной можно получить переходя к пределу со все более уменьшающимся шагом, пока не будет достигнута требуемая точность. Для этого на каждом шаге последовательности n приращение аргумента вычисляется по следующей формуле
$Delta x = Delta x_n = frac {Delta x_0}{a^n}$ ,
где
Δx₀ – начальное приращение аргумента, например, 0.1
a – некоторое число, большее 1, например, 10
n = 0, 1, …

Тогда
$y'(x_0) approx frac{Delta y_n}{Delta x_n}$

Последовательность останавливается при выполнении следующего условия
$frac{Delta y_n}{Delta x_n} - frac{Delta y_{n-1}}{Delta x_{n-1}} le epsilon$

Источник

Вычисление значений функции

Онлайн калькулятор поможет найти значения функции в заданном интервале, построить таблицу значений функции онлайн, табулировать функцию.
Вычисляет значения функции одной переменной y для заданных значений переменной x. Функция задается при помощи формулы, пример:
Построить таблицу значений функции f(x)=x/(x+1) на отрезке от 0 до 6 с шагом в единицу.

Синтаксис
основных функций:
x^a: x^a
|x|: abs(x)
√x: Sqrt[x]
ⁿ√x: x^(1/n)
a^x: a^x
log^ax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]

sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]

arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]

areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo

Пожалуйста напишите с чем связна такая низкая оценка:

Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Источник

bold{mathrm{Basic}}

bold{alphabetagamma}

bold{mathrm{ABGamma}}

bold{sincos}

bold{gedivrightarrow}

bold{overline{x}spacemathbb{C}forall}

bold{sumspaceintspaceproduct}

bold{begin{pmatrix}square&square\square&squareend{pmatrix}}

bold{H_{2}O}

square^{2}

x^{square}

sqrt{square}

nthroot[msquare]{square}

frac{msquare}{msquare}

log_{msquare}

theta

infty

int

frac{d}{dx}

ge	le	cdot	div	x^{circ}	(square)	\|square\|	(f:circ:g)	f(x)	ln	e^{square}
left(squareright)^{‘}	frac{partial}{partial x}	int_{msquare}^{msquare}	lim	sum	sin	cos	tan	cot	csc	sec

alpha	beta	gamma	delta	zeta	eta	theta	iota	kappa	lambda	mu
nu	xi	pi	rho	sigma	tau	upsilon	phi	chi	psi	omega

A	B	Gamma	Delta	E	Z	H	Theta	K	Lambda	M
N	Xi	Pi	P	Sigma	T	Upsilon	Phi	X	Psi	Omega

sin	cos	tan	cot	sec	csc	sinh	cosh	tanh	coth	sech
arcsin	arccos	arctan	arccot	arcsec	arccsc	arcsinh	arccosh	arctanh	arccoth	arcsech

begin{cases}square\squareend{cases}	begin{cases}square\square\squareend{cases}	=	ne	div	cdot	times	<	>	le	ge
(square)	[square]	▭:longdivision{▭}	times twostack{▭}{▭}	+ twostack{▭}{▭}	– twostack{▭}{▭}	square!	x^{circ}	rightarrow	lfloorsquarerfloor	lceilsquarerceil

overline{square}	vec{square}	in	forall	notin	exist	mathbb{R}	mathbb{C}	mathbb{N}	mathbb{Z}	emptyset
vee	wedge	neg	oplus	cap	cup	square^{c}	subset	subsete	superset	supersete

int	intint	intintint	int_{square}^{square}	int_{square}^{square}int_{square}^{square}	int_{square}^{square}int_{square}^{square}int_{square}^{square}	sum	prod
lim	lim _{xto infty }	lim _{xto 0+}	lim _{xto 0-}	frac{d}{dx}	frac{d^2}{dx^2}	left(squareright)^{‘}	left(squareright)^{”}	frac{partial}{partial x}

(2times2)	(2times3)	(3times3)	(3times2)	(4times2)	(4times3)	(4times4)	(3times4)	(2times4)	(5times5)
(1times2)	(1times3)	(1times4)	(1times5)	(1times6)	(2times1)	(3times1)	(4times1)	(5times1)	(6times1)	(7times1)

mathrm{Радианы}	mathrm{Степени}	square!	(	)	%	mathrm{очистить}
arcsin	sin	sqrt{square}	7	8	9	div
arccos	cos	ln	4	5	6	times
arctan	tan	log	1	2	3	–
pi	e	x^{square}	0	.	bold{=}	+

Подпишитесь, чтобы подтвердить свой ответ

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

y=frac{x^2+x+1}{x}
f(x)=x^3
f(x)=ln (x-5)
f(x)=frac{1}{x^2}
y=frac{x}{x^2-6x+8}
f(x)=sqrt{x+3}
f(x)=cos(2x+5)
f(x)=sin(3x)
Показать больше

Описание

Изучите функции шаг за шагом

functions-calculator

Блог-сообщения, имеющие отношение к Symbolab

Functions

A function basically relates an input to an output, there’s an input, a relationship and an output. For every input…

Введите Задачу

Сохранить в блокнот!

Войти

Источник

Инструкции:

Используйте этот калькулятор для вычисления линейного приближения для заданной функции в указанной вами точке, показывая все шаги. Пожалуйста, введите функцию и точку в поле формы ниже.

Калькулятор линейной аппроксимации

Этот

калькулятор линеаризации

позволит вычислить линейное приближение, также известное как

Касательная линия

для любой данной действительной функции в данной действительной точке.

Вам необходимо указать допустимую функцию, например, f(x) = x*sin(x) или f(x) = x^2 – 2x + 1, или любую допустимую функцию, которая является дифференцируемой, и точку (x_0) где функция корректно определена. Эта точка может быть любым допустимым числовым выражением, например, 1/3.

Как только вы укажете действительную функцию и точку, вы нажмете “Рассчитать”, и все расчеты будут показаны для вас.

Линейное приближение или приближение первого порядка ищет приближение данной функции линией в заданной точке (x_0). Естественно, для кривых линейная аппроксимация будет грубой, хотя основная идея заключается в том, что аппроксимация будет точной для точек, близких к (x_0).

Линейное приближение

Идея состоит в том, чтобы найти прямую, проходящую через точку ((x_0, f(x_0))) и "едва касающуюся" функции (f(x)). Формальное математическое определение “едва касаясь” дается идеей

Касательная линия

для чего нам необходимо

вычислить производную

функции.

На самом деле формула для линейной аппроксимации в точке (x_0) зависит от производной (f'(x_0)) следующим образом

[displaystyle y = f(x_0) + f'(x_0) (x – x_0) ]

Этот

формула линейной аппроксимации

по существу определяет

уравнение линии

которая проходит через точку ((x_0, f(x_0))), поэтому и называется "линейной аппроксимацией", так как определяет линейную функцию, совпадающую с (f(x)) в точке (x_0) и очень близкую к (f(x)) для значений (x), близкие к (x_0).

Шаги для нахождения линейной аппроксимации

Шаг 1:

У вас должна быть заданная функция f(x) и точка x0. Функция должна быть дифференцируемой в точке x0
Шаг 2:

Вычислите f(x0) и f'(x0), которые являются функцией и производной функции f в точке x0
Шаг 3:

Определим линейное приближение как y = f(x_0) + f'(x_0) (x – x_0), которое представляет собой формулу линеаризации, представленную выше.

Эта линия (y = f(x_0) + f'(x_0) (x – x_0)) представляет приближение первого порядка, также известное как локальное линейное приближение.

Связь с касательной линией

Как вы уже, наверное, догадались, линейное приближение – это то же самое, что и

Касательная линия

в данной точке. Тогда вычисление линейной аппроксимации точно такое же, как и вычисление касательной линии

Другое название того же – приближение первого порядка или приближение касательной линии, которые также часто используются в исчислении.

Дифференциальная и линейная аппроксимация

Другое распространенное понятие — понятие дифференциала, которое тесно связано с понятием линейного приближения и является просто его производным. Действительно, дифференциал (или конечная разность) определяется как (Delta y = y – f(x_0)). Тогда, основываясь на формуле первого приближения, формула для дифференциала имеет вид

[displaystyle Delta y = y – f(x_0) = f'(x_0) (x – x_0) = f'(x_0) Delta x ]

Естественно, это выглядит точно так же, как формула линейной аппроксимации, за исключением того, что член (f(x_0) передается слева.

Пример: вычисление аппроксимации первого порядка.

Рассмотрим следующее: (f(x) = x^2 – 2x + 3), найти его приближение первого порядка в (x_0 = 1).

Отвечать:

Предоставленная функция — (displaystyle f(x)=x^2-2x+3), и нам нужно найти линейное приближение вокруг точки x = 1. Итак, сначала нам нужна производная.

( displaystyle frac{d}{dx}left(x^2-2x+3right))

By linearity: (frac{d}{dx}left( x^2-2x+3 right) = frac{d}{dx}left(x^2right)-frac{d}{dx}left(2xright)+frac{d}{dx}left(3right)), so plugging that in:

( displaystyle = ,,)

(displaystyle frac{d}{dx}left(x^2right)-frac{d}{dx}left(2xright)+frac{d}{dx}left(3right))

The derivative of a constant is 0, so then:

( displaystyle = ,,)

(displaystyle frac{d}{dx}left(x^2right)-frac{d}{dx}left(2xright))

Directly: (frac{d}{dx}left( 2x right) = 2) and using the Power Rule for polynomial terms: (frac{d}{dx}left( x^2 right) = 2x)

( displaystyle = ,,)

(displaystyle 2x-2)

Линейное Приближение

: Уравнение для линейного приближения, которое мы ищем в точке (x_0 = 2), задается следующей формулой

[y = y_0 + f'(x_0)(x – x_0) ]

Обратите внимание, что по определению (displaystyle y_0 = f(x_0)), которое подразумевает, что нам нужно подключить функцию в точке (x_0 = 2):

[y_0 = f(x_0) = fleft(2right) = 2^2-2cdot 2+3 = 3]

Делаем то же самое, но теперь для производной в точке (x_0 = 2), так что тогда

[f'(x_0) = f’left(2right) = 2cdot 2-2 = 2 ]

Теперь с этим мы возвращаемся к формуле линейной аппроксимации:

[y = y_0 + f'(x_0)(x – x_0) ][Rightarrow y = 3+2left(x-2right) = 2x-1 ]

Заключение

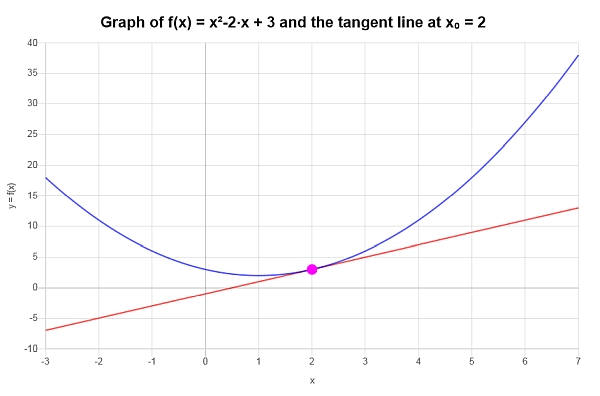
: Мы заключаем, что линейная аппроксимация для (displaystyle f(x)=x^2-2x+3) в точке (x_0 = 2) определяется следующим образом:

[y = 2x-1 ]

Графически:

Пример: больше аппроксимации первого порядка

Для функции : (f(x) = x sin(x)) и точки (x_0 = 2) найдите соответствующее приближение первого порядка.

Отвечать:

В этом случае функция, которая нам нужна для работы: (displaystyle f(x)=xsinleft(xright)).

Теперь вычислим его производную:

( displaystyle frac{d}{dx}left(xsinleft(xright)right))

Using the Product Rule: (frac{d}{dx}left( xsinleft(xright) right) = frac{d}{dx}left(xright) cdot sinleft(xright)+x cdot frac{d}{dx}left(sinleft(xright)right))

( displaystyle = ,,)

(displaystyle frac{d}{dx}left(xright) cdot sinleft(xright)+x cdot frac{d}{dx}left(sinleft(xright)right))

Directly differentiating: (frac{d}{dx}left( sinleft(xright) right) = cosleft(xright))

( displaystyle = ,,)

(displaystyle frac{d}{dx}left(xright) cdot sinleft(xright)+x cdot cosleft(xright))

( displaystyle = ,,)

(displaystyle xcosleft(xright)+sinleft(xright))

Линейное Приближение

: Уравнение линейной аппроксимации имеет вид:

[y = y_0 + f'(x_0)(x – x_0) ]

где (displaystyle y_0 = f(x_0)), то мы вычисляем:

[y_0 = f(x_0) = fleft(2right) = 2sinleft(2right)]

Для производной в (x_0 = 2) мы находим, что:

[f'(x_0) = f’left(2right) = 2cosleft(2right)+sinleft(2right) ]

Теперь мы готовы подставить их обратно в формулу аппроксимации первого порядка:

[y = y_0 + f'(x_0)(x – x_0) ][Rightarrow y = 2sinleft(2right)+2cosleft(2right)+sinleft(2right)left(x-2right)
= 2xcosleft(2right)+xsinleft(2right)-4cosleft(2right) ]

Заключение

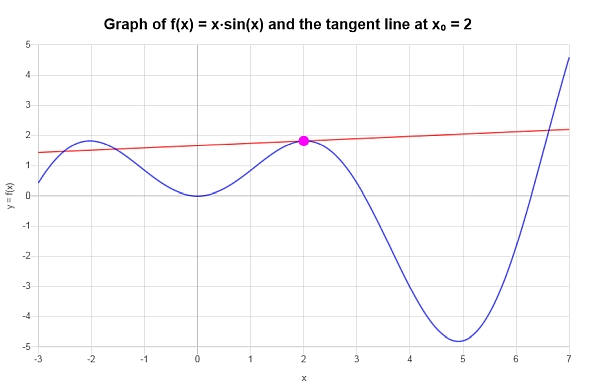
: Делается вывод, что линейная аппроксимация (displaystyle f(x)=xsinleft(xright)) в заданной точке (x_0 = 2) вычисляется как:

[y = 2xcosleft(2right)+xsinleft(2right)-4cosleft(2right) ]

Графически мы получаем следующий график:

Пример: расчет линейного приближения

Вычислите приближение первого порядка для ( f(x) = frac{sin(x)}{x}) в (x = frac{pi}{4}).

Отвечать:

Предусмотрена следующая функция: (displaystyle f(x)=frac{sinleft(xright)}{x}), для которой нам нужно вычислить ее производную.

Функция уже упрощена, поэтому мы можем перейти непосредственно к вычислению ее производной:

( displaystyle frac{d}{dx}left(frac{sinleft(xright)}{x}right))

Using the Quotient Rule: (frac{d}{dx}left( frac{sinleft(xright)}{x} right) = frac{x cdot frac{d}{dx}left(sinleft(xright)right)-sinleft(xright)cdot frac{d}{dx}left(xright)}{x^2})

( displaystyle = ,,)

(displaystyle frac{x cdot frac{d}{dx}left(sinleft(xright)right)-sinleft(xright)cdot frac{d}{dx}left(xright)}{x^2})

We know that (frac{d}{dx}left(xright) = 1)

( displaystyle = ,,)

(displaystyle frac{x cdot frac{d}{dx}left(sinleft(xright)right)-sinleft(xright)}{x^2})

Directly differentiating: (frac{d}{dx}left( sinleft(xright) right) = cosleft(xright))

( displaystyle = ,,)

(displaystyle frac{x cdot cosleft(xright)-sinleft(xright)}{x^2})

( displaystyle = ,,)

(displaystyle frac{xcosleft(xright)-sinleft(xright)}{x^2})

Аппроксимация Первого Порядка

: Уравнение для соответствующего приближения первого порядка для заданной функции (displaystyle f(x)=frac{sinleft(xright)}{x}) в заданной точке (x_0 = frac{pi}{4}) задается следующим образом:

[y = y_0 + f'(x_0)(x – x_0) ]

Подставляем соответствующие значения:

[y_0 = f(x_0) = fleft(frac{pi}{4}right) = frac{sinleft(frac{pi{}}{4}right)}{frac{pi{}}{4}} = frac{2sqrt{2}}{pi{}}]

[f'(x_0) = f’left(frac{pi}{4}right) = frac{cosleft(frac{pi{}}{4}right)}{frac{pi{}}{4}}-frac{sinleft(frac{pi{}}{4}right)}{left(frac{pi{}}{4}right)^2}
= frac{2sqrt{2}}{pi{}}-frac{8sqrt{2}}{pi{}^2} ]

Теперь мы можем подставить это в формулу:

[y = y_0 + f'(x_0)(x – x_0) ]

[Rightarrow y = frac{2sqrt{2}}{pi{}}+frac{2sqrt{2}}{pi{}}-frac{8sqrt{2}}{pi{}^2}left(x-frac{1}{4}pi{}right) =
-frac{1}{2}sqrt{2}+frac{2sqrt{2}x}{pi{}}+frac{4sqrt{2}}{pi{}}-frac{8sqrt{2}x}{pi{}^2} ]

Заключение

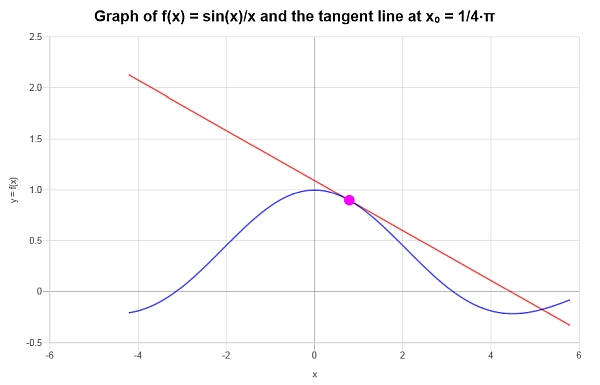
: Таким образом, мы можем заключить, что приближение первого порядка для данной функции (displaystyle f(x)=frac{sinleft(xright)}{x}) в данной точке (x_0 = frac{pi}{4}) определяется выражением

[y = -frac{1}{2}sqrt{2}+frac{2sqrt{2}x}{pi{}}+frac{4sqrt{2}}{pi{}}-frac{8sqrt{2}x}{pi{}^2} ]

Графически получается следующее:

Другие калькуляторы производных инструментов

Помимо этого

калькулятор линеаризации

, вы можете найти много вещей, которые делают разные вещи на основе производных. Дифференциация является важной операцией в исчислении, физике, технике и экономике с широким спектром приложений.

Существует также способ провести линейную аппроксимацию для большего количества переменных, например, для функции f(x, y)), и в этом случае формула линейной аппроксимации становится (f(x, y) = f(x_0, y_0) + frac{partial f}{partial x}(x_0, y_0)(x-x_0) + frac{partial f}{partial y}(x_0, y_0)(y-y_0)), поэтому в этом случае чтобы найти линеаризацию, нам нужно использовать

частные производные

Нахождение линеаризации функции далеко не единственное, что вы можете делать с производными. Дифференциация — относительно простая операция с простыми правилами, такими как

Правило Продукта

правило квоты

Правило цепи

что делает расчет производных относительно простой операцией.

Хотя предполагается, что она должна быть простой, рекомендуется использовать

производный калькулятор

чтобы получить все показанные шаги, с четким упоминанием всех

Правила производных

используется.

Источник

Вычисление производной по ее определению

Вычисление производной по ее определению

Вычисление значений функции

Номер Строки

Калькулятор линейной аппроксимации

Линейное приближение

Шаги для нахождения линейной аппроксимации

Связь с касательной линией

Дифференциальная и линейная аппроксимация

Пример: вычисление аппроксимации первого порядка.

Пример: больше аппроксимации первого порядка

Пример: расчет линейного приближения

Другие калькуляторы производных инструментов

Вам также может понравиться

Как найти массу на ось

Как исправить ошибку 523 на сайте

Как найти sin 160

Добавить комментарий Отменить ответ