Дифференциалом функции
называется главная (линейная по
) часть приращения функции. Чтобы понять данное определение, рассмотрим следующий рисунок.
На рисунке изображён график функции
и
касательной
к ней в точке
.
Дадим аргументу функции
некоторое приращение
,
тогда функция
также получит некоторое приращение
.
Величина
называется
дифференциалом функции
.
При этом, из графика следует, что
равно приращению ординаты касательной, проведённой в точке
к функции
.
Именно поэтому дифференциалом называют линейную часть приращения функции, т.е. приращение ординаты касательной.
Из рисунка следует, что угол наклона касательной
,
который она образует с положительным направлением оси
и
– равны. Кроме того, тангенс угла наклона касательной равен значению производной функции в точке касания:
Из треугольника
следует, что:
Таким образом, дифференциал функции выражается следующей формулой:
Рассмотрим ещё такой момент: из рисунка следует, что
, причем
. Причем, чем меньше
, тем меньший вклад в величину
вносит значение
. Т.е. при достаточно малых значениях
, можно считать, что
. Данное соотношение позволяет вычислять приближенное значение функции в точке
, если известно её значение в точке
.
Дифференциал высшего порядка (например порядка
) определяется как дифференциал от дифференциала
-ого порядка:
Например, дифференциал второго порядка вычисляется следующим образом:
Аналогичным образом получаем формулу для вычисления дифференциала
-ого порядка:
где
–
-ая производная функции
по переменной
.
Пару слов стоит сказать о вычислении дифференциала функции многих переменных, который в этом случае называется
полным дифференциалом. Полный дифференциал функции, зависящей от
-переменных
определяется по формуле:
Выражения для дифференциалов высших порядков функции многих переменных можно получить исходя из общей формулы:
В общем случае, для возведения суммы в
-ую степень необходимо воспользоваться формулой бинома Ньютона. Рассмотрим процесс получения формулы полного дифференциала второго порядка функции двух переменных:
Наш онлайн калькулятор способен вычислить дифференциалы разных порядков для любых функций одной или нескольких переменных с описанием подробного решения на русском языке.
Описание метода вычисления значения производной можно найти под калькулятором.
Вычисление производной по ее определению
Начальное приращение аргумента
Параметр изменения приращения
Точность вычисления
Знаков после запятой: 4
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Вычисление производной по ее определению
Задача численного дифференцирования возникает когда функция задана таблично, или когда прямое дифференцирование затруднено (например, при сложном аналитическом виде функции). Если функция задана аналитически, то можно применить вычисление значения производной по ее определению.
В этом случае у нас есть некоторая функция , для которой нам надо вычислить значение производной в точке x₀. Мы предполагаем, что эта функция определена в окрестности точки x₀ и имеет производную в этой точке. Исходя из определения производной
существует предел отношения приращения функции Δy к приращению аргумента Δx при Δx→0, где
Значение производной можно получить переходя к пределу со все более уменьшающимся шагом, пока не будет достигнута требуемая точность. Для этого на каждом шаге последовательности n приращение аргумента вычисляется по следующей формуле
,
где
Δx₀ – начальное приращение аргумента, например, 0.1
a – некоторое число, большее 1, например, 10
n = 0, 1, …
Тогда
Последовательность останавливается при выполнении следующего условия
Вычисление приближенно с помощью дифференциала
С одной стороны, вычисление дифференциала значительно проще, чем вычисление приращения, с другой стороны, dy≈∆y и допускаемая при этом погрешность может быть сделана сколь угодно малой за счет уменьшения ∆x. Эти обстоятельства позволяют во многих случаях заменять ∆y величиной dy. Из приближенного равенства dy≈∆y, учитывая, что ∆y = f(x) – f(x0), а dy=f’(x0)(x-x0), получим
f(x) ≈ f(x0) + f’(x0)(x–x0), (1)
где x-x0 = ∆x.
Пример№1. Вычислить .
Решение. Взяв функцию , имеем:
. Полагая x0=16 (выбираем сами, чтобы корень извлекался), ∆x = 0,02, получим:
Пример №2. Вычислить значение функции f(x) = ex в точке x=0.1.
Решение. В качестве x0 возьмем число 0, то есть x0=0, тогда ∆x=x-x0 =0.1 и e0.1≈e0 + e00.1 = 1+0.1 = 1.1. По таблице e0.1≈1.1052. Ошибка получилась незначительная.
Отметим еще одно важное свойство дифференциала. Формула для нахождения дифференциала dy=f’(x)dx верна как в случае, когда x – независимая переменная, так и в случае, когда x – функция от новой переменной t. Это свойство дифференциала называется свойством инвариантности его формы. Например, для функции y=tg(x) дифференциал запишется в виде 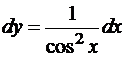
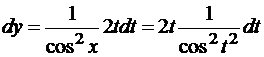
Если вместо формулы (2) воспользовались бы неинвариантной формулой (1), то в случае, когда x – функция, мы не могли бы подобным образом продолжить вычисление dy, так как ∆x, вообще говоря, не совпадает с dx.
Пример №3
Извлечь квадратный корень из 3654.
Решение. Надо найти значение функции при x=3654. Легко вычисляются значения f(x) и
при x=3600. Формула (1) при a=3600, h=54 дает
. Здесь все знаки верны.
Пример №4. Найти 102,1.
Решение. Полагаем f(x)=10x , так что . Формула (1) при a=2, h=0,1 дат:
.
Этот результат грубоват (с точностью до четвертой значащей цифры 102,1=125,9).
Если таким же образом вычислить 102,01 (теперь h=0,01), получим 102,3. Здесь все знаки верны.
Пример №5. Найти без таблиц tg 46о.
Решение. Полагаем f(x)=tg x, a=45о, h=1о=0,0175 радиана; тогда имеем: . Значит, tg 45о=1+2·0,0175=1,0350.
Неверен только последний знак; из таблиц имеем tg 46o=1, 0355.
Полезно заметить следующие приближенные формулы (a-малая величина):
,
; (2)
,
; (3)
,
; (4)
,
; (5)
,
; (6)
Формулы (2)-(6) являются частными случаями формулы (1+a)n≈1+na; последняя получается из (1), если положить f(x)=xn, a=1,h=a.
ln(1+a)≈a, ln(1-a)≈-a; (7)
ea≈1+a, ; (8)
sin a≈a, , tg a≈a; (9)
Инструкции:
Используйте этот дифференциальный калькулятор, чтобы найти дифференциал функции, которую вы предоставляете, в заданной точке, которую вы предоставляете, показывая все шаги. Пожалуйста, введите функцию и точку в поле формы ниже.
Дифференциальный калькулятор
Этот калькулятор позволит вам вычислить дифференциал предоставляемой вами функции в указанную вами точку, показывая все этапы процесса.
Предоставляемая вами функция может быть любой допустимой дифференцируемой функцией, такой как f(x) = x^2 + 2x или f(x) = x^2*sin(x), просто упомянем два примера.
Затем, когда вы указали функцию и точку для дифференциального расчета, просто нажмите “Рассчитать”, чтобы просмотреть все этапы показанного процесса.
Идея
Дифференциал
находится вплотную с линией касательной и
Линейное Приближение
, так как дифференциал точно измеряет изменение y вдоль
Касательная линия
в заданной точке.
Что такое дифференциал?
В дифференциальном исчислении идея состоит в том, что производные дают вам информацию о мгновенной скорости изменения функции в данной точке.
Понятие дифференциала использует
скорость изменения
определяется производной в данной точке (x_0), чтобы аппроксимировать поведение функции ее
Касательная линия
.
Формула дифференциала основана на идее, что
[displaystyle Delta y approx f'(x_0) Delta x ]
где (Delta y = y – f(x_0)) и (Delta x = x – x_0). Для дифференциала (dy) определим
[displaystyle dy = f'(x_0) dx ]
Это (расплывчатое) определение основано на идее, что линейная аппроксимация и функция приближаются к одному и тому же поведению, когда (x) достаточно близко к (x_0).
Шаги для вычисления дифференциала
-
Шаг 1:
Определите функцию f(x) и точку x0, в которой вы хотите вычислить дифференциал -
Шаг 2:
Вычислите производную f'(x) и оцените ее в x0, чтобы получить f'(x0). Упростите его, если это необходимо -
Шаг 3:
Используйте формулу (displaystyle dy = f'(x_0) dx )
Иногда вы встретите дифференциал, записанный как (displaystyle Delta y = f'(x_0) Delta x = f'(x_0)(x-x_0) ), как форму указания на то, что вы будете использовать дифференциал для оценки изменений y, измеренных (Delta y).
Дифференциальный калькулятор dy
Используя
Дифференциальный калькулятор
может сэкономить ваше время в процессе расчета производной. Идея дифференциала всегда была странной в том смысле, что она кажется нечетко определенной.
Хотя существует способ формального определения дифференциалов и их операций (предмет, называемый дифференциальными формами), большинство математиков не видят причин для существования дифференциалов, поскольку они не предоставляют никакой новой информации, которую производная или приближение первого порядка не предоставлять.
Полная дифференциальная интерпретация
Наиболее распространенное применение и интерпретация дифференциала – это использование в его “конечном” выражении:
[displaystyle Delta y = f'(x_0) Delta x = f'(x_0)(x-x_0) ]
где вы хотите оценить изменение y, измеренное (Delta y), по изменению x, измеренному (Delta x), и производной в точке.
Иногда это (Delta y) называют
полная вариация
или же
полный дифференциал
.
Советы и рекомендации
Не забывайте, что дифференциал можно рассматривать как теоретическое определение (displaystyle dy = f'(x_0) dx ), которое указывает на бесконечно малую вариацию у, вызванную бесконечно малой вариацией х.
Его также можно использовать в его полной дифференциальной форме, в которой у вас есть
[displaystyle Delta y approx f'(x_0)(x-x_0)]
который сообщает вам приблизительное изменение y при изменении x (от (x_0) до (x)).
Центр всего алгебраического калькулятора начинается с мощности основных чисел дробей.
Пример: дифференциальный калькулятор
Рассмотрим функцию: (f(x) = x^2). Найдите его дифференциал в точке (x_0 = 1).
Отвечать:
В случае этого первого примера мы работаем с функцией (displaystyle f(x)=x^2), для которой нам нужно вычислить ее дифференциал в точке (x_0 = 1).
Функция уже упрощена, поэтому мы можем перейти непосредственно к вычислению ее производной:
( displaystyle frac{d}{dx}left(x^2right))
In this case we use the Power Rule for polynomial terms: (frac{d}{dx}left( x^2 right) = 2x)
( displaystyle = ,,)
(displaystyle 2x)
Дифференциал
: Формула для дифференциала функции (displaystyle f(x)=x^2) в точке (x_0 = 1):
[dy = f'(x_0)(x – x_0) ]
Мы определяем (displaystyle y_0 = f(x_0)), поэтому подстановка значения точки (x_0 = 1) в функцию приводит к:
[y_0 = f(x_0) = fleft(1right) = 1^2 = 1]
Также подстановка значения точки (x_0 = 1) в вычисленную производную приводит к:
[f'(x_0) = f’left(1right) = 2cdot 1 = 2 ]
Итак, теперь мы подставляем это значение в дифференциальную формулу, чтобы получить:
[dy = f'(x_0)(x – x_0) ][Rightarrow dy = 2left(x-1right) ][Rightarrow dy = 2x-2 ]
Вывод
: Следовательно, мы находим, что дифференциал для функции (displaystyle f(x)=x^2) в точке (x_0 = 1) равен:
[dy = 2x-2 ]
Пример: дифференциальный расчет
Для заданной функции: (f(x) = x^3 + 3x^2 – 2) найти дифференциал в точке (x_0 = 2).
Отвечать:
Теперь нам нужно найти дифференциал для функции (displaystyle f(x)=x^3+3x^2-2),
( displaystyle frac{d}{dx}left(x^3+3x^2-2right))
By linearity, we know (frac{d}{dx}left( x^3+3x^2-2 right) = frac{d}{dx}left(x^3right)+3 cdot frac{d}{dx}left(x^2right)-frac{d}{dx}left(2right)), so plugging that in:
( displaystyle = ,,)
(displaystyle frac{d}{dx}left(x^3right)+3 cdot frac{d}{dx}left(x^2right)-frac{d}{dx}left(2right))
Since the derivative of a constant is 0, we get that:
( displaystyle = ,,)
(displaystyle frac{d}{dx}left(x^3right)+3 cdot frac{d}{dx}left(x^2right))
Using the Power Rule for polynomial terms: (frac{d}{dx}left( x^2 right) = 2x) and (frac{d}{dx}left( x^3 right) = 3x^2)
( displaystyle = ,,)
(displaystyle 3x^2+3 cdot 2x)
( displaystyle = ,,)
(displaystyle 3x^2+3cdot 2x)
We reduce the integers that can be multiplied: (displaystyle 3times2 = 6)
( displaystyle = ,,)
(displaystyle 3x^2+6x)
Directly reorganizing/simplifying/expanding
( displaystyle = ,,)
(displaystyle 3left(x+2right)x)
Дифференциальный Расчет
: Мы используем следующую формулу для дифференциала, который нам нужно построить для данной функции (displaystyle f(x)=x^3+3x^2-2), в данной точке (x_0 = frac{1}{2}):
[dy = f'(x_0)(x – x_0) ]
Заметьте, что (displaystyle y_0 = f(x_0)), что означает, что вычисляя функцию в (x_0 = frac{1}{2}), мы находим:
[y_0 = f(x_0) = fleft(frac{1}{2}right) = left(frac{1}{2}right)^3+3left(frac{1}{2}right)^2-2 = -frac{9}{8}]
Тогда получим производную в точке (x_0 = frac{1}{2}):
[f'(x_0) = f’left(frac{1}{2}right) = 3left(frac{1}{2}right)^2+6cdot frac{1}{2} = frac{15}{4} ]
Следовательно, мы получаем следующее
[dy = f'(x_0)(x – x_0) ][Rightarrow dy = left(frac{15}{4}right)left(x-frac{1}{2}right) ][Rightarrow dy = frac{15}{4}x-frac{15}{8} ]
Вывод
: Окончательный вывод состоит в том, что искомый дифференциал определяется выражением:
[dy = frac{15}{4}x-frac{15}{8} ]
Дифференциальный пример
Нам дана функция: (f(x) = frac{sin(x)}{x}). Найдите его дифференциал в точке (x_0 = frac{pi}{2}).
Решение:
Предусмотрена следующая функция: (displaystyle f(x)=frac{sinleft(xright)}{x}), для которой нужно вычислить ее дифференциал в точке (x_0 = frac{pi}{2}).
Функция уже упрощена, поэтому мы можем перейти непосредственно к вычислению ее производной:
( displaystyle frac{d}{dx}left(frac{sinleft(xright)}{x}right))
Using the Quotient Rule: (frac{d}{dx}left( frac{sinleft(xright)}{x} right) = frac{x cdot frac{d}{dx}left(sinleft(xright)right)-sinleft(xright)cdot frac{d}{dx}left(xright)}{x^2})
( displaystyle = ,,)
(displaystyle frac{x cdot frac{d}{dx}left(sinleft(xright)right)-sinleft(xright)cdot frac{d}{dx}left(xright)}{x^2})
We already know that (frac{d}{dx}left(xright) = 1)
( displaystyle = ,,)
(displaystyle frac{x cdot frac{d}{dx}left(sinleft(xright)right)-sinleft(xright)}{x^2})
Directly differentiating: (frac{d}{dx}left( sinleft(xright) right) = cosleft(xright))
( displaystyle = ,,)
(displaystyle frac{x cdot cosleft(xright)-sinleft(xright)}{x^2})
So then after simplifying:
( displaystyle = ,,)
(displaystyle frac{xcosleft(xright)-sinleft(xright)}{x^2})
Расчет
: Теперь пришло время найти дифференциал, связанный с (displaystyle f(x)=frac{sinleft(xright)}{x}), для заданной точки (x_0 = frac{pi}{2}). Используемая формула:
[dy = f'(x_0)(x – x_0) ]
Подставляем значение точки (x_0 = frac{pi}{2}) в вычисленную производную, что приводит к:
[f'(x_0) = f’left(frac{pi}{2}right) = frac{cosleft(frac{pi{}}{2}right)}{frac{pi{}}{2}}-frac{sinleft(frac{pi{}}{2}right)}{left(frac{pi{}}{2}right)^2}
= -frac{4}{pi{}^2} ]
Поэтому, используя дифференциальную формулу:
[dy = f'(x_0)(x – x_0) ][Rightarrow dy = left(-frac{4}{pi{}^2}right)left(x-frac{1}{2}pi{}right) ][Rightarrow dy = frac{2}{pi{}}-frac{4x}{pi{}^2} ]
Вывод
: Соответствующий дифференциал:
[dy = frac{2}{pi{}}-frac{4x}{pi{}^2} ]
Другие калькуляторы дифференцирования
Поиск производных
без сомнения, является ключевым элементом исчисления. Производные предоставляют информацию, необходимую для понимания
скорость изменения
функций. поскольку они имеют тесную связь.
К счастью, поиск деривативов — это систематический процесс (не обязательно простой), если вы будете следовать определенным правилам.
правила дифференциации
. Чаще всего используются правила
Правило Продукта
,
Правило квоты
и
Правило цепи
.
Линейный или
приближения первого порядка
концептуально попытаться аппроксимировать функцию линией, по крайней мере локально, и может многое рассказать о поведении функции, близкой к определенной точке.
вычислить значение функции с помощью дифференциала функции
Вы искали вычислить значение функции с помощью дифференциала функции? На нашем сайте вы можете получить ответ на любой математический вопрос здесь. Подробное
решение с описанием и пояснениями поможет вам разобраться даже с самой сложной задачей и вычислить приближенно, не
исключение. Мы поможем вам подготовиться к домашним работам, контрольным, олимпиадам, а так же к поступлению
в вуз.
И какой бы пример, какой бы запрос по математике вы не ввели – у нас уже есть решение.
Например, «вычислить значение функции с помощью дифференциала функции».
Применение различных математических задач, калькуляторов, уравнений и функций широко распространено в нашей
жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Математику человек
использовал еще в древности и с тех пор их применение только возрастает. Однако сейчас наука не стоит на
месте и мы можем наслаждаться плодами ее деятельности, такими, например, как онлайн-калькулятор, который
может решить задачи, такие, как вычислить значение функции с помощью дифференциала функции,вычислить приближенно,вычислить приближенно с помощью дифференциала,вычислить приближенно с помощью дифференциала онлайн калькулятор,вычислить приближенное значение,вычислить приближенное значение функции,как вычислить приближенно с помощью дифференциала,как найти приближенное значение,найти приближенное значение,найти приближенное значение функции с помощью дифференциала онлайн,приближенно вычислить с помощью дифференциала онлайн,приближенное вычисление,приближенное значение функции,приближенное значение функции с помощью дифференциала,приближенные вычисления с помощью дифференциала,с помощью дифференциала найти приближенное значение функции онлайн,с помощью дифференциала приближенно вычислить,с помощью дифференциала приближенно вычислить онлайн. На этой странице вы найдёте калькулятор,
который поможет решить любой вопрос, в том числе и вычислить значение функции с помощью дифференциала функции. Просто введите задачу в окошко и нажмите
«решить» здесь (например, вычислить приближенно с помощью дифференциала).
Где можно решить любую задачу по математике, а так же вычислить значение функции с помощью дифференциала функции Онлайн?
Решить задачу вычислить значение функции с помощью дифференциала функции вы можете на нашем сайте https://pocketteacher.ru. Бесплатный
онлайн решатель позволит решить онлайн задачу любой сложности за считанные секунды. Все, что вам необходимо
сделать – это просто
ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как правильно ввести
вашу задачу на нашем сайте. А если у вас остались вопросы, то вы можете задать их в чате снизу слева на странице
калькулятора.
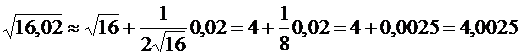
.jpg)
