Как найти приближенное значение корня онлайн

Метод Ньютона является численным, т.е. корень уравнения находится приближенно. При этом можно заранее задать точность его нахождения.

Пусть нам дано уравнение

Формула для поиска корня уравнения выглядит следующим образом:

и

– приближённые значения корня уравнения

на
-ой и
()-ой итерациях соответственно,

– значение функции

в точке
,

– значение производной функции

в точке
.

Как видно, для того чтобы начать работу необходимо задать точку

– начальное приближение для корня уравнения
. От выбора точки

зависит сойдётся ли алгоритм к решению или нет. Сходимость метода квадратичная, но она резко ухудшается если мы ищем кратный корень уравнения, т.е. если

и одновременно
, где

– кратный корень уравнения
.

Вычисления по приведённой выше формуле можно продолжать до бесконечности, соответственно на практике необходим некоторый критерий, который будет определять нужно ли нам продолжать вычисления или нет. Как правило, используется критерий останова вычислений на основе приращения или же на основе близости функции

к нулю в некоторой точке
.

Критерий останова вычислений на основе приращения задаётся следующей формулой:

т.е. различие (по модулю) между двумя последовательными приближениями к корню уравнения (

и

) должны быть меньше, некоторой наперёд заданной величины
.

Критерий останова вычислений на основе близости функции к нулю определяется следующей формулой:

т.е. отличие (по модулю) между функцией

в некоторой точке

и нулём меньше
.

В тоже время, если последовательность

к корню не сходится, то критерии останова не сработают и процесс поиска корня будет продолжаться бесконечно. Чтобы предотвратить такую ситуацию, на практике вычисления прекращают после некоторого, заданного количества итераций.

На рисунке ниже приведена геометрическая интерпретация процесса поиска корня уравнения

методом Ньютона.

В точке

мы строим
касательную к графику функции
. Уравнение касательной в этой точке имеет вид:

Находим точку пересечения полученной касательной с осью абсцисс, т.е. рассматриваем точку с координатами
. Подставляя координаты указанной точки в уравнение касательной, получаем следующее соотношение:

Из данного уравнения находим
:

Продолжая данный процесс, получим формулу метода Ньютона, приведенную выше. Из-за того, что на каждой итерации фактически происходит построение касательной, метод Ньютона также иногда называют методом касательных.

При решении различных задач из курса математики и физики ученики и студенты часто сталкиваются с необходимостью извлечения корней второй, третьей или n-ой степени. Конечно, в век информационных технологий не составит труда решить такую задачу при помощи калькулятора. Однако возникают ситуации, когда воспользоваться электронным помощником невозможно.

К примеру, на многие экзамены запрещено приносить электронику. Кроме того, калькулятора может не оказаться под рукой. В таких случаях полезно знать хотя бы некоторые методы вычисления радикалов вручную.

Извлечение квадратного корня при помощи таблицы квадратов

Один из простейших способов вычисления корней заключается в использовании специальной таблицы. Что же она собой представляет и как ей правильно воспользоваться?

При помощи таблицы можно найти квадрат любого числа от 10 до 99. При этом в строках таблицы находятся значения десятков, в столбах — значения единиц. Ячейка на пересечении строки и столбца содержит в себе квадрат двузначного числа. Для того чтобы вычислить квадрат 63, нужно найти строку со значением 6 и столбец со значением 3. На пересечении обнаружим ячейку с числом 3969.

Поскольку извлечение корня — это операция, обратная возведению в квадрат, для выполнения этого действия необходимо поступить наоборот: вначале найти ячейку с числом, радикал которого нужно посчитать, затем по значениям столбика и строки определить ответ. В качестве примера рассмотрим вычисление квадратного корня 169.

Находим ячейку с этим числом в таблице, по горизонтали определяем десятки — 1, по вертикали находим единицы — 3. Ответ: √169 = 13.

Аналогично можно вычислять корни кубической и n-ой степени, используя соответствующие таблицы.

Преимуществом способа является его простота и отсутствие дополнительных вычислений. Недостатки же очевидны: метод можно использовать только для ограниченного диапазона чисел (число, для которого находится корень, должно быть в промежутке от 100 до 9801). Кроме того, он не подойдёт, если заданного числа нет в таблице.

Разложение на простые множители

Если таблица квадратов отсутствует под рукой или с её помощью оказалось невозможно найти корень, можно попробовать разложить число, находящееся под корнем, на простые множители. Простые множители — это такие, которые могут нацело (без остатка) делиться только на себя или на единицу. Примерами могут быть 2, 3, 5, 7, 11, 13 и т. д.

Рассмотрим вычисление корня на примере √576. Разложим его на простые множители. Получим следующий результат: √576 = √(2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 2 ∙ 3 ∙ 3) = √(2 ∙ 2 ∙ 2)² ∙ √3². При помощи основного свойства корней √a² = a избавимся от корней и квадратов, после чего подсчитаем ответ: 2 ∙ 2 ∙ 2 ∙ 3 = 24.

Что же делать, если у какого-либо из множителей нет своей пары? Для примера рассмотрим вычисление √54. После разложения на множители получаем результат в следующем виде: √54 = √(2 ∙ 3 ∙ 3 ∙ 3) = √3² ∙ √(2 ∙ 3) = 3√6. Неизвлекаемую часть можно оставить под корнем. Для большинства задач по геометрии и алгебре такой ответ будет засчитан в качестве окончательного. Но если есть необходимость вычислить приближённые значения, можно использовать методы, которые будут рассмотрены далее.

Метод Герона

Как поступить, когда необходимо хотя бы приблизительно знать, чему равен извлечённый корень (если невозможно получить целое значение)? Быстрый и довольно точный результат даёт применение метода Герона. Его суть заключается в использовании приближённой формулы:

√R = √a + (R — a) / 2√a,

где R — число, корень которого нужно вычислить, a — ближайшее число, значение корня которого известно.

Рассмотрим, как работает метод на практике, и оценим, насколько он точен. Рассчитаем, чему равен √111. Ближайшее к 111 число, корень которого известен — 121. Таким образом, R = 111, a = 121. Подставим значения в формулу:

√111 = √121 + (111 — 121) / 2 ∙ √121 = 11 — 10 / 22 ≈ 10,55.

Теперь проверим точность метода:

10,55² = 111,3025.

Погрешность метода составила приблизительно 0,3. Если точность метода нужно повысить, можно повторить описанные ранее действия:

√111 = √111,3025 + (111 — 111,3025) / 2 ∙ √111,3025 = 10,55 — 0,3025 / 21,1 ≈ 10,536.

Проверим точность расчёта:

10,536² = 111,0073.

После повторного применения формулы погрешность стала совсем незначительной.

Вычисление корня делением в столбик

Этот способ нахождения значения квадратного корня является чуть более сложным, чем предыдущие. Однако он является наиболее точным среди остальных методов вычисления без калькулятора.

Допустим, что необходимо найти квадратный корень с точностью до 4 знаков после запятой. Разберём алгоритм вычислений на примере произвольного числа 1308,1912.

1. Разделим лист бумаги на 2 части вертикальной чертой, а затем проведём от неё ещё одну черту справа, немного ниже верхнего края. Запишем число в левой части, разделив его на группы по 2 цифры, двигаясь в правую и левую сторону от запятой. Самая первая цифра слева может быть без пары. Если же знака не хватает в правой части числа, то следует дописать 0. В нашем случае получится 13 08,19 12.
2. Подберём самое большое число, квадрат которого будет меньше или равен первой группе цифр. В нашем случае это 3. Запишем его справа сверху; 3 — первая цифра результата. Справа снизу укажем 3×3 = 9; это понадобится для последующих расчётов. Из 13 в столбик вычтем 9, получим остаток 4.
3. Припишем следующую пару чисел к остатку 4; получим 408.
4. Число, находящееся сверху справа, умножим на 2 и запишем справа снизу, добавив к нему _ x _ =. Получим 6_ x _ =.
5. Вместо прочерков нужно подставить одно и то же число, меньшее или равное 408. Получим 66×6 = 396. Напишем 6 справа сверху, т. к. это вторая цифра результата. Отнимем 396 от 408, получим 12.
6. Повторим шаги 3—6. Поскольку снесённые вниз цифры находятся в дробной части числа, необходимо поставить десятичную запятую справа сверху после 6. Запишем удвоенный результат с прочерками: 72_ x _ =. Подходящей цифрой будет 1: 721×1 = 721. Запишем её в ответ. Выполним вычитание 1219 — 721 = 498.
7. Выполним приведённую в предыдущем пункте последовательность действий ещё три раза, чтобы получить необходимое количество знаков после запятой. Если не хватает знаков для дальнейших вычислений, у текущего слева числа нужно дописать два нуля.

В результате мы получим ответ: √1308,1912 ≈ 36,1689. Если проверить действие при помощи калькулятора, можно убедиться, что все знаки были определены верно.

Поразрядное вычисление значения квадратного корня

Метод обладает высокой точностью. Кроме того, он достаточно понятен и для него не требуется запоминать формулы или сложный алгоритм действий, поскольку суть способа заключается в подборе верного результата.

Извлечём корень из числа 781. Рассмотрим подробно последовательность действий.

1. Выясним, какой разряд значения квадратного корня будет являться старшим. Для этого возведём в квадрат 0, 10, 100, 1000 и т. д. и выясним, между какими из них находится подкоренное число. Мы получим, что 10² < 781 < 100², т. е. старшим разрядом будут десятки.
2. Подберём значение десятков. Для этого будем по очереди возводить в степень 10, 20, …, 90, пока не получим число, превышающее 781. Для нашего случая получим 10² = 100, 20² = 400, 30² = 900. Значение результата n будет находиться в пределах 20 < n <30.
3. Аналогично предыдущему шагу подбирается значение разряда единиц. Поочерёдно возведём в квадрат 21,22, …, 29: 21² = 441, 22² = 484, 23² = 529, 24² = 576, 25² = 625, 26² = 676, 27² = 729, 28² = 784. Получаем, что 27 < n < 28.
4. Каждый последующий разряд (десятые, сотые и т. д. ) вычисляется так же, как было показано выше. Расчёты проводятся до тех пор, пока не будет достигнута необходимая точность.

Видео

Из видео вы узнаете, как извлекать квадратные корни без использования калькулятора.

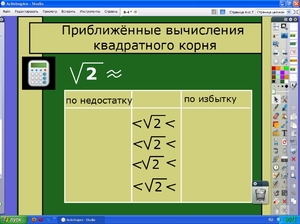
Вы уже научились находить значения некоторых квадратных
корней. Например, таких как:

Но бывает так, что необходимо найти квадратный
корень из числа, который уже нельзя так сходу определить. Тогда приходят к
нахождению приближённых значений квадратного корня.

Например:

Надо найти .

До этого мы с вами уже говорили, что нет
такого целого числа, квадрат которого бы равнялся двум.

Обратимся к параболе.

 Прямая  пересекает
параболу в двух точках. Абсцисса первой точки расположена между числами -1 и -2,
абсцисса второй точки между числами 1 и 2.

 А т.к. нас интересует арифметический
квадратный корень, то рассматриваем только точку в первой координатной четверти
(т.е. с положительной абсциссой). По рисунку можно лишь сказать, что значение
корня из двух расположено между числами 1 и 2.

Попробуем все же вычислить приближённое
значение  с
двумя знаками после запятой. Будем рассуждать следующим образом:

Т.к. нужно вычислить  с
точностью до двух знаков после запятой, то мы можем уже остановиться и не
продолжать вычисления дальше. Поэтому имеем

Это и будет ответом. Если бы необходимо было
вычислить ещё более точное значение, нужно было бы продолжать вычисления,
повторяя снова и снова цепочку рассуждений. Данный приём позволяет извлекать арифметический
квадратный корень с любой точностью.

Можно показать наши рассуждения относительно
значения  на координатной прямой.

В первом шаге  показано, что значение  расположено между числами 1 и 2.  

Во втором шаге нашли значение корня с
точностью до десятых. И пришли к выводу, что это значение заключено между
числами 1,4 и 1,5.

Затем, в третьем шаге показано, что значение  расположено
между числами 1,41 и 1,42 с точностью до сотых. И т.д..

В практических расчётах для нахождения
приближённых значений квадратных корней используют специальные
таблицы или вычислительную технику.

Рассмотрим, как можно находить значения
квадратных корней с помощью калькулятора.

Для этого используют клавишу, на которой
изображён знак квадратного корня. Чтобы извлечь корень из некоторого числа,
нужно ввести это число в калькулятор. Пауза нажать клавишу со знаком корня. И
на экране высветится приближённое значение корня.

Убедимся в правильности работы калькулятора.
Сначала давайте попробуем найти значение корня, которого вы уже
помните наизусть.

Например:

Нужно найти значение .
Конечно, вы с ходу скажите, что оно равно 5. Проверим. Вводим в калькулятор
число 25, затем нажимаем волшебную клавишу со знаком корня и
видим… значение равно 5.

Проверим, правильно ли мы рассуждали
относительно значения .
Вводим число 2 в калькулятор, нажимаем клавишу с корнем и видим
такие цифры: 1, запятая, 4, 1 и дальше ещё много циферок. Обратите внимание, получили
бесконечную непериодическую дробь, т.е. значение  –
иррациональное число. Но т.к. нам нужно было найти приближённое
значение  с
точностью до сотых, то мы убедились, что .

Задание:         

Сравните числа.

Решение:

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Извлечь корень онлайн

Поддержать сайт

Приближенное вычисление корней

Пусть
нужно извлечь корень
.
Всегда можно подобрать такое целое
число,
чтобыбыло возможно ближе к,
тогда

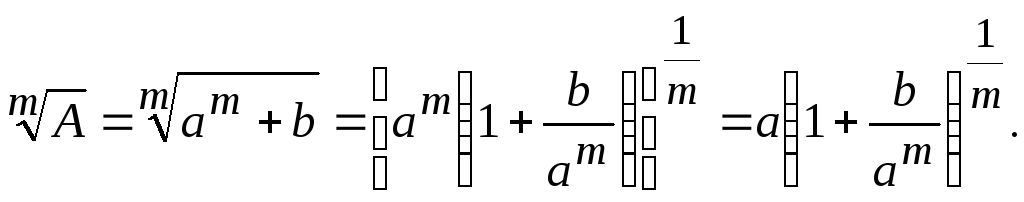
При
условии
последнее выражение можно вычислить,
используя биномиальный ряд:

,

.

Пример
24.
Вычислить
с точностью до 0,0001.

Решение

Используя
биномиальный ряд

,
при
,
получим

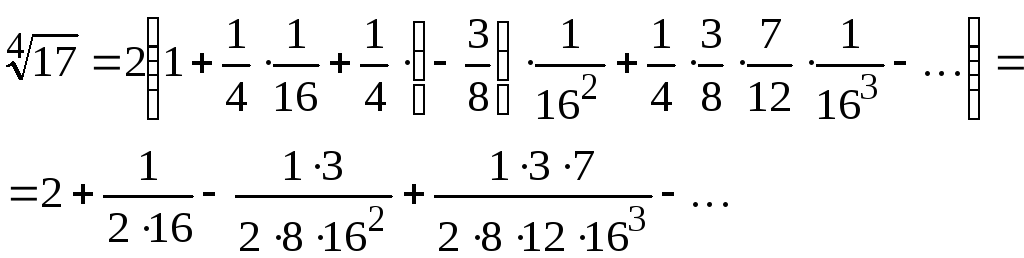
Это
знакочередующийся ряд.

; .

Поэтому,
ограничившись суммой первых трех членов,
получаем
.

Приближенное вычисление определенных интегралов

Многие
практически нужные интегралы не могут
быть вычислены с помощью формулы
Ньютона-Лейбница, так как первообразная
не может быть выражена через конечное
число элементарных функций.

Однако,
если подынтегральная функция разлагается
в степенной ряд, а пределы интегрирования
принадлежат области сходимости, то
можно вычислить определенный интеграл
с заданной степенью точности.

Пример
25.
Вычислить
с точностью 0,0001.

Решение

1)
Разложим подынтегральную функцию в
ряд:

,

.

1. Проинтегрируем
   его почленно

1. Получили
   знакочередующийся ряд. Для обеспечения
   требуемой точности достаточно взять
   сумму первых 7 членов, так как при
   

при

.

4)
Вычислим приближенно интеграл с одной
запасной цифрой.

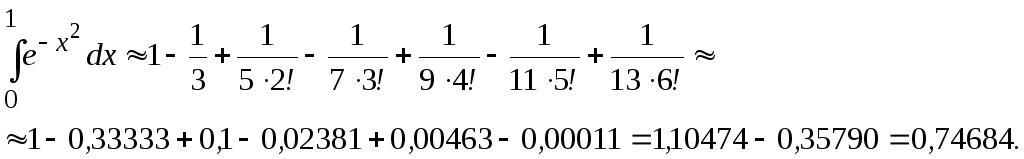
Округляя,
получим
.

Приближенное решение дифференциальных уравнений

Степенные
ряды широко используются при интегрировании
дифференциальных уравнений. В этом
случае решение задачи Коши

;
;ищется в виде степенного ряда.

Пример
26.
Найти первые пять членов разложения в
степенной ряд решения задачи Коши
,.

Решение

Так
как начальное условие задано при
,
то

(начальное
условие).

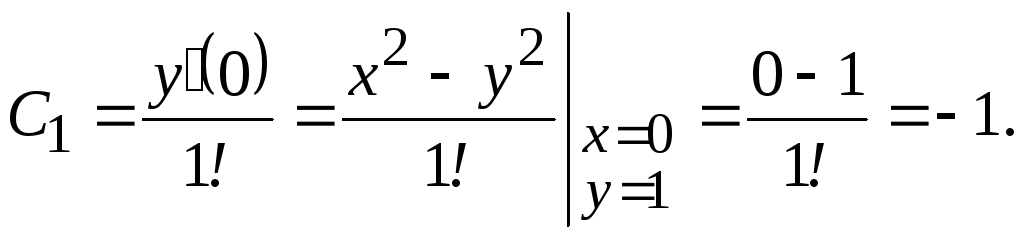
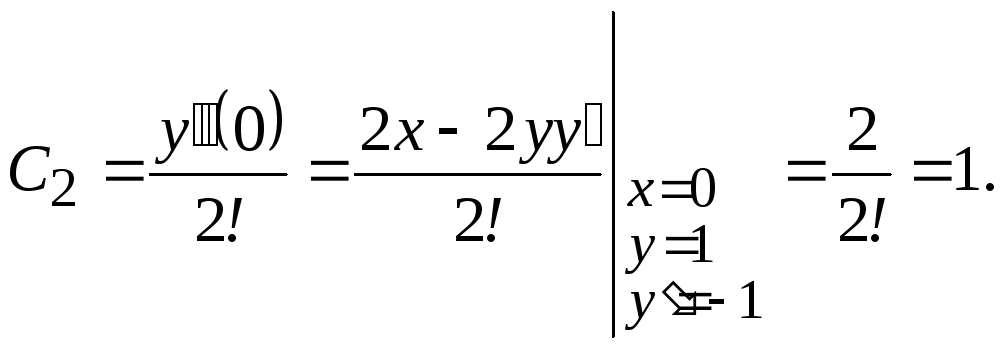
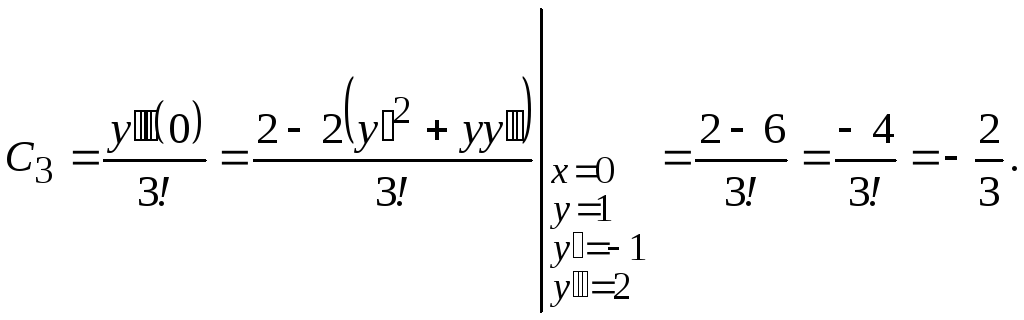
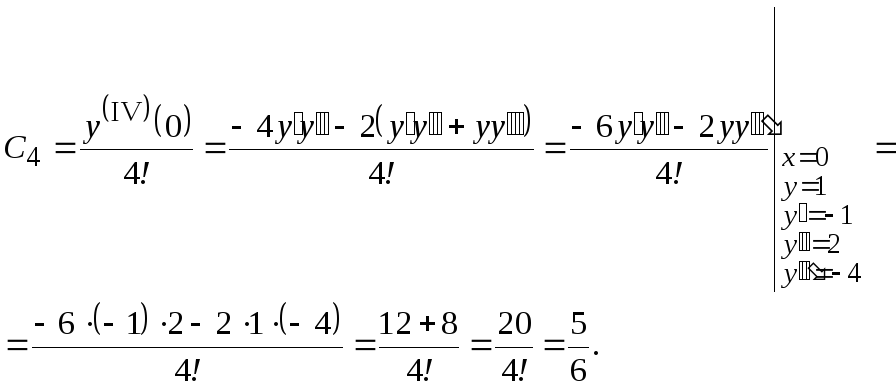
Получаем
ряд

Литература

1
Пискунов Н.С. Дифференциальное и
интегральное исчисление, т.2. – М.: Наука,
1976 (и последующие издания).

2
Минюк С.А., Самаль С.А., Шевченко Л.И.
Высшая математика для экономистов, т.1
– Мн.: Элайда, 2003.

3
Минюк С.А., Ровба Е.А. Высшая математика.
– ГрГУ, 2000.

4
Колобов А.М. Избранные главы высшей
математики. – Мн.: Высшая школа, 1965.

5
Данко П.Е., Попов А.Г., Кожевникова Т.Я.
Высшая математика в упражнениях и
задачах. – М.: Высшая школа, 1989.

6
Гусак А.А. Пособие к решению задач по
высшей математике. – Мн.: Вышэйшая школа,
1967.

7
Гурский Е.И. Руководство к решению задач
по высшей математике. Часть I.
– Мн.: Вышэйшая школа, 1989.

С
О Д Е Р Ж А Н И Е

ЧИСЛОВЫЕ РЯДЫ Числовой ряд. Общий член ряда Сходящиеся и расходящиеся ряды Основные свойства сходящихся рядов Признаки сходимости числовых рядов Необходимый признак сходимости ряда Знакоположительные числовые ряды Достаточные признаки сходимости знакоположительных рядов ЗНАКОЧЕРЕДУЮЩИЕСЯ И ЗНАКОПЕРЕМЕННЫЕ РЯДЫ Знакочередующиеся ряды Знакопеременные ряды ФУНКЦИОНАЛЬНЫЕ РЯДЫ Функциональный ряд и его область сходимости Степенные ряды РАЗЛОЖЕНИЕ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ В СТЕПЕННЫЕ РЯДЫ ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ С ПОМОЩЬЮ СТЕПЕННЫХ РЯДОВ Приближенное вычисление значений некоторых функций Приближенное вычисление корней Приближенное вычисление определенных интегралов Приближенное вычисление дифференциальных уравнений Литература

3 3 3 4 5 5 6 7 15 15 17 20 20 21 24 26 26 28 29 30 31

План
2004/2005, поз.103

Гладкова
Галина Александровна

Гладков
Лев Львович

Соседние файлы в предмете Высшая математика

• #
• #
• #
• #
• #