Как найти приближенное значение с помощью графика - Сайт, где вы сможете решить свои вопросы

Евгений Фомин

Мудрец

(13839),
закрыт

11 лет назад

Задание: построить график функций y=3^x и, используя этот график, найти приближенно:
1) 3^23; 2) 3^-1,5 ну и так далее.
Как найти число на графике???
P.S. Я думаю что надо сделать из чисел функцию а именно:
1) y=3^2/3; 2) y=3^-1,5
Ну или подскажите как бы вы сделали! Очень надо!
P.S.S. ^-возведение в степень.

Игорь Щёголев

Мыслитель

(7018)

11 лет назад

Если вас просят найти приближенно по графику, значит вам нужно найти на оси Ох значение 2/3 (0,(6) ), восстановить перпендикуляр из этой точки, и найти ординату пересечения этого перпендикуляра с графиком вашей функции, это и будет приближенное значение. Так как построение графическое, то ни о какой точности говорить не приходится (а вот если вы посчитаете 3^23- это будет точное аналитическое выражение).

Источник

Вычислить приближенное значение функции

Исследуем график функции y=f(x), для этого задайте функцию f(x).

Примеры

С применением степени
(квадрат и куб) и дроби

С применением синуса и косинуса

Гиберболические синус и косинус

Гиберболические тангенс и котангенс

Гиберболические арксинус и арккосинус

Гиберболические арктангенс и арккотангенс

Что исследует?

Для периодических функций идет исследование графика функции только на промежутке периода

Наш калькулятор позволяет исследовать график функции. Но пока что нет возможности находить область определения функции

Что умеет находить этот калькулятор:

Область определения функции: Да. Умеет определять только точки, в которых знаменатель функции обращается в нуль, но в остальных случаях:
Умеет определять точки пересечения графика функции с осями координат: Да
Экстремумы функции: интервалы (отрезки) возрастания и убывания функции: Да
Точки перегибов графика функции: перегибы: интервалы выпуклости, вогнутости (впуклости): Да
Вертикальные асимптоты : Да (это завязано с областью определения функции, на точки, где знаменатель функции обращается в нуль)
Горизонтальные асимптоты графика функции: Да
Наклонные асимптоты графика функции: Да
Четность и нечетность функции: Да
Минимум и максимум функции: Да

Правила ввода выражений и функций

3.14159.. e Число e — основание натурального логарифма, примерно равно

2,7183.. i Комплексная единица oo Символ бесконечности — знак для бесконечности

Применение дифференциала в приближенных вычислениях

Напомним, что дифференциалом функции называется выражение . Дифференциал функции можно применять для приближенного вычисления функции в окрестности точки зная значение функции и ее производной в самой точке .

Приближенная формула имеет вид:

Если представить геометрически, то мы вычисляем значение функции ,как если бы она была касательной в точке .

Имеется два момента, которые нужно учесть.

Первое . Мы не знаем, насколько функция может измениться при переходе от точки к точке . Это зависит от того насколько меняется ее производная.

И второе , мы не можем оценить точность нашего вычисления. Поэтому задачу о вычислении приближенного значения функции ставят так: найти значение функции в точке alt=»изменение точки х0″ width=»87″ height=»25″ />используя дифференциал. Иногда просят оценить погрешность или относительную погрешность, зная точное значение в точке alt=»изменение точки х0″ width=»87″ height=»25″ />.

Приведем несколько примеров.

Пример 1

Пусть мы хотим найти приближенное значение функции в точке , используя дифференциал, зная значение функции и ее производной в точке : и оценить абсолютную и относительную погрешность. По приближенной формуле имеем:.

Поскольку , то абсолютная погрешность , и относительная погрешность.

Посмотрим, как влияет расстояние между точками и на погрешность и относительную погрешность. Пусть мы хотим найти приближенное значение функции в точке . Тогда, применяя приближенную формулу, найдем: . С другой стороны , так что абсолютная погрешность , и относительная погрешность .

Мы видим, что при удалении точки достаточно далеко от исходной , погрешность может сильно возрасти.

Сделаем следующий вывод: для достаточно близких точек погрешность может быть вполне удовлетворительной. Но самое главное, мы не можем вычислить значение в близкой точке с нужной нам точностью. Это можно сделать, используя формулу Тейлора и взяв в ней достаточное число членов.

Рассмотрм еще несколько примеров.

Пример 2

Найти приближенное значение , используя дифференциал. Находим:

Подставим в приближенную формулу: .

Найдем абсолютную и относительную погрешности наших вычислений. Точное значение .

Абсолютная погрешность , относительная погрешность .

Относительная погрешность маленькая. Это связано с тем, что мы взяли значение в точке близкой к исходной точке .

Пример 3

Найти приближенное значение , используя дифференциал. Исходной точкой, в которой мы знаем значение функции и ее производной, берем точку.

По приближенной формуле находим: .

По калькулятору найдем точное значение функции .

Оценим абсолютную погрешность: .

Относительная погрешность.

Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.

Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.

Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.

Решение.

Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).

В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.

В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.

Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.

Применение производной к приближенным вычислениям

Выберем на кривой (y=f(x)) начальную точку (A(x_0,y_0)). Если мы начнем перемещаться к точке (B(x,y)), то приращению аргумента (triangle x=AC) соответствует приращение функции (triangle y=BC). Если считать, что кривая приблизительно совпадает со своей касательной при малых приращениях (triangle x), то (BCapprox MC) и (triangle yapprox dy).

п.2. Алгоритм приближенных вычислений с помощью дифференциала

На входе: функция (y=f(x)), точка x*, в которой нужно посчитать значение функции
Шаг 1. Определяем ближайшую к x* начальную точку (x_0), для которой значение (y_0=f(x_0)) известно или легко находится.
Шаг 2. Находим выражение для первой производной (f'(x)).
Шаг 3. Находим значение производной в начальной точке (f'(x_0))
Шаг 4. Находим линейное приближение значения функции $$ y^*approx f(x_0)+f'(x_0)(x^*-x_0) $$ На выходе: значение y*

Например:
1) Найдем значение корня (sqrt)
Функция (y=sqrt, x^*=65)
Начальная точка (x_0=64). Начальное значение функции (y_0=sqrt=8)
Производная: (f'(x)=frac>)
Производная в начальной точке: (f'(x_0)=frac>=frac)
Подставляем: (y^*=sqrtapprox 8+frac(65-64)=8+frac=8,0625)
Оценим относительную ошибку для полученного результата.
Значение, полученное на калькуляторе: (sqrtapprox 8,062258). Откуда: $$ partial=fraccdot 100textapprox 0,003text $$ Таким образом, в данном случае линейное приближение имеет высокую точность, т.к. для (x_0=64) и (x^*=65) кривая (y=sqrt) очень близка к прямой, т.е. своей касательной.

2) Найдем значение корня (sqrt)
Пусть начальная точка (x_0=4). Начальное значение функции (y_0=sqrt=2)
Производная в начальной точке: (f'(x_0)=frac>=frac14)
(y^*=sqrtapprox 2+frac14 (5-4)=2,25)
Значение, полученное на калькуляторе: (sqrtapprox 2,23607) $$ partial=fraccdot 100textapprox 0,06text $$ Точность стала хуже. Однако, её можно повысить, если взять (x_0=4,84).

3) Найдем (sqrt) при (x_0=4,84).
(y_0=sqrt =2,2)
Производная в начальной точке: (f'(x_0 )=frac=frac)
(y^*=sqrtapprox 2,2+frac(5-4,84)=2,2+frac=2,2+frac=2,23636…)
Значение (sqrtapprox 2,23607) $$ partial=fraccdot 100textapprox 0,01text $$ Точность повысилась.

Вывод: точку (x_0) следует выбирать, исходя из поведения функции (y=f(x)) в окрестности (x^*). Чем ближе (x_0) к (x^*) и чем ближе кривая к касательной, тем точнее будет линейное приближение с помощью дифференциала.

п.3. Приближение с точностью до квадрата приращения

Например:
1) Найдем квадратичное слагаемое для (x^*=65, x_0=64, y=sqrt)
Вторая производная: (f»(x)=left(frac>right)’=frac12cdotleft(-frac12right)cdotfrac>=-frac>) $$ frac(x^*-x_0)^2=-frac=-fracapprox -0,0002 $$ Значит, квадратичное слагаемое дает поправку в 4-м знаке.
Используя полученное выше линейное приближение, получаем: $$ y^*=sqrtapprox 8,0625-0,0002=8,0623approx 8,062 $$ Квадратичное слагаемое указывает, что округлить результат нужно до 3-го знака после запятой.

2) Найдем квадратичное слагаемое для (x^*=5, x_0=4, y=sqrt) $$ frac(x^*-x_0)^2=-frac=-fracapprox -0,02 $$ Получаем: $$ y^*=sqrtapprox 2,25-0,02=2,23approx 2,2 $$ Квадратичное слагаемое указывает, что округлить результат нужно до 1-го знака после запятой.

3) Найдем квадратичное слагаемое для (x^*=5, x_0=4,84, y=sqrt) $$ frac(x^*-x_0)^2=-frac=-fracapprox -0,0003 $$ Получаем: $$ y^*=sqrtapprox 2,2367-0,0003=2,2364approx 2,236 $$ Квадратичное слагаемое указывает, что округлить результат нужно до 3-го знака после запятой.

п.4. Полезные формулы приближений для функций вблизи нуля

Рассмотрим свойства приближений некоторых функций при (x_0=0) и (triangle x=xrightarrow 0).
В разложении ограничимся слагаемым (y(0)) и линейным приближением. Только если линейное приближение равно 0, будем учитывать слагаемое квадратичного приближения.
1) (y=sinx)
(y’=cosx, y»=-sinx)
(y(0)=0, y'(0)=1, y»(0)=0)
(sinxapprox 0+1cdot x-frac02cdot x^2approx x)

4) (y=e^x)
(y’=y»=e^x)
(y(0)=y'(0)=y»(0)=1)
(e^xapprox 1+1cdot x+frac12cdot x^2approx 1+x)
Пренебрегаем (frac) как очень малым слагаемым.

Источник

Взаимосвязи графика функции и графика ее производной

Приближенное и точное определение производной функции

Приближенным значением производной функции в точке $x_{0}$ со сдвигом 0,01 называется значение

$f’left(x_0right)approx frac{fleft(x_0+0,01right)-fleft(x_0right)}{left(x_0+0,01right)-left(x_0right)}$ $f’left(aright)approx frac{fleft(a+hright)-fleft(aright)}{left(a+hright)-left(aright)}$ Точное: $f’left(aright)=lim frac{fleft(a+hright)-fleft(aright)}{left(a+hright)-left(aright)}$ при $lim h=0$

Производная в точке – это отношение: (приращение самой функции) / (малое приращение аргумента в этой точке).
Физический смысл – производная функции показывает скорость изменения функции: роста или убывания функции.
Геометрический смысл – производная в каждой точке равна тангенсу угла наклона касательной, проведенной к ее графику.

Пример 1: Дана функция $fleft(xright)=x^3-3x+2$ . Вычислить приближенное производную $f’left(x_0right)$

в точке $x_0=1,2$ со сдвигом $h=0,2$ ? $Rightarrow$ $f’left(1,2right)approx frac{bigtriangleup fleft(xright)}{bigtriangleup x}approx frac{fleft(1,2+0,2right)-fleft(1,2right)}{1,4-1,2}=frac{1,4^3-3cdot 1,4+2-left(1,2^3-3cdot 1,2+2right)}{0,2}=1,555$
В реальности мы получили тангенс угла наклона секущей, проходящей в точках графика $left(1,2;fleft(1,2right)right)$ и $left(1,4;fleft(1,4right)right)$
в точке $x_0=0,5$ со сдвигом $h=0,0001$ ? $Rightarrow$ $f’left(0,4right)approx frac{fleft(0,4+hright)-fleft(0,4right)}{left(0,4+hright)-0,4}=frac{left(0,4+hright)^3-3cdot left(0,4+hright)+2-left(0,4^3-3cdot 0,4+2right)}{h}=frac{left(0,4+hright)^3-0,4^3}{h}-frac{3cdot left(0,4+hright)-3cdot 0,4}{h}=frac{0,4^3+3cdot 0,4^2cdot h+3cdot 0,4h^2+h^3-0,4^3}{h}-3=left(3cdot 0,4^2-3right)+hcdot left(3cdot 0,4+hright)approx 2,5201$
точное производное $f’left(0,4right)=3cdot 0,4^2-3=2,52$ при $hsim 0$ !
в точке $x_0=0,5$ со сдвигом $h=0,0001$ ? $Rightarrow$ $f’left(0,4right)approx frac{fleft(0,4+hright)-fleft(0,4right)}{left(0,4+hright)-0,4}=frac{left(0,4+hright)^3-3cdot left(0,4+hright)+2-left(0,4^3-3cdot 0,4+2right)}{h}=frac{left(0,4+hright)^3-0,4^3}{h}-frac{3cdot left(0,4+hright)-3cdot 0,4}{h}=frac{0,4^3+3cdot 0,4^2cdot h+3cdot 0,4h^2+h^3-0,4^3}{h}-3=left(3cdot 0,4^2-3right)+hcdot left(3cdot 0,4+hright)approx 2,5201$
точное производное $f’left(0,4right)=3cdot 0,4^2-3=2,52$ при $hsim 0$ !
$f’left(-0,6right)$ “На глаз по графику” ? $Rightarrow$ значения $fleft(-0,6right)approx 3,6$ и в сдвинутой $fleft(-0,4right)approx 3,1$. скорость изменения, наклон $f’left(-0,6right)approx frac{fleft(-0,4right)-fleft(-0,6right)}{-0,4-left(-0,6right)}approx frac{3,1-3,6}{0,2}=-2,5$

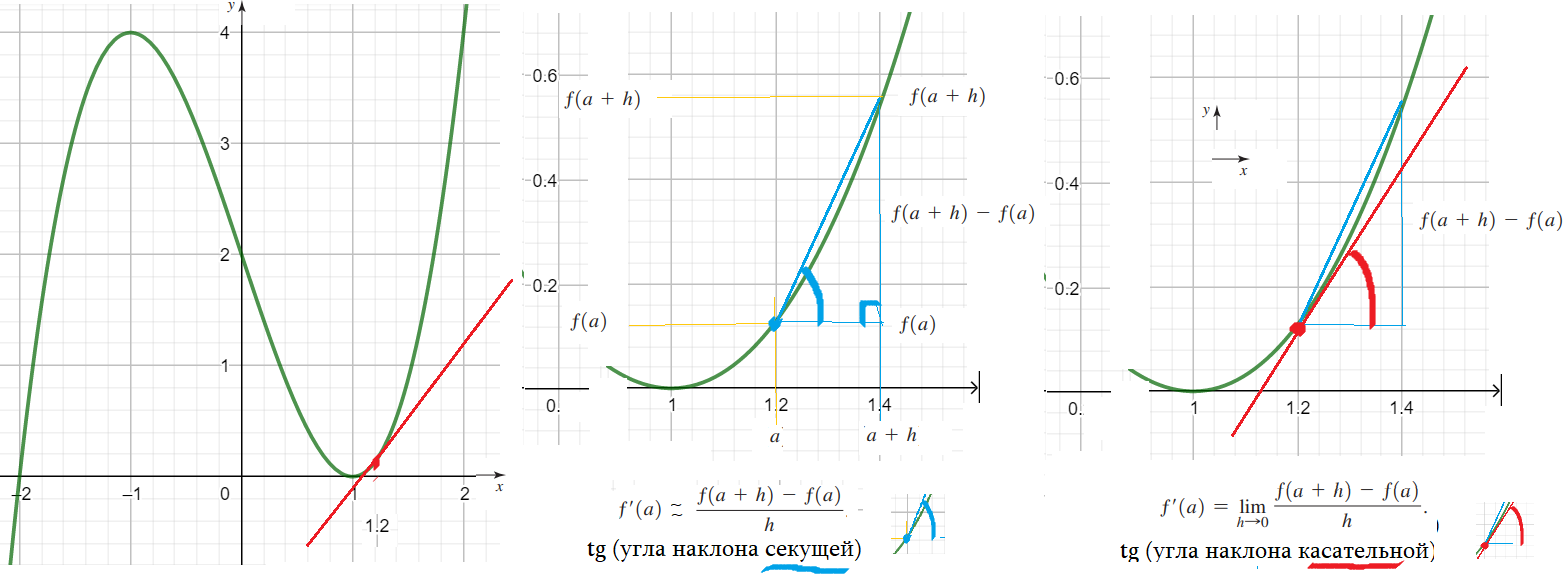
Секущая графика функции – прямая, проходящая в точках графика $left(x_1;fleft(x_1right)right) и left(x_2;fleft(x_2right)right)$.
Наклон секущей – тангенс угла наклона секущей к х – оси, равен $tg s=frac{fleft(x_2right)-fleft(x_1right)}{x_2-x_1}$.
Касательной к графику в точке х = а – предел секущих в точках $left(a;fleft(aright)right) и left(a+h;fleft(a+hright)right)$ при h стремящемся к нулю.
Наклон касательной – тангенс угла $k=frac{fleft(x+0,000001right)-fleft(xright)}{x+0,000001-x}$ . Точнее, “примерно равен”. Точнее: при малом h !.
….еще точнее “в пределе равен”. lim $frac{fleft(a+hright)-fleft(aright)}{h}$. Точка (a+h; f(a+h)) сближается с точкой (a; f(a)) при малом h !.
Производная f'(a) равен тангенсу угла наклона касательной к графику функции f в точке (a, f(a)).

Пример 2: По графику функции найти производную – наклон касательной в указанной точке.

Смотрим на касательную в точке х = 3. Для нахождения тангенса наклона надо “увидеть” прямоугольный треугольник с катетами вдоль х- и у- осей и с гипотенузой вдоль касательной.
Считаем по клеткам: f'(3) = – 1 : 3 1 клетка по у – оси вниз (-), 3 клетки по х – оси вправо (+) .
На 2-м рисунке: g'(5) = 2 : 2 2 клетки по у – оси вверх (+), 2 клетки по х – оси вправо (+) .

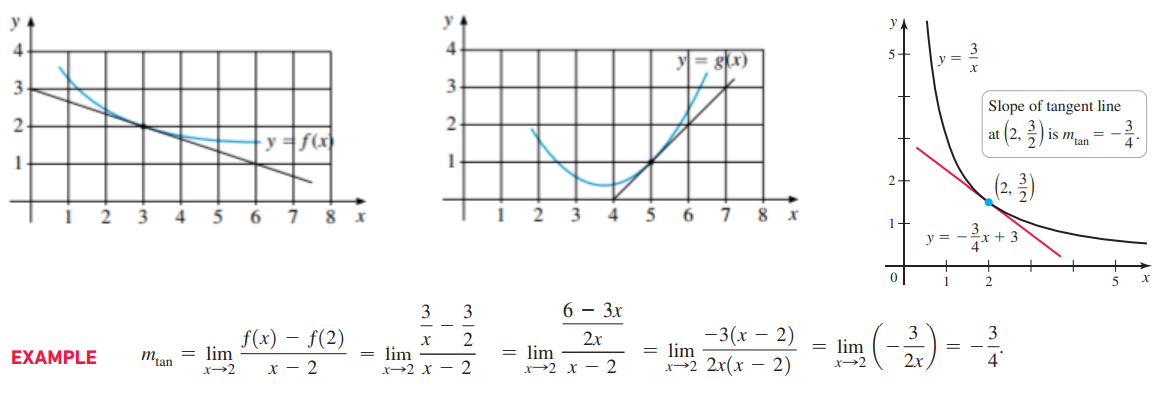
Уравнение касательной к графику функции $y=fleft(xright)$ в точке $x=x_0$ : $y=fleft(x_0right)+f’left(x_0right)cdotleft(x-x_0right)$ – касательная, прямая

Функция $y=fleft(xright)$ и её касательная $y=ax+b$ в точке касания $x=x_0$ имеют одинаковые значения, наклон, производные.
Наклон касательной = производное функции $a=f’left(x_0right)$ определяет как “течет” график: растет, убывает?
Наклон положительный – касательная справа-налево – производная положительна – функция растет – график функции “течет” вверх.
Наклон отрицательный – касательная слево-направо – производная отрицательна – функция убывает – график функции “течет” вниз, по склону.

Производная – как детектор поведения функции

Вопрос: Как влияет на поведение функции $fleft(x_0right)$ около точки $x=x_0$ значение производной $f’left(x_0right)$ ?

Из определения производной в точке $x=x_0$ $Rightarrow$ $f’left(x_0right)approxfrac{fleft(x_0+0,01right)-fleft(x_0right)}{x_0+0,01-x_0}$
выразим значение функции чуть правее точки $x_0$ : $fleft(x_0+0,01right)approx fleft(x_0right)+0,01f’left(x_0right)$. Значит, функция будет иметь большее значение правее от $x_0$ , если только $f’left(x_0right) > 0$.
Аналогичные рассуждения для значения функции чуть левее. Из $f’left(x_0right)approxfrac{fleft(x_0-0,01right)-fleft(x_0right)}{x_0-0,01-x_0}$ $Rightarrow$ $fleft(x_0-0,01right)approx fleft(x_0right)-0,01cdot f’left(x_0right)$ $Leftrightarrow$ понятно почему поведение функции левее $x_0$ зависит от знака производной в точке $x_0$.
Сформулирует ответы на вопрос о влиянии знака производной в данной точке:
если $f’left(x_0right) > 0$ то $fleft(x_0-0,01right) < fleft(x_0right) < fleft(x_0+0,01right)$ $Rightarrow $ функция растет (см. слева направо).
если $f’left(x_0right) < 0$ то $fleft(x_0-0,01right) > fleft(x_0right) > fleft(x_0+0,01right)$ $Rightarrow $ функция убывает, график идет вниз.
если $f’left(x_0right)=0$ то ситуации более запутанные: при $fleft(x_0-0,01right) < fleft(x_0right) > fleft(x_0+0,01right)$ точка $x=x_0$ называется точкой максимума. В нем функция “выше”, чем по-соседству хоть слева, хоть справа.
В случае $fleft(x_0-0,01right) > fleft(x_0right) < fleft(x_0+0,01right)$, $x=x_0$ – точка минимума. Если ни то, ни другое, то точка перегиба.

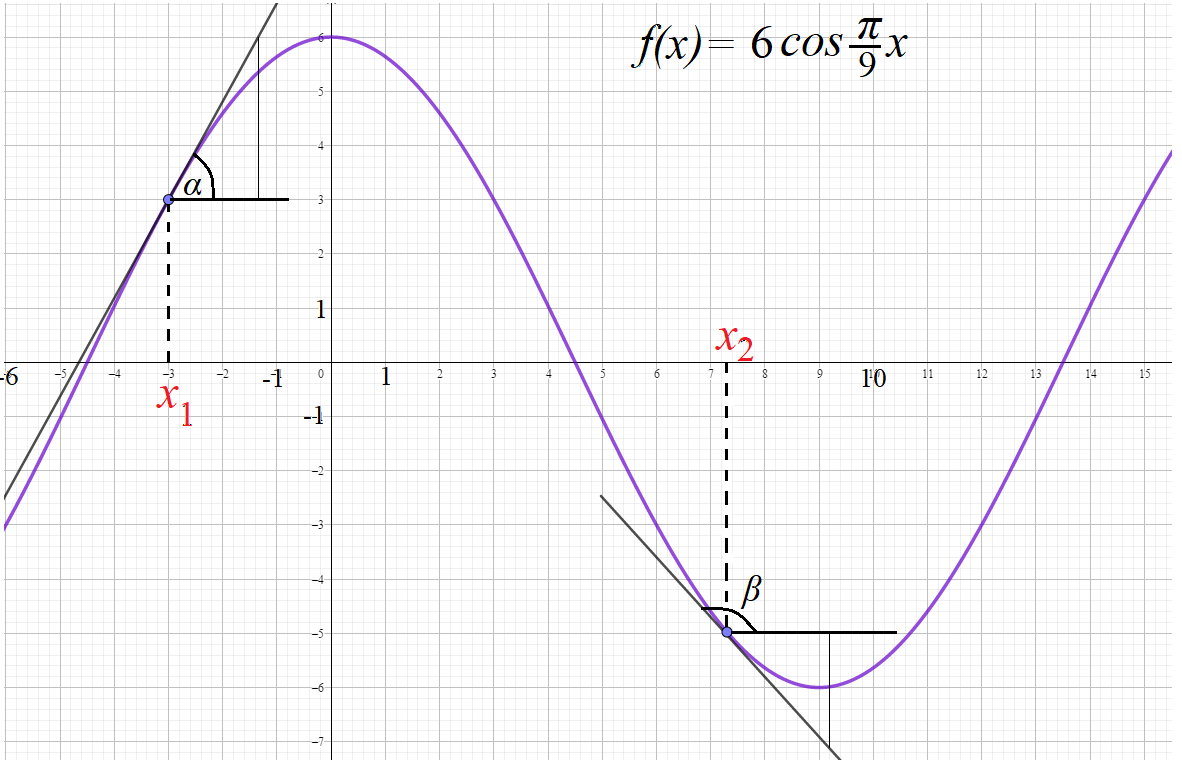
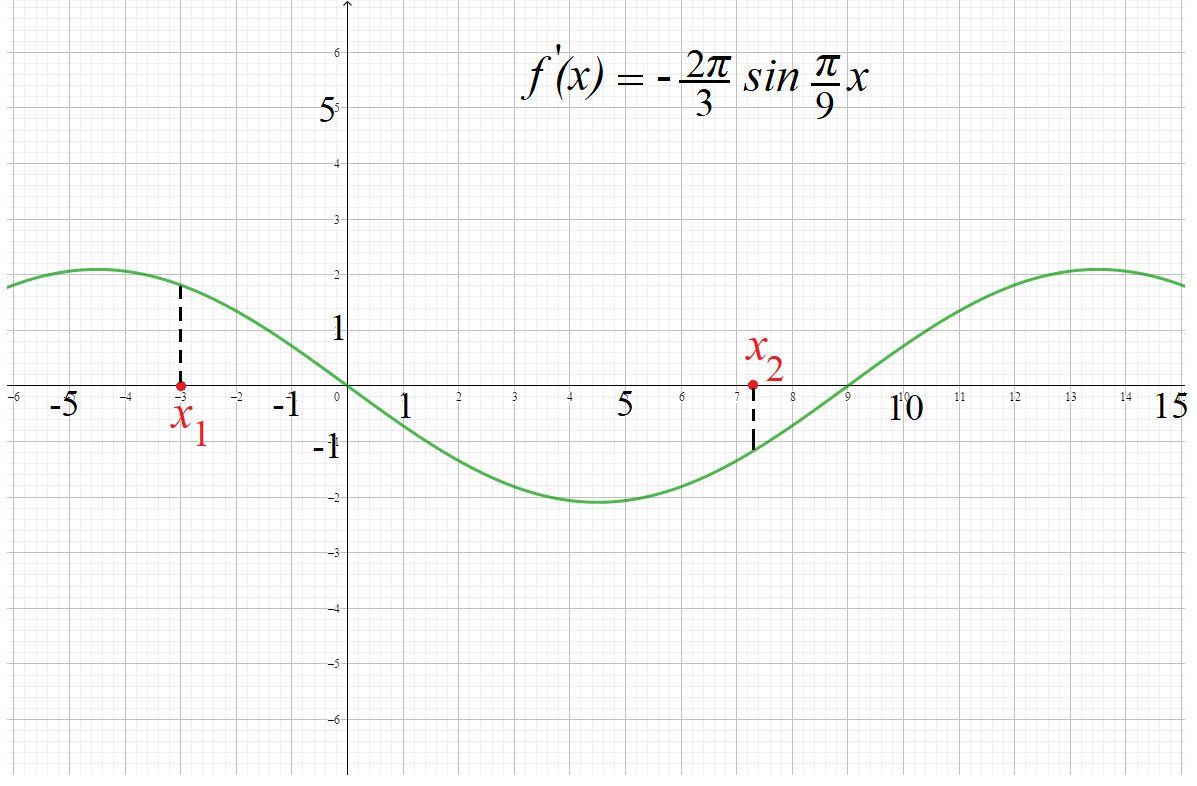
Пример 2: Каково взаимовлияние графика $fleft(xright)=6cosfrac{pi}{9}x$ и графике ее производной $f’left(xright)=-frac{2pi}{3}sinfrac{pi}{9}x$

Производная от какой-то функции – это некая, связанная с ней функция, характеризующая поведение самой функции
Рассмотрим точку $x_1=-3$ . В нем сама функция равна $fleft(-3right)=6cosfrac{pi}{9}(-3)=3$ , а ее производная – $f’left(-3right)=-frac{2pi}{3}sinfrac{pi}{9}(-3)approx1,77$,
График график проходит в точке $(-3;3)$. Каково поведение графика около этой точки? Растет или убывает?
Насколько быстро растет или убывает? На все эти вопросы ответы дает производная. Производная здесь $(-3;3)$ положительна, поэтому растет!
Около точки $x_1=-3$ функция приближенно $fleft(xright)approx 3+1,77cdot(x+7)$
Т.к. производная равна $1$, то тангенс угла наклона касательной, проведенной к графику нашей функции в данной точке ($-3; 3$) равен $1$.
Значит, касательная направлена под углом $45$ градусов, ведь $tg45=1$.
Значит, функция около этой точки растет “умеренно”, примерно под углом 45 градусов.

Значение производной $f’left(x_0right)$ в какой-либо точке указывает на рост или убывание исходной функции $fleft(xright)$ около этой точки $x_0$. Зная числовое значение производной, можно определить как ведет себя функция: стоит ли на месте, растет или убывает и как быстро изменяется. Производная от функции помогает узнать в каждой точке характер скорости изменений, поведения графика самой функции.

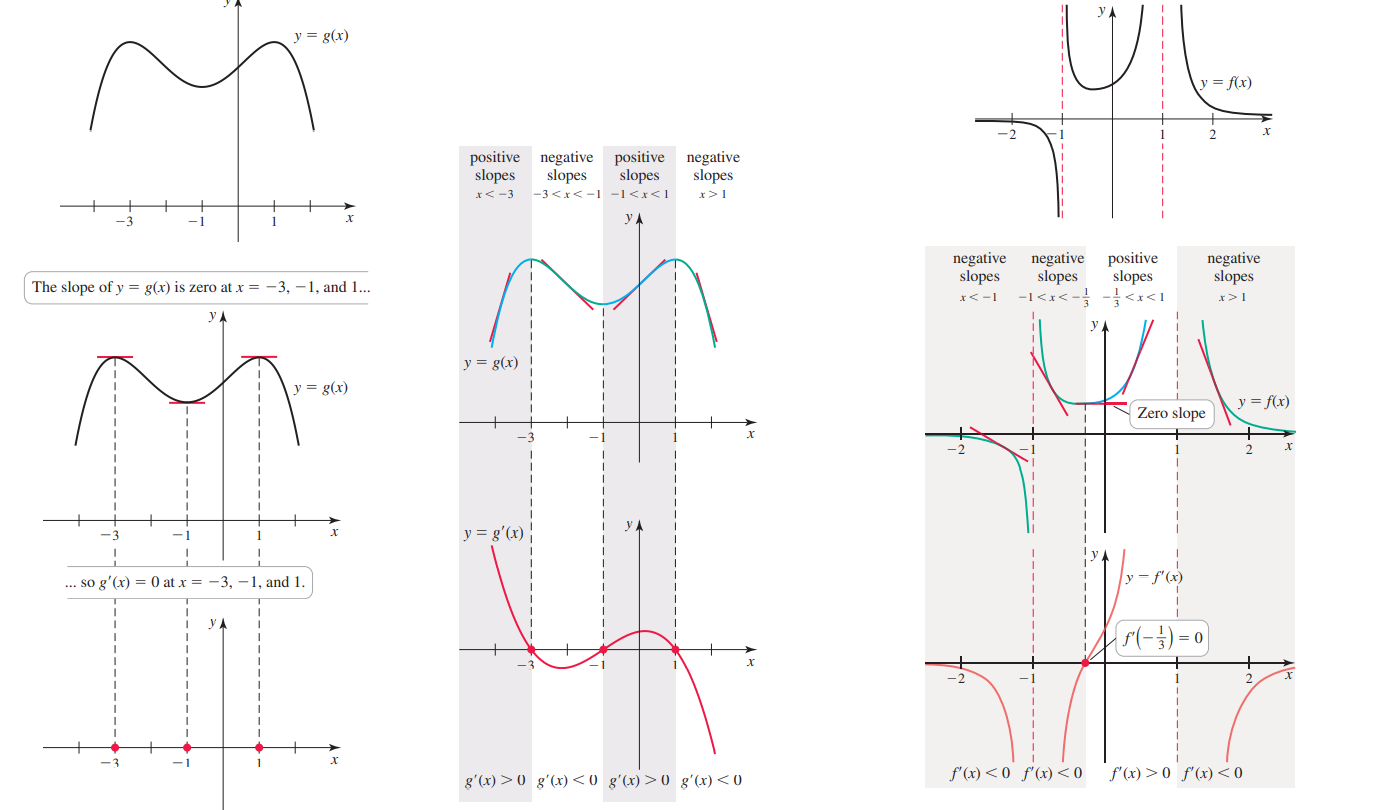
В тех точках, где функция растет – график поднимается вверх (если смотреть слева направо) – касательная к графику в этой точке наклонена вправо – – тангенс наклона положительный – производная в этой точке имеет положительное значение.
В тех точках, где функция убывает – график опускается вниз (если смотреть слева направо) – касательная к графику в этой точке наклонена влево – – тангенс наклона отрицательный, тупой угол – производная в этой точке имеет отрицательное значение.
Производная = 0 функция “остановилась”, “касательная горизонтальна” точка экстремума: минимум, максимум или перегиб.
Вторая производная в точке x показывает скорость изменения скорости, т.е. ускорение в этой точке. Вторая производная = 0 означает “ускорение обнулилось”. больше нуля – выпоукло вниз (min), меньше нуля – вверх (max).

Пример 3: Указать интервалы монотонности функции $fleft(xright)=x^3-3x+2$ . ;

$f’left(xright)=left(x^3-3x+2right)’=3x^2-3$ находим производную от нашей функции
$f’left(xright)>0$ $3x^2-3>0$ $left(-infty ;-1right) left(1;infty right)$ интервалы возрастания, неравенство больше
$f’left(xright)<0$ $3x^2-3<0$ $left(-1;1right)$ интервалы убывания, производное минус
$M_f$ области монотонности $ left(-infty ;-1right)+left(-1;1right)+left(1;infty right)$

Точки экстремумов функции. min-max

Из $f’left(x_0right)approxfrac{fleft(x_0+0,01right)-fleft(x_0right)}{x_0+0,01-x_0}$ выразим значение функции чуть правее точки $x_0$ : $fleft(x_0+0,01right)approx fleft(x_0right)+0,01f’left(x_0right)$.
Значит, функция будет иметь большее значение правее от $x_0$ , если только $f’left(x_0right) > 0$.

Аналогичные рассуждения для значения функции чуть левее. Из $f’left(x_0right)approxfrac{fleft(x_0-0,01right)-fleft(x_0right)}{x_0-0,01-x_0}$ $Rightarrow$ $fleft(x_0-0,01right)approx fleft(x_0right)-0,01cdot f’left(x_0right)$ $Leftrightarrow$ понятно почему поведение функции левее $x_0$ зависит от знака производной в точке $x_0$.

Итак:

если $f’left(x_0right) > 0$ то $fleft(x_0-0,01right) < fleft(x_0right) < fleft(x_0+0,01right)$ $Rightarrow $ функция растет (см. слева направо).
если $f’left(x_0right) < 0$ то $fleft(x_0-0,01right) > fleft(x_0right) > fleft(x_0+0,01right)$ $Rightarrow $ функция убывает, график идет вниз.
если $f’left(x_0right)=0$ то ситуации более запутанные: при $fleft(x_0-0,01right) < fleft(x_0right) > fleft(x_0+0,01right)$ точка $x=x_0$ называется точкой максимума. В нем функция “выше”, чем по-соседству хоть слева, хоть справа.
В случае $fleft(x_0-0,01right) > fleft(x_0right) < fleft(x_0+0,01right)$, $x=x_0$ – точка минимума. Если ни то, ни другое, то точка перегиба.

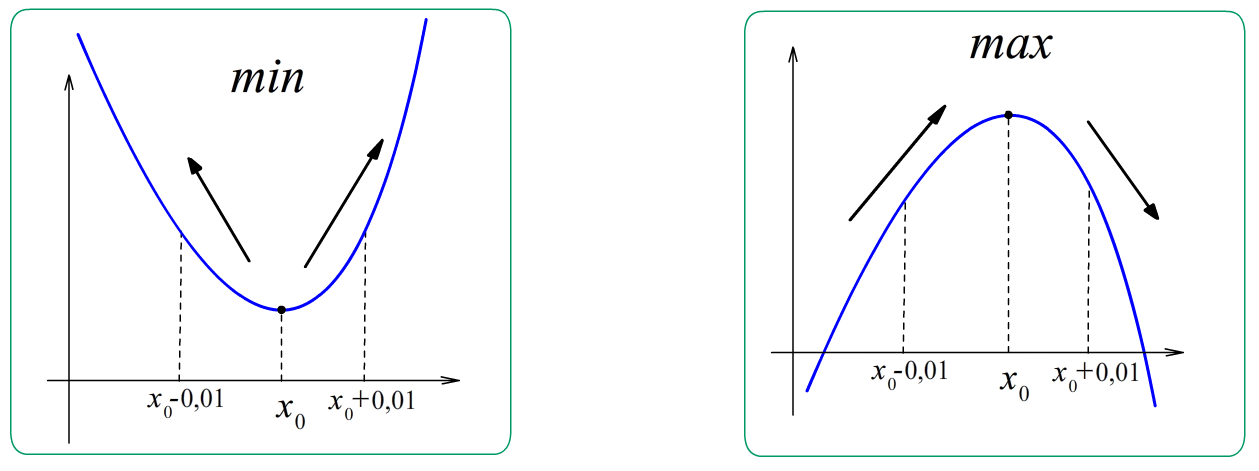
Определение: Точка, в которой производная обнуляется, называется экстремумом (минимум, максимум, перегиб).
В этой точке наклон графика равен нулю, т.е. касательная к графику горизонтальна.

Точка максимума – если функция растет, “застывает” в $x_0$” , затем убывает.
Производная функции больше нуля, в $x_0$ обнуляется, затем отрицательна.

Точка минимума наоборот – если функция убывает, “застывает” в $x_0$” , затем растет.
Производная меньше нуля, равна нулю в $x_0$”, затем положительна.

Нахождение точки минимума (максимума) функции $y=fleft(xright)$:

Точка минимума – это $x$ – число, в котором производная равна нулю, а сама исходная функция от убывания переходит к возрастанию. Надо “взять” производную исходной функции и составить уравнение экстремума “производная равна нулю”. Среди точек экстремума найти точку минимума.

Есть три способа:

по поведению “рост / убывание” исходной функции ;
либо поведение “отрицательности / положительности” производной;
либо знак второй производной в этой точке; если 2-ая производная (“производная от производной”) в точке $x_0$ положительна, то это минимум.

min: $f’left(x_0right)=0$ , $fleft(x_0-0,01right) > fleft(x_0right) < fleft(x_0+0,01right)$ , $f’left(x_0-0.01right) < 0$ , $f’left(x_0+0.01right) > 0$ ; $f”left(x_0right) > 0$.

max: $f’left(x_0right)=0$ , $fleft(x_0-0,01right) < fleft(x_0right) > fleft(x_0+0,01right)$ , $f’left(x_0-0.01right) > 0$ , $f’left(x_0+0.01right) < 0$ ; $f”left(x_0right) < 0$.

Обозначения множеств, областей

$D_f$ область определения функции

$Z_f$ область знакопостоянства, интервалы положительности, отрицательности

$M_f$ области монотонности функции, интервалы возрастания, убывания

$X_f$ экстремумы функции, перечисление х – точек

$T_f$ уравнение касательной к функции в указанной х – точке

$E_f$ области значений функции, все у – значений

Упражнения:

Источник

Теоретический материал:

Численное
дифференцирование используется для
приближенного вычисления производных
функции заданной таблицей и для функций,
которые по разным причинам неудобно
или невозможно дифференцировать
аналитически. В последнем случае
вычисляется таблица функции в окрестности
исследуемой точки и по этим значениям
вычисляется приближенное значение
производной.

Рассмотрим численный
метод решения дифференциального
уравнения первого порядка вида у’=f(x,y),
который носит название метода Эйлера.

y₁=y₀+h*f(x₀,y₀)

x₁=x₀+h

Расчетные
формулы для 1-го шага

y_i+1=y_i+h*f(x_i,y_i)

x_i+1=x_i+h

Расчетные
формулы для i-го шага

Примеры вычислений

Дано у’= xy²,
x₀=0,
y₀
=2, (или по другому y(0)=2),
h=0,1.
Найти с точностью до десятых y(0,2)
(т.е. y₂).

Алгоритм
решения поместим для удобства в таблицу.

шаг i	x_i	y_i	у’= x_iy_i²	Δy=h*f(x_i,y_i)
0	0	2	0·2²=0	0,1·0=0
1	0+0,1=0,1	2+0=2	0,1·2²=0,4	0,1·0,4=0,04
2	0,1+0,1=0,2	2+0,04=2,04⋲2

Ответ: y(0,2)⋲2

Задание для
практической работы по теме «Решить
приближенно дифференциальное уравнение
вида y’=f(x,y) с начальным условием y(x₀)=y₀
(задачи Коши) методом Эйлера»

Вычислить значение
y(0,3)
для функции заданного вида с начальными
условиями y(0)=2
методом Эйлера.

Вариант 1. у’=y-x²y,

Вариант 2. у’=y+x²y

Вариант 3.
у’=(1-2x)·y²

Вариант 4. у’=(1-x²)·y

Вариант 5. у’=(y²-y)·x

Вариант 6. у’=4x-2y

Вариант 7. у’=2x-y

Вариант 8. у’=x+3y

Вариант 9. у’=4x+y

Вариант 10. у’=3x-2y+5

Практическая
работа № 18

Тема 4.3: “Приближенное вычисление значения функции y(X) в точке с помощью производной”.

Цель:
Вычислять
приближенное
значения функции y(x) в точке с помощью
производной.

Теоретический материал:

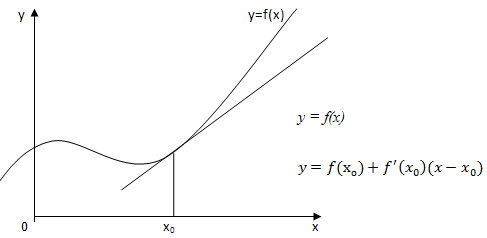
Вспомним уравнение
касательной к графику функции f(x) в точке
с абсциссой

.
Объяснение
по графику и записи рисунка. Каково
взаимное расположение точек графика
функции и точек касательной вблизи
точки касания с абсциссой

?
(Ответ: очень близко расположены). Что
это означает? Если функция y= f(x)
дифференцируема в точке

,
то значения функции в точках из окрестности
точки

очень
мало отличаются от значений функции,
задающей уравнение касательной, и для
всех значений х
из окрестности точки

можно
записать:

f(x)≈

.

Поскольку

x,
можно записать

f(x)≈
x

Пример вычисления

Пусть дана функция

и надо найти её значение при х=2,03.
Заметим, что при х
= 2 легко
вычислить f(2)=

=
77.

Применяя выведенную
формулу, получим: f(x)=f(2,03),

,
Δ x=
х-x₀=
2,03-2 =0,03;

f(2,03)=77+172·0,03=77+5,16=82,16.

Если произвести
вычисления на калькуляторе, то получается
f(2,03)=82,297634.
Как видим, приближенное значение,
полученное при помощи формулы, очень
мало отличается от точного значения
функции в данной точке.

Задание для
практической работы по теме
«Приближенное
вычисление значения функции y(x) в точке
с помощью производной»

Вычислить:

приближенное
значения функции y(x) с помощью производной;
точное значения
функции y(x) с помощью ПК или калькулятора;
абсолютную и
относительную погрешность.

Вариант1: 1,04¹⁵

Вариант2:

Вариант3: 0,99¹⁵

Вариант4:

Вариант5: 1,04¹⁰

Вариант6:

Вариант7: 0,98²⁵

Вариант8:

Вариант9: 1,02⁵⁰

Вариант10:

Практическая
работа № 19

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Вычислить приближенное значение функции

Примеры

Что исследует?

Правила ввода выражений и функций

Применение дифференциала в приближенных вычислениях

Применение производной к приближенным вычислениям

п.2. Алгоритм приближенных вычислений с помощью дифференциала

п.3. Приближение с точностью до квадрата приращения

п.4. Полезные формулы приближений для функций вблизи нуля

Взаимосвязи графика функции и графика ее производной

Точки экстремумов функции. min-max

Обозначения множеств, областей

Упражнения:

Теоретический материал:

Примеры вычислений

Тема 4.3: “Приближенное вычисление значения функции y(X) в точке с помощью производной”.

Теоретический материал:

Пример вычисления

Вам также может понравиться

Как найти страницу с помощью фото

Завал стопы во внутрь у детей как исправить

Как найти человека если знаешь его инстаграмм

Добавить комментарий Отменить ответ