Математика, 4 класс
Урок №14. Измерение площади фигуры с помощью палетки
Перечень вопросов, рассматриваемых в теме:
Площадь геометрической фигуры.
Вычисление площади фигур произвольной формы, используя палетку.
Глоссарий по теме:
Площадь – свойство фигур занимать место на плоскости.
Длина – свойство предмета “быть протяжённым в пространстве”
Палетка – прозрачная пластинка, разделенная на единицы площади.
Основная и дополнительная литература по теме урока:
- Математика: 4 класс: учебник в 2 ч. Ч.1/ М.И.Моро, М.А.Бантова, Г.В.Бельтюкова, С.И.Волкова, С.В.Степанова – М. Просвещение, 2016. – с. 36-38
- Всероссийские проверочные работе. Математика. Рабочая тетрадь 4 класс в 2 ч. Ч 1/ под.ред. Н.А. Сопруновой – М.; Просвещение, 2016. – с. 50 -68
Теоретический материал для самостоятельного изучения
Вычислите площадь прямоугольника, если известно, что его длина равна 8см, а ширина 5см.
Вы уже знаете, чтобы найти площадь прямоугольника, нужно длину умножить на ширину. S= 8 ∙ 5 = 40 см2
А теперь попробуйте вычислить площадь данной фигуры:

Сегодня мы узнаем, что для нахождения площади фигур можно использовать палетку. Палетка – это прозрачная плёнка, которая может быть разбита на квадратные дециметры, квадратные сантиметры, квадратные миллиметры. Простейшая палетка – лист кальки, разделенный на квадратные сантиметры. Палетку используют для измерения площади фигур, ограниченных кривой линией.
Чтобы найти площадь данной фигуры, нужно:
1) На данную фигуру наложить палетку. Не сдвигать!
2)Сосчитать, сколько целых клеток- квадратных единиц – содержится в фигуре.
Целых 34 клетки.
3) Сосчитать, сколько нецелых квадратных единиц содержится в фигуре.
Неполных 8 клеток.
4) Количество нецелых квадратных единиц разделить на 2, примерно столько целых квадратных единиц они образуют.
8 : 2 = 4
5) Сложить числа, полученные в пунктах 2 и 4.
6) В ответе записать, что площадь фигуры приблизительно равна найденной сумме.
S = 34 + (8 : 2) = 38 см2
Ответ: S = 38 см2
Задания тренировочного модуля:
1. Определите, какая фигура имеет большую площадь, а какая – меньшую, и решите ребус соответствия.
Правильный ответ: Прямоугольник – большую, круг – меньшую.
Сторона клетки фигуры на рисунке равна 1 см. Найдите её площадь и периметр.
Правильный ответ:
Площадь 7 см2
Периметр 12 см
Довольно точно можно вычислить площадь прямоугольной фигуры, но для фигуры неправильной формы можно найти её приближённую площадь. Для этого удобно использовать палетку.
Палетка — это прозрачная плёнка (или калька), расчерченная на равные квадраты со стороной (1) см.
Самостоятельно сделай палетку.
С её помощью ты сможешь быстро находить приближённую площадь разных фигур.
Для нахождения приближённой площади фигуры нужно:
1) наложить палетку на фигуру;
2) посчитать число (a) целых клеток внутри фигуры;
3) посчитать количество (b) клеток, частично входящих в фигуру;
4) вычислить приближённую площадь
S≈a+b:2
.
Поясним также, зачем нужно делить (b) на два.
(b) — число клеток, частично входящих в фигуру. У одних большая часть входит в фигуру, у других — меньшая. Из них можно составить приближённо (b:2) полных клеток (если (b) нечётно, то можно сначала увеличить (b) на (1), а потом уже разделить на (2)).
Обрати внимание!
Для записи приближённого равенства используется знак
≈
.
Найдём с помощью палетки приближённую площадь фигуры (B) неправильной формы.
1. Наложим палетку на фигуру (B).
2. Посчитаем количество (a) клеток, целиком находящихся внутри фигуры (закрашены зелёным цветом):
3. Посчитаем количество (b) клеток, частично входящих в фигуру (B) (закрашены синим). Таких клеток (17) — это нечётное число, поэтому увеличим это число на (1) и поделим на (2):
17+1=18,18:2≈9.
4. Сложим числа, полученные в пунктах (2) и (3), и запишем приближённую площадь фигуры (B):
S≈16+9=25см2.
Обрати внимание!
Нужно понимать разницу между оценкой площади и нахождением её приближённого значения!
Оценка площади записывается неравенством
a<S<b
.
Приближённое значение площади — это число, которое можно найти по формуле
S≈a+b:2
.
Источники:
Изображение: палетка. © ЯКласс.
Изображения: фигура. © ЯКласс.
|
Что такое палетка для 3-4 класса по математике и как ею пользоваться? Палеткой для такого предмета, как – Математика является прозрачный листок, на котором нанесена ровная сетка, а именно квадратики, которые обладают одним размером, чаще всего со стороной в 1 сантиметр. Данная палетка предназначена для того, чтобы вычислять площадь различных фигур. Для того, чтобы пользоваться палеткой, вам предстоит наложить поверх фигуры изготовленную нами палетки, а далее заняться счетом. Нужно посчитать, сколько квадратиков было помещено в центре. Важно то, что нужно разделить сколько целых квадратиков было помещено и сколько попадают от части в данную фигуру. Формула площади фигуры с помощью палетки: автор вопроса выбрал этот ответ лучшим Палетка это прозрачная сеточка разграфованная перпендикулярными линиями, образующими обычно квадратики со сторонами десять на десять миллиметров (1 см.) Используется для определения (достаточно приблизительного) площади не правильных фигур, площадь которых не получается вычислить путем арифметических действий, как например площадь квадрата, треугольника или круга. Бывают фигуры с размытыми, неправильными границами, ну предположим чернильное пятно, вот для вычисления площади таких геометрических форм и нужна палетка. Наложили на фигуру, посчитали квадратики внутри границ фигуры. Палетка это прозрачный листок с нанесённой на него сеткой с размером ячейки в 1 см. Палетку можно изготовить самостоятельно из прозрачной обложки для тетради или из листа кальки. На кусок прозрачного пластика (или кальки) наносится шариковой ручкой сетка размером 10 Х 10 см со стороной ячейки в 1 см. Палетка нужна для приближенного измерения площадей или отсчёта координат: Надо наложить палетку на изображенную фигуру и подсчитать количество квадратиков. Площадь фигуры (выраженная в сантиметрах) равна количеству квадратиков внутри фигуры, плюс половина количества квадратиков, через которые проходит граница фигуры. S=N+M/2
Для определения площади (в сантиметрах) можно воспользоваться формулой Пика : S=M/2+N-1
Mefody66 5 лет назад Палетка – это шаблон для измерения площадей фигур. Обычно в виде прозрачной пластинки с нарисованными параллельными и перпендикулярными линиями. Пользоваться очень просто – накладываешь пластинку на фигуру и считаешь: 1) Количество целых клеток внутри фигуры N. 2) Количество клеток M, через которые проходит граница фигуры. Если граница проходит строго по линиям палетки, эти места не учитываем. Считаем только клетки, которые пересекаются границей фигуры. 3) Площадь очень близка к числу S = N + M/2. -Irinka- 4 года назад В математике, в начальных классах для определения площади фигур используется палеткав- прозрачный листок на который нанесена сетка, в виде квадраиов. Квадратв в сетке имеют одинаковые размеры, сторона квадрата равна 1 сантиметру. Для вычисления площади необходимо наложить данную сетку поверх фигуры и сосчитать сначала сколько целых, полных квадратов, затем отдельно считаем сколько неполных квадратиков, частично затрагивающих сетку палетки. Делим количество неполных квардатов пополам и это значение суммируем с количеством полных квардатов. Примерная площадь фигуры определена. Вот как производятся вычисления. ВитаМиночка 4 года назад Плпеткой называют листок, изготовленный из прозрачного полиэтилена, на который нанесена сетка из квадратов (обычно сторона квадрата = 1 см.). Используется данная сеточка для определения площади фигуры. Чтобы измерить площадь, необходимо положить палетку поверх фигуры и отметить её границы. Следующим шагом необходимо посчитать количество целых и количество неполных квадратов. Площадь фигуры будет определяться по формуле: S=N+M/2 N – целые квадраты; M – неполные квадраты. Стоит отметить, что полученная цифра будет считаться очень приблизительной, т.к. площадь и размер неполных квадратов различна. В Рокотов 4 года назад Интересный метод предлагается сегодня при современном обучении младших школьников математике. Им предлагается изготовить самостоятельно квадрат 10х10 с ячейками в 1 сантиментр, для того, чтобы было проще измерять площадь фигуры с неровными краями. Прозрачная сетка накладывается на неровноочерченную поверхность и считается внутри количество квадратов полных(назовем их P) и неполных (N)площадь S будет равна P*N/2. Так визуально детям удобнее понять из чего получается то или иное математическое значение. Бархатные лапки 4 года назад Действительно, с помощью палетки можно рассчитать площади разных фигур. Школьникам наверняка больше вычислять площади именно таким образом, ведь тут немного замешано творчество и задание выполнить будет не так скучно. Пользоваться палеткой в принципе не так сложно, выполняем следующие шаги: Палетку можно сделать дома самому, вот тут неплохая инструкция, для этого можно взять обычные обложки для тетрадок и с них сделать палетку. юлия03 4 года назад При помощи палетки рассчитывается площадь фигур. Что удивительно, я не помню чтобы у меня такая была в детстве когда я училась. На самой палетке нанесена сетка из квадратов. Палетку можно купить или сделать самим. Пользоваться ею просто. Кладем палетку на фигуру сверху, потом считаем количество целых и не полных квадратов. kellymilena 4 года назад Ровная сетка сверху нанесена на тонкий прозрачный листок под названием палетка для математики. Такое устройство нужно, чтобы самостоятельно считать площадь самых разных фигур. Для этого аккуратно накладываем палетку на нужную фигуру и считаем суммарный результат. Знаете ответ? |
Привет, ребята!
Вы знаете, я хотела узнать площадь
нашей страны, но мне это не сразу удалось сделать. Дело в том, что её границы
имеют неправильную форму – это не прямоугольник, не квадрат, и даже не круг.
Я обратилась за помощью к нашей царице, и она
рассказала мне, как находить площадь любой, самой искривлённой фигуры. Царица
дала мне вот такое простое приспособление. Это прозрачная пластина или плёнка с
разлиновкой в клеточку. Называется она – палетка. В
зависимости от размера фигуры, площадь которой надо узнать, палетка может быть
разделена на квадратные миллиметры, квадратные сантиметры или квадратные
дециметры.
Представьте
себе, что надо узнать площадь вот такой фигуры.
Накладываем
на неё палетку.
Сначала
считаем, сколько всего целых квадратиков. Их тридцать четыре. Теперь считаем
все оставшиеся кусочки. Их восемь. Люди договорились, что каждые два
кусочка засчитывают за один полный квадратик. Поэтому количество кусочков
делим на два. Получилось четыре.
Складываем
тридцать четыре и четыре. Это тридцать восемь. Значит, площадь этой фигуры – примерно
тридцать восемь квадратиков.
Так
как в школе чаще всего пользуются палетками, разделёнными на квадратные
сантиметры, то вы бы сказали, что площадь данной фигуры примерно равна тридцати
восьми квадратным сантиметрам. Почему примерно? Потому что площадь фигуры по
палетке вряд ли возможно определить абсолютно точно, ведь редко два кусочка
могут идеально заменить целый квадратик.
А
теперь попробуем найти площадь вот такой, совершенно бесформенной фигуры.
Опять
накладываем на неё палетку. Считаем целые квадратики.
Их
семнадцать. Теперь считаем кусочки. Их двадцать четыре. Количество кусочков
делим на два и полученное число прибавляем к семнадцати. Получилось примерно
двадцать девять квадратных сантиметров.
Иногда
случается и так, что количество кусочков – нечётное число,
например, тринадцать или двадцать пять. Тогда делим на два ближайшее чётное
число, больше данного на один. Ведь всё равно при помощи палетки точно площадь
фигуры измерить невозможно. А вот почему берём чётное число больше данного, вы
узнаете в пятом классе.
Запомнили,
ребята, как мы определяем площадь фигур с помощью палетки?
̶ Накладываем
палетку на фигуру.
̶ Считаем
количество целых квадратов.
̶ Считаем
количество кусочков.
̶ Количество
кусочков делим на два…
̶ Складываем
полученное число с количеством целых квадратов….
̶ Записываем
ответ.
Видите,
всё просто!
Кстати,
именно так, используя план местности и палетку, можно найти площадь участка
земли, или озера, или целого города, и даже страны. Вот этим я сейчас и
займусь. Пока, ребята!
Для определения
площадей небольших участков с
криволинейными контурами на плане
применяют палетки, в основном прямолинейные.
К прямолинейным палеткам относятся
известные и наиболее распространенные
квадратные и параллельные палетки.
Квадратная палетка
представляет собой сеть взаимно
перпендикулярных линий, проведенных
через 1–2 мм на прозрачном целлулоиде,
плексигласе, фотопленке, стекле или
кальке.
Площадь фигуры
определяется простым подсчетом клеток
палетки, наложенной на фигуру. Доли
клеток, рассекаемых контуром на части,
учитываются на глаз (рис. 13). Квадратной
палеткой не рекомендуется определять
площади больше 2 см2
на плане. Недостаток ее применения
(помимо того, что площади долей клеток,
рассекаемых контуром, приходится
оценивать на глаз) в том, что подсчет
количества целых клеток нередко
сопровождается грубыми погрешностями.
-
Рис. 13
Рис.
14
Рис.
15
Такие недостатки
не наблюдаются при определении площадей
параллельной палеткой, представляющей
собой листок прозрачного целлулоида,
плексигласа или кальки, на котором
нанесены параллельные линии преимущественно
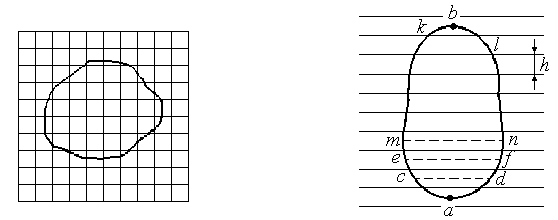
через 2 мм одна от другой. Площадь контура
определяют этой палеткой следующим
образом. Накладывают ее на контур так,
чтобы крайние точки a
и b
разместились посредине между параллельными
линиями палетки. Тогда, весь контур
оказывается разделенным параллельными
линиями на фигуры, близкие к трапециям,
с одинаковыми высотами, причем отрезки
параллельных линий внутри контура
являются средними линиями трапеций
(рис.14). Пунктиром показаны основания
этих трапеций.
Сумма площадей
трапеций, т.е. площадь контура, равна
.
Следовательно,
чтобы получить площадь контура, нужно
взять сумму средних линий, т.е. сумму
отрезков параллельных прямых внутри
контура, и умножить на расстояние между
ними.
Для упрощения
определения площади сумму средних линий
последовательно набирают в раствор
циркуля, которую определяют по масштабной
линейке и полученную длину умножают на
h,
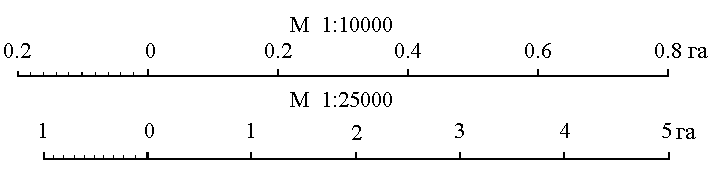
м (рис.15). Чтобы не выполнять подобных
вычислений, для каждого масштаба строят
специальную шкалу, по которой отсчитывают
площадь контура, зная сумму средних
линий.
Расчет шкалы: М
1:10000,
h
= 2 мм, при
длине шкалы 1
см площадь равна (0.2 см
100 м)
(1 см
100 м) = 2000
м2
= 0.2
га. Параллельной палеткой не следует
определять площади больше 10 см2
на плане.
4.5. Точность вычисления площадей графическим способом и с помощью палетки
При разбивке
участка на простейшие фигуры точность
вычисления для различных вариантов не
будет одинаковой. Площадь треугольника
графическим способом вычисляется
точнее, чем площади других фигур.
Следовательно, площадь при разбивке
участка на треугольники вычисляется
точнее, чем при разбивке на другие фигуры
(трапеции, прямоугольники). При разбивке
участка на треугольники из всех вариантов
будет лучшим тот, в котором треугольники
будут равносторонними или высота
h
примерно
равна
основанию a.
Погрешность
уменьшается, если вычислять площадь
треугольника не как
,
а по формуле
Герона
,
где
.
Это дает уточнение до 13% даже для
равностороннего треугольника. Основание
треугольника может быть во много раз
меньше высоты, если оно измеряется на
местности, а не на плане.
При разбивке
площади на треугольники погрешность
площади участка
,
где M
–
знаменатель численного масштаба плана.
Если
вычисляют два раза, то
.
Число треугольников,
на которое разбивается участок, не
влияет на погрешность площади. Поэтому
при разбивке участка на треугольники
не надо стремиться к тому, чтобы их было
меньше. Точность однократного определения
площади квадратной и параллельной
палетками, а также ротометром
характеризуется эмпирической формулой
.