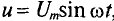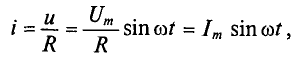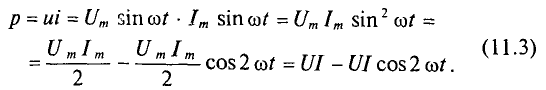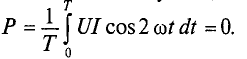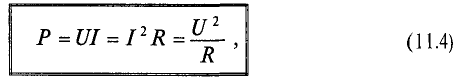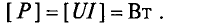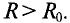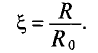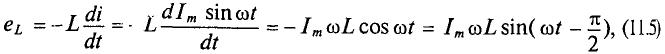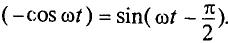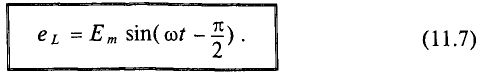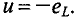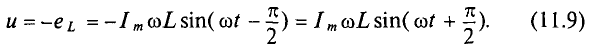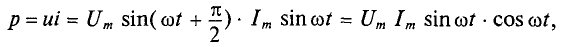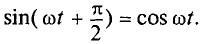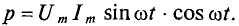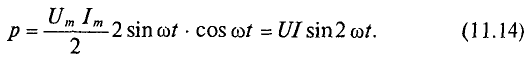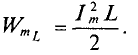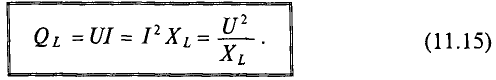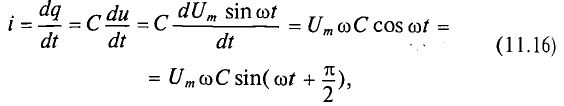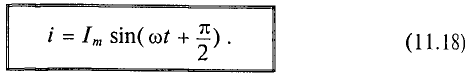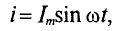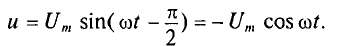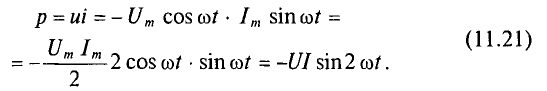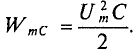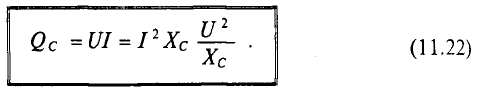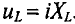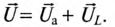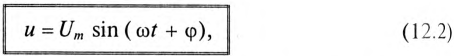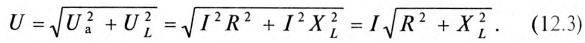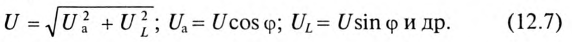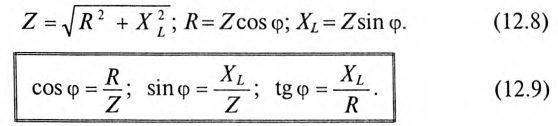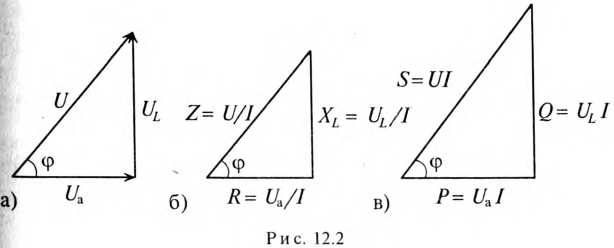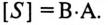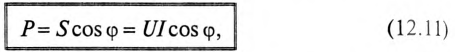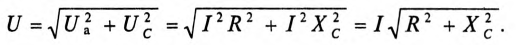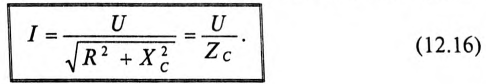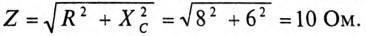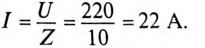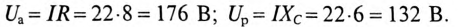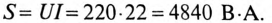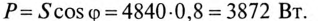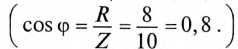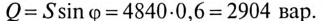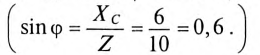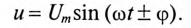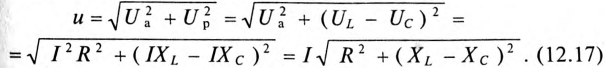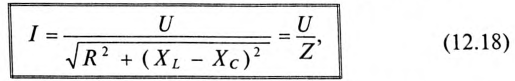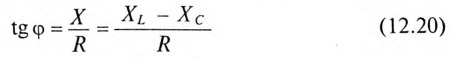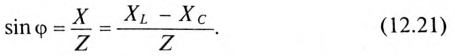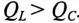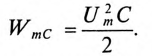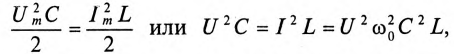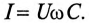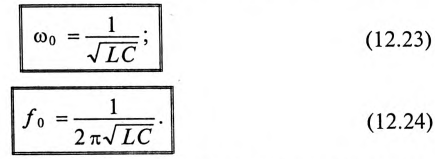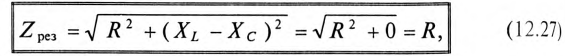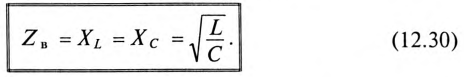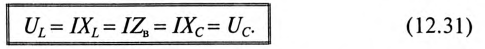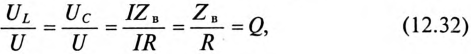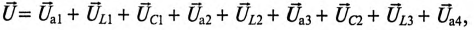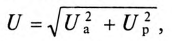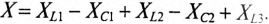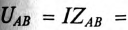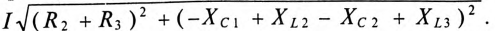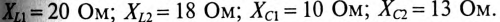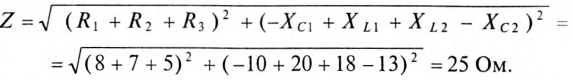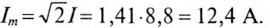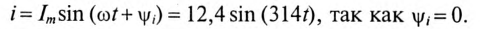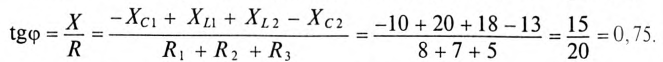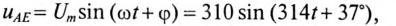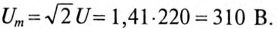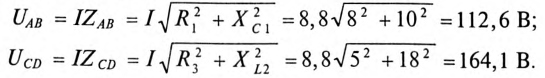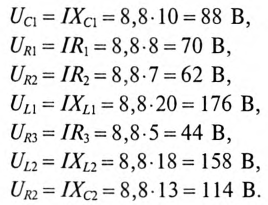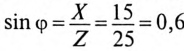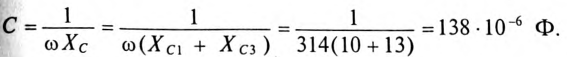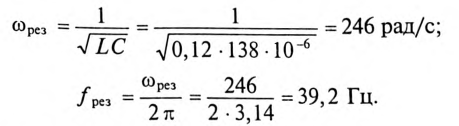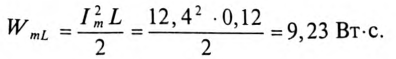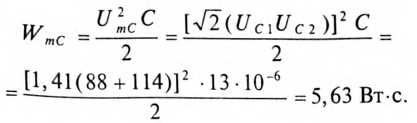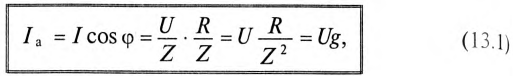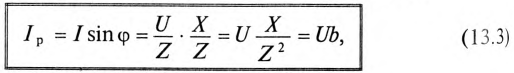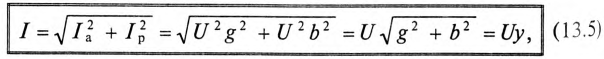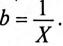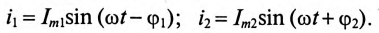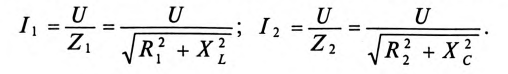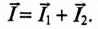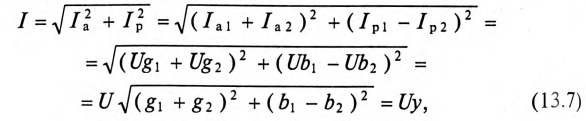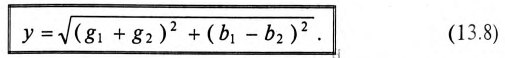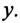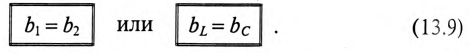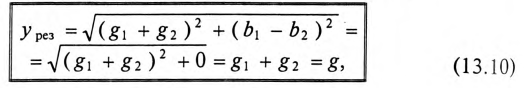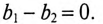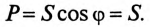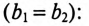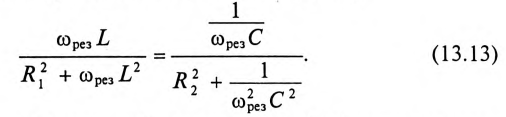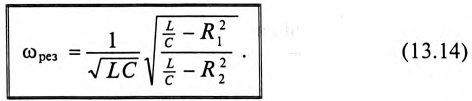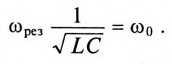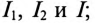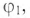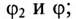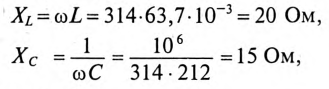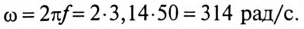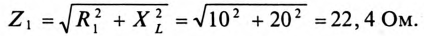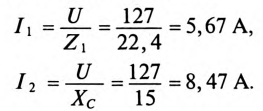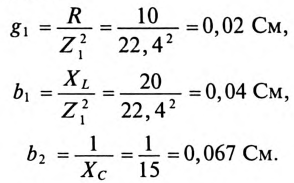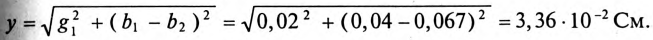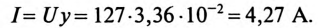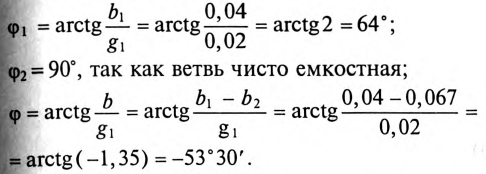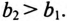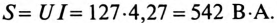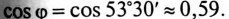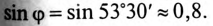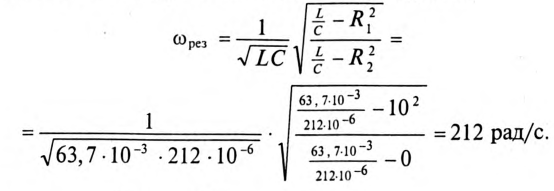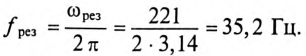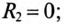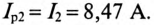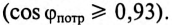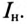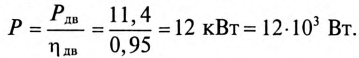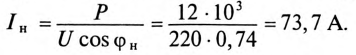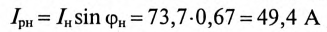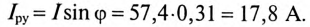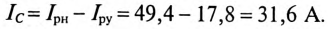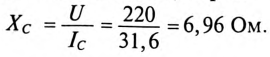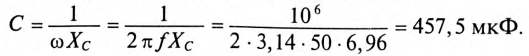Приложенное напряжение и падение напряжения на участке цепи.
Напряжения, действующие в электрических цепях, условно можно разделить на два типа:
– приложенное к цепи напряжение;
– падение напряжения на участках цепи или на всей цепи.
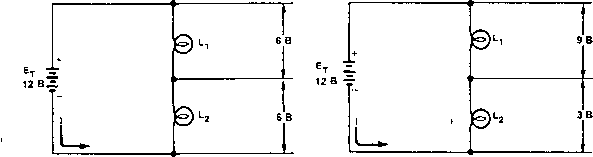
Приложенное напряжение это напряжение, подведенное к цепи (рис. 1.).
Рисунок 1. Приложенное напряжение и падение напряжения на участке цепи.
Источник напряжения подключен к цепи, поток электронов перемещается от минуса к плюсу источника напряжения. Если источник напряжения имеет значение напряжения 12 вольт (например, автомобильная аккумуляторная батарея), то приложенное напряжение будет иметь значение так же 12 вольт.
При движении потока электронов по цепи они встречает, как мы знаем, сопротивление. Таким образом, когда электроны проходят через нагрузку (или другие элементы цепи), то они теряют энергию. Та энергия, которую электроны отдали в нагрузку, называется падением напряжения на участке цепи . В основном эта энергия выделяется на нагрузке в виде тепла. Энергия, которая отдается в нагрузку, равна энергии сообщаемой электронам источником напряжения.
Если автомобильный аккумулятор напряжением 12 вольт подключить к автомобильной 12 вольтовой лампе, то приложенное к цепи напряжение будет равно 12 вольт, а падение напряжения на лампе так же будет 12 вольт (рис. 2.). Энергия в объеме 100% потребляется в цепи.
Рисунок 2. Пример приложенного напряжения в 12 В и падения напряжения на лампе.
Если к тому же 12-вольтовому автомобильному аккумулятору подключить две соединенные последовательно 6-вольтовые лампочки, то при том же приложенном напряжении в 12 В падение напряжение на лампочках будет по 6 вольт (рис. 3.). В этом случае все равно общее падение напряжение будет 12 вольт.
Рисунок 3.
В другом случае если взять две лампочки на разное напряжение, к примеру на 9 и 3 вольта, и включить их последовательно в цепь с источником напряжения 12 вольт, то соответственно на 9-ти вольтовой лампочке будет падать 9 вольт, а на 3-х вольтовой 3 вольта (рис. 4.). Как и всегда общее падение напряжения на лампочках равно 12 вольт.
Рисунок 4.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
В
электрических и электронных цепях
существует два типа напряжений —
приложенное напряжение и падение
напряжения.
Потенциал
или напряжение, подведенное к цепи,
называется приложенным
напряжением (рис.
3-23). Напряжение подсоединено к цепи,
ток течет от отрицательного вывода
источника напряжения и возвращается к
положительному выводу источника
напряжения. 12-вольтовая батарея,
подсоединенная к цепи дает приложенное
к цепи напряжение 12 вольт.
При
перемещении электронов по цепи они
встречают сопротивление. Проходя через
нагрузку, электроны теряют энергию.
Отданная энергия называется падением
напряжения (рис.
3-24). В большинстве случаев энергия
отдается в виде тепла. Энергия, которую
теряют электроны в цепи, равна энергии,
сообщаемой им источником.
Еще
раз повторим, что энергия, введенная в
цепь, называется приложенным
напряжением. Энергия, выделяемая в
цепи на нагрузке, называется падением
напряжения. Падение напряжения имеет
место, когда в цепи течет ток. Ток течет
по цепи от отрицательного полюса к
положительному. Внутри источника
напряжения ток течет от положительного
электрода к отрицательному.
Падение
напряжения в цепи равно приложенному
к цепи напряжению, так как энергия не
может создаваться или уничтожаться, а
только переходит из одной формы в
другую. Если 12-вольтовый источник
подсоединен к 12-воль- товой лампе, то
источник напряжения обеспечивает
приложенное напряжение 12 вольт, а на
лампе происходит падение напряжения
12 вольт. Вся энергия потребляется в
цепи. Если две одинаковые 6-вольтовые
лампы подсоединены последовательно
к тому же 12-вольтовому источ-
|
Г— |
+ |
+ |
|
|
приложенное |
: |
Е |
|
|
напряжение |
– |
||
|
U |
падение
напряжения
Рис.
3-23. Потенциал, приложенный к цепи,
называется приложенным напряжением.
Рис.
3-24. Энергия, поглощенная цепью при
прохождении тока через нагрузку
(сопротивление), называется падением
напряжения. Падение напряжения имеет
место при протекании тока в цепи.
Рис.
3-26. Когда две лампы, рассчитанные на
различное напряжение последовательно
подсоединены к 12-вольтовому источнику,
падение напряжения на каждой лампе
будет разным, в зависимости от
напряжения, на которое рассчитана
лампа, и ее сопротивления.
Рис.
3-25. На каждой из двух одинаковых
6-вольтовых ламп, подключенных к
источнику 12 вольт, происходит одинаковое
падение напряжения по 6 вольт.
нику
(рис. 3-25), то на каждой лампе происходит
падение напряжения б вольт, а общее
падение напряжения равно 12 вольт. Если
две разные лампы соединены последовательно,
например как 9-вольтовая и 3-вольтовая
лампы (рис. 3-26), то на 9-вольтовой лампе
происходит падение напряжения 9 вольт,
а на 3-вольтовой лампе — 3 вольта. Сумма
падений напряжения равна приложенному
напряжению 12 вольт.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
09.02.201529.19 Mб24Глинка, Н.Л. – Общая химия – 2000.djvu
Содержание:
Электрические цепи синусоидального тока:
В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R, индуктивностью L и емкостью С. В технике часто применяются цепи переменного тока, в которых преобладает один или два из этих параметров.
При анализе работы и расчетах цепей исходят из того, что для мгновенных значений переменного тока можно использовать все правила и законы постоянного тока.
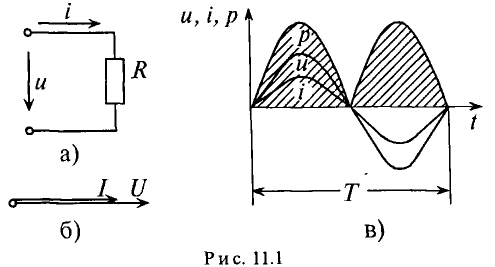
Цепь с активным сопротивлением
Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).
Если к активному сопротивлению R (рис. 11.1) приложено синусоидальное напряжение
где
Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны (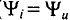
Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:
Это вытекает из выражения (11.1), если левую и правую части уравнения разделить на 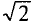
Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка цепи, к которому приложено напряжение U. Такая интерпретация закона Ома справедлива как для мгновенных, так и для действующих и амплитудных значений синусоидального тока.
Активная мощность
Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения ка, т. е. р = ui. Это действие производится над кривыми тока и ряжения в определенном масштабе (рис. 11.1в). В результате учена временная диаграмма мгновенной мощности р. Как видно из временной диаграммы, мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению (рис. 11.1в). Эта мощность (энергия) необратима. От источника она поступает на потребитель и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной.
Поэтому и сопротивление R, на котором происходит подобное образование, называется активным сопротивлением, цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии.
Количественно мощность в цепи с активным сопротивлением определяется следующим образом:
Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин -постоянной мощности UI и переменной 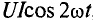
Средняя за период мощность, равная постоянной составляющей мгновенной мощности UI, является активной мощностью Р. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть
Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:
где U- действующее значение напряжения; I— действующее значение тока.
Единицей активной мощности является ватт:
Поверхностный эффект и эффект близости
Сопротивление проводника постоянному току 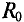
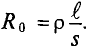
Оказывается, что сопротивление проводника переменному току больше его омического сопротивления за счет так называемого поверхностного эффекта и эффекта близости, т. е.
Увеличение активного сопротивления вызвано неодинаковой плотностью тока в различных сечениях проводника (рис. 11.2а).
На рис. 11.2а изображено магнитное поле проводника цилиндрического сечения. Если по проводнику проходит переменный ток, то он создает переменный магнитный поток внутри и вне проводника. Этот поток в различных сечениях проводника индуктирует ЭДС самоиндукции, которая, согласно правилу Ленца. противодействует изменению тока как причине создания ЭДС Очевидно, центр проводника охвачен большим количеством магнитных линий (большее потокосцепление), чем слои, близкие к поверхности. Следовательно, в центре проводника ЭДС (сопротивление) больше, чем на поверхности проводника. Плотность на поверхности больше, чем в центре. Поэтому это явление и называется поверхностным эффектом.
Таким образом, поверхностный эффект уменьшает сечение проводника для переменного тока, а следовательно, увеличивает активное сопротивление R.
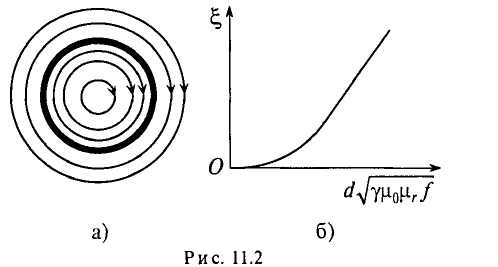
Отношение активного сопротивления проводника к его сопротивлению определяет коэффициент поверхностного эффекта 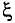
График зависимости коэффициента поверхностного эффекта от параметра проводника d, его удельной проводимости 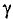
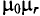

При токах большой частоты 
На величину активного сопротивления проводника R оказывает влияние и эффект близости.
Если токи в двух параллельных проводах, расположенных близко друг к другу, направлены в одну сторону, то элементы сечения водников, удаленных на большее расстояние друг от друга, цепляются с меньшим магнитным потоком и имеют большую плотность тока (заштриховано на рис. 11.3а), чем элементы сечения проводников, расположенные близко друг к другу.
Если же токи в близко расположенных параллельных проводах направлены в различные стороны, то большая плотность тока на-дается в элементах сечения проводников, расположенных ближе друг к другу (заштриховано на рис. 11.36).
Таким образом, эффект близости в проводниках также влияет активное сопротивление проводников за счет наведения в различных элементах сечений проводников различных ЭДС взаимоиндукции, направление которых определяется правилом Ленца.
Цепь с идеальной индуктивностью
Идеальной называют индуктивность L такой катушки, активным сопротивлением R и емкостью С которой можно пренебречь, т.е. R= О и С=0.
Если в цепи идеальной катушки индуктивностью L (рис. 11.4а) проходит синусоидальный ток 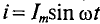
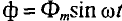
так как
Очевидно, эта ЭДС достигает своего амплитудного значения 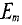
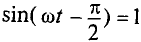
Тогда
Таким образом, ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90° = 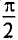
По второму закону Кирхгофа для мгновенных значений можно записать
Откуда
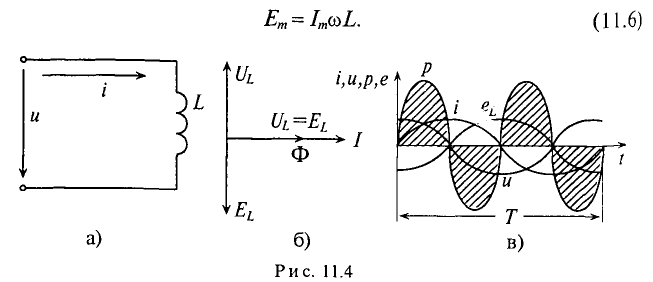
Тогда напряжение, приложенное к цепи с идеальной индуктивностью (см. (11.5)):
Очевидно, напряжение достигает своего амплитудного значения Um тогда, когда 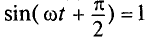
Следовательно,
Таким образом, напряжение, приложенное к цепи с идеальной ин-ивностью, как и ток в этой цепи, изменяется по синусоидально-жону, но опережает ток по фазе на угол 90°= 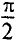
Резюмируя все вышесказанное, можно сделать вывод: для существования тока в цепи с идеальной индуктивностью необходимо ожить к цепи напряжение, которое в любой момент времени но по величине, но находится в противофазе с ЭДС, вызванной таким током (рис. 11.46, в).
Временная диаграмма (рис. 11.4в) еще раз иллюстрирует правило Ленца: ЭДС 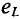
Если уравнение (11.10) разделить на 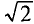
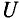
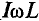
Это уравнение (11.12а) и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением XL.
Таким образом,
Закон Ома для этой цепи можно записать иначе:
Индуктивное сопротивление XL — это противодействие, которое ЭДС самоиндукции eL оказывает изменению тока.
Реактивная мощность в цепи с индуктивностью
Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока
где
Следовательно,
Полученное уравнение умножают и делят на 2:
Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.
Следовательно, среднее значение этой мощности за период Яс, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р= 0.
Временная диаграмма (рис. 11,4в) подтверждает этот вывод. На диаграмме видно, что мгновенная мощность (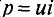
То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии по (9.12) равно
Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.
Таким образом, в цепи переменного тока с идеальной катушки мощность не потребляется (Р= 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода.
Такая колеблющаяся мощность (энергия), в отличие от активной, потребляемой, называется реактивной.
Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q]=вар (вольт-ампер реактивный).
Величина реактивной мощности в рассматриваемой цепи определяется выражением
Так как реактивная мощность QL имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера, т. е. XL.
Цепь с емкостью
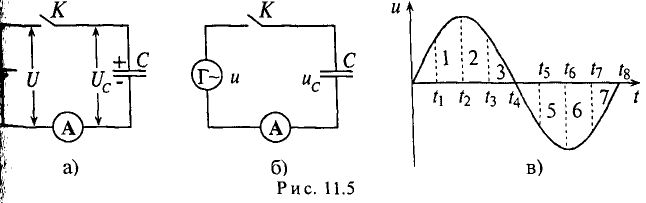
Если конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора ходит в цепи очень короткое время, пока напряжение на конденсаторе Uc не станет равным напряжению источника U.
Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I=0).
Если же конденсатор подключить к источнику с синусоидальным напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжена конденсаторе Uc отстает по фазе от напряжения источника и зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 – конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.
Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение 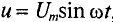
где q= Си согласно (6.3).
Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда 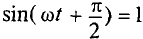
Тогда
Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°=
Следовательно, напряжение отстает по фазе от тока на 90° = 
Если уравнение (11.17) разделить на 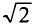
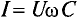
Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью.
Очевидно, знаменатель этого равенства является сопротивлением конденсатора Хс, которое называется емкостным сопротивлением:
Когда закон Ома для цепи с конденсатором можно записать:
Емкостное сопротивление – это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11,5а).
Реактивная мощность в цепи с конденсатором
Если в цепи конденсатора емкостью 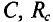
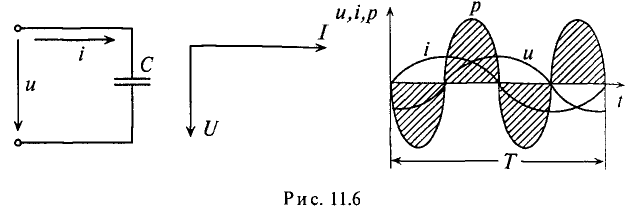
Напряжение и, приложенное к этому конденсатору (рис. 11.6), будет равно
Мгновенная мощность в цепи с конденсатором
Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 11.6в).
Следовательно, активная мощность Р в рассматриваемой цепи 1С. 11.6а), равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р= 0.
Это следует и из временной диаграммы (рис. 11.6в). На временной диаграмме видно, что изменение мгновенной мощности р по синусоидальному закону происходит с двойной частотой: 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора.
Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно
В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.
Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Такая колеблющаяся, но не потребляемая мощность называется реактивной мощностью.
Величина реактивной мощности в цепи конденсатора определяется выражением
Из временных диаграмм (рис. 11.4в, 11.6в) видно, что реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении (11.21) – аналитическом выражении мгновенной мощности в цепи с конденсатором.
Так как реактивная мощность Qc имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением Х емкостного характера (Хс).
Расчет линейных электрических цепей синусоидального тока
Расчет электрических цепей синусоидального тока производится преимущественно с помощью векторных диаграмм. В нашей главе рассматривается расчет неразветвленных цепей синусоидального тока, содержащих активное сопротивление R, активность L и емкость С в различных сочетаниях.
Цепь с активным сопротивлением и индуктивностью
Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток 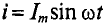
Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать
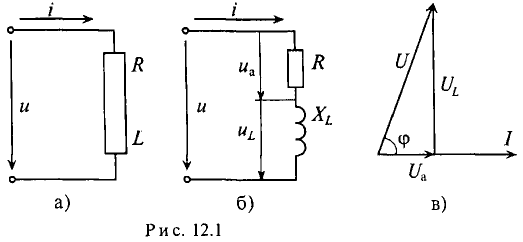
Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенными активным сопротивлением R и индуктивным сопротивлением XL (рис. 12.16).
Активное напряжение (рис. 11.16) совпадет по фазе с током и может быть записано 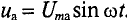
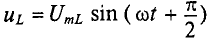
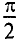
Мгновенное значение напряжения, приложенного к цепи, определяется алгебраической суммой мгновенных значений напряжений 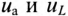
Это равенство лежит в основе построения векторной диаграммы (рис. 12.1 в).
Из векторной диаграммы (рис. 12.1 в) видно, что напряжение U, приложенное к реальной катушке, опережает по фазе ток 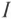
где ф — это международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.
Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника, по векторной диаграмме (рис. 12.1 в) определяется напряжение
Откуда
Равенство (12.4) является математическим выражением закона Ома для цепи синусоидального тока с активным R и индуктивным XL сопротивлениями в неразветвленной цепи.
Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным, или кажущимся, сопротивлением цепи синусоидального тока. Обозначается кажущееся (полное) сопротивление любой цепи переменного тока буквой Z:
где Zk — полное, или кажущееся, сопротивление реальной катушки.
Тогда закон Ома для любой цепи переменного тока в общем виде можно записать
где Z — кажущееся сопротивление этой цепи.
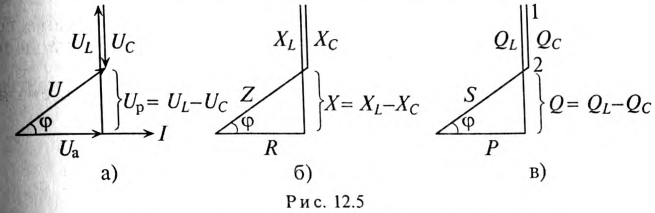
Треугольники напряжений, сопротивлений, мощностей
Треугольник, все стороны которого изображены векторами напряжений, называется треугольником напряжений. Пользуясь векторной диаграммой для неразветвленной цепи с активным и индуктивным сопротивлениями (рис. 12.1в), выделяем треугольник напряжений (рис. 12.2а).
Связь между напряжениями в данной цепи можно рассматривать как соотношение между сторонами и углами прямоугольного треугольника:
Если все стороны треугольника напряжений разделить на ве-1ину тока в цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают сопротивления цепи, т. е. получится треугольник составлений (рис. 12.16). Сопротивления не являются векторными величинами. Из треугольника сопротивлений можно определить:
Обычно тригометрические функции угла ф определяются из треугольника сопротивлений отношением (12.9).
Если все стороны треугольника напряжений умножить на величину тока цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают мощности цепи, т.е. получится треугольник мощностей (рис. 12.2в).
Произведение напряжения и тока цепи характеризует полную мощность цепи
которая измеряется в вольт-амперах, т.е.
Однако потребляется в цепи только часть полной мощности – активная мощность
где cos ф показывает, какая часть полной мощности 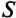
Полная мощность цепи S называется кажущейся. Из того же треугольника мощностей (рис. 12.2в) записать:
Построив треугольники напряжений, сопротивлений и мощностей для любой цепи синусоидального тока, по выражениям (12.7)—(12.14) можно рассчитать параметры этой цепи.
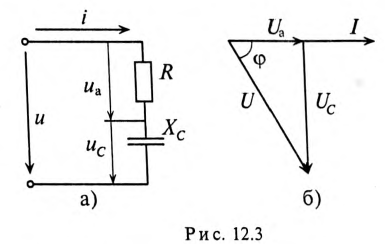
Цепь с активным сопротивлением и емкостью
Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток 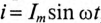
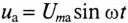
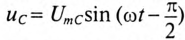
Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол ф < 90°, т. е.
Действующее значение напряжения U, приложенного к этой цепи, определяется по векторной диаграмме (рис. 12.3):
Откуда математическое выражение закона Ома для этой цепи:
Пример 12.1
К цепи с последовательно включенными сопротивлениями R= 8 Ом и Хс= 6 Ом (рис. 12.3а) приложено напряжение U= 220 В. Определить ток цепи I, напряжение на активном 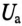
Решение
Для определения тока вычислим полное сопротивление цепи
Тогда ток будет равен
Напряжения на участках:
Полная мощность
Активная мощность
Реактивная мощность
Неразветвленная цепь с активным сопротивлением, индуктивностью и емкостью
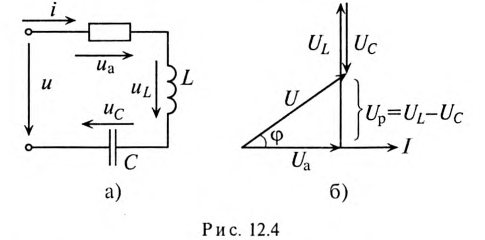
Если в неразветвленной цепи с R, L и С (рис. 12.4а) протекает синусоидальный ток 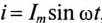
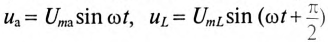
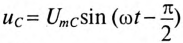
Мгновенное значение напряжения цепи определяется по формуле
Так как в рассматриваемой цепи включены два реактивных сопротивления XL и Хс, то возможны три режима работы цепи:
Векторная диаграмма цепи для режима 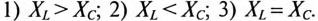
Знак перед углом сдвига фаз ф зависит от режима работы цепи Если в рассматриваемой цепи преобладает индуктивное напряжение (сопротивление), т. е. 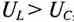
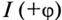
Если в цепи преобладает емкостное напряжение (сопротивление), т.е. 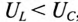
Из векторной диаграммы (рис. 12.46) следует:
Сопротивление R может включать в себя сопротивление самостоятельного резистора или активное сопротивление реальной катушки и конденсатора.
Математическое выражение закона Ома для неразветвленной цепи с активным сопротивлением, индуктивностью и емкость:
где Z — полное (или кажущееся) сопротивление неразветвленной цепи с R, L и С, т. е.
На рис. 12.5 изображены треугольники напряжений, сопротивлений и мощностей для рассматриваемой цепи.
Знак и значение угла ф можно определить из треугольника сопротивлений (рис. 12.56):
или
Из выражений (12.20) и (12.21) видно, что если 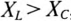
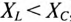
Из треугольника мощностей (рис. 12.5в) видно, что в цепи с R, L и С кроме активной мощности 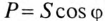
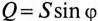
Из треугольника мощностей (рис. 12.5в) видно, что реактивная мощность, которая загружает источник и провода, Q= QL– Qc. Эта реактивная мощность (энергия) колеблется между источником и магнитным полем катушки индуктивности, так как
Полная мощность цепи определяется по формуле
Колебательный контур
Электрические цепи, в которых происходят периодические изменения токов, напряжений, энергии называются колебательными.
Для того чтобы исследовать резонансные явления, необходимо иметь представления о процессах в колебательном контуре, состоящем из идеальной катушки и конденсатора без потерь.
Если конденсатор емкостью С зарядить до напряжения Um, то в электрическом поле этого конденсатора накопится энергия, максимальное значение которой согласно выражению (6.21):
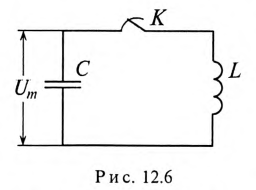
Если к заряженному конденсатору подключить индуктивность L замыканием ключа К (рис. 12.6), то конденсатор будет
разряжаться через индуктивность переменным током i. При этом в индуктивности L создается ЭДС самоиндукции eL, и в магнитном поле ее накапливается энергия, максимальное значение которой (9.12):
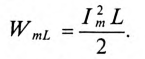
Источником энергии в этом контуре является конденсатор. Ток в контуре, состоящем из индуктивности L и конденсатора С, не прекращается даже когда конденсатор полностью разрядится. За счет ЭДС самоиндукции и энергии, накопившейся в магнитном поле индуктивности, конденсатор будет заряжаться, и энергия магнитного поля индуктивности переходит в электрическое поле конденсатора. При этом источником энергии в этом контуре является индуктивность. Дальше процесс повторяется.
Таким образом, в замкнутом контуре, состоящем из индуктивности и емкости, происходит колебание энергии между электрическим полем конденсатора С и магнитным полем индуктивности L. Поэтому такой замкнутый контур называется колебательным контуром.
Колебание энергии в колебательном контуре происходит с определенной частотой 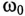
так как из (11.19) в цепи переменного тока с емкостью
Откуда
Таким образом, частота собственных колебаний колебательного контура определяется параметрами этого контура L и С.
Если в колебательном контуре отсутствуют потери (идеальный контур), то колебания в нем будут незатухающими с неизменной амплитудой. Если в колебательном контуре имеется активное сопротивление, т.е. возникают потери, то колебания энергии в нем будут затухающие, с уменьшающейся амплитудой, если эти потери не компенсируются.
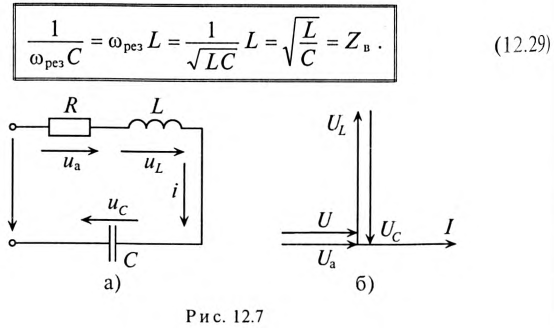
Резонанс напряжений
Если в цепи синусоидального тока с последовательно соединенными конденсатором емкостью С и катушкой с сопротивлением R И индуктивностью L (рис. 12.7а) равны реактивные сопротивления, то в цепи наступает резонанс напряжений. Равенство реактивных сопротивлений является условием резонанса напряжений.
Из (12.25) следует 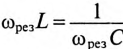
Из (12.26) следует, что резонанс напряжений имеет место в неразветвленной цепи с L и С тогда, когда частота вынужденных колебаний (частота источника) 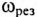
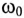
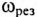
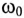
Полное (кажущееся) сопротивление цепи (рис. 12.7а) при резонансе напряжений определяется по формуле
так как XL-Xc=0.
То есть полное сопротивление неразветвленной цепи при резонансе напряжений 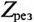
Следовательно, ток в неразветвленной цепи при резонансе напряжений максимальный:
Реактивные сопротивления при резонансе напряжений равны между собой, т. е.
(12.29)
Таким образом, реактивные сопротивления при резонансе напряжений равны (каждое) волновому сопротивлению 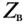
Напряжения на индуктивности UL и на емкости Uc при резонансе напряжений равны между собой, так как равны сопротивления, см. (12.25).
Равенство (12.31) определяет название «резонанс напряжений».
Так как UL и Uc изменяются в противофазе, то напряжение в резонансном режиме равно напряжению на активном сопротивлении 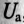
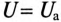
При резонансе напряжений каждое из реактивных напряжений UL и Uc может оказаться большим, чем напряжение цепи U.
где Q — добротность резонансного контура.
Добротность контура Q показывает, во сколько раз напряжение на индуктивности UL и емкости Uc (каждое) больше напряжения цепи U.
Высокая добротность резонансного контура (при малом активном сопротивлении контура) нашла широкое применение в радиотехнике, в частности в антенном контуре.
Из векторной диаграммы (рис. 12.76) видно, что при резонансе напряжение цепи U совпадает по фазе с током 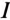
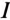
Колеблющаяся между магнитным полем индуктивности и электрическим полем емкости мощность (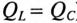
Из выражения (12.33) следует, что при отсутствии активной Мощности Р (активного сопротивления R) резонансный контур становится при резонансе идеальным колебательным контуром. Следовательно, при наличии активного сопротивления R источник расходует свою мощность на компенсацию потерь в контуре, за счет чего колебания в цепи будут незатухающими.
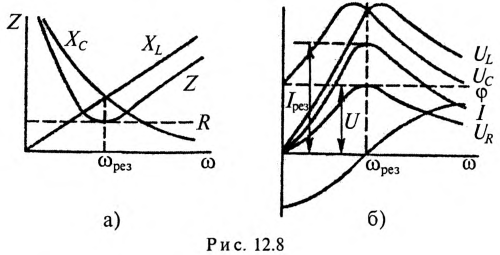
Кроме активного сопротивления R резонансной цепи и напряжения, приложенного к ней, все параметры резонансной цепи (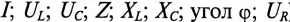
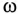
Эти изменения параметров резонансной цепи наглядно иллюстрируются резонансными кривыми, изображенными на рис. 12.8.
На резонансных кривых четко просматриваются значения этих параметров при частоте резонанса 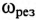
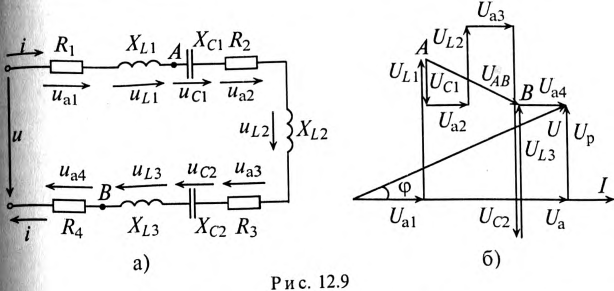
Общий случай неразветвленной цепи
Для неразветвленной цепи, содержащей несколько активных и реактивных сопротивлений различного характера (рис. 12.9а), справедливо геометрическое равенство напряжений (баланс напряжений)
которое лежит в основе построения векторной диаграммы (рис. 12.96).
Таким образом, напряжение цепи равно геометрической сумме напряжений на всех участках этой цепи.
Из векторной диаграммы следует (рис. 12.96)
где 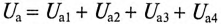
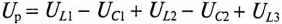
Те же рассуждения можно отнести и к сопротивлениям:
– полное сопротивление цепи 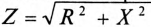
– активное сопротивление цепи 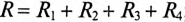
– реактивное сопротивление цепи
Напряжение на каком-либо участке неразветвленной цепи (рис. 12.9а), например на участке АВ, определяется так:_
Вектор напряжения UAB показан на векторной диаграмме (рис. 12.96).
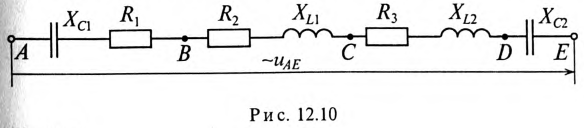
Пример 12.2
Напряжение, приложенное к неразветвленной цепи (рис. 12.10) U=220 В, частота тока сети f = 50 Гц. Начальная фаза тока 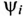
Сопротивление участков цепи: 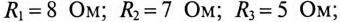
Требуется:
1. Вычислить ток цепи I и записать его мгновенное значение.
2. Записать мгновенное значение напряжения цепи иАЕ, определив предварительно угол ср и характер цепи.
3. Определить напряжение между точками АВ и CD.
4. Построить в масштабе векторную диаграмму цепи, определив едварительно напряжение на каждом сопротивлении.
5. Определить мощности S, Р и Q цепи.
6. Определить частоту, при которой в цепи наступит резонанс напряжений, и ток при резонансе.
7. Определить максимальную энергию, запасенную в магнитном поле катушек WmL и электрическом поле конденсаторов WmC. Как нужно изменить емкость конденсаторов, чтобы в цепи пил резонанс напряжений при частоте f = 50 Гц?
Решение
1. Для определения тока цепи I необходимо вычислить полное сопротивление цепи:
Действующее значение тока 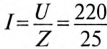
Угловая частота 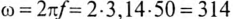
Мгновенное значение тока цепи:
2. Угол сдвига фаз ф и характер цепи определяется через tg ф:
Таким образом, угол ф = 37° (из таблицы), характер цепи индуктивный (+ф).
Тогда мгновенное значение напряжения цепи
где
3. Напряжение на участках:
4. Для построения векторной диаграммы определяются напряжения:
Векторная диаграмма цепи (отображает только характер участков, но не величины напряжений на них) изображена на рис. 12.11.
5. Полная мощность цепи 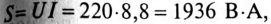
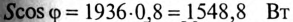
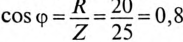
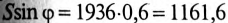
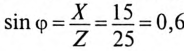
6. Для определения частоты резонанса вычисляется индуктивность L и емкость С цепи:
Тогда
Ток цепи при резонансе 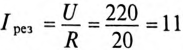
7. Максимальная энергия, запасенная в магнитном поле катушек:
Максимальная энергия, запасенная в электрическом поле конденсаторов:
8. Условие резонанса XL = XC.
По условию задачи 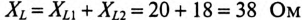
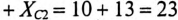
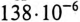
т. е. емкость конденсаторов нужно уменьшить на
Разветвленная цепь синусоидального тока
Активный и реактивный токи:
Для расчета разветвленных цепей синусоидального тока вводятся расчетные величины активного и реактивного токов цепи.
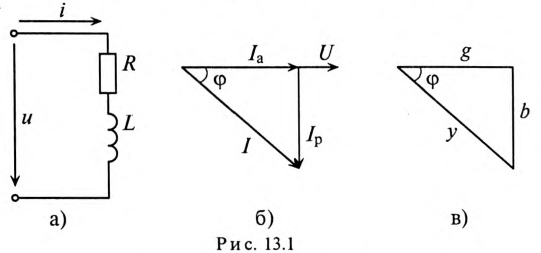
Если к цепи, содержащей активное сопротивление R и индуктивное XL (рис. 13.1а), приложено синусоидальное напряжение 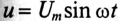
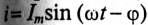
Векторная диаграмма в этом случае изображена на рис. 13.16.
Ток цепи I (рис. 13.16) раскладывается на две составляющие, одна из которых 



Активный и реактивный токи физического смысла не имеют. Они являются расчетными величинами, так как в неразветвленной цепи (рис. 13.1а) ток на всех участках имеет одинаковое значение. Однако понятия активный 

13.2. Проводимости
Из треугольника токов для рассматриваемой цепи (рис. 13.16) следует: 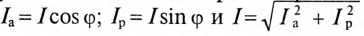
С другой стороны, известно, что 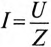
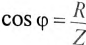
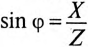
Тогда
где g — активная проводимость цепи, равная
Величина, на которую умножают напряжение, чтобы получить ток, называют проводимостью.
А так как g определяет активный ток 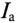
Таким образом, активная проводимость g определяется величиной активного сопротивления, деленного на квадрат полного (кажущегося) сопротивления цепи.
Величина реактивного тока определяется выражением
где b — реактивная проводимость цепи, равная
Величина полного тока цепи равна
где 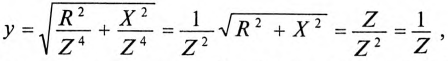
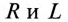
Таким образом, у — полная, или кажущаяся, проводимость цепи:
Полная (кажущаяся) проводимость цепи «у» является обратной величиной полного (кажущегося) сопротивления цепи.
Активная 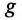
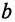
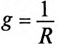
Если же в неразветвленной цепи (или ветви) включены сопротивления 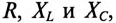
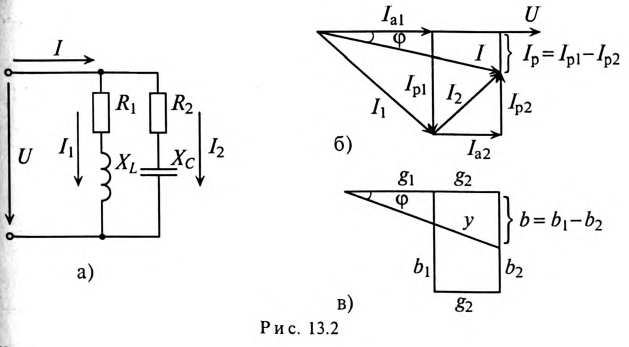
Параллельное соединение катушки и конденсатора
Если к источнику синусоидального напряжения 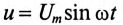
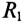
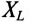
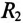
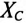
Действующие значения этих токов будут соответственно равны
Ток в неразветвленной цепи 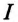
Для определения этого тока строится векторная диаграмма цепи (рис. 13.26), из которой следует:
где
Таким образом, ток в неразветвленной части цепи 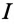
Реактивные проводимости в ветвях имеют различные знаки, так как сопротивления в ветвях различного характера (индуктивное и емкостное).
Треугольник проводимостей рассматриваемой цепи изображен на рис. 13.2в.
Характер разветвленной цепи определяется так же, как и неразветвленной. Если ток цепи 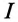
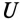
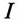
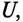
Резонанс токов
Резонанс токов в цепи (рис. 13.2а) с параллельным включением катушки и конденсатора (в различных ветвях) возникает при равенстве реактивных проводимостей в ветвях:
Выражение (13.9) является условием резонанса токов в разветвленных цепях синусоидального тока. Полная (кажущаяся) проводимость при этом условии
так как
Таким образом, полная проводимость цепи при резонансе токов 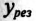
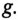
Реактивные токи в ветвях при резонансе токов равны между собой
Это равенство и определяет название «резонанс токов».
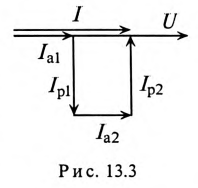
На основании равенства (13.12) строится векторная диаграмма при резонансе токов (рис. 13.3). Реактивные токи находятся в противофазе, поэтому ток в неразветвленной части цепи 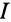
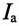
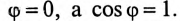
Эта активная мощность компенсирует потери на активном сопротивлении в параллельном резонансном контуре. Мощность (энергия), которая колеблется между электрическим полем конденсатора и магнитным полем индуктивности при резонансе, не является реактивной, так как не загружает источник и провода.
Частота резонанса токов в параллельном резонансном контуре может быть определена из условия резонанса токов, т. е. равенства реактивных проводимостей в ветвях
После ряда преобразований равенства (13.13) определяется частота резонанса токов
Резонансная частота зависит не только от параметров колебательного контура 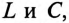
Если в резонансном контуре отсутствуют активные сопротивления в ветвях, то частота резонанса токов 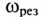
Если в резонансном контуре 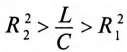
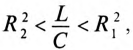
Резонанс токов нашел широкое применение в радиотехнике и выпрямительной технике (в резонансных фильтрах) и др.
Пример 13.1
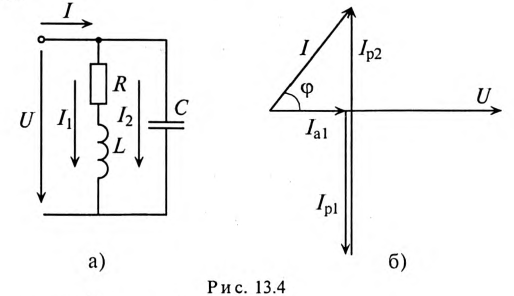
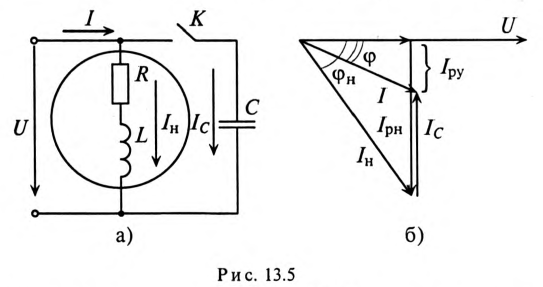
Напряжение, приложенное к параллельно включенным катушке и конденсатору (рис. 13.4а), 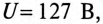
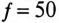
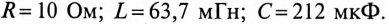
1) токи всех участков цепи:
2) углы сдвига фаз этих токов относительно напряжения:
3) полную S, активную Р и реактивную Q мощности цепи;
4) частоту, при которой наступит резонанс токов в этой цепи. Построить векторную диаграмму.
Решение
1. Сопротивление участков цепи:
где
Сопротивление 1-й ветви:
Токи в ветвях соответственно равны
Для определения тока 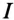
Тогда полная проводимость цепи будет равна
Ток в неразветвленной части цепи
2. Углы сдвига фаз:
.
Знак «минус» перед значением угла 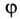
3. Полная мощность цепи
Активная мощность цепи 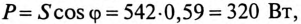
Реактивная мощность цепи 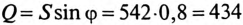
4. Угловая частота резонанса токов в цепи равна
Откуда
Для построения векторной диаграммы определяют активные и реактивные токи в ветвях:
Векторная диаграмма для рассматриваемой цепи изображена на рис. 13.46.
На векторной диаграмме видно, что ток I опережает напряжение U на угол 53°30′ (цепь емкостного характера).
Коэффициент мощности
Номинальные параметры, т.е. мощность источника 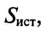
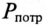
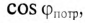
Из (13.15) следует, что чем меньше 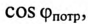
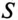
Ток в цепи потребителя с определенным 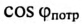
Из (13.16) видно, что чем меньше 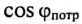
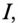
Таким образом, низкий коэффициент мощности потребителя 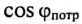

Однако 

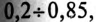
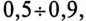
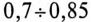
Так как большинство потребителей представляет собой нагрузку индуктивного характера, то для улучшения 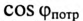
Из векторной диаграммы (рис. 13.56) видно, что с подключением конденсатора С (ключ К замкнут) появляется 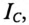
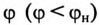
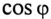
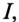
Для повышения коэффициента мощности 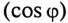
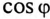
Коэффициент мощности можно повысить, увеличив активную нагрузку. При этом увеличивается потребляемая энергия, что экономически нерационально (уменьшается КПД установки).
Пример 13.2
Асинхронный двигатель, включенный в сеть с напряжением 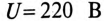
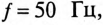
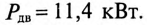
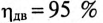
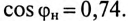
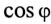
Решение
Мощность, потребляемая двигателем из сети:
Ток нагрузки 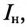
Реактивная составляющая тока двигателя 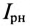
(по таблице 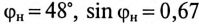
Ток установки 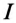
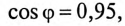
При 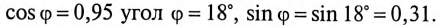
Ток конденсатора 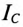
Емкостное сопротивление конденсаторов
Емкость конденсаторов, которые нужно подключить параллельно двигателю для улучшения 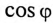
- Электрические цепи несинусоидального тока
- Несинусоидальный ток
- Электрические цепи с распределенными параметрами
- Резистивные электрические цепи и их расчёт
- Резонанс токов
- Трехфазные симметричные цепи
- Трехфазные несимметричные цепи
- Вращающееся магнитное поле
Вся прикладная электротехника базируется на одном догмате — это закон Ома для участка цепи. Без понимания принципа этого закона невозможно приступать к практике, поскольку это приводит к многочисленным ошибкам. Имеет смысл освежить эти знания, в статье мы напомним трактовку закона, составленного Омом, для однородного и неоднородного участка и полной цепи.
Классическая формулировка
Этот простой вариант трактовки, известный нам со школы.
Однородный открытый участок электроцепи
Формула в интегральной форме будет иметь следующий вид:
Формула в интегральной форме
То есть, поднимая напряжение, мы тем самым увеличиваем ток. В то время, как увеличение такого параметра, как «R», ведет к снижению «I». Естественно, что на рисунке сопротивление цепи показано одним элементом, хотя это может быть последовательное, параллельное (вплоть до произвольного)соединение нескольких проводников.
В дифференциальной форме закон мы приводить не будем, поскольку в таком виде он применяется, как правило, только в физике.
Как строятся
Монтаж вторичных цепей осуществляется с учетом ряда правил. Так, каждое устройство может быть подключено к 1 или нескольким источникам тока. Это определяют, принимая во внимание потребляемую мощность, нужную точность, протяженность.
Если речь идет о многообмоточном трансформаторе, вторичная цепь является независимым источником тока. Все вторичные приспособления, которые присоединяются к ТТ одной фазы, соединяют со вторичной обмоткой в определенном порядке. Приспособления и соединительные цепи должны составить замкнутую систему. Нельзя размыкать вторичную цепь трансформатора тока, если имеется ток в первичной. Поэтому в ней никогда не устанавливают автоматические выключатели, предохранители.
Формулировка для полной цепи
Трактовка для полной цепи будет несколько иной, чем для участка, поскольку в законе, составленном Омом, еще учитывает параметр «r», это сопротивление источника ЭДС. На рисунке ниже проиллюстрирована подобная схема.
Схема с подключенным с источником
Учитывая «r» ЭДС, формула предстанет в следующем виде:
Заметим, если «R» сделать равным 0, то появляется возможность рассчитать «I», возникающий во время короткого замыкания.
Напряжение будет меньше ЭДС, определить его можно по формуле:
Собственно, падение напряжения характеризуется параметром «I*r». Это свойство характерно многим гальваническим источникам питания.
О заземлении
Заземление для защиты всегда вставляют во вторичную цепь. Делается это посредством объединения соответствующего устройства с одним из фазных проводов либо нулевой точкой вторичной системы. Заземление делают на точке, которая находится максимально близко к сборкам зажимов ТН либо рядом с его выводами.
В проводах на подвергшейся заземлению фазе на вторичной цепи работу по установке автоматических выключателей между ней и местом заземления рубильника не осуществляют. Выводы обмоток трансформатора напряжения, которые были заземлены, не соединяют. Жилы контрольных кабелей прокладывают до места назначения – к примеру, до шинок. Не соединяют и выводы, подвергшиеся заземлению на разных трансформаторах напряжения.
В процессе использования может повредиться трансформатор напряжения, вторичные цепи с защитой которого соединены с устройствами автоматики, измерений и так далее. Во избежание случаев повреждений осуществляют резервирование.
Если имеется схема, включающая двойную систему сборных шин, ТН резервируют друг друга взаимно, когда из работы выводится один из трансформаторов. Если в схеме имеется 2 системы сборных шин, в процессе переключения соединения с одной системы на вторую автоматически переключаются цепи напряжения.
Всегда исключают вероятность того, что заземленные цепи обоих трансформаторов соединятся. Это крайне важно. Практика доказывает, что если это произойдет, работа защитной релейной системы, автоматических устройств будет серьезно нарушена.
Необходимо всегда следить за тем, чтобы разъемные контакты находились в хорошем состоянии, а также за вторичными цепями напряжения, оперативного тока, которые отходят от них.
Неоднородный участок цепи постоянного тока
Под таким типом подразумевается участок, где помимо электрического заряда производится воздействие других сил. Изображение такого участка показано на рисунке ниже.
Схема неоднородного участка
Формула для такого участка (обобщенный закон) будет иметь следующий вид:
Формула для неоднородного участка цепи
Особенности
В трансформаторах напряжения, которые помещают на электростанции либо подстанции с рядом распределительных устройств, размещают релейные щиты и щиты управления достаточно далеко друг от друга, заземляя их в месте, удаленном от трансформатора напряжения. Из-за такой особенности невозможно установить автоматические выключатели, которые бы защищали трансформатор в случае замыкания цепи.
Вторичная цепь, питание которой осуществляется с помощью аккумулятора, обладает некоторыми нюансами. Их всегда учитывают, выбирая предохранители.
Понятие «вторичные цепи» относится к проводам и кабелям, в том числе объединяющим оборудование, предназначенное для измерения величин в первичной цепи.
Их применяют в заливочных и разливочных кранах, которые работают с жидкими металлами. Также используются и в быстроходных кранах. В обоих случаях цепи представлены проводами с медными жилами, а также с термостойкой изоляцией.
Важно учитывать, что предохранители должны быть открыты для того чтобы без труда их осматривать и ремонтировать, не понижая напряжения на всей сборке.
Цепь состоит из изолированных проводов, объединенных в потоки. Если в одном потоке проводов больше 25 штук, то работа с ними становится чрезмерно сложной.
Каждый поток кладут по самому короткому пути, помещая его в горизонтальном либо вертикальном направлении. Допустимо отклонять их от этих положений лишь на 6 мм в каждом метре длины. Формируя потоки, провода никогда не скрещивают. Каждое ответвление проводится под прямыми углами. Важно чтобы ряды их были ровными. Обычно на поток берется 10-15 проводов. В нижних рядах находятся самые длинные провода, а в верхних – с наименьшей длиной.
Если вторичная цепь в шкафах и панелях включает медные провода, то во внешних соединениях – между шкафами и панелями – контрольные кабели. Иногда внешнее соединение реализуется с применением проводов в стальных трубах.
Практическое использование
Видео: Закон Ома для участка цепи — практика расчета цепей.
Собственно, к любому участку цепи можно применить этот закон. Пример приведен на рисунке.
Применяем закон к любому участку цепи
Используя такой план, можно вычислить все необходимые характеристики для неразветвленного участка. Рассмотрим более детальные примеры. Находим силу тока Рассмотрим теперь более определенный пример, допустим, возникла необходимость узнать ток, протекающий через лампу накаливания. Условия:
- Напряжение – 220 В;
- R нити накала – 500 Ом.
Решение задачи будет выглядеть следующим образом: 220В/500Ом=0,44 А.
Рассмотрим еще одну задачу со следующими условиями:
- R=0,2 МОм;
- U=400 В.
В этом случае, в первую очередь, потребуется выполнить преобразование: 0,2 МОм = 200000 Ом,после чего можно приступать к решению: 400 В/200000 Ом=0,002 А (2 мА). Вычисление напряжения Для решения мы также воспользуемся законом, составленным Омом. Итак задача:
- R=20 кОм;
- I=10 мА.
Преобразуем исходные данные:
- 20 кОм = 20000 Ом;
- 10 мА=0,01 А.
Решение: 20000 Ом х 0,01 А = 200 В.
Незабываем преобразовывать значения, поскольку довольно часто ток может быть указан в миллиамперах.
Сопротивление.
Несмотря на то, что общий вид способа для расчета параметра «R» напоминает нахождение значения «I», между этими вариантами существуют принципиальные различия. Если ток может меняться в зависимости от двух других параметров, то R (на практике) имеет постоянное значение. То есть по своей сути оно представляется в виде неизменной константы.
Если через два разных участка проходит одинаковый ток (I), в то время как приложенное напряжение (U) различается, то, опираясь на рассматриваемый нами закон, можно с уверенностью сказать, что там где низкое напряжение «R» будет наименьшим.
Рассмотрим случай когда разные токи и одинаковое напряжение на несвязанных между собой участках. Согласно закону, составленному Омом, большая сила тока будет характерна небольшому параметру «R».
Рассмотрим несколько примеров.
Допустим, имеется цепь, к которой подведено напряжение U=50 В, а потребляемый ток I=100 мА. Чтобы найти недостающий параметр, следует 50 В / 0,1 А (100 мА), в итоге решением будет – 500 Ом.
Вольтамперная характеристика позволяет наглядно продемонстрировать пропорциональную (линейную) зависимость закона. На рисунке ниже составлен график для участка с сопротивлением равным одному Ому (почти как математическое представление закона Ома).
Изображение вольт-амперной характеристики, где R=1 Ом
Изображение вольт-амперной характеристики
Вертикальная ось графика отображает ток I (A), горизонтальная – напряжение U(В). Сам график представлен в виде прямой линии, которая наглядно отображает зависимость от сопротивления, которое остается неизменным. Например, при 12 В и 12 А «R» будет равно одному Ому (12 В/12 А).
Обратите внимание, что на приведенной вольтамперной характеристике отображены только положительные значения. Это указывает, что цепь рассчитана на протекание тока в одном направлении. Там где допускается обратное направление, график будет продолжен на отрицательные значения.
Заметим, что оборудование, вольт-амперная характеристика которого отображена в виде прямой линии, именуется — линейным. Этот же термин используется для обозначения и других параметров.
Помимо линейного оборудования, есть различные приборы, параметр «R» которых может меняться в зависимости от силы тока или приложенного напряжения. В этом случая для расчета зависимости нельзя использовать закон Ома. Оборудование такого типа называется нелинейным, соответственно, его вольт-амперные характеристики не будут отображены в виде прямых линий.
Результат понижения напряжения
Распространено явление, когда входное напряжение определяется ниже установленной нормы. Проседание по длине кабеля возникает по причине прохождения высокого тока, который вызывает увеличение сопротивления. Также потери возрастают на линиях большой протяженности, что характерно для сельской местности.
Согласно нормативам, потери от трансформатора до самого удаленного участка должны составлять не более 9%. Результат отклонения параметров от нормы может быть следующим:
- сбой работы энергозависимых установок и оборудования, осветительных приборов;
- выход электроприборов из строя при низких показателях напряжения на входе;
- снижение вращающего момента при пуске электродвигателя или компрессорной установки;
- пусковой ток приводит к перегреву и отключению двигателя;
- неравномерная токовая нагрузка в начале линии и на удаленном конце;
- осветительные приборы работают вполнакала;
- потери электроэнергии, недоиспользование мощности тока.
Изменяются характеристики и параметры эксплуатации электрических приборов. Например, из-за слабой мощности увеличивается время нагрева воды бойлером. Снижение напряжения приводит к сбоям в электронике.
В рабочем режиме потери напряжения в кабеле могут быть до 5%. Это значение допустимо для сетей энергетической отрасли, так как токи большой мощности доставляются на дальние расстояния. К таким линиям предъявляются повышенные требования. Поэтому при потерях в быту следует уделить внимание вторичным сетям распределения энергии.
Вывод
Как уже упоминалось в начале статьи, вся прикладная электротехника базируется на законе, составленном Омом. Незнание этого базового догмата может привести к неправильному расчету, который, в свою очередь, станет причиной аварии.
Подготовка электриков как специалистов начинается с изучения теоретических основ электротехники. И первое, что они должны запомнить – это закон составленный Омом, поскольку на его основе производятся практически все расчеты параметров электрических цепей различного назначения.
Понимание основного закона электротехники поможет лучше разбираться в работе электрооборудования и его основных компонентов. Это положительно отразится на техническом обслуживании в процессе эксплуатации.
Самостоятельная проверка, разработка, а также опытное изучение узлов оборудования – все это существенно упрощается, если использовать закон Ома для участка цепи. При этом не требуется проводить всех измерений, достаточно снять некоторые параметры и, проведя несложные расчеты, получить необходимые значения.
Потенциал
Напряженность электрического поля характеризует его силовые свойства. Для количественной характеристики энергетических возможностей поля было введено понятие потенциала. Потенциал электростатического поля φ — это отношение потенциальной энергии Wp заряда в поле к величине заряда q:
$ φ = {Wpover {q * U}} $ (3).
Тогда напряжение между двумя точками электрической цепи (1-ой и 2-ой) можно выразить так:
$ U = φ_1 – φ_2 $ (4).
То есть становится более понятным физический смысл величины напряжения — это разность потенциалов в начальной точке 1 и конечной точке 2.
Для понимания смыслового значения напряжения можно воспользоваться аналогией с гравитационным полем, которое тоже является потенциальным. Масса тела m аналогична величине заряда q, а высота h, с которой может упасть, например, камень или поток воды, вращающий турбину, аналогична напряжению U. Напомним выражение для потенциальной энергии тела массы m в гравитационном поле Земли:
$ Е_p = m * g * h $ (5),
где: g — ускорение свободного падения, 9,8 м/с2. Видно, что формулы (2) и (4), полученные для разных потенциальных полей, очень похожи.
История открытия
Зависимость между током, напряжением и сопротивлением в электрической цепи была установлена опытным путём в 1827 году. Занимаясь исследованиями электричества, Георг Симон Ом проводил ряд экспериментов над проводниками, изучая их проводимость, и в частности, подключая последовательно к источнику энергии тонкие проводники, выполненные из различных материалов. Изменяя их длину, он получал определённую силу тока. Им было установлено, что на результаты экспериментов влияет источник электрической энергии, сопротивление которого оказывалось выше, чем у используемых в опытах проводников.
По совету своего наставника Поггендорфа Ом собрал термоэлектрическую батарею, отказавшись от использования химических элементов, применив вместо них открытую Зеебеком термопару медь-висмут. Для измерения параметров цепи им использовались крутильные весы, с магнитной стрелкой сконструированные Кулоном.
На основании своих исследований физик-экспериментатор пришёл к выводу, что отклонение стрелки зависит от определённой силы, названной силой тока. Когда стрелка отклонялась, Ом закручивал весы таким образом, чтобы она возвращалась в своё начальное положение. Угол, на который закручивалась нить, он считал пропорциональной силе тока. Изменяя условия, Ом вывел математическую зависимость, составив уравнение. Выглядело оно следующим образом: Х = а/b + x, где за Х принималась сила, отклоняющая магнитную стрелку, за а — длина исследуемого образца, а b+x обозначали интенсивность и считались постоянной величиной.
В 1862 году в журнале «Физика и химия» публикуется статья Ома под названием «Определение закона, по которому металлы проводят контактное электричество». Результаты его исследований не производят впечатления на других ученых, и его выводы остаются незамеченными. Ом продолжает эксперименты, выясняя, что электричество можно рассмотреть наподобие теплового потока. Подобно разнице температур, благодаря которой совершается тепловое движение, некой величиной можно описать движение электрического заряда. Так он вводит понятие ЭДС.
Открытие Ома было принято учёным миром уже после его смерти. Существенный вклад в это внесли русские учёные Ленц и Якоби. В 1842 году Лондонское Королевское общество наградило физика золотой медалью, а закон, открытый им, был назван его именем.
Диагностика
Когда проблема появляется в системе зажигания, которую относят к распределительному виду, то это влияет на все цилиндры двигателя. Его запуск превращается в весьма трудную задачу. Когда двигатель работает, но пропускает порой зажигание, и при этом загорается лампа «Проверить двигатель», то пришла пора применения диагностического сканера. С его помощью проверяют код, который связан с пропуском зажигания.
Тем не менее такая проблема может быть связана со сбоями в подаче топлива, по этой причине нельзя сразу точно диагностировать неисправность в катушке, свечах либо высоковольтных проводах.
И тут важно знание первичных и вторичных цепей. Если отсутствует соответствующий кол, то обязательно измеряют сопротивление в цепях. Для этого используют цифровой мультиметр. Важно посмотреть, в каком состоянии находятся свечи зажигания, каков зазор между контактами. Нередко на неисправности указывает цвет нагара на свечах. Вероятно, пропуск появился по причине наличия масляных отложений, сильного нагара. Важно осмотреть высоковольтные провода, чтобы удостовериться в том, что сопротивление в них находится в пределах установленной нормы.
Когда установлено, что катушка, ее цепи в норме, то можно предположить, что топливная форсунка загрязнилась либо повредилась. Поэтому обязательно проверяют ее. Когда вероятность ее неисправности исключена, то проверкам подвергают компрессию, клапаны, смотрят, не произошла ли утечка прокладки головки блока цилиндров.
Но если двигатель прокручивается, а искры нет, то, вероятно, неисправность находится в цепи управления. Проверку осуществляют руководствуясь рядом строгих правил.
«Не знаешь Ома – сиди дома» — пословица старых электриков. Действительно, этот закон очень важен для понимания того, как связаны напряжение, ток и сопротивление, или проще говоря — от чего зависит ток и мощность нагрузки и как их рассчитать.
Для понимания этих базовых вещей нужно знать закон Ома для участка цепи и закон Ома для полной цепи. Главное различие между ними, что первый распространяется на отдельный участок или элемент и учитывает только его сопротивление и приложенное к нему напряжение, а второй учитывает и внутреннее сопротивление источника питания. Давайте разберёмся подробнее.
Закон Ома для участка цепи
Самый простой и всем известный со школы вариант — закон Ома для участка цепи. Его определение звучит следующим образом:
В виде формулы это выглядит так:
I=U/R,
где I — ток, U — напряжение, R— сопротивление.
То есть чтобы определить силу тока нужно знать напряжение на участке цепи (на элементе) и его сопротивление.
Напряжение на элементе равно произведению тока на сопротивление, то есть чтобы найти напряжение нужно знать ток в участке цепи и его сопротивление:
U=IR
Чтобы найти сопротивление по закону Ома, нужно знать напряжение и ток:
R=U/I
К сведению: правильнее говорить «падение напряжения», но для упрощения в разговорной речи говорят просто «напряжение на элементе» или «… на участке цепи».
Электрическое сопротивление измеряется в Омах, величина 1 Ом выражает такое сопротивление проводника, при котором по нему будет протекать ток в 1 ампер, если к нему приложить напряжение в 1 вольт.
Как запомнить эти формулы?
В виде формулы это выглядит так:
I=U/R,
где I — ток, U — напряжение, R— сопротивление.
То есть чтобы определить силу тока нужно знать напряжение на участке цепи (на элементе) и его сопротивление.
Напряжение на элементе равно произведению тока на сопротивление, то есть чтобы найти напряжение нужно знать ток в участке цепи и его сопротивление:
U=IR
Чтобы найти сопротивление по закону Ома, нужно знать напряжение и ток:
R=U/I
К сведению: правильнее говорить «падение напряжения», но для упрощения в разговорной речи говорят просто «напряжение на элементе» или «… на участке цепи».
Электрическое сопротивление измеряется в Омах, величина 1 Ом выражает такое сопротивление проводника, при котором по нему будет протекать ток в 1 ампер, если к нему приложить напряжение в 1 вольт.
Как запомнить эти формулы?
Для запоминания формул закона Ома есть удобная мнемоническая подсказка так называемый «треугольник Ома». В нём сверху размещена буква U, а снизу I и R. Как несложно догадаться, они обозначают напряжение, ток и сопротивление соответственно.
Для запоминания формул закона Ома есть удобная мнемоническая подсказка так называемый «треугольник Ома». В нём сверху размещена буква U, а снизу I и R. Как несложно догадаться, они обозначают напряжение, ток и сопротивление соответственно.
Как пользоваться треугольником? Всё просто — закройте пальцем величину, которую нужно найти, а оставшиеся не закрытыми буквы нужно умножить или разделить друг на друга, что подробно проиллюстрировано ниже.
Есть еще одна шпаргалка в виде круга разделенного на сегменты, где перечислены все необходимые формулы, кроме перечисленных выше, добавлены и формулы для вычисления мощности.
Примеры
Итак, чтобы научиться рассчитывать напряжение на участке цепи, решим простенькую задачу. У нас есть цепь, состоящая из 3 резисторов и идеального источника с напряжением 12В постоянного тока. Пусть участком цепи у нас будет резистор R2, найдём напряжение на нём.
Дано:
U= 12 В;
R1= 1 кОм;
R2= 2 кОм;
R3= 3 кОм;
Найти:
I — ?;
U(R2) — ?;
По закону Ома чтобы найти напряжение нужно знать ток через участок цепи и его сопротивление.
U=IR
Последнее у нас известно, поэтому нужно найти ток в цепи, элементы соединены последовательно, поэтому ток через каждый из них одинаков, и чтобы найти его силу — нужно сначала найти общее сопротивление всех элементов, но сначала переведём его в Омы:
R1 = 1 кОм = 1000 Ом; R2 = 2 кОм = 2000 Ом; R3 = 3 кОм = 3000 Ом.
Теперь найдём общее сопротивление:
Rобщ=R1+R2+R3=1000+2000+3000= 6000 Ом
Тогда ток в цепи равен:
I= U/R = 12/6000 = 0,002 А
И наконец падение напряжения на резисторе R2:
U(R2) = I*U(R2) = 0,002*2000=4В
Итого, на выводах резистора R2 будет 4 вольта.
Закон Ома для полной цепи
Определение закона Ома для полной цепи вы видите ниже, жирным выделено основное отличие от закона для участка цепи.
В формуле добавляется внутреннее сопротивление источника питания, а напряжение заменяется на ЭДС:
I=E/(R+r),
где I – ток, E – ЭДС, R – сопротивление, r- внутреннее сопротивление источника.
Внутреннее сопротивление источника обуславливается его устройством, например, сечением вторичной обмотки трансформатора, химическим составом, степенью заряда и состоянием электродов аккумуляторов и батареек и так далее. На схеме условно рисуется в виде резистора внутри источника, но на самом деле никакого «внутреннего» или «скрытого» сопротивления там нет, как было отмечено выше.
Почему важно учитывать внутреннее сопротивление источника? Всё очень просто — вы замечали, как погасают лампочки в автомобиле, когда стартер запускает двигатель? Это происходит из-за просадок на проводах и в аккумуляторе от высоких пусковых токов. В принципе, подобное мы наблюдаем, когда лампы накаливания «просаживаются» по яркости во время пуска мощной нагрузки, например, электродвигателей.
Примеры
Давайте проанализируем, как влияет внутреннее сопротивление источника на напряжение нагрузки. Допустим, что у нас есть какой-то источник с внутренним сопротивлением (r) в 1 Ом и ЭДС (E) в 12 Вольт. И есть 3 разных нагрузки, с сопротивлением (R) каждой из них: 10, 5 и 1 Ом соответственно. Нагрузку будем подключать по очереди, по одной для каждого расчета.
Рассчитаем ток первой нагрузки:
I1=E/(R1+r)=12/(10+1)=1.09 А
Рассчитаем напряжение на нагрузке:
U1=I1*R1=1.09*10=10.9 В
Сразу видим, что на нагрузке уже не 12, а 10 вольт, посчитаем другие варианты:
Рассчитаем ток второй нагрузки:
I2=E/(R2+r)=12/(5+1)=2 А
Рассчитаем напряжение на нагрузке:
U2=I2*R2=2*5=10 В
Рассчитаем ток третей нагрузки:
I3=E/(R3+r)=12/(1+1)=6 А
Рассчитаем напряжение:
U3=I3*R3=6*1=6 В
Как вы можете видеть на внутреннем сопротивлении падает какое-то напряжение, и падение напряжение прямо пропорционально току нагрузки. При этом до нагрузки доходит всё меньше и меньше напряжения.
Сделаем то же самое, но для источника с внутренним сопротивлением 0.1 Ома. Рассчитаем ток первой нагрузки:
I1=E/(R1+r)=12/(10+0,1)=1.18 А
Рассчитаем напряжение:
U1=I1*R1=1.18*10=11.8 В
Ток второй нагрузки:
I2=E/(R2+r)=12/(5+0,1)=2,35 А
Рассчитаем напряжение на нагрузке:
U2=I2*R2=2,35*5=11.75 В
Рассчитаем ток третей нагрузки:
I3=E/(R3+r)=12/(1+0,1)=10,9 А
Рассчитаем напряжение:
U3=I3*R3=10,9*1=10,9 В
Для удобства соберем все результаты расчётов в одну таблицу.
Из таблицы мы видим, что чем меньше внутреннее сопротивление источника — тем меньше просаживается напряжение под нагрузкой.
Заключение
Георг Симон Ом жил в 1786-1854 годах, в 1826 году вывел теоретически и подтвердил с помощью опытов закон выражающий связь напряжения, тока и сопротивления. Этот закон назвали в честь открывателя — законом Ома, а также единицу измерения электрического сопротивления.
Закон Ома — один из важнейших и основополагающих в электротехнике, он широко используется при расчетах электрических схем.
Пишите в комментариях, понравился ли вам такой формат теоретической статьи и какие статьи хотите увидеть в будущем?