Данная статья рассматривает действия над дробями. Будут сформированы и обоснованы правила сложения, вычитания, умножения, деления или возведения в степень дробей вида AB, где A и B могут быть числами, числовыми выражениями или выражениями с переменными. В заключении будут рассмотрены примеры решения с подробным описанием.
Правила выполнения действий с числовыми дробями общего вида
Числовые дроби общего вида имеют числитель и знаменатель, в которых имеются натуральные числа или числовые выражения. Если рассмотреть такие дроби, как 35, 2,84, 1+2·34·(5-2), 34+782,3-0,8, 12·2, π1-23+π, 20,5ln 3, то видно, что числитель и знаменатель может иметь не только числа, но и выражения различного плана.
Существуют правила, по которым идет выполнение действий с обыкновенными дробями. Оно подходит и для дробей общего вида:
- При вычитании дробей с одинаковыми знаменателями складываются только числители, а знаменатель остается прежним, а именно: ad±cd=a±cd, значения a, c и d≠0 являются некоторыми числами или числовыми выражениями.
- При сложении или вычитании дроби при разных знаменателях, необходимо произвести приведение к общему, после чего произвести сложение или вычитание полученных дробей с одинаковыми показателями. Буквенно это выглядит таком образом ab±cd=a·p±c·rs, где значения a, b≠0, c, d≠0, p≠0, r≠0, s≠0 являются действительными числами, а b·p=d·r=s. Когда p=d и r=b, тогда ab±cd=a·d±c·db·d.
- При умножении дробей выполняется действие с числителями, после чего со знаменателями, тогда получим ab·cd=a·cb·d, где a, b≠0, c, d≠0 выступают в роли действительных чисел.
- При делении дроби на дробь первую умножаем на вторую обратную, то есть производим замену местами числителя и знаменателя: ab:cd=ab·dc.
Обоснование правил
Существуют следующие математические моменты, на которые следует опираться при вычислении:
- дробная черта означает знак деления;
- деление на число рассматривается как умножение на его обратное значение;
- применение свойства действий с действительными числами;
- применение основного свойства дроби и числовых неравенств.
С их помощью можно производить преобразования вида:
ad±cd=a·d-1±c·d-1=a±c·d-1=a±cd;ab±cd=a·pb·p±c·rd·r=a·ps±c·es=a·p±c·rs;ab·cd=a·db·d·b·cb·d=a·d·a·d-1·b·c·b·d-1==a·d·b·c·b·d-1·b·d-1=a·d·b·cb·d·b·d-1==(a·c)·(b·d)-1=a·cb·d
Примеры
В предыдущем пункте было сказано про действия с дробями. Именно после этого дробь нуждается в упрощении. Подробно эта тема была рассмотрена в пункте о преобразовании дробей.
Для начала рассмотрим пример сложения и вычитания дробей с одинаковым знаменателем.
Даны дроби 82,7 и 12,7, то по правилу необходимо числитель сложить, а знаменатель переписать.
Решение
Тогда получаем дробь вида 8+12,7. После выполнения сложения получаем дробь вида 8+12,7=92,7=9027=313. Значит, 82,7+12,7=8+12,7=92,7=9027=313.
Ответ: 82,7+12,7=313
Имеется другой способ решения. Для начала производится переход к виду обыкновенной дроби, после чего выполняем упрощение. Это выглядит таким образом:
82,7+12,7=8027+1027=9027=313
Произведем вычитание из 1-23·log23·log25+1 дроби вида 233·log23·log25+1.
Так как даны равные знаменатели, значит, что мы выполняем вычисление дроби при одинаковом знаменателе. Получим, что
1-23·log23·log25+1-233·log23·log25+1=1-2-233·log23·log25+1
Имеются примеры вычисления дробей с разными знаменателями. Важный пункт – это приведение к общему знаменателю. Без этого мы не сможем выполнять дальнейшие действия с дробями.
Процесс отдаленно напоминает приведение к общему знаменателю. То есть производится поиск наименьшего общего делителя в знаменателе, после чего добавляются недостающие множители к дробям.
Если складываемые дроби не имеют общих множителей, тогда им может стать их произведение.
Рассмотрим на примере сложения дробей 235+1 и 12.
Решение
В данном случае общим знаменателем выступает произведение знаменателей. Тогда получаем, что 2·35+1. Тогда при выставлении дополнительных множителей имеем, что к первой дроби он равен 2, а ко второй 35+1. После перемножения дроби приводятся к виду 42·35+1. Общее приведение 12 будет иметь вид 35+12·35+1. Полученные дробные выражения складываем и получаем, что
235+1+12=2·22·35+1+1·35+12·35+1==42·35+1+35+12·35+1=4+35+12·35+1=5+352·35+1
Ответ: 235+1+12=5+352·35+1
Когда имеем дело с дробями общего вида, тогда о наименьшем общем знаменателе обычно дело не идет. В качестве знаменателя нерентабельно принимать произведение числителей. Для начала необходимо проверить, имеется ли число, которое меньше по значению, чем их произведение.
Рассмотрим на примере 16·215 и 14·235, когда их произведение будет равно 6·215·4·235=24·245. Тогда в качестве общего знаменателя берем 12·235.
Рассмотрим примеры умножений дробей общего вида.
Для этого необходимо произвести умножение 2+16 и 2·53·2+1.
Решение
Следую правилу, необходимо переписать и в виде знаменателя написать произведение числителей. Получаем, что 2+16·2·53·2+12+1·2·56·3·2+1. Когда дробь будет умножена, можно производить сокращения для ее упрощения. Тогда 5·332+1:1093=5·332+1·9310.
Используя правило перехода от деления к умножению на обратную дробь, получим дробь, обратную данной. Для этого числитель и знаменатель меняются местами. Рассмотрим на примере:
5·332+1:1093=5·332+1·9310
После чего должны выполнить умножение и упростить полученную дробь. Если необходимо, то избавиться от иррациональности в знаменателе. Получаем, что
5·332+1:1093=5·33·9310·2+1=5·210·2+1=32·2+1==3·2-12·2+1·2-1=3·2-12·22-12=3·2-12
Ответ: 5·332+1:1093=3·2-12
Данный пункт применим, когда число или числовое выражение может быть представлено в виде дроби, имеющую знаменатель, равный 1, тогда и действие с такой дробью рассматривается отдельным пунктом. Например, выражение 16·74-1·3 видно, что корень из 3 может быть заменен другим 31 выражением. Тогда эта запись будет выглядеть как умножение двух дробей вида 16·74-1·3=16·74-1·31.
Выполнение действие с дробями, содержащими переменные
Правила, рассмотренные в первой статье , применимы для действий с дробями, содержащими переменные. Рассмотрим правило вычитания, когда знаменатели одинаковые.
Необходимо доказать, что A, C и D (D не равное нулю) могут быть любыми выражениями, причем равенство AD±CD=A±CD равноценно с его областью допустимых значений.
Необходимо взять набор переменных ОДЗ. Тогда А, С, D должны принимать соответственные значения a0, c0 и d0. Подстановка вида AD±CD приводит разность вида a0d0±c0d0, где по правилу сложения получаем формулу вида a0±c0d0. Если подставить выражение A±CD, тогда получаем ту же дробь вида a0±c0d0. Отсюда делаем вывод, что выбранное значение, удовлетворяющее ОДЗ, A±CD и AD±CD считаются равными.
При любом значении переменных данные выражения будут равны, то есть их называют тождественно равными. Значит это выражение считается доказываемым равенством вида AD±CD=A±CD.
Примеры сложения и вычитания дробей с переменными
Когда имеются одинаковые знаменатели, необходимо только складывать или вычитать числители. Такая дробь может быть упрощена. Иногда приходится работать с дробями, которые являются тождественно равными, но при первом взгляде это незаметно, так как необходимо выполнять некоторые преобразования. Например, x23·x13+1 и x13+12 или 12·sin 2α и sin a·cos a. Чаще всего требуется упрощение исходного выражения для того, чтобы увидеть одинаковые знаменатели.
Вычислить:1) x2+1x+x-2-5-xx+x-2, 2)lg2x+4x·(lg x+2)+4·lg xx·(lg x+2), x-1x-1+xx+1.
Решение
- Чтобы произвести вычисление, необходимо вычесть дроби, которым имеют одинаковые знаменатели. Тогда получаем, что x2+1x+x-2-5-xx+x-2=x2+1-5-xx+x-2. После чего можно выполнять раскрытие скобок с приведением подобных слагаемых. Получаем, чтоx2+1-5-xx+x-2=x2+1-5+xx+x-2=x2+x-4x+x-2
- Так как знаменатели одинаковые, то остается только сложить числители, оставив знаменатель:lg2x+4x·(lg x+2)+4·lg xx·(lg x+2)=lg2x+4+4x·(lg x+2)
Сложение было выполнено. Видно, что можно произвести сокращение дроби. Ее числитель может быть свернут по формуле квадрата суммы, тогда получим (lg x+2)2 из формул сокращенного умножения. Тогда получаем, что
lg2x+4+2·lg xx·(lg x+2)=(lg x+2)2x·(lg x+2)=lg x+2x - Заданные дроби вида x-1x-1+xx+1 с разными знаменателями. После преобразования можно перейти к сложению.
Рассмотрим двоякий способ решения.
Первый способ заключается в том, что знаменатель первой дроби подвергается разложению на множители при помощи квадратов, причем с ее последующим сокращением. Получим дробь вида
x-1x-1=x-1(x-1)·x+1=1x+1
Значит, x-1x-1+xx+1=1x+1+xx+1=1+xx+1.
В таком случае необходимо избавляться от иррациональности в знаменателе.
Получим:
1+xx+1=1+x·x-1x+1·x-1=x-1+x·x-xx-1
Второй способ заключается в умножении числителя и знаменателя второй дроби на выражение x-1. Таким образом, мы избавляемся от иррациональности и переходим к сложению дроби при наличии одинакового знаменателя. Тогда
x-1x-1+xx+1=x-1x-1+x·x-1x+1·x-1==x-1x-1+x·x-xx-1=x-1+x·x-xx-1
Ответ: 1) x2+1x+x-2-5-xx+x-2=x2+x-4x+x-2, 2)lg2x+4x·(lg x+2)+4·lg xx·(lg x+2)=lg x+2x, 3)x-1x-1+xx+1=x-1+x·x-xx-1.
В последнем примере получили, что приведение к общему знаменателю неизбежно. Для этого необходимо упрощать дроби. Для сложения или вычитая всегда необходимо искать общий знаменатель, который выглядит как произведение знаменателей с добавлением дополниетльных множителей к числителям.
Вычислить значения дробей: 1) x3+1×7+2·2, 2) x+1x·ln2(x+1)·(2x-4)-sin xx5·ln(x+1)·(2x-4), 3) 1cos2x-x+1cos2x+2·cos x·x+x
Решение
- Никаких сложных вычислений знаменатель не требует, поэтому нужно выбрать их произведение вида 3·x7+2·2, тогда к первой дроби x7+2·2 выбирают как дополнительный множитель, а 3 ко второй. При перемножении получаем дробь вида x3+1×7+2·2=x·x7+2·23·x7+2·2+3·13·x7+2·2==x·x7+2·2+33·x7+2·2=x·x7+2·2·x+33·x7+2·2
- Видно, что знаменатели представлены в виде произведения, что означает ненужность дополнительных преобразований. Общим знаменателем будет считаться произведение вида x5·ln2x+1·2x-4. Отсюда x4 является дополнительным множителем к первой дроби, а ln(x+1) ко второй. После чего производим вычитание и получаем, что:
x+1x·ln2(x+1)·2x-4-sin xx5·ln(x+1)·2x-4==x+1·x4x5·ln2(x+1)·2x-4-sin x·lnx+1×5·ln2(x+1)·(2x-4)==x+1·x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4)=x·x4+x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4) - Данный пример имеет смысл при работе со знаменателями дробями. Необходимо применить формулы разности квадратов и квадрат суммы, так как именно они дадут возможность перейти к выражению вида 1cos x-x·cos x+x+1(cos x+x)2. Видно, что дроби приводятся к общему знаменателю. Получаем, что cos x-x·cos x+x2.
После чего получаем, что
1cos2x-x+1cos2x+2·cos x·x+x==1cos x-x·cos x+x+1cos x+x2==cos x+xcos x-x·cos x+x2+cos x-xcos x-x·cos x+x2==cos x+x+cos x-xcos x-x·cos x+x2=2·cos xcos x-x·cos x+x2
Ответ:
1) x3+1×7+2·2=x·x7+2·2·x+33·x7+2·2, 2) x+1x·ln2(x+1)·2x-4-sin xx5·ln(x+1)·2x-4==x·x4+x4-sin x·ln(x+1)x5·ln2(x+1)·(2x-4), 3) 1cos2x-x+1cos2x+2·cos x·x+x=2·cos xcos x-x·cos x+x2.
Примеры умножения дробей с переменными
При умножении дробей числитель умножается на числитель, а знаменатель на знаменатель. Тогда можно применять свойство сокращения.
Произвести умножение дробей x+2·xx2·ln x2·ln x+1 и 3·x213·x+1-2sin2·x-x.
Решение
Необходимо выполнить умножение. Получаем, что
x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)==x-2·x·3·x213·x+1-2×2·ln x2·ln x+1·sin (2·x-x)
Число 3 переносится на первое место для удобства подсчетов, причем можно произвести сокращение дроби на x2, тогда получим выражение вида
3·x-2·x·x13·x+1-2ln x2·ln x+1·sin (2·x-x)
Ответ: x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)=3·x-2·x·x13·x+1-2ln x2·ln x+1·sin (2·x-x).
Деление
Деление у дробей аналогично умножению, так как первую дробь умножают на вторую обратную. Если взять к примеру дробь x+2·xx2·ln x2·ln x+1 и разделить на 3·x213·x+1-2sin2·x-x, тогда это можно записать таким образом, как
x+2·xx2·ln x2·ln x+1:3·x213·x+1-2sin(2·x-x), после чего заменить произведением вида x+2·xx2·ln x2·ln x+1·3·x213·x+1-2sin(2·x-x)
Возведение в степень
Перейдем к рассмотрению действия с дробями общего вида с возведением в степень. Если имеется степень с натуральным показателем, тогда действие рассматривают как умножение одинаковых дробей. Но рекомендовано использовать общий подход, базирующийся на свойствах степеней. Любые выражения А и С, где С тождественно не равняется нулю, а любое действительное r на ОДЗ для выражения вида ACr справедливо равенство ACr=ArCr. Результат – дробь, возведенная в степень. Для примера рассмотрим:
x0,7-π·ln3x-2-5x+12,5==x0,7-π·ln3x-2-52,5x+12,5
Порядок выполнения действий с дробями
Действия над дробями выполняются по определенным правилам. На практике замечаем, что выражение может содержать несколько дробей или дробных выражений. Тогда необходимо все действия выполнять в строгом порядке: возводить в степень, умножать, делить, после чего складывать и вычитать. При наличии скобок первое действие выполняется именно в них.
Вычислить 1-xcos x-1cos x·1+1x.
Решение
Так как имеем одинаковый знаменатель, то 1-xcos x и 1cos x, но производить вычитания по правилу нельзя, сначала выполняются действия в скобках, после чего умножение, а потом сложение. Тогда при вычислении получаем, что
1+1x=11+1x=xx+1x=x+1x
При подстановке выражения в исходное получаем, что 1-xcos x-1cos x·x+1x. При умножении дробей имеем: 1cos x·x+1x=x+1cos x·x. Произведя все подстановки, получим 1-xcos x-x+1cos x·x. Теперь необходимо работать с дробями, которые имеют разные знаменатели. Получим:
x·1-xcos x·x-x+1cos x·x=x·1-x-1+xcos x·x==x-x-x-1cos x·x=-x+1cos x·x
Ответ: 1-xcos x-1cos x·1+1x=-x+1cos x·x.
Здравствуйте, дорогие читатели, подписчики и гости канала. В этой статье рассмотрим различные вычисления с дробями, которые встречаются в шестом задании ОГЭ по математике. В июле 2.07.2021 года состоится последняя пересдача по математике в основной этап. Дополнительный этап будет уже в сентябре.
Давайте начнем разбор заданий.
1) Умножение дробь на дробь. Чтобы умножить дробь на дробь, нужно числитель умножить на числитель, знаменатель на знаменатель, при возможности сократить.
2) Деление дроби на дробь. При делении дробь на дробь, первая дробь переписывается, вторая дробь переворачивается, а деление заменяется на умножение.
3) Вычитание и умножение дробей. Несколько действий.
Способ №1. Находим общий знаменатель при вычитании. Чтобы найти общий знаменатель, нужно найти такое число, которое будет делиться на первое и второе число. В нашем случае это числа 10 и 20. Общий знаменатель 20.
Способ №2. Распределительный закон умножения. Чтобы умножить число на сумму можно умножить это число на каждое слагаемое, и результат сложить. Также это действует и при вычитании.
Также встречаются выражения, в которых не стоит находить общий знаменатель, поскольку это будет сложно. Приведу два примера:
Пример №1
Пример №2
4) Умножение целого числа на дробь. При умножении целого числа на дробь, целое число умножается на числитель, а знаменатель остается без изменений.
5) Сложение, деление и умножение смешанных чисел.
При сложении, вычитании, умножении и делении смешанных чисел иногда легче перевести смешанное число в неправильную дробь. Чтобы смешанное число перевести в неправильную дробь, нужно целую часть умножить на знаменатель, к полученному значению прибавить числитель дробной части и записать это в числитель, а знаменатель оставить прежним.
6) Вынесение общего множителя за скобку.
7) Действия с десятичными дробями
В итоге у нас получилось, что числитель дроби умножили на 100 (10*10=100), значит и знаменатель дроби тоже умножаем на 100, чтобы значение дроби не изменилось.
И еще один пример:
8) Десятичные дроби и действия со степенями
При возведении отрицательного числа в четную степень, получится число положительное. При возведении отрицательного числа в нечетную степень, получится число отрицательное.
И последнее выражение
Для отработки этих примеров, можно воспользоваться сайтом. Там много аналогичных задания, а эта статья вам будет в помощь при их решений.
Спасибо, что дочитали. Вы меня очень поддержите, если поставите лайк и подпишитесь на мой блог.
Доля целого
Доля это каждая из равных частей, на которые поделено целое.
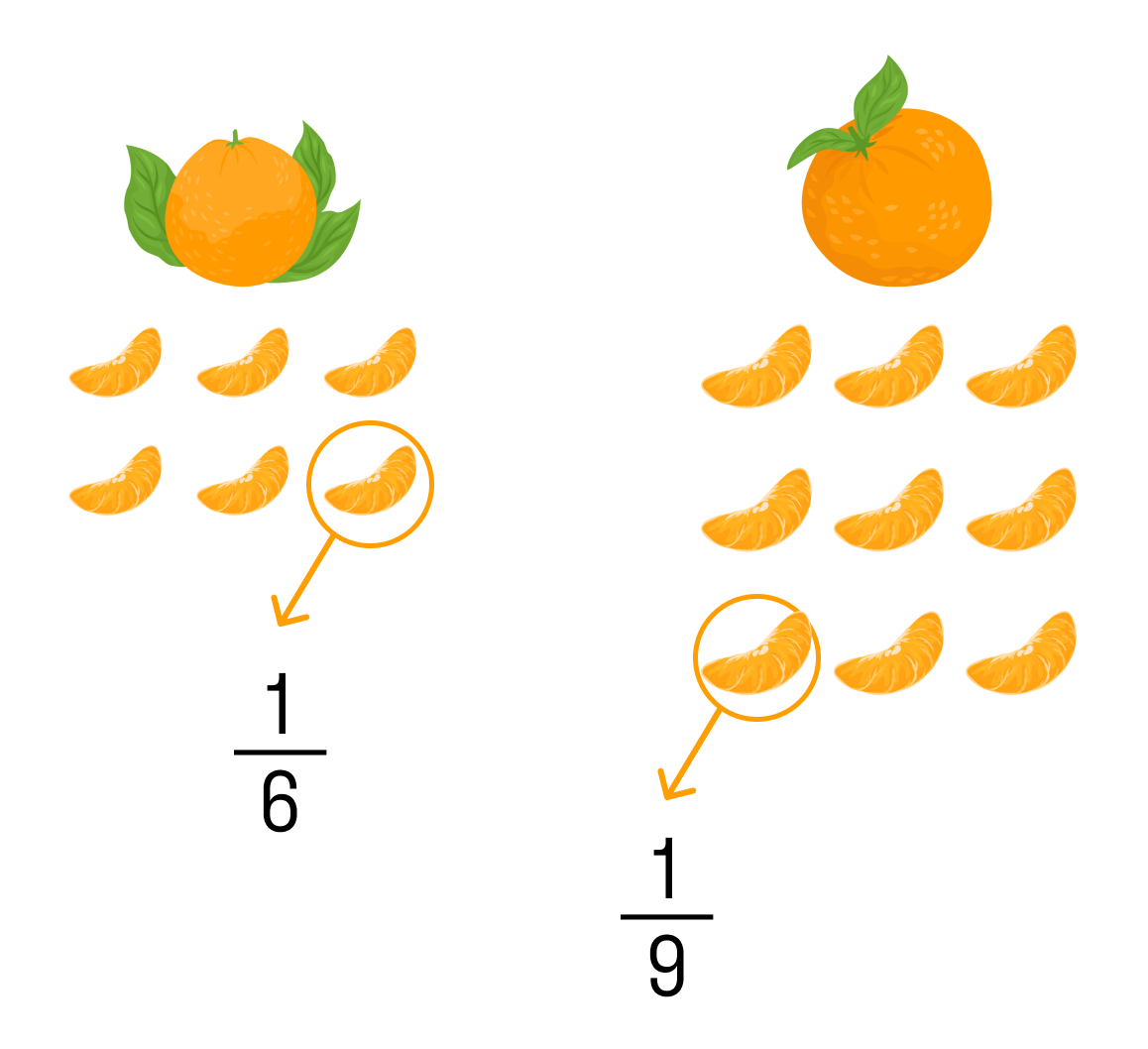
Для примера возьмем два мандарина. Когда мы их почистим, то получим в каждом мандарине разное количество долек или долей. В одном может быть 6, а в другом — целых 9. Размеры долей у каждого мандарина тоже разные.
У каждой доли есть свое название: оно зависит от количества долей в конкретном предмете. Если в мандарите шесть долей — каждая из них будет определяться, как одна шестая от целого.
- Половина — одна вторая доля предмета или 1/2.
- Треть — одна третья доля предмета или 1/3.
- Четверть — одна четвертая доля предмета или 1/4.
Понятие доли можно применить не только к предметам, но и величинам. Так, например, картина занимает четверть стены — при этом ее ширина треть метра.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.

Как устроена обыкновенная дробь
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа.
Такие дроби записываются с помощью двух натуральных чисел и горизонтальной черты, которая называется чертой дроби. Иногда ставится не горизонтальная черта, а косая.
Числитель обыкновенной дроби m/n — это натуральное число m, которое стоит над чертой. Числитель это делимое — то, что мы делим.
Знаменатель обыкновенной дроби m/n — натуральное число n, которое стоит под чертой. Знаменатель это делитель — то, на сколько делим.
Черта между числителем и знаменателем — символ деления.
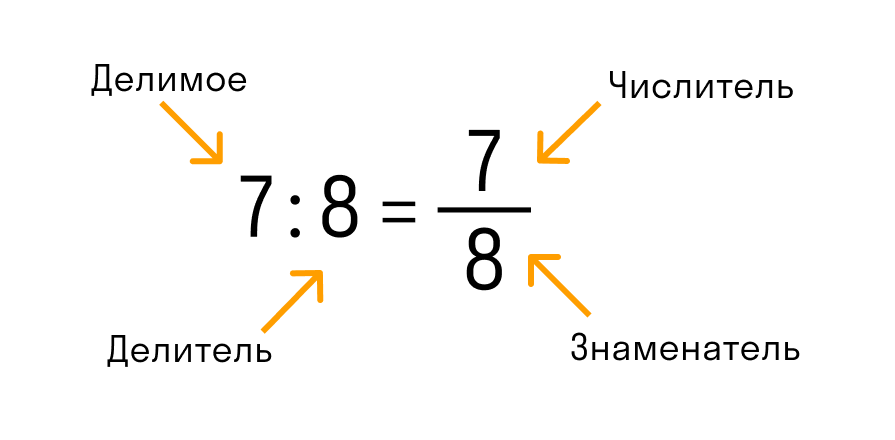
Равные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых справедливо равенство: a * d = b * c. Пример равных дробей: 1/2 и 2/4, так как 1 * 4 = 2 * 2.
Неравные обыкновенные дроби — обыкновенные дроби a/b и c/d, для которых равенство: a * d = b * c не является верным.
Как устроена десятичная дробь
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. Выходит, что десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
- 0,3
- 4,23
- 9,939
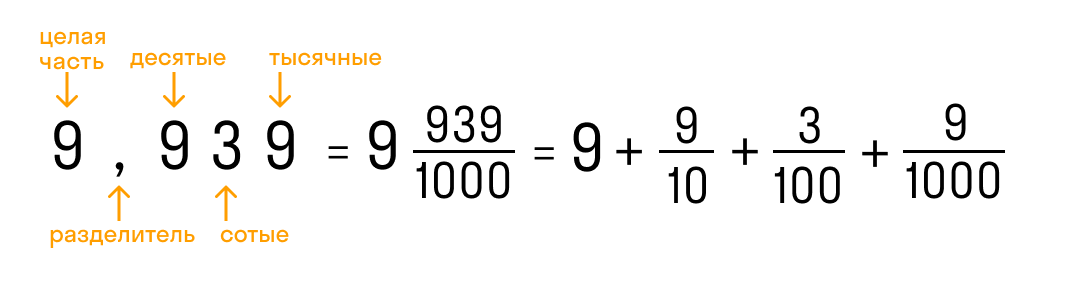
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства дробей
Основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же отличное от нуля число, то получится дробь, равная данной. Формула выглядит так:
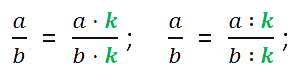 где a, b, k — натуральные числа.
где a, b, k — натуральные числа.
- Дробь не имеет значения, если знаменатель равен нулю.
- Дробь равна нулю, если числитель равен нулю, а знаменатель — нет.
- Две дроби a/b и c/d называются равными, если a * d = b * c.
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
- Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
- Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д.
- Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если в знаменателе обыкновенной дроби числа 10, 100, 1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.
Действия с дробями
С дробями можно выполнять те же действия, что и с обычными числами: складывать, вычитать, умножать и делить. А еще дроби можно сокращать и сравнивать между собой. Давайте попробуем.
Сравнение дробей
Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
Сравним 1/5 и 4/5. Как рассуждаем:
- В обеих дробях знаменатель равен 5.
- В первой дроби числитель равен 1, во второй дроби равен 4.
1 < 4
- Поэтому первая дробь 1/5 меньше второй 4/5.
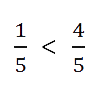
Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
Сравним 1/2 и 1/8. Как рассуждаем:
Представим, что у нас есть торт. Так как знаменатель первой дроби равен 2, то делим торт на две части и забираем себе одну, то есть половину торта.
Знаменатель второй дроби равен 8, делим торт на восемь частей и забираем крохотный кусочек. Половина торта больше больше маленького кусочка.
Таким образом 1/2 > 1/8.

Чтобы сравнить дроби с разными знаменателями, нужно привести дроби к общему знаменателю. А после приведения дробей к общему знаменателю, можно применить правило сравнения дробей с одинаковыми знаменателями.
Пример. Сравнить 2/7 и 1/14.
Как рассуждаем:
- Приведем дроби к общему знаменателю:
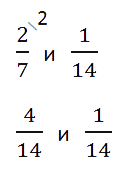
- Сравним дроби с одинаковыми знаменателями:
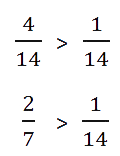
Ответ: 2/7 > 1/14.
Важно запомнить: любая неправильная дробь больше любой правильной. Потому что неправильная дробь всегда больше или равна 1, а правильная дробь всегда меньше 1.
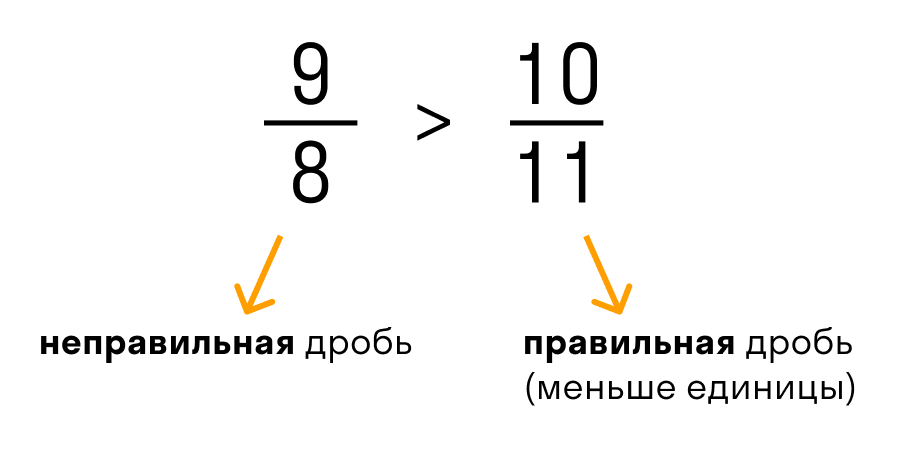
Чтобы сравнить дроби с разными числителями и знаменателями, нужно:
- привести дроби к общему знаменателю;
- сравнить полученные дроби.
Чтобы привести дроби к общему знаменателю, нужно:
- Найти общее кратное знаменателей дробей, которое станет их общим знаменателем.
- Разделить общий знаменатель на знаменатель данных дробей, то есть найти для каждой дроби дополнительный множитель.
- Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Сокращение дробей
Сокращение дроби — это деление числителя и знаменателя дроби на одно и то же натуральное число. Сократить дробь значит сделать ее короче и проще для восприятия. Например, дробь 1/3 выглядит намного проще и красивее, чем 27/81.
Сокращение дроби выглядит так: зачеркивают числитель и знаменатель, а рядом записывают результаты деления числителя и знаменателя на одно и то же число.
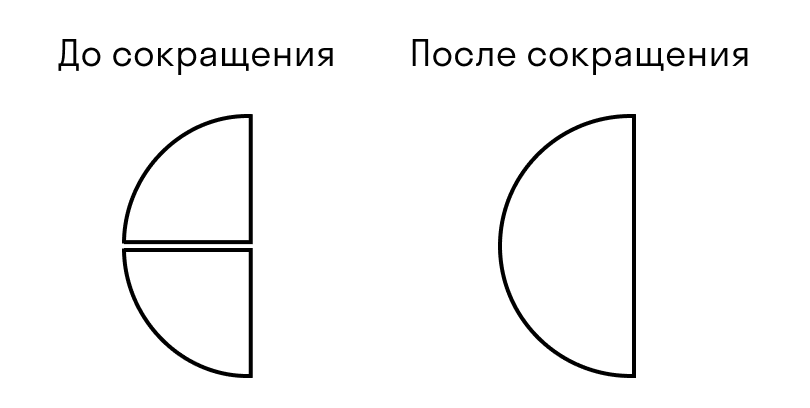
В этом примере делим обе части дроби на двойку.
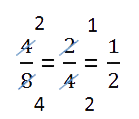
Можно никуда не спешить и сокращать дроби последовательно, в несколько действий.
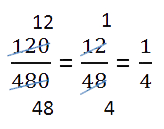
Сложение и вычитание дробей
При сложении и вычитании дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель.
Не забудьте проверить, можно ли сократить дробь и выделить целую часть.
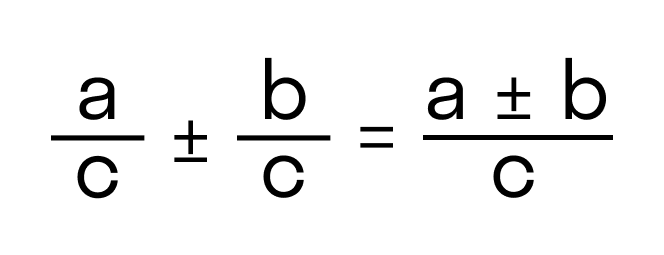
При сложении и вычитании дробей с разными знаменателями нужно найти наименьший общий знаменатель, сложить или вычесть полученные дроби (используем предыдущее правило).
Вот, что делать:
- Найдем наименьшее общее кратное для определения единого делителя.
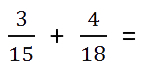
Для этого запишем в столбик числа, которые в сумме дают значения делителей. Далее перемножаем полученное и получаем НОК.
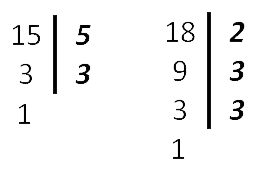
НОК (15, 18) = 3 * 2 * 3 * 5 = 90
- Найдем дополнительные множители для каждой дроби. Для этого НОК делим на каждый знаменатель:
90 : 15 = 6,
90 : 18 = 5.
Полученные числа запишем справа сверху над числителем.
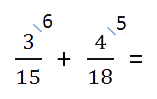
- Воспользуемся одним из основных свойств дробей: перемножим числитель и знаменатель на дополнительный множитель. После умножения знаменатель должен быть равен наименьшему общему кратному, которое мы ранее высчитывали. Затем можно перейти к сложению.
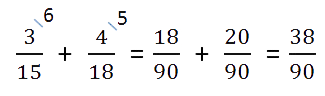
- Проверим полученный результат:
- если числитель больше знаменателя, нужно преобразовать дробь в смешанное число;
- если есть что сократить, нужно выполнить сокращение.
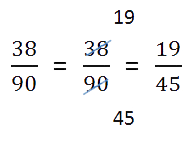
Ход решения одной строкой:
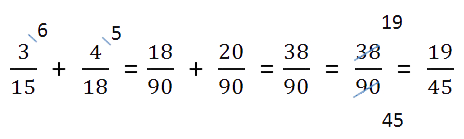
Сложение или вычитание смешанных чисел можно привести к отдельному сложению их целых частей и дробных частей. Для этого нужно действовать поэтапно:
- Сложить целые части.
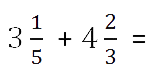
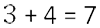
- Сложить дробные части.
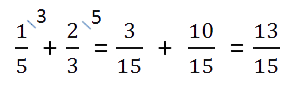
Необходимо приводить к общему, если знаменатели разные. Для этого воспользуемся знаниями из предыдущего примера.
- Суммировать полученные результаты.
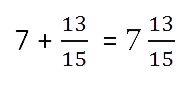
Если при сложении дробных частей получилась неправильная дробь, нужно выделить ее целую часть и прибавить к полученной ранее целой части.
Умножение и деление дробей
Произведение двух дробей равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
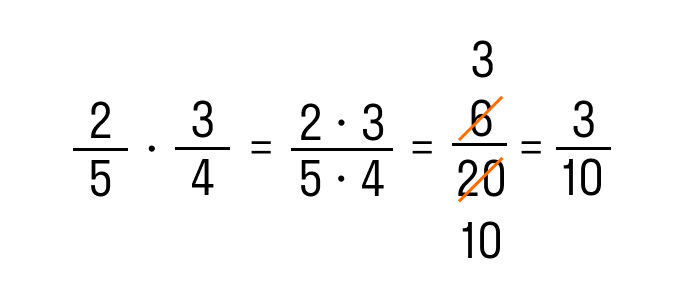
Не забываем про сокращение. Это может облегчить вычисления.

Чтобы умножить два смешанных числа, надо:
- преобразовать смешанные дроби в неправильные;
- перемножить числители и знаменатели дробей;
- сократить полученную дробь;
- если получилась неправильная дробь, преобразовать в смешанную.

Чтобы разделить дробь на дробь нужно выполнить следующую последовательность действий:
- числитель первой умножить на знаменатель второй, результат произведения записать в числитель новой дроби;
- знаменатель первой умножить на числитель второй, результат произведения записать в знаменатель новой дроби.
Другими словами это правило звучит так: чтобы разделить одну дробь на другую, надо первую умножить на обратную от второй.
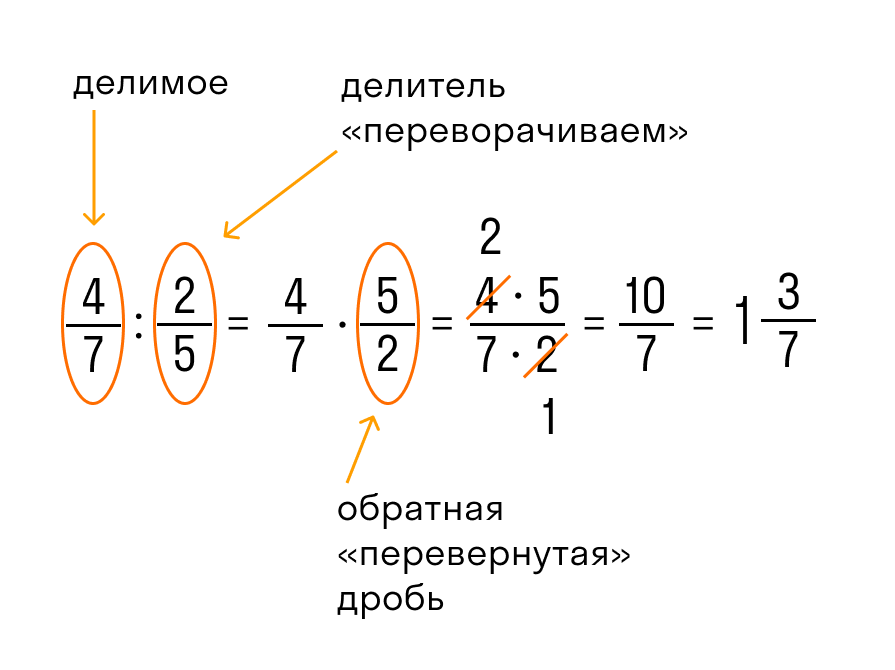
Числа, произведение которых равно 1, называют взаимно обратными.
Как делить дроби с разными знаменателями? На самом деле одинаковые или разные знаменатели у дробей — неважно, потому что все дроби делятся по правилу, описанному выше.
Для деления смешанных чисел необходимо:
- представить числа в виде неправильных дробей;
- разделить то, что получилось друг на друга.
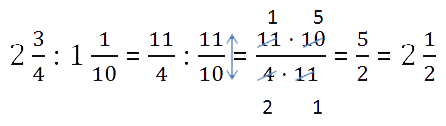
Дроби можно складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой. В принципе всё что можно делать с обычными числами, можно делать и с дробями.
Сложение дробей с одинаковыми знаменателями
Сложение дробей бывает двух видов:
- Сложение дробей с одинаковыми знаменателями;
- Сложение дробей с разными знаменателями.
Сначала изýчим сложение дробей с одинаковыми знаменателями. Тут всё просто. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения.
Например, слóжим дроби ![]() и
и ![]() . Складываем числители, а знаменатель оставляем без изменения:
. Складываем числители, а знаменатель оставляем без изменения:
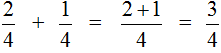
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если к ![]() пиццы прибавить
пиццы прибавить ![]() пиццы, то получится
пиццы, то получится ![]() пиццы:
пиццы:
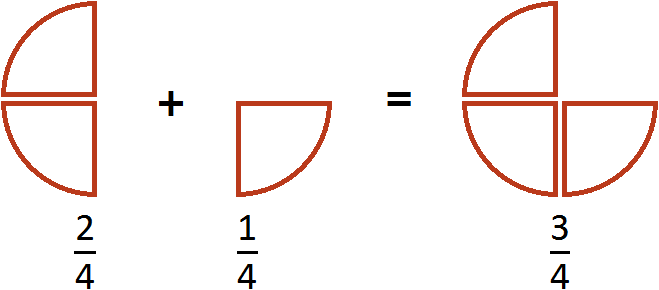
Пример 2. Сложить дроби ![]() и
и ![]() .
.
Опять же складываем числители, а знаменатель оставляем без изменения:
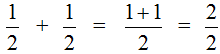
В ответе получилась неправильная дробь ![]() . Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
. Если наступает конец задачи, то от неправильных дробей принято избавляться. Чтобы избавится от неправильной дроби, нужно выделить в ней целую часть. В нашем случае целая часть выделяется легко — два разделить на два будет один:
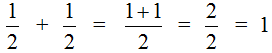
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на две части. Если к ![]() пиццы прибавить еще
пиццы прибавить еще ![]() пиццы, то получится одна целая пицца:
пиццы, то получится одна целая пицца:
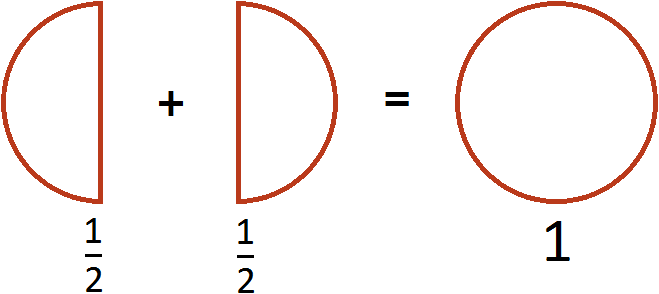
Пример 3. Сложить дроби ![]() и
и ![]() .
.
Опять же складываем числители, а знаменатель оставляем без изменения:
![]()
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если к ![]() пиццы прибавить ещё
пиццы прибавить ещё ![]() пиццы, то получится
пиццы, то получится ![]() пиццы:
пиццы:
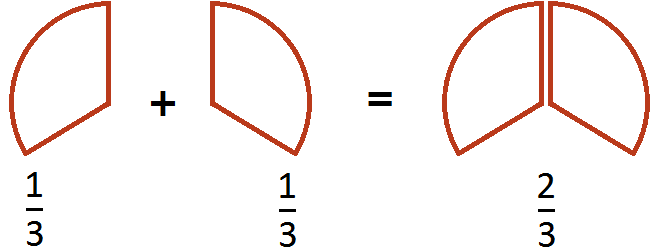
Пример 4. Найти значение выражения 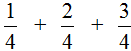
Этот пример решается точно также, как и предыдущие. Числители необходимо сложить, а знаменатель оставить без изменения:
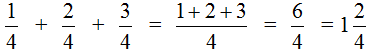
Попробуем изобразить наше решение с помощью рисунка. Если к ![]() пиццы прибавить
пиццы прибавить ![]() пиццы и ещё прибавить
пиццы и ещё прибавить пиццы, то получится 1 целая и ещё
![]() пиццы.
пиццы.

Как видите в сложении дробей с одинаковыми знаменателями нет ничего сложного. Достаточно понимать следующие правила:
- Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Сложение дробей с разными знаменателями
Теперь научимся складывать дроби с разными знаменателями. Когда складывают дроби, знаменатели этих дробей должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, дроби ![]() и
и ![]() сложить можно, поскольку у них одинаковые знаменатели.
сложить можно, поскольку у них одинаковые знаменатели.
А вот дроби ![]() и
и ![]() сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
сразу сложить нельзя, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Существует несколько способов приведения дробей к одинаковому знаменателю. Сегодня мы рассмотрим только один из них, поскольку остальные способы могут показаться сложными для начинающего.
Суть этого способа заключается в том, что сначала ищется наименьшее общее кратное (НОК) знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель. Аналогично поступают и со второй дробью — НОК делят на знаменатель второй дроби и получают второй дополнительный множитель.
Затем числители и знаменатели дробей умножаются на свои дополнительные множители. В результате этих действий, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем.
Пример 1. Сложим дроби и
![]()
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
В первую очередь находим наименьшее общее кратное знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 2. Наименьшее общее кратное этих чисел равно 6
НОК (2 и 3) = 6
Теперь возвращаемся к дробям и
![]() . Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
. Сначала разделим НОК на знаменатель первой дроби и получим первый дополнительный множитель. НОК это число 6, а знаменатель первой дроби это число 3. Делим 6 на 3, получаем 2.
Полученное число 2 это первый дополнительный множитель. Записываем его к первой дроби. Для этого делаем небольшую косую линию над дробью и записываем над ней найденный дополнительный множитель:
![]()
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби и получаем второй дополнительный множитель. НОК это число 6, а знаменатель второй дроби — число 2. Делим 6 на 2, получаем 3.
Полученное число 3 это второй дополнительный множитель. Записываем его ко второй дроби. Опять же делаем небольшую косую линию над второй дробью и записываем над ней найденный дополнительный множитель:
![]()
Теперь у нас всё готово для сложения. Осталось умножить числители и знаменатели дробей на свои дополнительные множители:
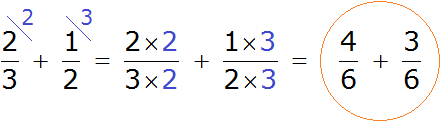
Посмотрите внимательно к чему мы пришли. Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как складывать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
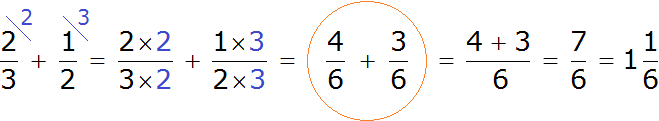
Таким образом, пример завершается. К прибавить
![]() получается
получается ![]() .
.
Попробуем изобразить наше решение с помощью рисунка. Если к пиццы прибавить
![]() пиццы, то получится одна целая пицца и еще одна шестая пиццы:
пиццы, то получится одна целая пицца и еще одна шестая пиццы:
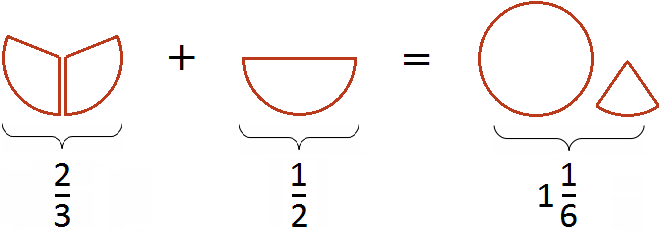
Приведение дробей к одинаковому (общему) знаменателю также можно изобразить с помощью рисунка. Приведя дроби и
![]() к общему знаменателю, мы получили дроби
к общему знаменателю, мы получили дроби ![]() и
и ![]() . Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
. Эти две дроби будут изображаться теми же кусками пицц. Различие будет лишь в том, что в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю).
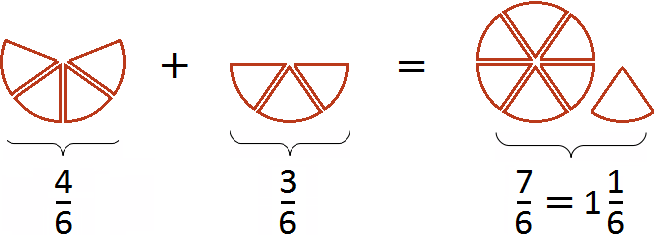
Первый рисунок изображает дробь ![]() (четыре кусочка из шести), а второй рисунок изображает дробь
(четыре кусочка из шести), а второй рисунок изображает дробь ![]() (три кусочка из шести). Сложив эти кусочки мы получаем
(три кусочка из шести). Сложив эти кусочки мы получаем ![]() (семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили
(семь кусочков из шести). Эта дробь неправильная, поэтому мы выделили в ней целую часть. В результате получили ![]() (одну целую пиццу и еще одну шестую пиццы).
(одну целую пиццу и еще одну шестую пиццы).
Отметим, что мы с вами расписали данный пример слишком подробно. В учебных заведениях не принято писать так развёрнуто. Нужно уметь быстро находить НОК обоих знаменателей и дополнительные множители к ним, а также быстро умножать найденные дополнительные множители на свои числители и знаменатели. Находясь в школе, данный пример нам пришлось бы записать следующим образом:
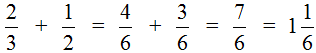
Но есть и обратная сторона медали. Если на первых этапах изучения математики не делать подробных записей, то начинают появляться вопросы рода «а откуда вон та цифра?», «почему дроби вдруг превращаются совсем в другие дроби?«.
Поэтому на первых этапах советуем записывать каждую мелочь. Хвастаться можно лишь в будущем, когда будут усвоены азы.
Чтобы легче было складывать дроби с разными знаменателями, можно воспользоваться следующей пошаговой инструкцией:
- Найти НОК знаменателей дробей;
- Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби;
- Умножить числители и знаменатели дробей на свои дополнительные множители;
- Сложить дроби, у которых одинаковые знаменатели;
- Если в ответе получилась неправильная дробь, то выделить её целую часть;
Пример 2. Найти значение выражения 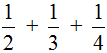 .
.
Воспользуемся инструкцией, которая приведена выше.
Шаг 1. Найти НОК знаменателей дробей
Находим НОК знаменателей обеих дробей. Знаменатели дробей это числа 2, 3 и 4
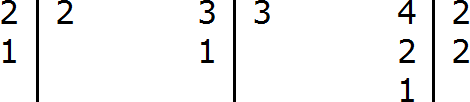
![]()
Шаг 2. Разделить НОК на знаменатель каждой дроби и получить дополнительный множитель для каждой дроби
Делим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби это число 2. Делим 12 на 2, получаем 6. Получили первый дополнительный множитель 6. Записываем его над первой дробью:
![]()
Теперь делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби это число 3. Делим 12 на 3, получаем 4. Получили второй дополнительный множитель 4. Записываем его над второй дробью:
![]()
Теперь делим НОК на знаменатель третьей дроби. НОК это число 12, а знаменатель третьей дроби это число 4. Делим 12 на 4, получаем 3. Получили третий дополнительный множитель 3. Записываем его над третьей дробью:
![]()
Шаг 3. Умножить числители и знаменатели дробей на свои дополнительные множители
Умножаем числители и знаменатели на свои дополнительные множители:
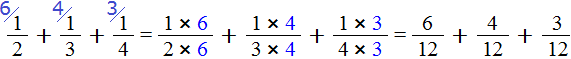
Шаг 4. Сложить дроби у которых одинаковые знаменатели
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби, у которых одинаковые (общие) знаменатели. Осталось сложить эти дроби. Складываем:
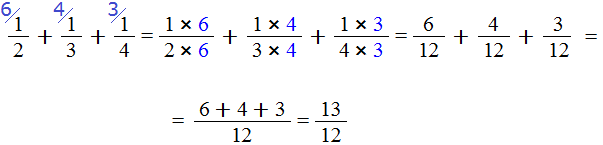
Сложение не поместилось на одной строке, поэтому мы перенесли оставшееся выражение на следующую строку. Это допускается в математике. Когда выражение не помещается на одну строку, его переносят на следующую строку, при этом надо обязательно поставить знак равенства (=) на конце первой строки и в начале новой строки. Знак равенства на второй строке говорит о том, что это продолжение выражения, которое было на первой строке.
Шаг 5. Если в ответе получилась неправильная дробь, то выделить в ней целую часть
У нас в ответе получилась неправильная дробь. Мы должны выделить у неё целую часть. Выделяем:
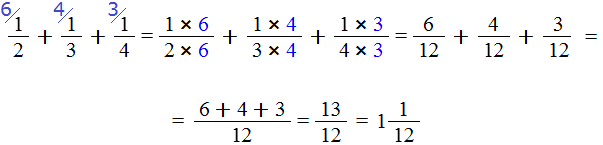
Получили ответ ![]()
Вычитание дробей с одинаковыми знаменателями
Вычитание дробей бывает двух видов:
- Вычитание дробей с одинаковыми знаменателями
- Вычитание дробей с разными знаменателями
Сначала изучим вычитание дробей с одинаковыми знаменателями.
Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения.
Например, найдём значение выражения 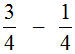 . Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
. Чтобы решить этот пример, надо из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения. Так и сделаем:
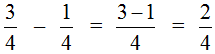
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на четыре части. Если от ![]() пиццы отрезать
пиццы отрезать ![]() пиццы, то получится
пиццы, то получится ![]() пиццы:
пиццы:
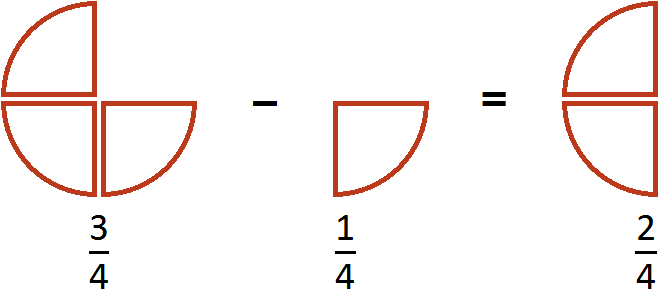
Пример 2. Найти значение выражения 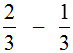 .
.
Опять же из числителя первой дроби вычитаем числитель второй дроби, а знаменатель оставляем без изменения:
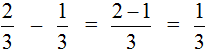
Этот пример можно легко понять, если вспомнить про пиццу, которая разделена на три части. Если от ![]() пиццы отрезать
пиццы отрезать ![]() пиццы, то получится
пиццы, то получится ![]() пиццы:
пиццы:
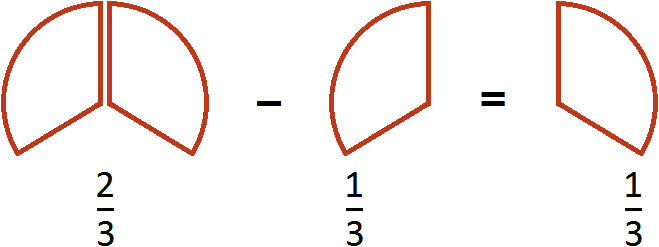
Пример 3. Найти значение выражения 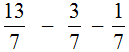
Этот пример решается точно также, как и предыдущие. Из числителя первой дроби нужно вычесть числители остальных дробей:
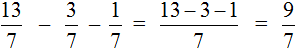
В ответе получилась неправильная дробь. Выделим в ней целую часть:
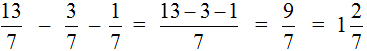
Как видите в вычитании дробей с одинаковыми знаменателями ничего сложного нет. Достаточно понимать следующие правила:
- Чтобы вычесть из одной дроби другую, нужно из числителя первой дроби вычесть числитель второй дроби, а знаменатель оставить без изменения;
- Если в ответе получилась неправильная дробь, то нужно выделить в ней целую часть.
Вычитание дробей с разными знаменателями
Теперь научимся вычитать дроби у которых разные знаменатели. Когда вычитают дроби их знаменатели должны быть одинаковыми. Но одинаковыми они бывают не всегда.
Например, от дроби ![]() можно вычесть дробь
можно вычесть дробь ![]() , поскольку у этих дробей одинаковые знаменатели. А вот от дроби
, поскольку у этих дробей одинаковые знаменатели. А вот от дроби ![]() нельзя вычесть дробь
нельзя вычесть дробь ![]() , поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
, поскольку у этих дробей разные знаменатели. В таких случаях дроби нужно приводить к одинаковому (общему) знаменателю.
Общий знаменатель находят по тому же принципу, которым мы пользовались при сложении дробей с разными знаменателями. В первую очередь находят НОК знаменателей обеих дробей. Затем НОК делят на знаменатель первой дроби и получают первый дополнительный множитель, который записывается над первой дробью. Аналогично НОК делят на знаменатель второй дроби и получают второй дополнительный множитель, который записывается над второй дробью.
Затем дроби умножаются на свои дополнительные множители. В результате этих операций, дроби у которых были разные знаменатели, обращаются в дроби, у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем.
Пример 1. Найти значение выражения: 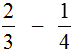
У этих дробей разные знаменатели, поэтому нужно привести их к одинаковому (общему) знаменателю.
Сначала находим НОК знаменателей обеих дробей. Знаменатель первой дроби это число 3, а знаменатель второй дроби — число 4. Наименьшее общее кратное этих чисел равно 12
НОК (3 и 4) = 12
Теперь возвращаемся к дробям ![]() и
и ![]()
Найдём дополнительный множитель для первой дроби. Для этого разделим НОК на знаменатель первой дроби. НОК это число 12, а знаменатель первой дроби — число 3. Делим 12 на 3, получаем 4. Записываем четвёрку над первой дробью:
![]()
Аналогично поступаем и со второй дробью. Делим НОК на знаменатель второй дроби. НОК это число 12, а знаменатель второй дроби — число 4. Делим 12 на 4, получаем 3. Записываем тройку над второй дробью:
![]()
Теперь у нас всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
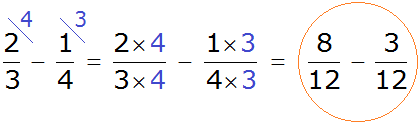
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример до конца:
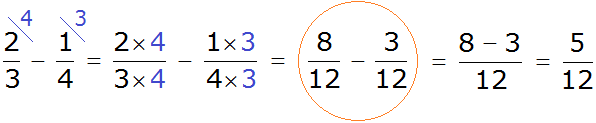
Получили ответ ![]()
Попробуем изобразить наше решение с помощью рисунка. Если от ![]() пиццы отрезать
пиццы отрезать ![]() пиццы, то получится
пиццы, то получится ![]() пиццы
пиццы
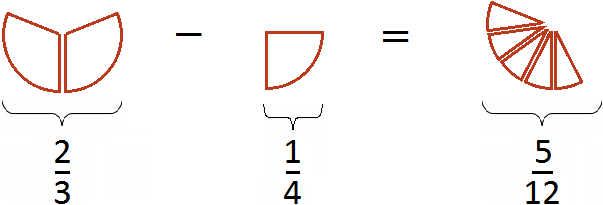
Это подробная версия решения. Находясь в школе, нам пришлось бы решить этот пример покороче. Выглядело бы такое решение следующим образом:
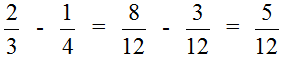
Приведение дробей ![]() и
и ![]() к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби
к общему знаменателю также может быть изображено с помощью рисунка. Приведя эти дроби к общему знаменателю, мы получили дроби ![]() и
и ![]() . Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
. Эти дроби будут изображаться теми же кусочками пицц, но в этот раз они будут разделены на одинаковые доли (приведены к одинаковому знаменателю):
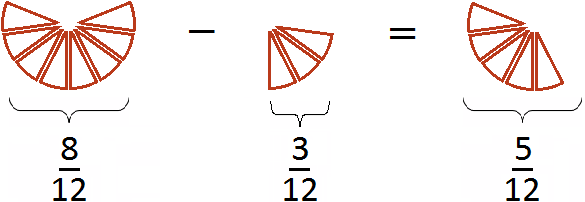
Первый рисунок изображает дробь ![]() (восемь кусочков из двенадцати), а второй рисунок — дробь
(восемь кусочков из двенадцати), а второй рисунок — дробь ![]() (три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь
(три кусочка из двенадцати). Отрезав от восьми кусочков три кусочка мы получаем пять кусочков из двенадцати. Дробь ![]() и описывает эти пять кусочков.
и описывает эти пять кусочков.
Пример 2. Найти значение выражения 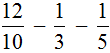
У этих дробей разные знаменатели, поэтому сначала нужно привести их к одинаковому (общему) знаменателю.
Найдём НОК знаменателей этих дробей.
Знаменатели дробей это числа 10, 3 и 5. Наименьшее общее кратное этих чисел равно 30
НОК (10, 3, 5) = 30
Теперь находим дополнительные множители для каждой дроби. Для этого разделим НОК на знаменатель каждой дроби.
Найдём дополнительный множитель для первой дроби. НОК это число 30, а знаменатель первой дроби — число 10. Делим 30 на 10, получаем первый дополнительный множитель 3. Записываем его над первой дробью:
![]()
Теперь находим дополнительный множитель для второй дроби. Разделим НОК на знаменатель второй дроби. НОК это число 30, а знаменатель второй дроби — число 3. Делим 30 на 3, получаем второй дополнительный множитель 10. Записываем его над второй дробью:
![]()
Теперь находим дополнительный множитель для третьей дроби. Разделим НОК на знаменатель третьей дроби. НОК это число 30, а знаменатель третьей дроби — число 5. Делим 30 на 5, получаем третий дополнительный множитель 6. Записываем его над третьей дробью:
![]()
Теперь всё готово для вычитания. Осталось умножить дроби на свои дополнительные множители:
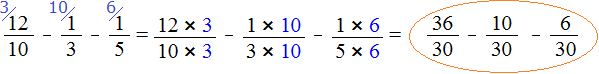
Мы пришли к тому, что дроби у которых были разные знаменатели, превратились в дроби у которых одинаковые (общие) знаменатели. А как вычитать такие дроби мы уже знаем. Давайте дорешаем этот пример.
Продолжение примера не поместится на одной строке, поэтому переносим продолжение на следующую строку. Не забываем про знак равенства (=) на новой строке:
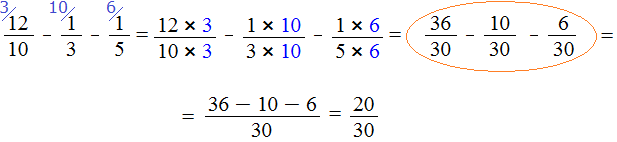
В ответе получилась правильная дробь, и вроде бы нас всё устраивает, но она слишком громоздка и некрасива. Надо бы сделать её проще. А что можно сделать? Можно сократить эту дробь.
Чтобы сократить дробь ![]() , нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
, нужно разделить её числитель и знаменатель на наибольший общий делитель (НОД) чисел 20 и 30.
Итак, находим НОД чисел 20 и 30:
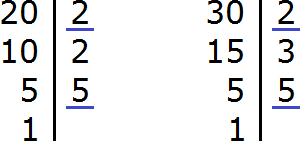
![]()
Теперь возвращаемся к нашему примеру и делим числитель и знаменатель дроби ![]() на найденный НОД, то есть на 10
на найденный НОД, то есть на 10
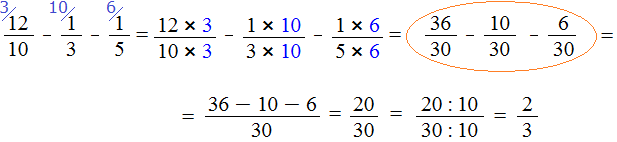
Получили ответ ![]()
Умножение дроби на число
Чтобы умножить дробь на число, нужно числитель данной дроби умножить на это число, а знаменатель оставить без изменений.
Пример 1. Умножить дробь ![]() на число 1.
на число 1.
Умножим числитель дроби ![]() на число 1
на число 1
![]()
Запись ![]() можно понимать, как взять половину 1 раз. К примеру, если
можно понимать, как взять половину 1 раз. К примеру, если ![]() пиццы взять 1 раз, то получится
пиццы взять 1 раз, то получится ![]() пиццы
пиццы
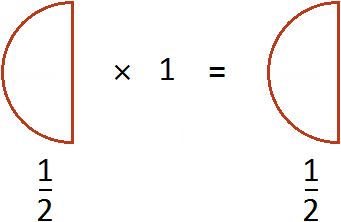
Из законов умножения мы знаем, что если множимое и множитель поменять местами, то произведение не изменится. Если выражение ![]() , записать как
, записать как ![]() , то произведение по прежнему будет равно
, то произведение по прежнему будет равно ![]() . Опять же срабатывает правило перемножения целого числа и дроби:
. Опять же срабатывает правило перемножения целого числа и дроби:
![]()
Эту запись можно понимать, как взятие половины от единицы. К примеру, если имеется 1 целая пицца и мы возьмем от неё половину, то у нас окажется ![]() пиццы:
пиццы:
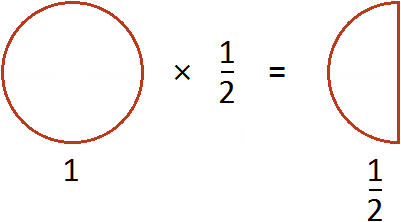
Пример 2. Найти значение выражения ![]()
Умножим числитель дроби ![]() на 4
на 4
![]()
В ответе получилась неправильная дробь. Выделим в ней целую часть:
![]()
Выражение ![]() можно понимать, как взятие двух четвертей 4 раза. К примеру, если
можно понимать, как взятие двух четвертей 4 раза. К примеру, если ![]() пиццы взять 4 раза, то получится две целые пиццы
пиццы взять 4 раза, то получится две целые пиццы
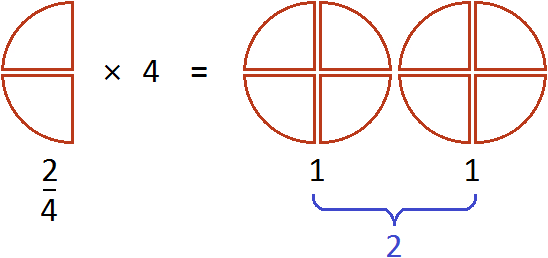
А если поменять множимое и множитель местами, то получим выражение ![]() . Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
. Оно тоже будет равно 2. Это выражение можно понимать, как взятие двух пицц от четырех целых пицц:
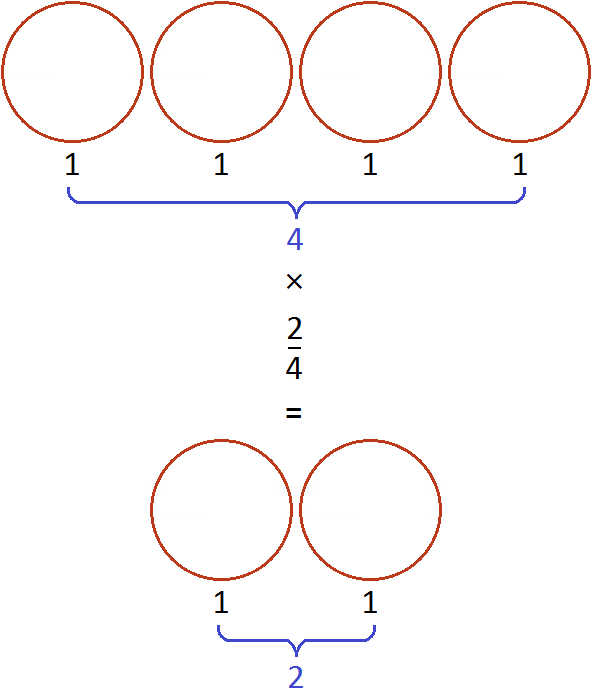
Число, которое умножается на дробь, и знаменатель дроби разрешается сокращать, если они имеют общий делитель, бóльший единицы.
Например, выражение ![]() можно вычислить двумя способами.
можно вычислить двумя способами.
Первый способ. Умножить число 4 на числитель дроби, а знаменатель дроби оставить без изменений:
![]()
Второй способ. Умножаемую четвёрку и четвёрку, находящуюся в знаменателе дроби , можно сократить. Сократить эти четвёрки можно на 4, поскольку наибольший общий делитель для двух четвёрок есть сама четвёрка:
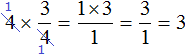
Получился тот же результат 3. После сокращения четвёрок, на их месте образуются новые числа: две единицы. Но перемножение единицы с тройкой, и далее деление на единицу ничего не меняет. Поэтому решение можно записать покороче:
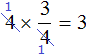
Сокращение может быть выполнено даже тогда, когда мы решили воспользоваться первым способом, но на этапе перемножения числа 4 и числителя 3 решили воспользоваться сокращением:
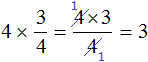
А вот к примеру выражение ![]() можно вычислить только первым способом — умножить число 7 на числитель дроби
можно вычислить только первым способом — умножить число 7 на числитель дроби ![]() , а знаменатель оставить без изменений:
, а знаменатель оставить без изменений:
![]()
Связано это с тем, что число 7 и знаменатель дроби ![]() не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
не имеют общего делителя, бóльшего единицы, и соответственно не сокращаются.
Некоторые ученики по ошибке сокращают умножаемое число и числитель дроби. Делать этого нельзя. Например, следующая запись не является правильной:
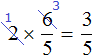
Сокращение дроби подразумевает, что и числитель и знаменатель будет разделён на одно и тоже число. В ситуации с выражением 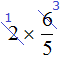 деление выполнено только в числителе, поскольку записать
деление выполнено только в числителе, поскольку записать 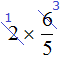 это всё равно, что записать
это всё равно, что записать 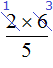 . Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
. Видим, что деление выполнено только в числителе, а в знаменателе никакого деления не происходит.
Умножение дробей
Чтобы перемножить дроби, нужно перемножить их числители и знаменатели. Если в ответе получится неправильная дробь, нужно выделить в ней целую часть.
Пример 1. Найти значение выражения ![]() .
.
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
![]()
Получили ответ ![]() . Желательно сократить данную дробь. Дробь
. Желательно сократить данную дробь. Дробь ![]() можно сократить на 2. Тогда окончательное решение примет следующий вид:
можно сократить на 2. Тогда окончательное решение примет следующий вид:
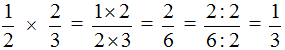
Выражение ![]() можно понимать, как взятие
можно понимать, как взятие пиццы от половины пиццы. Допустим, у нас есть половина пиццы:

Как взять от этой половины две третьих? Сначала нужно поделить эту половину на три равные части:

И взять от этих трех кусочков два:
У нас получится ![]() пиццы. Вспомните, как выглядит пицца, разделенная на три части:
пиццы. Вспомните, как выглядит пицца, разделенная на три части:

Один кусок от этой пиццы и взятые нами два кусочка будут иметь одинаковые размеры:
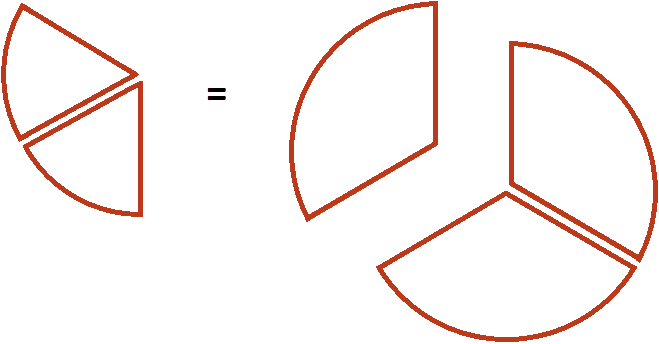
Другими словами, речь идет об одном и том же размере пиццы. Поэтому значение выражения ![]() равно
равно ![]()
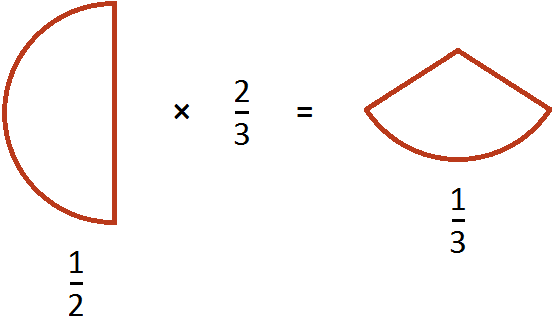
Пример 2. Найти значение выражения ![]()
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
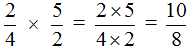
В ответе получилась неправильная дробь. Выделим в ней целую часть:
![]()
Пример 3. Найти значение выражения ![]()
Умножаем числитель первой дроби на числитель второй дроби, а знаменатель первой дроби на знаменатель второй дроби:
![]()
В ответе получилась правильная дробь, но будет хорошо, если её сократить. Чтобы сократить эту дробь, нужно числитель и знаменатель данной дроби разделить на наибольший общий делитель (НОД) чисел 105 и 450.
Итак, найдём НОД чисел 105 и 450:
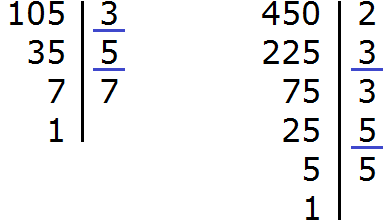
![]()
Теперь делим числитель и знаменатель нашего ответа на НОД, который мы сейчас нашли, то есть на 15
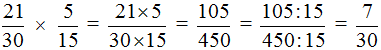
Представление целого числа в виде дроби
Любое целое число можно представить в виде дроби. Например, число 5 можно представить как ![]() . От этого пятёрка своего значения не поменяет, поскольку выражение
. От этого пятёрка своего значения не поменяет, поскольку выражение ![]() означает «число пять разделить на единицу», а это, как известно равно пятёрке:
означает «число пять разделить на единицу», а это, как известно равно пятёрке:
![]()
Обратные числа
Сейчас мы познакомимся с очень интересной темой в математике. Она называется «обратные числа».
Определение. Обратным к числу a называется число, которое при умножении на a даёт единицу.
Давайте подставим в это определение вместо переменной a число 5 и попробуем прочитать определение:
Обратным к числу 5 называется число, которое при умножении на 5 даёт единицу.
Можно ли найти такое число, которое при умножении на 5, даёт единицу? Оказывается можно. Представим пятёрку в виде дроби:
![]()
Затем умножить эту дробь на саму себя, только поменяем местами числитель и знаменатель. Другими словами, умножим дробь ![]() на саму себя, только перевёрнутую:
на саму себя, только перевёрнутую:
![]()
Что получится в результате этого? Если мы продолжим решать этот пример, то получим единицу:
![]()
Значит обратным к числу 5, является число ![]() , поскольку при умножении 5 на
, поскольку при умножении 5 на ![]() получается единица.
получается единица.
Обратное число можно найти также для любого другого целого числа.
Примеры:
- обратным числа 2 является дробь

- обратным числа 3 является дробь

- обратным числа 4 является дробь

Найти обратное число можно также для любой другой дроби. Для этого достаточно перевернуть её.
Примеры:
Деление дроби на число
Допустим, у нас имеется половина пиццы:

Разделим её поровну на двоих. Сколько пиццы достанется каждому?
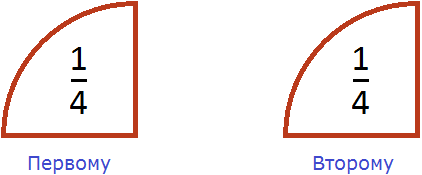
Видно, что после разделения половины пиццы получилось два равных кусочка, каждый из которых составляет ![]() пиццы. Значит каждому достанется по
пиццы. Значит каждому достанется по ![]() пиццы.
пиццы.
Деление дробей выполняется с помощью обратных чисел. Обратные числа позволяют заменить деление умножением.
Чтобы разделить дробь на число, нужно эту дробь умножить на число, обратное делителю.
Пользуясь этим правилом, запишем деление нашей половины пиццы на две части.
Итак, требуется разделить дробь ![]() на число 2. Здесь делимым является дробь
на число 2. Здесь делимым является дробь ![]() , а делителем число 2.
, а делителем число 2.
Чтобы разделить дробь ![]() на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь
на число 2, нужно эту дробь умножить на число, обратное делителю 2. Обратное делителю 2 это дробь ![]() . Значит нужно умножить
. Значит нужно умножить ![]() на
на ![]()
![]()
Получили ответ ![]() . Значит при делении половины на две части получается четверть.
. Значит при делении половины на две части получается четверть.
Попробуем понять механизм этого правила. Для этого рассмотрим следующий простейший пример. Пусть у нас имеется одна целая пицца:
Умножим её на 2. То есть повторим её два раза (или возьмём два раза). В результате будем иметь две пиццы:
Теперь угостим этими пиццами двоих друзей. То есть разделим две пиццы на 2. Тогда каждому достанется по одной пицце:
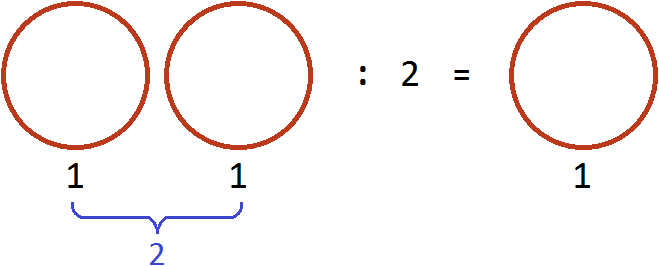
Разделить две пиццы на 2 это всё равно, что взять половину от этих пицц, то есть умножить число 2 на дробь ![]()
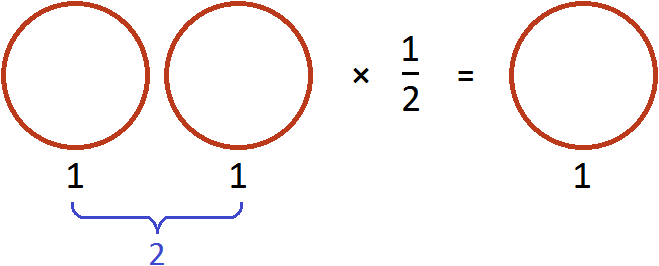
В обоих случаях получился один и тот же результат.
Тоже самое происходило, когда мы делили половину пиццы на две части. Чтобы разделить ![]() на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь
на 2, мы умножили эту дробь на число, обратное делителю 2. А обратное делителю 2 это дробь ![]()
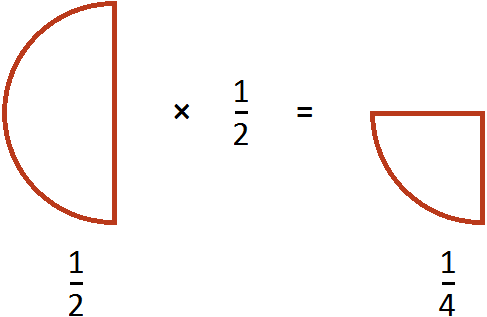
Пример 2. Найти значение выражения ![]()
Умножим первую дробь на число, обратное делителю:
![]()
Допустим, имеется четверть пиццы и нужно разделить её на двоих:
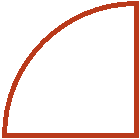
Если разделить эту четверть на две части, то каждая получившаяся часть будет одной восьмой частью целой пиццы:
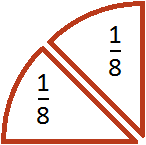
Заменять деление умножением можно не только при работе с дробями, но и с обычными числами. Например, все мы знаем, что 10 разделить на 2 будет 5
10 : 2 = 5
Заменим в этом примере деление умножением. Чтобы разделить число 10 на число 2, можно умножить число 10 на число, обратное числу 2. А обратное числу 2 это дробь ![]()
![]()
Как видно результат не изменился. Мы снова получили ответ 5.
Можно сделать вывод, что деление можно заменять умножением при условии, что вместо делителя будет подставлено обратное ему число.
Пример 3. Найти значение выражения ![]()
Умножим первую дробь на число, обратное делителю. Обратное делителю число это дробь
![]()
Допустим, имелось ![]() пиццы:
пиццы:

Как разделить такую пиццу на шестерых? Если каждый из трех кусков разделить пополам, то можно получить 6 равных кусков
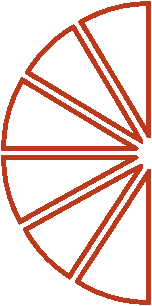
Эти шесть кусков являются шестью кусками из двенадцати. А один из этих кусков составляет ![]() . Поэтому при делении
. Поэтому при делении ![]() на 6 получается
на 6 получается ![]()
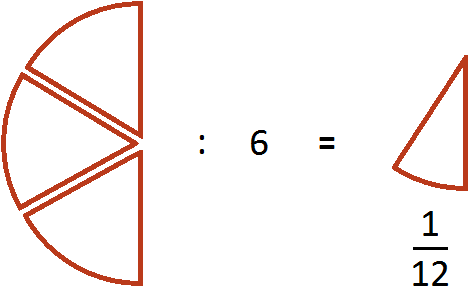
Деление числа на дробь
Правило деления числа на дробь такое же, как и правило деления дроби на число.
Чтобы разделить число на дробь, нужно умножить это число на дробь, обратную делителю.
Например, разделим число 1 на ![]() .
.
Чтобы разделить число 1 на ![]() , нужно это число 1 умножить на дробь, обратную дроби
, нужно это число 1 умножить на дробь, обратную дроби ![]() . А обратная дроби
. А обратная дроби ![]() это дробь
это дробь ![]()
![]()
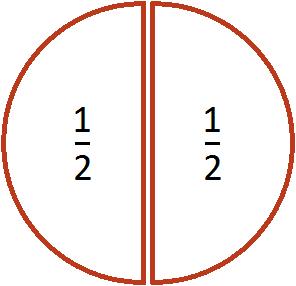
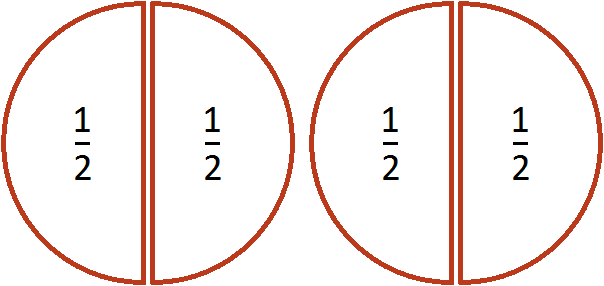
Выражение ![]() можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:
можно понимать, как определение количества половин в одной целой пицце. Допустим, имеется одна целая пицца:

Если зададим вопрос «сколько раз половина содержится в этой пицце», то ответом будет 2. Действительно, половина содержится в одной целой пицце два раза
Пример 2. Найти значение выражения ![]()
Умножим число 2 на дробь, обратную делителю. А обратная делителю дробь это дробь ![]()
![]()
Допустим, у нас имеются две целые пиццы:
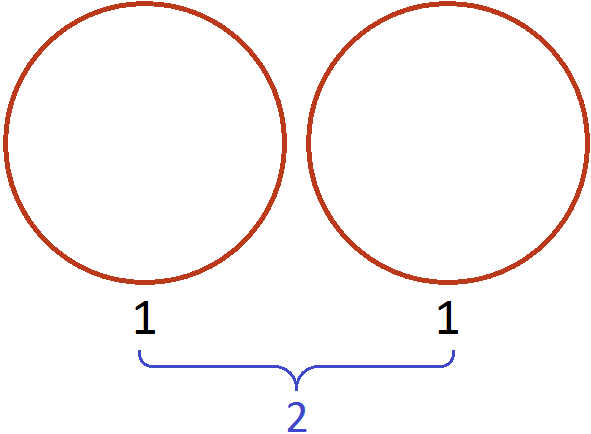
Если зададим вопрос «сколько раз половина содержится в двух пиццах», то ответом будет 4. Действительно, половина содержится в двух пиццах четыре раза:
Деление дробей
Чтобы разделить дробь на дробь, нужно первую дробь умножить на дробь, обратную второй.
Например, разделим ![]() на
на ![]()
Чтобы разделить ![]() на
на ![]() , нужно
, нужно ![]() умножить на дробь, обратную дроби
умножить на дробь, обратную дроби ![]() . А обратная дроби
. А обратная дроби ![]() это дробь
это дробь ![]()
![]()
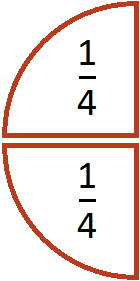
Допустим, имеется половина пиццы:

Если зададим вопрос «сколько раз четверть пиццы содержится в этой половине», то ответом будет 2. Действительно, четверть пиццы содержится в половине пиццы два раза:
Пример 1. Найти значение выражения ![]()
Умножаем первую дробь на дробь, обратную второй. Грубо говоря, умножаем первую дробь на перевёрнутую вторую:
![]()
Пример 2. Найти значение выражения ![]()
Умножаем первую дробь на дробь обратную второй:
![]()
Здесь советуем остановиться и потренироваться. Решите несколько примеров, приведенных ниже. Можете использовать материалы сайта, как справочник. Это позволит вам научиться работать с литературой.
Каждая следующая тема будет более сложной, поэтому нужно тренироваться.
Задания для самостоятельного решения:
Задание 1. Найдите значение выражения:
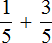
Решение:
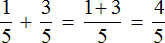
Задание 2. Найдите значение выражения:
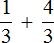
Решение:
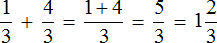
Задание 3. Найдите значение выражения:
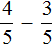
Решение:
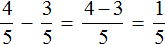
Задание 4. Найдите значение выражения:
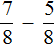
Решение:
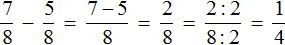
Задание 5. Найдите значение выражения:
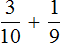
Решение:
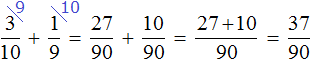
Задание 6. Найдите значение выражения:
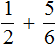
Решение:
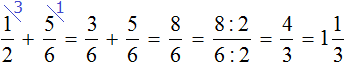
Задание 7. Найдите значение выражения:
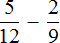
Решение:
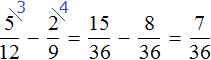
Задание 8. Найдите значение выражения:
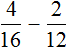
Решение:
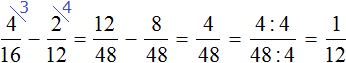
Задание 9. Найдите значение выражения:
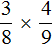
Решение:
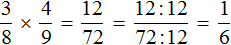
Задание 10. Найдите значение выражения:
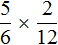
Решение:
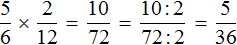
Задание 11. Найдите значение выражения:
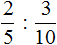
Решение:
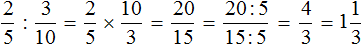
Задание 12. Найдите значение выражения:

Решение:
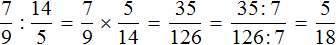
Задание 13. Найдите значение выражения:
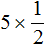
Решение:
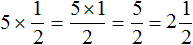
Задание 14. Найдите значение выражения:
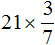
Решение:
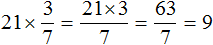
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Download Article
Download Article
Calculating fractions are one of the most useful math skills to develop. Before you begin working with them, learn how to identify parts and types of fractions. Then you can move on to adding and subtracting them. For more complex calculations, learn how to multiply and divide them. In most cases, you’ll also need to simplify or reduce the fraction.
-

1
Find a fraction. Fractions are written as 1 number placed over a dividing line with 1 number below it.
-

2
Identify the numerator. The number on top is called the numerator and it tells you how many parts of the fraction there are.[1]
- For example, in the fraction 1/5, 1 is the numerator.
Advertisement
-

3
Locate the denominator. The number on the bottom is called the denominator. This number tells you how many parts make up the whole number.[2]
- For example, in the fraction 1/5, 5 is the denominator so there should be 5 parts in the fraction.
-

4
Determine if the fraction is proper or improper. If the numerator is less than the denominator, the fraction is proper. For an improper fraction, the numerator is greater than the denominator.[3]
- For example, 3/4 is a proper fraction and 5/3 is an improper fraction.
- If you have a whole number with a fraction, it’s called a mixed fraction. For example, 1 1/2 is a mixed fraction.
Advertisement
-

1
Identify fractions with like denominators. If you need to add or subtract fractions, they need to have common denominators before you make your calculations. Look at the denominator on the fractions to see if they’re the same (like).
-

2
Find a common denominator if the denominators are unlike. If your denominators aren’t the same, you’ll need to change the fractions so they have the same denominators. To find a common denominator, multiply each part of a fraction by the denominator of the other fraction.[4]
- For example, to find a common denominator for 1/3 + 2/5, multiply the 1 and 3 by 5 and multiply the 2 and 5 by 3. You should get 5/15 + 6/15. Then you can calculate the fractions.
-

3
Add or subtract the numerators to calculate the fractions. Once you’ve found a common denominator and multiplied the numerators if necessary, you’re ready to add or subtract. Add or subtract the numerators and place the result over a dividing line. Put the common denominator below the line.[5]
- For example, 3/6 – 2/6 = 1/6.
- Avoid adding or subtracting denominators.
-

4
Simply the sum if necessary. If you’ve had to find a common denominator, you may end up with a large fraction that can be simplified. For example, if you added 8/32 +12/32, you’d get 20/32. This can be reduced to 5/8.[6]
Advertisement
-

1
Turn mixed fractions or whole numbers into improper fractions. To make it easier to multiply, you’ll need to work with proper or improper fractions. If you have a whole number or mixed fraction that you want to multiply, turn it into its fraction.
- For example, to multiply 2/5 by 7, turn 7 into a fraction. Then you can multiply 2/5 by 7/1.
- If you have a mixed fraction such as 1 1/3, turn it into an improper fraction, 4/3 before you multiply.
-

2
Multiply the numerators and denominators. Instead of adding the numerators, multiply both of them and write the result over your dividing line. You’ll also need to multiply the denominators and put the result under the line.[7]
- For example, to multiply 1/3 by 3/4, multiply 1 by 3 to get the numerator. Multiply 3 by 4 to get the denominator. Your answer will be 3/12.
-

3
Simplify your result. In many cases, you’ll need to reduce the result to a simplified fraction, especially if you started with improper fractions.Identify the greatest common factor and use it to simplify the numerator and denominator.[8]
- For example, if your answer is 3/12, 3 is the greatest common factor. Reduce the fraction by 3 to get 1/4.
Advertisement
-

1
Invert the second fraction. The simplest way to divide fractions, even those with unlike denominators, is to flip the second fraction before you calculate the sum.
- For example, with 5/4 ÷ 1/2 you should flip the 1/2 fraction so it appears as 2/1.
-

2
Multiply the numerators and denominators. Multiply the fractions straight across to multiply the numerators. Put the result over a dividing line and multiply the denominators. Put the result under the dividing line.[9]
- To continue the example, you’d multiply 5/4 by 2/1 to get 10/4.
-

3
Simplify the results, if needed. If your answer is an improper fraction or can be reduced, simplify the fraction. Use the greatest common factor to reduce the fraction.[10]
- For example, the greatest common factor for 10/4 is 2 so your simplified answer is 5/2.
- Since this is an improper fraction, turn it into a whole number with a fraction. 5/2 becomes 2 1/2.
Advertisement
Add New Question
-
Question
What is 5/8 times 16?

To multiply a fraction by a whole number, multiply the numerator by the whole number to get the new numerator. The denominator remains unchanged. (5/8)(16) = 80/8 = 10.
-
Question
How do I calculate 2/3 × -5/6?

(2/3)(-5/6) = [(2)(-5)] / [(3)(6)] = -10/18 = -5/9.
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Always write your fractions neatly to reduce your risk for calculation errors.
-
If you’re working with complex fractions, you’ll need to take a few extra steps to simplify them, but that’s still a necessary part of the process.
Advertisement
References
About This Article
Article SummaryX
To calculate fractions by adding or subtracting, start by finding a common denominator of the two numbers. Simply multiply the fraction by the denominator of the other fraction to make the denominators the same. For example, to find a common denominator for 1/3 + 2/5, multiply the 1 and 3 by 5 and multiply the 2 and 5 by 3 to get 5/15 + 6/15. Then, add or subtract the numerators, and use the common denominator as the denominator for your answer. For example, 5/15 + 6/15 would be 11/16. Be sure to simplify your answer if possible! If you want to learn how to multiply fractions together, keep reading the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 90,200 times.
Reader Success Stories
-

Pavithra Poojani
Mar 19, 2020
“Thanks for the explanation, it helped me to be successful.”
