Время чтения: 8 минут.
Задание 6 решается за несколько секунд, если ты умеешь работать с графиками и таблицами. Давай разберемся, как легко и быстро разбираться в данных, представленных графически.
Диаграммы и графики – что это?📈
Для начала давай разберемся, что такое графики и диаграммы.
График – это отражение зависимости одной величины от другой. Пример: график зависимости температуры воздуха от времени суток.
Диаграмма – показывает соотношение каких-либо величин. Пример: доля населения Азии в общей численности населения Земли.
Чаще всего данные на диаграмме представлены в процентах (%).
Решение заданий из ВПР📝
Столбчатые диаграммы📊
Задачи со столбчатыми диаграммами решаются проще всего. Обычно нужно подсчитать общее количество чего-либо, либо определить наибольшее/наименьшее число из общего количества.
Пример №1: На диаграмме показаны виды кровли домов жителей поселка. По вертикальной оси указано количество домов. Сколько домов в данном поселке?
Решение: По диаграмме можно определить, сколько домов с каждым видом кровли. С железной крышей – 5 домов, с соломенной крышей – 9 домов, с черепичной – 8 домов и с деревянной – 7 домов. Складываем и получаем ответ!
Пример №2: На диаграмме показаны результаты проверочной работы, проведенной в 6 «А» классе. По вертикальной оси указано число учеников. Назовите средний балл по классу за эту проверочную работу.
Решение: Для расчета среднего балла используем формулу среднего арифметического – сумму всех оценок делим на число учеников.
Круговые диаграммы🔘
Задания с круговыми диаграммами решаются как задачи на проценты: находится процент от числа или число по его проценту.
Разбор задач на части представлен в статье:
Пример №3: На диаграмме представлен отчет о тратах семьи за прошедший месяц. По данным диаграммы, определите, сколько рублей потратила семья на одежду, если известно, что на коммунальные услуги было истрачено 7000 рублей?
Решение: Сначала находим число по его проценту – сколько семья потратила за месяц в целом. Затем из общего числа определяем, сколько денег было потрачено конкретно на одежду.
Формулы для решения ниже👇
Пример №4: На диаграмме показаны результаты контрольной работы в 6 «В» классе. Сколько процентов ребят получило отметку выше «3»?
Решение: Данная задача отличается тем, что нужно найти, какую часть одно число составляет от другого (в процентах). Для этого используется третья формула из задач на проценты.
На этом все! Остались вопросы? Напиши о них в комментариях!👇
Обязательно подпишись на канал, чтобы не пропустить больше полезных статей!🧠
#впр #огэ #егэ #математика #репетитор #6класс #алгебра #геометрия #диаграммы #задачинапроценты
Школьники, которые готовятся к сдаче ЕГЭ по математике и рассчитывают на получение достойных баллов по итогам прохождения аттестационного испытания, обязательно должны уметь справляться с заданиями, где требуется выполнить анализ данных с помощью диаграмм. Подобные задачи включаются в экзамен ежегодно. Если задания ЕГЭ на выполнение анализа данных по диаграммам вызывают у вас определенные затруднения, рекомендуем вам повторить эту тему.
Вместе с образовательным проектом «Школково» вы сможете восполнить пробелы в знаниях. Наши специалисты подготовили и систематизировали весь необходимый материал, который может потребоваться вам для выполнения заданий ЕГЭ на проведение анализа данных с помощью диаграмм.
Прежде всего мы рекомендуем выпускникам на этапе подготовки к прохождению аттестационного испытания вспомнить основные понятия и правила. Для этого необходимо посетить раздел «Теоретическая справка».
Для закрепления полученных знаний и приобретения практического навыка предлагаем выполнить задания по темам «Построение графиков и диаграмм и анализ статических данных» и «Определение величины по графикам ЕГЭ» подобные тем, которые присутствуют в ЕГЭ. Для каждого упражнения на сайте представлены алгоритм решения и правильный ответ. При этом учащиеся могут попрактиковаться как с простыми, так и с более сложными заданиями по теме «Анализ данных с помощью диаграмм».
В случае необходимости школьники имеют возможность сохранить упражнение в «Избранное», чтобы затем обсудить алгоритм нахождения правильного ответа с преподавателем. Практиковаться в решении задач, в которых требуется выполнить анализ данных по диаграммам и графикам, имеют возможность учащиеся из Москвы и любого другого российского города.
Круговая диаграмма


4
Средняя оценка: 4
Всего получено оценок: 643.
4
Средняя оценка: 4
Всего получено оценок: 643.
Если говорить честно, то в математике 5 класса круговая диаграмма используется крайне редко. Но это возможность наглядной подачи информации, что используется на презентациях любых предметов школьного курса. Поэтому изучим принцип построения круговой диаграммы, ее преимущества и недостатки.
Что такое круговая диаграмма?
Круговой диаграммой называют круг, разделенный на сектора. Величина сектора показывает, сколько раз то или иное число повторяется в ряде. К примеру, на круговой диаграмме можно отразить процентное соотношение троечников, хорошистов и отличников в классе.
Достоинства и недостатки круговой диаграммы.
Наравне с круговой диаграммой используется столбчатая диаграмма, гистограммы и графики.
Круговая диаграмма обладает следующими недостатками:
- На круговой диаграмме нельзя отобразить несколько рядов. На графике или столбчатой гистограмме можно отобразить любое количество рядов. Это удобно, так как позволяет сравнивать ряды между собой. Круговая диаграмма дает возможность оценить тенденцию ряда: т.е. наиболее повторяющиеся в ряду элементы.
- На диаграмме нельзя отобразить изменение функции. Для этого можно использовать только график.
- На диаграмме нельзя наглядно изобразить более 7 элементов. Если в ряду 200, 300 и более элементов, то эффект наглядности пропадает. Зрителю будет просто невозможно разглядеть процентное соотношение элементов. Поэтому было выведено максимальное число элементов ряда, за которым эффект наглядности круговой диаграммы пропадает: это число 7.
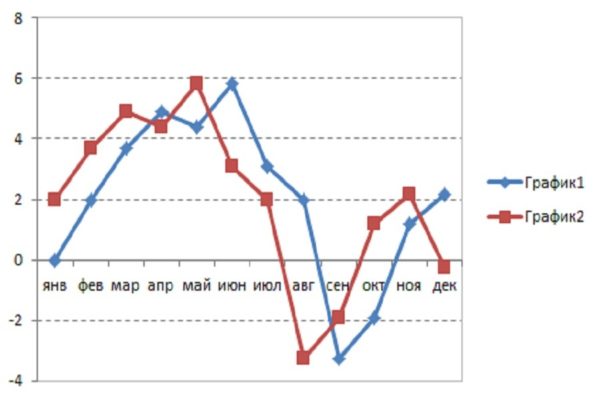
Но при всех своих недостатках, круговая диаграмма обладает одним огромным достоинством: на ней очень удобно показывать тенденцию ряда. Все элементы простого ряда просто и наглядно будут выглядеть на круговой диаграмме.
Как строить круговую диаграмму?
Для того, чтобы построить круговую диаграмму, нам нужно узнать, сколько градусов нужно отвести каждому сектору.
Для этого используется следующая формула:
$$а={nover{N}} *360 $$
В формуле буква а это градусная мера сектора, соответствующая определенному элементу, n – число одинаковых элементов в ряде, N – общее число всех элементов в ряде. Посчитанное значение округляется до целых. После расчета все сектора наносятся на круг.
При построении круговой диаграммы, общее число элементов принимается за целое. Целый круг это 360 градусов. То есть каждый сектор занимает какую-то часть от 360 градусов. Из этих рассуждений и появилась формула.
Для нанесения частей на круговую диаграмму необходимо:
- Провести радиус перпендикулярно вниз.
- От радиуса отложить наибольший из получившихся углов. Так мы получим первый сектор, его нужно подписать, заштриховать или раскрасить отдельным цветом. Значение всех цветов и штриховок выписывается ниже диаграммы, иначе рисунок будет невозможно прочитать
- От проведенного радиуса откладывается наибольший из оставшихся углов. Так получается следующий сектор.
- Пункт 3 повторяется, пока не кончатся сектора.

Что мы узнали?
Мы узнали, что такое круговая диаграмма. Поговорили о плюсах и минусах этого вида подачи информации. Сказали о других видах информационных рисунков, выделили плюсы и минусы круговой диаграммы в сравнении с другими информационными рисунками. Привели алгоритм построения круговой диаграммы и формулу расчета секторов, необходимую для этого построения.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-

Анастасия Минай
4/5
-

Olezh Dushnov
4/5
-

Almas Izbasarov
4/5
-

Елена Котова
5/5
-

Анастасия Родионова
5/5
-

Софа Вдовина
4/5
-

Ольга Поспелова
5/5
-

Юксель Саркаров
5/5
Оценка статьи
4
Средняя оценка: 4
Всего получено оценок: 643.
А какая ваша оценка?
Круговые графики: круг делится на меньшие части. Каждая часть представлена в процентах от всего круга. Круговая диаграмма или круговая диаграмма используется для визуального представления информации и данных. Показывает относительные размеры данных.
Представьте, что вы опрашиваете своих друзей, чтобы найти то мороженое, которое им больше всего нравится
Для построения кругового графика сформируйте данные в таблице выше
Шаг 1: сложите все значения в таблице
Шаг 2: Затем разделите каждое значение на сумму и умножьте на 100, чтобы получить процент
Шаг 3: Вы можете показать эти данные, используя график Cicle следующим образом:
Легко увидеть, какие вкусы мороженого больше всего нравятся, а какие вкусы наименее нравятся, с первого взгляда.
В этом уроке мы решаем проблемы, связанные с поиском процентов от общей суммы в круговых диаграммах.
Рассмотрим следующие решенные примеры для лучшего понимания.
Ниже приведен круговой график, показывающий ежемесячные расходы Натана. Сколько он тратит на еду в процентах?
Шаг 1:
Общие расходы = 400 долл. США + 320 долл. США + 240 долл. США + 640 долл. США = 1600 долл. США
Шаг 2:
Расходы на еду = 640 долларов
Процент расходов на продукты питания = frac6401600 times100=4%
Некоторые из пятиклассников были опрошены на предмет их любимого цвета. Круговая диаграмма показывает результаты опроса. Какой процент и сколько ученикам нравится желтый цвет?
Шаг 1:
Процент желтого
= 20%
Количество тех, кто любит зеленый = 75
Шаг 2:
Процент тех, кто любит зеленый = 60%
Количество тех, кто любит желтый = frac2060 times75=25
Г-н Нильсен спросил учеников в своем классе, как они проводят свой досуг. Ответы, как показано на круговой диаграмме. Если в классе 40 учеников, сколько учеников проводят свободное время в рисовании?
Шаг 1:
Количество учеников в классе = 40
Процент студентов, которые проводили время в рисовании = 10%
Количество тех, кто любит зеленый = 75
Шаг 2:
Количество студентов, проводящих время в рисовании
= 10% от 40
frac10100 times40=4
В прошлом уроке мы научились работать с транспортиром. Мы выяснили, что градусная мера развернутого угла равняется $180°$, это также градусная мера полуокружности. А следовательно, градусная мера самой окружности в два раза больше: $180°cdot2=360°$
Градусная мера любой окружности равняется $360°$.
В этом уроке мы познакомимся с круговыми диаграммами.
Круговая диаграмма — это схема с секторами, которая помогает наглядно показать какое-либо соотношение.
Задача №1
Рассмотрим ситуацию: у Образавра есть два яблока, три апельсина и одна груша. Давайте поможем ему наглядно показать соотношение фруктов в виде круговой диаграммы.
Для начала найдем общее количество фруктов: $$2 space яблока + 3 space апельсина + 1 space груша = 6 space фруктов$$
Теперь начертим окружность и расчертим в ней $6$ равных секторов. Как нам это сделать? Вспомним, что в окружности $360°$. Тогда разделим $360°$на $6$: $$360°:6=60°$$
Выходит, каждый сектор должен занимать по $60°$. С помощью транспортира построим все секторы, получаем рисунок 3.
Теперь вспомним, что яблоки занимают два сектора, апельсины – три сектора, а груша – один. Изобразим все фрукты в секторах, получим рисунок 4.
Остается стереть линии между одинаковыми фруктами и получить окончательную круговую диаграмму, рисунок 5. Каждый сектор обязательно подписываем!
Таким образом, круговая диаграмма дает нам возможность сравнить количество фруктов, не сравнивая их численные значения. По полученной диаграмме видно, что у Образавра больше всего апельсинов, а меньше всего — груш.
Бывают ситуации, когда градусные меры секторов не получаются такими же удобными, как в случае с фруктами. И тогда первый способ построения становится сложным.
Рассмотрим второй вариант построения круговых диаграмм.
Задача №2
В классах 5 «А» и 5 «Б» по $20$ детей. Оба класса написали контрольную работу по математике. Результаты 5 «А»: $12$ пятерок, $4$ четверки, $3$ тройки и $1$ двойка. Результаты 5 «Б»: $10$ пятерок, $5$ четверок и $5$ троек.
Для сравнения результатов этих классов построим две круговые диаграммы.
В данном случае неудобно вычерчивать по $20$ одинаковых секторов, как мы это делали раньше. В работе с большим количеством вариантов проще сразу работать с разными секторами.
Начнем с класса 5 «А». Всего в классе $20$ детей, а в окружности $360°$, значит говорим, что $20$ — это $360°$. Тогда найдем, сколько градусов занимает один ребенок: $$20 — 360°$$ $$1 — X°$$
$$X=frac{1cdot360°}{20}=18°$$
Теперь найдем, сколько градусов занимают ученики с разными оценками, для этого умножаем их количества на $18°$:
$12cdot18°=216°$ — такое количество градусов в диаграмме занимают дети из класса 5 «А», написавшие контрольную на пятерки.
$4cdot18°=72°$ — написали на четверки;
$3cdot18°=54°$ — написали на тройки;
$1cdot18°=18°$ — написали на двойки.
Аналогично для класса 5 «Б», сразу запишем ответ:
$10spaceдетей$ – $180°$ — такое количество градусов в диаграмме занимают дети из класса 5 «Б», написавшие контрольную на пятерки.
$5spaceдетей$ – $90°$ — столько детей написали на четверки;
$5spaceдетей$ – $90°$ — столько написали на тройки;
Теперь мы можем воспользоваться транспортиром и изобразить две диаграммы с результатами контрольной работы для двух классов:
Далее закрасим сектора для наглядности и подпишем каждый из них. Получаем конечные диаграммы:
С помощью круговых диаграмм мы можем сравнить результаты двух классов. Пусть «5» и «4» — хорошие оценки, а «3» и «2» — плохие. Тогда по диаграммам мы можем сказать, что результаты контрольной работы в классе 5 «А» лучше, чем в классе 5 «Б», потому что в классе «А» площадь зелёных зон больше.
Построение круговой диаграммы по процентам
Среди учеников начальной школы был проведен опрос на тему: «Какое ваше любимое время года?» $55%$ учеников выбрали лето, $20%$ выбрали зиму, $15%$ выбрали весну, и $10%$ — осень. Воспользуйтесь транспортиром, чтобы изобразить результаты опроса в виде круговой диаграммы.
Всего у нас есть $100%$, значит $100%$ занимают всю площадь окружности, то есть все $360°$. $$100% — 360°$$ $$1% — X°$$ $$X°=frac{360°}{100}=3.6°$$
Умножьте $3.6°$ на $55%, 20%, 15%spaceиspace10%$, чтобы узнать, сколько градусов в диаграмме займёт каждый сектор. По полученным результатам начертите круговую диаграмму.
Сравните свою диаграмму с рисунком 8. Вы могли расположить сектора с временами года в другой последовательности. Чтобы понять, правильно ли вы начертили диаграмму, посмотрите, сколько градусов занимают ваши секторы, правильный ответ:
$55% -198°$
$20% -72°$
$15% -54°$
$10% -36°$
