#хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳
Продолжаем готовиться к ОГЭ по математике. В этой статье рассмотрим решение задач «с теплицей». В нашем канале мы уже публиковали задачи № 1 -5 из ОГЭ «на шины», «на мобильную связь», «на ОСАГО» и вот «теплицы». И каждый раз читаю комментарии вроде: «зачем?», «кому это надо?», «где пригодиться?», «да и вообще это не математика».
Так вот, как раз эти задачи о том — «где может пригодиться математика»! Это задачи практико-ориентированной направленности. А кто-то наоборот говорит: «И это экзамен для 9 –го класса?!», — намекая на слишком простые задания.
К сожалению, практика показывает, что именно такие задачи хуже всего решают 9-классники, им проще решить уравнения, неравенства, теорию вероятности и др. задачи.
Прежде, чем решать задачи, внимательно прочитайте условие, выпишите все величины и формулы, которые могут понадобиться.
Итак,
NP = 4,5 м = 450 см — длина теплицы;
Длина дуги MCDM (длина полуокружности) = 5,2 м — длина металлической дуги;
Напомню, что формула для вычисления длины окружности С = 2πR = = Dπ, где R — радиус, D — диаметр (в данном случае, D = MN — ширина теплицы).
Задание 1.
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
Решение:
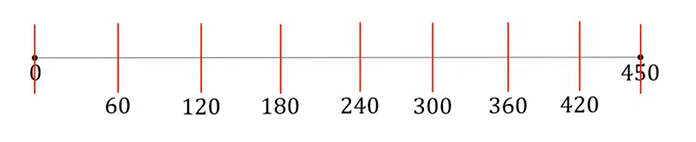
Суть задачи в том, что нужно длину теплицы NP разделить на промежутки (отрезки) длиной не более 60 см. Поэтому всю длину 450 см мы делим на 60 см:
450 : 60 = 7,5 частей (берём 8 частей).
Внимание: основная ошибка в том, что ребята ошибочно думают, что это и есть количество дуг, но это количество отрезков. Посмотрите на рисунок ниже — дуг на 1 больше, включая крайние дуги.
Итак, 8 + 1 = 9
Ответ: 9.
Задание 2
Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.
Решение
1) Из условия задачи мы отметили, что MN = D (диаметр окружности), C = Dπ, следовательно, чтобы найти диаметр D, необходимо D = C / π
2) По условию, 5,2 м — длина полуокружности, следовательно, вся длина C = 5,2 × 2 = 10,4
3) D = 10,4 / π = 10,4 / 3,14 ≈ 3,312 ≈ 3,3 (округлили до десятых).
Т.о. MN = 3,3 м
Ответ: 3,3 м.
Задание 3
Найдите примерную площадь участка внутри теплицы в квадратных метрах. Ответ округлите до целых.
Решение
Как следует из условия, фундамент для теплицы имеет форму прямоугольника, таким образом, для того, чтобы найти площадь внутри теплицы, нужно найти площадь прямоугольника MNPK (см. рис.):
S = MN × NP (MN нашли во 2 задаче, NP — берём из условия)
S = 3,3 × 4,5 = 14,85 ≈ 15 квадратных метров (округлили до целых)
Ответ: 15.
Задание 4
Сколько квадратных метров плёнки нужно купить для теплицы с учётом передней и задней стенок, включая дверь? Для крепежа плёнку нужно покупать с запасом 10 %. Число π возьмите равным 3,14. Ответ округлите до целых.
Решение
1) Найдём сначала сколько понадобится квадратных метров плёнки для каркаса теплицы: это площадь прямоугольника со сторонами NP и длиной полуокружности (дуга MCDN) = 5,2 м.
S = 4,5 × 5,2 = 23,4 м^2
2) Передняя и задняя стенка, включая дверь, представляют собой две полуокружности или целую окружность, т.е. требуется найти площадь круга.
3) Всего понадобится плёнки:
23,4 + 8,55 = 31,95 + 3,19 (добавили 10 %) = 35,14 ≈ 35 м^2
Ответ: 35.
Примечание: непонятно, что это за плёнка, которая продаётся в форме окружности. В реальной жизни мы бы купили прямоугольник и вырезали из него круг. Но это уже вопрос не ко мне, а к составителю этих заданий. Но!!! Девятиклассник может подумать так же, и решит эту задачу именно практично и не получит свой заслуженный 1 балл.
Задание 5
Найдите примерную высоту входа в теплицу в метрах. Число π возьмите равным 3,14. Ответ округлите до десятых.
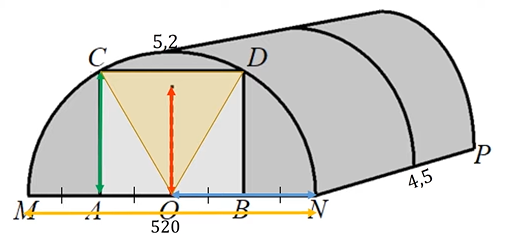
1. Рассмотрим ∆ OCD — равносторонний, т.к.
CO = OD = R;
A — середина MO = R, B — середина ON = R (по условию), следовательно, AB = СD = R.
Таким образом, CO = OD = CD = R.
OH — высота, это и есть искомая высота входа в теплицу.
2. Рассмотрим ∆ DHO — прямоугольный, ∟D = 60 °,
√3 ≈ 1,7; R = D / 2 = 3,3 / 2 = 1,65
OH = 1,7 ×1,65 / 2 = 1,4 м
Ответ: 1,4.
Почему я так подробно разбираю решение этих задач? Потому что цель моей статьи — помочь выпускникам 9-ых классов разобраться в этих задачах и успешно пройти это испытание. И я надеюсь, моя статья вам в этом поможет!
Читайте наш канал в телеграм – по этой ссылке
#хакнем_математика 👈 подпишись на рубрику, содержащую интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳
Автор: #ирина_чудневцева главный редактор и соавтор канала Хакнем Школа, 43 года, город Ярославль
Другие статьи автора:
Хотите опубликовать свой пост в «Хакнем Школа»? Напишите нам на почту: story@haknem.com
В 2022 учебном году выпускники 9 классов будут сдавать ОГЭ по обновлённым заданиям. Представляем вам вариант тренировочной работы по математике в формате ОГЭ от СтатГрада. Обычно статградовские задания, используемые на пробных тестированиях в школах, максимально приближены к реальным экзаменационным вариантам. Рассказываем, как работать с новыми заданиями про теплицу.
Хотите БЕСПЛАТНО разобрать с опытным преподавателем все детали новых усложнённых вариантов ОГЭ по математике 2023 года – приходите на пробное занятие в Lancman School. Решите продолжить готовиться к ОГЭ вместе с нами весь год – дадим скидку после бесплатного пробного занятия.
Любой вопрос смело пишите сюда. Мы 13 лет готовим к ОГЭ на высокие баллы. Прокачиваем знания даже самых слабых учеников. Гаранитруем получение оценки “5” на ОГЭ. Офисы Курсов ОГЭ Lancman School есть на каждой ветке московского метро.
Если хотите сэкономить, но получить при этом качественную подготовку, записывайтесь на наши онлайн-курсы ОГЭ-2023 по русскому языку, математике, обществознанию и английскому языку.
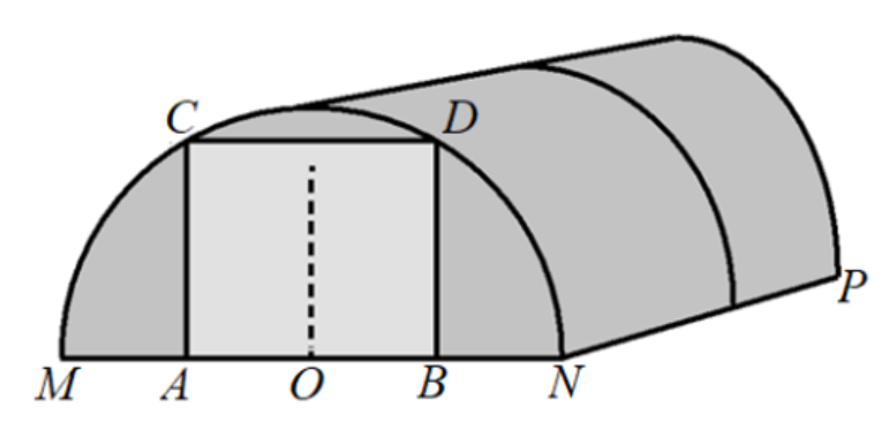
Алексей Юрьевич решил построить на дачном участке теплицу длиной NP = 4,5 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Алексей Юрьевич заказывает металлические дуги в форме полуокружностей длиной 5,2 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B — середины отрезков MO и ON соответственно.
1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
Решение:
Решать подобные задания лучше наглядным способом, то есть нарисовать предварительно дугу и делать на ней необходимые пометки.
Ответ: 9.
2. Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.
Решение:
Длину МN необходимо искать, исходя из дуги, используя формулу длины окружности. Поскольку MN – это полуокружность, то ее длина равна πR.
πR=5,2
3,14R=5,2
R=5,2/3,14
MN=2 × 520/314=520/157
MN=3,31
Ответ: 3,3
3. Найдите примерную площадь участка внутри теплицы в квадратных метрах. Ответ округлите до целых.
Решение:
Площадь участка внутри теплицы представляет собой прямоугольник, и его площадь равна MN × NP.
S=520/157 × 4,5= 2340/157=14,9… При округлению получаем 15.
Можно взять ответ в 3,3 из предыдущего задания для решения.
S=3,3 × 4,5=14,85. При округлении тоже получаем 15.
Ответ: 15.
4. Сколько квадратных метров плёнки нужно купить для теплицы с учётом передней и задней стенок, включая дверь? Для крепежа плёнку нужно покупать с запасом 10 %. Число π возьмите равным 3,14. Ответ округлите до целых.
Решение:
Для начала необходимо посчитать площадь крыши теплицы. Она представляет собой прямоугольник со сторонами, равными 4,5 и 5,2.
S крыши=5,2 × 4,5=23,4
Остаётся посчитать площадь двух полуокружностей (перед и задняя часть теплицы). Вместе это одна окружность – значит, можно не считать площадь 2 раза.
S стенок=3,14 × (260/157)в квадрате=314/100 × 260/157 × 260/157=1352/157
К данной площади необходимо добавить 10%, поскольку плёнки надо купить с запасом. Прибавляем по 10% к уже имеющимся цифрам.
S крыши=25,74
S стенок=9,47…
Складываем и округляем. Получаем примерно 35 метров плёнки.
Ответ: 35.
5. Найдите примерную высоту входа в теплицу в метрах. Число π возьмите равным 3,14. Ответ округлите до десятых.
Решение:
Задача геометрическая: нам надо представить, что перед нами равносторонний треугольник.
Итак, перед нами равносторонний треугольник СOD. Найдя его высоту, мы найдём высоту входа в теплицу. Будем использовать формулу высоты равностороннего треугольника. Сторона треугольника COD равна радиусу окружности, которую мы уже знаем (260/157).
h=1,40… Округляем до 1,4.
Ответ: 1,4.
Ваш ребёнок – школьник 1-11 класса? Вы учитель? Отлично! Мы пишем для вас. Узнавайте от нас первыми новости образования, актуальную информацию об экзаменах и просто полезные советы. Кнопка подписки прямо под постом!
Фото: pixabay.com
Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.
Требуется: найти примерную ширину MN теплицы в метрах
Дано: теплица, её длина = 4.5 метров.
Ширина: диаметр полукруга металлической дуги = 5.2 метров.
Число π = 3,14. Результат округлить до 1 числа после запятой.
Виртуальная окружность или две дуги = 5.2 х 2 = 10.4
Диаметр или ширина теплицы равна 10.4/π = 10.4/3.14 = 3.31
Округляем до десятой получается, что MN теплицы в метрах = 3.3 метра.
Можно и площадь вычислить, но это в следующем вопросе.
автор вопроса выбрал этот ответ лучшим
Tanyetta
[298K]
11 месяцев назад
Данная задача, является достаточно актуальной, ведь сейчас начинается дачный период и каждый дачник, что-то докупает для своего садового участка. Нам предстоит решить математическую задачку, чтобы определить ширину MN теплицы в метрах. Из условия задачи нам известно, что Алексей Юрьевич решил приобрести на свою любимую дачу теплицу длиной 4,5 метра и для этого, он уже сделал прямоугольный фундамент. Далее Алексей Юрьевич заказывает металлические дуги в форме полуокружностей, длина которых составляет 5,2 метра каждая и пленку для обтягивания теплицы.
- 5,2 * 2 = 10,4 (метров) – составляет окружность двух дуг.
- L = 2пR = пD, L = 10,4/3,4=3,31 (метр) – ширина теплицы.
Ответ: 3,3 метра составляет ширина теплицы.
Пашенька
[189K]
более года назад
Планируя строить теплицу, Алексей Юрьевич решил, что она должна быть полукруглой. Мне кажется, что это не самый лучший вариант, но не мне судить хозяина теплицу. По условию нам дана длина теплицу, а также нам известна длина дуги – 5.2 м.
- Зная длину дуги, можно подсчитать длину окружности:
5.2х2=10.4 – м – длина окружности.
- Теперь мы знаем длину окружности, поэтому из формулы L=2пR мы можем вывести значение значение диаметра
- L = пД, Д = L/п, Д = 10.4/3,4=3,31=3,3 – метра.
Ответ: 3.3
Niki M
[390K]
более года назад
Чем больше теплица в пересчете на квадратный метр, тем дешевле она получается.
В зависимости от местоположения и использования существуют разные типы теплиц: теплицы, односкатные теплицы и политоннели.
Классический вариант – отдельно стоящая теплица.
Что мы имеем по задаче:
4.5 – длина.
5.2 – ширина дуги – у нас их две.
5.2х2=10.4
Далее решаем по формуле:
Росинка Роса
[477K]
более года назад
Примерная ширина теплицы вычисляется по формуле длины окружности.
Для решения задачи у нас есть необходимые и избыточные данные.
Избыточными являются сведение о длине теплицы, а также о ее фундаменте.
Необходимое сведение – длина дугового пролета в форме полуокружности.
Если длина полуокружности известна, умножим ее на 2 и получим длину окружности, в которой диаметр и будет шириной нашей теплицы.
Производим вычисления:
5,2 Х 2 = 10,4
Это число нам надо разделить на число ПИ (3.14) и получим искомый диаметр, он же – ширина теплицы, которую героически самостоятельно возводит на своем дачном участке Алексей Юрьевич.
10,4 : 3,14 = 3,31
Округляем до десятых долей
3,3 метра.
Знаете ответ?
Версия для печати и копирования в MS Word
Найдите примерную ширину MN теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.
Алексей Юрьевич решил построить на дачном участке теплицу длиной NP = 4,5 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Алексей Юрьевич заказывает металлические дуги в форме полуокружностей длиной 5,2 м каждая и плёнку для обтяжки. В передней стенке планируется вход, показанный на рисунке прямоугольником ACDB. Точки A и B — середины отрезков MO и ON соответственно.
Спрятать решение
Решение.
Ширина MN представляет собой диаметр окружности. Длина окружности равна 5,2 · 2 = 10,4. Зная о том, что длина окружности может быть вычислена по формуле имеем
Таким образом, D = 3,3.
Ответ: 3,3.
1
Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
2
Найдите примерную площадь участка внутри теплицы в квадратных метрах. Ответ округлите до целых.
3
Сколько квадратных метров плёнки нужно купить для теплицы с учётом передней и задней стенок, включая дверь? Для крепежа плёнку нужно покупать с запасом 10 %. Число π возьмите равным 3,14. Ответ округлите до целых.
4
Найдите примерную высоту входа в теплицу в метрах. Число π возьмите равным 3,14. Ответ округлите до десятых.
Разбор заданий 1-5 ОГЭ по математике о строительстве
теплицы.
Решение типовых «сюжетных» заданий № 1-5 с общим рисунком
из КИМ ОГЭ-2020 и ОГЭ-2021 использует целый ряд межпредметных связей, развивает
вариативность, умение анализировать информацию и делать правильный выбор.
Основными трудностями при работе с этими заданиями может
являться сложный прикладного характера материал и лимит времени урока. Поэтому
необходимо формировать и развивать у обучающихся навык « смыслового чтения».
Необходимо научить их выделять ключевые фразы и основные вопросы из текста,
разбираться в изображениях рисунков, планов и масштабе фигур на рисунках,
анализировать и пользоваться информацией из таблиц.
При разборе заданий «о теплице» необходимо вспомнить
понятие дуги окружности, радиуса, диаметра, длины окружности. Обратить
внимание, что количество частей при разрезании отрезка на единицу меньше, чем
количество граничных точек. Необходимо правильно округлять результат
вычислений. Оценка иррациональных чисел требует повышенного внимания.
Задача о теплице является практико-ориентированной задачей.
Сложность данной задачи заключается в том, что в 5 задании требуется найти
приближенное значение арифметического квадратного корня.

Алексей Иванович решил построить на дачном участке теплицу
длиной NP = 6,5 м. Для этого он сделал прямоугольный фундамент. Для каркаса
теплицы Алексей Иванович заказывает металлические дуги в форме полуокружностей
длиной 6,1 м каждая и пленку для обтяжки. В передней стенке планируется вход,
показанный на рисунке прямоугольником ACDB. Точки A и B — середины отрезков MO
и ON соответственно.
Задание 1. Какое наименьшее количество дуг
нужно заказать чтобы расстояние между соседними дугами было не более 75 см?
Решение. Из первого предложения текста задачи, мы узнаем,
что длина теплицы составляет 6,5 метров. Поэтому, первым делом находим
количество интервалов, между дугами.
650:75=8,6=9
Получаем 9 интервалов, между
дугами
Теперь найдем, сколько
будет дуг. Количество дуг = количество интервалов +1 = 9+1 = 10 дуг.
Ответ:1
Задание 2. Найдите примерную ширину MN
теплицы в метрах. Число π возьмите равным 3,14. Результат округлите до десятых.
Решение.
Ширина
теплицы – это отрезок MN. Поскольку теплица состоит из дуг, то MN – это диаметр окружности.
Диаметр
окружности связан с длиной окружности следующей формулой:
L=2пR=пD
В этой формуле, L-длина окружности, D- диаметр окружности,
“пи”=3,14
Длину окружности, найдем из следующей
информации: “….металлические дуги в форме полуокружности длиной 6,1
метра….”
Поскольку известна длина
полуокружности – 6,1 м, то длина окружности равна: L=6,1*2=12,2
12,2=3,14D
D=12,2:3,14=3,89м
Из этих расчетов получаем, что ширина
теплицы (с округлением до десятых) равна 3,9м
Ответ: 3,9
Задание 3. Найдите примерную площадь участка
внутри теплицы в квадратных метрах. Ответ округлите до целых.
Решение.
Площадь участка внутри теплицы представляет собой прямоугольник со
сторонами MN и NP. NP = 6,5 м., MN – это диаметр окружности, MN=3,9м S=MN*NP=3,9*6,5=25,35м2
Из этих расчетов получаем, что примерная
площадь внутри теплицы (с округлением до целых) равна 25м2
Ответ: 25
Задание 4. Сколько квадратных метров пленки
нужно купить для теплицы с учетом передней и задней стенок, включая дверь? Для
крепежа пленку нужно покупать с запасом 10%. Число π возьмите равным 3,14.
Ответ округлите до целых.
Решение.
Чтобы узнать сколько метров пленки нужно купить для теплицы, нужно
вычислить площадь ее поверхности. Площадь ее поверхности состоит из двух равных
полуокружностей (круга)и прямоугольника.
Пленку нужно купить с запасом 10%.
Это 5,16м от площади всей поверхности. 51,59+5,16=56,75м2 (с округлением до
целых) 57м2
Ответ: 57
Задание 5. Найдите примерную высоту входа в
теплицу в метрах. Число π возьмите равным 3,14. Ответ округлите до десятых.
Решение:
Для расчета высоты теплицы, нам необходимо
сделать дополнительные построения. Проводим OD.
Получаем прямоугольный треугольник, ОDB. Дальше
по теореме Пифагора, выразим BD.
При таком решении, получаем неизвлекаемый
корень из 3. На экзамене, хорошо, что хоть кто- нибудь вспомнит, что примерно
он равен 1,7.
Ответ: 1,7