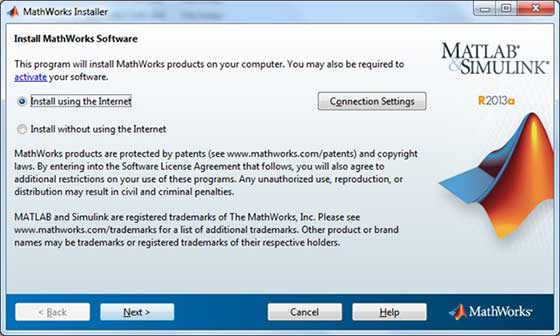
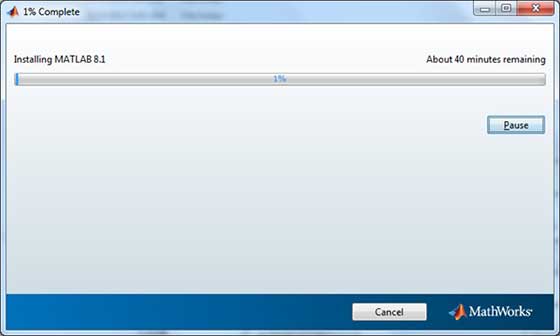
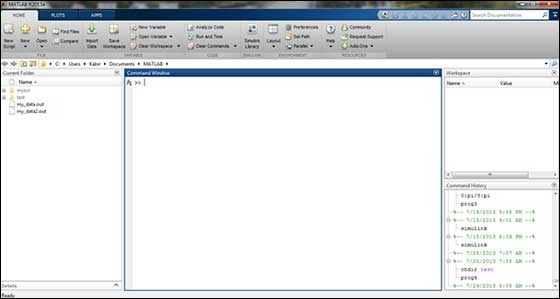
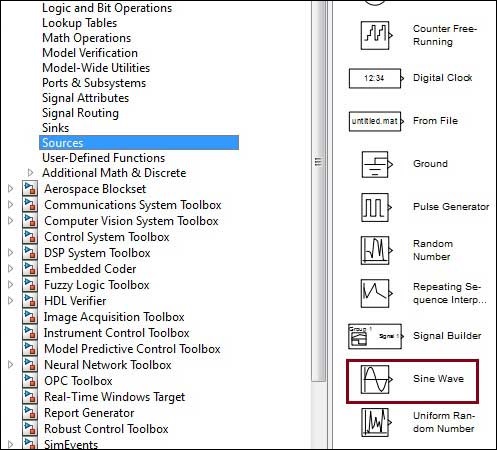
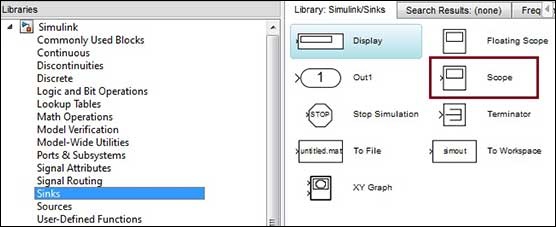
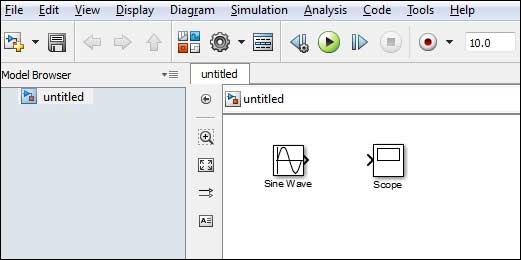
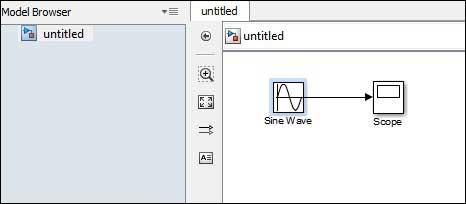
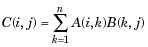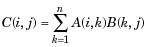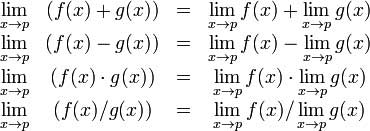Мы заметили, что вы часто ищете примеры MATLAB, потому что хотите познакомиться с особенностями языка или найти готовое решения своей проблемы.
Чтобы помочь вам быстрее находить красивые и понятные примеры, мы подготовили специальное хранилище примеров кода MATLAB, доступное всем желающим. Доступно оно по ссылке:
Примеры MATLAB (MATLAB-Examples)
Достоинства хранилища примеров MATLAB-Examples
- Все примеры русскоязычные
- Примеры разбиты по темам
- Имеется интерактивное оглавление
- Посмотреть примеры можно без запуска MATLAB
- Открыть примеры в MATLAB можно одной командой
Как посмотреть примеры
Чтобы посмотреть примеры, переходите по ссылке, листайте страницу вниз и пользуйтесь оглавлением.
Фрагмент оглавления
Нажмите на название примера, чтобы перейти в папку с ним.
В папке с примером мы рекомендуем открыть файл PDF и изучать пример по нему. Также внизу страницы примера вы найдете ссылки на полезные материалы и на другие примеры по теме.
Фрагмент страницы примера
Как скачать и попробовать примеры в MATLAB
На главной странице вы найдете инструкцию по скачиванию примеров.
Мы рекомендуем следующий способ:
- Запустите MATLAB
- Выполните команду:
eval(webread('https://exponenta.ru/install/examples'))
После этого примеры автоматически загрузятся на ваш компьютер и откроется интерактивное оглавление.
На компьютере мы рекомендуем открывать и изучать .mlx-файлы, созданные в редакторе MATLAB Live Editor.
Какая версия MATLAB понадобится?
Примеры довольно простые, поэтому должны работать даже в старых релизах MATLAB.
Тем не менее мы всегда рекомендуем использовать новейший релиз, пробную версию которого вы можете бесплатно получить за минуту по ссылке.
Не хватает примеров?
Напишите в комментариях к этой статье, каким примеров вам не хватает, чтобы мы их оформили и добавили.
Давайте сделаем интересную подборку примеров вместе!
В комментариях смело предлагайте свои интересные примеры, мы их оформим и выложим с указанием вашего авторства.
Старайтесь предлагать примеры, которые не слишком сложные и могут быть интересны широкой аудитории.
Нам важна ваша обратная связь!
Если эти примеры или сам проект MATLAB-Examples показались вам интересными, пожалуйста, сообщите нам об этом, чтобы мы понимали, сколько сил в это стоит вкладывать. Это можно сделать несколькими способами:
- Оставить комментарий к этой статье
- Повысить или понизить рейтинг этой статьи
- Поставить звездочку репозиторию на GitHub
Спасибо!
Здравствуйте, уважаемые читатели. В этой небольшой статье речь пойдет о работе с символьными переменными в Matlab. На простых примерах мы разберем преобразование символьных выражений, а…
Доброго времени суток! В этой статье мы поговорим о решении систем нелинейных алгебраических уравнений в Matlab. Вслед за решением нелинейных уравнений, переходим к их системам,…
Доброго времени суток. В этой статье мы разберем решение простых нелинейных уравнений с помощью средств Matlab. Посмотрим в действии как стандартные функции, так и сами…
Здравствуйте, уважаемые читатели. Продолжаем разбираться в Matlab. И сегодня наша тема связанна с численной оптимизацией — нахождением локальных и глобальных экстремумов функций одной или нескольких…
Доброго времени суток! Сегодня мы поговорим о решении ОДУ (обыкновенных дифференциальных уравнений) в Matlab. Перед тем как мы начнём обсуждать данную тему, советую вам ознакомиться…
Доброго времени суток! Мы продолжаем говорить о численных методах. И сегодня мы поговорим о реализации численных методов интегрирования в среде Matlab. Численное интегрирование в Matlab…
Доброго времени суток! Сегодня мы продолжаем говорить об обработке статических данных (ранее разбирали апроксимацию и интерполяцию в Matlab). Численное дифференцирование в Matlab. Теория Процесс дифференцирования…
Приветствую! Сегодня продолжаем говорить об обработке экспериментальных данных. Сегодняшняя статья — продолжение предыдущей темы: Интерполяция в Matlab. Настоятельно советую с ней ознакомиться перед чтением данной…
Доброго времени суток! Сегодня поговорим о работе с данными полученными «экспериментально». Подразумевается, что даны значения по двум или более координатам (точки), с которыми в задаче…
Доброго времени суток, читатели! Сегодня мы поговорим о матрицах в Matlab, об их применении в решении систем линейных алгебраических уравнений. Подробно разберем методы решения, и…
MATLAB – Обзор
MATLAB (матричная лаборатория) – это язык программирования высокого уровня четвертого поколения и интерактивная среда для численных расчетов, визуализации и программирования.
MATLAB разработан MathWorks.
Это позволяет матричные манипуляции; построение графиков функций и данных; реализация алгоритмов; создание пользовательских интерфейсов; взаимодействие с программами, написанными на других языках, включая C, C ++, Java и FORTRAN; анализировать данные; разработать алгоритмы; и создавать модели и приложения.
Он имеет множество встроенных команд и математических функций, которые помогают вам в математических вычислениях, создании графиков и выполнении численных методов.
Сила вычислительной математики MATLAB
MATLAB используется во всех аспектах вычислительной математики. Ниже приведены некоторые часто используемые математические вычисления, где он используется чаще всего:
- Работа с матрицами и массивами
- 2-D и 3-D Печать и графика
- Линейная алгебра
- Алгебраические уравнения
- Нелинейные функции
- Статистика
- Анализ данных
- Исчисление и дифференциальные уравнения
- Численные расчеты
- интеграция
- Трансформации
- Кривая Фитинг
- Различные другие специальные функции
Особенности MATLAB
Ниже приведены основные характеристики MATLAB –
-
Это язык высокого уровня для численных расчетов, визуализации и разработки приложений.
-
Он также предоставляет интерактивную среду для итеративного исследования, проектирования и решения проблем.
-
Он предоставляет обширную библиотеку математических функций для линейной алгебры, статистики, анализа Фурье, фильтрации, оптимизации, численного интегрирования и решения обыкновенных дифференциальных уравнений.
-
Он предоставляет встроенную графику для визуализации данных и инструменты для создания пользовательских графиков.
-
Интерфейс программирования MATLAB предоставляет инструменты для разработки, позволяющие повысить качество сопровождения кода и максимально повысить производительность.
-
Он предоставляет инструменты для создания приложений с пользовательскими графическими интерфейсами.
-
Он предоставляет функции для интеграции алгоритмов на основе MATLAB с внешними приложениями и языками, такими как C, Java, .NET и Microsoft Excel.
Это язык высокого уровня для численных расчетов, визуализации и разработки приложений.
Он также предоставляет интерактивную среду для итеративного исследования, проектирования и решения проблем.
Он предоставляет обширную библиотеку математических функций для линейной алгебры, статистики, анализа Фурье, фильтрации, оптимизации, численного интегрирования и решения обыкновенных дифференциальных уравнений.
Он предоставляет встроенную графику для визуализации данных и инструменты для создания пользовательских графиков.
Интерфейс программирования MATLAB предоставляет инструменты для разработки, позволяющие повысить качество сопровождения кода и максимально повысить производительность.
Он предоставляет инструменты для создания приложений с пользовательскими графическими интерфейсами.
Он предоставляет функции для интеграции алгоритмов на основе MATLAB с внешними приложениями и языками, такими как C, Java, .NET и Microsoft Excel.
Использование MATLAB
MATLAB широко используется в качестве вычислительного инструмента в науке и технике, охватывающего области физики, химии, математики и всех технических потоков. Он используется в различных областях, в том числе –
- Обработка сигналов и связь
- Обработка изображений и видео
- Системы управления
- Тест и Измерение
- Вычислительные финансы
- Вычислительная биология
MATLAB – Настройка среды
Настройка локальной среды
Настройка среды MATLAB производится в несколько кликов. Установщик можно скачать здесь .
MathWorks предоставляет лицензионный продукт, пробную версию, а также студенческую версию. Вам необходимо зайти на сайт и немного подождать их одобрения.
После загрузки установщика программное обеспечение можно установить с помощью нескольких кликов.
Понимание среды MATLAB
Среду разработки MATLAB можно запустить из иконки, созданной на рабочем столе. Основное рабочее окно в MATLAB называется рабочим столом. Когда MATLAB запущен, рабочий стол отображается в макете по умолчанию –
Рабочий стол имеет следующие панели –
-
Текущая папка – эта панель позволяет получить доступ к папкам и файлам проекта.
-
Окно команд – это основная область, где команды можно вводить в командной строке. На это указывает командная строка (>>).
-
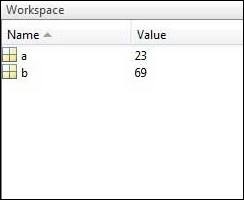
Рабочая область – Рабочая область показывает все переменные, созданные и / или импортированные из файлов.
-
История команд – эта панель показывает или возвращает команды, которые вводятся в командной строке.
Текущая папка – эта панель позволяет получить доступ к папкам и файлам проекта.
Окно команд – это основная область, где команды можно вводить в командной строке. На это указывает командная строка (>>).
Рабочая область – Рабочая область показывает все переменные, созданные и / или импортированные из файлов.
История команд – эта панель показывает или возвращает команды, которые вводятся в командной строке.
Настройка GNU Octave
Если вы хотите использовать Octave на своем компьютере (Linux, BSD, OS X или Windows), пожалуйста, скачайте последнюю версию с Download GNU Octave . Вы можете проверить данные инструкции по установке для вашей машины.
MATLAB – базовый синтаксис
Среда MATLAB ведет себя как сверхсложный калькулятор. Вы можете вводить команды в командной строке >>.
MATLAB – это интерпретируемая среда. Другими словами, вы даете команду, а MATLAB выполняет ее сразу.
Руки на практике
Введите правильное выражение, например,
Live Demo
5 + 5
И нажмите ENTER
Когда вы нажимаете кнопку «Выполнить» или нажимаете Ctrl + E, MATLAB выполняет его немедленно, и возвращается результат –
ans = 10
Давайте рассмотрим еще несколько примеров –
Live Demo
3 ^ 2 % 3 raised to the power of 2
Когда вы нажимаете кнопку «Выполнить» или нажимаете Ctrl + E, MATLAB выполняет его немедленно, и возвращается результат –
ans = 9
Другой пример,
Live Demo
sin(pi /2) % sine of angle 90 o
Когда вы нажимаете кнопку «Выполнить» или нажимаете Ctrl + E, MATLAB выполняет его немедленно, и возвращается результат –
ans = 1
Другой пример,
Live Demo
7/0 % Divide by zero
Когда вы нажимаете кнопку «Выполнить» или нажимаете Ctrl + E, MATLAB выполняет его немедленно, и возвращается результат –
ans = Inf warning: division by zero
Другой пример,
Live Demo
732 * 20.3
Когда вы нажимаете кнопку «Выполнить» или нажимаете Ctrl + E, MATLAB выполняет его немедленно, и возвращается результат –
ans = 1.4860e+04
MATLAB предоставляет некоторые специальные выражения для некоторых математических символов, таких как pi для π, Inf для ∞, i (и j) для √-1 и т. Д. Nan означает «не число».
Использование точки с запятой (;) в MATLAB
Точка с запятой (;) указывает на конец оператора. Однако, если вы хотите подавить и скрыть вывод MATLAB для выражения, добавьте точку с запятой после выражения.
Например,
Live Demo
x = 3; y = x + 5
Когда вы нажимаете кнопку «Выполнить» или нажимаете Ctrl + E, MATLAB выполняет его немедленно, и возвращается результат –
y = 8
Добавление комментариев
Символ процента (%) используется для обозначения строки комментария. Например,
x = 9 % assign the value 9 to x
Вы также можете написать блок комментариев, используя операторы комментариев к блоку% {и%}.
Редактор MATLAB включает в себя инструменты и элементы контекстного меню, которые помогут вам добавлять, удалять или изменять формат комментариев.
Обычно используемые операторы и специальные символы
MATLAB поддерживает следующие часто используемые операторы и специальные символы –
| оператор | Цель |
|---|---|
| + | Плюс; оператор сложения. |
| – | Минус; оператор вычитания. |
| * | Скалярный и матричный оператор умножения. |
| . * | Оператор умножения массива. |
| ^ | Скалярный и матричный оператор возведения в степень. |
| . ^ | Оператор возведения в степень массива. |
| Оператор левого деления. | |
| / | Оператор правого деления. |
| . | Массив левого делителя. |
| ./ | Массив оператора правого деления. |
| : | Двоеточие; генерирует регулярно расположенные элементы и представляет всю строку или столбец. |
| () | Скобки; заключает в себе аргументы функций и индексы массивов; переопределяет приоритет |
| [] | Скобки; элементы массива вложений. |
| , | Десятичная точка. |
| … | Многоточие; оператор продолжения строки |
| , | Comma; разделяет операторы и элементы подряд |
| ; | Точка с запятой; разделяет столбцы и подавляет отображение. |
| % | Знак процента; обозначает комментарий и задает форматирование. |
| _ | Цитировать знак и транспонировать оператора. |
| ._ | Несопряженный оператор транспонирования. |
| знак равно | Оператор присваивания. |
Специальные переменные и константы
MATLAB поддерживает следующие специальные переменные и константы –
| название | Имея в виду |
|---|---|
| анс | Самый последний ответ. |
| прибыль на акцию | Точность точности с плавающей точкой. |
| I, J | Мнимая единица √-1. |
| Inf | Бесконечность. |
| NaN | Неопределенный числовой результат (не число). |
| число Пи | Число π |
Именование переменных
Имена переменных состоят из буквы, за которой следует любое количество букв, цифр или подчеркивания.
MATLAB чувствителен к регистру .
Имена переменных могут быть любой длины, однако MATLAB использует только первые N символов, где N задается функцией namelengthmax .
Сохранение вашей работы
Команда save используется для сохранения всех переменных в рабочей области в виде файла с расширением .mat в текущем каталоге.
Например,
save myfile
Вы можете перезагрузить файл в любое время позже, используя команду загрузки .
load myfile
MATLAB – Переменные
В среде MATLAB каждая переменная является массивом или матрицей.
Вы можете назначить переменные простым способом. Например,
Live Demo
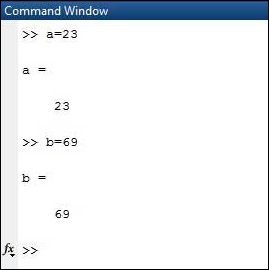
x = 3 % defining x and initializing it with a value
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
x = 3
Он создает матрицу 1 на 1 с именем x и сохраняет значение 3 в своем элементе. Давайте посмотрим на другой пример,
Live Demo
x = sqrt(16) % defining x and initializing it with an expression
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
x = 4
Пожалуйста, обратите внимание, что –
-
Как только переменная введена в систему, вы можете обратиться к ней позже.
-
Переменные должны иметь значения, прежде чем они будут использованы.
-
Когда выражение возвращает результат, который не присвоен какой-либо переменной, система назначает его переменной с именем ans, которая может быть использована позже.
Как только переменная введена в систему, вы можете обратиться к ней позже.
Переменные должны иметь значения, прежде чем они будут использованы.
Когда выражение возвращает результат, который не присвоен какой-либо переменной, система назначает его переменной с именем ans, которая может быть использована позже.
Например,
Live Demo
sqrt(78)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 8.8318
Вы можете использовать эту переменную ANS –
Live Demo
sqrt(78); 9876/ans
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 1118.2
Давайте посмотрим на другой пример –
Live Demo
x = 7 * 8; y = x * 7.89
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
y = 441.84
Несколько назначений
Вы можете иметь несколько назначений на одной строке. Например,
Live Demo
a = 2; b = 7; c = a * b
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
c = 14
Я забыл переменные!
Команда who отображает все имена переменных, которые вы использовали.
who
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Your variables are: a ans b c
Команда whos показывает немного больше о переменных –
- Переменные в настоящее время в памяти
- Тип каждой переменной
- Память, выделенная для каждой переменной
- Являются ли они сложными переменными или нет
whos
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Attr Name Size Bytes Class ==== ==== ==== ==== ===== a 1x1 8 double ans 1x70 757 cell b 1x1 8 double c 1x1 8 double Total is 73 elements using 781 bytes
Команда очистки удаляет все (или указанные) переменные из памяти.
clear x % it will delete x, won't display anything
clear % it will delete all variables in the workspace
% peacefully and unobtrusively
Длинные Задания
Длинные назначения могут быть расширены до другой строки с помощью эллипсов (…). Например,
Live Demo
initial_velocity = 0; acceleration = 9.8; time = 20; final_velocity = initial_velocity + acceleration * time
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
final_velocity = 196
Формат Команда
По умолчанию MATLAB отображает числа с четырьмя знаками после запятой. Это известно как короткий формат .
Однако, если вы хотите большей точности, вам нужно использовать команду форматирования .
Команда format long отображает 16 цифр после десятичной дроби.
Например –
Live Demo
format long x = 7 + 10/3 + 5 ^ 1.2
MATLAB выполнит приведенный выше оператор и вернет следующий результат:
x = 17.2319816406394
Другой пример,
Live Demo
format short x = 7 + 10/3 + 5 ^ 1.2
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
x = 17.232
Команда формата банка округляет числа до двух десятичных знаков. Например,
Live Demo
format bank daily_wage = 177.45; weekly_wage = daily_wage * 6
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
weekly_wage = 1064.70
MATLAB отображает большие числа с использованием экспоненциальной записи.
Команда format short e позволяет отображать в экспоненциальной форме с четырьмя десятичными знаками плюс показатель степени.
Например,
Live Demo
format short e 4.678 * 4.9
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 2.2922e+01
Команда format long e позволяет отображать в экспоненциальной форме с четырьмя десятичными знаками плюс показатель степени. Например,
Live Demo
format long e x = pi
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
x = 3.141592653589793e+00
Команда format rat дает наиболее близкое рациональное выражение, полученное в результате вычисления. Например,
Live Demo
format rat 4.678 * 4.9
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 34177/1491
Создание векторов
Вектор – это одномерный массив чисел. MATLAB позволяет создавать два типа векторов –
- Векторы строк
- Векторы столбцов
Векторы строк создаются путем заключения набора элементов в квадратных скобках с использованием пробела или запятой для разделения элементов.
Например,
Live Demo
r = [7 8 9 10 11]
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
r = 7 8 9 10 11
Другой пример,
Live Demo
r = [7 8 9 10 11]; t = [2, 3, 4, 5, 6]; res = r + t
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
res =
9 11 13 15 17
Векторы столбцов создаются заключением набора элементов в квадратные скобки с использованием точки с запятой (;) для разделения элементов.
Live Demo
c = [7; 8; 9; 10; 11]
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
c =
7
8
9
10
11
Создание Матрицы
Матрица – это двумерный массив чисел.
В MATLAB матрица создается путем ввода каждой строки в виде последовательности элементов, разделенных пробелами или запятыми, и конец строки обозначается точкой с запятой. Например, давайте создадим матрицу 3 на 3 как –
Live Demo
m = [1 2 3; 4 5 6; 7 8 9]
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
m =
1 2 3
4 5 6
7 8 9
MATLAB – Команды
MATLAB – интерактивная программа для численных расчетов и визуализации данных. Вы можете ввести команду, набрав ее в командной строке MATLAB ‘>>’ в окне команд .
В этом разделе мы предоставим списки часто используемых общих команд MATLAB.
Команды для управления сеансом
MATLAB предоставляет различные команды для управления сеансом. В следующей таблице приведены все такие команды:
| команда | Цель |
|---|---|
| CLC | Очищает командное окно. |
| Чисто | Удаляет переменные из памяти. |
| существовать | Проверяет наличие файла или переменной. |
| Глобальный | Объявляет переменные глобальными. |
| Помогите | Ищет справочную тему. |
| Ищу | Поиск записей справки по ключевому слову. |
| уволиться | Останавливается MATLAB. |
| кто | Перечисляет текущие переменные. |
| Whos | Перечисляет текущие переменные (длинный дисплей). |
Команды для работы с системой
MATLAB предоставляет различные полезные команды для работы с системой, такие как сохранение текущей работы в рабочей области в виде файла и загрузка файла позже.
Он также предоставляет различные команды для других действий, связанных с системой, таких как отображение даты, отображение списка файлов в каталоге, отображение текущего каталога и т. Д.
В следующей таблице приведены некоторые часто используемые системные команды:
| команда | Цель |
|---|---|
| CD | Изменяет текущий каталог. |
| Дата | Отображает текущую дату. |
| удалять | Удаляет файл. |
| дневник | Включает / выключает запись в дневниковый файл. |
| реж | Перечисляет все файлы в текущем каталоге. |
| нагрузка | Загружает переменные рабочей области из файла. |
| дорожка | Отображает путь поиска. |
| PWD | Отображает текущий каталог. |
| спасти | Сохраняет переменные рабочей области в файл. |
| тип | Отображает содержимое файла. |
| какие | Перечисляет все файлы MATLAB в текущем каталоге. |
| wklread | Читает файл электронной таблицы .wk1. |
Команды ввода и вывода
MATLAB предоставляет следующие команды ввода и вывода –
| команда | Цель |
|---|---|
| Индик.точки | Отображает содержимое массива или строки. |
| fscanf | Чтение отформатированных данных из файла. |
| формат | Управляет форматом отображения экрана. |
| fprintf | Выполняет отформатированные записи на экран или в файл. |
| вход | Отображает подсказки и ждет ввода. |
| ; | Подавляет трафаретную печать. |
Команды fscanf и fprintf ведут себя как функции C scanf и printf. Они поддерживают следующие коды формата –
| Код формата | Цель |
|---|---|
| % s | Форматировать как строку. |
| % d | Форматировать как целое число. |
| % е | Формат как значение с плавающей запятой. |
| % е | Формат как значение с плавающей запятой в научной нотации. |
| %г | Формат в наиболее компактной форме:% f или% e. |
| п | Вставьте новую строку в выходную строку. |
| т | Вставьте вкладку в выходной строке. |
Функция форматирования имеет следующие формы, используемые для числового отображения:
| Функция формата | Отображать до |
|---|---|
| формат короткий | Четыре десятичных знака (по умолчанию). |
| форматировать долго | 16 десятичных цифр. |
| формат короткой электронной | Пять цифр плюс показатель степени. |
| формат длинная электронная | 16 цифр плюс показатели. |
| формат банка | Две десятичные цифры. |
| формат + | Положительный, отрицательный или ноль. |
| формат крыса | Рациональное приближение. |
| формат компактный | Подавляет некоторые переводы строки. |
| свободный формат | Сбрасывает в менее компактный режим отображения. |
Векторные, матричные и матричные команды
В следующей таблице показаны различные команды, используемые для работы с массивами, матрицами и векторами.
| команда | Цель |
|---|---|
| кошка | Объединяет массивы. |
| находить | Находит индексы ненулевых элементов. |
| длина | Вычисляет количество элементов. |
| LINSPACE | Создает равномерно расположенный вектор. |
| logspace | Создает логарифмически разнесенный вектор. |
| Максимум | Возвращает самый большой элемент. |
| мин | Возвращает наименьший элемент. |
| тычок | Продукт каждого столбца. |
| перекроить | Изменяет размер. |
| размер | Вычисляет размер массива. |
| Сортировать | Сортирует каждый столбец. |
| сумма | Суммирует каждый столбец. |
| глаз | Создает идентичную матрицу. |
| те, | Создает массив из них. |
| нули | Создает массив нулей. |
| пересекать | Вычисляет матричные перекрестные произведения. |
| точка | Вычисляет матричные точечные произведения. |
| йе | Вычисляет определитель массива. |
| фактура | Вычисляет обратную матрицу. |
| pinv | Вычисляет псевдообратную матрицу. |
| ранг | Вычисляет ранг матрицы. |
| RREF | Вычисляет приведенную форму ряда эшелонов. |
| клетка | Создает массив ячеек. |
| celldisp | Отображает массив ячеек. |
| cellplot | Отображает графическое представление массива ячеек. |
| num2cell | Преобразует числовой массив в массив ячеек. |
| по рукам | Соответствует спискам ввода и вывода. |
| iscell | Определяет массив ячеек. |
Команды построения
MATLAB предоставляет многочисленные команды для построения графиков. В следующей таблице приведены некоторые из наиболее часто используемых команд для построения графиков:
| команда | Цель |
|---|---|
| ось | Устанавливает пределы оси. |
| fplot | Интеллектуальное построение функций. |
| сетка | Отображает линии сетки. |
| сюжет | Создает график xy. |
| Распечатать | Печать графика или сохранение графика в файл. |
| заглавие | Размещает текст в верхней части сюжета. |
| xlabel | Добавляет текстовую метку к оси X. |
| ylabel | Добавляет текстовую метку к оси Y. |
| оси | Создает объекты осей. |
| близко | Закрывает текущий сюжет. |
| закрыть все | Закрывает все участки. |
| фигура | Открывает новое окно фигуры. |
| gtext | Включает размещение метки с помощью мыши. |
| держать | Замораживает текущий сюжет. |
| легенда | Размещение легенды мышью. |
| обновление | Перерисовывает текущее окно рисунка. |
| задавать | Определяет свойства объектов, таких как оси. |
| подзаговор | Создает участки в подокнах. |
| текст | Размещает строку на рисунке. |
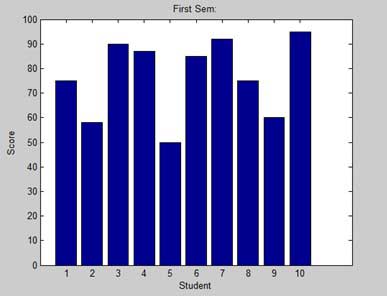
| бар | Создает гистограмму. |
| loglog | Создает лог-лог сюжет. |
| полярный | Создает полярный сюжет. |
| semilogx | Создает полулогичный сюжет. (логарифмическая абсцисса). |
| semilogy | Создает полулогичный сюжет. (логарифмическая ордината). |
| лестница | Создает лестничный участок. |
| стебель | Создает стволовый сюжет. |
MATLAB – M-Files
До сих пор мы использовали среду MATLAB в качестве калькулятора. Тем не менее, MATLAB также является мощным языком программирования, а также интерактивной вычислительной средой.
В предыдущих главах вы узнали, как вводить команды из командной строки MATLAB. MATLAB также позволяет записывать серии команд в файл и исполнять файл как единое целое, например, писать функцию и вызывать ее.
М-файлы
MATLAB позволяет писать два вида программных файлов –
-
Скрипты – файлы скриптов – это программные файлы с расширением .m . В этих файлах вы пишете серию команд, которые вы хотите выполнить вместе. Скрипты не принимают входные данные и не возвращают никаких выходных данных. Они оперируют данными в рабочей области.
-
Функции – файлы функций также являются программными файлами с расширением .m . Функции могут принимать входные и выходные данные. Внутренние переменные являются локальными для функции.
Скрипты – файлы скриптов – это программные файлы с расширением .m . В этих файлах вы пишете серию команд, которые вы хотите выполнить вместе. Скрипты не принимают входные данные и не возвращают никаких выходных данных. Они оперируют данными в рабочей области.
Функции – файлы функций также являются программными файлами с расширением .m . Функции могут принимать входные и выходные данные. Внутренние переменные являются локальными для функции.
Вы можете использовать редактор MATLAB или любой другой текстовый редактор для создания ваших .m файлов. В этом разделе мы обсудим файлы сценариев. Файл сценария содержит несколько последовательных строк команд MATLAB и вызовов функций. Вы можете запустить скрипт, набрав его имя в командной строке.
Создание и запуск файла скрипта
Для создания файлов скриптов вам необходимо использовать текстовый редактор. Вы можете открыть редактор MATLAB двумя способами:
- Использование командной строки
- Использование IDE
Если вы используете командную строку, введите edit в командной строке. Это откроет редактор. Вы можете напрямую ввести edit и затем имя файла (с расширением .m)
edit Or edit <filename>
Приведенная выше команда создаст файл в директории MATLAB по умолчанию. Если вы хотите сохранить все программные файлы в определенной папке, вам придется указать полный путь.
Давайте создадим папку с именем progs. Введите следующие команды в командной строке (>>) –
mkdir progs % create directory progs under default directory chdir progs % changing the current directory to progs edit prog1.m % creating an m file named prog1.m
Если вы создаете файл в первый раз, MATLAB предложит вам подтвердить его. Нажмите Да.
В качестве альтернативы, если вы используете IDE, выберите NEW -> Script. Это также открывает редактор и создает файл с именем Untitled. Вы можете назвать и сохранить файл после ввода кода.
Введите следующий код в редакторе –
Live Demo
NoOfStudents = 6000; TeachingStaff = 150; NonTeachingStaff = 20; Total = NoOfStudents + TeachingStaff ... + NonTeachingStaff; disp(Total);
После создания и сохранения файла вы можете запустить его двумя способами:
-
Нажав кнопку « Выполнить» в окне редактора или
-
Просто введите имя файла (без расширения) в командной строке: >> prog1
Нажав кнопку « Выполнить» в окне редактора или
Просто введите имя файла (без расширения) в командной строке: >> prog1
В командной строке отображается результат –
6170
пример
Создайте файл сценария и введите следующий код –
Live Demo
a = 5; b = 7; c = a + b d = c + sin(b) e = 5 * d f = exp(-d)
Когда приведенный выше код компилируется и выполняется, он дает следующий результат –
c = 12 d = 12.657 e = 63.285 f = 3.1852e-06
MATLAB – Типы данных
MATLAB не требует никакого объявления типа или операторов измерения. Всякий раз, когда MATLAB встречает новое имя переменной, он создает переменную и выделяет соответствующее пространство памяти.
Если переменная уже существует, то MATLAB заменяет исходный контент новым контентом и выделяет новое место для хранения, где это необходимо.
Например,
Total = 42
Вышеприведенный оператор создает матрицу 1 на 1 с именем «Total» и сохраняет в ней значение 42.
Типы данных, доступные в MATLAB
MATLAB предоставляет 15 основных типов данных. Каждый тип данных хранит данные в форме матрицы или массива. Размер этой матрицы или массива составляет минимум 0 на 0, и это может увеличиться до матрицы или массива любого размера.
В следующей таблице приведены наиболее часто используемые типы данных в MATLAB.
| Sr.No. | Тип данных и описание |
|---|---|
| 1 |
int8 8-разрядное целое число со знаком |
| 2 |
uint8 8-битное целое число без знака |
| 3 |
int16 16-разрядное целое число со знаком |
| 4 |
uint16 16-разрядное целое число без знака |
| 5 |
int32 32-разрядное целое число со знаком |
| 6 |
uint32 32-разрядное целое число без знака |
| 7 |
int64 64-разрядное целое число со знаком |
| 8 |
uint64 64-разрядное целое число без знака |
| 9 |
не замужем числовые данные одинарной точности |
| 10 |
двойной числовые данные двойной точности |
| 11 |
логический логические значения 1 или 0, представляют истину и ложь соответственно |
| 12 |
голец символьные данные (строки хранятся как вектор символов) |
| 13 |
массив ячеек массив индексированных ячеек, каждая из которых может хранить массив другого измерения и типа данных |
| 14 |
состав C-подобные структуры, каждая структура имеет именованные поля, способные хранить массив другого измерения и типа данных |
| 15 |
ручка функции указатель на функцию |
| 16 |
пользовательские классы объекты, созданные из определенного пользователем класса |
| 17 |
Java-классы объекты, построенные из класса Java |
int8
8-разрядное целое число со знаком
uint8
8-битное целое число без знака
int16
16-разрядное целое число со знаком
uint16
16-разрядное целое число без знака
int32
32-разрядное целое число со знаком
uint32
32-разрядное целое число без знака
int64
64-разрядное целое число со знаком
uint64
64-разрядное целое число без знака
не замужем
числовые данные одинарной точности
двойной
числовые данные двойной точности
логический
логические значения 1 или 0, представляют истину и ложь соответственно
голец
символьные данные (строки хранятся как вектор символов)
массив ячеек
массив индексированных ячеек, каждая из которых может хранить массив другого измерения и типа данных
состав
C-подобные структуры, каждая структура имеет именованные поля, способные хранить массив другого измерения и типа данных
ручка функции
указатель на функцию
пользовательские классы
объекты, созданные из определенного пользователем класса
Java-классы
объекты, построенные из класса Java
пример
Создайте файл сценария со следующим кодом –
Live Demo
str = 'Hello World!' n = 2345 d = double(n) un = uint32(789.50) rn = 5678.92347 c = int32(rn)
Когда приведенный выше код компилируется и выполняется, он дает следующий результат –
str = Hello World! n = 2345 d = 2345 un = 790 rn = 5678.9 c = 5679
Преобразование типов данных
MATLAB предоставляет различные функции для преобразования значения из одного типа данных в другой. В следующей таблице приведены функции преобразования типов данных –
| функция | Цель |
|---|---|
| голец | Преобразовать в массив символов (строку) |
| int2str | Преобразовать целочисленные данные в строку |
| mat2str | Преобразовать матрицу в строку |
| num2str | Преобразовать число в строку |
| str2double | Преобразовать строку в значение двойной точности |
| str2num | Преобразовать строку в число |
| native2unicode | Преобразуйте числовые байты в символы Юникода |
| unicode2native | Преобразование символов Юникода в числовые байты |
| base2dec | Преобразовать базовую N числовую строку в десятичное число |
| BIN2DEC | Преобразовать строку двоичного числа в десятичное число |
| dec2base | Преобразовать десятичное число в базовое число N в строке |
| DEC2BIN | Преобразовать десятичное число в двоичное число в строке |
| DEC2HEX | Преобразовать десятичное число в шестнадцатеричное число в строке |
| HEX2DEC | Преобразовать строку шестнадцатеричного числа в десятичное число |
| hex2num | Преобразовать строку шестнадцатеричного числа в число с двойной точностью |
| num2hex | Преобразование одинарных и двойных символов в шестнадцатеричные строки IEEE |
| cell2mat | Преобразовать массив ячеек в числовой массив |
| cell2struct | Преобразовать массив ячеек в массив структур |
| cellstr | Создать массив строк из массива символов |
| mat2cell | Конвертировать массив в массив ячеек с потенциально разными размерами ячеек |
| num2cell | Преобразовать массив в массив ячеек с ячейками одинакового размера |
| struct2cell | Преобразовать структуру в массив ячеек |
Определение типов данных
MATLAB предоставляет различные функции для определения типа данных переменной.
В следующей таблице приведены функции для определения типа данных переменной –
| функция | Цель |
|---|---|
| является | Определить состояние |
| это | Определите, является ли ввод объектом указанного класса |
| iscell | Определите, является ли ввод массивом ячеек |
| iscellstr | Определите, является ли ввод массивом строк |
| ischar | Определить, является ли элемент массивом символов |
| isfield | Определите, является ли входное поле структурным массивом |
| isfloat | Определите, является ли ввод массивом с плавающей точкой |
| ishghandle | Истинно для дескрипторов объектов Handle Graphics |
| isinteger | Определите, является ли ввод целочисленным массивом |
| isjava | Определите, является ли ввод Java-объектом |
| ISLOGICAL | Определите, является ли ввод логическим массивом |
| IsNumeric | Определите, является ли ввод числовым массивом |
| IsObject | Определите, является ли ввод объектом MATLAB |
| реально | Проверьте, является ли входной массив реальным |
| isscalar | Определите, является ли вход скалярным |
| isstr | Определите, является ли ввод символьным массивом |
| isstruct | Определите, является ли ввод структурным массивом |
| isvector | Определите, является ли входной вектор |
| учебный класс | Определить класс объекта |
| validateattributes | Проверьте правильность массива |
| Whos | Перечислите переменные в рабочей области, с размерами и типами |
пример
Создайте файл сценария со следующим кодом –
Live Demo
x = 3 isinteger(x) isfloat(x) isvector(x) isscalar(x) isnumeric(x) x = 23.54 isinteger(x) isfloat(x) isvector(x) isscalar(x) isnumeric(x) x = [1 2 3] isinteger(x) isfloat(x) isvector(x) isscalar(x) x = 'Hello' isinteger(x) isfloat(x) isvector(x) isscalar(x) isnumeric(x)
Когда вы запускаете файл, он дает следующий результат –
x = 3
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x = 23.540
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x =
1 2 3
ans = 0
ans = 1
ans = 1
ans = 0
x = Hello
ans = 0
ans = 0
ans = 1
ans = 0
ans = 0
MATLAB – Операторы
Оператор – это символ, который указывает компилятору выполнять определенные математические или логические манипуляции. MATLAB предназначен для работы преимущественно с целыми матрицами и массивами. Следовательно, операторы в MATLAB работают как со скалярными, так и нескалярными данными. MATLAB допускает следующие виды элементарных операций –
- Арифметические Операторы
- Операторы отношений
- Логические Операторы
- Побитовые операции
- Операции над множествами
Арифметические Операторы
MATLAB допускает два различных типа арифметических операций –
- Матричные арифметические операции
- Массив арифметических операций
Матричные арифметические операции аналогичны определенным в линейной алгебре. Операции с массивами выполняются поэлементно, как в одномерном, так и в многомерном массиве.
Матричные операторы и операторы массива дифференцируются символом точки (.). Однако, поскольку операция сложения и вычитания одинакова для матриц и массивов, оператор одинаков для обоих случаев. Следующая таблица дает краткое описание операторов –
Показать примеры
| Sr.No. | Оператор и описание |
|---|---|
| 1 |
+ Дополнение или унарный плюс. A + B добавляет значения, хранящиеся в переменных A и B. A и B должны иметь одинаковый размер, если только один не является скаляром. Скаляр можно добавить в матрицу любого размера. |
| 2 |
– Вычитание или унарный минус. AB вычитает значение B из A. A и B должны иметь одинаковый размер, если только он не является скаляром. Скаляр можно вычесть из матрицы любого размера. |
| 3 |
* Матричное умножение. C = A * B – линейное алгебраическое произведение матриц A и B. Точнее, Для нескалярных A и B число столбцов в A должно быть равно количеству строк в B. Скаляр может умножить матрицу любого размера. |
| 4 |
. * Умножение массивов. A. * B – это поэлементное произведение массивов A и B. A и B должны иметь одинаковый размер, если только один из них не является скаляром. |
| 5 |
/ Косая черта или матрица правого деления. B / A примерно такой же, как B * inv (A). Точнее, B / A = (A ‘ B’) ‘. |
| 6 |
./ Массив правого деления. A./B – матрица с элементами A (i, j) / B (i, j). A и B должны иметь одинаковый размер, если только один из них не является скаляром. |
| 7 |
Обратная косая черта или матрица левого деления. Если A – квадратная матрица, A B – примерно то же самое, что inv (A) * B, за исключением того, что она вычисляется другим способом. Если A является матрицей n-на-n и B является вектором столбцов с n компонентами, или матрицей с несколькими такими столбцами, то X = A B является решением уравнения AX = B. Предупреждающее сообщение отображается, если А плохо масштабировано или почти единственное число. |
| 8 |
. Массив покинул деление. A. B – матрица с элементами B (i, j) / A (i, j). A и B должны иметь одинаковый размер, если только один из них не является скаляром. |
| 9 |
^ Матрица власти. X ^ p есть X в степени p, если p скаляр. Если p является целым числом, мощность вычисляется путем повторного возведения в квадрат. Если целое число отрицательно, X инвертируется первым. Для других значений p в расчет включаются собственные значения и собственные векторы, например, если [V, D] = eig (X), то X ^ p = V * D. ^ p / V. |
| 10 |
. ^ Массив власти. A. ^ B – это матрица с элементами A (i, j) степени B (i, j). A и B должны иметь одинаковый размер, если только один из них не является скаляром. |
| 11 |
‘ Матрица транспонировать. A ‘- линейная алгебраическая транспонирование A. Для комплексных матриц это комплексная сопряженная транспонирование. |
| 12 |
«. Массив транспонировать. A.» это транспонирование массива A. Для сложных матриц это не связано с сопряжением. |
+
Дополнение или унарный плюс. A + B добавляет значения, хранящиеся в переменных A и B. A и B должны иметь одинаковый размер, если только один не является скаляром. Скаляр можно добавить в матрицу любого размера.
–
Вычитание или унарный минус. AB вычитает значение B из A. A и B должны иметь одинаковый размер, если только он не является скаляром. Скаляр можно вычесть из матрицы любого размера.
*
Матричное умножение. C = A * B – линейное алгебраическое произведение матриц A и B. Точнее,
Для нескалярных A и B число столбцов в A должно быть равно количеству строк в B. Скаляр может умножить матрицу любого размера.
. *
Умножение массивов. A. * B – это поэлементное произведение массивов A и B. A и B должны иметь одинаковый размер, если только один из них не является скаляром.
/
Косая черта или матрица правого деления. B / A примерно такой же, как B * inv (A). Точнее, B / A = (A ‘ B’) ‘.
./
Массив правого деления. A./B – матрица с элементами A (i, j) / B (i, j). A и B должны иметь одинаковый размер, если только один из них не является скаляром.
Обратная косая черта или матрица левого деления. Если A – квадратная матрица, A B – примерно то же самое, что inv (A) * B, за исключением того, что она вычисляется другим способом. Если A является матрицей n-на-n и B является вектором столбцов с n компонентами, или матрицей с несколькими такими столбцами, то X = A B является решением уравнения AX = B. Предупреждающее сообщение отображается, если А плохо масштабировано или почти единственное число.
.
Массив покинул деление. A. B – матрица с элементами B (i, j) / A (i, j). A и B должны иметь одинаковый размер, если только один из них не является скаляром.
^
Матрица власти. X ^ p есть X в степени p, если p скаляр. Если p является целым числом, мощность вычисляется путем повторного возведения в квадрат. Если целое число отрицательно, X инвертируется первым. Для других значений p в расчет включаются собственные значения и собственные векторы, например, если [V, D] = eig (X), то X ^ p = V * D. ^ p / V.
. ^
Массив власти. A. ^ B – это матрица с элементами A (i, j) степени B (i, j). A и B должны иметь одинаковый размер, если только один из них не является скаляром.
‘
Матрица транспонировать. A ‘- линейная алгебраическая транспонирование A. Для комплексных матриц это комплексная сопряженная транспонирование.
«.
Массив транспонировать. A.» это транспонирование массива A. Для сложных матриц это не связано с сопряжением.
Операторы отношений
Реляционные операторы также могут работать как со скалярными, так и с нескалярными данными. Реляционные операторы для массивов выполняют поэлементное сравнение двух массивов и возвращают логический массив одинакового размера с элементами, установленными в логическое 1 (истина), где отношение истинно, и элементами, установленными в логическое 0 (ложь), где оно не.
В следующей таблице показаны реляционные операторы, доступные в MATLAB.
Показать примеры
| Sr.No. | Оператор и описание |
|---|---|
| 1 |
< Меньше, чем |
| 2 |
<= Меньше или равно |
| 3 |
> Лучше чем |
| 4 |
> = Больше или равно |
| 5 |
== Равно |
| 6 |
~ = Не равно |
<
Меньше, чем
<=
Меньше или равно
>
Лучше чем
> =
Больше или равно
==
Равно
~ =
Не равно
Логические Операторы
MATLAB предлагает два типа логических операторов и функций –
-
Поэлементный – Эти операторы работают с соответствующими элементами логических массивов.
-
Короткое замыкание – эти операторы работают со скалярными и логическими выражениями.
Поэлементный – Эти операторы работают с соответствующими элементами логических массивов.
Короткое замыкание – эти операторы работают со скалярными и логическими выражениями.
Поэлементные логические операторы работают поэлементно на логических массивах. Символы &, | и ~ являются операторами логических массивов И, ИЛИ и НЕ.
Логические операторы короткого замыкания допускают короткое замыкание на логических операциях. Символы && и || являются логическими операторами короткого замыкания И и ИЛИ.
Показать примеры
Побитовые операции
Битовые операторы работают с битами и выполняют побитовые операции. Таблицы истинности для &, | и ^ следующие:
| п | Q | P & Q | р | Q | р ^ д |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
Предположим, если А = 60; и B = 13; Теперь в двоичном формате они будут выглядеть следующим образом –
A = 0011 1100
B = 0000 1101
—————–
A & B = 0000 1100
A | B = 0011 1101
A ^ B = 0011 0001
~ A = 1100 0011
MATLAB предоставляет различные функции для побитовых операций, таких как «побитовое и», «побитовое или» и «побитовое не», операция сдвига и т. Д.
В следующей таблице приведены часто используемые побитовые операции –
Показать примеры
| функция | Цель |
|---|---|
| Битанд (а, б) | Побитовое И целых чисел А и В |
| bitcmp (а) | Побитовое дополнение |
| BITGET (а, позы) | Получить бит в указанной позиции pos , в целочисленном массиве a |
| битор (а, б) | Побитовое ИЛИ целых чисел a и b |
| bitset (a, pos) | Установить бит в определенном месте поз |
| битное смещение (а, к) | Возвращает смещение влево на k бит, что эквивалентно умножению на 2 k . Отрицательные значения k соответствуют сдвигу битов вправо или делению на 2 | k | и округление до ближайшего целого числа в сторону отрицательного бесконечного. Все биты переполнения усекаются. |
| битксор (а, б) | Побитовое XOR целых чисел a и b |
| swapbytes | Порядок замены байт |
Операции над множествами
MATLAB предоставляет различные функции для операций над множествами, такие как объединение, пересечение и тестирование для множества множеств и т. Д.
В следующей таблице приведены некоторые часто используемые операции над множествами:
Показать примеры
| Sr.No. | Описание функции |
|---|---|
| 1 |
пересекаются (А, В) Установить пересечение двух массивов; возвращает значения, общие для A и B. Возвращаемые значения находятся в отсортированном порядке. |
| 2 |
пересекаются (A, B, ‘строки’) Обрабатывает каждую строку A и каждую строку B как отдельные объекты и возвращает строки, общие как для A, так и для B. Строки возвращенной матрицы расположены в отсортированном порядке. |
| 3 |
IsMember (А, В) Возвращает массив того же размера, что и A, содержащий 1 (true), где элементы A находятся в B. В других местах он возвращает 0 (false). |
| 4 |
IsMember (A, B, ‘строк’) Обрабатывает каждую строку A и каждую строку B как отдельные объекты и возвращает вектор, содержащий 1 (true), где строки матрицы A также являются строками B. В другом месте возвращается 0 (false). |
| 5 |
issorted (А) Возвращает логическое 1 (истина), если элементы A расположены в отсортированном порядке, и логическое 0 (ложь) в противном случае. Вход A может быть вектором или массивом строк размером 1 на 1 или 1 на N. A считается отсортированным, если A и выходные данные сортировки (A) равны. |
| 6 |
issorted (A, ‘row’) Возвращает логическое 1 (истина), если строки двумерной матрицы A расположены в отсортированном порядке, и логическое 0 (ложь) в противном случае. Матрица A считается отсортированной, если A и выходные данные sortrows (A) равны. |
| 7 |
setdiff (А, В) Устанавливает разницу двух массивов; возвращает значения в A, которых нет в B. Значения в возвращенном массиве расположены в отсортированном порядке. |
| 8 |
setdiff (А, В, ‘строк’) Обрабатывает каждую строку A и каждую строку B как отдельные объекты и возвращает строки из A, которых нет в B. Строки возвращенной матрицы расположены в отсортированном порядке. Опция ‘rows’ не поддерживает массивы ячеек. |
| 9 |
setxor Устанавливает эксклюзивное ИЛИ из двух массивов |
| 10 |
союз Устанавливает объединение двух массивов |
| 11 |
уникальный Уникальные значения в массиве |
пересекаются (А, В)
Установить пересечение двух массивов; возвращает значения, общие для A и B. Возвращаемые значения находятся в отсортированном порядке.
пересекаются (A, B, ‘строки’)
Обрабатывает каждую строку A и каждую строку B как отдельные объекты и возвращает строки, общие как для A, так и для B. Строки возвращенной матрицы расположены в отсортированном порядке.
IsMember (А, В)
Возвращает массив того же размера, что и A, содержащий 1 (true), где элементы A находятся в B. В других местах он возвращает 0 (false).
IsMember (A, B, ‘строк’)
Обрабатывает каждую строку A и каждую строку B как отдельные объекты и возвращает вектор, содержащий 1 (true), где строки матрицы A также являются строками B. В другом месте возвращается 0 (false).
issorted (А)
Возвращает логическое 1 (истина), если элементы A расположены в отсортированном порядке, и логическое 0 (ложь) в противном случае. Вход A может быть вектором или массивом строк размером 1 на 1 или 1 на N. A считается отсортированным, если A и выходные данные сортировки (A) равны.
issorted (A, ‘row’)
Возвращает логическое 1 (истина), если строки двумерной матрицы A расположены в отсортированном порядке, и логическое 0 (ложь) в противном случае. Матрица A считается отсортированной, если A и выходные данные sortrows (A) равны.
setdiff (А, В)
Устанавливает разницу двух массивов; возвращает значения в A, которых нет в B. Значения в возвращенном массиве расположены в отсортированном порядке.
setdiff (А, В, ‘строк’)
Обрабатывает каждую строку A и каждую строку B как отдельные объекты и возвращает строки из A, которых нет в B. Строки возвращенной матрицы расположены в отсортированном порядке.
Опция ‘rows’ не поддерживает массивы ячеек.
setxor
Устанавливает эксклюзивное ИЛИ из двух массивов
союз
Устанавливает объединение двух массивов
уникальный
Уникальные значения в массиве
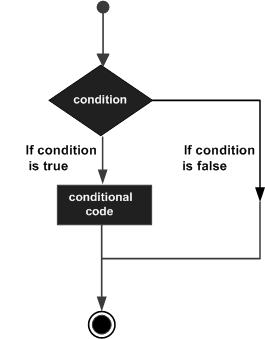
MATLAB – принятие решений
Структуры принятия решений требуют, чтобы программист указал одно или несколько условий, которые должны быть оценены или протестированы программой, вместе с оператором или инструкциями, которые должны быть выполнены, если условие определено как истинное, и, необязательно, другие операторы, которые должны быть выполнены, если условие определяется как ложное.
Ниже приводится общая форма типичной структуры принятия решений, встречающейся в большинстве языков программирования.
MATLAB предоставляет следующие типы заявлений о принятии решений. Нажмите на следующие ссылки, чтобы проверить их детали –
| Sr.No. | Заявление и описание |
|---|---|
| 1 | if … end
Оператор if … end состоит из логического выражения, за которым следует один или несколько операторов. |
| 2 | если … еще … конец заявления
За оператором if может следовать необязательный оператор else , который выполняется, когда логическое выражение имеет значение false. |
| 3 | Если … elseif … elseif … else … конец заявления
За оператором if может следовать один (или несколько) необязательных elseif … и оператор else , что очень полезно для проверки различных условий. |
| 4 | вложенные операторы if
Вы можете использовать один оператор if или elseif внутри другого оператора if или elseif . |
| 5 | заявление о переключении
Оператор switch позволяет проверять переменную на соответствие списку значений. |
| 6 | вложенные операторы switch
Вы можете использовать один оператор switch внутри другого оператора (ов) switch . |
Оператор if … end состоит из логического выражения, за которым следует один или несколько операторов.
За оператором if может следовать необязательный оператор else , который выполняется, когда логическое выражение имеет значение false.
За оператором if может следовать один (или несколько) необязательных elseif … и оператор else , что очень полезно для проверки различных условий.
Вы можете использовать один оператор if или elseif внутри другого оператора if или elseif .
Оператор switch позволяет проверять переменную на соответствие списку значений.
Вы можете использовать один оператор switch внутри другого оператора (ов) switch .
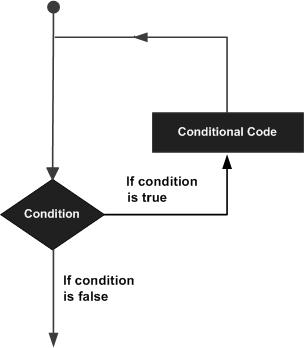
MATLAB – Типы петель
Может возникнуть ситуация, когда вам нужно выполнить блок кода несколько раз. Как правило, операторы выполняются последовательно. Первый оператор в функции выполняется первым, затем следует второй и так далее.
Языки программирования предоставляют различные управляющие структуры, которые допускают более сложные пути выполнения.
Оператор цикла позволяет нам выполнять оператор или группу операторов несколько раз, и в большинстве языков программирования ниже приводится общая форма инструкции цикла.
MATLAB предоставляет следующие типы циклов для обработки требований циклов. Нажмите на следующие ссылки, чтобы проверить их детали –
| Sr.No. | Тип и описание петли |
|---|---|
| 1 | в то время как цикл
Повторяет оператор или группу операторов, пока данное условие выполняется. Он проверяет условие перед выполнением тела цикла. |
| 2 | для цикла
Выполняет последовательность операторов несколько раз и сокращает код, который управляет переменной цикла. |
| 3 | вложенные циклы
Вы можете использовать один или несколько циклов внутри любого другого цикла. |
Повторяет оператор или группу операторов, пока данное условие выполняется. Он проверяет условие перед выполнением тела цикла.
Выполняет последовательность операторов несколько раз и сокращает код, который управляет переменной цикла.
Вы можете использовать один или несколько циклов внутри любого другого цикла.
Заявления о контроле цикла
Операторы управления циклом изменяют выполнение от его нормальной последовательности. Когда выполнение покидает область действия, все автоматические объекты, созданные в этой области, уничтожаются.
MATLAB поддерживает следующие управляющие операторы. Нажмите на следующие ссылки, чтобы проверить их детали.
| Sr.No. | Контрольное заявление и описание |
|---|---|
| 1 | заявление о нарушении
Завершает оператор цикла и передает выполнение в оператор, следующий сразу за циклом. |
| 2 | продолжить заявление
Заставляет петлю пропускать оставшуюся часть своего тела и немедленно проверять свое состояние перед повторением. |
Завершает оператор цикла и передает выполнение в оператор, следующий сразу за циклом.
Заставляет петлю пропускать оставшуюся часть своего тела и немедленно проверять свое состояние перед повторением.
MATLAB – Векторы
Вектор – это одномерный массив чисел. MATLAB позволяет создавать два типа векторов –
- Векторы строк
- Векторы столбцов
Строки Векторы
Векторы строк создаются путем заключения набора элементов в квадратных скобках с использованием пробела или запятой для разделения элементов.
Live Demo
r = [7 8 9 10 11]
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
r = 7 8 9 10 11
Векторы столбцов
Векторы столбцов создаются заключением набора элементов в квадратные скобки с использованием точки с запятой для разделения элементов.
Live Demo
c = [7; 8; 9; 10; 11]
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
c =
7
8
9
10
11
Ссылка на элементы вектора
Вы можете ссылаться на один или несколько элементов вектора несколькими способами. I- й компонент вектора v обозначается как v (i). Например –
Live Demo
v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements v(3)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 3
Когда вы ссылаетесь на вектор с двоеточием, например, v (:), в нем отображаются все компоненты вектора.
Live Demo
v = [ 1; 2; 3; 4; 5; 6]; % creating a column vector of 6 elements v(:)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans =
1
2
3
4
5
6
MATLAB позволяет вам выбрать диапазон элементов из вектора.
Например, давайте создадим вектор-строку rv из 9 элементов, затем мы будем ссылаться на элементы с 3 по 7, написав rv (3: 7), и создадим новый вектор с именем sub_rv .
Live Demo
rv = [1 2 3 4 5 6 7 8 9]; sub_rv = rv(3:7)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
sub_rv = 3 4 5 6 7
Векторные операции
В этом разделе давайте обсудим следующие векторные операции –
-
Сложение и вычитание векторов
-
Скалярное Умножение Векторов
-
Транспонирование вектора
-
Добавление векторов
-
Величина вектора
-
Вектор Дот Продукт
-
Векторы с равномерно расположенными элементами
Сложение и вычитание векторов
Скалярное Умножение Векторов
Транспонирование вектора
Добавление векторов
Величина вектора
Вектор Дот Продукт
Векторы с равномерно расположенными элементами
MATLAB – Матрица
Матрица – это двумерный массив чисел.
В MATLAB вы создаете матрицу, вводя элементы в каждой строке в виде чисел, разделенных запятыми или пробелами, и используя точки с запятой, чтобы отметить конец каждой строки.
Например, давайте создадим матрицу 4 на 5 a –
Live Demo
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
a =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
4 5 6 7 8
Ссылка на элементы матрицы
Для ссылки на элемент в m- й строке и n- м столбце матрицы mx мы пишем:
mx(m, n);
Например, чтобы обратиться к элементу во 2- й строке и 5- м столбце матрицы a , как создано в последнем разделе, мы набираем –
Live Demo
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a(2,5)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 6
Для ссылки на все элементы в m- м столбце мы набираем A (:, m).
Создадим вектор-столбец v из элементов 4- й строки матрицы a –
Live Demo
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; v = a(:,4)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
v =
4
5
6
7
Вы также можете выбрать элементы в столбцах с m по n, для этого мы напишем:
a(:,m:n)
Давайте создадим меньшую матрицу, взяв элементы из второго и третьего столбцов –
Live Demo
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a(:, 2:3)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans =
2 3
3 4
4 5
5 6
Таким же образом вы можете создать подматрицу, взяв подчасть матрицы.
Live Demo
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a(:, 2:3)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans =
2 3
3 4
4 5
5 6
Таким же образом вы можете создать подматрицу, взяв подчасть матрицы.
Например, давайте создадим подматрицу sa, взяв внутреннюю часть a –
3 4 5 4 5 6
Для этого напишите –
Live Demo
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; sa = a(2:3,2:4)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
sa =
3 4 5
4 5 6
Удаление строки или столбца в матрице
Вы можете удалить всю строку или столбец матрицы, назначив пустой набор квадратных скобок [] для этой строки или столбца. По сути, [] обозначает пустой массив.
Например, давайте удалим четвертый ряд –
Live Demo
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a( 4 , : ) = []
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
a =
1 2 3 4 5
2 3 4 5 6
3 4 5 6 7
Далее, давайте удалим пятый столбец –
Live Demo
a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]; a(: , 5)=[]
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
a =
1 2 3 4
2 3 4 5
3 4 5 6
4 5 6 7
пример
В этом примере давайте создадим матрицу 3 на 3 m, затем дважды скопируем вторую и третью строки этой матрицы, чтобы создать матрицу 4 на 3.
Создайте файл сценария со следующим кодом –
Live Demo
a = [ 1 2 3 ; 4 5 6; 7 8 9]; new_mat = a([2,3,2,3],:)
Когда вы запускаете файл, он показывает следующий результат –
new_mat =
4 5 6
7 8 9
4 5 6
7 8 9
Матричные Операции
В этом разделе давайте обсудим следующие основные и часто используемые матричные операции –
-
Сложение и вычитание матриц
-
Отдел матриц
-
Скалярные операции матриц
-
Транспонировать матрицы
-
Конкатенирующие матрицы
-
Умножение матриц
-
Определитель матрицы
-
Инверсия матрицы
Сложение и вычитание матриц
Отдел матриц
Скалярные операции матриц
Транспонировать матрицы
Конкатенирующие матрицы
Умножение матриц
Определитель матрицы
Инверсия матрицы
MATLAB – Массивы
Все переменные всех типов данных в MATLAB являются многомерными массивами. Вектор – это одномерный массив, а матрица – это двумерный массив.
Мы уже обсуждали векторы и матрицы. В этой главе мы обсудим многомерные массивы. Однако перед этим давайте обсудим некоторые специальные типы массивов.
Специальные массивы в MATLAB
В этом разделе мы обсудим некоторые функции, которые создают специальные массивы. Для всех этих функций один аргумент создает квадратный массив, двойные аргументы создают прямоугольный массив.
Функция нулей () создает массив всех нулей –
Например –
Live Demo
zeros(5)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans =
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
Функция ones () создает массив всех единиц –
Например –
Live Demo
ones(4,3)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans =
1 1 1
1 1 1
1 1 1
1 1 1
Функция eye () создает единичную матрицу.
Например –
Live Demo
eye(4)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans =
1 0 0 0
0 1 0 0
0 0 1 0
0 0 0 1
Функция rand () создает массив равномерно распределенных случайных чисел по (0,1) –
Например –
Live Demo
rand(3, 5)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 0.8147 0.9134 0.2785 0.9649 0.9572 0.9058 0.6324 0.5469 0.1576 0.4854 0.1270 0.0975 0.9575 0.9706 0.8003
Магический Квадрат
Магический квадрат – это квадрат, который дает одинаковую сумму, когда его элементы добавляются построчно, по столбцам или по диагонали.
Функция magic () создает массив магических квадратов. Требуется исключительный аргумент, который дает размер квадрата. Аргумент должен быть скаляром, большим или равным 3.
Live Demo
magic(4)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 16 2 3 13 5 11 10 8 9 7 6 12 4 14 15 1
Многомерные массивы
В MATLAB массив, имеющий более двух измерений, называется многомерным массивом. Многомерные массивы в MATLAB являются расширением нормальной двумерной матрицы.
Обычно для создания многомерного массива мы сначала создаем двумерный массив и расширяем его.
Например, давайте создадим двумерный массив a.
Live Demo
a = [7 9 5; 6 1 9; 4 3 2]
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
a = 7 9 5 6 1 9 4 3 2
Массив a является массивом 3 на 3; мы можем добавить третье измерение к, предоставив такие значения, как –
Live Demo
a(:, :, 2)= [ 1 2 3; 4 5 6; 7 8 9]
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
a = ans(:,:,1) = 0 0 0 0 0 0 0 0 0 ans(:,:,2) = 1 2 3 4 5 6 7 8 9
Мы также можем создавать многомерные массивы, используя функции ones (), zeros () или rand ().
Например,
Live Demo
b = rand(4,3,2)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
b(:,:,1) = 0.0344 0.7952 0.6463 0.4387 0.1869 0.7094 0.3816 0.4898 0.7547 0.7655 0.4456 0.2760 b(:,:,2) = 0.6797 0.4984 0.2238 0.6551 0.9597 0.7513 0.1626 0.3404 0.2551 0.1190 0.5853 0.5060
Мы также можем использовать функцию cat () для построения многомерных массивов. Он объединяет список массивов по указанному измерению –
Синтаксис для функции cat () –
B = cat(dim, A1, A2...)
Куда,
-
B – новый созданный массив
-
A1 , A2 , … массивы, которые будут объединены
-
dim – это размер, по которому объединяются массивы.
B – новый созданный массив
A1 , A2 , … массивы, которые будут объединены
dim – это размер, по которому объединяются массивы.
пример
Создайте файл сценария и введите в него следующий код –
Live Demo
a = [9 8 7; 6 5 4; 3 2 1]; b = [1 2 3; 4 5 6; 7 8 9]; c = cat(3, a, b, [ 2 3 1; 4 7 8; 3 9 0])
Когда вы запускаете файл, он отображает –
c(:,:,1) =
9 8 7
6 5 4
3 2 1
c(:,:,2) =
1 2 3
4 5 6
7 8 9
c(:,:,3) =
2 3 1
4 7 8
3 9 0
Функции массива
MATLAB предоставляет следующие функции для сортировки, вращения, перестановки, изменения формы или смещения содержимого массива.
| функция | Цель |
|---|---|
| длина | Длина вектора или наибольшее измерение массива |
| ndims | Количество размеров массива |
| numel | Количество элементов массива |
| размер | Размеры массива |
| iscolumn | Определяет, является ли ввод вектором столбца |
| пустой | Определяет, является ли массив пустым |
| ismatrix | Определяет, является ли ввод матричным |
| isrow | Определяет, является ли ввод вектором строки |
| isscalar | Определяет, является ли вход скалярным |
| isvector | Определяет, является ли входной вектор |
| blkdiag | Создает блочную диагональную матрицу из входных аргументов. |
| circshift | Смещает массив по кругу |
| ctranspose | Комплексное сопряженное транспонирование |
| диаг | Диагональные матрицы и диагонали матрицы |
| flipdim | Переворачивает массив по указанному измерению |
| fliplr | Отразить матрицу слева направо |
| flipud | Переворачивает матрицу вверх-вниз |
| ipermute | Инвертирует перестановочные размеры массива ND |
| переставлять | Переставляет размеры массива ND |
| repmat | Реплики и массив плиток |
| перекроить | Перекраивает массив |
| rot90 | Поворот матрицы на 90 градусов |
| shiftdim | Смещает размеры |
| issorted | Определяет, находятся ли заданные элементы в отсортированном порядке |
| Сортировать | Сортирует элементы массива в порядке возрастания или убывания |
| sortrows | Сортирует строки в порядке возрастания |
| выжимать | Удаляет одиночные размеры |
| транспонировать | транспонировать |
| векторизовать | Векторизованное выражение |
Примеры
Следующие примеры иллюстрируют некоторые из функций, упомянутых выше.
Длина, Размер и Количество элементов –
Создайте файл сценария и введите в него следующий код –
Live Demo
x = [7.1, 3.4, 7.2, 28/4, 3.6, 17, 9.4, 8.9]; length(x) % length of x vector y = rand(3, 4, 5, 2); ndims(y) % no of dimensions in array y s = ['Zara', 'Nuha', 'Shamim', 'Riz', 'Shadab']; numel(s) % no of elements in s
Когда вы запускаете файл, он показывает следующий результат –
ans = 8 ans = 4 ans = 23
Круговое смещение элементов массива –
Создайте файл сценария и введите в него следующий код –
Live Demo
a = [1 2 3; 4 5 6; 7 8 9] % the original array a b = circshift(a,1) % circular shift first dimension values down by 1. c = circshift(a,[1 -1]) % circular shift first dimension values % down by 1 % and second dimension values to the left % by 1.
Когда вы запускаете файл, он показывает следующий результат –
a = 1 2 3 4 5 6 7 8 9 b = 7 8 9 1 2 3 4 5 6 c = 8 9 7 2 3 1 5 6 4
Сортировка массивов
Создайте файл сценария и введите в него следующий код –
Live Demo
v = [ 23 45 12 9 5 0 19 17] % horizontal vector sort(v) % sorting v m = [2 6 4; 5 3 9; 2 0 1] % two dimensional array sort(m, 1) % sorting m along the row sort(m, 2) % sorting m along the column
Когда вы запускаете файл, он показывает следующий результат –
v = 23 45 12 9 5 0 19 17 ans = 0 5 9 12 17 19 23 45 m = 2 6 4 5 3 9 2 0 1 ans = 2 0 1 2 3 4 5 6 9 ans = 2 4 6 3 5 9 0 1 2
Cell Array
Массивы ячеек – это массивы индексированных ячеек, где каждая ячейка может хранить массив разных измерений и типов данных.
Функция cell используется для создания массива cell. Синтаксис для функции ячейки –
C = cell(dim) C = cell(dim1,...,dimN) D = cell(obj)
Куда,
-
С – массив ячеек;
-
dim – скалярное целое число или вектор целых чисел, который определяет размеры массива ячеек C;
-
dim1, …, dimN – скалярные целые числа, которые определяют размеры C;
-
obj является одним из следующих –
- Массив или объект Java
- .NET массив типа System.String или System.Object
С – массив ячеек;
dim – скалярное целое число или вектор целых чисел, который определяет размеры массива ячеек C;
dim1, …, dimN – скалярные целые числа, которые определяют размеры C;
obj является одним из следующих –
пример
Создайте файл сценария и введите в него следующий код –
Live Demo
c = cell(2, 5); c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5}
Когда вы запускаете файл, он показывает следующий результат –
c =
{
[1,1] = Red
[2,1] = 1
[1,2] = Blue
[2,2] = 2
[1,3] = Green
[2,3] = 3
[1,4] = Yellow
[2,4] = 4
[1,5] = White
[2,5] = 5
}
Доступ к данным в массивах ячеек
Существует два способа обращения к элементам массива ячеек:
- Заключение индексов в первую скобку () для ссылки на наборы ячеек
- Заключение индексов в фигурные скобки {} для ссылки на данные в отдельных ячейках
Когда вы заключаете индексы в первую скобку, это относится к набору ячеек.
Индексы массива ячеек в гладких скобках относятся к наборам ячеек.
Например –
Live Demo
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5}; c(1:2,1:2)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans =
{
[1,1] = Red
[2,1] = 1
[1,2] = Blue
[2,2] = 2
}
Вы также можете получить доступ к содержимому ячеек путем индексации с помощью фигурных скобок.
Например –
Live Demo
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5}; c{1, 2:4}
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = Blue ans = Green ans = Yellow
MATLAB – двоеточие
Двоеточие (:) является одним из самых полезных операторов в MATLAB. Он используется для создания векторов, массивов индексов и определения для итераций .
Если вы хотите создать вектор строки, содержащий целые числа от 1 до 10, вы пишете –
Live Demo
1:10
MATLAB выполняет инструкцию и возвращает вектор строки, содержащий целые числа от 1 до 10 –
ans =
1 2 3 4 5 6 7 8 9 10
Если вы хотите указать значение приращения, отличное от единицы, например:
Live Demo
100: -5: 50
MATLAB выполняет инструкцию и возвращает следующий результат –
ans = 100 95 90 85 80 75 70 65 60 55 50
Давайте возьмем другой пример –
Live Demo
0:pi/8:pi
MATLAB выполняет инструкцию и возвращает следующий результат –
ans =
Columns 1 through 7
0 0.3927 0.7854 1.1781 1.5708 1.9635 2.3562
Columns 8 through 9
2.7489 3.1416
Вы можете использовать оператор двоеточия, чтобы создать вектор индексов для выбора строк, столбцов или элементов массивов.
Следующая таблица описывает его использование для этой цели (у нас есть матрица A) –
| Формат | Цель |
|---|---|
| А (:, J) | это j-й столбец А. |
| А (я, 🙂 | это шестой ряд А. |
| А (:, 🙂 | эквивалентный двумерный массив Для матриц это то же самое, что и A. |
| А (J: к) | является A (j), A (j + 1), …, A (k). |
| A (:, J: к) | является A (:, j), A (:, j + 1), …, A (:, k). |
| А (:,:, к) | является k- й страницей трехмерного массива A. |
| A (I, J, K, 🙂 | является вектором в четырехмерном массиве A. Вектор включает в себя A (i, j, k, 1), A (i, j, k, 2), A (i, j, k, 3) и так далее. |
| А (:) | это все элементы А, рассматриваемые как один столбец. В левой части оператора присваивания A (:) заполняет A, сохраняя свою форму ранее. В этом случае правая сторона должна содержать то же количество элементов, что и A. |
пример
Создайте файл сценария и введите в нем следующий код –
Live Demo
A = [1 2 3 4; 4 5 6 7; 7 8 9 10] A(:,2) % second column of A A(:,2:3) % second and third column of A A(2:3,2:3) % second and third rows and second and third columns
Когда вы запускаете файл, он показывает следующий результат –
A =
1 2 3 4
4 5 6 7
7 8 9 10
ans =
2
5
8
ans =
2 3
5 6
8 9
ans =
5 6
8 9
MATLAB – Числа
MATLAB поддерживает различные числовые классы, которые включают целые числа со знаком и без знака, а также числа с плавающей запятой одинарной и двойной точности. По умолчанию MATLAB сохраняет все числовые значения как числа с плавающей запятой двойной точности.
Вы можете сохранить любое число или массив чисел в виде целых чисел или чисел одинарной точности.
Все числовые типы поддерживают базовые операции с массивами и математические операции.
Преобразование в различные числовые типы данных
MATLAB предоставляет следующие функции для преобразования в различные числовые типы данных –
| функция | Цель |
|---|---|
| двойной | Преобразует в число с двойной точностью |
| не замужем | Преобразует в число с одинарной точностью |
| int8 | Преобразует в 8-разрядное целое число со знаком |
| int16 | Преобразует в 16-разрядное целое число со знаком |
| int32 | Преобразует в 32-разрядное целое число со знаком |
| int64 | Преобразует в 64-разрядное целое число со знаком |
| uint8 | Преобразует в 8-разрядное целое число без знака |
| uint16 | Преобразует в 16-разрядное целое число без знака |
| uint32 | Преобразует в 32-разрядное целое число без знака |
| uint64 | Преобразует в 64-разрядное целое число без знака |
пример
Создайте файл сценария и введите следующий код –
Live Demo
x = single([5.32 3.47 6.28]) .* 7.5 x = double([5.32 3.47 6.28]) .* 7.5 x = int8([5.32 3.47 6.28]) .* 7.5 x = int16([5.32 3.47 6.28]) .* 7.5 x = int32([5.32 3.47 6.28]) .* 7.5 x = int64([5.32 3.47 6.28]) .* 7.5
Когда вы запускаете файл, он показывает следующий результат –
x = 39.900 26.025 47.100 x = 39.900 26.025 47.100 x = 38 23 45 x = 38 23 45 x = 38 23 45 x = 38 23 45
пример
Давайте расширим предыдущий пример немного подробнее. Создайте файл сценария и введите следующий код –
Live Demo
x = int32([5.32 3.47 6.28]) .* 7.5 x = int64([5.32 3.47 6.28]) .* 7.5 x = num2cell(x)
Когда вы запускаете файл, он показывает следующий результат –
x =
38 23 45
x =
38 23 45
x =
{
[1,1] = 38
[1,2] = 23
[1,3] = 45
}
Самые маленькие и самые большие целые числа
Функции intmax () и intmin () возвращают максимальное и минимальное значения, которые могут быть представлены всеми типами целых чисел.
Обе функции принимают в качестве аргумента целочисленный тип данных, например, intmax (int8) или intmin (int64), и возвращают максимальное и минимальное значения, которые вы можете представить в целочисленном типе данных.
пример
В следующем примере показано, как получить наименьшее и наибольшее значения целых чисел. Создайте файл сценария и напишите в нем следующий код –
Live Demo
% displaying the smallest and largest signed integer data str = 'The range for int8 is:nt%d to %d '; sprintf(str, intmin('int8'), intmax('int8')) str = 'The range for int16 is:nt%d to %d '; sprintf(str, intmin('int16'), intmax('int16')) str = 'The range for int32 is:nt%d to %d '; sprintf(str, intmin('int32'), intmax('int32')) str = 'The range for int64 is:nt%d to %d '; sprintf(str, intmin('int64'), intmax('int64')) % displaying the smallest and largest unsigned integer data str = 'The range for uint8 is:nt%d to %d '; sprintf(str, intmin('uint8'), intmax('uint8')) str = 'The range for uint16 is:nt%d to %d '; sprintf(str, intmin('uint16'), intmax('uint16')) str = 'The range for uint32 is:nt%d to %d '; sprintf(str, intmin('uint32'), intmax('uint32')) str = 'The range for uint64 is:nt%d to %d '; sprintf(str, intmin('uint64'), intmax('uint64'))
Когда вы запускаете файл, он показывает следующий результат –
ans = The range for int8 is: -128 to 127 ans = The range for int16 is: -32768 to 32767 ans = The range for int32 is: -2147483648 to 2147483647 ans = The range for int64 is: 0 to 0 ans = The range for uint8 is: 0 to 255 ans = The range for uint16 is: 0 to 65535 ans = The range for uint32 is: 0 to -1 ans = The range for uint64 is: 0 to 18446744073709551616
Самые маленькие и самые большие числа с плавающей точкой
Функции realmax () и realmin () возвращают максимальное и минимальное значения, которые могут быть представлены числами с плавающей запятой.
Обе функции при вызове с аргументом ‘single’ возвращают максимальное и минимальное значения, которые вы можете представить с помощью типа данных с одинарной точностью, а при вызове с аргументом ‘double’ возвращают максимальное и минимальное значения, которые вы можете представить с помощью тип данных двойной точности.
пример
В следующем примере показано, как получить наименьшее и наибольшее числа с плавающей запятой. Создайте файл сценария и напишите в нем следующий код –
Live Demo
% displaying the smallest and largest single-precision % floating point number str = 'The range for single is:nt%g to %g andnt %g to %g'; sprintf(str, -realmax('single'), -realmin('single'), ... realmin('single'), realmax('single')) % displaying the smallest and largest double-precision % floating point number str = 'The range for double is:nt%g to %g andnt %g to %g'; sprintf(str, -realmax('double'), -realmin('double'), ... realmin('double'), realmax('double'))
Когда вы запускаете файл, он показывает следующий результат –
ans = The range for single is:
-3.40282e+38 to -1.17549e-38 and
1.17549e-38 to 3.40282e+38
ans = The range for double is:
-1.79769e+308 to -2.22507e-308 and
2.22507e-308 to 1.79769e+308
MATLAB – Струны
Создать строку символов в MATLAB довольно просто. На самом деле, мы использовали это много раз. Например, вы вводите следующее в командной строке –
Live Demo
my_string = 'Tutorials Point'
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
my_string = Tutorials Point
MATLAB рассматривает все переменные как массивы, а строки – как символьные массивы. Давайте используем команду whos для проверки созданной выше переменной –
whos
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
Name Size Bytes Class Attributes my_string 1x16 32 char
Интересно, что вы можете использовать функции преобразования чисел, такие как uint8 или uint16, чтобы преобразовать символы в строке в их числовые коды. Функция char преобразует вектор целых чисел обратно в символы –
пример
Создайте файл сценария и введите в него следующий код –
Live Demo
my_string = 'Tutorial''s Point'; str_ascii = uint8(my_string) % 8-bit ascii values str_back_to_char= char(str_ascii) str_16bit = uint16(my_string) % 16-bit ascii values str_back_to_char = char(str_16bit)
Когда вы запускаете файл, он показывает следующий результат –
str_ascii = 84 117 116 111 114 105 97 108 39 115 32 80 111 105 110 116 str_back_to_char = Tutorial's Point str_16bit = 84 117 116 111 114 105 97 108 39 115 32 80 111 105 110 116 str_back_to_char = Tutorial's Point
Прямоугольный массив символов
Строки, которые мы обсуждали до сих пор, являются одномерными символьными массивами; Однако нам нужно хранить больше, чем это. Нам нужно хранить более объемные текстовые данные в нашей программе. Это достигается путем создания прямоугольных массивов символов.
Простейший способ создания прямоугольного массива символов состоит в объединении двух или более одномерных массивов символов по вертикали или по горизонтали, как требуется.
Вы можете комбинировать строки по вертикали одним из следующих способов –
-
Используя оператор конкатенации MATLAB [] и разделяя каждую строку точкой с запятой (;). Обратите внимание, что в этом методе каждая строка должна содержать одинаковое количество символов. Для строк разной длины вы должны заполнять пробелами по мере необходимости.
-
Использование функции char . Если строки имеют разную длину, более короткие строки облагаются символьными символами, чтобы в каждой строке было одинаковое количество символов.
Используя оператор конкатенации MATLAB [] и разделяя каждую строку точкой с запятой (;). Обратите внимание, что в этом методе каждая строка должна содержать одинаковое количество символов. Для строк разной длины вы должны заполнять пробелами по мере необходимости.
Использование функции char . Если строки имеют разную длину, более короткие строки облагаются символьными символами, чтобы в каждой строке было одинаковое количество символов.
пример
Создайте файл сценария и введите в него следующий код –
Live Demo
doc_profile = ['Zara Ali '; ... 'Sr. Surgeon '; ... 'R N Tagore Cardiology Research Center'] doc_profile = char('Zara Ali', 'Sr. Surgeon', ... 'RN Tagore Cardiology Research Center')
Когда вы запускаете файл, он показывает следующий результат –
doc_profile = Zara Ali Sr. Surgeon R N Tagore Cardiology Research Center doc_profile = Zara Ali Sr. Surgeon RN Tagore Cardiology Research Center
Вы можете комбинировать строки горизонтально одним из следующих способов –
-
Используя оператор конкатенации MATLAB, [] и разделяя входные строки запятой или пробелом. Этот метод сохраняет любые конечные пробелы во входных массивах.
-
Используя функцию конкатенации строк, strcat . Этот метод удаляет завершающие пробелы во входных данных.
Используя оператор конкатенации MATLAB, [] и разделяя входные строки запятой или пробелом. Этот метод сохраняет любые конечные пробелы во входных массивах.
Используя функцию конкатенации строк, strcat . Этот метод удаляет завершающие пробелы во входных данных.
пример
Создайте файл сценария и введите в него следующий код –
Live Demo
name = 'Zara Ali '; position = 'Sr. Surgeon '; worksAt = 'R N Tagore Cardiology Research Center'; profile = [name ', ' position ', ' worksAt] profile = strcat(name, ', ', position, ', ', worksAt)
Когда вы запускаете файл, он показывает следующий результат –
profile = Zara Ali , Sr. Surgeon , R N Tagore Cardiology Research Center profile = Zara Ali,Sr. Surgeon,R N Tagore Cardiology Research Center
Объединение строк в массив ячеек
Из нашего предыдущего обсуждения ясно, что объединение строк разной длины может быть проблематичным, поскольку все строки в массиве должны быть одинаковой длины. Мы использовали пробелы в конце строк, чтобы выровнять их длину.
Однако более эффективный способ объединения строк – преобразование полученного массива в массив ячеек.
Массив ячеек MATLAB может содержать различные размеры и типы данных в массиве. Массивы ячеек обеспечивают более гибкий способ хранения строк различной длины.
Функция cellstr преобразует массив символов в массив строк.
пример
Создайте файл сценария и введите в него следующий код –
Live Demo
name = 'Zara Ali '; position = 'Sr. Surgeon '; worksAt = 'R N Tagore Cardiology Research Center'; profile = char(name, position, worksAt); profile = cellstr(profile); disp(profile)
Когда вы запускаете файл, он показывает следующий результат –
{
[1,1] = Zara Ali
[2,1] = Sr. Surgeon
[3,1] = R N Tagore Cardiology Research Center
}
Строковые функции в MATLAB
MATLAB предоставляет множество строковых функций для создания, объединения, анализа, сравнения и манипулирования строками.
В следующей таблице приведено краткое описание строковых функций в MATLAB –
| функция | Цель |
|---|---|
| Функции для хранения текста в символьных массивах, комбинирования символьных массивов и т. Д. | |
| заготовки | Создать строку пустых символов |
| cellstr | Создать массив строк из массива символов |
| голец | Преобразовать в массив символов (строку) |
| iscellstr | Определите, является ли ввод массивом строк |
| ischar | Определить, является ли элемент массивом символов |
| Sprintf | Форматировать данные в строку |
| strcat | Конкатенация строк по горизонтали |
| strjoin | Соединить строки в массиве ячеек в одну строку |
| Функции для идентификации частей строк, поиска и замены подстрок | |
| ischar | Определить, является ли элемент массивом символов |
| isletter | Элементы массива, которые являются буквенными буквами |
| isspace | Элементы массива, которые являются пробелами |
| isstrprop | Определить, относится ли строка к указанной категории |
| sscanf | Считать отформатированные данные из строки |
| strfind | Найти одну строку в другой |
| strrep | Найти и заменить подстроку |
| strsplit | Разделить строку по указанному разделителю |
| strtok | Отдельные части строки |
| validatestring | Проверьте правильность текстовой строки |
| symvar | Определить символические переменные в выражении |
| регулярное выражение | Соответствие регулярному выражению (с учетом регистра) |
| regexpi | Соответствие регулярному выражению (без учета регистра) |
| regexprep | Заменить строку с помощью регулярного выражения |
| regexptranslate | Перевести строку в регулярное выражение |
| Функции для сравнения строк | |
| зЬгстр | Сравнить строки (с учетом регистра) |
| strcmpi | Сравнить строки (без учета регистра) |
| strncmp | Сравните первые n символов строк (с учетом регистра) |
| strncmpi | Сравните первые n символов строк (без учета регистра) |
| Функции для изменения строки в верхний или нижний регистр, создания или удаления пробела | |
| deblank | Снять задние заготовки с конца струны |
| strtrim | Удалить начальные и конечные пробелы из строки |
| ниже | Преобразовать строку в нижний регистр |
| верхний | Преобразовать строку в верхний регистр |
| strjust | Обоснуйте массив символов |
Примеры
Следующие примеры иллюстрируют некоторые из вышеупомянутых строковых функций –
Форматирование строк
Создайте файл сценария и введите в него следующий код –
Live Demo
A = pi*1000*ones(1,5); sprintf(' %f n %.2f n %+.2f n %12.2f n %012.2f n', A)
Когда вы запускаете файл, он показывает следующий результат –
ans = 3141.592654
3141.59
+3141.59
3141.59
000003141.59
Строки соединения
Создайте файл сценария и введите в него следующий код –
Live Demo
%cell array of strings str_array = {'red','blue','green', 'yellow', 'orange'}; % Join strings in cell array into single string str1 = strjoin(str_array, "-") str2 = strjoin(str_array, ",")
Когда вы запускаете файл, он показывает следующий результат –
str1 = red-blue-green-yellow-orange str2 = red,blue,green,yellow,orange
Поиск и замена строк
Создайте файл сценария и введите в него следующий код –
Live Demo
students = {'Zara Ali', 'Neha Bhatnagar', ... 'Monica Malik', 'Madhu Gautam', ... 'Madhu Sharma', 'Bhawna Sharma',... 'Nuha Ali', 'Reva Dutta', ... 'Sunaina Ali', 'Sofia Kabir'}; % The strrep function searches and replaces sub-string. new_student = strrep(students(8), 'Reva', 'Poulomi') % Display first names first_names = strtok(students)
Когда вы запускаете файл, он показывает следующий результат –
new_student =
{
[1,1] = Poulomi Dutta
}
first_names =
{
[1,1] = Zara
[1,2] = Neha
[1,3] = Monica
[1,4] = Madhu
[1,5] = Madhu
[1,6] = Bhawna
[1,7] = Nuha
[1,8] = Reva
[1,9] = Sunaina
[1,10] = Sofia
}
Сравнение строк
Создайте файл сценария и введите в него следующий код –
Live Demo
str1 = 'This is test' str2 = 'This is text' if (strcmp(str1, str2)) sprintf('%s and %s are equal', str1, str2) else sprintf('%s and %s are not equal', str1, str2) end
Когда вы запускаете файл, он показывает следующий результат –
str1 = This is test str2 = This is text ans = This is test and This is text are not equal
MATLAB – Функции
Функция – это группа операторов, которые вместе выполняют задачу. В MATLAB функции определены в отдельных файлах. Имя файла и функции должны совпадать.
Функции работают с переменными в их собственном рабочем пространстве, которое также называется локальным рабочим пространством , отдельно от рабочего пространства, к которому вы обращаетесь в командной строке MATLAB, которое называется базовым рабочим пространством .
Функции могут принимать более одного входного аргумента и могут возвращать более одного выходного аргумента.
Синтаксис оператора функции –
function [out1,out2, ..., outN] = myfun(in1,in2,in3, ..., inN)
пример
Следующая функция с именем mymax должна быть записана в файл с именем mymax.m . Он принимает пять чисел в качестве аргумента и возвращает максимум чисел.
Создайте файл функции с именем mymax.m и введите в него следующий код –
function max = mymax(n1, n2, n3, n4, n5) %This function calculates the maximum of the % five numbers given as input max = n1; if(n2 > max) max = n2; end if(n3 > max) max = n3; end if(n4 > max) max = n4; end if(n5 > max) max = n5; end
Первая строка функции начинается с ключевого слова function . Это дает название функции и порядок аргументов. В нашем примере функция mymax имеет пять входных аргументов и один выходной аргумент.
Строки комментариев, которые идут сразу после оператора функции, содержат текст справки. Эти строки печатаются при вводе –
help mymax
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
This function calculates the maximum of the five numbers given as input
Вы можете вызвать функцию как –
mymax(34, 78, 89, 23, 11)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 89
Анонимные функции
Анонимная функция похожа на встроенную функцию в традиционных языках программирования, определенную в одной инструкции MATLAB. Он состоит из одного выражения MATLAB и любого количества входных и выходных аргументов.
Вы можете определить анонимную функцию прямо в командной строке MATLAB или в функции или скрипте.
Таким образом, вы можете создавать простые функции без необходимости создавать файл для них.
Синтаксис для создания анонимной функции из выражения:
f = @(arglist)expression
пример
В этом примере мы напишем анонимную функцию с именем power, которая будет принимать два числа в качестве входных данных и возвращать первое число, возведенное в степень второго числа.
Создайте файл сценария и введите в нем следующий код –
Live Demo
power = @(x, n) x.^n; result1 = power(7, 3) result2 = power(49, 0.5) result3 = power(10, -10) result4 = power (4.5, 1.5)
Когда вы запускаете файл, он отображает –
result1 = 343 result2 = 7 result3 = 1.0000e-10 result4 = 9.5459
Основные и подфункции
Любая функция, кроме анонимной, должна быть определена в файле. Каждый файл функции содержит требуемую первичную функцию, которая появляется первой, и любое количество необязательных подфункций, которые идут после основной функции и используются ею.
Первичные функции могут быть вызваны из-за пределов файла, который их определяет, либо из командной строки, либо из других функций, но подфункции не могут быть вызваны из командной строки или других функций вне файла функции.
Подфункции видны только основной функции и другим подфункциям в файле функций, который их определяет.
пример
Напишем функцию с именем quadratic, которая будет вычислять корни квадратного уравнения. Функция будет принимать три входа: квадратичный коэффициент, линейный коэффициент и постоянный член. Это вернуло бы корни.
Файл функций quadratic.m будет содержать основную функцию quadratic и вспомогательный диск , который вычисляет дискриминант.
Создайте файл функции quadratic.m и введите в него следующий код –
function [x1,x2] = quadratic(a,b,c) %this function returns the roots of % a quadratic equation. % It takes 3 input arguments % which are the co-efficients of x2, x and the %constant term % It returns the roots d = disc(a,b,c); x1 = (-b + d) / (2*a); x2 = (-b - d) / (2*a); end % end of quadratic function dis = disc(a,b,c) %function calculates the discriminant dis = sqrt(b^2 - 4*a*c); end % end of sub-function
Вы можете вызвать вышеуказанную функцию из командной строки как –
quadratic(2,4,-4)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 0.7321
Вложенные функции
Вы можете определить функции в теле другой функции. Это так называемые вложенные функции. Вложенная функция содержит любой или все компоненты любой другой функции.
Вложенные функции определены в области действия другой функции и имеют общий доступ к рабочему пространству содержащей функции.
Вложенная функция имеет следующий синтаксис:
function x = A(p1, p2) ... B(p2) function y = B(p3) ... end ... end
пример
Перепишем функцию quadratic из предыдущего примера, однако на этот раз функция диска будет вложенной функцией.
Создайте файл функции quadratic2.m и введите в него следующий код –
function [x1,x2] = quadratic2(a,b,c) function disc % nested function d = sqrt(b^2 - 4*a*c); end % end of function disc disc; x1 = (-b + d) / (2*a); x2 = (-b - d) / (2*a); end % end of function quadratic2
Вы можете вызвать вышеуказанную функцию из командной строки как –
quadratic2(2,4,-4)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 0.73205
Частные функции
Закрытая функция – это основная функция, которая видна только ограниченной группе других функций. Если вы не хотите показывать реализацию функции (й), вы можете создать их как частные функции.
Закрытые функции находятся в подпапках со специальным именем private .
Они видны только функциям в родительской папке.
пример
Перепишем квадратичную функцию. На этот раз, однако, функция диска, вычисляющая дискриминант, будет частной функцией.
Создайте подпапку с именем private в рабочем каталоге. Сохраните в нем следующий файл функции disc.m –
function dis = disc(a,b,c) %function calculates the discriminant dis = sqrt(b^2 - 4*a*c); end % end of sub-function
Создайте функцию quadratic3.m в вашем рабочем каталоге и введите в нее следующий код:
function [x1,x2] = quadratic3(a,b,c) %this function returns the roots of % a quadratic equation. % It takes 3 input arguments % which are the co-efficient of x2, x and the %constant term % It returns the roots d = disc(a,b,c); x1 = (-b + d) / (2*a); x2 = (-b - d) / (2*a); end % end of quadratic3
Вы можете вызвать вышеуказанную функцию из командной строки как –
quadratic3(2,4,-4)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 0.73205
Глобальные переменные
Глобальные переменные могут совместно использоваться более чем одной функцией. Для этого вам нужно объявить переменную как глобальную во всех функциях.
Если вы хотите получить доступ к этой переменной из базовой рабочей области, объявите переменную в командной строке.
Глобальное объявление должно произойти до того, как переменная будет фактически использована в функции. Рекомендуется использовать заглавные буквы для имен глобальных переменных, чтобы отличать их от других переменных.
пример
Давайте создадим файл функции с именем medium.m и наберем в нем следующий код:
function avg = average(nums) global TOTAL avg = sum(nums)/TOTAL; end
Создайте файл сценария и введите в нем следующий код –
global TOTAL; TOTAL = 10; n = [34, 45, 25, 45, 33, 19, 40, 34, 38, 42]; av = average(n)
Когда вы запустите файл, он покажет следующий результат –
av = 35.500
MATLAB – импорт данных
Импорт данных в MATLAB означает загрузку данных из внешнего файла. Функция importdata позволяет загружать различные файлы данных разных форматов. Он имеет следующие пять форм –
| Sr.No. | Описание функции |
|---|---|
| 1 |
A = importdata (имя файла) Загружает данные в массив A из файла, обозначенного именем файла . |
| 2 |
A = importdata (‘- pastespecial’) Загружает данные из системного буфера обмена, а не из файла. |
| 3 |
A = importdata (___, delimiterIn) Интерпретирует delimiterIn как разделитель столбцов в файле ASCII, имени файла или данных буфера обмена. Вы можете использовать delimiterIn с любым из входных аргументов в приведенных выше синтаксисах. |
| 4 |
A = importdata (___, delimiterIn, headerlinesIn) Загружает данные из файла ASCII, имени файла или буфера обмена, считывая числовые данные, начиная со строки headerlinesIn + 1 . |
| 5 |
[A, delimiterOut, headerlinesOut] = importdata (___) Возвращает обнаруженный символ разделителя для входного файла ASCII в delimiterOut и обнаруженное количество строк заголовка в headerlinesOut , используя любой из входных аргументов в предыдущих синтаксисах. |
A = importdata (имя файла)
Загружает данные в массив A из файла, обозначенного именем файла .
A = importdata (‘- pastespecial’)
Загружает данные из системного буфера обмена, а не из файла.
A = importdata (___, delimiterIn)
Интерпретирует delimiterIn как разделитель столбцов в файле ASCII, имени файла или данных буфера обмена. Вы можете использовать delimiterIn с любым из входных аргументов в приведенных выше синтаксисах.
A = importdata (___, delimiterIn, headerlinesIn)
Загружает данные из файла ASCII, имени файла или буфера обмена, считывая числовые данные, начиная со строки headerlinesIn + 1 .
[A, delimiterOut, headerlinesOut] = importdata (___)
Возвращает обнаруженный символ разделителя для входного файла ASCII в delimiterOut и обнаруженное количество строк заголовка в headerlinesOut , используя любой из входных аргументов в предыдущих синтаксисах.
По умолчанию Octave не поддерживает функцию importdata () , поэтому вам придется искать и устанавливать этот пакет, чтобы следующие примеры работали с вашей установкой Octave.
Пример 1
Давайте загрузим и отобразим файл изображения. Создайте файл сценария и введите в нем следующий код –
filename = 'smile.jpg'; A = importdata(filename); image(A);
Когда вы запускаете файл, MATLAB отображает файл изображения. Однако вы должны сохранить его в текущем каталоге.
Пример 2
В этом примере мы импортируем текстовый файл и указываем разделитель и заголовок столбца. Давайте создадим ASCII-файл, разделенный пробелами, с заголовками столбцов с именем weeklydata.txt .
Наш текстовый файл weeklydata.txt выглядит так –
SunDay MonDay TuesDay WednesDay ThursDay FriDay SaturDay 95.01 76.21 61.54 40.57 55.79 70.28 81.53 73.11 45.65 79.19 93.55 75.29 69.87 74.68 60.68 41.85 92.18 91.69 81.32 90.38 74.51 48.60 82.14 73.82 41.03 0.99 67.22 93.18 89.13 44.47 57.63 89.36 13.89 19.88 46.60
Создайте файл сценария и введите в нем следующий код –
filename = 'weeklydata.txt'; delimiterIn = ' '; headerlinesIn = 1; A = importdata(filename,delimiterIn,headerlinesIn); % View data for k = [1:7] disp(A.colheaders{1, k}) disp(A.data(:, k)) disp(' ') end
Когда вы запускаете файл, он показывает следующий результат –
SunDay 95.0100 73.1100 60.6800 48.6000 89.1300 MonDay 76.2100 45.6500 41.8500 82.1400 44.4700 TuesDay 61.5400 79.1900 92.1800 73.8200 57.6300 WednesDay 40.5700 93.5500 91.6900 41.0300 89.3600 ThursDay 55.7900 75.2900 81.3200 0.9900 13.8900 FriDay 70.2800 69.8700 90.3800 67.2200 19.8800 SaturDay 81.5300 74.6800 74.5100 93.1800 46.6000
Пример 3
В этом примере давайте импортируем данные из буфера обмена.
Скопируйте следующие строки в буфер обмена –
Математика проста
Создайте файл сценария и введите следующий код –
A = importdata('-pastespecial')
Когда вы запускаете файл, он показывает следующий результат –
A = 'Mathematics is simple'
Низкоуровневый файловый ввод / вывод
Функция importdata является высокоуровневой функцией. Низкоуровневые функции ввода / вывода файлов в MATLAB позволяют максимально контролировать чтение или запись данных в файл. Однако эти функции нуждаются в более подробной информации о вашем файле для эффективной работы.
MATLAB предоставляет следующие функции для операций чтения и записи на уровне байтов или символов:
| функция | Описание |
|---|---|
| fclose | Закройте один или все открытые файлы |
| feof | Тест на конец файла |
| FERROR | Информация об ошибках файлового ввода-вывода |
| fgetl | Чтение строки из файла, удаление символов новой строки |
| fgets | Читать строку из файла, сохраняя символы новой строки |
| Еореп | Откройте файл или получите информацию об открытых файлах |
| fprintf | Записать данные в текстовый файл |
| Fread | Чтение данных из двоичного файла |
| frewind | Переместить индикатор положения файла в начало открытого файла |
| fscanf | Читать данные из текстового файла |
| FSEEK | Переместить в указанную позицию в файле |
| ftell | Положение в открытом файле |
| FWRITE | Записать данные в двоичный файл |
Импорт текстовых файлов данных с низкоуровневым вводом / выводом
MATLAB предоставляет следующие функции для низкоуровневого импорта файлов текстовых данных –
-
Функция fscanf читает отформатированные данные в текстовом или ASCII-файле.
-
Функции fgetl и fgets читают по одной строке файла за раз, где символ новой строки разделяет каждую строку.
-
Функция fread считывает поток данных на уровне байтов или битов.
Функция fscanf читает отформатированные данные в текстовом или ASCII-файле.
Функции fgetl и fgets читают по одной строке файла за раз, где символ новой строки разделяет каждую строку.
Функция fread считывает поток данных на уровне байтов или битов.
пример
У нас есть текстовый файл данных «myfile.txt», сохраненный в нашем рабочем каталоге. Файл хранит данные об осадках за три месяца; Июнь, июль и август за 2012 год.
Данные в myfile.txt содержат повторные наборы измерений времени, месяца и количества осадков в пяти местах. Данные заголовка хранят количество месяцев M; таким образом, у нас есть M наборов измерений.
Файл выглядит так –
Rainfall Data Months: June, July, August M = 3 12:00:00 June-2012 17.21 28.52 39.78 16.55 23.67 19.15 0.35 17.57 NaN 12.01 17.92 28.49 17.40 17.06 11.09 9.59 9.33 NaN 0.31 0.23 10.46 13.17 NaN 14.89 19.33 20.97 19.50 17.65 14.45 14.00 18.23 10.34 17.95 16.46 19.34 09:10:02 July-2012 12.76 16.94 14.38 11.86 16.89 20.46 23.17 NaN 24.89 19.33 30.97 49.50 47.65 24.45 34.00 18.23 30.34 27.95 16.46 19.34 30.46 33.17 NaN 34.89 29.33 30.97 49.50 47.65 24.45 34.00 28.67 30.34 27.95 36.46 29.34 15:03:40 August-2012 17.09 16.55 19.59 17.25 19.22 17.54 11.45 13.48 22.55 24.01 NaN 21.19 25.85 25.05 27.21 26.79 24.98 12.23 16.99 18.67 17.54 11.45 13.48 22.55 24.01 NaN 21.19 25.85 25.05 27.21 26.79 24.98 12.23 16.99 18.67
Мы импортируем данные из этого файла и отображаем эти данные. Сделайте следующие шаги –
-
Откройте файл с помощью функции fopen и получите идентификатор файла.
-
Опишите данные в файле с помощью спецификаторов формата , таких как « % s » для строки, « % d » для целого числа или « % f » для числа с плавающей запятой.
-
Чтобы пропустить буквенные символы в файле, включите их в описание формата. Чтобы пропустить поле данных, используйте звездочку (‘*’) в спецификаторе.
Например, чтобы прочитать заголовки и вернуть единственное значение для M, мы пишем –
M = fscanf(fid, '%*s %*sn%*s %*s %*s %*snM=%dnn', 1);
-
По умолчанию fscanf считывает данные в соответствии с нашим описанием формата, пока не найдет совпадения для данных или не достигнет конца файла. Здесь мы будем использовать цикл для чтения 3 наборов данных и каждый раз будем читать 7 строк и 5 столбцов.
-
Мы создадим структуру с именем mydata в рабочей области для хранения данных, считанных из файла. Эта структура имеет три поля – время , месяц и массив raindata .
Откройте файл с помощью функции fopen и получите идентификатор файла.
Опишите данные в файле с помощью спецификаторов формата , таких как « % s » для строки, « % d » для целого числа или « % f » для числа с плавающей запятой.
Чтобы пропустить буквенные символы в файле, включите их в описание формата. Чтобы пропустить поле данных, используйте звездочку (‘*’) в спецификаторе.
Например, чтобы прочитать заголовки и вернуть единственное значение для M, мы пишем –
По умолчанию fscanf считывает данные в соответствии с нашим описанием формата, пока не найдет совпадения для данных или не достигнет конца файла. Здесь мы будем использовать цикл для чтения 3 наборов данных и каждый раз будем читать 7 строк и 5 столбцов.
Мы создадим структуру с именем mydata в рабочей области для хранения данных, считанных из файла. Эта структура имеет три поля – время , месяц и массив raindata .
Создайте файл сценария и введите в нем следующий код –
filename = '/data/myfile.txt'; rows = 7; cols = 5; % open the file fid = fopen(filename); % read the file headers, find M (number of months) M = fscanf(fid, '%*s %*sn%*s %*s %*s %*snM=%dnn', 1); % read each set of measurements for n = 1:M mydata(n).time = fscanf(fid, '%s', 1); mydata(n).month = fscanf(fid, '%s', 1); % fscanf fills the array in column order, % so transpose the results mydata(n).raindata = ... fscanf(fid, '%f', [rows, cols]); end for n = 1:M disp(mydata(n).time), disp(mydata(n).month) disp(mydata(n).raindata) end % close the file fclose(fid);
Когда вы запускаете файл, он показывает следующий результат –
12:00:00 June-2012 17.2100 17.5700 11.0900 13.1700 14.4500 28.5200 NaN 9.5900 NaN 14.0000 39.7800 12.0100 9.3300 14.8900 18.2300 16.5500 17.9200 NaN 19.3300 10.3400 23.6700 28.4900 0.3100 20.9700 17.9500 19.1500 17.4000 0.2300 19.5000 16.4600 0.3500 17.0600 10.4600 17.6500 19.3400 09:10:02 July-2012 12.7600 NaN 34.0000 33.1700 24.4500 16.9400 24.8900 18.2300 NaN 34.0000 14.3800 19.3300 30.3400 34.8900 28.6700 11.8600 30.9700 27.9500 29.3300 30.3400 16.8900 49.5000 16.4600 30.9700 27.9500 20.4600 47.6500 19.3400 49.5000 36.4600 23.1700 24.4500 30.4600 47.6500 29.3400 15:03:40 August-2012 17.0900 13.4800 27.2100 11.4500 25.0500 16.5500 22.5500 26.7900 13.4800 27.2100 19.5900 24.0100 24.9800 22.5500 26.7900 17.2500 NaN 12.2300 24.0100 24.9800 19.2200 21.1900 16.9900 NaN 12.2300 17.5400 25.8500 18.6700 21.1900 16.9900 11.4500 25.0500 17.5400 25.8500 18.6700
MATLAB – Вывод данных
Экспорт данных (или вывод) в MATLAB означает запись в файлы. MATLAB позволяет вам использовать ваши данные в другом приложении, которое читает файлы ASCII. Для этого MATLAB предоставляет несколько вариантов экспорта данных.
Вы можете создать следующий тип файлов –
-
Прямоугольный файл данных ASCII с разделителями из массива.
-
Дневник (или журнал) файла нажатий клавиш и результирующего текстового вывода.
-
Специализированный файл ASCII с использованием низкоуровневых функций, таких как fprintf.
-
MEX-файл для доступа к вашей подпрограмме C / C ++ или Fortran, которая записывает в определенный формат текстового файла.
Прямоугольный файл данных ASCII с разделителями из массива.
Дневник (или журнал) файла нажатий клавиш и результирующего текстового вывода.
Специализированный файл ASCII с использованием низкоуровневых функций, таких как fprintf.
MEX-файл для доступа к вашей подпрограмме C / C ++ или Fortran, которая записывает в определенный формат текстового файла.
Помимо этого, вы также можете экспортировать данные в электронные таблицы.
Существует два способа экспорта числового массива в виде файла данных с разделителями ASCII:
-
Использование функции сохранения и указание спецификатора -ascii
-
Использование функции dlmwrite
Использование функции сохранения и указание спецификатора -ascii
Использование функции dlmwrite
Синтаксис для использования функции сохранения –
save my_data.out num_array -ascii
где my_data.out – созданный файл данных ASCII с разделителями, num_array – числовой массив, а -ascii – спецификатор.
Синтаксис использования функции dlmwrite –
dlmwrite('my_data.out', num_array, 'dlm_char')
где my_data.out – созданный файл данных ASCII с разделителями, num_array – числовой массив, а dlm_char – символ разделителя.
пример
Следующий пример демонстрирует концепцию. Создайте файл сценария и введите следующий код –
Live Demo
num_array = [ 1 2 3 4 ; 4 5 6 7; 7 8 9 0]; save array_data1.out num_array -ascii; type array_data1.out dlmwrite('array_data2.out', num_array, ' '); type array_data2.out
Когда вы запускаете файл, он показывает следующий результат –
1.0000000e+00 2.0000000e+00 3.0000000e+00 4.0000000e+00 4.0000000e+00 5.0000000e+00 6.0000000e+00 7.0000000e+00 7.0000000e+00 8.0000000e+00 9.0000000e+00 0.0000000e+00 1 2 3 4 4 5 6 7 7 8 9 0
Обратите внимание, что команда save -ascii и функция dlmwrite не работают с массивами ячеек в качестве входных данных. Чтобы создать файл ASCII с разделителями из содержимого массива ячеек, вы можете
-
Либо преобразуйте массив ячеек в матрицу, используя функцию cell2mat
-
Или экспортируйте массив ячеек, используя низкоуровневые функции файлового ввода-вывода.
Либо преобразуйте массив ячеек в матрицу, используя функцию cell2mat
Или экспортируйте массив ячеек, используя низкоуровневые функции файлового ввода-вывода.
Если вы используете функцию сохранения для записи массива символов в файл ASCII, он записывает в файл эквивалент символов ASCII.
Например, давайте напишем слово «привет» в файл –
Live Demo
h = 'hello'; save textdata.out h -ascii type textdata.out
MATLAB выполняет вышеуказанные операторы и отображает следующий результат. это символы строки ‘hello’ в 8-значном формате ASCII.
1.0400000e+02 1.0100000e+02 1.0800000e+02 1.0800000e+02 1.1100000e+02
Запись в дневник
Дневниковые файлы – это журналы активности вашего сеанса MATLAB. Функция дневника создает точную копию вашей сессии в файле на диске, исключая графику.
Чтобы включить функцию дневника, введите –
diary
При желании вы можете дать имя файла журнала, скажем –
diary logdata.out
Чтобы отключить функцию дневника –
diary off
Вы можете открыть файл дневника в текстовом редакторе.
Экспорт данных в текстовые файлы данных с низкоуровневым вводом / выводом
До сих пор мы экспортировали числовые массивы. Однако вам может потребоваться создать другие текстовые файлы, включая комбинации числовых и символьных данных, непрямоугольные выходные файлы или файлы со схемами кодирования, отличными от ASCII. Для этих целей MATLAB предоставляет низкоуровневую функцию fprintf .
Как и в низкоуровневых операциях с файлами ввода-вывода, перед экспортом необходимо открыть или создать файл с помощью функции fopen и получить идентификатор файла. По умолчанию fopen открывает файл только для чтения. Вы должны указать разрешение на запись или добавление, например, «w» или «a».
После обработки файла его необходимо закрыть с помощью функции fclose (fid) .
Следующий пример демонстрирует концепцию –
пример
Создайте файл сценария и введите в нем следующий код –
Live Demo
% create a matrix y, with two rows x = 0:10:100; y = [x; log(x)]; % open a file for writing fid = fopen('logtable.txt', 'w'); % Table Header fprintf(fid, 'Log Functionnn'); % print values in column order % two values appear on each row of the file fprintf(fid, '%f %fn', y); fclose(fid); % display the file created type logtable.txt
Когда вы запускаете файл, он показывает следующий результат –
Log Function 0.000000 -Inf 10.000000 2.302585 20.000000 2.995732 30.000000 3.401197 40.000000 3.688879 50.000000 3.912023 60.000000 4.094345 70.000000 4.248495 80.000000 4.382027 90.000000 4.499810 100.000000 4.605170
MATLAB – Печать
Чтобы построить график функции, вам необходимо выполнить следующие шаги:
-
Определите x , указав диапазон значений для переменной x , для которой должна быть построена функция
-
Определите функцию, y = f (x)
-
Вызовите команду plot , как plot (x, y)
Определите x , указав диапазон значений для переменной x , для которой должна быть построена функция
Определите функцию, y = f (x)
Вызовите команду plot , как plot (x, y)
Следующий пример продемонстрирует концепцию. Построим простую функцию y = x для диапазона значений x от 0 до 100 с шагом 5.
Создайте файл сценария и введите следующий код –
x = [0:5:100]; y = x; plot(x, y)
Когда вы запускаете файл, MATLAB отображает следующий график –
Давайте возьмем еще один пример для построения функции y = x 2 . В этом примере мы нарисуем два графика с одной и той же функцией, но во второй раз мы уменьшим значение приращения. Обратите внимание, что при уменьшении приращения график становится более плавным.
Создайте файл сценария и введите следующий код –
x = [1 2 3 4 5 6 7 8 9 10]; x = [-100:20:100]; y = x.^2; plot(x, y)
Когда вы запускаете файл, MATLAB отображает следующий график –
Немного измените файл кода, уменьшите приращение до 5 –
x = [-100:5:100]; y = x.^2; plot(x, y)
MATLAB рисует более плавный график –
Добавление заголовка, меток, линий сетки и масштабирования на графике
MATLAB позволяет добавлять заголовки, метки вдоль осей X и Y, линии сетки, а также настраивать оси для улучшения графика.
-
Команды xlabel и ylabel генерируют метки вдоль оси x и оси y.
-
Команда title позволяет вам разместить заголовок на графике.
-
Команда grid on позволяет вам разместить линии сетки на графике.
-
Команда осевого равенства позволяет создать график с одинаковыми масштабными коэффициентами и пробелами на обеих осях.
-
Команда оси квадрат создает квадратный график.
Команды xlabel и ylabel генерируют метки вдоль оси x и оси y.
Команда title позволяет вам разместить заголовок на графике.
Команда grid on позволяет вам разместить линии сетки на графике.
Команда осевого равенства позволяет создать график с одинаковыми масштабными коэффициентами и пробелами на обеих осях.
Команда оси квадрат создает квадратный график.
пример
Создайте файл сценария и введите следующий код –
x = [0:0.01:10]; y = sin(x); plot(x, y), xlabel('x'), ylabel('Sin(x)'), title('Sin(x) Graph'), grid on, axis equal
MATLAB создает следующий график –
Рисование нескольких функций на одном графике
Вы можете нарисовать несколько графиков на одном графике. Следующий пример демонстрирует концепцию –
пример
Создайте файл сценария и введите следующий код –
x = [0 : 0.01: 10]; y = sin(x); g = cos(x); plot(x, y, x, g, '.-'), legend('Sin(x)', 'Cos(x)')
MATLAB создает следующий график –
Установка цветов на графике
MATLAB предоставляет восемь основных вариантов цвета для рисования графиков. В следующей таблице приведены цвета и их коды –
| Код | цвет |
|---|---|
| вес | белый |
| К | черный |
| б | синий |
| р | красный |
| с | Cyan |
| г | зеленый |
| м | фуксин |
| Y | желтый |
пример
Нарисуем график двух полиномов
-
f (x) = 3x 4 + 2x 3 + 7x 2 + 2x + 9 и
-
г (х) = 5х 3 + 9х + 2
f (x) = 3x 4 + 2x 3 + 7x 2 + 2x + 9 и
г (х) = 5х 3 + 9х + 2
Создайте файл сценария и введите следующий код –
x = [-10 : 0.01: 10]; y = 3*x.^4 + 2 * x.^3 + 7 * x.^2 + 2 * x + 9; g = 5 * x.^3 + 9 * x + 2; plot(x, y, 'r', x, g, 'g')
Когда вы запускаете файл, MATLAB генерирует следующий график –
Настройка весов оси
Команда оси позволяет вам установить масштаб оси. Вы можете указать минимальное и максимальное значения для осей x и y, используя команду оси следующим образом:
axis ( [xmin xmax ymin ymax] )
Следующий пример показывает это –
пример
Создайте файл сценария и введите следующий код –
x = [0 : 0.01: 10]; y = exp(-x).* sin(2*x + 3); plot(x, y), axis([0 10 -1 1])
Когда вы запускаете файл, MATLAB генерирует следующий график –
Генерация подзаговоров
Когда вы создаете массив графиков на одном и том же рисунке, каждый из этих графиков называется вложенным графиком. Команда subplot используется для создания подзаговоров.
Синтаксис для команды –
subplot(m, n, p)
где, m и n – количество строк и столбцов массива графика, а p указывает, куда поместить конкретный график.
Каждый график, созданный командой subplot, может иметь свои характеристики. Следующий пример демонстрирует концепцию –
пример
Давайте создадим два участка –
у = е -1,5х грех (10х)
у = е- 2х грех (10х)
Создайте файл сценария и введите следующий код –
x = [0:0.01:5]; y = exp(-1.5*x).*sin(10*x); subplot(1,2,1) plot(x,y), xlabel('x'),ylabel('exp(–1.5x)*sin(10x)'),axis([0 5 -1 1]) y = exp(-2*x).*sin(10*x); subplot(1,2,2) plot(x,y),xlabel('x'),ylabel('exp(–2x)*sin(10x)'),axis([0 5 -1 1])
Когда вы запускаете файл, MATLAB генерирует следующий график –
MATLAB – Графика
В этой главе мы продолжим изучение графических и графических возможностей MATLAB. Мы обсудим –
- Рисование гистограмм
- Рисование контуров
- Трехмерные участки
Рисование гистограмм
Команда bar рисует двухмерную гистограмму. Давайте возьмем пример, чтобы продемонстрировать идею.
пример
Пусть у нас будет воображаемый класс с 10 учениками. Мы знаем, что процент оценок, полученных этими студентами, составляет 75, 58, 90, 87, 50, 85, 92, 75, 60 и 95. Мы нарисуем гистограмму для этих данных.
Создайте файл сценария и введите следующий код –
x = [1:10]; y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95]; bar(x,y), xlabel('Student'),ylabel('Score'), title('First Sem:') print -deps graph.eps
Когда вы запускаете файл, MATLAB отображает следующую гистограмму –
Рисование контуров
Линия контура функции двух переменных – это кривая, вдоль которой функция имеет постоянное значение. Контурные линии используются для создания контурных карт путем объединения точек равной высоты над данным уровнем, например среднего уровня моря.
MATLAB предоставляет функцию контура для рисования контурных карт.
пример
Создадим контурную карту, которая показывает контурные линии для данной функции g = f (x, y). Эта функция имеет две переменные. Итак, нам нужно будет сгенерировать две независимые переменные, то есть два набора данных x и y. Это делается путем вызова команды meshgrid .
Команда meshgrid используется для генерации матрицы элементов, которые задают диапазон по x и y, а также задают приращение в каждом случае.
Построим нашу функцию g = f (x, y), где −5 ≤ x ≤ 5, −3 ≤ y ≤ 3. Давайте возьмем приращение 0,1 для обоих значений. Переменные установлены как –
[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);
Наконец, нам нужно назначить функцию. Пусть наша функция будет: x 2 + y 2
Создайте файл сценария и введите следующий код –
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables g = x.^2 + y.^2; % our function contour(x,y,g) % call the contour function print -deps graph.eps
Когда вы запускаете файл, MATLAB отображает следующую контурную карту –
Давайте немного изменим код, чтобы украсить карту
[x,y] = meshgrid(-5:0.1:5,-3:0.1:3); %independent variables g = x.^2 + y.^2; % our function [C, h] = contour(x,y,g); % call the contour function set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2) print -deps graph.eps
Когда вы запускаете файл, MATLAB отображает следующую контурную карту –
Трехмерные участки
Трехмерные графики в основном отображают поверхность, определенную функцией от двух переменных, g = f (x, y).
Как и прежде, чтобы определить g, мы сначала создаем набор точек (x, y) над областью функции, используя команду meshgrid . Далее мы назначаем саму функцию. Наконец, мы используем команду прибоя для создания графика поверхности.
Следующий пример демонстрирует концепцию –
пример
Давайте создадим трехмерную карту поверхности для функции g = xe – (x 2 + y 2 )
Создайте файл сценария и введите следующий код –
[x,y] = meshgrid(-2:.2:2); g = x .* exp(-x.^2 - y.^2); surf(x, y, g) print -deps graph.eps
Когда вы запускаете файл, MATLAB отображает следующую трехмерную карту –
Вы также можете использовать команду сетки для создания трехмерной поверхности. Однако команда surf отображает как соединительные линии, так и грани поверхности в цвете, тогда как команда mesh создает поверхность каркаса с цветными линиями, соединяющими определяющие точки.
MATLAB – алгебра
До сих пор мы видели, что все примеры работают как в MATLAB, так и в его GNU, альтернативно называемом Octave. Но для решения основных алгебраических уравнений и MATLAB, и Octave немного отличаются, поэтому мы постараемся охватить MATLAB и Octave в отдельных разделах.
Мы также обсудим факторизацию и упрощение алгебраических выражений.
Решение основных алгебраических уравнений в MATLAB
Функция решения используется для решения алгебраических уравнений. В простейшем виде функция решения принимает в качестве аргумента уравнение, заключенное в кавычки.
Например, давайте решим для х в уравнении х-5 = 0
solve('x-5=0')
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 5
Вы также можете вызвать функцию решения как –
y = solve('x-5 = 0')
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
y = 5
Вы можете даже не включать правую часть уравнения –
solve('x-5')
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 5
Если в уравнение входит несколько символов, то по умолчанию MATLAB предполагает, что вы решаете для x, однако функция решения имеет другую форму –
solve(equation, variable)
где вы также можете упомянуть переменную.
Например, давайте решим уравнение v – u – 3t 2 = 0, для v. В этом случае мы должны написать –
solve('v-u-3*t^2=0', 'v')
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 3*t^2 + u
Решение основных алгебраических уравнений в октаве
Функция корней используется для решения алгебраических уравнений в Octave, и вы можете написать приведенные выше примеры следующим образом:
Например, давайте решим для х в уравнении х-5 = 0
Live Demo
roots([1, -5])
Octave выполнит приведенный выше оператор и вернет следующий результат –
ans = 5
Вы также можете вызвать функцию решения как –
Live Demo
y = roots([1, -5])
Octave выполнит приведенный выше оператор и вернет следующий результат –
y = 5
Решение квадратичных уравнений в MATLAB
Функция решения также может решать уравнения более высокого порядка. Он часто используется для решения квадратных уравнений. Функция возвращает корни уравнения в массиве.
В следующем примере решается квадратное уравнение x 2 -7x +12 = 0. Создайте файл сценария и введите следующий код –
eq = 'x^2 -7*x + 12 = 0'; s = solve(eq); disp('The first root is: '), disp(s(1)); disp('The second root is: '), disp(s(2));
Когда вы запускаете файл, он показывает следующий результат –
The first root is: 3 The second root is: 4
Решение квадратичных уравнений в октаве
В следующем примере решается квадратное уравнение x 2 -7x +12 = 0 в октаве. Создайте файл сценария и введите следующий код –
Live Demo
s = roots([1, -7, 12]); disp('The first root is: '), disp(s(1)); disp('The second root is: '), disp(s(2));
Когда вы запускаете файл, он показывает следующий результат –
The first root is: 4 The second root is: 3
Решение уравнений высшего порядка в MATLAB
Функция решения также может решать уравнения более высокого порядка. Например, давайте решим кубическое уравнение как (x-3) 2 (x-7) = 0
solve('(x-3)^2*(x-7)=0')
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 3 3 7
В случае уравнений более высокого порядка корни длинные, содержащие много членов. Вы можете получить числовое значение таких корней, преобразовав их в двойные. В следующем примере решается уравнение четвертого порядка x 4 – 7x 3 + 3x 2 – 5x + 9 = 0.
Создайте файл сценария и введите следующий код –
eq = 'x^4 - 7*x^3 + 3*x^2 - 5*x + 9 = 0'; s = solve(eq); disp('The first root is: '), disp(s(1)); disp('The second root is: '), disp(s(2)); disp('The third root is: '), disp(s(3)); disp('The fourth root is: '), disp(s(4)); % converting the roots to double type disp('Numeric value of first root'), disp(double(s(1))); disp('Numeric value of second root'), disp(double(s(2))); disp('Numeric value of third root'), disp(double(s(3))); disp('Numeric value of fourth root'), disp(double(s(4)));
Когда вы запускаете файл, он возвращает следующий результат –
The first root is: 6.630396332390718431485053218985 The second root is: 1.0597804633025896291682772499885 The third root is: - 0.34508839784665403032666523448675 - 1.0778362954630176596831109269793*i The fourth root is: - 0.34508839784665403032666523448675 + 1.0778362954630176596831109269793*i Numeric value of first root 6.6304 Numeric value of second root 1.0598 Numeric value of third root -0.3451 - 1.0778i Numeric value of fourth root -0.3451 + 1.0778i
Обратите внимание, что последние два корня являются комплексными числами.
Решение уравнений высшего порядка в октаве
В следующем примере решается уравнение четвертого порядка x 4 – 7x 3 + 3x 2 – 5x + 9 = 0.
Создайте файл сценария и введите следующий код –
Live Demo
v = [1, -7, 3, -5, 9]; s = roots(v); % converting the roots to double type disp('Numeric value of first root'), disp(double(s(1))); disp('Numeric value of second root'), disp(double(s(2))); disp('Numeric value of third root'), disp(double(s(3))); disp('Numeric value of fourth root'), disp(double(s(4)));
Когда вы запускаете файл, он возвращает следующий результат –
Numeric value of first root 6.6304 Numeric value of second root -0.34509 + 1.07784i Numeric value of third root -0.34509 - 1.07784i Numeric value of fourth root 1.0598
Решение системы уравнений в MATLAB
Функция решения также может быть использована для генерации решений систем уравнений, включающих более одной переменной. Давайте рассмотрим простой пример, чтобы продемонстрировать это использование.
Давайте решим уравнения –
5x + 9y = 5
3x – 6y = 4
Создайте файл сценария и введите следующий код –
s = solve('5*x + 9*y = 5','3*x - 6*y = 4'); s.x s.y
Когда вы запускаете файл, он показывает следующий результат –
ans = 22/19 ans = -5/57
Таким же образом вы можете решать большие линейные системы. Рассмотрим следующую систему уравнений –
х + 3й -2z = 5
3x + 5y + 6z = 7
2x + 4y + 3z = 8
Решающая система уравнений в октаве
У нас есть немного другой подход к решению системы ‘n’ линейных уравнений с ‘n’ неизвестными. Давайте рассмотрим простой пример, чтобы продемонстрировать это использование.
Давайте решим уравнения –
5x + 9y = 5
3x – 6y = 4
Такая система линейных уравнений может быть записана в виде единого матричного уравнения Ax = b, где A – матрица коэффициентов, b – вектор столбцов, содержащий правую часть линейных уравнений, а x – вектор столбцов, представляющий решение как показано в программе ниже –
Создайте файл сценария и введите следующий код –
Live Demo
A = [5, 9; 3, -6]; b = [5;4]; A b
Когда вы запускаете файл, он показывает следующий результат –
ans = 1.157895 -0.087719
Таким же образом, вы можете решить большие линейные системы, как указано ниже –
х + 3й -2z = 5
3x + 5y + 6z = 7
2x + 4y + 3z = 8
Разложение и сбор уравнений в MATLAB
Функция расширения и сбора расширяет и собирает уравнение соответственно. Следующий пример демонстрирует понятия –
Когда вы работаете со многими символическими функциями, вы должны объявить, что ваши переменные являются символическими.
Создайте файл сценария и введите следующий код –
syms x %symbolic variable x syms y %symbolic variable x % expanding equations expand((x-5)*(x+9)) expand((x+2)*(x-3)*(x-5)*(x+7)) expand(sin(2*x)) expand(cos(x+y)) % collecting equations collect(x^3 *(x-7)) collect(x^4*(x-3)*(x-5))
Когда вы запускаете файл, он показывает следующий результат –
ans = x^2 + 4*x - 45 ans = x^4 + x^3 - 43*x^2 + 23*x + 210 ans = 2*cos(x)*sin(x) ans = cos(x)*cos(y) - sin(x)*sin(y) ans = x^4 - 7*x^3 ans = x^6 - 8*x^5 + 15*x^4
Расширяя и собирая уравнения в октаве
Вам нужно иметь символьный пакет, который обеспечивает расширение и функцию сбора для расширения и сбора уравнения, соответственно. Следующий пример демонстрирует понятия –
Когда вы работаете со многими символическими функциями, вы должны объявить, что ваши переменные являются символическими, но у Octave другой подход к определению символических переменных. Обратите внимание на использование Sin и Cos , которые также определены в символической упаковке.
Создайте файл сценария и введите следующий код –
% first of all load the package, make sure its installed. pkg load symbolic % make symbols module available symbols % define symbolic variables x = sym ('x'); y = sym ('y'); z = sym ('z'); % expanding equations expand((x-5)*(x+9)) expand((x+2)*(x-3)*(x-5)*(x+7)) expand(Sin(2*x)) expand(Cos(x+y)) % collecting equations collect(x^3 *(x-7), z) collect(x^4*(x-3)*(x-5), z)
Когда вы запускаете файл, он показывает следующий результат –
ans = -45.0+x^2+(4.0)*x ans = 210.0+x^4-(43.0)*x^2+x^3+(23.0)*x ans = sin((2.0)*x) ans = cos(y+x) ans = x^(3.0)*(-7.0+x) ans = (-3.0+x)*x^(4.0)*(-5.0+x)
Факторизация и упрощение алгебраических выражений
Факторная функция разлагает выражение, а функция упрощения упрощает выражение. Следующий пример демонстрирует концепцию –
пример
Создайте файл сценария и введите следующий код –
syms x syms y factor(x^3 - y^3) factor([x^2-y^2,x^3+y^3]) simplify((x^4-16)/(x^2-4))
Когда вы запускаете файл, он показывает следующий результат –
ans = (x - y)*(x^2 + x*y + y^2) ans = [ (x - y)*(x + y), (x + y)*(x^2 - x*y + y^2)] ans = x^2 + 4
MATLAB – Исчисление
MATLAB предоставляет различные способы решения задач дифференциального и интегрального исчисления, решения дифференциальных уравнений любой степени и расчета пределов. Лучше всего, вы можете легко построить графики сложных функций и проверить максимумы, минимумы и другие точки канцелярских товаров на графике, решив исходную функцию, а также ее производную.
В этой главе будут рассмотрены проблемы исчисления. В этой главе мы обсудим концепции предисчисления, то есть вычисления пределов функций и проверки свойств пределов.
В следующей главе Дифференциал мы вычислим производную выражения и найдем локальные максимумы и минимумы на графе. Мы также обсудим решение дифференциальных уравнений.
Наконец, в главе « Интеграция» мы обсудим интегральное исчисление.
Расчет лимитов
MATLAB предоставляет функцию предела для расчета пределов. В своей основной форме функция limit принимает выражение в качестве аргумента и находит предел выражения, когда независимая переменная стремится к нулю.
Например, давайте вычислим предел функции f (x) = (x 3 + 5) / (x 4 + 7), когда x стремится к нулю.
syms x limit((x^3 + 5)/(x^4 + 7))
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 5/7
Функция предела относится к области символьных вычислений; вам нужно использовать функцию syms, чтобы сообщить MATLAB, какие символические переменные вы используете. Вы также можете вычислить предел функции, так как переменная стремится к некоторому числу, отличному от нуля. Чтобы вычислить lim x-> a (f (x)), мы используем команду limit с аргументами. Первое – это выражение, а второе – число, к которому подходит x , здесь это a .
Например, давайте вычислим предел функции f (x) = (x-3) / (x-1), поскольку x стремится к 1.
limit((x - 3)/(x-1),1)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = NaN
Давайте возьмем другой пример,
limit(x^2 + 5, 3)
MATLAB выполнит приведенный выше оператор и вернет следующий результат –
ans = 14
Расчет лимитов с использованием октавы
Ниже приведена октавная версия приведенного выше примера с использованием символического пакета, попробуйте выполнить и сравнить результат –
pkg load symbolic symbols x = sym("x"); subs((x^3+5)/(x^4+7),x,0)
Octave выполнит приведенный выше оператор и вернет следующий результат –
ans = 0.7142857142857142857
Проверка основных свойств пределов
Алгебраическая предельная теорема обеспечивает некоторые основные свойства пределов. Это следующие –
Давайте рассмотрим две функции –
- f (x) = (3x + 5) / (x – 3)
- г (х) = х 2 + 1.
Давайте вычислим пределы функций при стремлении x к 5 для обеих функций и проверим основные свойства пределов, используя эти две функции и MATLAB.
пример
Создайте файл сценария и введите в него следующий код –
syms x f = (3*x + 5)/(x-3); g = x^2 + 1; l1 = limit(f, 4) l2 = limit (g, 4) lAdd = limit(f + g, 4) lSub = limit(f - g, 4) lMult = limit(f*g, 4) lDiv = limit (f/g, 4)
Когда вы запускаете файл, он отображает –
l1 = 17 l2 = 17 lAdd = 34 lSub = 0 lMult = 289 lDiv = 1
Проверка основных свойств лимитов с использованием октавы
Ниже приведена октавная версия приведенного выше примера с использованием символического пакета, попробуйте выполнить и сравнить результат –
pkg load symbolic symbols x = sym("x"); f = (3*x + 5)/(x-3); g = x^2 + 1; l1 = subs(f, x, 4) l2 = subs (g, x, 4) lAdd = subs (f+g, x, 4) lSub = subs (f-g, x, 4) lMult = subs (f*g, x, 4) lDiv = subs (f/g, x, 4)
Octave выполнит приведенный выше оператор и вернет следующий результат –
l1 = 17.0 l2 = 17.0 lAdd = 34.0 lSub = 0.0 lMult = 289.0 lDiv = 1.0
Левый и Правосторонний Пределы
Когда функция имеет разрыв для некоторого конкретного значения переменной, в этой точке ограничение не существует. Другими словами, пределы функции f (x) имеют разрыв при x = a, когда значение предела, когда x приближается к x с левой стороны, не равно значению предела, когда x приближается с правой стороны.
Это приводит к концепции пределов для левшей и правшей. Предел для левой руки определяется как предел как x -> a слева, т. Е. X приближается к a для значений x <a. Правосторонний предел определяется как предел как x -> a справа, т. Е. X приближается к a для значений x> a. Когда левосторонний лимит и правосторонний лимит не равны, этот предел не существует.
Давайте рассмотрим функцию –
f (x) = (x – 3) / | x – 3 |
Покажем, что lim x-> 3 f (x) не существует. MATLAB помогает нам установить этот факт двумя способами –
- Построить график функции и показать разрыв.
- Вычисляя пределы и показывая, что оба они разные.
Пределы для левшей и правшей вычисляются путем передачи строк символов ‘left’ и ‘right’ в команду limit в качестве последнего аргумента.
пример
Создайте файл сценария и введите в него следующий код –
f = (x - 3)/abs(x-3); ezplot(f,[-1,5]) l = limit(f,x,3,'left') r = limit(f,x,3,'right')
Когда вы запускаете файл, MATLAB рисует следующий график
После этого отображается следующий вывод –
l = -1 r = 1
MATLAB – Дифференциал
MATLAB предоставляет команду diff для вычисления символьных производных. В простейшей форме вы передаете функцию, которую вы хотите дифференцировать, команде diff в качестве аргумента.
Например, давайте вычислим производную функции f (t) = 3t 2 + 2t -2
пример
Создайте файл сценария и введите в него следующий код –
syms t f = 3*t^2 + 2*t^(-2); diff(f)
Когда приведенный выше код компилируется и выполняется, он дает следующий результат –
ans = 6*t - 4/t^3
Ниже приведен октавный эквивалент приведенного выше расчета –
pkg load symbolic symbols t = sym("t"); f = 3*t^2 + 2*t^(-2); differentiate(f,t)
Octave выполняет код и возвращает следующий результат –
ans = -(4.0)*t^(-3.0)+(6.0)*t
Проверка элементарных правил дифференциации
Кратко сформулируем различные уравнения или правила дифференцирования функций и проверим эти правила. Для этого мы напишем f ‘(x) для производной первого порядка и f “(x) для производной второго порядка.
Ниже приведены правила для дифференциации –
Правило 1
Для любых функций f и g и любых действительных чисел a и b являются производными функции –
h (x) = af (x) + bg (x) относительно x определяется как –
h ‘(x) = af’ (x) + bg ‘(x)
Правило 2
Правила сумм и вычитаний гласят, что если f и g две функции, то f ‘и g’ являются их производными соответственно, тогда
( f + g) ‘= f’ + g ‘
(f – g) ‘= f’ – g ‘
Правило 3
Правило произведения гласит, что если f и g две функции, f ‘и g’ являются их производными соответственно, то
(fg) ‘= f’.g + g’.f
Правило 4
Правило отношения гласит, что если f и g две функции, f ‘и g’ являются их производными соответственно, то
(f / g) ‘= (f’.g – g’.f) / g 2
Правило 5
Полиномиальное или элементарное степенное правило гласит, что если y = f (x) = x n , то f ‘= n. х (н-1)
Прямым результатом этого правила является то, что производная любой константы равна нулю, т. Е. Если y = k , любая константа, то
f ‘= 0
Правило 6
Правило цепочки гласит, что производная функции функции h (x) = f (g (x)) по x равна
h ‘(x) = f’ (g (x)). g ‘(x)
пример
Создайте файл сценария и введите в него следующий код –
syms x syms t f = (x + 2)*(x^2 + 3) der1 = diff(f) f = (t^2 + 3)*(sqrt(t) + t^3) der2 = diff(f) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = diff(f) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = diff(f) f = (x^2 + 1)^17 der5 = diff(f) f = (t^3 + 3* t^2 + 5*t -9)^(-6) der6 = diff(f)
Когда вы запускаете файл, MATLAB отображает следующий результат –
f = (x^2 + 3)*(x + 2) der1 = 2*x*(x + 2) + x^2 + 3 f = (t^(1/2) + t^3)*(t^2 + 3) der2 = (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2 f = (x^2 + 1)^17 der5 = 34*x*(x^2 + 1)^16 f = 1/(t^3 + 3*t^2 + 5*t - 9)^6 der6 = -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7
Ниже приведен октавный эквивалент приведенного выше расчета –
pkg load symbolic symbols x = sym("x"); t = sym("t"); f = (x + 2)*(x^2 + 3) der1 = differentiate(f,x) f = (t^2 + 3)*(t^(1/2) + t^3) der2 = differentiate(f,t) f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) der3 = differentiate(f,x) f = (2*x^2 + 3*x)/(x^3 + 1) der4 = differentiate(f,x) f = (x^2 + 1)^17 der5 = differentiate(f,x) f = (t^3 + 3* t^2 + 5*t -9)^(-6) der6 = differentiate(f,t)
Octave выполняет код и возвращает следующий результат –
f = (2.0+x)*(3.0+x^(2.0)) der1 = 3.0+x^(2.0)+(2.0)*(2.0+x)*x f = (t^(3.0)+sqrt(t))*(3.0+t^(2.0)) der2 = (2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0)) f = (1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0)) der3 = (-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x) f = (1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x) der4 = (1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x) f = (1.0+x^(2.0))^(17.0) der5 = (34.0)*(1.0+x^(2.0))^(16.0)*x f = (-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0) der6 = -(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)
Производные экспоненциальных, логарифмических и тригонометрических функций
В следующей таблице приведены производные от часто используемых экспоненциальных, логарифмических и тригонометрических функций.
| функция | производный |
|---|---|
| топор с | c ax. ln ca (ln – натуральный логарифм) |
| е х | е х |
| ln x | 1 / х |
| ln c x | 1 / x.ln c |
| х х | х х (1 + лн х) |
| грех (х) | сов (х) |
| сов (х) | -sin (х) |
| тангенс (х) | sec 2 (x), или 1 / cos 2 (x), или 1 + tan 2 (x) |
| кроватка (х) | -csc 2 (x) или -1 / sin 2 (x) или – (1 + кроватка 2 (x)) |
| с (х) | с (х) .tan (х) |
| CSC (х) | -csc (х) .cot (х) |
пример
Создайте файл сценария и введите в него следующий код –
syms x y = exp(x) diff(y) y = x^9 diff(y) y = sin(x) diff(y) y = tan(x) diff(y) y = cos(x) diff(y) y = log(x) diff(y) y = log10(x) diff(y) y = sin(x)^2 diff(y) y = cos(3*x^2 + 2*x + 1) diff(y) y = exp(x)/sin(x) diff(y)
Когда вы запускаете файл, MATLAB отображает следующий результат –
y = exp(x) ans = exp(x) y = x^9 ans = 9*x^8 y = sin(x) ans = cos(x) y = tan(x) ans = tan(x)^2 + 1 y = cos(x) ans = -sin(x) y = log(x) ans = 1/x y = log(x)/log(10) ans = 1/(x*log(10)) y = sin(x)^2 ans = 2*cos(x)*sin(x) y = cos(3*x^2 + 2*x + 1) ans = -sin(3*x^2 + 2*x + 1)*(6*x + 2) y = exp(x)/sin(x) ans = exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2
Ниже приведен октавный эквивалент приведенного выше расчета –
pkg load symbolic symbols x = sym("x"); y = Exp(x) differentiate(y,x) y = x^9 differentiate(y,x) y = Sin(x) differentiate(y,x) y = Tan(x) differentiate(y,x) y = Cos(x) differentiate(y,x) y = Log(x) differentiate(y,x) % symbolic packages does not have this support %y = Log10(x) %differentiate(y,x) y = Sin(x)^2 differentiate(y,x) y = Cos(3*x^2 + 2*x + 1) differentiate(y,x) y = Exp(x)/Sin(x) differentiate(y,x)
Octave выполняет код и возвращает следующий результат –
y = exp(x) ans = exp(x) y = x^(9.0) ans = (9.0)*x^(8.0) y = sin(x) ans = cos(x) y = tan(x) ans = 1+tan(x)^2 y = cos(x) ans = -sin(x) y = log(x) ans = x^(-1) y = sin(x)^(2.0) ans = (2.0)*sin(x)*cos(x) y = cos(1.0+(2.0)*x+(3.0)*x^(2.0)) ans = -(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0)) y = sin(x)^(-1)*exp(x) ans = sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)
Вычисление производных высшего порядка
Для вычисления старших производных функции f мы используем синтаксис diff (f, n) .
Вычислим вторую производную функции y = f (x) = x .e -3x
f = x*exp(-3*x); diff(f, 2)
MATLAB выполняет код и возвращает следующий результат –
ans = 9*x*exp(-3*x) - 6*exp(-3*x)
Ниже приведен октавный эквивалент приведенного выше расчета –
pkg load symbolic symbols x = sym("x"); f = x*Exp(-3*x); differentiate(f, x, 2)
Octave выполняет код и возвращает следующий результат –
ans = (9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)
пример
В этом примере давайте решим проблему. Учитывая, что функция y = f (x) = 3 sin (x) + 7 cos (5x) . Нам нужно выяснить, выполняется ли уравнение f “+ f = -5cos (2x) .
Создайте файл сценария и введите в него следующий код –
syms x y = 3*sin(x)+7*cos(5*x); % defining the function lhs = diff(y,2)+y; %evaluting the lhs of the equation rhs = -5*cos(2*x); %rhs of the equation if(isequal(lhs,rhs)) disp('Yes, the equation holds true'); else disp('No, the equation does not hold true'); end disp('Value of LHS is: '), disp(lhs);
Когда вы запускаете файл, он показывает следующий результат –
No, the equation does not hold true Value of LHS is: -168*cos(5*x)
Ниже приведен октавный эквивалент приведенного выше расчета –
pkg load symbolic symbols x = sym("x"); y = 3*Sin(x)+7*Cos(5*x); % defining the function lhs = differentiate(y, x, 2) + y; %evaluting the lhs of the equation rhs = -5*Cos(2*x); %rhs of the equation if(lhs == rhs) disp('Yes, the equation holds true'); else disp('No, the equation does not hold true'); end disp('Value of LHS is: '), disp(lhs);
Octave выполняет код и возвращает следующий результат –
No, the equation does not hold true Value of LHS is: -(168.0)*cos((5.0)*x)
Нахождение максимумов и минимумов кривой
Если мы ищем локальные максимумы и минимумы для графика, мы в основном ищем самые высокие или самые низкие точки на графике функции в определенной местности или для определенного диапазона значений символической переменной.
Для функции y = f (x) точки на графе, где граф имеет нулевой наклон, называются стационарными точками . Другими словами, стационарные точки – это где f ‘(x) = 0.
Чтобы найти стационарные точки функции, которую мы дифференцируем, нам нужно установить производную равной нулю и решить уравнение.
пример
Найдем стационарные точки функции f (x) = 2x 3 + 3x 2 – 12x + 17
Сделайте следующие шаги –
Сначала давайте введем функцию и построим ее график.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y)
MATLAB выполняет код и возвращает следующий график –
Вот октавный эквивалентный код для приведенного выше примера –
pkg load symbolic symbols x = sym('x'); y = inline("2*x^3 + 3*x^2 - 12*x + 17"); ezplot(y) print -deps graph.eps
Наша цель – найти некоторые локальные максимумы и минимумы на графике, поэтому давайте найдем локальные максимумы и минимумы для интервала [-2, 2] на графике.
syms x y = 2*x^3 + 3*x^2 - 12*x + 17; % defining the function ezplot(y, [-2, 2])
MATLAB выполняет код и возвращает следующий график –
Вот октавный эквивалентный код для приведенного выше примера –
pkg load symbolic symbols x = sym('x'); y = inline("2*x^3 + 3*x^2 - 12*x + 17"); ezplot(y, [-2, 2]) print -deps graph.eps
Далее, давайте вычислим производную.
g = diff(y)
MATLAB выполняет код и возвращает следующий результат –
g = 6*x^2 + 6*x - 12
Вот октавный эквивалент приведенного выше расчета –
pkg load symbolic symbols x = sym("x"); y = 2*x^3 + 3*x^2 - 12*x + 17; g = differentiate(y,x)
Octave выполняет код и возвращает следующий результат –
g = -12.0+(6.0)*x+(6.0)*x^(2.0)
Давайте решим производную функцию g, чтобы получить значения, где она становится равной нулю.
s = solve(g)
MATLAB выполняет код и возвращает следующий результат –
s = 1 -2
Ниже приведен октавный эквивалент приведенного выше расчета –
pkg load symbolic symbols x = sym("x"); y = 2*x^3 + 3*x^2 - 12*x + 17; g = differentiate(y,x) roots([6, 6, -12])
Octave выполняет код и возвращает следующий результат –
g = -12.0+(6.0)*x^(2.0)+(6.0)*x ans = -2 1
Это согласуется с нашим сюжетом. Итак, давайте оценим функцию f в критических точках x = 1, -2. Мы можем подставить значение в символическую функцию с помощью команды subs .
subs(y, 1), subs(y, -2)
MATLAB выполняет код и возвращает следующий результат –
ans = 10 ans = 37
Ниже приведен октавный эквивалент приведенного выше расчета –
pkg load symbolic symbols x = sym("x"); y = 2*x^3 + 3*x^2 - 12*x + 17; g = differentiate(y,x) roots([6, 6, -12]) subs(y, x, 1), subs(y, x, -2)
ans = 10.0 ans = 37.0-4.6734207789940138748E-18*I
Следовательно, минимальное и максимальное значения для функции f (x) = 2x 3 + 3x 2 – 12x + 17 в интервале [-2,2] составляют 10 и 37.
Решение дифференциальных уравнений
MATLAB предоставляет команду dsolve для символического решения дифференциальных уравнений.
Наиболее простой формой команды dsolve для поиска решения одного уравнения является
dsolve('eqn')
где eqn – текстовая строка, используемая для ввода уравнения.
Он возвращает символическое решение с набором произвольных констант, которые MATLAB помечает C1, C2 и так далее.
Вы также можете указать начальные и граничные условия для задачи в виде списка с разделителями-запятыми после уравнения в виде –
dsolve('eqn','cond1', 'cond2',…)
В целях использования команды dsolve производные обозначены знаком D. Например, уравнение типа f ‘(t) = -2 * f + стоимость (t) вводится как –
‘Df = -2 * f + cos (t)’
Высшие производные обозначены следующим за D порядком производной.
Например, уравнение f “(x) + 2f ‘(x) = 5sin3x должно быть введено как –
‘D2y + 2Dy = 5 * sin (3 * x)’
Давайте рассмотрим простой пример дифференциального уравнения первого порядка: y ‘= 5y.
s = dsolve('Dy = 5*y')
MATLAB выполняет код и возвращает следующий результат –
s = C2*exp(5*t)
Давайте рассмотрим другой пример дифференциального уравнения второго порядка: y “- y = 0, y (0) = -1, y ‘(0) = 2.
dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')
MATLAB выполняет код и возвращает следующий результат –
ans = exp(t)/2 - (3*exp(-t))/2
MATLAB – Интеграция
Интеграция имеет дело с двумя принципиально разными типами проблем.
-
В первом типе дается производная функции, и мы хотим найти функцию. Поэтому мы в основном обращаем вспять процесс дифференциации. Этот обратный процесс известен как антидифференцирование, или нахождение примитивной функции, или нахождение неопределенного интеграла .
-
Второй тип проблем включает сложение очень большого количества очень маленьких величин, а затем определение предела, когда размер величин приближается к нулю, а число членов стремится к бесконечности. Этот процесс приводит к определению определенного интеграла .
В первом типе дается производная функции, и мы хотим найти функцию. Поэтому мы в основном обращаем вспять процесс дифференциации. Этот обратный процесс известен как антидифференцирование, или нахождение примитивной функции, или нахождение неопределенного интеграла .
Второй тип проблем включает сложение очень большого количества очень маленьких величин, а затем определение предела, когда размер величин приближается к нулю, а число членов стремится к бесконечности. Этот процесс приводит к определению определенного интеграла .
Определенные интегралы используются для определения площади, объема, центра тяжести, момента инерции, работы, выполняемой силой, и во многих других приложениях.
Поиск неопределенного интеграла с помощью MATLAB
По определению, если производная функции f (x) есть f ‘(x), то мы говорим, что неопределенный интеграл от f’ (x) по x равен f (x). Например, поскольку производная (по x) x 2 равна 2x, мы можем сказать, что неопределенный интеграл от 2x равен x 2 .
В символах –
f ‘(x 2 ) = 2x , следовательно,
∫ 2xdx = x 2 .
Неопределенный интеграл не является уникальным, потому что производная x 2 + c для любого значения константы c также будет 2x.
Это выражается в символах как –
∫ 2xdx = x 2 + c .
Где c называется «произвольной константой».
MATLAB предоставляет команду int для вычисления интеграла выражения. Чтобы вывести выражение для неопределенного интеграла функции, мы пишем –
int(f);
Например, из нашего предыдущего примера –
syms x int(2*x)
MATLAB выполняет приведенный выше оператор и возвращает следующий результат –
ans = x^2
Пример 1
В этом примере давайте найдем интеграл некоторых часто используемых выражений. Создайте файл сценария и введите в нем следующий код –
syms x n int(sym(x^n)) f = 'sin(n*t)' int(sym(f)) syms a t int(a*cos(pi*t)) int(a^x)
Когда вы запускаете файл, он показывает следующий результат –
ans = piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)]) f = sin(n*t) ans = -cos(n*t)/n ans = (a*sin(pi*t))/pi ans = a^x/log(a)
Пример 2
Создайте файл сценария и введите в нем следующий код –
syms x n int(cos(x)) int(exp(x)) int(log(x)) int(x^-1) int(x^5*cos(5*x)) pretty(int(x^5*cos(5*x))) int(x^-5) int(sec(x)^2) pretty(int(1 - 10*x + 9 * x^2)) int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2) pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))
Обратите внимание, что функция pretty возвращает выражение в более читаемом формате.
Когда вы запускаете файл, он показывает следующий результат –
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ------------
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2
Нахождение определенного интеграла с помощью MATLAB
По определению, определенный интеграл в основном является пределом суммы. Мы используем определенные интегралы, чтобы найти области, такие как область между кривой и осью x и область между двумя кривыми. Определенные интегралы могут также использоваться в других ситуациях, где требуемое количество может быть выражено как предел суммы.
Функция int может использоваться для определенной интеграции, передавая пределы, по которым вы хотите вычислить интеграл.
Вычислять
мы пишем,
int(x, a, b)
Например, для расчета стоимости 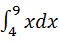
int(x, 4, 9)
MATLAB выполняет приведенный выше оператор и возвращает следующий результат –
ans = 65/2
Ниже приведен октавный эквивалент приведенного выше расчета –
pkg load symbolic symbols x = sym("x"); f = x; c = [1, 0]; integral = polyint(c); a = polyval(integral, 9) - polyval(integral, 4); display('Area: '), disp(double(a));
Octave выполняет код и возвращает следующий результат –
Area: 32.500
Альтернативное решение может быть дано с помощью функции quad (), предоставляемой Octave следующим образом:
pkg load symbolic symbols f = inline("x"); [a, ierror, nfneval] = quad(f, 4, 9); display('Area: '), disp(double(a));
Octave выполняет код и возвращает следующий результат –
Area: 32.500
Пример 1
Вычислим площадь, заключенную между осью x и кривой y = x 3 -2x + 5 и ординатами x = 1 и x = 2.
Требуемая площадь определяется как –
Создайте файл сценария и введите следующий код –
f = x^3 - 2*x +5; a = int(f, 1, 2) display('Area: '), disp(double(a));
Когда вы запускаете файл, он показывает следующий результат –
a = 23/4 Area: 5.7500
Ниже приведен октавный эквивалент приведенного выше расчета –
pkg load symbolic symbols x = sym("x"); f = x^3 - 2*x +5; c = [1, 0, -2, 5]; integral = polyint(c); a = polyval(integral, 2) - polyval(integral, 1); display('Area: '), disp(double(a));
Octave выполняет код и возвращает следующий результат –
Area: 5.7500
Альтернативное решение может быть дано с помощью функции quad (), предоставляемой Octave следующим образом:
pkg load symbolic symbols x = sym("x"); f = inline("x^3 - 2*x +5"); [a, ierror, nfneval] = quad(f, 1, 2); display('Area: '), disp(double(a));
Octave выполняет код и возвращает следующий результат –
Area: 5.7500
Пример 2
Найдите площадь под кривой: f (x) = x 2 cos (x) для −4 ≤ x ≤ 9.
Создайте файл сценария и напишите следующий код –
f = x^2*cos(x); ezplot(f, [-4,9]) a = int(f, -4, 9) disp('Area: '), disp(double(a));
Когда вы запускаете файл, MATLAB строит график –
Выход дан ниже –
a = 8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9) Area: 0.3326
Ниже приведен октавный эквивалент приведенного выше расчета –
pkg load symbolic symbols x = sym("x"); f = inline("x^2*cos(x)"); ezplot(f, [-4,9]) print -deps graph.eps [a, ierror, nfneval] = quad(f, -4, 9); display('Area: '), disp(double(a));
MATLAB – многочлены
MATLAB представляет полиномы как векторы строк, содержащие коэффициенты, упорядоченные по убыванию степеней. Например, уравнение P (x) = x 4 + 7x 3 – 5x + 9 может быть представлено как –
р = [1 7 0 -5 9];
Оценка полиномов
Функция polyval используется для оценки полинома по указанному значению. Например, чтобы оценить наш предыдущий полином p при x = 4, введите –
Live Demo
p = [1 7 0 -5 9]; polyval(p,4)
MATLAB выполняет вышеуказанные операторы и возвращает следующий результат –
ans = 693
MATLAB также предоставляет функцию поливалма для вычисления матричного полинома. Матричный полином – это полином с матрицами в качестве переменных.
Например, давайте создадим квадратную матрицу X и оценим многочлен p, в X –
Live Demo
p = [1 7 0 -5 9]; X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8]; polyvalm(p, X)
MATLAB выполняет вышеуказанные операторы и возвращает следующий результат –
ans =
2307 -1769 -939 4499
2314 -2376 -249 4695
2256 -1892 -549 4310
4570 -4532 -1062 9269
Нахождение корней полиномов
Функция корней вычисляет корни многочлена. Например, чтобы вычислить корни нашего полинома p, наберите
Live Demo
p = [1 7 0 -5 9]; r = roots(p)
MATLAB выполняет вышеуказанные операторы и возвращает следующий результат –
r = -6.8661 + 0.0000i -1.4247 + 0.0000i 0.6454 + 0.7095i 0.6454 - 0.7095i
Функция poly является обратной функцией корней и возвращается к полиномиальным коэффициентам. Например –
p2 = poly(r)
MATLAB выполняет вышеуказанные операторы и возвращает следующий результат –
p2 =
Columns 1 through 3:
1.00000 + 0.00000i 7.00000 + 0.00000i 0.00000 + 0.00000i
Columns 4 and 5:
-5.00000 - 0.00000i 9.00000 + 0.00000i
Фитинг полиномиальной кривой
Функция polyfit находит коэффициенты полинома, который соответствует набору данных в смысле наименьших квадратов. Если x и y – это два вектора, содержащие данные x и y, которые нужно подогнать к полиному n-степени, то мы получим полином, подгоняющий данные, написав:
p = polyfit(x,y,n)
пример
Создайте файл сценария и введите следующий код –
Live Demo
x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67]; %data p = polyfit(x,y,4) %get the polynomial % Compute the values of the polyfit estimate over a finer range, % and plot the estimate over the real data values for comparison: x2 = 1:.1:6; y2 = polyval(p,x2); plot(x,y,'o',x2,y2) grid on
Когда вы запускаете файл, MATLAB отображает следующий результат –
p = 4.1056 -47.9607 222.2598 -362.7453 191.1250
И строит следующий график –
MATLAB – Преобразования
MATLAB предоставляет команду для работы с преобразованиями, такими как преобразования Лапласа и Фурье. Преобразования используются в науке и технике как инструмент для упрощения анализа и анализа данных с другой стороны.
Например, преобразование Фурье позволяет нам преобразовывать сигнал, представленный как функцию времени, в функцию частоты. Преобразование Лапласа позволяет преобразовать дифференциальное уравнение в алгебраическое уравнение.
MATLAB предоставляет команды laplace , fourier и fft для работы с преобразованиями Laplace, Fourier и Fast Fourier.
Преобразование Лапласа
Преобразование Лапласа функции времени f (t) задается следующим интегралом:
Преобразование Лапласа также обозначается как преобразование f (t) в F (s). Вы можете видеть, что этот процесс преобразования или интеграции преобразует функцию f (t) символической переменной t в другую функцию F (s) с другой переменной s.
Преобразование Лапласа превращает дифференциальные уравнения в алгебраические. Чтобы вычислить преобразование Лапласа функции f (t), напишите –
laplace(f(t))
пример
В этом примере мы вычислим преобразование Лапласа некоторых часто используемых функций.
Создайте файл сценария и введите следующий код –
syms s t a b w laplace(a) laplace(t^2) laplace(t^9) laplace(exp(-b*t)) laplace(sin(w*t)) laplace(cos(w*t))
Когда вы запускаете файл, он показывает следующий результат –
ans = 1/s^2 ans = 2/s^3 ans = 362880/s^10 ans = 1/(b + s) ans = w/(s^2 + w^2) ans = s/(s^2 + w^2)
Обратное преобразование Лапласа
MATLAB позволяет нам вычислять обратное преобразование Лапласа, используя команду ilaplace .
Например,
ilaplace(1/s^3)
MATLAB выполнит приведенную выше инструкцию и отобразит результат –
ans = t^2/2
пример
Создайте файл сценария и введите следующий код –
syms s t a b w ilaplace(1/s^7) ilaplace(2/(w+s)) ilaplace(s/(s^2+4)) ilaplace(exp(-b*t)) ilaplace(w/(s^2 + w^2)) ilaplace(s/(s^2 + w^2))
Когда вы запускаете файл, он показывает следующий результат –
ans = t^6/720 ans = 2*exp(-t*w) ans = cos(2*t) ans = ilaplace(exp(-b*t), t, x) ans = sin(t*w) ans = cos(t*w)
Преобразования Фурье
Преобразования Фурье обычно преобразуют математическую функцию времени f (t) в новую функцию, иногда обозначаемую или F, аргумент которой – частота с единицами циклов / с (герц) или радианами в секунду. Новая функция тогда называется преобразованием Фурье и / или частотным спектром функции f.
пример
Создайте файл сценария и введите в нем следующий код –
syms x f = exp(-2*x^2); %our function ezplot(f,[-2,2]) % plot of our function FT = fourier(f) % Fourier transform
Когда вы запускаете файл, MATLAB строит следующий график –
Следующий результат отображается –
FT = (2^(1/2)*pi^(1/2)*exp(-w^2/8))/2
Построение преобразования Фурье как –
ezplot(FT)
Дает следующий график –
Обратные преобразования Фурье
MATLAB предоставляет команду ifourier для вычисления обратного преобразования Фурье функции. Например,
f = ifourier(-2*exp(-abs(w)))
MATLAB выполнит приведенную выше инструкцию и отобразит результат –
f = -2/(pi*(x^2 + 1))
MATLAB – GNU Octave Tutorial
GNU Octave – это язык программирования высокого уровня, такой как MATLAB, и он в основном совместим с MATLAB. Он также используется для численных расчетов.
Octave имеет следующие общие черты с MATLAB:
- матрицы являются фундаментальным типом данных
- имеет встроенную поддержку комплексных чисел
- имеет встроенные математические функции и библиотеки
- поддерживает пользовательские функции
GNU Octave также является свободно распространяемым программным обеспечением. Вы можете распространять его и / или изменять его в соответствии с условиями Стандартной общественной лицензии GNU (GPL), опубликованной Free Software Foundation.
Матлаб против Октавы
Большинство программ MATLAB работают в Octave, но некоторые из программ Octave могут не работать в MATLAB, потому что Octave допускает некоторый синтаксис, которого нет в MATLAB.
Например, MATLAB поддерживает только одинарные кавычки, но Octave поддерживает одинарные и двойные кавычки для определения строк. Если вы ищете учебник по Octave, просим пройти этот учебник с самого начала, который охватывает как MATLAB, так и Octave.
Совместимые примеры
Почти все примеры, описанные в этом руководстве, совместимы как с MATLAB, так и с Octave. Давайте попробуем следующий пример в MATLAB и Octave, который дает тот же результат без каких-либо изменений синтаксиса –
В этом примере создается трехмерная карта поверхности для функции g = xe – (x 2 + y 2 ) . Создайте файл сценария и введите следующий код –
[x,y] = meshgrid(-2:.2:2); g = x .* exp(-x.^2 - y.^2); surf(x, y, g) print -deps graph.eps
Когда вы запускаете файл, MATLAB отображает следующую трехмерную карту –
Несовместимые примеры
Хотя все основные функции MATLAB доступны в Octave, есть некоторые функции, например, Дифференциальное и интеграционное исчисление, которые не совпадают точно в обоих языках. В этом руководстве были приведены примеры обоих типов, в которых они различались по синтаксису.
Рассмотрим следующий пример, где MATLAB и Octave используют разные функции для получения области кривой: f (x) = x 2 cos (x) для −4 ≤ x ≤ 9. Ниже приводится версия кода MATLAB –
f = x^2*cos(x); ezplot(f, [-4,9]) a = int(f, -4, 9) disp('Area: '), disp(double(a));
Когда вы запускаете файл, MATLAB строит график –
Следующий результат отображается
a = 8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9) Area: 0.3326
Но чтобы дать область той же кривой в Octave, вам придется использовать символический пакет следующим образом:
pkg load symbolic symbols x = sym("x"); f = inline("x^2*cos(x)"); ezplot(f, [-4,9]) print -deps graph.eps [a, ierror, nfneval] = quad(f, -4, 9); display('Area: '), disp(double(a));
МАТЛАБ – Симулинк
Simulink – это среда моделирования и проектирования на основе моделей для динамических и встроенных систем, интегрированная с MATLAB. Simulink, также разработанный MathWorks, представляет собой инструмент языка графического программирования потоков данных для моделирования, моделирования и анализа многодоменных динамических систем. В основном это графический инструмент для построения блок-схем с настраиваемым набором библиотек блоков.
Это позволяет включать алгоритмы MATLAB в модели, а также экспортировать результаты моделирования в MATLAB для дальнейшего анализа.
Simulink поддерживает –
- системный дизайн
- моделирование
- автоматическая генерация кода
- тестирование и проверка встроенных систем
Существует несколько других дополнительных продуктов, предоставляемых MathWorks и сторонними аппаратными и программными продуктами, которые доступны для использования с Simulink.
Следующий список дает краткое описание некоторых из них –
-
Stateflow позволяет разрабатывать конечные автоматы и блок-схемы.
-
Simulink Coder позволяет генерировать исходный код на C для автоматической реализации систем в реальном времени.
-
xPC Target вместе с системами реального времени на базе x86 обеспечивают среду для имитации и тестирования моделей Simulink и Stateflow в реальном времени на физической системе.
-
Встроенный кодер поддерживает определенные встроенные цели.
-
HDL Coder позволяет автоматически генерировать синтезируемые VHDL и Verilog.
-
SimEvents предоставляет библиотеку графических строительных блоков для моделирования систем массового обслуживания.
Stateflow позволяет разрабатывать конечные автоматы и блок-схемы.
Simulink Coder позволяет генерировать исходный код на C для автоматической реализации систем в реальном времени.
xPC Target вместе с системами реального времени на базе x86 обеспечивают среду для имитации и тестирования моделей Simulink и Stateflow в реальном времени на физической системе.
Встроенный кодер поддерживает определенные встроенные цели.
HDL Coder позволяет автоматически генерировать синтезируемые VHDL и Verilog.
SimEvents предоставляет библиотеку графических строительных блоков для моделирования систем массового обслуживания.
Simulink способен систематически проверять и проверять модели посредством проверки стиля моделирования, отслеживания требований и анализа охвата модели.
Simulink Design Verifier позволяет выявлять ошибки проектирования и генерировать сценарии тестирования для проверки модели.
Использование Simulink
Чтобы открыть Simulink, введите рабочее пространство MATLAB –
simulink
Simulink открывается с помощью браузера библиотеки . Браузер библиотеки используется для построения имитационных моделей.
В левой части окна вы найдете несколько библиотек, распределенных по категориям на основе различных систем, щелкнув по каждой из них, вы увидите блоки дизайна на правой панели окна.
Модели зданий
Чтобы создать новую модель, нажмите кнопку « Создать» на панели инструментов браузера библиотеки. Это открывает новое безымянное окно модели.
Модель Simulink – это блок-схема.
Элементы модели добавляются путем выбора соответствующих элементов в браузере библиотеки и перетаскивания их в окно модели.
Кроме того, вы можете скопировать элементы модели и вставить их в окно модели.
Примеры
Перетащите элементы из библиотеки Simulink, чтобы создать свой проект.
В этом примере для моделирования будут использоваться два блока – Источник (сигнал) и Раковина (область). Генератор сигналов (источник) генерирует аналоговый сигнал, который затем будет графически визуализирован областью действия (приемником).
Начните с перетаскивания необходимых блоков из библиотеки в окно проекта. Затем соедините блоки вместе, что можно сделать, перетаскивая соединители из точек соединения одного блока в точки другого.
Давайте перетащим блок «Синусоида» в модель.
Выберите «Sinks» из библиотеки и перетащите блок «Scope» в модель.
Перетащите сигнальную линию с выхода блока синусоидальной волны на вход блока Scope.
Запустите симуляцию, нажав кнопку « Выполнить », сохраняя все параметры по умолчанию (вы можете изменить их из меню симуляции)
Вы должны получить ниже график из области видимости.
Символьные вычисления в Matlab
Здравствуйте, уважаемые читатели. В этой небольшой статье речь пойдет о работе с символьными переменными в Matlab. На простых примерах мы разберем преобразование символьных выражений, а также символьное дифференцирование и интегрирование.
Создание символьного выражения в Matlab
Иногда символьные выражения крайне необходимы, именно поэтому важно уметь их объявлять в Matlab. Обычно используют два способа. Первый — использование оператора syms.
Таким простым способом мы создали две символьные переменные. Пока они ничего не делают и не представляют какой либо ценности, но чуть позже мы увидим, что они могут быть полезны.
Второй способ — использование команды sym.
При ее использовании, можно сразу задать функцию, полином или выражение:
Символьные выражения полезны тем, что вычисления с ними производятся без погрешностей.
Преобразования символьных выражений в Matlab
Возможны несколько типов преобразований:
- Функция раскрытия скобок expand
Для примера зададим символьное выражение и попробуем раскрыть скобки:
- Функция упрощения simplify
Данная функция помогает упростить символьное выражение в Matlab. Возьмем для примера такое выражение.
- Функция разложения на множители factor
Данная функция помогает преобразовать символьное выражение, например, в полином в Matlab. Иногда, это бывает очень важно и необходимо.
Вычисление значения символьных выражений в Matlab
Конечно, символьные выражения это интересный инструмент в Matlab, но хотелось бы находить значение этого выражения при каких-то заданных значениях переменной.
Для этого можно воспользоваться несколькими функциями. Сначала нужно заменить все переменные на число с помощью оператора subs. Затем перевести полученное выражение в числовое с помощью оператора double. Разберем пример:
Стоит отметить, что после выполнения оператора subs, выражение все еще остается символьным. Поэтому далее выполняется оператор double.
Если же у функции несколько переменных, то придется использовать subs несколько раз.
Символьное дифференцирование в Matlab
На нашем сайте уже были статьи по численному дифференцированию в среде Matlab, но любой численный метод может давать погрешности. А вычисление в символьном виде может быть очень полезным и точным.
Итак, символьное дифференцирование осуществляется оператором diff. При вызове функции следует указать переменную, по которой будет производиться дифференцирование.
В этом примере функция зависит от одной переменной, поэтому производная считается по ней автоматически. Если нужно вычислить вторую производную:
Теперь посмотрим на функцию от нескольких переменных:
Очевидно, что после получения производных, с ними можно выполнить все действия, описанные выше.
Символьное интегрирование в Matlab
Наряду с дифференцированием, в Matlab можно выполнять символьное интегрирование. Иногда это бывает удобнее, чем численное интегрирование. Символьное интегрирование в Matlab выполняется оператором int.
Оператор выполняется практически также, как и оператор дифференцирования.
Также, возможен расчет определенного интеграла:
Другие функции
В Matlab реализовано множество функций для работы с символьными вычислениями. Помимо тех, что были рассмотрены, следует выделить следующие функции:
- ezplot(f) — построение графика функции
- solve(f) — решение символьных уравнений и систем
- taylor(f) — разложение символьной функции в ряд тейлора
- limit(f) — вычисление предела
Эти и многие другие функции в Matlab имеют свои опции и параметры. Очевидно, что среда Matlab дает широкие возможности разработчику при работе с символьными вычислениями.
Заключение
На этом статья подходит к концу. Символьные вычисления в Matlab являются дополнительным инструментом разработчика, и с помощью этой статьи можно ознакомиться с этим инструментом.
Все примеры очень просты и в исходниках не нуждаются. На этом все, встретимся в следующей статье.
Основы работы в символьных переменных в системе MATLAB
Цель работы:изучить систему команд расширения MATLAB (Toolbox) для работы с символьными переменными Symbolic Math.
Расширение (Toolbox) Symbolic Math предназначено для работы с математическими выражениями в символьных переменных, то есть в привычном для нас виде, когда переменная не заменяется ее числовым значением, может входить в разные функции, выражения и уравнения, а также преобразовываться в любых доступных формах с помощью известных алгебраических преобразований. Кроме того, указанное расширение дает возможность символьного интегрирования и дифференцирования, с последующей подстановкой числовых значений, упрощением и преобразованием вновь получаемых математических зависимостей.
Основные команды, используемые для работы с символьными переменными:
1. Общие операции:
– syms – создает символьные переменные упрощенным способом. Формат команды: syms vol1 vol2 …, где vol1, vol2 и т.д. – имена создаваемых символьных переменных. Для создания символьных переменных может также применяться команда sym, которая применяется в следующем формате: vol1 = sym(‘vol1’). Таким образом, в скобках, заключенное в апострофы, задается имя создаваемой переменной. Такая запись является чересчур громоздкой, поэтому рекомендуется применять упрощенную команду syms, при этом, создаваемые переменные просто перечисляются через пробел после самой команды. Ставить знак «;» после команды syms не требуется;
– pretty – выдает символьное выражение в многоуровневом представлении (в привычном нам виде). Формат записи команды: pretty(vol), где vol – имя переменной, в которой хранится символьное выражение. Например, символьное выражение:
A = (2*x+y*x*2+y^2)/(2*a+3*b) в линейной форме записи, будет преобразовано командой pretty в:
2. Решение уравнений:
– solve – решение алгебраических уравнений, в том числе их систем. Формат записи:
solve (‘eqn1′,’eqn2’. ‘eqnN’,’var1,var2. varN’), где eqn1, eqn2 и т.д. – уравнения, решения которых нужно найти.
Таким образом, в качестве аргументов этой функции используются уравнения, заключенные в апострофы и разделенные запятыми. После уравнений приводится список переменных, которые нужно определить. Если уравнение одно и содержит одну переменную указывать относительно какой переменной его решать не требуется;
– dsolve – решение дифференциальных уравнений. Формат записи:
– simplify – упрощение выражения;
– expand – раскрывает все скобки в выражении;
– collect – выносит общий множитель за скобки;
– subs – подстановка числовых значений вместо символьных.
Формат записи для всех команд одинаков:
vol2 = command(vol1), где vol1 – преобразуемая переменная, vol2 – переменная, в которую будет записан результат преобразования, command – одна из указанных выше команд.
– diff – дифференцирование выражения. Формат записи:
diff(vol1, n), где n – порядок дифференцирования;
– int – интегрирование выражения. Формат записи: int(vol1,a,b), где a и b – верхний и нижний пределы интегрирования, в случае нахождения определенного интеграла;
– limit – нахождение предела выражения. Формат записи:
limit(vol1,x,a,’ident’), где x – имя переменной которая стремится к пределу, a – численное значение, к которому стремится переменная x, ident – может принимать значения left и right, т.е. это указание, в какую сторону стремится величина x – направление для односторонних пределов.
Пример №1: Необходимо задать выражение A = (x*2+y^3-3*z)*3*x+4*y^3, упростить его и определить значение A в точке (1,2,1).
Выполняется следующим образом:
% после выполнения этой команды в рабочей области (workspace появятся три символьные переменные x, y и z
% результат выполнения команды:
% показывает как выражение было занесено в переменную А. В отдельных случаях, когда возможно упростить вводимое выражение, оно будет упрощено и выдано на экран уже в упрощенном виде. Как видно из результата применения команды, все составляющие в скобке были помножены на 3.
% для дополнительного контроля можно применить команду
% результат ее применения:
% (6 x + 3 y – 9 z) x + 4 y
% раскрываем скобки, запоминаем результат в переменной А1
% результат: A1 = 6*x^2+3*x*y^3-9*x*z+4*y^3
% группируем переменные в выражении А1 и выносим общие множители за скобки. Результат: A2 = 6*x^2+(3*y^3-9*z)*x+4*y^3
% задаем значения переменных x, y и z соответственно заданной точке (1,2,1). при этом в рабочей области появятся уже числовые переменные с соответствующими значениями.
% подставляем численные значения в наше выражение, получаем результат:
% Возможно присваивание численных значений только части символьных переменных выражения. Для иллюстрации этого вернем переменные x, y и z в символьный вид:
% результат в этом случае: A3 = 62-9*z
Пример №2: Необходимо решить независимые уравнения
x+20=10, 3*x^2+2*x-10=0 и 4*x+5*x^3=-12.
Выполняется следующим образом:
% MATLAB выдал два корня уравнения в неупрощенном виде, для их упрощения необходимо повторить ответ в командном окне (скопировать его и заново ввести в командное окно)
Пример №3: Необходимо решить независимые уравнения
x+y=35, 3*x^2+2*y=0 и 4*x+5*y^3=-12 относительно переменной x.
Выполняется следующим образом:
Пример №4: Необходимо найти неопределенный интеграл и дифференциал выражения 3*a^5*sin(a).
Выполняется следующим образом:
Пример №5: Необходимо найти определенный интеграл выражения 3*a^5*sin(a), для пределов от -10 до 100.
Выполняется следующим образом:
Пример №6: Необходимо продифференцировать выражение 3*a^5*sin(a) четыре раза.
Выполняется следующим образом:
Пример №7: Необходимо получить передаточную функцию трех последовательно соединенных звеньев: , и . А также определить передаточную функцию замкнутой системы, состоящей из звеньев W1, W2 и W3 – в прямой ветви, и звена – в обратной связи, при условии отрицательной обратной связи.
Выполняется следующим образом:
syms k1 k2 k3 T1 T2 T3 p
% передаточная функция последовательно соединенных звеньев:
MATLAB — алгебра
До сих пор мы видели, что все примеры работают как в MATLAB, так и в его GNU, альтернативно называемом Octave. Но для решения основных алгебраических уравнений и MATLAB, и Octave немного отличаются, поэтому мы постараемся охватить MATLAB и Octave в отдельных разделах.
Мы также обсудим факторизацию и упрощение алгебраических выражений.
Решение основных алгебраических уравнений в MATLAB
Функция решения используется для решения алгебраических уравнений. В простейшем виде функция решения принимает в качестве аргумента уравнение, заключенное в кавычки.
Например, давайте решим для х в уравнении х-5 = 0
MATLAB выполнит приведенный выше оператор и вернет следующий результат —
Вы также можете вызвать функцию решения как —
MATLAB выполнит приведенный выше оператор и вернет следующий результат —
Вы можете даже не включать правую часть уравнения —
MATLAB выполнит приведенный выше оператор и вернет следующий результат —
Если в уравнение входит несколько символов, то по умолчанию MATLAB предполагает, что вы решаете для x, однако функция решения имеет другую форму —
где вы также можете упомянуть переменную.
Например, давайте решим уравнение v — u — 3t 2 = 0, для v. В этом случае мы должны написать —
MATLAB выполнит приведенный выше оператор и вернет следующий результат —
Решение основных алгебраических уравнений в октаве
Функция корней используется для решения алгебраических уравнений в Octave, и вы можете написать приведенные выше примеры следующим образом:
Например, давайте решим для х в уравнении х-5 = 0
Octave выполнит приведенный выше оператор и вернет следующий результат —
Вы также можете вызвать функцию решения как —
Octave выполнит приведенный выше оператор и вернет следующий результат —
Решение квадратичных уравнений в MATLAB
Функция решения также может решать уравнения более высокого порядка. Он часто используется для решения квадратных уравнений. Функция возвращает корни уравнения в массиве.
В следующем примере решается квадратное уравнение x 2 -7x +12 = 0. Создайте файл сценария и введите следующий код —
Когда вы запускаете файл, он показывает следующий результат —
Решение квадратичных уравнений в октаве
В следующем примере решается квадратное уравнение x 2 -7x +12 = 0 в октаве. Создайте файл сценария и введите следующий код —
Когда вы запускаете файл, он показывает следующий результат —
Решение уравнений высшего порядка в MATLAB
Функция решения также может решать уравнения более высокого порядка. Например, давайте решим кубическое уравнение как (x-3) 2 (x-7) = 0
MATLAB выполнит приведенный выше оператор и вернет следующий результат —
В случае уравнений более высокого порядка корни длинные, содержащие много членов. Вы можете получить числовое значение таких корней, преобразовав их в двойные. В следующем примере решается уравнение четвертого порядка x 4 — 7x 3 + 3x 2 — 5x + 9 = 0.
Создайте файл сценария и введите следующий код —
Когда вы запускаете файл, он возвращает следующий результат —
Обратите внимание, что последние два корня являются комплексными числами.
Решение уравнений высшего порядка в октаве
В следующем примере решается уравнение четвертого порядка x 4 — 7x 3 + 3x 2 — 5x + 9 = 0.
Создайте файл сценария и введите следующий код —
Когда вы запускаете файл, он возвращает следующий результат —
Решение системы уравнений в MATLAB
Функция решения также может быть использована для генерации решений систем уравнений, включающих более одной переменной. Давайте рассмотрим простой пример, чтобы продемонстрировать это использование.
Давайте решим уравнения —
Создайте файл сценария и введите следующий код —
Когда вы запускаете файл, он показывает следующий результат —
Таким же образом вы можете решать большие линейные системы. Рассмотрим следующую систему уравнений —
Решающая система уравнений в октаве
У нас есть немного другой подход к решению системы ‘n’ линейных уравнений с ‘n’ неизвестными. Давайте рассмотрим простой пример, чтобы продемонстрировать это использование.
Давайте решим уравнения —
Такая система линейных уравнений может быть записана в виде единого матричного уравнения Ax = b, где A — матрица коэффициентов, b — вектор столбцов, содержащий правую часть линейных уравнений, а x — вектор столбцов, представляющий решение как показано в программе ниже —
Создайте файл сценария и введите следующий код —
Когда вы запускаете файл, он показывает следующий результат —
Таким же образом, вы можете решить большие линейные системы, как указано ниже —
Разложение и сбор уравнений в MATLAB
Функция расширения и сбора расширяет и собирает уравнение соответственно. Следующий пример демонстрирует понятия —
Когда вы работаете со многими символическими функциями, вы должны объявить, что ваши переменные являются символическими.
Создайте файл сценария и введите следующий код —
Когда вы запускаете файл, он показывает следующий результат —
Расширяя и собирая уравнения в октаве
Вам нужно иметь символьный пакет, который обеспечивает расширение и функцию сбора для расширения и сбора уравнения, соответственно. Следующий пример демонстрирует понятия —
Когда вы работаете со многими символическими функциями, вы должны объявить, что ваши переменные являются символическими, но у Octave другой подход к определению символических переменных. Обратите внимание на использование Sin и Cos , которые также определены в символической упаковке.
Создайте файл сценария и введите следующий код —
Когда вы запускаете файл, он показывает следующий результат —
Факторизация и упрощение алгебраических выражений
Факторная функция разлагает выражение, а функция упрощения упрощает выражение. Следующий пример демонстрирует концепцию —
пример
Создайте файл сценария и введите следующий код —
Когда вы запускаете файл, он показывает следующий результат —
[spoiler title=”источники:”]
http://poisk-ru.ru/s36222t14.html
http://coderlessons.com/tutorials/kompiuternoe-programmirovanie/uznaite-matlab/matlab-algebra
[/spoiler]