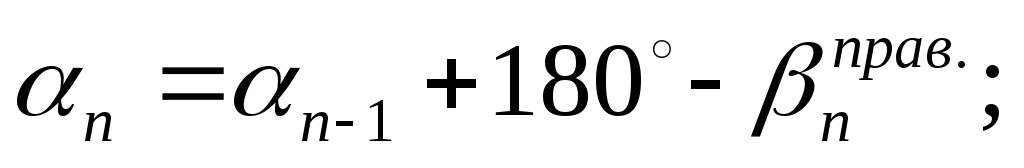ОБЩИЕ УКАЗАНИЯ
Тахеометрическая съемка является одним из методов топографической съемки местности и производится обычно на небольших участках для получения плана в крупном масштабе с изображениями на нем предметов, контуров и рельефа местности.
Процесс тахеометрической съемки состоит из двух стадий работ:
-
полевые инструментальные измерения на местности;
-
камеральная обработка результатов полевых измерений на местности и составление топографического плана.
Опорную сеть при тахеометрической съемке составляют пункты триангуляции, полигонометрии, аналитических сетей, находящиеся на участке. Для сгущения имеющейся геодезической опорной сети прокладывают высотные теодолитные ходы или замкнутые полигоны, а между ними — съемочные тахеометрические ходы.
В высотных теодолитных ходах горизонтальные и вертикальные углы измеряют теодолитом, а стороны — мерными лентами или дальномерами ДНТ или ДД-3, ДЦ-5.
В тахеометрических ходах стороны измеряют нитяным дальномером, а горизонтальные и вертикальные углы теодолитом.
Слово тахеометрия в переводе с греческого языка означает «быстрое измерение». Быстрота при этой съемке достигается тем, что одним наведением трубы инструмента на рейку получают плановое и высотное положение определяемой точки, т.е. получают расстояние, определяемое по дальномеру, направление по горизонтальному лимбу и превышение, отсчитываемое по рейке или вычисляемое по углу наклона.
Тахеометрическая съемка производится техническими теодолитами (тахеометрами) или более совершенными — номограммными тахеометрами.
Цель методических указаний — помочь студентам приобрести практический опыт при выполнении второй стадии тахеометрической съемки, т.е. в камеральной обработке результатов полевых измерений.
Методические указания содержат сведения, которые помогут студентам при изучении устройства теодолита Т30, его поверок и методики измерения углов.
2. КАМЕРАЛЬНАЯ ОБРАБОТКА ТЕОДОЛИТНЫХ ХОДОВ
2.1. Вычисление дирекционного угла примычной стороны теодолитного хода
При примыкании теодолитных ходов к исходным пунктам измеряют углы между примыкающей (рис. 1).
Исходными данными для вычисления дирекционных углов сторон хода являются известные дирекционные углы примычных сторон, Если дирекционный угол
задан, то его вычисляют по координатам исходных пунктов путем решения обратной геодезической задачи.
Сущность решения обратной задачи заключается в вычислении дирекционного угла и расстояния между двумя пунктами по известным координатам этих пунктов (рис.2).
Формулы для решения обратных задач:
(1)
где — известные координаты первого (начального) пункта, на котором находится наблюдатель;
— известные координаты другого пункта, видимого наблюдателем с первого (начального).
Известные координаты пунктов Д, С и В студент выбирает из табл.1 для своего варианта.
В табл. 2 приведено решение обратной задачи для варианта 30. Сходимость длин сторон вычисленных в результате действий 12 и 13 таблицы являются контролем правильности решения задачи. При нахождении дирекционного угла по таблицам натуральных значений тригонометрических функций или на микрокалькуляторе всегда получаем его румб (r).
Поэтому необходимо определить, в какой четверти окружности расположен вычисленный дирекционный угол. Это можно установить по знакам приращений координат, пользуясь табл. 3.
Дирекционный угол примычной стороны (В-1) вычисляют дважды, используя направления двух исходных сторон опорной сети:
(2)
где » — примычные углы, выбираемые из табл. 4.
Если разность дирекционных углов примычной стороны (В-1) не превышает то среднее значение на этих углов принимается для дальнейших вычислений.
Таблица 1
|
№ варианта |
Пункт С |
Пункт Д |
Пуни В |
|||
|
X,м |
X Y,м |
X,м |
Y,м |
X Y |
Ybbbb H,м |
|
|
5260 |
7448 |
526 |
7449 |
Координаты пункта В одинаковыдля всех вариантов Х=5262 591.47У=7448 200.00 |
||
|
I |
154.46 |
611.46 |
2003.92 |
653.03 |
166.88 |
|
|
2 |
152.46 |
599.40 |
1996.74 |
650.11 |
170.21 |
|
|
3 |
150.51 |
587.34 |
1989.57 |
647.15 |
170.54 |
|
|
4 |
148.63 |
575.26 |
1982.42 |
644.16 |
170.87 |
|
|
5 |
147.80 |
563Л8 |
1975.29 |
641.13 |
171.20 |
|
|
6 |
145.03 |
551.08 |
1960.17 |
638.06 |
171.53 |
|
|
7 |
143.33 |
538.98 |
1961.07 |
634.96 |
171,86 |
|
|
8 |
141.68 |
526,87 |
1953.98 |
631.83 |
172.19 |
|
|
9 |
140.10 |
514.75 |
1946.91 |
628.66 |
172,52 |
|
|
10 |
138.57 |
502.63 |
1939.85 |
625.45 |
172.85 |
|
|
11 |
137.10 |
490.49 |
1932.81 |
622.21 |
173.18 |
|
|
12 |
135.69 |
478.35 |
1925.78 |
618.94 |
173.51 |
|
|
13 |
. 134.35 |
466.21 |
1918.78 |
615.63 |
173.84 |
|
|
14 |
133.06 |
454.05 |
1911.78 |
612.28 |
174.17 |
|
|
15 |
131.84 |
441.89 |
1904.81 |
608.91 |
174.50 |
|
|
5259 |
7448 |
5261 |
7449 |
|||
|
16 |
955.08 |
645.12 |
928.12 |
840.49 |
174.83 |
|
|
17 |
952.91 |
632.08 |
920.01 |
837.19 |
175.16 |
|
|
18 |
950.81 |
619,03 |
911.92 |
833.85 |
175.49 |
|
|
19 |
948.77 |
605.96 |
903.85 |
830.47 |
175,82 |
|
|
20 |
946.80 |
592.89 |
895.80 |
827.04 |
176,15 |
|
|
21 |
944.88 |
579.81 |
887.76 |
823.58 |
.176,48 |
|
|
22 |
943.04 |
566.71 |
879.74 |
820.09 |
176,81 |
|
|
23 |
941.26 |
553.61 |
871.74 |
816.54 |
177,14 |
|
|
24 |
939.54 |
540.50 |
863.75 |
812.97 |
177.47 |
|
|
25 |
937.89 |
527.39 |
855.78 |
809.35 |
177.80 |
|
|
26 |
936.31 |
514.26 |
847.84 |
805.69 |
178.13 |
|
|
27 |
934.78 |
501.13 |
839.90 |
801.99 |
178.46 |
|
|
28 |
933.33 |
487.98 |
831.99 |
798.26 |
178.79 |
|
|
29 |
931.93 |
474.84 |
824.10 |
794.48 |
179.12 |
|
|
30 |
930.61 |
461.68 |
816.22 |
790.67 |
179.45 |
Таблица 2
|
Порядок действий |
1 2 формулы |
Д В |
С В |
|
2 1 5=2-1 4 3 6=4-3 7=6:5 8 9 10 11 12=5×10 13=6×11 |
cos sin |
5 62591.47 5 61816.22 +775.25 7 448200.00 7 449790.67 -1590.67 -2.051815 64.01663 64°00’59″9 295°59’00»1 —0,438110 + 0,898921 1769.53 1769.53 |
5 262591.47 5 259930.61 + 2660.86 7 448200.00 7 448461.68 -261.68 — 0,098344 5,616601 5°36’59″8 354°23’00″2 — 0,995199 + 0,097871 2673.72 2673.70 |
Решение 2.
αВС = 5о02,7′ + 180о – 274о16,8′ = – 89о14,1′ + 360о = 270о45,9′, поскольку значение дирекционного угла получилось отрицательным.
3. Исходные данные: αАВ = 201о42’08”; β (правый по ходу) = 36о14’32”. Решение 3. ( через дирекционный угол исходящего направления).
αВА = 201о42’08” – 180о = 211о42’08”.
αВС = 21о42’08” – 36о14’32” = – 14о32’24” + 360о = 345о27’36”.
Целью привязки теодолитных ходов к пунктам Государственной геодезии-ческой сети 1, 2, 3 и 4 классов, а также к пунктам съемочной сети 1 и 2 разрядов является определение с заданной точностью координат вершин ука-занных ходов.
В зависимости от расположения теодолитного хода на местности, условий съемки, сложности ситуации и других факторов схемы и способы привязки элементов теодолитного хода могут быть различными. Во многих случаях приходится выполнять дополнительные геодезические построения. Тем более, что любая привязка должна иметь надежный контроль, который, чаще всего, обеспечивается избыточными измерениями и дополнительными геодезиическими построениями.
Под элементом теодолитного хода понимают одну из его точек, координаты которой необходимо найти, и дирекционный угол линии теодолитного хода, исходящей из определяемой точки.
Здесь мы рассмотрим некоторые из основных способов привязки теодолитных ходов, которые чаще всего встречаются на практике, приведем схемы, предусматривающие комбинированное использование способов привязки. Однако следует иметь ввиду, что на практике могут встретиться случаи, когда ни один из рассмотренных способов не может быть реализован в силу действия различных факторов. Геодезист и маркшейдер должны уметь проектировать частные схемы привязок, которые обеспечат построение съемочного обоснования с необходимой точностью.
68.1. Способ примыкания
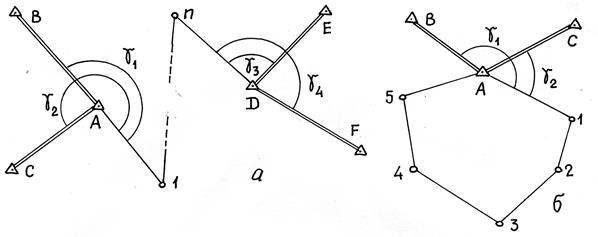
На рис. 7.2 приведены сравнительно простейшие способы привязки теодолитных ходов. Для разомкнутого хода – это привязка начальной и конечной линий минимально к двум исходным направлениям с включением пункта высокого класса в теодолитный ход в местах примыкания. Замкнутый теодолитный ход может быть привязан на два исходных направления с включением пункта высокого класса непосредственно в ход (рис. 7.2 б), либо с помощью дополнительного полигонометрического хода (рис. 7.2 в) от исходных пунктов (привязка ходом). Методика выполнения привязки с помощью указанных схем следующая.
Привязка разомкнутого теодолитного хода на двух его концах выполняется с использованием примычных (горизонтальных) углов γ1, γ2, γ3 и γ4 (рис.
172

7.5). В результате дважды определяют дирекционные углы направлений А-1
и n-D.
|
α А1( |
АВ ) = α ВА + γ 1 , |
(7.12) |
|
|
α А1( АС ) = α СА + γ 2 |
|||
|
α nD (DE ) |
= α DE |
− γ 3 + 180 0 |
|
|
α nD (DF ) |
= α DF |
− γ 4 + 180 0 , |
(7.13) |
Рис. 7.5. Привязка разомкнутого и замкнутого теодолитных ходов Разомкнутый ход (а), замкнутый ход (б)
где αВА , αСА , αDE , αDF – дирекционные углы исходных направлений – находят из решения обратных геодезических задач по координатам исходных пунктов; на схеме углы γ1 и γ2 – левые по ходу, углы γ3 и γ4 – правые по ходу.
Если разница полученных дирекционных углов допустима (для технических теодолитных ходов – не более 1′), т.е.
|
α А1 |
= |
α А1( АВ ) − α А1( АС ) |
≤ 1′ |
, |
(7.14) |
|||||
|
α nD |
= |
α nD ( DE ) − α nD ( DF ) |
≤ 1′ |
|||||||
|
то вычисляют средние арифметические значения углов |
||||||||||
|
α А1 |
= 0,5(α А1( АВ ) + α А1( АС ) ) |
(7.15) |
||||||||
|
α nD |
= 0,5(α nD ( DE ) − α nD ( DF ) ) |
|||||||||
и в дальнейшем принимают их за исходные.
Аналогично выполняют привязку линии А1 в замкнутом теодолитном ходе (рис. 7.5 б).
Примычные углы измеряют теодолитом повышенной точности, чем рекомендуемый для измерений в теодолитных ходах. Иногда приходится пользоваться для измерения примычных углов и для измерения горизонтальных углов в вершинах хода одним и тем же теодолитом. В этом случае примычные углы измеряют несколькими полными приемами каждый (3 – 5 полных приемов с перестановкой лимба горизонтального круга и с повторным центрированием и горизонтированием теодолита перед каждым приемом). Целесообразно, чтобы примычные углы имели вес в 1,5 – 2 раза больший, чем вес углов дальнейших геодезических построений.
173

68.2. Прямая угловая засечка
Положение точки М теодолитного хода определяют из решения треугольников АВМ и ВСМ по результатам измерения горизонтальных углов β1, β2, β3 и β4 при исходных направлениях АВ и ВС (рис. 7.6 а). Горизонтальный угол β5 , измеренный в вершине М между направлениями ВМ и МN, используют для передачи дирекционного угла с направления ВМ на линию теодолитного хода MN.
Рис. 7.6. Прямая угловая засечка. а) схема 1; б) схема 2
Координаты точки М удобно вычислять по формулам Юнга:
|
Х M = |
Х Аctgβ 2 + X B ctgβ 1 + YB − YA |
||
|
ctgβ 1 |
+ ctgβ 2 |
||
|
YM = |
YActgβ 2 + YB ctgβ 1 + X A − X B |
||
|
ctgβ 1 |
+ ctgβ 2 |
Для контроля аналогичные вычисления выполняют из решения второго треугольника. Точность определения прямоугольных координат не должна быть меньше установленной инструкцией.
Для передачи дирекционного угла на линию MN вычисляют из решения обратной геодезической задачи дирекционный угол направления BM (αBM), а затем получают дирекционный угол αMN по формуле
αMN = αВM + 180о – β5 (7.18) На схеме привязки горизонтальный угол β5 является правым по ходу ВMN,
поэтому в формуле (7.18) перед ним стоит знак минус.
Часто прямую угловую засечку выполняют сразу для точек М и N. Тогда координаты точки N определяют так же, как и координаты точки М, а значение горизонтального угла β5 используют как контрольное. Аналогичный угол целесообразно измерить и в точке N.
Оценка точности определения координат пункта M относительно исходных пунктов А, В и С выполняется по следующим формулам:
|
mM (1) = mβ |
SAM |
2 + |
SBM |
2 |
, |
(7.19) |
||
|
ρ ′′ sin(β 1 |
+ β |
2 ) |
174

|
mM (2) = mβ |
SBM |
2 + |
SCM |
2 |
, |
(7.20) |
|||||
|
ρ ′′ sin(β 3 |
+ β |
4 ) |
|||||||||
|
, |
(7.21) |
||||||||||
|
mM = 0,5 |
mM (1) |
2 |
+ mM (2) |
2 |
где mM(1) и mM(2) – соответственно средние квадратические погрешности определения положения точки М из первого и второго треугольников; mβ – средняя квадратическая погрешность измерения горизонтального угла (сек); ρ” = 206265″ – число секунд в радиане; S – расстояния (горизонтальные проложения) между исходными пунктами и определяемой точкой, вычисляемые по теореме синусов в соответствующем треугольнике.
При проектировании рассмотренной схемы привязки следует стремиться к тому, чтобы горизонтальные углы γ при определяемой точке были не меньше 30о и не больше 150о. Большая точность достигается при углах γ в пределах 109о – 110о при примерно равных расстояниях до нее от исходных пунктов..
|
Пример 7.4. Привязка способом прямой угловой засечки. |
||||||||||||||||||||||||||
|
Исходные данные (схема рис. 7.6 а): |
||||||||||||||||||||||||||
|
ХА = 3946,547 м |
ХВ = 3763,211 м |
ХС = 4015,338 м |
||||||||||||||||||||||||
|
YA = 4105,854 м |
YВ = 4568,642 м |
YС = 4905,039 м |
||||||||||||||||||||||||
|
β1 = 63018’10”; |
β2 = 59044’58”; |
β3 = 61047’20”; β4 = 70003’50”; β5 = 86055’45”. |
||||||||||||||||||||||||
|
Решение. |
||||||||||||||||||||||||||
|
Из треугольника АВМ (1): |
||||||||||||||||||||||||||
|
X M (1) |
= |
3946 ,547 ctg 59 0 44′58′′ + 3763 ,211 ctg 63 018′10′′ − 4105 ,854 + |
4568 ,642 |
= |
4287 ,7648 м; |
|||||||||||||||||||||
|
ctg 59 0 44′58′′ + ctg 63 018′10′′ |
||||||||||||||||||||||||||
|
YM (1) |
= |
4105 ,854 ctg 59 0 44′58′′ + 4568 ,642 ctg 63 018′10′′ + 3946 ,547 − |
3763 ,211 |
= |
4488 ,9427 м |
|||||||||||||||||||||
|
ctg 59 0 44′58′′ + |
ctg 63 018′10′′ |
|||||||||||||||||||||||||
|
Аналогичные вычисления выполняем в треугольнике ВСМ (2): |
||||||||||||||||||||||||||
|
ХМ(2) = 4287,7594 м ; |
YM(2) = 4488,9353 м. |
|||||||||||||||||||||||||
|
В результате получены невязки в координатах: |
||||||||||||||||||||||||||
|
fX = XM(1) – XM(2) = 0,0054 м; |
fY = YM(1) – YM(2) =0,0074 м; fАБС = 0,00916 м. |
|||||||||||||||||||||||||
|
Значение fАБС является критерием качества решения задачи привязки. |
||||||||||||||||||||||||||
|
При допустимом значении абсолютной невязки вычисляют среднее значение ко- |
||||||||||||||||||||||||||
|
ординат точки М: ХМ = 4287,762 м ; YM = 4488,939 м. |
||||||||||||||||||||||||||
|
Выполним оценку точности засечки по формулам (7.19) – (7.21), приняв mβ = 2,0″. |
||||||||||||||||||||||||||
|
Из решения обратной геодезической задачи с точностью до 1 м вычислим |
||||||||||||||||||||||||||
|
значения |
||||||||||||||||||||||||||
|
S 1 ≈ 513 м, |
S2 ≈ 531 м, |
S3 ≈ 497 м. |
||||||||||||||||||||||||
|
Значения sin для оценки точности округлим до 0,50. |
||||||||||||||||||||||||||
|
2 |
′′ |
|||||||||||||||||||||||||
|
M1 |
= |
5132 |
+ 5312 |
= |
0,0085м = 8,5мм . |
|||||||||||||||||||||
|
206265′′ sin1230 |
||||||||||||||||||||||||||
|
2 |
′′ |
|||||||||||||||||||||||||
|
M 2 |
= |
5312 + 497 2 |
= 0,0083 м = 8,3мм . |
|||||||||||||||||||||||
|
20626 5′′ sin 121,5 |
0 |
|||||||||||||||||||||||||
|
Средняя погрешность засечки М = |
8,52 + 8,32 |
= 5,9мм . |
||||||||||||||||||||||||
|
2 |
Здесь следует сделать некоторые замечания.
1. Средняя погрешность по значению меньше частных погрешностей, полученных по оценкам в соответствующих треугольниках. Это полностью согласуется с положениями теории погрешностей (гл. 3). Координаты точки М получены независимо из ре-
175
шения двух треугольников, т.е. определены дважды. В связи с этим средняя погрешность относится к значению средних арифметических координат точки М.
2. Практическая погрешность (невязка) составила порядка 9 мм, т.е. на 3 мм больше. Оценка точности выполнялась по теоретическим формулам, для идеального случая, когда влияние других погрешностей исключается, не учитывается. При выполнении практических работ в результатах измерений содержатся и другие погрешности, что и повлияло на окончательное практическое значение точности определения координат точки М. При этом следует иметь ввиду, что все погрешности имеют вероятностный характер, и не исключено, что оценочные их значения могут в каких-то случаях оказаться и больше, чем их практические величины.
Вычислим дирекционный угол направления MN.
Из решения обратной геодезической задачи по координатам точек В и М вычислим значение дирекционного угла направления ВМ:
|
Х = |
+ 524,551м; |
Y = |
− 79,703 м;(IVчетверть ); r |
= 80 |
21′ 37′′;α |
ВМ |
= 3510 |
21′ 37′′. |
|
|
BM |
|||||||||
|
α MN |
= 3510 21′ 37 ′′ |
+ 180 0 |
− 86 0 55 ′45 ′′ = 444 0 25 ′52 ′′ = |
84 0 25 ′52 ′′. |
Часто видимость между пунктами А – В и В – С может отсутствовать. В этом случае возможно использование другой схемы прямой угловой засечки (рис. 7.6 б), решение которой выполняется по формулам Гаусса (тангенсов или котангенсов).
Формулы тангенсов:
|
X М = |
X Atgα AP − X B tgα BP − YA + YB |
, |
(7.22) |
|||
|
tgα AМ − tgα BМ |
(7.23) |
|||||
|
YМ |
= YA + ( X М − X A )tgα AМ = YB + (X М − |
X B )tgα BМ |
||||
|
Формулы котангенсов: |
||||||
|
YМ = YActgα AМ − YB ctgα BМ − X A + |
X B |
, |
(7.24) |
|||
|
ctgα AМ − ctgα BМ |
(7.25) |
|||||
|
X М |
= X A + (YМ − YA )ctgα AМ = X B + (YМ − YB )ctgα BМ |
|||||
|
Для контроля выполняют аналогичную привязку с точек В и С. |
Значения дирекционных углов в приведенных формулах получают в результате решения азимутальной привязки от соответствующих исходных
|
направлений: |
|
|
αАМ = αАD ± β1 , |
(7.26) |
|
αBМ = αBE ± β2 , |
(7.27) |
|
αCМ = αCF ± β3 |
(7.28) |
Знак «плюс» – для левых по ходу углов (как это показано на рис. 7.4), знак «минус» – для правых по ходу углов. На схеме рис. 7.6 б горизонтальные углы – левые по ходу.
При использовании для вычислений микрокалькуляторов формулы тангенсов не следует применять, если дирекционные углы близки к 90о ± 5о или 270о ± 5о, а формулы котангенсов – если дирекционные углы близки к 0о ± 5о или 180о ± 5о. Это обязательно следует проверить и, при возможности, перейти к другим построениям. В любом случае использование приведенной схемы привязки необходимо начинать с вычисления (или с оценки) величин дирекционных углов.
176
Содержание
- 47. Привязка теодолитных ходов к пунктам геодезической опорной сети.
- 48.Прямая геодезическая засечка.
- 49. Обратная геодезическая засечка.
- 50.Сущность геометрического нивелирования «Вперед»
- Привязка теодолитных ходов к пунктам геодезической опорной сети
- 9.5. Привязка теодолитных ходов.
- 9.6. Камеральная обработка результатов измерений.
- 9.7. Прямая геодезическая задача.
- 9.8. Обратная геодезическая задача.
- Раздел 10. Топографическая съемка
- Привязка теодолитных ходов
47. Привязка теодолитных ходов к пунктам геодезической опорной сети.
Привязка к опорным геодезическим пунктам имеет целью: получить возможность вести с заданной точностью предстоящие геодезические работы в системе координат и отметок исходных опорных пунктов; осуществлять контроль и выдерживать необходимую точность выполняемых геодезических работ. Для более полного и падежного контроля теодолитный ход, строительную сетку, красную линию, нивелирный ход привязывают не менее чем к двум опорным пунктам. Привязка теодолитного хода заключается в измерении двух примычных углов на опорных пунктах.
Привязка теодолитных ходов к пунктам опорной геодезической сети.
Теодолитные ходы обычно прокладывают между исходными (опорными) пунктами государственной геодезической сети или сетей сгущения. Координаты опорных пунктов (X и Y) определены в общегосударственной системе координат. Поэтому привязка теодолитного хода производится для определения координат точек хода и дирекционных углов его сторон в единой общегосударственной системе.
Плановая привязка теодолитного хода заключается в измерении горизонтальных углов и длин сторон от исходных пунктов к точкам теодолитного хода. Рассмотрим способы привязки замкнутого и разомкнутого теодолитных ходов.
48.Прямая геодезическая засечка.
Засечка геодезическая, способ определения положения точки (опорного пункта в геодезии, орудия или цели в артиллерии) путём измерения длин отрезков, соединяющих эту точку с некоторыми заданными точками, или углов между направлениями этих отрезков. В зависимости от вида измеряемых величин различают линейные и угловые.
Засечка геодезическая, способ определения положения точки (опорного пункта в геодезии, орудия или цели в артиллерии) путём измерения длин отрезков, соединяющих эту точку с некоторыми заданными точками, или углов между направлениями этих отрезков. В зависимости от вида измеряемых величин различают линейные и угловые З. г.
Прямая геодезическая угловая засечка применяется для определения координат дополнительной точки на основании двух исходных пунктов с известными координатами. Для беспечения надежного контроля измерений и повышения точности определения положения искомого пункта на практике, как правило, применяют многократные прямые засечки не менее чем с трех исходных пунктов
49. Обратная геодезическая засечка.
На местности находят приближенное положение К’выносимой проектной точкиК(рис. 1.49). Над точкойК’ устанавливают теодолит и с требуемой точностью измеряют углы β1, β2как минимум на три опорные точки с известными координатами. По формулам обратной угловой засечки вычисляют координаты точкиК’ и сравнивают их с проектными значениями. По разности координат определяют величины редукций Δх, Δу или угловой Ө и линейныйеэлементы и смещают точку в проектное положениеК.
Р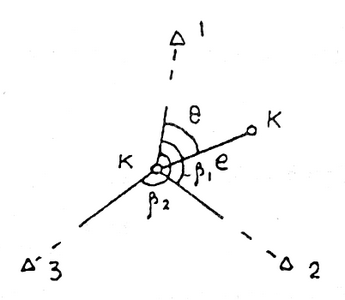
Для контроля на точке Кизмеряют углы и по ним вычисляют координаты точкиКи сравнивают их с проектными. При недопустимых расхождениях измерения повторяют.
50.Сущность геометрического нивелирования «Вперед»
При нивелировании вперед нивелир устанавливают над пунктом, измеряют его высоту и снимают отсчет по рейке, установленной над другим пунктом. В данном случае превышение равно разности между высотой нивелира и отсчетом по передней рейке.
Предельное расстояние от нивелира до реек при нивелировании 100 – 150 м. Следовательно, с одной станции, если позволяют условия местности, можно нивелировать точки, расстояния между которыми не превышают 200 – 300 м. Расстояния большей протяженности нивелируют с нескольких станций, связанных между собой общими точками. Точки, общие для двух смежных станций, называют связующими, их высоты, как правило, вычисляют последовательно по направлению нивелирования через превышения. Остальные нивелируемые точки называются промежуточными, ими, обычно, являются характерные точки местности. Их высоту вычисляют через горизонт прибора, т.е. горизонт прибора минус отсчет на промежуточную точку. Горизонтом прибора называется высота визирной оси зрительной трубы нивелира над уровнем моря или над условным уровнем.
Источник
Привязка теодолитных ходов к пунктам геодезической опорной сети
Для получения координат точек теодолитных ходов в общегосударственной системе координат и для осуществления контроля измерений теодолитные ходы следует привязывать к пунктам геодезической опорной сети. Сущность привязки состоит в передаче с опорных пунктов плановых координат как минимум на одну из точек теодолитного хода и дирекционного угла на одну или несколько его сторон. Координаты опорных пунктов и дирекционные углы исходных направлений выбираются из каталогов пунктов геодезической сети.
Существуют следующие наиболее характерные случаи привязки теодолитных ходов и полигонов:
11.5.1 Теодолитный ход непосредственно примыкает к пункту опорной сети (рис. 11.1 б). В данном случае пункт А геодезической опорной сети с известными координатами XA и YA является одновременно вершиной теодолитного полигона. С пункта А имеется видимость на другой пункт В геодезической сети; дирекционный угол направления ВА известен. Для передачи дирекционного угла на одну из сторон (А-1) следует измерить примычной угол j между исходной и определяемой сторонами.
11.5.2 Теодолитный ход проложен между двумя пунктами опорной сети (рис. 11.1 а). Начальная и конечная точки А и С разомкнутого теодолитного хода являются пунктами опорной сети, координаты которых известны. С каждого из конечных пунктов должно быть видно хотя бы по одному пункту опорной сети, например В и D. Дирекционные углы исходных сторон ВА и CD известны. Непосредственная привязка заключается в измерении на конечных пунктах А и С примычных углов jA и jC между исходными направлениями АВ и CD и соответственно первой и последней сторонами хода.
11.5.3 Теодолитный ход не примыкает к пунктам опорной сети. В этом случае от ближайшего пункта опорной сети прокладывают специальный подходной теодолитный ход к одной из сторон теодолитного хода. С целью контроля измерений и и повышения надежности привязки привязочный ход должен быть замкнутым (рис. 11.2 а).
Если вблизи теодолитного хода расположены как минимум два пункта геодезической опорной сети, с которых имеется видимость на одну из точек хода, то его привязка может выполнена прямой геодезической засечкой (рис. 11.2 б). для этого на исходных пунктах А и В измеряют горизонтальные углы a и b между исходной стороной и направлением на определяемую точку. В точке 1 измеряют примычные углы j1 и j2.
При наличии видимости с определяемой точки на три пункта опорной сети привязка осуществляется обратной геодезической засечкой. В этом случае с определяемой точки измеряют углы a и b между направлениями на исходные пункты, координаты которых известны (рис. 11.2 в). Для передачи дирекционного угла на сторону теодолитного хода измеряют примычные углы j.
11.5.4 В районе прокладки теодолитного хода отсутствуют пункты опорной сети. В этом случае дирекционные углы одной или нескольких сторон хода могут быть вычислены исходя из значений истинных азимутов направлений, которые устанавливаются на основе астрономических наблюдений небесных светил либо определены с помощью гирокомпасов или гиротеодолитов. Зная величину сближения меридианов, рассчитывают дирекционные углы этих сторон. Координаты начальной точки теодолитного хода задаются условно.
где а – подходной ход;
б – прямая геодезическая засечка;
в – обратная геодезическая засечка.
Рисунок 11.2 – Случаи привязки теодолитного хода к опорным пунктам
Источник
9.5. Привязка теодолитных ходов.
Для того, чтобы связать теодолитный ход с другими ходами в единое плановое съемочное обоснование, выполняется его привязка к пунктам опорной геодезической сети. Наиболее простой способ привязки при помощи измерения примычных углов (рис. 9.6.).
Рис. 9.6. Схема привязки теодолитных ходов
9.6. Камеральная обработка результатов измерений.
Конечной целью камеральной обработки теодолитного хода является получение уравненных значений координат точек. Она включает следующие процессы:
где t = 1 – точность отсчетного устройства теодолита. Если fβ≤ fβ теор. то вычисляют поправки 

Вычисление дирекционных углов и румбов
В зависимости от четверти по формулам связи переходят к румбам.
Вычисление приращений координат и координат точек. В основе данных вычислений лежит прямая (обратная) геодезические задачи.
9.7. Прямая геодезическая задача.
По известным координатам одной точки, дирекционному углу и горизонтальному проложению линии АВ, определить координаты второй точки (рис. 9.7.).
Рис.9.7. Прямая и обратная геодезические задачи
9.8. Обратная геодезическая задача.
По известным координатам двух точек определить дирекционный угол и горизонтальное проложение линии АВ.
Из ∆АОВ 
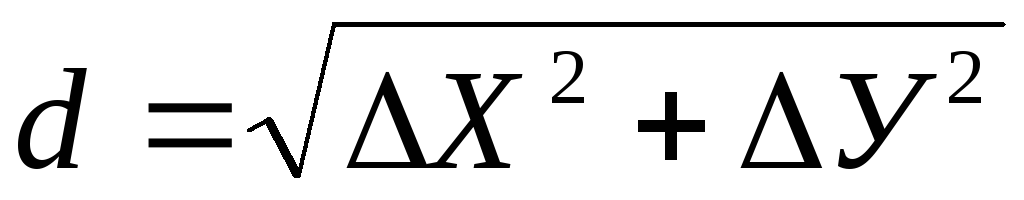
Вычисление приращений координат производят по таблицам приращений или с помощью калькулятора. Алгебраическая сумма приращений координат в замкнутом полигоне должна равняться нулю. По вычисленным ∆Х и ∆У находим невязки 



Раздел 10. Топографическая съемка
Съемкой называется комплекс геодезических работ необходимых для составления планов и карт. В процессе съемки с пунктов опорной геодезической сети или съемочного обоснования определяют плановые положения контуров и предметов местности и производят определение точек по высоте для изображения рельефа. Топографическая съемка состоит из подготовительных и полевых работ. В процессе полевых работ производят осмотр участка местности, закрепляют точки съемочного обоснования и выполняют необходимые угловые, линейные и высотные измерения. В зависимости от размеров участка, цели создания плана, масштабов съемки бывают:
глазомерная (для приближенного изображения участка местности в произвольном масштабе);
теодолитная (получение контурного плана без рельефа);
тахеометрическая (получение топографического плана);
мензульная (получение топографического плана в полевых условиях).
стереотопографическая (получение топографических планов и карт на большие территории с использованием материалов аэрофотосъемки и стереокомпараторов).
По материалам съемок создаются планы, карты, цифровые модели местности. В последнее десятилетие все большие масштабы приобретают технологии создания планов и карт в виде цифровых моделей или электронных планов. Цифровые модели местности создаются на ЭВМ, путем преобразования топографической информации о местности в цифровую форму. Цифровая модель местности состоит из независимых составляющих, представляющих: рельеф, инженерные коммуникации, здания и сооружения, гидрографию и др. Точность цифровых моделей или электронных планов должна соответствовать точности соответствующих масштабов топографических планов.
Источник
Привязка теодолитных ходов
Целью привязки теодолитных ходов к пунктам Государственной геодезической сети 1, 2, 3 и 4 классов, а также к пунктам съёмочной сети 1 и 2 разрядов является определение с заданной точностью координат вершин указанных ходов.
В зависимости от расположения теодолитного хода на местности, условий съёмки, сложности ситуации и других факторов схемы и способы привязки элементов теодолитного хода могут быть различными. Во многих случаях приходится выполнять дополнительные геодезические построения. Тем более, что любая привязка должна иметь надёжный контроль, который, чаще всего, обеспечивается избыточными измерениями и дополнительными геодезиическими построениями.
Под элементом теодолитного хода понимают одну из его определяемых точек, координаты которой необходимо найти, и дирекционный угол линии теодолитного хода, исходящей из определяемой точки.
Здесь будут рассмотрены некоторые из основных способов привязки теодолитных ходов, которые чаще всего встречаются на практике, приведены схемы, предусматривающие комбинированное использование способов привязки. Однако следует иметь в виду, что на практике могут встретиться случаи, когда ни один из рассмотренных способов не может быть выполнен в силу действия различных факторов. Геодезист и маркшейдер должны уметь проектировать частные схемы привязок, которые обеспечат построение съёмочного обоснования с необходимой точностью.
73.1. Способ примыкания
На рис. 7.2 приведены сравнительно простейшие способы привязки теодолитных ходов. Для разомкнутого хода – это привязка начальной и конечной линий оптимально к двум исходным направлениям с включением пункта высокого класса в теодолитный ход в местах примыкания. Замкнутый теодолитный ход может быть привязан на два исходных направления с включением пункта высокого класса непосредственно в ход (рис. 7.2 б) либо с помощью дополнительного полигонометрического хода (рис. 7.2 в) от исходных пунктов (привязка ходом). Методика выполнения привязки с помощью указанных схем следующая.
Рис. 7.5. Привязка разомкнутого и замкнутого теодолитных ходов:
разомкнутый ход (а), замкнутый ход (б).
Привязка разомкнутого теодолитного хода на двух его концах выполняется с использованием примычных (горизонтальных) углов γ1, γ2, γ3 и γ4 (рис. 7.5). В результате дважды определяют дирекционные углы направлений А-1 и n-D.


где αВА , αСА , αDE , αDF – дирекционные углы исходных направлений (находят из решения обратных геодезических задач по координатам исходных пунктов); на схеме углы γ1 и γ2 – левые по ходу, углы γ3 и γ4 – правые по ходу.
Если разница полученных дирекционных углов допустима (для технических теодолитных ходов – не более 1′), т.е.

то вычисляют средние арифметические значения углов

и в дальнейшем принимают их за исходные.
Аналогично выполняют привязку линии А1 в замкнутом теодолитном ходе (рис. 7.5 б).
Примычные углы измеряют теодолитом повышенной точности, чем рекомендуемый для измерений в теодолитных ходах. Иногда приходится пользоваться для измерения примычных углов и для измерения горизонтальных углов в вершинах хода одним и тем же теодолитом. В этом случае примычные углы измеряют несколькими полными приёмами каждый (3 – 5 полных приёмов с перестановкой лимба горизонтального круга и с повторным центрированием и горизонтированием теодолита перед каждым приёмом). Целесообразно, чтобы примычные углы имели вес в 1,5 – 3 раза больший, чем вес углов дальнейших геодезических построений.
73.2. Прямая угловая засечка
Положение точки М теодолитного хода определяют из решения треугольников АВМ и ВСМ по результатам измерения горизонтальных углов β1, β2, β3 и β4 при исходных направлениях АВ и ВС (рис. 7.6 а). Горизонтальный угол β5 , измеренный в вершине М между направлениями ВМ и МN, используют для передачи дирекционного угла с направления ВМ на линию теодолитного хода MN.
Рис. 7.6. Прямая угловая засечка:
Координаты точки М чаще всего вычисляют по формулам Юнга:



Для контроля аналогичные вычисления выполняют из решения второго треугольника. Точность определения прямоугольных координат не должна быть меньше установленной инструкцией.
Для передачи дирекционного угла на линию MN из решения обратной геодезической задачи вычисляют дирекционный угол направления BM (αBM), а затем получают дирекционный угол αMN по формуле
На схеме привязки горизонтальный угол β5 является правым по ходу ВMN, поэтому в формуле (7.18) перед ним стоит знак минус.
Часто прямую угловую засечку выполняют сразу для двух точек, М и N. Тогда координаты точки N определяют так же, как и координаты точки М, а значение горизонтального угла β5 используют как контрольное. Аналогичный угол целесообразно измерить и в точке N.
Оценка точности определения координат пункта M относительно исходных пунктов А, В и С выполняется по следующим формулам:


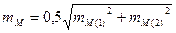
где mM(1) и mM(2) – соответственно средние квадратические погрешности определения положения точки М из первого и второго треугольников; mβ – средняя квадратическая погрешность измерения горизонтального угла (сек); ρ» = 206265″ – число секунд в радиане; S – расстояния (горизонтальные проложения) между исходными пунктами и определяемой точкой, вычисляемые по теореме синусов в соответствующем треугольнике.
При проектировании рассмотренной схемы привязки следует стремиться к тому, чтобы горизонтальные углы γ при определяемой точкебыли не меньше 30 о и не больше 150 о . Большая точность достигается при углах γ в пределах 109 о – 110 о при примерно равных расстояниях до неё от исходных пунктов..
Пример 7.4.Привязка способом прямой угловой засечки.
Исходные данные (схема рис. 7.6 а):
Решение.
Из треугольника АВМ (1):


Аналогичные вычисления выполняем в треугольнике ВСМ (2):
В результате получены невязки в координатах:
Значение fАБС является критерием качества решения задачи привязки.
При допустимом значении абсолютной невязки вычисляют среднее значение координат точки М: ХМ = 4287,762 м ; YM = 4488,939 м.
Выполним оценку точности засечки по формулам (7.19) – (7.21), приняв mβ = 2,0″.
Из решения обратной геодезической задачи с точностью до 1 м вычислим значения S 1 ≈ 513 м, S2 ≈ 531 м, S3 ≈ 497 м (для оценки точности определения координат указанного округления до 1 м достаточно).
Значения sin для оценки точности округлим до 0,5 0 .


Средняя погрешность засечки 
Здесь следует сделать некоторые замечания.
1. Средняя погрешность по значению меньше частных погрешностей, полученных по оценкам в соответствующих треугольниках. Это полностью согласуется с положениями теории погрешностей (гл. 3). Координаты точки М получены независимо из решения двух треугольников, т.е. определены дважды. В связи с этим средняя погрешность относится к значениям средних арифметических координат точки М.
2. Практическая погрешность (невязка) составила порядка 9 мм, т.е. на 3 мм больше. Оценка точности выполнялась по теоретическим формулам, для идеального случая, когда влияние других погрешностей исключается, не учитывается. При выполнении практических работ в результатах измерений содержатся и другие погрешности, что и повлияло на окончательное практическое значение точности определения координат точки М. При этом следует иметь в виду, что все погрешности имеют вероятностный характер, и не исключено, что оценочные их значения могут в каких-то случаях оказаться и больше, чем их практические величины.
Вычислим дирекционный угол направления MN.
Из решения обратной геодезической задачи по координатам точек В и М вычислим значение дирекционного угла направления ВМ:
Часто видимость между пунктами А – В и В – С может отсутствовать. В этом случае возможно использование другой схемы прямой угловой засечки (рис. 7.6 б), решение которой выполняется по формулам Гаусса (тангенсов или котангенсов).
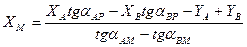



Для контроля выполняют аналогичную привязку с точек В и С.
Значения дирекционных углов в приведенных формулах получают в результате решения азимутальной привязки от соответствующих исходных направлений:
Знак «плюс» — для левых по ходу углов (как это показано на рис. 7.4), знак «минус» — для правых по ходу углов. На схеме рис. 7.6 б горизонтальные углы – левые по ходу.
При использовании для вычислений микрокалькуляторов формулы тангенсов не следует применять, если дирекционные углы близки к 90 о ± 5 о или 270 о ± 5 о , а формулы котангенсов – если дирекционные углы близки к 0 о ± 5 о или 180 о ± 5 о . Это обязательно следует проверить и, при возможности, перейти к другим построениям. В любом случае использование приведённой схемы привязки необходимо начинать с вычисления (или с оценки) величин дирекционных углов.
73.3. Линейная засечка
Этот способ часто используют в тех случаях, когда имеется возможность измерения расстояний S светодальномером либо непосредственно компарированной рулеткой в одно уложение (рис. 7.7). Такие схемы обычно используют при небольших расстояниях между пунктами А и В, расположенными, например, на углах здания, и сравнительно большом расстоянии между пунктами В и С (в этом случае используют дополнительную точку Т, закрепляемую в створе линии ВС). Кроме того, при большом расстоянии между точками А и В можно и между ними (в створе) выбрать в удобном месте дополнительную точку при соблюдении примерного равенства расстояний S. Значения координат точки М вычисляют по формулам:



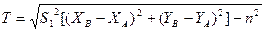
Формулы (7.29) и (7.30) используют в том случае, когда точка М находится слева от направления из точки А на точку В. В связи с этим перед вычислениями необходимо составить схему расположения точки М относительно исходных точек А и В и учесть это при записи разностей координат Х и Y.
Рис. 7.7. Линейная засечка.
Задача решается дважды относительно точек А и В и точек В и С (Т).
Часто решение линейной засечки выполняют по несколько измененным формулам:


где 


Значение h берут со знаком «плюс», если точка М находится слева от направления из точки А на точку В. Если точка М находится справа от указанного направления, то значение h берут со знаком «минус».
Приближённая оценка точности произведенной линейной засечки может быть выполнена по формулам:


где mS / S – относительная погрешность измерения линий; γ – угол засечки при определяемой точке (его вычисляют по теореме косинусов в соответствующем треугольнике).
Углы при определяемой точке не должны быть меньше 30 о и более 150 о . Большая точность достигается при углах γ в пределах 90 о .
Пример 7.5.Привязка способом линейной засечки.
Исходные данные (схема рис.7.7):
Стороны измерены с относительной погрешностью 1:10000.
Решение.
Из решения обратной геодезической задачи находим:


Определяем координаты точки Т (прямая геодезическая задача):
Воспользуемся формулами (7.29) и (7.30).
Для треугольника АВМ: n = 24551,453 ; D = 53072,306.
Для треугольника ВМТ: n = -11749,929 ; D = 57984,954.
Невязки в координатах:
Если это условие удовлетворяет необходимой точности привязки, то вычисляют средние значения координат точки М:
Выполним оценку точности определения координат точки М по формуле (7.34). Для этого по теореме косинусов найдем углы γ в треугольниках АМВ и ВМТ при точке М (вычисления достаточно выполнить с точностью до 0,5 0 ): γ1 = 69,2 0 ; γ2 = 34,7 0 .

Из треугольников АВМ и ВМТ соответственно получим:
mM1 = 0,037 м; mM2 = 0,082 м; средняя погрешность mM = 0,5 
73.4. Обратная угловая засечка
Привязка способом обратной угловой засечки может быть выполнена по трём исходным геодезическим пунктам, если определяемая точка не лежит на окружности, описанной по ним. Оптимально, когда определяемая точка находится внутри треугольника примерно на равных расстояниях от его вершин (рис. 7.8 а).
Удаление точки М от опасной окружности на 10% её радиуса уже обеспечивает решение задачи определения координат искомой точки. Для графической оценки положения точки М составляют схему привязки и контролируют выполнение условия 
Следует иметь в виду, что в данном случае не обеспечивается надёжный контроль привязки, поэтому целесообразно использовать для решения указанной задачи четыре исходных пункта, т.е. в определяемой точке необходимо ещё измерить угол β3 на исходный пункт D.
Рис. 7.8. Обратная угловая засечка.
Схема обратной угловой засечки (а). Построение инверсионных треугольников (б).
Координаты точки М находят по формулам С.Г.Молочкова:


где 



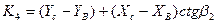
При наличии четвёртого пункта (D) координаты точки М могут быть получены дважды: при использовании пунктов D, A и B и при использовании пунктов А, В и С. При этом может оказаться, что точность определения координат будет различной, в связи с чем целесообразно установить, относительно каких пунктов следует определять координаты точки М, а какой из пунктов будет контрольным. Указанная задача решается методом инверсионных треугольников.
Построение инверсионных треугольников выполняется на графической схеме привязки, построенной в произвольном масштабе длин, но с таким расчётом, чтобы отрезки S были не менее 6 – 7 см. На этих отрезках откладывают в принятом масштабе значения параметров qi (градиентов):

Получают соответствующие инверсионные треугольники: 123 – для пунктов D, A и B и 234 – для пунктов А, В и С (рис. 7.8 б). Из точек 1, 2, 3 и 4 опускают высоты hi на соответствующие стороны и графически, в масштабе q, получают их значения.
Графическая оценка точности выполняется по формулам:


где М – средняя квадратическая погрешность определения координат точки М; mβ – средняя квадратическая погрешность измерения углов.
По минимальной величине М выбирают исходные пункты для вычисления координат по формулам (7.35) и (7.36).
Иногда координаты определяют два раза, по двум группам из трёх исходных пунктов, а оценку погрешности выполняют по средней её величине, как это делалось в предыдущих способах.
Контроль вычислений по четвёртому исходному пункту выполняют сравнением измеренного горизонтального угла (или углов, если пунктов более четырёх) с вычисленным его значением. Например, если контрольное направление выбрано на пункт D, то сравнивают

с тем же горизонтальным углом, измеренным в поле. Разница в полученных углах является критерием качества привязки. Для теодолитных ходов указанная разница не должна превышать 1′.
Передача дирекционного угла на определяемую линию MN выполняется с учётом значения горизонтального угла β4 (правого или левого по ходу).
Аналитическая оценка точности определения координат точки М (линейная погрешность mM) может быть выполнена по формуле

где 
Пример 7.6.Привязка способом обратной угловой засечки.
Исходные данные (схема рис. 7.8):
Решение.
По схеме, построенной в произвольном масштабе, но с соблюдением её геометрии по горизонтальным углам, получим длины отрезков S в мм и в метрах: S1 = 72,5 мм (3625 м); S2 = 54,0 мм 2700 м); S3 = 51,3 мм (2565 м); S4 = 59,2 мм (2960 м).
По формуле (7.37) вычислим значения градиентов (q1 = 56,9; q2 = 76,4; q3 = 80,4; q4 = 69,7) и построим их величины на схеме по соответствующим сторонам в условно выбранном масштабе. Получатся точки 1, 2, 3 и 4. В результате образованы два инверсионных треугольника 123 и 234.
Построим в инверсионных треугольниках высоты hi и графически в масштабе q измерим их значения: h1 = 91,0; h2 = 90,0; h3 = 97,0; h4 = 132,0.
Принимая mβ = 2,0″ (здесь необходимо учитывать фактическую точность измерения углов), по формулам (7.38) вычислим значения средних квадратических погрешностей: М1 = 0,030 м; М2 = 0,027 м.
Поскольку М2 меньше М1, то целесообразно для вычисления координат точки М использовать второй инверсионный треугольник (234), т.е. использовать для вычислений координат исходные точки В, С и D.
Далее решаем задачу по формулам Молочкова (7.35) и (7.36) для установленных исходных пунктов:






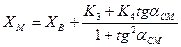

Контроль привязки выполняем по направлению на четвёртый исходный пункт А.
Из решения обратной геодезической задачи найдем дирекционные углы направлений MА и МВ: 



Как видим, различие составляет всего 0,5″, что для данных условий вполне допустимо.
Аналитическая оценка точности определения координат точки М по формуле (7.40) дает значение М = 0,0279 м = 28 мм. Все параметры, входящие в формулу (7.40), получены из решения обратной геодезической задачи по соответствующим направлениям ( 

Аналогичная задача привязки точки М (задача обратной однократной засечки) может быть решена по формулам И.Ю.Пранис-Праневича. Она решается для трёх исходных пунктов и двух измеренных горизонтальных углов в определяемой точке. Например, в соответствии со схемой рис. 7.8, для исходных пунктов А, В и С и измеренных углов β1 и β2 координаты точки М вычисляют по формулам:




Пример 7.7.Обратная однократная засечка (использование формул И.Ю.Пранис-Праневича).
Исходные данные примера 7.6.
Решение (для исходных пунктов А, В и С).
ctgαBM = (- 2789?170172)/(-4651,097936) = +0,599679949 (третья четверть – ЮЗ).
N = 398,5895246 + (- 3434,064933) = — 3035,475409.
Различия в значениях координат точки М по сравнению со значениями, полученными в примере 7.6, объясняются другими погрешностями измерений в схеме АВС по сравнению со схемой ВСD.
Такая же задача способом обратной однократной засечки может быть решена по измеренным направлениям (рис. 7.9) по формулам Деламбера.
Рис. 7.9. Обратная однократная угловая засечка
по измеренным направлениям.
Для указанной засечки необходимо иметь четыре исходных пункта, наблюдаемых с точки М. Горизонтальные измеренные углы β приводят к какому-либо начальному направлению на исходный пункт, например, на пункт А. Значения координат точки М вычисляют дважды по двум последовательным схемам: АВС и ВСD. При этом в схеме АВС за начальное направление принимают МА, а в схеме BCD – МВ. Из схемы АВС:





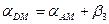
Аналогичные формулы, в соответствии со схемой привязки, составляют и для группы точек BCD.
Пример 7.8.Обратная однократная засечка по измеренным направлениям.
Исходные данные (см. пример 7.6).
Решение(для схемы АВС).
В соответствии с рис. 7.8 и 7.9, в схеме АВС
Тогда tgαАМ = -1,363648006 (вторая четверть – ЮВ), αАМ = 126 о 15’13»; αВМ = 210 о 57’01»; αСМ = 292 о 10’26»; αDМ = 71 о 00’42».
В результате получены значения координат ХМ = 3400,754 м, YМ = 6645,212 м. То есть такие же, как и при вычислениях по формулам И.Ю.Пранис-Праневича.
73.5. Комбинированные засечки
Кроме рассмотренных выше схем привязки используются схемы комбинированной засечки (рис. 7.10).
Рис. 7.10. Комбинированные засечки.
В схеме рис. 7.10 а положение точки М определяют способом обратной угловой засечки по углам β1 и β2 и для контроля – способом прямой угловой засечки по углам β3 и β4. При этом, например, угол β4 можно не измерять, а вычислить из треугольника АВМ по углам β1 и β3.
В схеме рис. 7.10 б дважды вычисляют дирекционный угол линии ВМ от направлений АВ и ВС, находят его среднее значение. Используя затем углы β1 и β2, находят дирекционные углы линий МD и МЕ. Далее по формулам Гаусса вычисляют координаты точки М из двух вариантов: относительно пунктов В и Е и затем пунктов В и D.
Часто привязку целесообразно выполнять для двух точек одновременно, включённых в определяемую линию теодолитного или полигонометрического хода. Такие привязки используются, например, в схемах, приведённых на рис. 7.10 в, г, д.
В схеме рис. 7.10 в координаты точек М1 и М2 определяют обратной засечкой по трём исходным пунктам, а координаты вспомогательной точки D – прямой засечкой с точек М1 и М2 и одного исходного пункта. Обычно координаты точки D определяют с пунктов М1 и А по формулам Юнга, а
относительно точек М1 и М2 – по формулам тангенсов или котангенсов (контрольное вычисление).
Схемы рис. 7.10 г и д используют при густой сети исходных пунктов.
В схеме рис. 7.10 г координаты точки М1 определяют по четырём исходным пунктам, а координаты точки М2 по трём исходным пунктам и точке М1. В схеме рис. 7.10 д, при отсутствии видимости между определяемыми пунктами, выбирают вспомогательную точку D. При этом координаты точек М1 и М2 находят по трём исходным пунктам, а координаты точки D – прямой засечкой с точек М1 и М2 и одного исходного пункта.
Схема рис. 7.11 представляет собой т.н. геодезический четырехугольник. При этом в указанной схеме подбирают такое положение точек M и N , чтобы все углы, кроме β1, были не менее 20 0 . В замкнутом треугольнике BCD при использовании линии MD в теодолитном ходе, угловая невязка не должна превышать 1,5′. Сначала, после уравнивания углов β2, β4, β5 и β7, вычисляют координаты точки D, а затем, из двух вариантов по формулам прямой угловой засечки, координаты точки М.
73.6. Задача П.А.Ганзена
Такую задачу (задачу о двух точках) решают при наличии всего двух исходных пунктов (рис. 7.12).
В этой схеме измеряют углы β5, β6, β7, и β8 при определяемых точках М и С. Из треугольников АСМ и ВСМ вычисляют углы β3 и β4. Значения углов β1 и β2 находят по формулам:

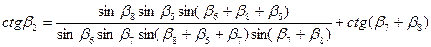
Далее решают прямые угловые засечки из треугольников АМВ и АВС. Для контроля вычисляют дирекционные углы линии СМ и направлений с определяемых точек на исходные пункты. По разностям дирекционных углов контролируют значения углов β.
Источник
Прямая и обратная геодезическая задачи. Обработка результатов измерений при теодолитной съемке
Лекция 2: ПРЯМАЯ И ОБРАТНАЯ
ГЕОДЕЗИЧЕСКАЯ ЗАДАЧИ
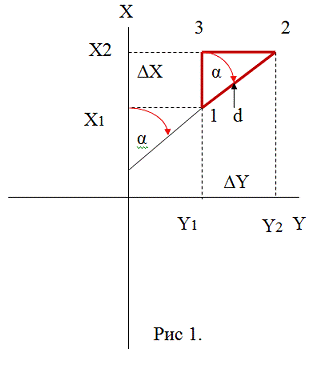
Прямая
геодезическая задача
Даны координаты первой точки Х1 и
У1,горизонтальное расстояние от первой до второй точки d
и дирекционный угол α1-2 линии
1-2. Нужно определить координаты Х2 и У2 второй точки.
Спроектируем точки 1и 2 на оси координат.
Проекция линии d на ось Х ,
очевидно, будет равна Δ Х = Х2 –
Х1, а на ось У, ΔУ = У2 – У1.
Из прямоугольного треугольника 1- 2
– 3
находим:
Δ Х= d·
cos ; Δ
У= d· sinα
Координаты точки 2 находим по формулам: Х2= Х1 + ΔХ;
Y2 = Y1
+ ΔY. В зависимости от
величины дирекционного угла приращения координат могут иметь различные знаки,
которые определяются знаками тригонометрических функций ( sinα
и cosα
) соответствующей четверти.
|
Приращения |
1-четверть |
2- |
3- |
4- |
|
ΔХ |
+ |
– |
– |
+ |
|
ΔY |
+ |
+ |
– |
– |
ОБРАТНАЯ ГЕОДЕЗИЧЕСКАЯ ЗАДАЧА
Даны координаты Х1 и У1 первой и Х2 и У2 второй
точек (см. рис.1).
Нужно определить дирекционный угол α
линии
1-2 и горизонтальное расстояние d.
Зная координаты первой и второй точек, легко определить приращение координат: ΔХ=
Х2 -Х1 и ΔY
= Y2 – Y1.
Отношении ΔУ
к ΔХ
позволяет определить тангенс угла.
tgr1-2 = ΔY/ΔX
Полученный угол является румбом направления 1-2.
Для перехода от румба к, дирекционному необходимо учесть знаки приращения
координат, (см. табл.1). Например У имеет знак минус, а Х знак + ,
следовательно направление находится в 4 четверти, а дирекционный угол
рассчитывается по формуле α =
360 – r .
Расстояние d
определяется по формулам:
d = ΔX/cosα
= (X2 – X1)/
cosα; d
= ΔY/sinα
= (Y2 – Y1)/sinα
Расстояние так же можно определить по теореме
Пифагора из прямоугольного треугольника 1- 2 – 3 см. рис.1.
d =
СЕТИ И СЪЕМКИ. ГЕОДЕЗИЧЕСКИЕ СЕТИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Совокупность измерений на местности
с целью составления плана или карты называется съемкой. Для ослабления ошибки
на результаты измерения геодезические работы ведутся от общего к частному, т.е.
съемка подробностей ведется с точек местности, координаты которых заранее
определены.
Геодезические сети России.
Создание топографических карт для
всей территории страны невозможно без построения единой сети опорных пунктов,
определенных с высокой точностью в единой системе координат и надежно
закрепленных на местности. Система опорных пунктов, составляет опорную
геодезическую сеть. Существуют плановые геодезические сети, в которых для
каждого пункта определяются плоские прямоугольные координаты в системе
Гаусса-Крюгера и высотные пункты со значением высот относительно нуля
Крондштатского футштока. По своему положению и точности определения пункты
делятся на классы. Пункты высшего класса расположены на большом расстоянии друг
от друга. В последствии, они сужаются, путем развития между ними сетей более
низкого класса.
Определение планового положения
(координаты) опорного пункта производится астрономическими и геодезическими
методами. Астрономический метод дает возможность получения географических
координат точек независимо друг от друга. При геодезическом способе создания
опорных сетей, астрономическим методом определяется положение одного или
нескольких опорных пунктов. Остальные пункты связываются с исходным
направлением путем построения простейших геометрических фигур, вершинами
которых являются опорные пункты и соответствующих измерений сторон и углов этих
фигур. При создании опорных сетей геодезический способ является основным, т.к.
он значительно точнее, чем астрономический. Поэтому государственные опорные
сети называются геодезическими сетями. Для определения планового положения
опорных пунктов применяются методы триангуляции, трилатерации и полигонометрии.
Метод триангуляции основан на
построении на местности сети треугольников, примыкающих друг к другу, в которых
измеряются все углы и длина одной из сторон. Остальные стороны вычисляются по
формулам тригонометрии. Метод трилатерации сводится к построению на местности
смежных треугольников и геодезических четырехугольников с измерением в каждом
из них всех сторон и диагоналей. Углы получают путем тригонометрических
вычислений.
После этих работ производится
определение координат всех опорных пунктов. В районах где видимость ограничена
(например лесной массив) и создание видимых опорных пунктов связано с большими
затратами, используется метод полигонометрии. Он сводится к построению на
местности ломаной линии с углами близкими 180 градусов. При применении
полигонометрических сетей замеряют все стороны – S1, S2, S3,…… Sn., углы
поворотов β1, β2, β 3… β n. и
примычные углы Q1, Q2, Q3….Qn
По исходным сторонам и углам, имея
координату исходной точки А и дирекционный угол исходного направления АВ
вычисляют координаты вершин полигонов, которые являются опорными пунктами,
закрепленные на местности строительством постоянных сооружений. Плановая
геодезическая сеть делится на четыре класса, где каждый последующий класс
опирается на точки более высокого класса. Государственная нивелирная сеть так
же делится на 4 класса. Нивелирная сеть 1 и 2 класса служит главной высотной
основой, посредством которой устанавливается единая система высот на всей
территории страны.
Нивелирные сети 3 и 4 классов служат
для развития высотных сетей и решения инженерных задач. Геодезические сети
местного значения являются обоснованием топографических съемок 1:5000 и 1:500
масштабов, и инженерных работ выполняемых в городах и других населенных
пунктах, а так же площадках промышленного строительства, при строительстве
подземных коммуникаций и в маркшейдерском деле. Они подразделяются на
аналитические сети 1 и 2 разряда и полигонометрические сети 1 и 2 разрядов.
Аналитические сети создаются методом триангуляции, а полигонометрические,
методом полигонометрии, между пунктов триангуляции. Все они опираются на сети
более высокого порядка. Высотная геодезическая сеть местного значения, выполняется
отдельными ходами, системой ходов и замкнутых полигонов между пунктами
нивелирования высших классов. После создания геодезической сети производится
съемка подробностей ситуации и рельефа. В зависимости от применяемых
инструментов и методов различают несколько видов съемок подробностей.
Теодолитная съемка выполняется
теодолитом и мерной лентой. При этом измеряются только расстояния и
горизонтальные углы. Расстояния можно измерять дальномерами соответствующей
точности.
Тахеометрическая съемка сочетает в
себе, контурную и вертикальную. Производится теодолитом, снабженным
вертикальным кругом и дальномером. Превышения измеряются тригонометрическим
нивелированием, путем измерения угла наклона с помощью вертикального круга. Она
позволяет отображать на плане не только горизонтальную ситуацию, но и рельеф.
Мензульная съемка производится с помощью мензулы и кипрегеля, инструментов
позволяющих непосредственно в поле получать план местности с изображением
рельефа.
Аэрофотосъемка, это съемка
специальным фотоаппаратом установленном на самолете. Она ведется, в сочетании с
геодезическими работами, необходимыми для привязки снимков к местности, в
плановом и высотном отношениях.
ТЕОДОЛИТНАЯ СЪМКА
Получение контурного плана местности
с помощью теодолита и мерной ленты (или дальномера) называется теодолитной
съемкой. При теодолитной съемке рельеф не изображается. Съемка ведется по
принципу от общего к частному, т. е. на местности выбираются и закрепляются
опорные точки, определяются их координаты, а с них ведется съемка подробностей.
Совокупность таких точек называется съемочной сетью, которая строится в виде
теодолитных ходов, представляющих с собой систему ломаных линий, в которых углы
измеряются теодолитом, а стороны мерной лентой или дальномером.
Теодолитные ходы.
Основные требования при проложении
теодолитных ходов следующие.
а) Выбирая положение точек
теодолитного хода надо стремиться, что бы вокруг точки была горизонтальная
площадка с твердым грунтом, с хорошим обзором соседних точек хода и удобством
съемки подробностей.
б) Стороны хода должны находиться на
твердых прямых участках местности с углами наклона не более 5 градусов и длиной
от 50 до 350 метров.
в) Теодолитные ходы прокладываются с
учетом надежного контроля. Поэтому в районах, где отсутствуют точки геодезической
сети или они располагаются близко друг от друга, рекомендуется прокладывать
замкнутые полигоны, внутри которых прокладываются диагональные ходы, образующие
узловые точки. Диагональные ходы позволяют сгущать систему съемочных точек и
осуществлять дополнительный контроль измерений.
Разомкнутые, вытянутые ходы прокладываются, как
правило, между опорными геодезическими точками, например, применяются при
трассировании вытянутых сооружений.
г) Для ограничения накопления ошибок угловых и
линейных измерений теодолитных ходов, установлены предельные значения их длин
между опорными и узловыми точками, в зависимости от точности инструмента и
масштаба съемки.
д) При прокладке теодолитных ходов на
незастроенных территориях необходима следующая густота съемочных точек:
:5000 1 точка на 7-8 га, или 14 точек на 1 км
:2000 1 точка на 4 га, или 25 точек на 1 км.
:1000 1 точка на1 га, или 100 точек на 1 км.
Порядок производства работ при прокладке
теодолитных ходов.
Работы по прокладке теодолитных ходов
производятся в следующем порядке.
1) Камеральная подготовка включает:
изучение картографического материала, каталогов плановой и высотной опорной
сетей, географического описания района и составление предварительного проекта
работ.
2) Рекогносцировка – в процессе, которой
отыскиваются пункты геодезической плановой и высотной сетей на местности и
окончательно устанавливаются вершины углов поворота теодолитных ходов.
Результаты рекогносцировки наносятся на карту самого крупного масштаба, а при
ее отсутствии, на схему, составленную в процессе работ.
) Прокладка теодолитных ходов состоит из
следующих этапов.
а) Закрепление точек поворотов ходов колышками
со сторожками, на которых указывается номер точки, название организации, год
работы. Через 1 км., устанавливают деревянные столбы или полигонометрические
центры, такие точки называются закладными.
б) измерение углов 30 секундным или 1 минутным
теодолитом, который перед замерами должен быть тщательно вымерен.
в) Измерение длин линий в прямом и обратном
направлениях.
Привязка теодолитных ходов к пунктам
геодезической опорной сети.
Для получения координат точек теодолитных ходов
в общегосударственной системе координат и для контроля измерений, теодолитные
ходы необходимо привязать к пунктам государственной геодезической сети или сети
местного значения.
Допустим, что в систему точек теодолитного хода
включена одна точка опорной сети.
Зная дирекционный угол
α2-3, линии 2-3, измерив примычный угол и зная
значения внутренних углов β1,
β2,
β3,
β4,
а также длин сторон хода
Мы имеем возможность вычислить координаты всех
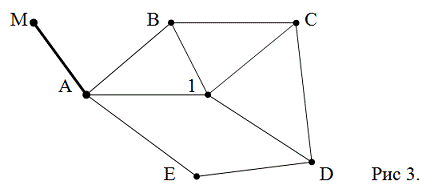
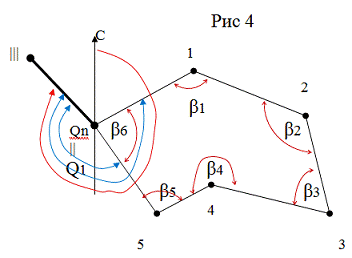
точек теодолитного хода в государственной системе координат. Кроме примычного Q1
угла ,рекомендуется измерять примычный угол Qn
,так как разность углов Q1
– Qn =
β6
может служить контролем правильности измерения примычных углов. Во втором
случае внутренние углы полигона β4, β5
являются одновременно примычными углами к твердой линии 4-5.
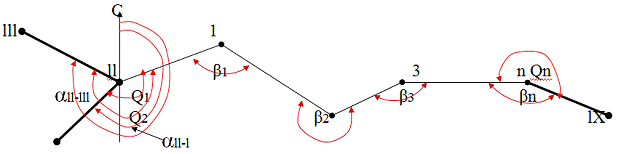
Разомкнутые, вытянутые ходы, прокладываются, как
правило, между двумя твердыми точками, а лучше между двумя твердыми сторонами.
Если есть возможность привязки к двум
направлениям lll – ll
и ll – l,
то измеряются два примычных угла Q1
и Q2, что дает
дополнительный контроль привязки, так как разность примычных углов, должна
равняться разности дирекционных Q2-Q1=
αlll-ll
– αll-l.
Нужно стремиться, что бы конечная точка вытянутого хода, являлась точкой
геодезической сети и что бы имелась возможность замерить примычный угол Qn.
Если ход не привязан к сети высшего класса, он называется висячим.
При отсутствии в непосредственной близости к
теодолитному ходу опорных точек, приходится прокладывать специальные
привязочные ходы.
В отдельных случаях допускается для ориентирования
теодолитного хода определения дирекционного угла путем измерения магнитного
азимута и введение в него поправок за склонение магнитной стрелки и сближения
меридианов.
СЪЕМКА ПОДРОБНОСТЕЙ
Производится с пунктов теодолитного хода в
соответствии с заданием и масштабом плана и определяет положение контуров и
точек ситуации на нем. Существует несколько способов съемки подробностей.
а) Метод ординат – съемка ситуации ведется
относительно теодолитного хода. Положение точек местности определяется прямоугольными
координатами.
б) Метод линейных засечек. Положение точки
определяется как вершина треугольника, стороны которого известны.
в) Метод угловых засечек, применяется для съемки
труднодоступных точек.
г) Полярный метод. Съемка ведется относительно
твердой линии, один конец которой принимается за полюс. Положение точки
определяется двумя координатами – горизонтальным углом, отсчитываемым от этой
линии до направления на данную точку и расстоянием от полюса до этой точки.
Углы, измеряются теодолитом установленном в полюсе, а расстояния мерной лентой
или дальномером.
д) Метод обхода. Осуществляется проложением
теодолитного хода, линии которого совпадают с контуром местности (например –
граница леса).
е) Метод перпендикуляров производится с помощью
экера или на глаз, когда определяемые точки под углом 90° выносятся на линию
теодолитного хода.
Лекция №3. ОБРАБОТКА РЕЗУЛЬТАТОВ
ИЗМЕРЕНИЙ ПРИ ТЕОДОЛИТНОЙ СЪЕМКЕ
Камеральная обработка результатов съемки
заключается в выполнение вычислительных и графических работ, целью которых
является определение координат точек теодолитного хода и построение плана
местности в заданном масштабе.
ОБРАБОТКА УГЛОВЫХ ИЗМЕРЕНИЙ
Практические измерения углов
сопровождаются ошибками. Величиной точности теодолитного хода является угловая невязка,
которая не должна превышать определенного предела (ƒβд = ±1’), где n- число
углов теодолитного хода.
Измерение углов замкнутого
теодолитного хода подробно рассмотрено в мультимедийной версии РГР №1. Сумма
внутренних углов замкнутого теодолитного хода определяется по формуле Σβтеор.= 180°(n – 2), где n – число
углов теодолитного хода.
В разомкнутом теодолитном ходе,
опирающемся на две твердые стороны, теоретическая сумма правых углов равна Σβп = αн – αк + n · 180°;
теоретическая сумма левых углов
равна Σβл = αк – αн + n · 180°. Где
αн и αк
дирекционные углы начальной и конечной сторон, к которым привязан теодолитный
ход.
Тогда угловая невязка разомкнутого
теодолитного хода для правых углов равна ƒβ = Σβптеор. – (αн – αк + n · 180°), а
для левых углов
Ƒβ = Σβлтеор. – (αк – αн + n · 180°).
Если определяемая невязка меньше или
равна допустимой невязке, рассчитываемой по формуле ƒβдоп. = 1’, то измерения признаются
удовлетворительными. После этого приступаем к увязке углов, т.е. уравниваем
полученную и теоретическую сумму углов. Для этого в измеренные углы вносим
поправки, которые равны полученной невязке деленной на число углов теодолитного
хода. Поправки вносятся с обратным знаком, т.е., если ƒβ имеет знак
плюс, то поправка δβ
= ƒβ/n имеет знак минус.
ВЫЧИСЛЕНИЕ ДИРЕКЦИОННЫХ УГЛОВ
ТЕОДОЛИТНОГО ХОДА
Допустим, что известен дирекционный
угол начальной стороны αн и все углы
β
теодолитного
хода. Необходимо вычислить дирекционные углы всех сторон хода.
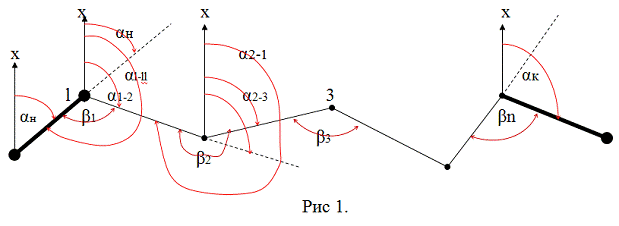
Определяем дирекционный угол стороны 1-2. Для
этого продолжим направление ll-1
за точку 1.
Из рисунка №1 следует, что α1-2
=
αl-ll
– β1, но αl
– ll = αн
+ 180°, поэтому
α1-2 =
αн
+
180° – β1. Соответственно α2-3
=
α1-2
+
180° – β2….. αn
=
αn-1+180 -βn.
Отсюда можно получить общую формулу всего
теодолитного хода:
αк =
αн
+ n · 180° – Σβ.
Последующий дирекционный угол равен предыдущему
дирекционному углу плюс 180° и минус правый внутренний угол.
Для левых углов формулы примут такой вид: αпосл.
= αпред.
– 180° +βл, т.е., последующий дирекционный угол равен
предыдущему углу минус 180°, плюс левый внутренний угол.
В замкнутом теодолитном ходе имеется возможность
надежного контроля, так как после вычисления дирекционного угла последней
стороны полигона, можно вычислить дирекционный угол начального направления.
Если значение вычисленного угла совпадает с исходным, то вычисления сделаны
правильно. В разомкнутом теодолитном ходе, опирающимся на две стороны,
вычисленные дирекционные углы сверяются со значениями, выписанными из каталогов
геодезических опорных точек.
ВЫЧИСЛЕНИЕ КООРДИНАТ ТЕОДОЛИТНОГО
ХОДА
геодезическая
сеть теодолитная съемка
Все измерения теодолитной съемки заносятся в
специальный журнал. Расчет координат замкнутого теодолитного хода подробно
рассмотрен в РГР№1. Для разомкнутого хода вычисление координат производится в
следующей последовательности.
. Вычисляется сумма измеренных углов
хода. Сумма теоретических углов подсчитывается по формуле: Σβтеор.=
αн
–
αк
+ n · 180°. Разница
теоретической и вычисленной сумм углов хода дают угловую невязку теодолитного
хода: ƒβпол.
= Σβтеор. – Σβпол.
2. Вычисляем допустимую невязку
хода по формуле: ƒβдоп. = 1’ Сравниваем полученную невязку с
допустимой. Если полученная невязка меньше или равна допустимой, то измерения
проведены правильно.
. Уравниваем измеренные углы,
т.е. разбрасываем равномерно полученную невязку на все углы с обратным знаком.
Сумма исправленных углов, должна быть равна теоретической сумме углов.
Исправленные углы записываем в ведомость координат теодолитного хода.
. Приступаем к вычислению
дирекционных углов по формулам:
αпосл.=
αпред.
+
180° – βп. или αпосл.
=
αпред.
–
180° + βл.
Полученные данные сверяем со значениями,
выписанными из каталогов геодезических опорных точек.
. Вычисляем румбы направлений сторон
теодолитного хода.
. Вычисляем периметр теодолитного хода,
равному сумме всех сторон (горизонтальных проложений) теодолитного хода.
. Определяем приращения координат по
формулам: ΔХ = d·cosα,
ΔY=
d·sinα.
Определяем знаки приращений координат.
. Сумму полученных приращений
сравнивается с теоретической суммой приращений координат, которая находится как
разность между координатой конечной и начальной опорных точек теодолитного
хода.
ΣΔХ = Хк – Хн;
ΣΔY = Yк
– Yн.
. По разности практической и
теоретической сумм приращений координат определяются линейные невязки
теодолитного хода.
ƒх = ΣΔХ
п.
– ΣΔХ теор. и ƒy
= ΣΔY п –
ΣΔY теор.
. Определяем абсолютную невязку
теодолитного хода по формуле:
ƒр = ±
. Определяем относительную
невязку теодолитного хода по формуле: ƒотн. = ƒр / Р, где Р
– периметр хода. Для удобства сравнения относительная невязка преобразуется в
простую дробь, где в числителе стоит единица. Для этого числитель и знаменатель
второй части равенства делим на ƒр. 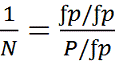
невязку с, допустимой невязкой. Величина допустимой невязки зависит от рельефа
местности. Так для выровненного рельефа величина допустимой невязки принимается
равной 1/N = 1/3000, а
для сильно кочковатой, болотистой местности ее величина равна 1/N = 1/1000.
. Убедившись, что полученная
невязка меньше или равна допустимой невязке, приступаем к увязке приращений
координат, т.е. вносим поправки в приращения координат по осям Х и У. Поправки
в приращения координат рассчитываются по формулам:
δх = (ƒх/Р)
· d, δy
= (ƒy/P)
· d, где ƒх
и ƒу
– невязки по осям Х и У, Р – периметр теодолитного хода, d
– длина стороны хода (горизонтальное проложение).
. Поправки в приращения координат
округляются до сотых, но сумма поправок должна быть равна невязке (ƒх
= δх1+δх2+…δхn;
ƒy=δy1
+ δy2 +… δyn).
Они вносятся с обратным знаком, например ƒх
имеет знак +, значит δх1,δх2…δхn,
вносятся со знаком минус. После внесения поправок в приращения координат, сумма
исправленных приращений должна быть равна теоретической сумме приращений
координат.
. Вычисляются координаты всех точек
теодолитного хода по формулам: Хпосл. = Х пред. + ΔХ;
Y посл. = Y
пред. + ΔY.
Если координаты последней полученной точки соответствуют значениям, полученным
из каталога геодезических опорных точек, то вычисления выполнены правильно.
ПОСТРОЕНИЕ ПЛАНА ТЕОДОЛИТНОЙ СЪЕМКИ
При построении плана теодолитной съемки,
предварительно строится координатная сетка, состоящая из нескольких квадратов,
длина стороны каждого 10 сантиметров. Построение координатной сетки
производится с помощью линейки Дробышева или штангенциркуля и масштабной
линейки. Первоначально определяются размеры координатной сетки, так что бы план
теодолитной сетки симметрично поместился внутри нее. Для этого берутся
минимальные и максимальные значение координат, по осям Х и У. Производится
оцифровка координатной сетки, т.е. берется целое значение меньше минимального
значения координаты по оси Х или У, кратное величине соответствующей 10 см. на
плане. Например: для 1:500 масштаба это 50 метров, для 1:2000 – 200 метров. С
особой тщательностью на координатную сетку выносятся точки теодолитного хода,
которые соединяются прямыми линиями. После этого с помощью транспортира и
измерительного циркуля на план выносятся результаты съемки подробностей. В
окончательном варианте план вычерчивается в туши, применяя топографические
условные знаки. предварительно с плана убираются все вспомогательные линии.
Подробно построение плана теодолитной съемки рассмотрено в мульти-медийной
версии РГР№1.