Как найти принадлежность точки к окружности

Перейти к содержанию

var x,y,r,h: real;

begin

    write('координаты точки: ');

    readln(x,y);

    write('радиус круга: ');

    readln(r);

    h := sqrt(x*x + y*y);

    if h > r then writeln('Точка не принадлежит кругу')

    else writeln('Точка принадлежит кругу');

end.

координаты точки: -1 -2

радиус круга: 5

Точка принадлежит кругу

#include 

#include 

main() {

    float x,y,r,h;

    printf("Координаты точки: ");

    scanf("%f%f", &x,&y);

    printf("Радиус круга: ");

    scanf("%f", &r);

    h = sqrt(x*x + y*y);

    printf("Гипотенуза равна %.2f. ", h);

    if (h > r) printf("Точка не принадлежит кругу.n");

    else printf("Точка принадлежит кругу.n");

}

Координаты точки: 4 5

Радиус круга: 10

Гипотенуза равна 6.40. Точка принадлежит кругу.

from math import sqrt

 
x = float(input("x="))

y = float(input("y="))

r = float(input("r="))

h = sqrt(x**2 + y**2)

print("Расстояние до точки от начала координат равно %.2f" % h)

if h > r:

    print("точка находится за пределами круга")

else:

    print("точка принадлежит кругу")



  


                       
  

x=10

y=-3

r=5

Расстояние до точки от начала координат равно 10.44

точка находится за пределами круга

алг точка_круг

нач

  вещ x,y,r,h

  вывод "Координаты точки: "

  ввод x,y

  вывод "Радиус круга: "

  ввод r

  h := sqrt(x**2 + y**2)

  если h > r то вывод "Не принадлежит"

   иначе вывод "Принадлежит"

  все

кон

Координаты точки: 1.6 -2.1

Радиус круга: 4

Принадлежит

input "x=", x

input "y=", y

input "r=", r

h = sqrt(x^2 + y^2)

if h > r then

        print "Не принадлежит"

else

        print "Принадлежит"

endif

Определение принадлежности точки кругу с центром в начале координат

Вводятся координаты (x;y) точки и радиус круга ( r ). Определить принадлежит ли данная точка кругу, если его центр находится в начале координат.

Будем считать, что точка принадлежит кругу, если находится внутри его или на его окружности.

Из любой точки координатной плоскости можно провести отрезок к началу координат. Если длина этого отрезка больше радиуса круга, то точка лежит за пределами круга и, следовательно, не принадлежит ему. Если же отрезок, соединяющий точку и начало координат, меньше радиуса круга с центром в начале координат или равен ему, то точка будет принадлежать кругу.

Отрезок между любой точкой и нулевой точкой (началом координат) является гипотенузой прямоугольного треугольника, катеты которого равны значениям x и y координаты данной точки.

Таким образом задача сводится по-сути к двум действия:

1. Нахождение длины отрезка между точкой и началом координат по теореме Пифагора (квадрат длины гипотенузы равен сумме квадратов длин катетов).
2. Сравнению полученного значения с радиусом круга.

Pascal

Определение принадлежности точки кругу с центром в начале координат паскаль

Язык Си

Для gcc компилировать с ключом -lm.

Python

Определение принадлежности точки кругу с центром в начале координат Python

Уравнение окружности.

Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.

В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.

Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:

Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.

Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:

Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2

Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3

Получаем:
(x – 2 ) 2 + (y – ( -3 )) 2 = 4 2
или
(x – 2 ) 2 + (y + 3 ) 2 = 16 .

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x – 2) 2 + (y + 3) 2 = 16.

Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.

В уравнение ( x – 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
( x – 2) 2 + ( y + 3) 2 = 16
( 2 – 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

Признак принадлежности четырёх точек одной окружности

Признак принадлежности четырёх точек одной окружности

Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.

Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,

Доказать: точки A, B, C, D лежат на одной окружности

Обозначим ∠ABD=∠ACD=α.

Опишем около треугольника ABD окружность.

Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.

Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:

Рассмотрим четырехугольник ACDF.

Отсюда следует, что четырёхугольник ABDF — вписанный.

Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.

[spoiler title=”источники:”]

http://www.profmeter.com.ua/communication/learning/course/course7/chapter0552/?LESSON_PATH=456.552

[/spoiler]

Признак принадлежности четырёх точек одной окружности

 Если точки B и C лежат в одной полуплоскости относительно прямой AD, и точки B и C видны из отрезка AD под одним углом (то есть ∠ABD=∠ACD), то точки A, B, C и D лежат на одной окружности.

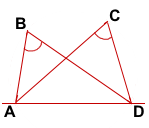
Дано: точки B и C лежат в одной полуплоскости относительно прямой AD,

∠ABD=∠ACD

Доказать: точки A, B, C, D лежат на одной окружности

Доказательство:

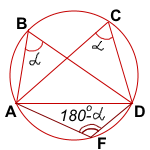Обозначим ∠ABD=∠ACD=α.

Опишем около треугольника ABD окружность.

Отметим на этой окружности произвольную точку F, лежащую относительно прямой AD в другой полуплоскости, чем точки B и C.

Четырёхугольник ABDF — вписанный в окружность. Следовательно, сумма его противолежащих углов равна 180°:

∠ABD+∠AFD=180°.

Отсюда ∠AFD=180°-∠ABD=180°-α.

Рассмотрим четырехугольник ACDF.

∠ACD+∠AFD=α+180°-α=180°.

Отсюда следует, что четырёхугольник ABDF — вписанный.

Поскольку около треугольника ABD можно описать только одну окружность, то точка C лежит на той же окружности, что и точки A, B и D.

Что и требовалось доказать.

Уравнение окружности.

Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.

В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.

Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.

Геометрическая интерпретация уравнения окружности – это линия окружности.

Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.

Окружность с центром в точке А и радиусом R поместим в координатную плоскость.

Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:

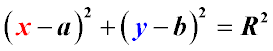
Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.

Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:

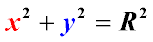
Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.

Примеры решения задач про уравнение окружности

Задача. Составить уравнение заданной окружности

Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.

Решение.
Обратимся к формуле уравнения окружности:
R² = (x-a)² + (y-b)²

Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3

Получаем:
(x – 2)² + (y – (-3))² = 4²
или
(x – 2)² + (y + 3)² = 16.

Задача. Принадлежит ли точка уравнению окружности

Проверить, принадлежит ли точка A(2;3) уравнению окружности (x – 2)² + (y + 3)² = 16.

Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.

В уравнение (x – 2)² + (y + 3)² = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3

Проверим истинность полученного равенства
(x – 2)² + (y + 3)² = 16
(2 – 2)² + (3 + 3)² = 16
0 + 36 = 16 равенство неверно

Таким образом, заданная точка не принадлежит заданному уравнению окружности.

0
 

 Площадь геометрической фигуры |

Описание курса

| Задачи про окружность