Как найти приобретенную скорость тела – Сайт, где вы сможете решить свои вопросы

Нахождение скорости по формулам и единица её измерения

Понятие и основные термины

Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.

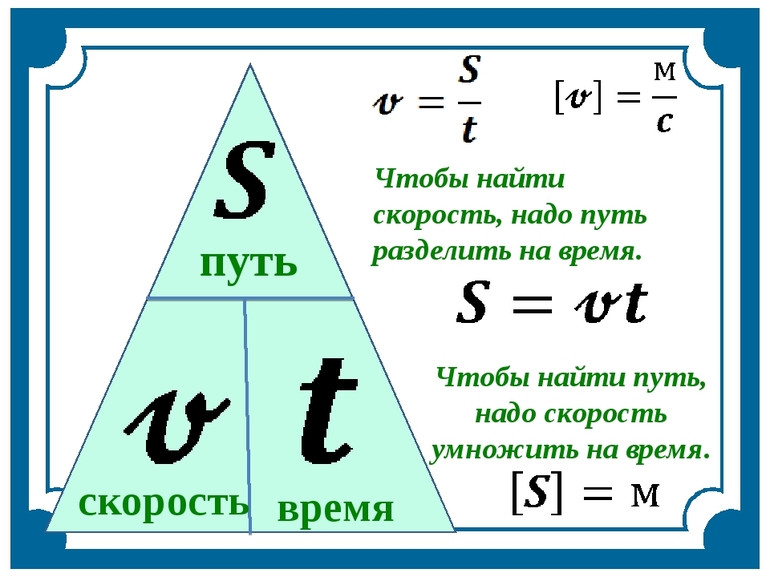
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:

S — расстояние (путь), пройденное материальной точкой или телом (м);
T — время за которое она преодолела путь (с).

Нахождение скорости по формулам

Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.

Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.

Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:

Нахождение скорости

неравномерную;
среднюю;
равномерно-переменную;
поступательную;
вращательную;
ускоренную.

Равноускоренное движение

Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.

Равноускоренное движение

Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.

В произвольно взятой точке скорость перемещения равна ускорению свободного падения.

Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:

V0 — начальная скорость;
A — ускорение (имеет постоянное значение);
t — время движения.

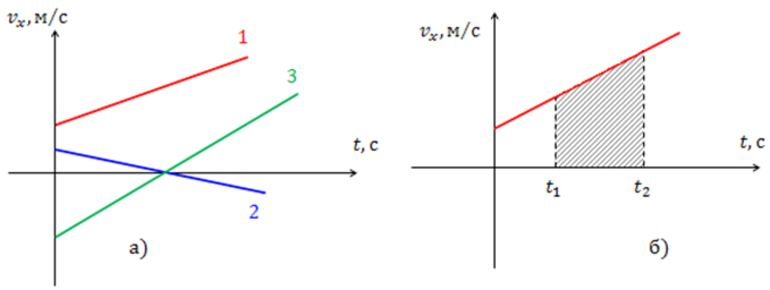
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.

Если на оси времени выделить промежуток Δt, то можно предположить, что движение будет равномерным и описываться некоторым параметром, равным мгновенному значению в середине отрезка. Эта моментальная величина является векторной. Она численно равна пределу, который пытается достигнуть скорость за промежуток времени, стремящийся к нулю. В физике это состояние описывается формулой мгновенной скорости: V = lim (Δ s/ Δ t) = r^-1(t). То есть, с математической точки зрения, это первая производная.

Исходя из этого можно утверждать, что движение Δs = v*Δt. Так как произведение ускорения на время определяется разницей V -V0, то верной будет запись: S = V0*t + A*t²/2 = (V² — V²0) /2*A.

Из этой формулы можно вывести выражение для нахождения конечной скорости материальной точки: V = (V²0 — 2* A * s)^½. Если же в начальный момент V0 = 0, то формулу можно упростить до вида: V = (2* A * s)^½.

Среднее значение

В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.

Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.

Среднее значение скорости

По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.

Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.

Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: {V} = V.

Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.

Угловая скорость

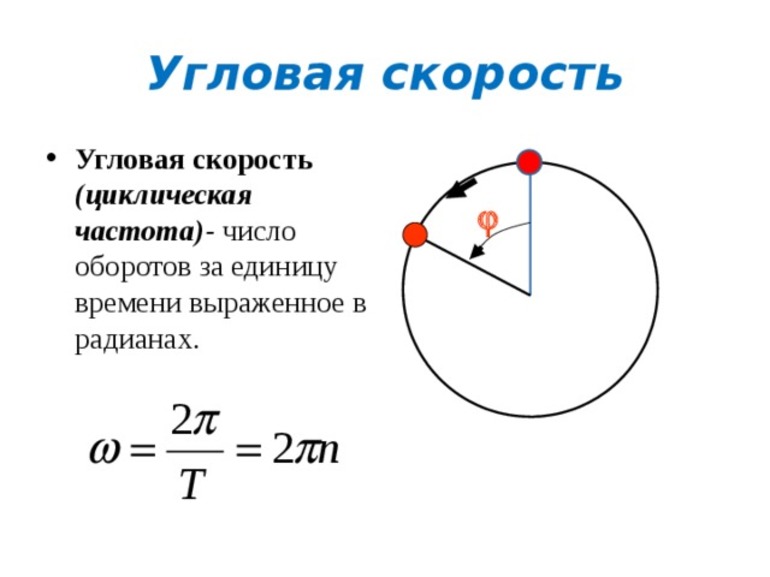
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.

В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.

Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).

Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.

Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.

Закон сложения

Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.

Закон сложения скоростей

Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.

Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.

Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.

Использование онлайн-калькулятора

Онлайн-калькулятор по физике

В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.

Из множества сайтов можно выделить три наиболее популярных среди потребителей:

Справочный портал «Калькулятор».
Allcalc.
Fxyz.

Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.

Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.

Источник

Скорость
${vec v}={frac {{mathrm {d}}{vec r}}{{mathrm {d}}t}}$
Размерность	LT⁻¹
Единицы измерения
СИ	м/с
СГС	см/с
Примечания
вектор

Классическая механика
История…
Фундаментальные понятия Пространство Время Масса Скорость Сила Механическая работа Энергия Импульс
Формулировки Ньютоновская механика Лагранжева механика Гамильтонова механика Формализм Гамильтона — Якоби Уравнения Рауса Уравнения Аппеля Теория Купмана — фон Неймана
Разделы Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика
Учёные Галилей Кеплер Ньютон Эйлер Лаплас Д’Аламбер Лагранж Гамильтон Коши
См. также: Портал:Физика

Ско́рость (стандартное обозначение: ${vec {v}}$ , от англ. velocity, исходно от лат. vēlōcitās) — векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта. По определению, равна производной радиус-вектора точки по времени^[1]. В СИ измеряется в метрах в секунду.

В русском языке этим же словом называют и скалярную величину — либо модуль вектора скорости, либо алгебраическую скорость точки, то есть проекцию вектора ${vec {v}}$ на касательную к траектории точки^[2]. В некоторых других языках для скалярной скорости имеются отдельные наименования, например англ. speed, лат. celeritas^{[значимость факта?]}.

Термин «скорость» используют в науке и в широком смысле, понимая под ним быстроту изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще подразумеваются изменения во времени, но также в пространстве или любой другой). Так, например, говорят об угловой скорости, скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения и т. д. Математически «быстрота изменения» характеризуется производной рассматриваемой величины.

Понятие «скорость» в классической механике[править | править код]

Случай материальной точки[править | править код]

Вектор скорости (мгновенной скорости) материальной точки в каждый момент времени определяется как производная по времени радиус-вектора ${{vec r}}$ текущего положения этой точки, так что^[3]:

${vec v}={{mathrm {d}}{{vec r}} over {mathrm {d}}t}equiv v_{{tau }}{{vec tau }},$

где ${{vec tau }}equiv {mathrm {d}}{{vec r}}/{mathrm {d}}s$ — единичный вектор касательной, проходящей через текущую точку траектории (он направлен в сторону возрастания дуговой координаты $s$ движущейся точки), а $v_{{tau }}equiv {dot {s}}$ — проекция вектора скорости на направление упомянутого единичного вектора, равная производной дуговой координаты по времени и именуемая алгебраической скоростью точки. В соответствии с приведёнными формулами, вектор скорости точки всегда направлен вдоль касательной, а алгебраическая скорость точки может отличаться от модуля $v$ этого вектора лишь знаком^[4]. При этом:

Пройденный точкой путь ${tilde {s}}$ за промежуток времени от $t_0$ до $t$ , находится как

${displaystyle {tilde {s}}=int _{t_{0}}^{t}|{dot {s}}|,mathrm {d} t;}$ .

Когда алгебраическая скорость точки всё время неотрицательна, путь совпадает с приращением дуговой координаты за время от $t_0$ до $t$ (если же при этом начало отсчёта дуговой координаты совпадает с начальным положением движущейся точки, то ${tilde {s}}$ будет просто совпадать с $s$ ).

Иллюстрация средней и мгновенной скорости

Если алгебраическая скорость точки не меняется с течением времени (или, что то же самое, модуль скорости постоянен), то движение точки называется^[5] равномерным (алгебраическое касательное ускорение ${ddot {s}}$ при этом тождественно равно нулю).

Предположим, что ${{ddot {s}}}geqslant {0}$ . Тогда при равномерном движении скорость точки (алгебраическая) будет равна отношению пройденного пути ${tilde {s}}$ к промежутку времени $t-t_{0}$ , за который этот путь был пройден:

${{dot {s}}}^{{,{mathrm {cp}}}}={{tilde {s}} over t-t_{0}};.$

В общем же случае аналогичные отношения

${{vec v}}^{{,,{mathrm {cp}}}}={{{vec r}}-{{vec r}}_{0} over t-t_{0}}equiv {Delta {{vec r}} over Delta {t}}$ и ${{dot {s}}}^{{,{mathrm {cp}}}}={s-s_{0} over t-t_{0}}equiv {Delta {s} over Delta {t}}$

определяют соответственно среднюю скорость точки^[6] и её среднюю алгебраическую скорость; если термином «средняя скорость» пользуются, то о величинах ${vec {v}}$ и ${dot {s}}$ говорят (чтобы избежать путаницы) как о мгновенных скоростях.

Различие между двумя введёнными выше понятиями средней скорости состоит в следующем. Во-первых, ${{vec v}}^{{,,{mathrm {cp}}}}$ — вектор, а ${{dot {s}}}^{{,{mathrm {cp}}}}$ — скаляр. Во-вторых, эти величины могут не совпадать по модулю. Так, пусть точка движется по винтовой линии и за время своего движения проходит один виток; тогда модуль средней скорости этой точки будет равен отношению шага винтовой линии (то есть расстояния между её витками) ко времени движения, а модуль средней алгебраической скорости — отношению длины витка ко времени движения.

Случай тела конечных размеров[править | править код]

Для тела протяжённых размеров понятие «скорости» (тела как такового, а не одной из его точек) не может быть определено; исключение составляет случай мгновенно-поступательного движения. Говорят, что абсолютно твёрдое тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны^[7]; тогда можно, разумеется, положить скорость тела равной скорости любой из его точек. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).

В общем же случае скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса модули скоростей точек на ободе относительно дороги принимают значения от нуля (в точке касания с дорогой) до удвоенного значения скорости центра колеса (в точке, диаметрально противоположной точке касания). Распределение скоростей точек абсолютно твёрдого тела описывается кинематической формулой Эйлера.

Начальная скорость[править | править код]

Начальная скорость ( ${displaystyle {vec {v}}_{0}}$ ) — это скорость материальной точки в момент, принимаемый за нуль по шкале времени (то есть при $t = 0$ )^[8].

Истолкование ${displaystyle {vec {v}}_{0}}$ как скорости, с которой тело начинает движение, не вполне корректно, поскольку покоившееся тело в принципе не может начать двигаться с отличной от нуля скоростью. При такой формулировке неявно подразумевается, что в короткий промежуток времени ${displaystyle t=[-Delta tldots 0]}$ действовала большая по величине сила, на пренебрежимо малом участке разогнавшая тело до скорости ${displaystyle {vec {v}}={vec {v}}_{0}}$ к моменту $t = 0$ .

Запись скорости в разных системах координат[править | править код]

В декартовых координатах[править | править код]

В прямоугольной декартовой системе координат^[9]:

${displaystyle mathbf {v} =v_{x}mathbf {i} +v_{y}mathbf {j} +v_{z}mathbf {k} .}$

При этом ${mathbf r}=x{mathbf i}+y{mathbf j}+z{mathbf k}$ , следовательно,

${displaystyle mathbf {v} ={frac {mathrm {d} (xmathbf {i} +ymathbf {j} +zmathbf {k} )}{mathrm {d} t}}={frac {mathrm {d} x}{mathrm {d} t}}mathbf {i} +{frac {mathrm {d} y}{mathrm {d} t}}mathbf {j} +{frac {mathrm {d} z}{mathrm {d} t}}mathbf {k} .}$

Таким образом, компоненты вектора скорости — это скорости изменения соответствующих координат материальной точки^[9]:

${displaystyle v_{x}={frac {mathrm {d} x}{mathrm {d} t}};v_{y}={frac {mathrm {d} y}{mathrm {d} t}};v_{z}={frac {mathrm {d} z}{mathrm {d} t}}.}$

В цилиндрических координатах[править | править код]

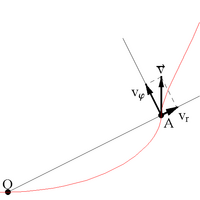
Скорость в полярных координатах

В цилиндрических координатах $R,varphi ,z$ ^[9]:

${displaystyle v_{R}={frac {mathrm {d} R}{mathrm {d} t}};v_{varphi }=R{frac {mathrm {d} varphi }{mathrm {d} t}};v_{z}={frac {mathrm {d} z}{mathrm {d} t}}.}$

$v_{varphi }$ носит название поперечной скорости, $v_{R}$ — радиальной.

В сферических координатах[править | править код]

В сферических координатах $R,varphi ,theta$ ^[9]:

${displaystyle v_{R}={frac {mathrm {d} R}{mathrm {d} t}};v_{varphi }=Rsin theta {frac {mathrm {d} varphi }{mathrm {d} t}};v_{theta }=R{frac {mathrm {d} theta }{mathrm {d} t}}.}$

Для описания плоского движения иногда используются полярные координаты, которые можно рассматривать как частный случай цилиндрических (c ${displaystyle z=}$ const) или сферических (с $theta =pi /2$ ).

Физическая и координатная скорости[править | править код]

В аналитической механике вышеприведённые и другие криволинейные координаты играют роль обобщённых координат; изменение положение тела описывается их зависимостью от времени. Производные от координат тела по времени при этом называются координатными скоростями (они могут иметь размерность отличную от м/c). Физической же скоростью является производная радиус-вектора по времени, а её составляющие в каждом случае задаются всем стоящим перед соответствующим ортом выражением.

Некоторые связанные со скоростью понятия[править | править код]

Ряд величин в классической механике выражается через скорость.

Импульс, или количество движения, — это мера механического движения точки, которая определяется как произведение массы точки на её скорость

${vec p}=m{vec v}$ .

Импульс является векторной величиной, его направление совпадает с направлением скорости. Для замкнутой системы выполняется закон сохранения импульса.

От скорости также зависит кинетическая энергия механической системы. Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения^[10]^[11]:

${displaystyle T={frac {mv^{2}}{2}}+{frac {{mathcal {I}}{vec {omega }}^{2}}{2}},}$

где $m$ — масса тела, $v$ — скорость центра масс тела, ${mathcal {I}}$ — момент инерции тела, ${vec omega }$ — угловая скорость тела.

Изменение скорости во времени характеризуется ускорением. Ускорение отражает изменение скорости как по величине (тангенциальное ускорение), так и по направлению (центростремительное ускорение)^[12]:

${vec a}={frac {{mathrm {d}}{vec v}}{{mathrm {d}}t}}={vec a}_{tau }+{vec a}_{n}={frac {{mathrm {d}}|{vec v}|}{{mathrm {d}}t}}{vec e}_{tau }+{v^{2} over r}{vec e}_{n},$

где $r$ — радиус кривизны траектории точки.

Преобразования Галилея и Лоренца для скорости[править | править код]

В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта $S$ была равна ${vec {v}}$ , а скорость системы отсчёта $S'$ относительно системы отсчёта $S$ равна $vec u$ , то скорость тела при переходе в систему отсчёта $S'$ будет равна^[9]

${displaystyle {vec {v}}'={vec {v}}-{vec {u}}.}$

Для скоростей, близких к скорости света, преобразования Галилея становятся несправедливы. При переходе из системы $S$ в систему $S'$ необходимо использовать преобразования Лоренца для скоростей^[9]:

$v_{x}'={frac {v_{x}-u}{1-(v_{x}u)/c^{2}}},v_{y}'={frac {v_{y}{sqrt {1-{frac {u^{2}}{c^{2}}}}}}{1-(v_{x}u)/c^{2}}},v_{z}'={frac {v_{z}{sqrt {1-{frac {u^{2}}{c^{2}}}}}}{1-(v_{x}u)/c^{2}}},$

в предположении, что скорость $vec u$ направлена вдоль оси $x$ системы $S$ . В пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.

Скорость в релятивистской механике[править | править код]

Четырёхмерная скорость[править | править код]

Одним из обобщений понятия скорости является четырёхмерная скорость (скорость в релятивистской механике^[9]). В специальной теории относительности каждому событию ставится в соответствие точка пространства Минковского, три координаты которого представляют собой декартовы координаты трёхмерного евклидова пространства, а четвёртая ― временну́ю координату $ct$ , где $c$ ― скорость света, $t$ ― время события. Компоненты четырёхмерного вектора скорости связаны с проекциями трёхмерного вектора скорости следующим образом^[9]:

$v_{0}={frac {c}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}};v_{1}={frac {v_{x}}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}};v_{2}={frac {v_{y}}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}};v_{3}={frac {v_{z}}{{sqrt {1-{frac {v^{2}}{c^{2}}}}}}}.$

Четырёхмерный вектор скорости является времениподобным вектором, то есть лежит внутри светового конуса^[9].

Существует также понятие четырёхимпульс, временна́я компонента которого равна $E/c$ (где $E$ — энергия). Для четырёхмерного импульса выполняется равенство^[13]:

${displaystyle p_{i}=m,v_{i}}$ ,

где $v_{i}$ — четырёхмерная скорость.

Понятие «быстрота»[править | править код]

В релятивистской механике угол между касательной к мировой линии частицы и осью времени в базовой системе отсчёта носит название быстроты (обозначается $theta$ ). Быстрота выражается формулой

$theta =c,{mathrm {Arth}},{frac {v}{c}}={frac {c}{2}}ln {frac {1+{dfrac {v}{c}}}{1-{dfrac {v}{c}}}},$

где ${mathrm {Arth}},x$ — ареатангенс, или гиперболический арктангенс. Быстрота стремится к бесконечности когда скорость стремится к скорости света. В отличие от скорости, для которой необходимо пользоваться преобразованиями Лоренца, быстрота аддитивна, то есть

$theta '=theta +theta _{0},$

где $theta _{0}$ — быстрота системы отсчёта $S'$ относительно системы отсчёта $S$ .

Некоторые скорости[править | править код]

Космические скорости[править | править код]

Анализ первой и второй космической скорости по Исааку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D — на эллиптическую. Снаряд E улетает в открытый космос

Небесная механика изучает поведение тел Солнечной системы и других небесных тел. Движение искусственных космических тел изучается в астродинамике. При этом рассматривается несколько вариантов движения тел, для каждого из которых необходимо придание определённой скорости. Для вывода спутника на круговую орбиту ему необходимо придать первую космическую скорость (например, искусственный спутник Земли); преодолеть гравитационное притяжение позволит вторая космическая скорость (например, объект запущенный с Земли, вышедший за её орбиту, но находящийся в Солнечной системе); третья космическая скорость нужна чтобы покинуть звёздную систему, преодолев притяжение звезды (например, объект запущенный с Земли, вышедший за её орбиту и за пределы Солнечной системы); четвёртая космическая скорость позволит покинуть галактику.

В небесной механике под орбитальной скоростью понимают скорость вращения тела вокруг барицентра системы.

Скорости распространения волн[править | править код]

Скорость звука[править | править код]

Скорость звука — скорость распространения упругих волн в среде, определяется упругостью и плотностью среды. Скорость звука не является постоянной величиной и зависит от температуры (в газах), от направления распространения волны (в монокристаллах). При заданных внешних условиях обычно не зависит от частоты волны и её амплитуды. В тех случаях, когда это не выполняется и скорость звука зависит от частоты, говорят о дисперсии звука. Впервые измерена Уильямом Дерхамом. Как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях скорость звука меньше, чем в твёрдых телах, поэтому при сжижении газа скорость звука возрастает.

Отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде называется числом Маха по имени австрийского учёного Эрнста Маха. Упрощённо, скорость, соответствующая 1 Маху при давлении в 1 атм (у земли на уровне моря), будет равна скорости звука в воздухе. Движение аппаратов со скоростью, сравнимой со скоростью звука, сопровождается рядом явлений, которые называются звуковой барьер. Скорости от 1,2 до 5 Махов называются сверхзвуковыми, скорости выше 5 Махов — гиперзвуковыми.

Скорость света[править | править код]

Время распространения светового луча в масштабной модели Земля-Луна. Для преодоления расстояния от поверхности Земли до поверхности Луны свету требуется 1,255 секунды.

Скорость света в вакууме — абсолютная величина скорости распространения электромагнитных волн в вакууме. Традиционно обозначается латинской буквой «c» (произносится как [це]). Скорость света в вакууме — фундаментальная постоянная, не зависящая от выбора инерциальной системы отсчёта (ИСО). Она относится к фундаментальным физическим постоянным, которые характеризуют не просто отдельные тела или поля, а свойства пространства-времени в целом. По современным представлениям, скорость света в вакууме — предельная скорость движения частиц и распространения взаимодействий.

Наиболее точное измерение скорости света 299 792 458 ± 1,2 м/с на основе эталонного метра было проведено в 1975 году. Теперь ввиду современного определения метра скорость света считается равной точно 299792458 м/с^[14].

Скорость гравитации[править | править код]

Скорость гравитации — скорость распространения гравитационных воздействий, возмущений и волн. До сих пор остаётся не определённой экспериментально, но согласно общей теории относительности должна совпадать со скоростью света.

Единицы измерения скорости[править | править код]

Линейная скорость:

Метр в секунду, (м/с), производная единица системы СИ
Километр в час, (км/ч)
узел (морская миля в час)
Число Маха, 1 Мах равен скорости звука; Max n в n раз быстрее. Как единица, зависящая от конкретных условий, должна дополнительно определяться.
Скорость света в вакууме (обозначается c)

Угловая скорость:

Радианы в секунду, принята в системах СИ и СГС. Физическая размерность 1/с.
Обороты в секунду (в технике)
градусы в секунду, грады в секунду

Соотношения между единицами скорости[править | править код]

1 м/с = 3,6 км/ч
1 узел = 1,852 км/ч = 0,514 м/c
Мах 1 ~ 330 м/c ~ 1200 км/ч (зависит от условий, в которых находится воздух)
c = 299 792 458 м/c

Исторический очерк[править | править код]

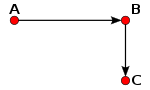
Две стадии движения брошенного тела по теории Авиценны: отрезок АВ — период «насильственного стремления», отрезок ВС — период «естественного стремления» (падение вертикально вниз)

Автолик из Питаны в IV веке до н. э. определил равномерное движение так: «О точке говорится, что она равномерно перемещается, если в равные времена она проходит равные и одинаковые величины». Несмотря на то, что в определении участвовали путь и время, их отношение считалось бессмысленным^[15], так как сравнивать можно было только однородные величины и скорость движения являлась чисто качественным, но не количественным понятием^[16]. Живший в то же время Аристотель делил движение на «естественное», когда тело стремится занять своё естественное положение, и «насильственное», происходящее под действием силы. В случае «насильственного» движения произведение величины «двигателя» и времени движения равно произведению величины «движимого» и пройденного пути, что соответствует формуле $Ft=ms$ , или $F=mv$ ^[15]. Этих же взглядов придерживался Авиценна в XI веке, хотя и предлагал другие причины движения^[17], а также Герард Брюссельский в конце XII —
начале XIII века. Герард написал трактат «О движении» — первый европейский трактат по кинематике — в котором сформулировал идею определения средней скорости движения тела (при вращении прямая, параллельная оси вращения, движется «одинаково с любой своей точкой», а радиус — «одинаково со своей серединой»)^[18].

В 1328 году увидел свет «Трактат о пропорциях или о пропорциях скоростей при движении» Томаса Брадвардина, в котором он нашёл несоответствие в физике Аристотеля и связи скорости с действующими силами. Брадвардин заметил, что по словесной формуле Аристотеля если движущая сила равна сопротивлению, то скорость равна 1, в то время как она должна быть равна 0. Он также представил свою формулу изменения скорости, которая хоть и была не обоснована с физической точки зрения, но представляла собой первую функциональную зависимость скорости от причин движения. Брадвардин называл скорость «количеством движения»^[19]. Уильям Хейтсбери, в трактате «О местном движении» ввёл понятие мгновенной скорости. В 1330—1340 годах он и другие ученики Брадвардина доказали так называемое «мертонское правило», которое означает равенство пути при равноускоренном движении и равномерном движении со средней скоростью^[20].

Всякая широта движения, униформно приобретаемая или теряемая, соответствует своему среднему градусу, так что столько же в точности будет пройдено благодаря этой приобретаемой широте, сколько и благодаря среднему градусу, если бы тело двигалось всё время с этим средним градусом.

— «Мертонское правило» в формулировке Суайнсхеда^[20]

В XIV веке Жан Буридан ввёл понятие импетуса^[21], благодаря чему была определена величина изменения скорости — ускорение. Николай Орем, ученик Буридана, предложил считать, что благодаря импетусу ускорение остаётся постоянным (а не скорость, как полагал сам Буридан), предвосхитив, таким образом, второй закон Ньютона^[22]. Орем также использовал графическое представление движения. В «Трактате о конфигурации качеств и движения» (1350) он предложил изображать отрезками перпендикулярных прямых количество и качество движения (время и скорость), иными словами, он нарисовал график изменения скорости в зависимости от времени^[23].

По мнению Тартальи, только вертикальное падение тела является «естественным» движением, а все остальные — «насильственные», при этом у первого типа скорость постоянно возрастает, а у второго — убывает. Два этих типа движения не могут проистекать одновременно. Тарталья считал, что «насильственные» движения вызваны ударом, результатом которого является «эффект», определяемый скоростью^[24]. С критикой работ Аристотеля и Тартальи выступал Бенедетти, который вслед за Оремом пользовался понятиями импетуса и ускорения^[25].

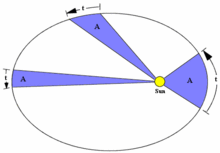
В 1609 году в работе «Новая астрономия» Кеплер сформулировал закон площадей, согласно которому секторная скорость планеты (площадь, описываемая отрезком планета — Солнце, за единицу времени) постоянна^[26]. В «Началах философии» Декарт сформулировал закон сохранения количества движения, которое в его понимании есть произведение количества материи на скорость^[27], при этом Декарт не принимал во внимание тот факт, что количество движения имеет не только величину, но и направление^[28]. В дальнейшем понятие «количество движения» развивал Гук, который понимал его как «степень скорости, присущей в определённом количестве вещества»^[29]. Гюйгенс, Валлис и Рен добавили к этому определению направление. В таком виде во второй половине XVII века количество движения стало важным понятием в динамике, в частности в работах Ньютона и Лейбница^[30]. При этом Ньютон не определял в своих работах понятие скорости^[31]. По-видимому, первая попытка явного определения скорости была сделана Валлисом в его трактате «Механика или геометрический трактат о движении» (1669—1671): «Скорость есть свойство движения, отражающееся в сравнении длины и времени; а именно, она определяет, какая длина в какое время проходится»^[32].

В XVII веке были заложены основы математического анализа, а именно интегрального и дифференциального исчисления. В отличие от геометрических построений Лейбница, теория «флюксий» Ньютона строится на потребностях механики и имеет в своём основании понятие скорости. В своей теории Ньютон рассматривает переменную величину «флюенту» и её скорость изменения — «флюксию»^[33].

Скорости в природе и технике[править | править код]

Основной источник: ^[34]

	Метры в секунду
Скорость улитки	${displaystyle 1{,}4times 10^{-2}}$
Скорость черепахи	${displaystyle 5{,}0times 10^{-2}}$
Средняя скорость здорового человека (произвольный темп)	${displaystyle 1{,}43}$
Рекорд скорости человека в ходьбе на 50 км	${displaystyle 3{,}4}$ ( ${displaystyle 3{,}92}$ )
Рекорд скорости человека в беге на дистанции 100 м	${displaystyle 1{,}0times 10^{1}}$ ( ${displaystyle 1{,}044times 10^{1}}$ )
Скорость гепарда	$31$
Максимальная скорость полёта сокола	$100$
Максимальная скорость локомотива на железной дороге	${displaystyle 110}$
Максимальная скорость автомобиля	${displaystyle 340}$ ^[35]
Средняя скорость молекулы азота при температуре 0 °C	$500$
Максимальная скорость пассажирского реактивного самолёта	$700$
Скорость движения Луны по орбите вокруг Земли	$1000$
Скорость искусственного спутника Земли	${displaystyle 8000}$
Скорость движения Земли по орбите вокруг Солнца	${displaystyle 30000}$
Скорость движения Солнца по орбите вокруг центра Галактики	${displaystyle 230000}$
Скорость электронов в кинескопе телевизора	${displaystyle 1{,}0times 10^{8}}$
Скорость движения самых далёких галактик	${displaystyle 1{,}4times 10^{8}}$
Максимальная скорость протонов в Большом адронном коллайдере	299 792 455
Скорость частицы Oh-My-God	299792457,9999999999999985310169558
Скорость безмассовых частиц (фотонов, глюонов, гравитонов)	299 792 458
Скорость тахионов и сверхбрадионов	> 299792458

Скорости движения живых существ[править | править код]

Сапсан (самое быстрое животное): самая высокая зарегистрированная скорость — 389 км/ч^[36];
Гепард (самое быстрое наземное животное): самая высокая зарегистрированная скорость — 98 км/ч^[37];
Меч-рыба: от 100 до 130 км в час^[37];
Чёрный марлин: самая высокая зарегистрированная скорость — 105 км/ч^[36];
Вилорогая антилопа: самая высокая зарегистрированная скорость — 88,5 км/ч^[36];
Лошадь (американский квортерхорс): 88 км/ч^[36];
Человек: самая высокая зарегистрированная скорость — 44,72 км/ч (Усэйн Болт)^[37].

Рекорды скорости транспортных средств[править | править код]

Самый быстрый рукотворный объект — Parker Solar Probe, 150 км/с (относительно Солнца) в 2021 году^[38].

Абсолютный рекорд скорости в воздухе был поставлен в 1976 году американским самолетом-разведчиком Lockheed SR-71 Blackbird — 3529,56 км/ч.

Рекорд скорости на земле был установлен в 2003 году на ракетных санях и составил 10 325 км/ч или 2868 м/с (по другим данным, 10 430 км/ч)^[39]

Самая высокая скорость на наземном управляемом транспортном средстве была достигнута на реактивном автомобиле Thrust SSC в 1997 году — 1228 км/ч.

Рекорд скорости на воде был поставлен в 1978 году австралийским судном с реактивным газотурбинным двигателем Spirit of Australia^[en] — 511,11 км/ч^[40]

См. также[править | править код]

Кинематика

Примечания[править | править код]

↑ Маркеев, 1990, с. 15.
↑ Старжинский, 1980, с. 154.
↑ Маркеев, 1990, с. 15—17.
↑ Старжинский, 1980, с. 154—155.
↑ Старжинский, 1980, с. 163.
↑ Старжинский, 1980, с. 152.
↑ Маркеев, 1990, с. 46—47.
↑ См. Всегда ли начальная скорость равна нулю? в справочнике «Студворк».
↑ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ Скорость // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
↑ Главный редактор А. М. Прохоров. Кинетическая энергия // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
↑ Главный редактор А. М. Прохоров. Вращательное движение // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
↑ Главный редактор А. М. Прохоров. Ускорение // Физический энциклопедический словарь.. — 1983. Физическая энциклопедия
↑ Главный редактор А. М. Прохоров. Импульс // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
↑ Определение метра Архивная копия от 26 июня 2013 на Wayback Machine (англ.) Резолюция 1 XVII Генеральной конференции по мерам и весам (1983)
↑ ¹ ² Яковлев, 2001, с. 21.
↑ Яковлев, 2001, с. 34.
↑ Яковлев, 2001, с. 29.
↑ Яковлев, 2001, с. 31—32.
↑ Яковлев, 2001, с. 32—34.
↑ ¹ ² Яковлев, 2001, с. 35.
↑ Яковлев, 2001, с. 35—36.
↑ Яковлев, 2001, с. 37.
↑ Яковлев, 2001, с. 37—38.
↑ Яковлев, 2001, с. 43.
↑ Яковлев, 2001, с. 45.
↑ Яковлев, 2001, с. 51—52.
↑ Яковлев, 2001, с. 59.
↑ Яковлев, 2001, с. 68.
↑ Яковлев, 2001, с. 77.
↑ Яковлев, 2001, с. 91.
↑ Яковлев, 2001, с. 96.
↑ Яковлев, 2001, с. 72—73.
↑ Яковлев, 2001, с. 64—66.
↑ Кабардин О.Ф., Орлов В.А., Пономарёва А.В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — Тираж 143 500 экз. — С. 44
↑ FIA World Land Speed Records (англ.). Federation Internationale de l’Automobile (10 июня 2012). Дата обращения: 3 декабря 2020. Архивировано 31 марта 2019 года.
↑ ¹ ² ³ ⁴ 12 самых быстрых животных в мире. Дата обращения: 17 июня 2022. Архивировано 29 июля 2021 года.
↑ ¹ ² ³ 12 самых быстрых животных в мире. Дата обращения: 17 июня 2022. Архивировано 22 сентября 2020 года.
↑ Самый быстрый объект, созданный человеком. Зонд Parker Solar Probe развил скорость около 150 км/с. Дата обращения: 17 июня 2022. Архивировано 17 мая 2021 года.
↑ Test sets world land speed record. www.af.mil. Дата обращения: 19 апреля 2016.
↑ Назло рекордам: почему люди не хотят передвигаться очень быстро

Литература[править | править код]

Маркеев А. П. Теоретическая механика. — М.: Наука, 1990. — 416 с. — ISBN 5-02-014016-3.
Старжинский В. М. Теоретическая механика. — М.: Наука, 1980. — 464 с.
Яковлев В. И. Предыстория аналитической механики. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — 328 с. — ISBN 5-93972-063-3.

Источник

Содержание:

Определение и формула скорости
Скорость в разных системах координат
Частные случаи формул для вычисления скорости
Единицы измерения скорости
Примеры решения задач

Определение и формула скорости

Определение

Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора
$bar{r}$ точки по времени (t). Обозначают скорость обычно буквой v.
Это векторная величина. Математически определение вектора мгновенной скорости записывается как:

$$bar{v}=frac{d bar{r}}{d t}=dot{bar{r}}(1)$$

Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения.
Модуль скорости можно определить как первую производную от длины пути (s) по времени:

$$v=frac{d s}{d t}=dot{s}(2)$$

Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.

Скорость в разных системах координат

Проекции скорости на оси декартовой системы координат запишутся как:

$$v_{x}=dot{x} ; v_{y}=dot{y} ; v_{z}=dot{z}(3)$$

Следовательно, вектор скоростив декартовых координатах можно представить:

$$bar{v}=dot{x} bar{i}+dot{y} bar{j}+dot{z} bar{k}(4)$$

где $bar{i}, bar{j}, bar{k}$ единичные орты. При этом модуль вектора скорости находят при помощи формулы:

$$v=sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}}(5)$$

В цилиндрических координатах модуль скорости вычисляют при помощи формулы:

$$v=sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}}(6)$$

в сферической системе координат:

$$v=sqrt{(r)^{2}+(r dot{theta})^{2}+(r dot{varphi} sin theta)^{2}}(7)$$

Частные случаи формул для вычисления скорости

Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const).
При равномерном движении скорость можно вычислить, применяя формулу:

$$v=frac{s}{t}(8)$$

где s– длина пути, t – время, за которое материальная точка преодолела путь s.

При ускоренном движении скорость можно найти как:

$$bar{v}=int_{t_{1}}^{t_{2}} bar{a} d t(9)$$

где $bar{a}$ – ускорение точки,
$t_{1} leq t leq t_{2}$ – отрезок времени, в течение которого рассматривается скорость.

Если движение является равнопеременным, то применяется следующая формула для вычисления скорости:

$$bar{v}=bar{v}_{0}+bar{a} t$$

где $bar{v}_0$ – начальная скорость движения,
$bar{a} = const$ .

Единицы измерения скорости

Основной единицей измерения скорости в системе СИ является: [v]=м/с²

В СГС: [v]=см/с²

Примеры решения задач

Пример

Задание. Движение материальной точки А задано уравнением:
$x=2 t^{2}-4 t^{3}$ . Точка начала свое движение при
t₀=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.

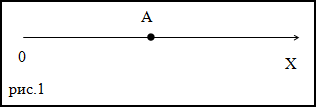
Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для
этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:

$$v=frac{d x}{d t}=4 t-12 t^{2}(1.1)$$

Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент
времении сравним результат с нулем:

$$v(t=0,5)=4 cdot 0,5-12(0,5)^{2}=-1 lt 0$$

Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.

Ответ. Против оси X.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Скорость материальной точки является функцией от времени вида:

$$v=10left(1-frac{t}{5}right)$$

где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии
10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.

Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:

$$x=int_{0}^{t} v d t=int_{0}^{t} 10left(1-frac{t}{5}right) d t=10 t-frac{10 t^{2}}{2 cdot 5}=10 t-t^{2}(2.1)$$

Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:

$$x=10 cdot 10-(10)^{2}=0(m)$$

Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат
приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:

$$
begin{array}{c}
10 t-t^{2}=10(2.2) \
t_{1}=5+sqrt{15} approx 8,8(c) ; t_{2}=5-sqrt{15} approx 1,13(c)
end{array}
$$

Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:

$$10 t-t^{2}=-10(2.3)$$

При решении уравнения (2.3) нам подойдет корень равный:

$$t_{3}=5+6=11 (c)$$

Ответ. 1) $x=0 mathrm{~m}$ 2) $t_{1}=8,8 mathrm{c}, t_{2}=1,13 c, t_{3}=11 c$

Читать дальше: Формула средней скорости.

Источник

Равномерное и неравномерное движение.

Рассмотрим движение автомобиля. Например, если автомобиль за каждую четверть часа (15 мин) проходит 15 км, за каждые полчаса (30 мин) – 30 км, а за каждый час – 60 км, считается, что он движется равномерно.

Неравномерное движение.

Если тело за любые равные промежутки времени проходит равные пути, его движение считается равномерным.

Равномерное движение встречается очень редко. Почти равномерно движется Земля вокруг Солнца, за год Земля делает один оборот вокруг Солнца.

Практически никогда водителю автомобиля не удается поддерживать равномерность движение – по разным причинам приходится то ускорять то замедлять езду. Движение стрелок часов (минутной и часовой) только кажется равномерным, в чем легко убедиться, наблюдая за движением секундной стрелки. Она то движется, то останавливается. Точно так же движутся и две остальные стрелки, только медленно, и поэтому их рывков не видно. Молекулы газов, ударяясь друг об друга, на какое-то время останавливаются, затем снова разгоняются. При следующих столкновениях, уже с другими молекулами, они снова замедляют свое движение в пространстве.

Все это примеры неравномерного движения. Так движется поезд, отходя от станции, проходя за одинаковые промежутки времени все бóльшие и бóльшие пути. Лыжник или конькобежец проходят на соревнованиях равные пути за различное время. Так движутся взлетающий самолет, открываемая дверь, падающая снежинка.

Если тело за равные промежутки времени проходит разные пути, то его движение называют неравномерным.

Неравномерное движение можно наблюдать на опыте. На рисунке изображена тележка с капельницей, из которой через одинаковые промежутки времени падают капли. При движении тележки под действием к ней груза мы видим, что расстояния между следами от капель неодинаковы. А это и означает, что за одинаковые промежутки времени тележка проходит разные пути.

Скорость. Единицы скорости.

Мы часто говорим, что одни тела движутся быстрее, другие медленнее. Например, по шоссе шагает турист, мчится автомобиль, в воздухе летит самолет. Допустим, что все они движутся равномерно, тем не менее движение этих тел будет отличаться.

Автомобиль движется быстрее пешехода, а самолет быстрее автомобиля. В физике величиной, характеризующей быстроту движения, называется скорость.

Предположим, что турист за 1 час проходит 5 км, автомобиль 90 км, а скорость самолета 850 км в час.

Скорость при равномерном движении тела показывает, какой путь прошло тело в единицу времени.

Таким образом, используя понятие скорости, мы можем теперь сказать, что турист, автомобиль и самолет движутся с различными скоростями.

При равномерном движении скорость тела остается постоянной.

Если велосипедист проезжает в течение 5 с путь, равный, 25 м, то его скорость будет равна 25м/5с = 5м/с.

Чтобы определить скорость при равномерном движении, надо путь, пройденный телом за какой-то промежуток времени, разделить на этот промежуток времени:

скорость = путь/время.

Скорость обозначают буквой v, путь – s, время – t. Формула для нахождения скорости будет иметь такой вид:

v=s/t.

Скорость тела при равномерном движении – это величина, равная отношению пути ко времени, за которое этот путь пройден.

В Международной системе (СИ) Скорость измеряют в метрах в секунду (м/с).

Это значит, что за единицу скорости принимается скорость такого равномерного движения, при котором за одну секунду тело проходит путь, равный 1 метру.

Скорость тела можно измерять также в километрах в час (км/ч), километрах в секунду (км/с), сантиметрах в секунду (см/с).

Пример. Поезд, двигаясь равномерно, за 2 ч проходит путь, равный 108 км. Вычислите скорость движения поезда.

Итак, s = 108 км; t = 2 ч; v = ?

Решение. v = s/t, v = 108 км/2 ч = 54 км/ч. Легко и просто.

Теперь, выразим скорость поезда в единицах СИ, т.е километры переведем в метры, а часы в секунды:

54 км/ч = 54000 м/ 3600 с = 15м/с.

Ответ: v = 54 км/ч, или 15 м/с.

Таким образом, числовое значение скорости зависит от выбранной единицы.

Скорость, кроме числового значения, имеет направление.

Например, если требуется указать, где будет находиться через 2 ч самолет, вылетевший из Владивостока, то необходимо указать, не только значение его скорости, но и его пункт назначения, т.е. его направление. Величины, которые, кроме числового значения (модуля), имеют еще и направление, называются векторными.

Скорость – это векторная физическая величина.

Все векторные величины обозначают соответствующими буквами со стрелочкой. Например, скорость обозначается символом v со стрелочкой, а модуль скорости той же буквой, но без стрелочки v.

Некоторые физические величины не имеют направления. Они характеризуются только числовым значением. Это время, объем, длина и др. Они являются скалярными.

Если при движении тела его скорость изменяется от одного участка пути к другому, то такое движение является неравномерным. Для характеристики неравномерного движения тела, введено понятие средней скорости.

Например, поезд от Москвы до Санкт-Петербурга идет со скоростью 80 км/ч. Какую скорость имеют ввиду? Ведь скорость поезда на остановках равна нулю, после остановки – увеличивается, а перед остановкой – уменьшается.

В данном случае поезд движется неравномерно, а значит, скорость, равная 80 км/ч, – это средняя скорость движения поезда.

Она определяется почти так же, как и скорость при равномерном движении.

Чтобы определить среднюю скорость тела при неравномерном движении, надо весь пройденный путь разделить на все время движения:

vср = s/t.

Следует напомнить, что только при равномерном движении отношение s/t за любой промежуток времени будет постоянно.

При неравномерном движении тела средняя скорость характеризует движение тела за весь промежуток времени. Она не поясняет, как двигалось тело в различные моменты времени этого промежутка.

В таблице 1 приводится средние скорости движения некоторых тел.

Таблица 1

Средние скорости движения некоторых тел, скорость звука, радиоволн и света.

наименование	скорость, м/с	наименование	скорость, м/с
Улитка	0,0014	Самолет Ил-18	180
Черепаха	0,05-0,4	Звук в воздухе при 0 °С	332
Муха комнатная	5	Пуля автомата Калашникова (при вылете из ствола)	715
Пешеход	1,3	Луна вокруг Земли	1000
Конькобежец	до 13	Молекула водорода (при 0 °С)	1693
Скворец	20	Молекула водорода (при 25 °С)	1770
Страус	22	Искусственный спутник Земли	8000
Тепловоз ТЭ10Л	до 28	Земля вокруг Солнца	30 000
Автомобиль “Жигули”	40	Свет и радиоволны	около 300 000 000

Расчет пути и времени движения.

Если известны скорость тела и время при равномерном движении, то можно найти пройденный им путь.

Поскольку v = s/t, то путь определяют по формуле

s = vt.

Чтобы определить путь, пройденный телом при равномерном движении, надо скорость тела умножить на время его движения.

Теперь, зная, что s = vt, можно найти время, в течение которого двигалось тело, т.е.

t = s/v.

Чтобы определить время при неравномерном движении, надо путь, пройденном телом, разделить на скорость его движения.

Если тело движется неравномерно, то, зная его среднюю скорость движения и время, за которое происходит это движение, находят путь:

s = vсрt.

Пользуясь этой формулой, можно определить время при неравномерном движении тела:

t = s/vср.

Инерция.

Наблюдения и опыты показывают, что скорость тела сама по себе измениться не может.

Опыт с тележками. Инерция.

Футбольный мяч лежит на поле. Ударом ноги футболист приводит его в движение. Но сам мяч не изменит свою скорость и не начнет двигаться, пока на него не подействуют другие тела. Пуля, вложенная в ствол ружья, не вылетит до тех пор, пока ее не вытолкнут пороховые газы.

Таким образом, и мяч и пуля не имеют свою скорость, пока на них не подействуют другие тела.

Футбольный мяч, катящийся по земле, останавливается из-за трения о землю.

Тело уменьшает свою скорость и останавливается не само по себе, а под действием других тел. Под действием другого тела происходит также изменение направления скорости.

Теннисный мяч меняет направление движения после удара о ракетку. Шайба после удара о клюшку хоккеиста также изменяет направление движения. Направление движения молекулы газа меняется при ударении ее с другой молекулой или со стенками сосуда.

Значит, изменение скорости тела (величина и направления) происходит в результате действия на него другого тела.

Проделаем опыт. Установим наклонно на столе доску. Насыплем на стол, на небольшом расстоянии от конца доски, горку песка. Поместим на наклонную доску тележку. Тележка, скатившись с наклонной доски быстро останавливается, попав в песок. Скорость тележки уменьшается очень быстро. Ее движение неравномерно.

Выровняем песок и вновь отпустим тележку с прежней высоты. Теперь тележка пройдет большее расстояние по столу, прежде чем остановится. Ее скорость изменяется медленнее, а движение становится ближе к равномерному.

Если совсем убрать песок с пути тележки, то препятствием ее движению будет только трение о стол. Тележка до остановки еще медленнее, и проедет она больше,чем в первый, и во второй разы.

Итак, чем меньше действие другого тела на тележку, тем дольше сохраняется скорость ее движения и тем ближе оно к равномерному.

Как же будет двигаться тело, если не него совсем не будут действовать другие тела? Как это можно установить на опыте? Тщательные опыты по изучению движения тел были впервые проведены Г. Галилеем. Они позволили установить, что если на тело не действуют другие тела, то оно находится или в покое, или движется прямолинейно, и равномерно относительно Земли.

Явление сохранения скорости тела при отсутствии действия на него других тел, называется инерцией.

Инерция – от латинского инерциа – неподвижность, бездеятельность.

Таким образом, движения тела при отсутствии действия на него другого тела, называется движением по инерции.

Например, пуля вылетевшая из ружья, так и летела бы, сохраняя свою скорость, если бы на нее не действовало другое тело – воздух (а точнее, молекулы газов, которые в нем находятся.). Вследствие этого скорость пули уменьшается. Велосипедист, перестав крутит педали, продолжает двигаться. Он смог бы сохранить скорость своего движения, если бы на него не действовала бы сила трения.

Итак, если на тело не действуют другие тела, то оно движется с постоянной скоростью.

Взаимодействие тел.

Вам уже известно, что при неравномерном движении скорость тела меняется с течением времени. Изменение скорости тела происходит под действием другого тела.

Опыт с тележками. Тележки приходят в движение относительно стола.

Проделаем опыт. К тележке прикрепим упругую пластинку. Затем изогнем ее и свяжем нитью. Тележка относительно стола находится в покое. Станет ли двигаться тележка, если упругая пластинка выпрямится?

Для этого перережем нить. Пластинка выпрямится. Тележка же останется на прежнем месте.

Затем вплотную к согнутой пластинке поставим еще одну такую же тележку. Вновь пережжем нить. После этого обе тележки приходят в движение относительно стола. Они разъезжаются в разные стороны.

Чтобы изменить скорость тележки, понадобилось второе тело. Опыт показал, что скорость тела меняется только в результате действия на него другого тела (второй тележки). В нашем опыте мы наблюдали, что в движение пришла и вторая тележка. Обе стали двигаться относительно стола.

Опыт с лодками. Обе лодки приходят в движение.

Тележки действуют друг на друга , т.е они взаимодействуют. Значит, действие одного тела на другое не может быть односторонним, оба тела действуют друг на друга, т. е. взаимодействуют.

Мы рассмотрели самый простой случай взаимодействия двух тел. Оба тела (тележки) до взаимодействия находились в покое относительно друг друга, и относительно стола.

Опыт с лодками. Лодка отходит в сторону, противоположную прыжку.

Например, пуля также находилась в покое относительно ружья перед выстрелом. При взаимодействии (во время выстрела) пуля и ружье движутся в разные стороны. Получается явление – отдачи.

Если человек, сидящий в лодке, отталкивает от себя другую лодку, то происходит взаимодействие. Обе лодки приходят в движение.

Если же человек прыгает с лодки на берег, то лодка отходит в сторону, противоположную прыжку. Человек подействовал на лодку. В свою очередь, и лодка действует на человека. Он приобретает скорость, которая направлена к берегу.

Итак, в результате взаимодействия оба тела могут изменить свою скорость.

Масса тела. Единица массы.

При взаимодействии двух тел скорости первого и второго тела всегда меняются.

Опыт с тележками. Одна больше другой.

Одно тело после взаимодействия приобретает скорость, которая может значительно отличаться от скорости другого тела. Например, после выстрела из лука скорость стрелы гораздо больше скорости, которую приобретает тетива лука после взаимодействия.

Почему так происходит? Проведем опыт, описанный в параграфе 18. Только теперь, возьмем тележки разного размера. После того, как нить пережгли, тележки разъезжаются с разными скоростями. Тележка, которая после взаимодействия движется медленнее, называется более массивной. У нее больше масса. Тележка, которая после взаимодействия движется с большей скоростью, имеет меньшую массу. Значит, тележки имеют разную массу.

Скорости, которые приобрели тележки в результате взаимодействия, можно измерить. По этим скоростям сравнивают массы взаимодействующих тележек.

Пример. Скорости тележек до взаимодействия равны нулю. После взаимодействия скорость одной тележки стала равна 10 м/с, а скорость другой 20 м/с. Поскольку скорость, которую приобрела вторая тележка, в 2 раза больше скорости первой, то и ее масса в 2 раза меньше массы первой тележки.

В случае, если после взаимодействия скорости изначально покоившихся тележек одинаковы, то их массы одинаковы. Так, в опыте, изображенном на рисунке 42, после взаимодействия тележки разъезжаются с равными скоростями. Следовательно, их массы были одинаковы. Если после взаимодействия тела приобрели разные скорости, то их массы различны.

Международный эталон килограмма. На картинке: эталон килограмма в США.

Во сколько раз скорость первого тела больше (меньше) скорости второго тела, во столько раз масса первого тела меньше (больше) массы второго.

Чем меньше меняется скорость тела при взаимодействии, тем большую массу оно имеет. Такое тело называется более инертным.

И наоборот, чем больше меняется скорость тела при взаимодействии, тем меньшую массу оно имеет, тем меньше оно инертно.

Значит, что для всех тел характерно свойство по-разному менять свою скорость при взаимодействии. Это свойство называется инертностью.

Масса тела – это физическая величина, которая характеризует его инертность.

Следует знать, что любое тело: Земля, человек, книга и т.д. – обладает массой.

Масса обозначается буквой m. За единицу массы в СИ принят килограмм (1 кг).

Килограмм – это масса эталона. Эталон изготовлен из сплава двух металлов: платины и иридия. Международный эталон килограмма хранится в г. Севре (близ Парижа). С международного эталона сделано более 40 точнейших копий, разосланных в разные страны. Одна из копий международного эталона находится в нашей стране, в институте метрологии им. Д. И. Менделеева в Санкт-Петербурге.

На практике используют и другие единицы массы: тонна (т), грамм (г), миллиграмм (мг).

1 т	= 1000 кг (10³ кг)	1 г	= 0,001 кг (10^-3 кг)
1 кг	= 1000 г (10³ г)	1 мг	= 0,001 г (10^-3 г)
1 кг	= 1 000 000 мг (10⁶ мг)	1 мг	= 0,000001 кг (10^-6 кг)

В дальнейшем при изучении физики понятие массы будет раскрыто глубже.

Измерение массы тела на весах.

Для того, чтобы измерить массу тела, можно использовать метод, описанный в параграфе 19.

Учебные весы.

Сравнивая скорости, приобретенные телами при взаимодействии, определяют, во сколько раз масса одного тела больше (или меньше) массы другого. Измерить массу тела этим способом можно, если масса одного из взаимодействующих тел известна. Таким способом определяют в науке массы небесных тел, а также молекул и атомов.

На практике массу тела можно узнать с помощью весов. Весы бывают различного типа: учебные, медицинские, аналитические, аптекарские, электронные и др.

Специальный набор гирь.

Рассмотрим учебные весы. Главной частью таких весов, является коромысло. К середине коромысла прикреплена стрелка – указатель, которая движется вправо или влево. К концам коромысла подвешены чашки. При каком условии весы будут находиться в равновесии?

Поместим на чашки весов тележки, которые применялись в опыте (см. § 18). поскольку при взаимодействии тележки приобрели одинаковые скорости, то мы выяснили, что их массы одинаковы. Следовательно, весы будут находится в равновесии. Это значит, что массы тел, лежащих на чашках весов, равны друг другу.

Теперь на одну чашку весов, поместим тело, массу которого надо узнать. На другую будем ставить гирьки, массы которых известны, до тех пор, пока весы не окажутся в равновесии. Следовательно, масса взвешиваемого тела будет равна общей массе гирь.

При взвешивании используется специальный набор гирь.

Различные весы предназначены для взвешивания разных тел, как очень тяжелых, так и очень легких. Так, например, с помощью вагонных весов можно определить массу вагона от 50 т до 150 т. Массу комара, равную 1мг, можно узнать с помощью аналитических весов.

Плотность вещества.

Взвешиваем два цилиндра равного объема. Один алюминиевый, а другой – свинцовый.

Тела, окружающие нас, состоят из различных веществ: дерева, железа, резины и т.д.

Масса любого тела зависит не только от его размеров, но и оттого, из какого вещества оно состоит. Поэтому тела, имеющие одинаковые объемы, но состоящие из разных веществ, имеют разные массы.

Проведем такой опыт. Взвесим два цилиндра одинакового объема, но состоящие из разных веществ. Например, один из – алюминия, другой из – свинца. Опыт показывает, что масса алюминиевого меньше свинцового, то есть, алюминий легче свинца.

В то же время тела с одинаковыми массами, состоящие из разных веществ, имеют разные объемы.

Железный брус массой 1 т занимает 0,13 кубических метров. А лед массой 1 т – объем 1,1 метров кубических.

Так, железный брус массой 1 т занимает объем 0,13 м³ , а лед с такой же массой в 1 т – объем 1,1 м³ . Объем льда почти в 9 раз больше объема железного бруса. Это объясняется тем, что разные вещества могут иметь разную плотность.

Отсюда следует, что тела объемом, например, 1 м³ каждое, состоящие из разных веществ, имеют разные массы. Приведем пример. Алюминий объемом 1 м³ имеет массу 2700 кг, свинец такого же объема имеет массу 11 300 кг. То есть, при одинаковом объеме (1 м³), свинец, имеет массу, превышающую массу алюминия, примерно в 4 раза.

Плотность показывает, чему равна масса вещества, взятого в определённом объёме.

Как же можно найти плотность какого-либо вещества?

Пример. Мраморная плита имеет объем 2м³ , а ее масса равна 5400 кг. Надо определить плотность мрамора.

Итак, нам известно, что мрамор объемом 2м³ имеет массу 5400 кг. Значит, 1 м³ мрамора будет иметь массу в 2 раза меньшую. В нашем случае – 2700 кг (5400 : 2 = 2700). Таким образом, плотность мрамора будет равна 2700 кг на 1 м³ .

Значит, если известна масса тела и его объем, можно определить плотность.

Чтобы найти плотность вещества, надо массу тела разделить на его объем.

Плотность это физическая величина, которая равна отношению массы тела к его объему:

плотность = масса/объем.

Обозначим величины, входящие в это выражение, буквами: плотность вещества – ρ (греч. буква “ро”), масса тела – m, его объем – V. Тогда получим формулу для вычисления плотности:

ρ = m/V.

Единицей плотности вещества в СИ является килограмм на кубический метр (1кг/м³).

Плотность вещества выражают очень часто и в граммах на кубический сантиметр (1г/см³ ).

Если плотность вещества выражена в кг/м³ , то ее можно перевести в г/см³ следующим образом.

Пример. Плотность серебра 10 500 кг/м³ . Выразите ее в г/см³ .

10 500 кг = 10 500 000 г (или 10,5 * 10⁶ г),

1м3 = 1 000 000 см³ (или 10⁶ см³ ).

Тогда ρ = 10 500 кг/м³ = 10,5 * 10⁶ / 10⁶ г/см³ = 10,5 г/см³ .

Следует помнить, что плотность одного и того же вещества в твердом, жидком и газообразном состояниях различна. Так, плотность льда равна 900 кг/м³ , воды 1000 кг/м³ , а водяного пара – 0,590 кг/м³ . Хотя все это состояния того же вещества – воды.

Ниже приведены таблицы плотностей некоторых твердых тел, жидкостей и газов.

Таблица 2

Плотности некоторых твердых тел (при норм. атм. давл., t = 20 °C)

Твердое тело	ρ, кг/м³	ρ, г/см³	Твердое тело	ρ, кг/м³	ρ, г/см³
Осмий	22 600	22,6	Мрамор	2700	2,7
Иридий	22 400	22,4	Стекло оконное	2500	2,5
Платина	21 500	21,5	Фарфор	2300	2,3
Золото	19 300	19,3	Бетон	2300	2,3
Свинец	11 300	11,3	Кирпич	1800	1,8
Серебро	10 500	10,5	Сахар-рафинад	1600	1,6
Медь	8900	8,9	Оргстекло	1200	1,2
Латунь	8500	8,5	Капрон	1100	1,1
Сталь, железо	7800	7,8	Полиэтилен	920	0,92
Олово	7300	7,3	Парафин	900	0,90
Цинк	7100	7,2	Лед	900	0,90
Чугун	7000	7	Дуб (сухой)	700	0,70
Корунд	4000	4	Сосна (сухая)	400	0,40
Алюминий	2700	2,7	Пробка	240	0,24

Таблица 3

Плотности некоторых жидкостей (при норм. атм. давл. t=20 °C)

Жидкость	ρ, кг/м³	ρ, г/см ³	Жидкость	ρ, кг/м³	ρ, г/см³
Ртуть	13 600	13,60	Керосин	800	0,80
Серная кислота	1 800	1,80	Спирт	800	0,80
Мед	1 350	1,35	Нефть	800	0,80
Вода морская	1030	1,03	Ацетон	790	0,79
Молоко цельное	1030	1,03	Эфир	710	0,71
Вода чистая	1000	1,00	Бензин	710	0,71
Масло подсолнечное	930	0,93	Жидкое олово (при t = 400 °C)	6800	6,80
Масло машинное	900	0,90	Жидкий воздух (при t = -194 °C)	860	0,86

Таблица 4

Плотности некоторых газов (при норм. атм. давл. t=20 °C)

Газ	ρ, кг/м³	ρ, г/см³	Газ	ρ, кг/м³	ρ, г/см³
Хлор	3,210	0,00321	Оксид углерода (2) (угарный газ)	1,250	0,00125
Оксид углерода (4) (углекислый газ)	1,980	0,00198	Природный газ	0,800	0,0008
Кислород	1,430	0,00143	Водяной пар (при t = 100 °C)	0,590	0,00059
Воздух (при 0 °C)	1,290	0,00129	Гелий	0,180	0,00018
Азот	1,250	0,00125	Водород	0,090	0,00009

Расчет массы и объема по его плотности.

Знать плотность веществ очень важно для различных практических целей. Инженер, проектируя машину, заранее по плотности и объему материала может рассчитать массу будущей машины. Строитель может определить, какова будет масса строящегося здания.

Следовательно, зная плотность вещества и объем тела, всегда можно определить его массу.

Поскольку плотность вещества можно найти по формуле ρ = m/V, то отсюда можно найти массу т.е.

m = ρV.

Чтобы вычислить массу тела, если известны его объем и плотность, надо плотность умножить на объем.

Пример. Определите массу стальной детали объем 120 см³.

По таблице 2 находим, что плотность стали равна 7,8 г/см³ . Запишем условие задачи и решим ее.

Дано:

V = 120 см³;

ρ = 7,8 г/см³;

m – ?

Решение:

m = ρ · V ,

m = 120 см³ · 7,8 г/см³ = 936 г.

Ответ: m = 936 г.

Если известна масса тела и его плотность, то объем тела можно выразить из формулы m = ρV, т.е. объем тела будет равен:

V = m/ρ.

Чтобы вычислить объем тела, если известна его масса и плотность, надо массу разделить на плотность.

Пример. Масса подсолнечного масла, заполняющего бутылку, равна 930 г. Определите объем бутылки.

По таблице 3 находим, что плотность подсолнечного масла равна 0,93 г/см³ .

Запишем условие задачи и решим ее.

Дано:

ρ = 0,93 г/см³

m = 930 г

V – ?

Решение:

V = m/ρ,

V = 930/0.93 г/см³ = 1000 см³ = 1л.

Ответ: V = 1 л.

Для определения объема пользуются формулой, как правило, в тех случаях, когда объем сложно найти с помощью простых измерений.

Сила.

Каждый из нас постоянно встречается с различными случаями действия тел друг на друга. В результате взаимодействия скорость движения какого-либо тела меняется. Вам уже известно, что скорость тела меняется тем больше, чем меньше его масса. Рассмотрим некоторые примеры, подтверждающие это.

Толкая руками вагонетку, мы можем привести ее в движение. Скорость вагонетки меняется под действием руки человека.

Кусочек железа, лежащий на пробке, опущенной в воду, притягивается магнитом. Кусочек железа и пробка изменяют свою скорость под действием магнита.

Действуя на пружину рукой, можно ее сжать. Сначала в движение приходит конец пружины. Затем движение передается остальным ее частям. Сжатая пружина, распрямляясь, может, например, привести в движение шарик.

При сжатии пружины действующим телом была рука человека. Когда пружина распрямляется, действующим телом является сама пружина. Она приводит в движение шарик.

Ракеткой или рукой можно остановить или изменить направление движения летящего мячика.

Во всех приведенных примерах одно тело под действием другого тела приходит в движение, останавливается, или изменяет направление своего движения.

Таким образом, скорость тела меняется при взаимодействии его с другими телами.

Часто не указывается какое тело и как действовало на данное тело. Просто говорится, что на тело действует сила или к нему приложена сила. Значит, силу можно рассматривать как причину изменения скорости движения.

Сила, действующая на тело, может не только изменить скорость своего тела, но и отдельных его частей.

Доска, лежащая на опорах, прогибается, если на нее садится человек.

Например, если надавить пальцами на ластик или кусочек пластилина, он сожмется и изменит свою форму. Это называется деформацией.

Деформацией называется любое изменение формы и размера тела.

Приведем другой пример. Доска, лежащая на опорах, прогибается, если на нее садится человек, или любой другой груз. Середина доски перемещается на большее расстояние, чем края.

Под действием силы скорость различных тел за одно и то же время может измениться одинаково. Для этого необходимо к этим телам приложить разные силы.

Так, чтобы привести в движение грузовую машину, необходима большая сила, чем для легкового автомобиля. Значит, числовое значение силы может быть различным: большим или меньшим. Что же такое сила?

Сила является мерой взаимодействия тел.

Сила – физическая величина, значит, ее можно измерить.

На чертеже сила отображается в виде отрезка прямой со стрелкой на конце.

Сила, как и скорость, является векторной величиной. Она характеризуется не только числовым значением, но и направлением. Сила обозначается буквой F со стрелочкой (как мы помним стрелочкой обозначается направление), а ее модуль тоже буквой F, но без стрелочки.

Когда говорят о силе, важно указывать, к какой точке тела приложена действующая сила.

На чертеже силу изображают в виде отрезка прямой со стрелкой на конце. Начало отрезка – точка А есть точка приложения силы. Длина отрезка условно обозначает в определенном масштабе модуль силы.

Итак, результат действия силы на тело зависит от ее модуля, направления и точки приложения.

Явление тяготения. Сила тяжести.

Выпустим камень из рук – он упадет на землю.

Если выпустить камень из рук – он упадет на землю. То же самое произойдет и с любым другим телом. Если мяч бросить в горизонтальном направлении, он не летит прямолинейно и равномерно. Его траекторией будет кривая линия.

Камень летит по кривой линии.

Искусственный спутник Земли также не летит по прямой, он летит вокруг Земли.

Искусственный спутник движется вокруг Земли.

В чем же причина наблюдаемых явлений? А вот в чем. На эти тела действует сила – сила притяжения к Земле. Из-за притяжения к Земле падают тела, поднятые над Землей, а потом опущенные. А также, из-за этого притяжения, мы ходим по Земле, а не улетаем в бесконечный Космос, где нет воздуха, чтоб дышать.

Листья деревьев опускаются на Землю, потому что Земля притягивает их. Благодаря притяжению к Земле течет вода в реках.

Земля притягивает к себе любые тела: дома, людей, Луну, Солнце, воду в морях и океанах и др. В свою очередь, и Земля притягивается ко всем этим телам.

Притяжение существует не только между Землей и перечисленными телами. Все тела притягиваются друг к другу. Притягиваются между собой Луна и Земля. Притяжение Земли к Луне вызывает приливы и отливы воды. Огромные массы воды поднимаются в океанах и морях дважды в сутки на много метров. Вам хорошо известно, что Земля и другие планеты движутся вокруг Солнца, притягиваясь к нему и друг к другу.

Притяжение всех тел Вселенной друг к другу называется всемирным тяготением.

Английский ученый Исаак Ньютон первым доказал и установил закон всемирного тяготения.

Согласно этому закону, силы притяжения между телами тем больше, чем больше массы этих тел. Силы притяжения между телами уменьшаются, если увеличивается расстояние между ними.

Для всех живущих на Земле одна из особенно важных значений имеет сила притяжения к Земле.

Сила, с которой Земля притягивает к себе тело, называется силой тяжести.

Сила тяжести обозначается буквой F с индексом: Fтяж . Она всегда направлена вертикально вниз.

Земной шар немного сплюснут у полюсов, поэтому тела, находящиеся у полюсов расположены немного ближе к центру Земли. Поэтому, сила тяжести на полюсе немного больше, чем на экваторе, или на других широтах. Сила тяжести на вершине горы несколько меньше, чем у ее подножия.

Сила тяжести прямо пропорциональна массе данного тела.

Если сравнивать два тела с разной массой, то тело с большей массой – тяжелее. Тело же с меньшей массой – легче.

Во сколько раз масса одного тела больше массы другого тела, во столько же раз и сила тяжести, действующая на первое тело, больше силы тяжести, действующей на второе. Когда массы тел одинаковы, то одинаковы и действующие на них силы тяжести.

Сила упругости. Закон Гука.

Вам уже известно, что на все тела, находящиеся на Земле, действует сила тяжести.

На книгу, лежащую на столе, также действует сила тяжести, но она не проваливается сквозь стол, а находится в покое. Повесим-ка тело на нити. Оно падать не будет.

Закон Гука. Опыт.

Почему же покоятся тела, лежащие на опоре или подвешенные на нити? По-видимому, сила тяжести уравновешивается какой-то другой силой. Что же это за сила и откуда она берется?

Проведем опыт. На середину горизонтально расположенной доски, расположенную на опоры, поставим гирю. Под действием силы тяжести гиря начнет двигаться вниз и прогнет доску, т.е. доска деформируется. При этом возникает сила, с которой доска действует на тело, расположенное на ней. Из этого опыта можно сделать вывод, что на гирю, кроме силы тяжести направленной вертикально вниз, действует другая сила. Эта сила направлена вертикально вверх. Она и уравновесила силу тяжести. Эту силу называют силой упругости.

Итак, сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение, называется силой упругости.

Силу упругости обозначают буквой F с индексом Fупр.

Чем сильнее прогибается опора(доска), тем больше сила упругости. Если сила упругости становится равной силе тяжести, действующей на тело, то опора и тело останавливаются.

Теперь подвесим тело на нити. Нить (подвес) растягивается. В нити (подвесе), также как и в опоре, возникает сила упругости. При растяжении подвеса сила упругости будет равна силе тяжести, то растяжение прекращается. Сила упругости возникает только при деформации тел. Если исчезает деформация тела, то исчезает и сила упругости.

Опыт с телом, подвешенным на нити.

Деформации бывают разных видов: растяжения, сжатия, сдвига, изгиба и кручения.

С двумя видами деформации мы уже познакомились – сжатия и изгиба. Более подробно эти и другие виды деформации вы изучите в старших классах.

Теперь попытаемся выяснить, от чего зависит сила упругости.

Файл:Opyt s pezinovym shnurom i girey.jpg

Модуль силы упругости упругости при растяжении (или сжатии) тела прямо пропорционален изменению длины тела.

Английский ученый Роберт Гук, современник Ньютона, установил, как зависит сила упругости от деформации.

Рассмотрим опыт. Возьмем резиновый шнур. Один его конец закрепим в штативе. Первоначальная длина шнура была l₀. Если к свободному концу шнура подвесить чашку с гирькой, то шнур удлинится. Его длина станет равной l. Удлинение шнура можно найти так:

Δl = l – l₀.

Если менять гирьки на чашке, то будет меняться и длина шнура, а значит, ее удлинение Δl .

Опыт показал, что модуль силы упругости при растяжении (или сжатии) тела прямо пропорционален изменению длины тела.

В этом и заключается закон Гука. Записывается закон Гука следующим образом:

Fупр = -kΔl,

Вес тела – это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.

где Δl – удлинение тела (изменение его длины), k – коэффициент пропорциональности, который называется жесткостью.

Жесткость тела зависит от формы и размеров, а также от материала, из которого оно изготовлено.

Закон Гука справедлив только для упругой деформации. Если после прекращения действий сил, деформирующих тело, оно возвращается в исходное положение, то деформация является упругой.

Более подробно закон Гука и виды деформаций вы изучите в старших классах.

Вес тела.

В повседневной жизни очень часто используется понятие “вес” . Попытаемся выяснить что же это за величина. В опытах, когда тело ставили на опору, сжималась не только опора, но и тело, притягиваемое Землей.

Деформированное, сжатое тело давит на опору с силой, которую называют весом тела. Если тело подвешено на нити, то растянута не только нить, но и само тело.

Вес тела – это сила, с которой тело вследствие притяжения к Земле действует на опору или подвес.

Вес тела – это векторная физическая величина и обозначается она буквой P со стрелочкой над этой буквой, направленная вправо.

Однако следует помнить, что сила тяжести приложена к телу, а вес приложен к опоре или подвесу.

Если тело и опора неподвижны или движутся равномерно и прямолинейно, то вес тела по своему числовому значению равен силе тяжести, т.е.

P = Fтяж.

Следует помнить, что сила тяжести является результатом взаимодействия тела и Земли.

Итак, Вес тела – это результат взаимодействия тела и опоры (подвеса). Опора (подвес) и тело при этом деформируются, что приводит к появлению силы упругости.

Единицы силы. Связь между силой тяжести и массой тела.

Вам уже известно, что сила – это физическая величина. Она кроме числового значения (модуля) имеет направление, т. е. это векторная величина.

Силу, как и любую физическую величину, можно измерить, сравнить с силой, принятой за единицу.

Единицы физических величин всегда выбирают условно. Так, за единицу силы можно принять любую силу. Например, можно принять за единицы силы силу упругости какой-то пружины, растянутой до определенной длины. За единицу силы, можно принять и силу тяжести, действующей на тело.

Вы знаете, что сила является причиной изменения скорости тела. Именно поэтому за единицу силы, принята сила, которая за время 1с изменяет скорость тела массой 1 кг на 1 м/с.

В честь английского физика Ньютона эта единица названа ньютоном (1 Н). Часто применяют и другие единицы – килоньютоны (кН), миллиньютоны (мН):

1кН=1000 Н, 1Н = 0,001 кН.

Попытаемся определить величину силы в 1 Н. Установлено, что 1 Н приблизительно равен силе тяжести, которая действует на тело массой 1/10 кг, или более точно 1/9,8 кг (т. е. около 102 г).

Необходимо помнить, что сила тяжести, действующая на тело, зависит от географической широты, на которой находится тело. Сила тяжести меняется при изменении высоты над поверхностью Земли.

Если известно, что единицей силы является 1 Н, то как рассчитать силу тяжести, которая действует на тело любой массы?

Известно, что, во сколько раз масса одного тела, больше массы другого тела, во столько же раз сила тяжести, действующей на первое тело, больше силы тяжести, действующей на второе тело. Таким образом, если на тело массой 1/9,8 кг действует сила тяжести равная 1 Н, то на тело 2/9,8 кг будет действовать сила тяжести, равная 2 Н.

На тело массой 5/9,8 кг – сила тяжести равная – 5 Н, 5,5/9,8 кг – 5,5 Н, и т. д. На тело массой 9,8/9,8 кг – 9,8 Н.

Поскольку 9,8/9,8 кг = 1 кг, то на тело массой в 1 кг будет действовать сила тяжести, равная 9,8 Н. Значение силы тяжести, действующей на тело массой 1 кг, можно записать так: 9,8 Н/кг.

Значит, если на тело массой 1 кг действует сила, равная 9,8 Н, то на тело массой 2 кг будет действовать сила, в 2 раза большая. Она будет равна 19,6 Н, и так далее.

Таким образом, чтобы определить силу тяжести, действующую на тело любой массы, необходимо 9,8 Н/кг умножить на массу этого тела.

Масса тела выражается в килограммах. Тогда получим, что:

Fтяж = 9,8 Н/кг · m.

Величину 9,8 Н/кг обозначают буквой g, и формула для силы тяжести будет иметь вид:

Fтяж = gm,

где m – масса, g – называется ускорением свободного падения. (Понятие ускорения свободного падения будет дано в 9 классе.)

При решении задач где не требуется большой точности, g = 9,8 Н/кг округляют до 10 Н/кг.

Вам уже известно, что P = Fтяж , если тело и опора неподвижны или движутся равномерно и прямолинейно. Следовательно, вес тела можно определить по формуле:

P = gm,

Пример. На столе стоит чайник с водой массой 1,5 кг. Определите силу тяжести и вес чайника. Покажите эти силы на рисунке 68.

Дано:

m = 1,5 кг

g ≈ 10 Н/кг

Fтяж – ?

P – ?

Решение:

Fтяж = gm,

P = gm,

Fтяж = P ≈ 10 Н/кг · 1,5 кг = 15 Н.

Ответ: Fтяж = P = 15 Н.

Теперь изобразим силы графически. Выберем масштаб. Пусть 3 Н будет равен отрезку длиной 0,3 см. Тогда силу в 15 Н. необходимо начертить отрезком длиной 1,5 см.

Следует учитывать, что сила тяжести действует на тело, а значит, приложена к самому телу. Вес действует на опору или подвес, т. е. приложен к опоре, в нашем случае к столу.

Динамометр.

Простейший динамометр.

На практике часто приходится измерять силу, с которой одно тело действует на другое. Для измерения силы используется прибор, который называется динамометр (от греч. динамис – сила, метрео – измеряю).

Динамометры бывают различного устройства. Основная их часть – стальная пружина, которой придают разную форму в зависимости от назначения прибора. Устройство простейшего динамометра основывается на сравнении любой силы с силой упругости пружины.

Простейший динамометр можно изготовить из пружины с двумя крючками, укрепленной на дощечке. К нижнему концу пружины прикрепляется указатель, а на доску наклеивается полоска бумаги.

Отметим на бумаге черточкой положение указателя при не натянутой пружине. Эта отметка будет нулевым делением.

Ручной динамометр – силомер.

Затем к крючку будем подвешивать груз массой 1/9,8 кг, т. е. 102 г.На этот груз будет действовать сила тяжести 1 Н. Под действием этой силы (1 Н) пружина растянется, указатель опустится вниз. Его новое положение отмечаем на бумаге и ставим цифру 1. После чего, подвешиваем груз массой 204 г и ставим отметку 2. Это означает, что в таком положении сила упругости пружины равна 2 Н. Подвесив груз массой 306 г, наносим отметку 3, и т. д.

Для того, чтобы нанести десятые доли ньютона, надо нанести деления – 0,1; 0,2; 0,3; 0,4 и т. д. Для этого расстояния между каждыми целыми отметками делятся на десять равных частей. Так можно сделать, учитывая, что сила упругости пружины Fупр увеличивается во столько раз, во сколько увеличивается ее удлинение Δl . Это следует из закона Гука: Fупр = kΔl, т. е. сила упругости тела при растяжении прямо пропорциональна изменению длины тела.

Тяговый динамометр.

Проградуированная пружина и будет простейшим динамометром.

С помощью динамометра измеряется не только сила тяжести, но и другие силы, такие как – сила упругости, сила трения и т. д.

Так, например, для измерения силы различных мышечных групп человека используется медицинские динамометры.

Для измерения мускульной силы руки при сжатии кисти в кулак применяется ручной динамометр – силомер.

Применяются также ртутные, гидравлические, электрические и другие динамометры.

В последнее время широко применяются электрические динамометры. У них имеется датчик, преобразующий деформацию в электрический сигнал.

Для измерения больших сил, таких, например, как тяговые усилия тракторов, тягачей, локомотивов, морских и речных буксиров, используют специальные тяговые динамометры. Ими можно измерить силы до нескольких десятков тысяч ньютонов.

Опыт. Равнодействующая двух сил, действующих на тело по одной прямой в одну сторону.

Сложение двух сил, направленных по одной прямой. Равнодействующая сил.

В большинстве случаев, с которыми мы встречаемся в жизни, на тело действует не одна, а сразу несколько сил. Так, например, на парашютиста, спускающегося на Землю, действуют сила тяжести и сила сопротивления воздуха. На тело, висящее на пружине, действуют две силы: сила тяжести и сила упругости пружины.

В каждом подобном случае можно заменить несколько сил, в действительности приложенных к телу, одной силой, равноценной по своему действию этим силам.

Сила, которая производит на тело такое же действие, как несколько одновременно действующих сил, называется равнодействующей этих сил.

Найдем равнодействующую этих двух сил, действующих на тело по одной прямой в одну сторону.

Обратимся к опыту. К пружине один под другим подвесим два груза массой 102 г и 204 г, т. е. весом 1 Н и 2 Н. Отметим длину, на которую растянулась пружина. Снимем эти грузы заменим одним грузом, который растягивает пружина на такую же длину. Вес этого груза оказывается равным 3 Н.

Из опыта следует, что: равнодействующая сил, направленных по одной прямой в одну и ту же сторону, а ее модуль равен сумме модулей составляющих сил.

На рисунке равнодействующая сил, действующих на тело, обозначена буквой R, а слагаемые силы – буквами F₁ и F₂. В этом случае

R = F₁ + F₂.

Выясним теперь, как найти равнодействующую двух сил, действующих на тело по одной прямой в разные стороны. Тело – столик динамометра. Поставим на столик гирю весом 5 Н, т.е. подействуем на него силой 5 Н, направленной вниз. Привяжем к столику нить и подействуем на него с силой, равной 2 Н, направленной вверх. Тогда динамометр покажет силу 3 Н. Эта сила есть равнодействующая двух сил: 5 Н и 2Н.

Итак, равнодействующая двух сил, направленных по одной прямой в противоположные стороны, направлена в сторону большей по модулю силы, а ее модуль равен разности модулей составляющих сил (рис.):

R = F₁ – F₂ .

Если к телу приложены две равные и направленные противоположно силы, то равнодействующая этих сил равна нулю. Например, если в нашем опыте за конец потянуть силой в 5 Н, то стрелка динамометра установится на нулевом делении. Равнодействующая двух сил в этом случае равна нулю:

R = 5 H – 5 H,

R = 0.

Тело под действием двух равных и противоположно направленных сил будет находится в покое или двигаться равномерно и прямолинейно.

Сила трения.

Сани скатившиеся с горы, в скором времени останавливаются.

Сани, скатившись с горы, движутся по горизонтальному пути неравномерно, скорость их постепенно уменьшается, и через некоторое время они останавливаются. Человек, разбежавшись, скользит на конька по льду, но, как бы ни был гладок лед, человек все-таки останавливается. Останавливается и велосипед, когда велосипедист прекращает крутить педали. Мы знаем, что причиной таких явлений, является сила. В данном случае это сила трения.

При соприкосновении одного тела с другим получается взаимодействие, препятствующее их относительному движению, которое называется трением. А сила, характеризующая это взаимодействие называется силой трения.

Сила трения – это еще один вид силы, отличающийся от рассмотренных ранее силы тяжести и силы упругости.

Одна из причин возникновения силы трения, является шероховатость поверхностей соприкасающихся тел.

Одна из причин возникновения силы трения является шероховатость поверхностей соприкасающихся тел.

Даже гладкие на вид поверхности тел имеют неровности, бугорки и царапины. На рисунке 79, а неровности изображены в увеличенном виде. Когда одно тело скользит или катится по поверхности другого, эти неровности цепляются друг за друга, так, что получается некоторая сила, задерживающая движение.

Другая причина трения – взаимное притяжение молекул соприкасающихся тел.

Возникновение силы трения обусловлено главным образом первой причиной, когда поверхности тел шероховаты. Но если поверхности хорошо отполированы, то при соприкосновении часть их молекул располагается очень близко друг от друга. В этом случае начинает заметно проявляться притяжение между молекулами соприкасающихся тел.

Опыт с бруском и динамометром. Измеряем силу трения.

Силу трения можно уменьшить во много раз, если ввести между трущимися поверхностями смазку. Слой смазки разъединяет поверхности трущихся тел. В этом случае соприкасаются не поверхности тел, а слои смазки. Смазка же в большинстве случаев жидкая, а трение слоев жидкости меньше, чем твердых поверхностей. Например, на коньках малое трение при скольжении по льду объясняется также действием смазки. Между коньками и льдом образуется тонкий слой воды. В технике в качестве смазки широко применяют различные масла.

При скольжении одного тела по поверхности другого возникнет трение, которое называют трением скольжения. Например, такое трение возникнет при движении саней и лыж по снегу.

Если же одно тело не скользит, а катится по поверхности другого, то трение, возникающее при этом, называют трением качения. Так, при движении колес вагона, автомобиля, при перекатывании бревен или бочек по земле проявляется трение качения.

Силу трения можно измерить. Например, чтобы измерить силу трения скольжения деревянного бруска по доске или по столу, надо прикрепить к нему динамометр. Затем равномерно двигать брусок по доске, держа динамометр горизонтально. Что при этом покажет динамометр? На брусок в горизонтальном направлении действуют две силы. Одна сила – сила упругости пружины динамометра, направленная в сторону движения. Вторая сила – это сила трения, направленная против движения. Так как брусок движется равномерно, то это значит, что равнодействующая этих двух сил равна нулю. Следовательно, эти силы равны по модулю, но противоположны по направлению. Динамометр показывает силу упругости (силу тяги), равную по модулю силе трения.

Таким образом, измеряя силу, с которой динамометр действует на тело при его равномерном движении, мы измеряем силу трения.

Если на брусок положить груз, например гирю, и измерить по описанному выше способу силу трения, то она окажется больше силы трения, измеренной без груза.

Чем больше сила, прижимающая тело к поверхности, тем больше возникающая при этом сила трения.

Положив деревянный брусок на круглые палочки, можно измерить силу трения качения. Она оказывается меньше силы трения скольжения.

Таким образом, при равных нагрузках сила трения качения всегда меньше силы трения скольжения. Именно поэтому, люди еще в древности применяли катки для перетаскивания больших грузов, а позднее стали использовать колесо.

Трение покоя.

Мы познакомились с силой трения, возникающей при движении одного тело по поверхности другого. Но можно ли говорить о силе трения между соприкасающимися твердыми телами, если они находятся в покое?

Когда тело находится в покое на наклонной плоскости, оно удерживается на ней силой трения. Действительно, если бы не было трения, то тело под действием тяжести соскользнуло бы вниз по наклонной плоскости. Рассмотрим случай, когда тело находится в покое на горизонтальной плоскости. Например, на полу стоит шкаф. Попробуем его передвинуть. Если бы шкаф нажать слабо, то с места он не сдвинется. Почему? Действующая сила в этом случае уравновешивается силой трения между полом и ножками шкафа. Так как эта сила существует между покоящимися друг относительно друга телами, то эта сила называется силой трения покоя.

На рисунке изображен транспортер, с помощью которого поднимаются тюки с хлóпком. Тюки удерживаются на ленте транспортера силой трения покоя.

Сила трения покоя удерживает гвоздь, вбитый в доску, не дает развязаться банту на ленте, удерживает нитку, которой сшиты два куска ткани, и т. п.

Трение в природе и технике.

Сила трения трения останавливает автомобиль при торможении, но без трения покоя он не смог бы и начать движение.

В природе и технике трение имеет большое значение. Трение может быть полезным и вредным. Когда оно полезно, его стараются увеличить, когда вредно – уменьшить.

Без трения покоя ни люди, ни животные не смогли бы ходить по земле, так как при ходьбе мы отталкиваемся от земли. Когда трение между подошвой обуви и земли (или льдом) малó, например, в гололедицу, то отталкиваться от земли очень трудно, ноги скользят. Чтобы ноги не скользили, тротуары посыпаются песком. Это увеличивает силу трения между подошвой обуви и льдом.

Не будь трения, предметы выскальзывали бы из рук.

Сила трения останавливает автомобиль при торможении, но без трения он не смог бы стоять на месте, буксовал. Что-бы увеличить трение, поверхность шин у автомобиля делаются с ребристыми выступами. Зимой, когда дорога бывает особенно скользкая, ее посыпают песком, очищают ото льда.

У многих растений и животных имеются различные органы, служащие для хватания (усики растений, хобот слона, цепкие хвосты лазающих животных). Все они имеют шероховатую поверхность для увеличения трения.

Для уменьшения трения, так же используются подшипники.

Вам уже известно, что в некоторых случаях трение вредно и с ним приходится бороться. Например, во всех машинах из-за трения нагреваются и изнашиваются движущиеся части. Для уменьшения трения соприкасающиеся поверхности делают гладкими, между ними вводят смазку. Что-бы уменьшить трение вращающихся валов машин и станков, их опирают на подшипники. Деталь подшипника, непосредственно соприкасающуюся с валом, называется вкладышем. Вкладыши делают из твердых металлов – бронзы, чугун или стали. Внутреннюю поверхность их покрывают особыми материалами, чаще всего баббитом (это сплав свинца или олова с другими металлами), и смазывают. Подшипники, в которых вал при вращении скользит по поверхности вкладыша, называют подшипниками скольжения.

Мы знаем, что сила трения качения при одинаковой нагрузке значительно меньше силы трения скольжения. На этом явлении основано применение шариковых и роликовых подшипников. В таких подшипниках вращающийся вал не скользит по неподвижному вкладышу подшипника, а катится по нему на стальных шариках или роликах.

Устройство простейших шарикового и роликового подшипников изображено на рисунке. Внутреннее кольцо подшипника, изготовленное из твердой стали, насажено на вал. Наружное же кольцо закреплено в корпусе машины. При вращении вала внутреннее кольцо катится на шариках или роликах, находящихся между кольцами. Замена в машине подшипников скольжения шариковыми или роликовыми подшипниками позволяет уменьшить силу трения в 20-30 раз.

Шариковые и роликовые подшипники используются в разнообразных машинах: автомобилях, токарных станках, электрических двигателях, велосипедах, и т. д. Без подшипников (они используют силу трения), невозможно представить современную промышленность и транспорт.

Ссылки

Уроки по физике за 7 класс по школьной программе

Источник

Когда лодка движется по течению, течение помогает лодке двигаться, и лодка начинает двигаться быстрее. Таким образом, скорость самой лодки и скорость течения объединяются.

Как рассчитать скорость формула

Скорость 90 км/ч означает, что объект проходит 90 км за один час.

Запишите тип скорости.

Формулы приводятся в математической нотации, а значения выражаются общими буквами (переменными).

V — скорость, V — расстояние, S — время, t — время.

Исходя из этого, уравнение скорости приобретает вид

Примените эту формулу для решения следующей задачи.

Автомобиль, движущийся с постоянной скоростью, проезжает 120 км за 2 часа. С какой скоростью двигался автомобиль?

Пройденное расстояние (дистанция) и время, затраченное на путь, были заменены формулой для нахождения скорости. V = 60 км/ч.

Теперь, исходя из формулы скорости, напишем формулу пути.

Поезд двигался со скоростью 50 км/ч в течение 3 часов равномерно. Какое расстояние было пройдено поездом за этот период?

Используя тип маршрута, мы нашли ответ. Поезд проехал 150 км за 3 часа.

Скорость — это физическая величина, определяющая расстояние, которое проходит объект за единицу времени. Поэтому уравнение для определения скорости (равномерного движения) может быть выражено как.

V, значение скорости — S, значение пройденного расстояния — T, время движения.

Скорость почти всегда выражается в м/с или км/ч, расстояние — в метрах (м) или километрах (км), а время — в секундах, минутах или часах.

Из перечисленных выше типов скоростей можно экспортировать определенные типы маршрутов.

Пройденное расстояние — это произведение скорости на время. Если известны расстояние и скорость, то время можно найти по следующей формуле

Разделите расстояние на скорость, чтобы найти время.

Вы можете использовать онлайн-калькуляторы для быстрого и точного расчета времени, скорости и расстояния в различных единицах измерения.

С древних времен людей волновала идея достижения сверхскорости, и никогда не волновала высота, летающих машин. На самом деле, это два очень тесно связанных понятия. То, насколько быстро вы сможете добраться из одной точки в другую на современном самолете, зависит исключительно от скорости. Рассматриваются методы и виды расчетов, а также время и расстояние.

Как же рассчитать скорость?

На самом деле, существует несколько методов расчета.

через формулу нахождения мощности;
через дифференциальные исчисления;
по угловым параметрам и так далее.

В этой статье описан самый простой метод, в котором используется самое простое уравнение. Он заключается в нахождении значения этого параметра из расстояния и времени. Кстати, формула разности также содержит эти значения. Формула выглядит следующим образом.

v — скорость объекта,
S — расстояние, которое пройдено или должно быть пройдено объектом,
t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, нет ничего сложного в том, чтобы быть первокурсником. Вы можете рассчитать скорость, с которой движется объект, подставив значения, соответствующие позициям букв. Например, давайте найдем значение скорости, с которой автомобиль проезжает 100 км за 1 час 30 минут. В большинстве случаев единицей измерения являются километры в час (км/ч), поэтому сначала нужно перевести 1 час 30 минут в часы. Это означает, что 1 час 30 минут равен 1,5 часа. Это потому, что 30 минут — это половина или 1/2 или 0,5 часа. Сумма 1 часа и 0,5 часа равна 1,5 часа.

Затем замените буквы алфавита на доступные значения.

Здесь v = 66,66 км/ч. Это значение очень приблизительное (неосведомленным лучше почитать о нем в специальной литературе), S = 100 км и t = 1,5ч.

С помощью этого простого метода скорость можно найти из времени и расстояния.

Что произойдет, если я захочу найти среднюю цену? Как правило, приведенный выше расчет приводит к среднему значению искомого параметра. Однако, если мы знаем, что скорость объекта не постоянна в определенном сечении по сравнению с другими сечениями, мы можем экспортировать более точные значения. В этом случае используйте тип.

V1, V2, V3 и VN — величины объектов на конкретном участке, n — количество этих участков, а VCR — средняя скорость на всех расстояниях.

Один и тот же тип можно записать по-разному, используя маршрут и время, которое объект прошел по этому маршруту.

vср=(S1+S2+. +Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
S1, S2, Sn — отдельные неравномерные участки всего пути,
t — общее время, за которое объект прошел все участки.

Можно также написать его, используя вычисления такого типа.

vср=S/(t1+t2+. +tn), где S — общее пройденное расстояние,
t1, t2, tn — время прохождения отдельных участков расстояния S.

Однако тот же тип можно записать и в более точной форме

vcp = s1/t1+s2/t2+. +sn/tn, где s1/t1, s2/t2 и sn/tn — типы для расчета скорости на отдельных участках общего маршрута S.

Поэтому очень легко найти необходимые параметры, используя вышеуказанные типы. Он очень прост и, как уже говорилось, используется в начальном образовании. Самый сложный тип основан на том же типе и тех же принципах структуры и расчета, но имеет другой, более сложный формат, больше переменных и разные коэффициенты. Это необходимо для получения наиболее точной цены индикатора.

Другие способы вычисления

Существуют и другие методы и способы, помогающие рассчитать значение этого параметра. Примером может служить тип вычислительной мощности.

n = f*v*cos a, где n — механическая мощность, и

cos a — косинус угла между вектором силы и скоростью.

Как рассчитать тип скорости

Скорость сближения — это расстояние, на которое два объекта приближаются друг к другу в единицах времени. Чтобы найти скорость сближения двух объектов, движущихся навстречу друг другу, необходимо суммировать скорости этих объектов.

Формула нахождения значений скорости, времени и расстояния

На самом деле, существует несколько методов расчета.

через формулу нахождения мощности;
через дифференциальные исчисления;
по угловым параметрам и так далее.

В данной статье рассматривается самый простой тип и самый простой метод — нахождение цены этого параметра через расстояние и время. Кстати, различные формулы включают эти значения. Мужчины следующие.

v — скорость объекта,
S — расстояние, которое пройдено или должно быть пройдено объектом,
t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, ничего сложного для первоклассников нет. Вы можете вычислить скорость, с которой движется объект, подставив вместо буквы соответствующее значение. Например, найдите значение скорости, с которой автомобиль проезжает 100 километров за 1 час 30 минут. В большинстве случаев единицей измерения является один километр в час (км/ч), который сначала необходимо перевести в один час и 30 минут. Поэтому один час и 30 минут равны 1,5 часа, так как 30 минут — это половина, или половина, или 0,5 часа. При сложении 1 часа и 0,5 часа получается 1,5 часа.

Затем замените буквы алфавита на доступные значения.

С помощью этого простого метода скорость можно найти из времени и расстояния.

V1, V2, V3 и VN — это значения для объектов на конкретном участке, n — количество этих участков, а VCR — средняя скорость на всех расстояниях.

vср=(S1+S2+. +Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
S1, S2, Sn — отдельные неравномерные участки всего пути,
t — общее время, за которое объект прошел все участки.

Можно также написать его, используя вычисления такого типа.

vср=S/(t1+t2+. +tn), где S — общее пройденное расстояние,
t1, t2, tn — время прохождения отдельных участков расстояния S.

Однако тот же тип можно записать и в более точной форме

vcp = s1/t1+s2/t2+. +sn/tn, где s1/t1, s2/t2 и sn/tn — типы для расчета скорости на отдельных участках общего маршрута S.

Другие способы вычисления

n = f*v*cos a, где n — механическая мощность, и

cos a — косинус угла между вектором силы и скоростью.

Нахождение среднего значения

Способы вычисления расстояния и времени

Также можно найти цены расстояния и времени, зная скорость. Например:.

s = v*t, где v дает понять, что это такое, и

s — расстояние, которое вы хотите найти, и

t — время, необходимое объекту для прохождения этого расстояния.

При этом рассчитывается цена расстояния.

В качестве альтернативы рассчитайте значение времени прохождения расстояния.

t = s/v, где v — та же скорость и

s — пройденное расстояние, и

В данном случае это время, за которое нужно найти цену.

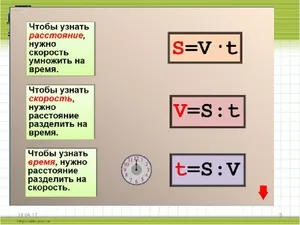
Скорость и расстояние

Существует несколько выражений этого типа и все остальные для нахождения среднего значения этих параметров. Самое главное — знать основные правила перевода и расчета. Еще важнее знать сами типы, причем желательно извне. Если вы не помните их, лучше запишите их. Это поможет, не сомневайтесь.

С помощью таких переводов можно легко найти время, расстояние и другие параметры, используя правильный способ их вычисления.

Водитель едет из города А в город Б, и через три часа к нему приближается мотоциклист со скоростью 60 км/ч. Водитель и мотоциклист встретились в 350 км от А. Расстояние между А и В составляет 470 км. Найдите скорость мотоциклиста.

Время

Время — это самое ценное, что у нас есть. Однако, помимо философии, время играет важную роль в математике.

Время — это продолжительность определенной деятельности или события.

Время обозначается латинской буквой t.

Наиболее распространенными единицами измерения времени являются секунды, минуты и часы.

на некоторое время.

Чтобы найти время, разделите расстояние на скорость.

Этот человек полезен, когда вы хотите узнать, сколько времени требуется вашему телу, чтобы преодолеть расстояние.

Взаимосвязь скорости, времени, расстояния

Скорость, время и расстояние тесно связаны между собой. Трудно представить себе человека без другого.

Если известны скорость и время движения, можно найти расстояние. Время равно скорости: s = v x t.

Работа 1. Мы вышли из нашего дома и посетили соседний двор. Нам потребовалось 15 минут, чтобы добраться до следующего сада. Наш спортивный браслет показывал, что наша скорость составляет 50 метров в минуту. Какое расстояние мы прошли?

Если мы проходим 50 метров в минуту, сколько из этих 50 метров мы проходим за 10 минут? Умножьте 50 метров в минуту на 15 минут, чтобы определить расстояние от дома до магазина.

Ответ: 750 метров пешком.

Если время и расстояние известны, найдите скорость: v = s:t.

Вопрос 2. Два ученика решили посмотреть, кто быстрее пробежит двор детской площадки. Расстояние между двором и детской площадкой составляет 100 метров. Первый выполняется за 25 секунд, а второй — за 50 секунд. Кто быстрее?

Самым быстрым считается тот, который проходит наибольшую длину за 1 секунду. Считается, что это самая высокая скорость. В этом вопросе скорость студента — это расстояние, пройденное за одну секунду.

Чтобы найти скорость, разделите расстояние на время. Чтобы найти скорость первого ученика, разделите 100 метров на время движения первого ученика, т.е. 25 секунд.

Если расстояние задано в метрах, а время движения в секундах, то скорость измеряется в метрах в секунду (м/с). Если расстояние указано в километрах, а продолжительность времени в часах, то скорость измеряется в километрах в час (км/ч).

В нашей задаче расстояние задано в виде измерения, а время в секундах. Это позволяет измерять скорость в метрах в секунду (м/с).

Таким образом, мы узнаем, что скорость первого ученика составляет 4 метра в секунду.

Затем мы можем найти скорость второго ученика. Для этого разделите расстояние на время движения второго ученика, т.е. 50 секунд.

Таким образом, скорость второго ученика составляет 2 метра в секунду.

Теперь вы можете сравнить скорость каждого ученика и определить, кто бежал быстрее.

Скорость первого ученика выше. Так он быстрее добирался до корта.

ОТВЕТ: первый ученик бежал быстрее.

Если скорость и расстояние известны, можно найти время: t = s:v.

Вопрос 3: Стадион находится в 500 метрах от школы. Мы должны идти туда пешком. Скорость составляет 100 метров в минуту. Сколько времени нужно, чтобы дойти от школы до стадиона?

Если мы проходим 100 метров в минуту, сколько минут в 100 метрах нам нужно, чтобы пройти 500 метров?

Чтобы ответить на этот вопрос, нужно разделить 500 метров на 1 минуту, то есть на расстояние, которое вам нужно пройти до 100. Затем требуется время, чтобы достичь этой стадии.

Ответ: дойти от школы до суда за пять минут.

Печатайте или рисуйте таблицы, особенно в математических курсах, чтобы быстрее запомнить и применить скорость, время и расстояние.

Например, определите угловую скорость преобразователя, когда подвешенная масса перемещается на 10 метров. Радиус руки равен 40 см. В начале подвеса он находится в состоянии покоя и начинает спускаться с ускорением A = 0,04 м/S2.

Единицы измерения скорости

Основной единицей измерения скорости в системе СИ является: V = M/S2

Задание. Движение точки A задается уравнением: $ x = 2 t^-4 t^$. Пойнт начинает свое движение.₀= 0 c. Как движется ось под осью в момент времени t = 0,5 с?

Решение. Найдите уравнение, определяющее скорость этой точки. Для этого получите первую производную по времени от функции x = x(t), заданной в условиях задачи.

Чтобы определить направление движения, заменим полученную функцию скорости на v = v(t) в (1.1) и сравним результат с нулем за время, определенное конвенцией.

Получив свою скорость в этой точке, материальная точка будет двигаться по оси x, так как ее скорость отрицательна.

Ответ. Ось x.

Мы уже помогли 4372 студентам старших классов и колледжей сдать экзамены, начиная с решения задач и заканчивая бакалаврской работой! Узнайте, сколько будет стоить ваша работа за 15 минут!

Задание. Скорость материала точки является функцией времени формы.

Скорость в м/с, время в с. Каковы координаты точки в момент времени t = 10 с? Считайте, что в момент t = 0 c точка начала двигаться вдоль оси x от своей начальной точки.

Разрешение. Точка движется вдоль оси x, и связь между координатами x и скоростью имеет следующий вид

Чтобы ответить на первый вопрос задачи, давайте поменяем в уравнении (2.1) время t = 10 c.

Чтобы определить точку, в которой достигается 10 м от начала, пусть уравнение (2.1) равно 10 и пусть следующее квадратное уравнение равно.

$ begin 10 t-t^= 10 (2.2) ǫ t_ = 5+ ǫ sqrt compx 8.8 (c); t_ = 5- sqrt amptx 1.13 (c) ǫ end $

Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала, когда x = -10. Решение квадратного уравнения:.

При решении уравнения (2.3) скорректируйте следующий маршрут

Ответ. 1) $ x = 0 mathrm $ 2) $ t_ = 8.8 mathrm, t_ = 1.13 c, t_ = 11 c $

Источник

Понятие и основные термины

Равноускоренное движение

Среднее значение

Угловая скорость

Закон сложения

Использование онлайн-калькулятора

Понятие «скорость» в классической механике[править | править код]

Случай материальной точки[править | править код]

Случай тела конечных размеров[править | править код]

Начальная скорость[править | править код]

Запись скорости в разных системах координат[править | править код]

В декартовых координатах[править | править код]

В цилиндрических координатах[править | править код]

В сферических координатах[править | править код]

Физическая и координатная скорости[править | править код]

Некоторые связанные со скоростью понятия[править | править код]

Преобразования Галилея и Лоренца для скорости[править | править код]

Скорость в релятивистской механике[править | править код]

Четырёхмерная скорость[править | править код]

Понятие «быстрота»[править | править код]

Некоторые скорости[править | править код]

Космические скорости[править | править код]

Скорости распространения волн[править | править код]

Скорость звука[править | править код]

Скорость света[править | править код]

Скорость гравитации[править | править код]

Единицы измерения скорости[править | править код]

Соотношения между единицами скорости[править | править код]

Исторический очерк[править | править код]

Скорости в природе и технике[править | править код]

Скорости движения живых существ[править | править код]

Рекорды скорости транспортных средств[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Определение и формула скорости

Скорость в разных системах координат

Частные случаи формул для вычисления скорости

Единицы измерения скорости

Примеры решения задач

Равномерное и неравномерное движение.

Скорость. Единицы скорости.

Расчет пути и времени движения.

Инерция.

Взаимодействие тел.

Масса тела. Единица массы.

Измерение массы тела на весах.

Плотность вещества.

Расчет массы и объема по его плотности.

Сила.

Явление тяготения. Сила тяжести.

Сила упругости. Закон Гука.

Вес тела.

Единицы силы. Связь между силой тяжести и массой тела.

Динамометр.

Сложение двух сил, направленных по одной прямой. Равнодействующая сил.

Сила трения.

Трение покоя.

Трение в природе и технике.

Ссылки

Как рассчитать скорость формула

Как же рассчитать скорость?

Другие способы вычисления

Формула нахождения значений скорости, времени и расстояния

Другие способы вычисления

Способы вычисления расстояния и времени

Время

Взаимосвязь скорости, времени, расстояния

Единицы измерения скорости

Вам также может понравиться

Как найти силу тока через батарейку

Образец как исправить ошибку в трудовой книжке в дате приказа

Как найти блоггеров в яндекс дзен

Добавить комментарий Отменить ответ