
Понятие и основные термины
Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.
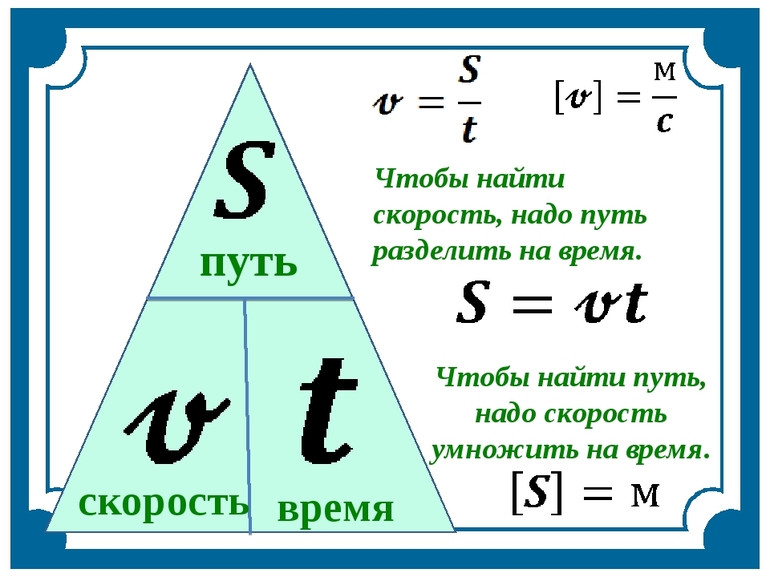
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:
- S — расстояние (путь), пройденное материальной точкой или телом (м);
- T — время за которое она преодолела путь (с).

Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.
Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.
Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:
- неравномерную;
- среднюю;
- равномерно-переменную;
- поступательную;
- вращательную;
- ускоренную.
Равноускоренное движение
Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.
Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.
В произвольно взятой точке скорость перемещения равна ускорению свободного падения.
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:
- V0 — начальная скорость;
- A — ускорение (имеет постоянное значение);
- t — время движения.
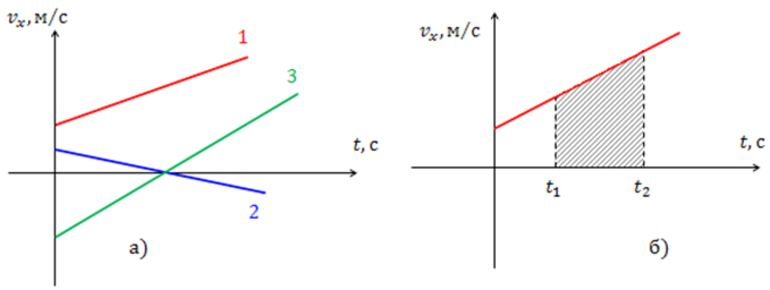
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.
Если на оси времени выделить промежуток Δt, то можно предположить, что движение будет равномерным и описываться некоторым параметром, равным мгновенному значению в середине отрезка. Эта моментальная величина является векторной. Она численно равна пределу, который пытается достигнуть скорость за промежуток времени, стремящийся к нулю. В физике это состояние описывается формулой мгновенной скорости: V = lim (Δ s/ Δ t) = r-1(t). То есть, с математической точки зрения, это первая производная.
Исходя из этого можно утверждать, что движение Δs = v*Δt. Так как произведение ускорения на время определяется разницей V -V0, то верной будет запись: S = V0*t + A*t2/2 = (V2 — V20) /2*A.
Из этой формулы можно вывести выражение для нахождения конечной скорости материальной точки: V = (V20 — 2* A * s)½. Если же в начальный момент V0 = 0, то формулу можно упростить до вида: V = (2* A * s)½.
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.

По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: {V} = V.
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
Угловая скорость
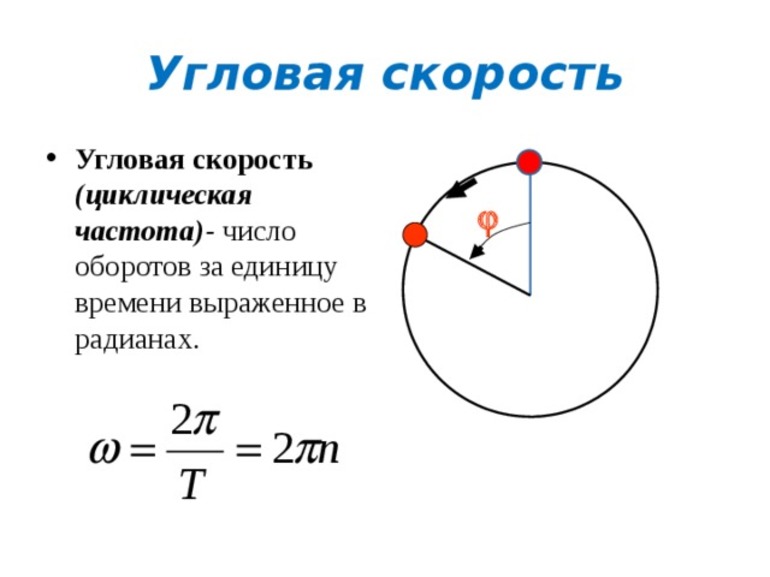
Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.
В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.
Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).
Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.
Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.

Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Использование онлайн-калькулятора

В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.
Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.
Из множества сайтов можно выделить три наиболее популярных среди потребителей:
- Справочный портал «Калькулятор».
- Allcalc.
- Fxyz.
Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.
Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.
Сергей Феликсович Савельев
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Понятие скорости
Когда мы сравниваем движение каких-либо тел, то говорим, что одни тела двигаются быстрее, а другие – медленнее. Такую простую терминологию мы используем в повседневной жизни, говоря, например, о движении транспорта. В физике быстрота движения тел характеризуется определенной величиной. Эта величина называется скоростью. Общее определение скорости (в случае, если тело движется равномерно):
Определение 1
Скорость при равномерном движении тела – это физическая величина, показывающая, какой путь прошло тело за единицу времени.
Под равномерным движением тела подразумевается, что скорость тела постоянна. Формула нахождения скорости: $v=frac{s}{t}$, $s$ – это пройденный телом путь (то есть длина линии), $t$ – время (то есть промежуток времени, за который пройден путь).
Согласно международной системе СИ, единица измерения линейной скорости является производной от двух основных единиц – метра и секунды, то есть измеряется в метрах в секунду (м/с). Это значит, что под единицей скорости понимается скорость такого равномерного движения, при котором путь в один метр тело проходит за одну секунду.
Также скорость часто измеряют в км/ч, км/с, см/с.
Рассмотрим простой пример задачи на вычисление скорости.
Пример 1
Задача. Двигаясь равномерно, поезд за 4 ч проходит 219 км. Найти его скорость движения.
Решение. $v=frac{219 км}{4 ч}=54,75frac{км}{ч}$. Переведём километры в метры и часы в секунды: $54,75frac{км}{ч}=frac{54750 м}{3600c}approx 15,2frac{м}{c}$.
Ответ. $54,75frac{км}{ч}$ или $15,2frac{м}{c}$.
Из примера мы видим, что числовое значение скорости отличается в зависимости от выбранной единицы измерения.
Кроме числового значения, скорость имеет направление. Числовое значение величины в физике называют модулем. Когда у физической величины есть и направление, то эту величину называют векторной. То есть скорость – это векторная физическая величина.
«Формула для расчета линейной скорости» 👇
На письме модуль скорости обозначается $v$, а вектор скорости – $vec v$.
В свою очередь, такие величины как путь, время, длина и другие характеризуются только числовым значением. Тогда говорят, что это скалярные физические величины.
В случае, когда движение является неравномерным, используют понятие средней скорости. Формула средней скорости: $v_{ср}=frac{s}{t}$, где $s$ – это весь пройденный телом путь, $t$ – всё время движения. Рассмотрим пример задачи на среднюю скорость, чтобы понять разницу.
Пример 2
Задача. Некоторый транспорт за 2,5 часа преодолевает путь в 213 км. Найти его $v_{ср}$.
Решение. $v_{ср}=frac{213 км}{2,5 ч}= 85,2 frac{км}{ч}=frac{213000 м}{9000 с}approx 23,7frac{м}{с} $.
Ответ. $85,2 frac{км}{ч}$ или $23,7frac{м}{с} $.
Линейная скорость
Определение линейной скорости относится к разделу физики о механике и подразделу о кинематике в рамках вопроса движения по окружности. В измерении скорости движения по окружности выделяют угловую скорость и линейную скорость.
Дадим определение линейной скорости.
Определение 2
Линейная скорость $V$ – это физическая величина, показывающая путь, который прошло тело за единицу времени.
Формула линейной скорости:
$V=frac{S}{t}$, где $S$ – путь, $t$ – время, за которое точка прошла путь $S$.
Также существует иной вариант этой формулы:
$V=frac{l}{t}$, где $l$ – путь, $t$ – время, за которое точка прошла по дуге $l$.
В некоторых учебниках линейная скорость также обозначается маленькой буквой $v$.
Есть ещё одна формула, по которой можно найти линейную скорость:
$v=frac{2pi R}{T}$.
$2pi$ соответствует полной окружности (360 угловым градусам).
$vec V$ направленена по касательной к тракетории.
Связь между линейной и угловой скоростями
Чтобы проследить связь между линейной и угловой скоростями, нужно дать определение угловой скорости.
Определение 3
Угловая скорость – это величина, которая равна отношению угла поворота отрезка, соединяющего точку с центром окружности, к промежутку времени, за который этот поворот произошёл.
Записывается эта формула следующим образом:
$omega = frac{phi}{t}$, где $phi$ – это угловое перемещение (или угол поворота, измеряется в радианах), $t$ – промежуток времени, за которое соврешено угловое перемещение.
В системе СИ угловая скорость измеряется в рад/с.
Угловую скорость также называют циклической частотой вращения, потому что при вращении твёрдого тела угловая скорость всех его точек одинакова.
Связь между $V$ и $omega$: $V=omega R$.
Эта формула выводится из определения модуля центростремительного ускорения.
Определение 4
Центростремительное ускорение $a$ – это ускорение точки при равномерном движении по окружности.
$a=frac{V^2}{R}$ и $a=omega^2 R$.
С помощью элементарных математических действий из этих двух формул выводится связь между $V$ и $omega$.
Таким образом, в данной статье мы разобрали следующие понятия:
- скорость;
- линейная и угловая скорость;
- связь между линейной и угловой скоростями.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Содержание:
- Определение и формула скорости
- Скорость в разных системах координат
- Частные случаи формул для вычисления скорости
- Единицы измерения скорости
- Примеры решения задач
Определение и формула скорости
Определение
Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора
$bar{r}$ точки по времени (t). Обозначают скорость обычно буквой v.
Это векторная величина. Математически определение вектора мгновенной скорости записывается как:
$$bar{v}=frac{d bar{r}}{d t}=dot{bar{r}}(1)$$
Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения.
Модуль скорости можно определить как первую производную от длины пути (s) по времени:
$$v=frac{d s}{d t}=dot{s}(2)$$
Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.
Скорость в разных системах координат
Проекции скорости на оси декартовой системы координат запишутся как:
$$v_{x}=dot{x} ; v_{y}=dot{y} ; v_{z}=dot{z}(3)$$
Следовательно, вектор скоростив декартовых координатах можно представить:
$$bar{v}=dot{x} bar{i}+dot{y} bar{j}+dot{z} bar{k}(4)$$
где $bar{i}, bar{j}, bar{k}$ единичные орты. При этом модуль вектора скорости находят при помощи формулы:
$$v=sqrt{(dot{x})^{2}+(dot{y})^{2}+(dot{z})^{2}}(5)$$
В цилиндрических координатах модуль скорости вычисляют при помощи формулы:
$$v=sqrt{(dot{rho})^{2}+(rho dot{varphi})^{2}+(dot{z})^{2}}(6)$$
в сферической системе координат:
$$v=sqrt{(r)^{2}+(r dot{theta})^{2}+(r dot{varphi} sin theta)^{2}}(7)$$
Частные случаи формул для вычисления скорости
Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const).
При равномерном движении скорость можно вычислить, применяя формулу:
$$v=frac{s}{t}(8)$$
где s– длина пути, t – время, за которое материальная точка преодолела путь s.
При ускоренном движении скорость можно найти как:
$$bar{v}=int_{t_{1}}^{t_{2}} bar{a} d t(9)$$
где $bar{a}$ – ускорение точки,
$t_{1} leq t leq t_{2}$ – отрезок времени, в течение которого рассматривается скорость.
Если движение является равнопеременным, то применяется следующая формула для вычисления скорости:
$$bar{v}=bar{v}_{0}+bar{a} t$$
где $bar{v}_0$ – начальная скорость движения,
$bar{a} = const$ .
Единицы измерения скорости
Основной единицей измерения скорости в системе СИ является: [v]=м/с2
В СГС: [v]=см/с2
Примеры решения задач
Пример
Задание. Движение материальной точки А задано уравнением:
$x=2 t^{2}-4 t^{3}$ . Точка начала свое движение при
t0=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.
Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для
этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:
$$v=frac{d x}{d t}=4 t-12 t^{2}(1.1)$$
Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент
времении сравним результат с нулем:
$$v(t=0,5)=4 cdot 0,5-12(0,5)^{2}=-1 lt 0$$
Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.
Ответ. Против оси X.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Скорость материальной точки является функцией от времени вида:
$$v=10left(1-frac{t}{5}right)$$
где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии
10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.
Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:
$$x=int_{0}^{t} v d t=int_{0}^{t} 10left(1-frac{t}{5}right) d t=10 t-frac{10 t^{2}}{2 cdot 5}=10 t-t^{2}(2.1)$$
Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:
$$x=10 cdot 10-(10)^{2}=0(m)$$
Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат
приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:
$$
begin{array}{c}
10 t-t^{2}=10(2.2) \
t_{1}=5+sqrt{15} approx 8,8(c) ; t_{2}=5-sqrt{15} approx 1,13(c)
end{array}
$$
Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:
$$10 t-t^{2}=-10(2.3)$$
При решении уравнения (2.3) нам подойдет корень равный:
$$t_{3}=5+6=11 (c)$$
Ответ. 1) $x=0 mathrm{~m}$ 2) $t_{1}=8,8 mathrm{c}, t_{2}=1,13 c, t_{3}=11 c$
Читать дальше: Формула средней скорости.
| Скорость | |
|---|---|
 |
|
| Размерность | LT−1 |
| Единицы измерения | |
| СИ | м/с |
| СГС | см/с |
| Примечания | |
| вектор |
| Классическая механика |
|---|
| История… |
|
Фундаментальные понятия
|
|
Формулировки
|
|
Разделы
|
|
Учёные
|
| См. также: Портал:Физика |
Ско́рость (стандартное обозначение: 
В русском языке этим же словом называют и скалярную величину — либо модуль вектора скорости, либо алгебраическую скорость точки, то есть проекцию вектора 
Термин «скорость» используют в науке и в широком смысле, понимая под ним быстроту изменения какой-либо величины (не обязательно радиус-вектора) в зависимости от другой (чаще подразумеваются изменения во времени, но также в пространстве или любой другой). Так, например, говорят об угловой скорости, скорости изменения температуры, скорости химической реакции, групповой скорости, скорости соединения и т. д. Математически «быстрота изменения» характеризуется производной рассматриваемой величины.
Понятие «скорость» в классической механике[править | править код]
Случай материальной точки[править | править код]
Вектор скорости (мгновенной скорости) материальной точки в каждый момент времени определяется как производная по времени радиус-вектора 
где 



Пройденный точкой путь 


.
Когда алгебраическая скорость точки всё время неотрицательна, путь совпадает с приращением дуговой координаты за время от 




Иллюстрация средней и мгновенной скорости
Если алгебраическая скорость точки не меняется с течением времени (или, что то же самое, модуль скорости постоянен), то движение точки называется[5] равномерным (алгебраическое касательное ускорение 
Предположим, что 


В общем же случае аналогичные отношения
и
определяют соответственно среднюю скорость точки[6] и её среднюю алгебраическую скорость; если термином «средняя скорость» пользуются, то о величинах 

Различие между двумя введёнными выше понятиями средней скорости состоит в следующем. Во-первых, 

Случай тела конечных размеров[править | править код]
Для тела протяжённых размеров понятие «скорости» (тела как такового, а не одной из его точек) не может быть определено; исключение составляет случай мгновенно-поступательного движения. Говорят, что абсолютно твёрдое тело совершает мгновенно-поступательное движение, если в данный момент времени скорости всех составляющих его точек равны[7]; тогда можно, разумеется, положить скорость тела равной скорости любой из его точек. Так, например, равны скорости всех точек кабинки колеса обозрения (если, конечно, пренебречь колебаниями кабинки).
В общем же случае скорости точек, образующих твёрдое тело, не равны между собой. Так, например, для катящегося без проскальзывания колеса модули скоростей точек на ободе относительно дороги принимают значения от нуля (в точке касания с дорогой) до удвоенного значения скорости центра колеса (в точке, диаметрально противоположной точке касания). Распределение скоростей точек абсолютно твёрдого тела описывается кинематической формулой Эйлера.
Начальная скорость[править | править код]
Начальная скорость (

Истолкование 
![{displaystyle t=[-Delta tldots 0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22025d25103c33e678f3cfa5e32d3266f03d9d5b)


Запись скорости в разных системах координат[править | править код]
В декартовых координатах[править | править код]
В прямоугольной декартовой системе координат[9]:
При этом 
Таким образом, компоненты вектора скорости — это скорости изменения соответствующих координат материальной точки[9]:
В цилиндрических координатах[править | править код]
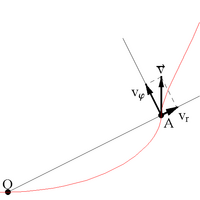
Скорость в полярных координатах
В цилиндрических координатах 


В сферических координатах[править | править код]
В сферических координатах 
Для описания плоского движения иногда используются полярные координаты, которые можно рассматривать как частный случай цилиндрических (c 

Физическая и координатная скорости[править | править код]
В аналитической механике вышеприведённые и другие криволинейные координаты играют роль обобщённых координат; изменение положение тела описывается их зависимостью от времени. Производные от координат тела по времени при этом называются координатными скоростями (они могут иметь размерность отличную от м/c). Физической же скоростью является производная радиус-вектора по времени, а её составляющие в каждом случае задаются всем стоящим перед соответствующим ортом выражением.
Некоторые связанные со скоростью понятия[править | править код]
Ряд величин в классической механике выражается через скорость.
Импульс, или количество движения, — это мера механического движения точки, которая определяется как произведение массы точки на её скорость
.
Импульс является векторной величиной, его направление совпадает с направлением скорости. Для замкнутой системы выполняется закон сохранения импульса.
От скорости также зависит кинетическая энергия механической системы. Для абсолютно твёрдого тела полную кинетическую энергию можно записать в виде суммы кинетической энергии поступательного и вращательного движения[10][11]:
где 



Изменение скорости во времени характеризуется ускорением. Ускорение отражает изменение скорости как по величине (тангенциальное ускорение), так и по направлению (центростремительное ускорение)[12]:
где 
Преобразования Галилея и Лоренца для скорости[править | править код]
В классической механике Ньютона скорости преобразуются при переходе из одной инерциальной системы отсчёта в другую согласно преобразованиям Галилея. Если скорость тела в системе отсчёта 





Для скоростей, близких к скорости света, преобразования Галилея становятся несправедливы. При переходе из системы 

в предположении, что скорость 


Скорость в релятивистской механике[править | править код]
Четырёхмерная скорость[править | править код]
Одним из обобщений понятия скорости является четырёхмерная скорость (скорость в релятивистской механике[9]). В специальной теории относительности каждому событию ставится в соответствие точка пространства Минковского, три координаты которого представляют собой декартовы координаты трёхмерного евклидова пространства, а четвёртая ― временну́ю координату 


Четырёхмерный вектор скорости является времениподобным вектором, то есть лежит внутри светового конуса[9].
Существует также понятие четырёхимпульс, временна́я компонента которого равна 

,
где 
Понятие «быстрота»[править | править код]
В релятивистской механике угол между касательной к мировой линии частицы и осью времени в базовой системе отсчёта носит название быстроты (обозначается 
где 
где 


Некоторые скорости[править | править код]
Космические скорости[править | править код]

Анализ первой и второй космической скорости по Исааку Ньютону. Снаряды A и B падают на Землю. Снаряд C выходит на круговую орбиту, D — на эллиптическую. Снаряд E улетает в открытый космос
Небесная механика изучает поведение тел Солнечной системы и других небесных тел. Движение искусственных космических тел изучается в астродинамике. При этом рассматривается несколько вариантов движения тел, для каждого из которых необходимо придание определённой скорости. Для вывода спутника на круговую орбиту ему необходимо придать первую космическую скорость (например, искусственный спутник Земли); преодолеть гравитационное притяжение позволит вторая космическая скорость (например, объект запущенный с Земли, вышедший за её орбиту, но находящийся в Солнечной системе); третья космическая скорость нужна чтобы покинуть звёздную систему, преодолев притяжение звезды (например, объект запущенный с Земли, вышедший за её орбиту и за пределы Солнечной системы); четвёртая космическая скорость позволит покинуть галактику.
В небесной механике под орбитальной скоростью понимают скорость вращения тела вокруг барицентра системы.
Скорости распространения волн[править | править код]
Скорость звука[править | править код]
Скорость звука — скорость распространения упругих волн в среде, определяется упругостью и плотностью среды. Скорость звука не является постоянной величиной и зависит от температуры (в газах), от направления распространения волны (в монокристаллах). При заданных внешних условиях обычно не зависит от частоты волны и её амплитуды. В тех случаях, когда это не выполняется и скорость звука зависит от частоты, говорят о дисперсии звука. Впервые измерена Уильямом Дерхамом. Как правило, в газах скорость звука меньше, чем в жидкостях, а в жидкостях скорость звука меньше, чем в твёрдых телах, поэтому при сжижении газа скорость звука возрастает.
Отношение скорости течения в данной точке газового потока к местной скорости распространения звука в движущейся среде называется числом Маха по имени австрийского учёного Эрнста Маха. Упрощённо, скорость, соответствующая 1 Маху при давлении в 1 атм (у земли на уровне моря), будет равна скорости звука в воздухе. Движение аппаратов со скоростью, сравнимой со скоростью звука, сопровождается рядом явлений, которые называются звуковой барьер. Скорости от 1,2 до 5 Махов называются сверхзвуковыми, скорости выше 5 Махов — гиперзвуковыми.
Скорость света[править | править код]
![]()
Время распространения светового луча в масштабной модели Земля-Луна. Для преодоления расстояния от поверхности Земли до поверхности Луны свету требуется 1,255 секунды.
Скорость света в вакууме — абсолютная величина скорости распространения электромагнитных волн в вакууме. Традиционно обозначается латинской буквой «c» (произносится как [це]). Скорость света в вакууме — фундаментальная постоянная, не зависящая от выбора инерциальной системы отсчёта (ИСО). Она относится к фундаментальным физическим постоянным, которые характеризуют не просто отдельные тела или поля, а свойства пространства-времени в целом. По современным представлениям, скорость света в вакууме — предельная скорость движения частиц и распространения взаимодействий.
Наиболее точное измерение скорости света 299 792 458 ± 1,2 м/с на основе эталонного метра было проведено в 1975 году. Теперь ввиду современного определения метра скорость света считается равной точно 299792458 м/с[14].
Скорость гравитации[править | править код]
Скорость гравитации — скорость распространения гравитационных воздействий, возмущений и волн. До сих пор остаётся не определённой экспериментально, но согласно общей теории относительности должна совпадать со скоростью света.
Единицы измерения скорости[править | править код]
Линейная скорость:
- Метр в секунду, (м/с), производная единица системы СИ
- Километр в час, (км/ч)
- узел (морская миля в час)
- Число Маха, 1 Мах равен скорости звука; Max n в n раз быстрее. Как единица, зависящая от конкретных условий, должна дополнительно определяться.
- Скорость света в вакууме (обозначается c)
Угловая скорость:
- Радианы в секунду, принята в системах СИ и СГС. Физическая размерность 1/с.
- Обороты в секунду (в технике)
- градусы в секунду, грады в секунду
Соотношения между единицами скорости[править | править код]
- 1 м/с = 3,6 км/ч
- 1 узел = 1,852 км/ч = 0,514 м/c
- Мах 1 ~ 330 м/c ~ 1200 км/ч (зависит от условий, в которых находится воздух)
- c = 299 792 458 м/c
Исторический очерк[править | править код]
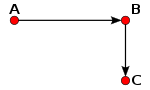
Две стадии движения брошенного тела по теории Авиценны: отрезок АВ — период «насильственного стремления», отрезок ВС — период «естественного стремления» (падение вертикально вниз)
Автолик из Питаны в IV веке до н. э. определил равномерное движение так: «О точке говорится, что она равномерно перемещается, если в равные времена она проходит равные и одинаковые величины». Несмотря на то, что в определении участвовали путь и время, их отношение считалось бессмысленным[15], так как сравнивать можно было только однородные величины и скорость движения являлась чисто качественным, но не количественным понятием[16]. Живший в то же время Аристотель делил движение на «естественное», когда тело стремится занять своё естественное положение, и «насильственное», происходящее под действием силы. В случае «насильственного» движения произведение величины «двигателя» и времени движения равно произведению величины «движимого» и пройденного пути, что соответствует формуле 

начале XIII века. Герард написал трактат «О движении» — первый европейский трактат по кинематике — в котором сформулировал идею определения средней скорости движения тела (при вращении прямая, параллельная оси вращения, движется «одинаково с любой своей точкой», а радиус — «одинаково со своей серединой»)[18].
В 1328 году увидел свет «Трактат о пропорциях или о пропорциях скоростей при движении» Томаса Брадвардина, в котором он нашёл несоответствие в физике Аристотеля и связи скорости с действующими силами. Брадвардин заметил, что по словесной формуле Аристотеля если движущая сила равна сопротивлению, то скорость равна 1, в то время как она должна быть равна 0. Он также представил свою формулу изменения скорости, которая хоть и была не обоснована с физической точки зрения, но представляла собой первую функциональную зависимость скорости от причин движения. Брадвардин называл скорость «количеством движения»[19]. Уильям Хейтсбери, в трактате «О местном движении» ввёл понятие мгновенной скорости. В 1330—1340 годах он и другие ученики Брадвардина доказали так называемое «мертонское правило», которое означает равенство пути при равноускоренном движении и равномерном движении со средней скоростью[20].
Всякая широта движения, униформно приобретаемая или теряемая, соответствует своему среднему градусу, так что столько же в точности будет пройдено благодаря этой приобретаемой широте, сколько и благодаря среднему градусу, если бы тело двигалось всё время с этим средним градусом.
— «Мертонское правило» в формулировке Суайнсхеда[20]
В XIV веке Жан Буридан ввёл понятие импетуса[21], благодаря чему была определена величина изменения скорости — ускорение. Николай Орем, ученик Буридана, предложил считать, что благодаря импетусу ускорение остаётся постоянным (а не скорость, как полагал сам Буридан), предвосхитив, таким образом, второй закон Ньютона[22]. Орем также использовал графическое представление движения. В «Трактате о конфигурации качеств и движения» (1350) он предложил изображать отрезками перпендикулярных прямых количество и качество движения (время и скорость), иными словами, он нарисовал график изменения скорости в зависимости от времени[23].
По мнению Тартальи, только вертикальное падение тела является «естественным» движением, а все остальные — «насильственные», при этом у первого типа скорость постоянно возрастает, а у второго — убывает. Два этих типа движения не могут проистекать одновременно. Тарталья считал, что «насильственные» движения вызваны ударом, результатом которого является «эффект», определяемый скоростью[24]. С критикой работ Аристотеля и Тартальи выступал Бенедетти, который вслед за Оремом пользовался понятиями импетуса и ускорения[25].
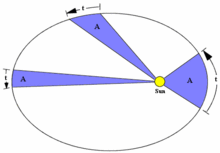
В 1609 году в работе «Новая астрономия» Кеплер сформулировал закон площадей, согласно которому секторная скорость планеты (площадь, описываемая отрезком планета — Солнце, за единицу времени) постоянна[26]. В «Началах философии» Декарт сформулировал закон сохранения количества движения, которое в его понимании есть произведение количества материи на скорость[27], при этом Декарт не принимал во внимание тот факт, что количество движения имеет не только величину, но и направление[28]. В дальнейшем понятие «количество движения» развивал Гук, который понимал его как «степень скорости, присущей в определённом количестве вещества»[29]. Гюйгенс, Валлис и Рен добавили к этому определению направление. В таком виде во второй половине XVII века количество движения стало важным понятием в динамике, в частности в работах Ньютона и Лейбница[30]. При этом Ньютон не определял в своих работах понятие скорости[31]. По-видимому, первая попытка явного определения скорости была сделана Валлисом в его трактате «Механика или геометрический трактат о движении» (1669—1671): «Скорость есть свойство движения, отражающееся в сравнении длины и времени; а именно, она определяет, какая длина в какое время проходится»[32].
В XVII веке были заложены основы математического анализа, а именно интегрального и дифференциального исчисления. В отличие от геометрических построений Лейбница, теория «флюксий» Ньютона строится на потребностях механики и имеет в своём основании понятие скорости. В своей теории Ньютон рассматривает переменную величину «флюенту» и её скорость изменения — «флюксию»[33].
Скорости в природе и технике[править | править код]
Основной источник: [34]
| Метры в секунду | |
|---|---|
| Скорость улитки | 
|
| Скорость черепахи | 
|
| Средняя скорость здорового человека (произвольный темп) | 
|
| Рекорд скорости человека в ходьбе на 50 км |  ( ( ) )
|
| Рекорд скорости человека в беге на дистанции 100 м |  ( ( ) )
|
| Скорость гепарда | 
|
| Максимальная скорость полёта сокола | 
|
| Максимальная скорость локомотива на железной дороге | 
|
| Максимальная скорость автомобиля |  [35] [35]
|
| Средняя скорость молекулы азота при температуре 0 °C | 
|
| Максимальная скорость пассажирского реактивного самолёта | 
|
| Скорость движения Луны по орбите вокруг Земли | 
|
| Скорость искусственного спутника Земли | 
|
| Скорость движения Земли по орбите вокруг Солнца | 
|
| Скорость движения Солнца по орбите вокруг центра Галактики | 
|
| Скорость электронов в кинескопе телевизора | 
|
| Скорость движения самых далёких галактик | 
|
| Максимальная скорость протонов в Большом адронном коллайдере | 299 792 455 |
| Скорость частицы Oh-My-God | 299792457,9999999999999985310169558 |
| Скорость безмассовых частиц (фотонов, глюонов, гравитонов) | 299 792 458 |
| Скорость тахионов и сверхбрадионов | > 299792458 |
Скорости движения живых существ[править | править код]
- Сапсан (самое быстрое животное): самая высокая зарегистрированная скорость — 389 км/ч[36];
- Гепард (самое быстрое наземное животное): самая высокая зарегистрированная скорость — 98 км/ч[37];
- Меч-рыба: от 100 до 130 км в час[37];
- Чёрный марлин: самая высокая зарегистрированная скорость — 105 км/ч[36];
- Вилорогая антилопа: самая высокая зарегистрированная скорость — 88,5 км/ч[36];
- Лошадь (американский квортерхорс): 88 км/ч[36];
- Человек: самая высокая зарегистрированная скорость — 44,72 км/ч (Усэйн Болт)[37].
Рекорды скорости транспортных средств[править | править код]
Самый быстрый рукотворный объект — Parker Solar Probe, 150 км/с (относительно Солнца) в 2021 году[38].
Абсолютный рекорд скорости в воздухе был поставлен в 1976 году американским самолетом-разведчиком Lockheed SR-71 Blackbird — 3529,56 км/ч.
Рекорд скорости на земле был установлен в 2003 году на ракетных санях и составил 10 325 км/ч или 2868 м/с (по другим данным, 10 430 км/ч)[39]
Самая высокая скорость на наземном управляемом транспортном средстве была достигнута на реактивном автомобиле Thrust SSC в 1997 году — 1228 км/ч.
Рекорд скорости на воде был поставлен в 1978 году австралийским судном с реактивным газотурбинным двигателем Spirit of Australia[en] — 511,11 км/ч[40]
См. также[править | править код]
- Кинематика
Примечания[править | править код]
- ↑ Маркеев, 1990, с. 15.
- ↑ Старжинский, 1980, с. 154.
- ↑ Маркеев, 1990, с. 15—17.
- ↑ Старжинский, 1980, с. 154—155.
- ↑ Старжинский, 1980, с. 163.
- ↑ Старжинский, 1980, с. 152.
- ↑ Маркеев, 1990, с. 46—47.
- ↑ См. Всегда ли начальная скорость равна нулю? в справочнике «Студворк».
- ↑ 1 2 3 4 5 6 7 8 9 Скорость // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- ↑ Главный редактор А. М. Прохоров. Кинетическая энергия // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
- ↑ Главный редактор А. М. Прохоров. Вращательное движение // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
- ↑ Главный редактор А. М. Прохоров. Ускорение // Физический энциклопедический словарь.. — 1983. Физическая энциклопедия
- ↑ Главный редактор А. М. Прохоров. Импульс // Физический энциклопедический словарь. — Советская энциклопедия. — М., 1983. Физическая энциклопедия
- ↑ Определение метра Архивная копия от 26 июня 2013 на Wayback Machine (англ.) Резолюция 1 XVII Генеральной конференции по мерам и весам (1983)
- ↑ 1 2 Яковлев, 2001, с. 21.
- ↑ Яковлев, 2001, с. 34.
- ↑ Яковлев, 2001, с. 29.
- ↑ Яковлев, 2001, с. 31—32.
- ↑ Яковлев, 2001, с. 32—34.
- ↑ 1 2 Яковлев, 2001, с. 35.
- ↑ Яковлев, 2001, с. 35—36.
- ↑ Яковлев, 2001, с. 37.
- ↑ Яковлев, 2001, с. 37—38.
- ↑ Яковлев, 2001, с. 43.
- ↑ Яковлев, 2001, с. 45.
- ↑ Яковлев, 2001, с. 51—52.
- ↑ Яковлев, 2001, с. 59.
- ↑ Яковлев, 2001, с. 68.
- ↑ Яковлев, 2001, с. 77.
- ↑ Яковлев, 2001, с. 91.
- ↑ Яковлев, 2001, с. 96.
- ↑ Яковлев, 2001, с. 72—73.
- ↑ Яковлев, 2001, с. 64—66.
- ↑ Кабардин О.Ф., Орлов В.А., Пономарёва А.В. Факультативный курс физики. 8 класс. — М.: Просвещение, 1985. — Тираж 143 500 экз. — С. 44
- ↑ FIA World Land Speed Records (англ.). Federation Internationale de l’Automobile (10 июня 2012). Дата обращения: 3 декабря 2020. Архивировано 31 марта 2019 года.
- ↑ 1 2 3 4 12 самых быстрых животных в мире. Дата обращения: 17 июня 2022. Архивировано 29 июля 2021 года.
- ↑ 1 2 3 12 самых быстрых животных в мире. Дата обращения: 17 июня 2022. Архивировано 22 сентября 2020 года.
- ↑ Самый быстрый объект, созданный человеком. Зонд Parker Solar Probe развил скорость около 150 км/с. Дата обращения: 17 июня 2022. Архивировано 17 мая 2021 года.
- ↑ Test sets world land speed record. www.af.mil. Дата обращения: 19 апреля 2016.
- ↑ Назло рекордам: почему люди не хотят передвигаться очень быстро
Литература[править | править код]
- Маркеев А. П. Теоретическая механика. — М.: Наука, 1990. — 416 с. — ISBN 5-02-014016-3.
- Старжинский В. М. Теоретическая механика. — М.: Наука, 1980. — 464 с.
- Яковлев В. И. Предыстория аналитической механики. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — 328 с. — ISBN 5-93972-063-3.
Формула скорости
Определение и формула скорости
Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора $bar$ точки по времени (t). Обозначают скорость обычно буквой v. Это векторная величина. Математически определение вектора мгновенной скорости записывается как:
Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения. Модуль скорости можно определить как первую производную от длины пути (s) по времени:
Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.
Скорость в разных системах координат
Проекции скорости на оси декартовой системы координат запишутся как:
Следовательно, вектор скоростив декартовых координатах можно представить:
где $bar, bar, bar$ единичные орты. При этом модуль вектора скорости находят при помощи формулы:
В цилиндрических координатах модуль скорости вычисляют при помощи формулы:
в сферической системе координат:
Частные случаи формул для вычисления скорости
Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const). При равномерном движении скорость можно вычислить, применяя формулу:
где s– длина пути, t – время, за которое материальная точка преодолела путь s.
При ускоренном движении скорость можно найти как:
Если движение является равнопеременным, то применяется следующая формула для вычисления скорости:
где $bar_0$ – начальная скорость движения, $bar = const$ .
Единицы измерения скорости
Основной единицей измерения скорости в системе СИ является: [v]=м/с 2
Примеры решения задач
Задание. Движение материальной точки А задано уравнением: $x=2 t^<2>-4 t^<3>$ . Точка начала свое движение при t0=0 c.Как будет двигаться рассматриваемая точка по отношению к оси X в момент времени t=0,5 с.

Решение. Найдем уравнение, которое будет задавать скорость рассматриваемой материальной точки, для этого от функции x=x(t), которая задана в условиях задачи, возьмем первую производную по времени, получим:
Для определения направления движения подставим в полученную нами функцию для скорости v=v(t) в (1.1) указанный в условии момент времении сравним результат с нулем:
Так как мы получили, что скорость в указанный момент времени отрицательна, следовательно, материальная точка движется против оси X.
Ответ. Против оси X.

Задание. Скорость материальной точки является функцией от времени вида:
где скорость в м/с, время в c. Какова координата точки в момент времени равный 10 с, в какой момент времени точка будет на расстоянии 10 м от начала координат? Считайте, что при t=0 c точка началадвижение из начала координат по оси X.
Решение. Точка движется по оси X, cвязь координаты x и скорости движения определена формулой:
Для ответа на первый вопрос задачи подставим в выражение (2.1) время t=10 c, имеем:
Для того чтобы определить в какой момент времени точка будет находиться на расстоянии 10 м от начала координат приравняем выражение (2.1) к 10 и решим, полученное квадратное уравнение:
$$ begin 10 t-t^<2>=10(2.2) \ t_<1>=5+sqrt <15>approx 8,8(c) ; t_<2>=5-sqrt <15>approx 1,13(c) end $$
Рассмотрим второй вариант нахождения точки на расстоянии 10 м от начала координат, когда x=-10. Решим квадратное уравнение:
При решении уравнения (2.3) нам подойдет корень равный:
Ответ. 1) $x=0 mathrm<
m>$ 2) $t_<1>=8,8 mathrm, t_<2>=1,13 c, t_<3>=11 c$
Формула скорости — обозначение, единицы измерения и примеры нахождения
Довольно часто в точных науках приходится сталкиваться с понятием скорость. Формула, дающаяся в школе на уроке математики, справедлива лишь для частного случая, при котором перемещение остаётся всегда постоянным. По сути, термин обозначает быстроту изменения чего-либо. Существует несколько видов движения и методов расчета.

Понятие и основные термины
Под скоростью понимается величина, определяющая быстроту и направление перемещения материальной точки в выбранной системе отсчёта. Термин широко применяется в математике, физике, химии. Так, с его помощью описывают реакции, изменения температуры, передвижение тел, используют как производную рассматриваемой величины.
Слово «скорость» произошло от латинского «velocitas», обозначающее движение. В качестве единицы измерения, согласно Международной системе единиц (СИ), для неё выбран метр, делённый на секунду (м/с). Обозначается скорость буквой V, вне зависимости от науки, в которой её применяют. Простейшая формула, с помощью которой определяют величину, выглядит следующим образом: V = S: t. Где:
- S — расстояние (путь), пройденное материальной точкой или телом (м);
- T — время за которое она преодолела путь (с).

Это обобщённое уравнение, но в то же время позволяющее получить представление о понятии. Часто это неравенство называют уравнением пути. Формула используется для вычисления только в том случае, если движение не изменяется на всём исследуемом участке.
Впервые с выражением знакомят учащихся на уроках математики в пятом классе. Учитель предлагает научиться решать простые задачи на нахождение характеристики при известной длине пройденного пути и потраченного на это времени. Например, автомобиль за четыре часа проехал 16 километров. Необходимо найти, с какой скоростью он двигался. Решение задачи сводится к двум действиям. В первом все заданные величины переводятся в систему СИ: 4 часа = 240 минут = 10240 секунд; 16 километров = 16000 метров. Во втором действии данные подставляют в формулу и вычисляют ответ: V = 16000/10240 = 1,6 м/с.
Но, помимо равномерного движения, то есть при котором скорость является константой, есть ещё и другие виды перемещений. Использовать обобщённое уравнение для них нельзя. Для каждого вида движения применяется своя формула. Существующую скорость разделяют на следующие виды:

- неравномерную;
- среднюю;
- равномерно-переменную;
- поступательную;
- вращательную;
- ускоренную.
Равноускоренное движение
Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.

Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.
В произвольно взятой точке скорость перемещения равна ускорению свободного падения.
Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:
- V0 — начальная скорость;
- A — ускорение (имеет постоянное значение);
- t — время движения.
Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.
Если на оси времени выделить промежуток Δt, то можно предположить, что движение будет равномерным и описываться некоторым параметром, равным мгновенному значению в середине отрезка. Эта моментальная величина является векторной. Она численно равна пределу, который пытается достигнуть скорость за промежуток времени, стремящийся к нулю. В физике это состояние описывается формулой мгновенной скорости: V = lim (Δ s/ Δ t) = r -1 (t). То есть, с математической точки зрения, это первая производная.
Исходя из этого можно утверждать, что движение Δs = v*Δt. Так как произведение ускорения на время определяется разницей V -V0, то верной будет запись: S = V0*t + A*t 2 /2 = (V 2 — V 2 0) /2*A.
Из этой формулы можно вывести выражение для нахождения конечной скорости материальной точки: V = (V 2 0 — 2* A * s) ½ . Если же в начальный момент V0 = 0, то формулу можно упростить до вида: V = (2* A * s) ½ .
Среднее значение
В кинематике для нахождения характеристики используется усреднённый параметр. Используют его при изучении движения материальной точки или любого физического тела. Для определения средней скорости используют две величины: скалярную и векторную. Первой обозначают путевое движение, а второй — перемещение.
Путевая скорость определяется как отношение расстояния пройденного тела ко времени, затраченному на его прохождение: V = Σs / Σt.

По сути, среднее значение находится как среднеарифметическое от всех скоростей, если рассматриваемая точка передвигалась одинаковые отрезки времени. В ином же случае найденная величина будет взвешенной среднеарифметической величиной.
Математически формулу средней скорости записывают так: V (t + Δ t) = Δ s/ Δ t = (s (t + Δ t) — s (t)) / Δ t. Учитывая, что Δs зависит от длины пути, которую преодолела точка за время Δt, верной будет запись: Δ s = s (t + Δt) — s (t). Если же затраченное время стремится к нулю, получится формула, совпадающая с выражением для нахождения мгновенной скорости.
Вектор материальной точки находится из отношения положения тела к отрезку времени: V (t + Δt) = Δr / Δt = (r (t + Δt) — r (t)) / Δt, где r — радиус-вектор. Когда тело выполняет равномерно-прямолинейное перемещение, то справедливым будет равенство: = V.
Например, мяч первую половину пути длиной 100 метров катился с одной скоростью в течение двадцати секунд, а вторую с другой и одну минуту. Необходимо вычислить среднюю скорость. Согласно формулам, интервал движения на первом участке пути будет равен: t1 = s/2*V1, а на втором t2 = s/2*V2. Решением задачи будет: Vср = s/(t1+t2) = s/(s/2*v1 + s/2*v2) = 2*V1*V2/(V1+V2) = 100/(20 +60) = 1,25 м/с.
Угловая скорость

Проявляется этот вид при вращении тела вокруг оси. Траектория представляет собой круговое движение. Основным параметром, учитывающимся при его нахождении, является угол поворота (f). Все элементарные угловые движения являются векторами. Обычный поворот равен углу вращения тела df за небольшой отрезок времени dt в противоположную сторону от хода часовой стрелки.
В математике формулу для нахождения углового параметра записывают как w = df/dt. Угловая скорость — аксиальная величина, располагающаяся вдоль мгновенной оси и совпадающая с поступательным вращением правого винта. Равномерное вращение, то есть движение, при котором происходит поворот на один и тот же угол, называют равномерным. Модуль угловой скорости определяют по формуле: w = f/t, где f — угол поворота, t — время, в течение которого происходило вращение. Учитывая, что Δf = 2p, формулу можно переписать до вида: w = 2p/T, то есть с использованием периода.
Существует связь между угловой скоростью и числом оборотов: w = 2*p*v. Это понятие используется для решения заданий при описании неравномерного вращения. Есть также выражение, связывающее линейную скорость с угловой: v = [w*R], где R — компонента, проведённая перпендикулярно к радиус-вектору. В качестве единицы измерения параметра используется радиан, делённый на секунду (рад/с).
Например, необходимо определить угловую скорость вариатора в тот момент, когда подвешенная масса пройдёт расстояние, равное 10 метрам. Радиус плеча составляет 40 сантиметров. В начальный момент подвес находится в состоянии покоя, а затем начинает опускаться с ускорением A = 0,04 м/с2.
Учитывая, что линейная скорость вариатора совпадает с движением груза по прямой, можно записать: V = (2*a*S)½. Должен получится ответ: V = (4*0,04*10)½ = 1,26 м/с. Угловую же скорость находят по формуле: w = v/R, так как R = 40 см = 0,4 м, то W = 1,26/0,4 = 3,15 рад/с.
Закон сложения
Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.

Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.
Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.
Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.
Использование онлайн-калькулятора

В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.
Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.
Из множества сайтов можно выделить три наиболее популярных среди потребителей:
Все они имеют интуитивно понятный интерфейс и, что примечательно, на своих страницах содержат таблицы всех формул, используемых для решения заданий, правильные условные обозначения и описания процессов вычисления.
Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.
Кинематика

Механика — это раздел физики, изучающий механическое движение тел.
Кинематика — это раздел механики, в котором изучается механическое движение тел без учета причин, вызывающих это движение.
Материальная точка — тело, обладающее массой, размерами которого в данной задаче можно пренебречь, если
- расстояние, которое проходит тело, много больше его размера;
- расстояние от данного тела до другого тела много больше его размера;
- тело движется поступательно.
Система отсчета — это тело отсчета, связанная с ним система координат и прибор для измерения времени.
Траектория — это линия, которую описывает тело при своем движении.
Путь — это скалярная величина, равная длине траектории.
Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением за данный промежуток времени.
Важно!
В процессе движения путь может только увеличиваться, а перемещение как увеличиваться, так и уменьшаться, например, когда тело поворачивает обратно.
При прямолинейном движении в одном направлении путь равен модулю перемещения, а при криволинейном — путь больше перемещения.
Перемещение на замкнутой траектории равно нулю.
Основная задача механики — определить положение тела в пространстве в любой момент времени.
Механическое движение и его виды
Механическое движение — это изменение положения тела в пространстве относительно других тел с течением времени.
Механическое движение может быть:
1. по характеру движения
- поступательным — это движение, при котором все точки тела движутся одинаково и любая прямая, мысленно проведенная в теле, остается параллельна сама себе;
- вращательным — это движение, при котором все точки твердого тела движутся по окружностям, расположенным в параллельных плоскостях;
- колебательным — это движение, которое повторяется в двух взаимно противоположных направлениях;
2. по виду траектории
- прямолинейным — это движение, траектория которого прямая линия;
- криволинейным — это движение, траектория которого кривая линия;
- равномерным — движение, при котором скорость тела с течением времени не изменяется;
- неравномерным — это движение, при котором скорость тела с течением времени изменяется;
- равноускоренным — это движение, при котором скорость тела увеличивается с течением времени на одну и ту же величину;
- равнозамедленным — это движение, при котором скорость тела уменьшается с течением времени на одну и ту же величину.
Относительность механического движения
Относительность движения — это зависимость характеристик механического движения от выбора системы отсчета.
Правило сложения перемещений
Перемещение тела относительно неподвижной системы отсчета равно векторной сумме перемещения тела относительно подвижной системы отсчета и перемещения подвижной системы отсчета относительно неподвижной системы отсчета:

где ( S ) — перемещение тела относительно неподвижной системы отсчета;
( S_1 ) — перемещение тела относительно подвижной системы отсчета;
( S_2 ) — перемещение подвижной системы отсчета относительно неподвижной системы отсчета.
Правило сложения скоростей
Скорость тела относительно неподвижной системы отсчета равна векторной сумме скорости тела относительно подвижной системы отсчета и скорости подвижной системы отсчета относительно неподвижной системы отсчета:

где ( v ) — скорость тела относительно неподвижной системы отсчета;
( v_1 ) — скорость тела относительно подвижной системы отсчета;
( v_2 ) — скорость подвижной системы отсчета относительно неподвижной системы отсчета.
Относительная скорость
Важно! Чтобы определить скорость одного тела относительно другого, надо мысленно остановить то тело, которое мы принимаем за тело отсчета, а к скорости оставшегося тела прибавить скорость остановленного, изменив направление его скорости на противоположное.
Пусть ( v_1 ) — скорость первого тела, а ( v_2 ) — скорость второго тела.
Определим скорость первого тела относительно второго ( v_ <12>) :

Определим скорость второго тела относительно первого ( v_ <21>) :

Следует помнить, что траектория движения тела и пройденный путь тоже относительны.
Если скорости направлены перпендикулярно друг к другу, то относительная скорость рассчитывается по теореме Пифагора:


Если скорости направлены под углом ( alpha ) друг к другу, то относительная скорость рассчитывается по теореме косинусов:


Скорость
Скорость — это векторная величина, характеризующая изменение перемещения данного тела относительно тела отсчета с течением времени.
Обозначение — ( v ) , единицы измерения — м/с (км/ч).

Средняя скорость — это векторная величина, равная отношению всего перемещения к промежутку времени, за которое это перемещение произошло:

Средняя путевая скорость — это скалярная величина, равная отношению всего пути, пройденного телом, к промежутку времени, за которое этот путь пройден:

Важно! Чтобы определить среднюю скорость на всем участке пути, надо время разделить на отдельные промежутки и все время представить в виде суммы этих промежутков.
Чтобы определить среднюю скорость за все время движения, надо путь разделить на отдельные участки и весь путь представить как сумму этих участков.
Мгновенная скорость — это скорость тела в данный момент времени или в данной точке траектории.
Мгновенная скорость направлена по касательной к траектории движения.
Ускорение
Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.
Обозначение — ( a ) , единица измерения — м/с 2 .
В векторном виде:

где ( v ) – конечная скорость; ( v_0 ) – начальная скорость;
( t ) – промежуток времени, за который произошло изменение скорости.
В проекциях на ось ОХ:


где ( a_n ) – нормальное ускорение, ( a_ <tau>) – тангенциальное ускорение.
Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.
Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если ( a_ <tau>) ≠ 0, ( a_n ) = 0, то тело движется по прямой;
если ( a_ <tau>) = 0, ( a_n ) = 0, ( v ) ≠ 0, то тело движется равномерно по прямой;
если ( a_ <tau>) = 0, ( a_n ) ≠ 0, тело движется равномерно по кривой;
если ( a_ <tau>) = 0, ( a_n ) = const, то тело движется равномерно по окружности;
если ( a_ <tau>) ≠ 0, ( a_n ) ≠ 0, то тело движется неравномерно по окружности.
Равномерное движение
Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.
Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)
График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ( t ) , тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ) , тело движется против оси ОХ.
Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)
График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью ( t ) , тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ( t ) , тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время ( t ) . Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ( x=x(t) ) .

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Прямолинейное равноускоренное движение
Прямолинейное равноускоренное движение – это движение по прямой, при котором тело движется с постоянным ускорением:

При движении с ускорением скорость может как увеличиваться, так и уменьшаться.
Скорость тела при равноускоренном движении рассчитывается по формуле:

При разгоне (в проекциях на ось ОХ):


При торможении (в проекциях на ось ОХ):


График ускорения (проекции ускорения) при равноускоренном движении представляет собой зависимость ускорения от времени:

График ускорения при равноускоренном движении – прямая, параллельная оси времени.
График 1 лежит над осью t, тело разгоняется, ( a_x ) > 0.
График 2 лежит под осью t, тело тормозит, ( a_x ) ( v_ <0x>) > 0, ( a_x ) > 0.

График 2 направлен вниз, тело движется равнозамедленно в положительном направлении оси ОХ, ( v_ <0x>) > 0, ( a_x ) ( v_ <0x>) ( a_x ) ( t_2-t_1 ) . Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).
Перемещение при равноускоренном движении рассчитывается по формулам:

Перемещение в ( n ) -ую секунду при равноускоренном движении рассчитывается по формуле:

Координата тела при равноускоренном движении рассчитывается по формуле:

Свободное падение (ускорение свободного падения)
Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.
Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).
Обозначение – ( g ) , единицы измерения – м/с 2 .
Важно! ( g ) = 9,8 м/с 2 , но при решении задач считается, что ( g ) = 10 м/с 2 .
Движение тела по вертикали
Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ( v_0 ) = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ( v ) = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально
Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали со скоростью ( v_0=v_ <0x>) ;
- равноускоренного движения по вертикали с ускорением свободного падения ( g ) и без начальной скорости ( v_<0y>=0 ) .



Скорость тела в любой момент времени:


Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)
Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:
- равномерного движения по горизонтали;
- равноускоренного движения по вертикали с ускорением свободного падения.



Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:


Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ( v_0 ) , с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ( alpha ) , под которым тело брошено, будет равен углу, под которым оно упадет.
При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Движение по окружности с постоянной по модулю скоростью
Движение по окружности с постоянной по модулю скоростью – простейший вид криволинейного движения.
Траектория движения – окружность. Вектор скорости направлен по касательной к окружности.
Модуль скорости тела с течением времени не изменяется, а ее направление при движении по окружности в каждой точке изменяется, поэтому движение по окружности – это движение с ускорением.
Ускорение, которое изменяет направление скорости, называется центростремительным.
Центростремительное ускорение направлено по радиусу окружности к ее центру.

Центростремительное ускорение – это ускорение, характеризующее быстроту изменения направления вектора линейной скорости.
Обозначение – ( a_ <цс>) , единицы измерения – м/с 2 .

Движение тела по окружности с постоянной по модулю скоростью является периодическим движением, т. е. его координата повторяется через равные промежутки времени.
Период – это время, за которое тело совершает один полный оборот.
Обозначение – ( T ) , единицы измерения – с.

где ( N ) – количество оборотов, ( t ) – время, за которое эти обороты совершены.
Частота вращения – это число оборотов за единицу времени.
Обозначение – ( nu ) , единицы измерения – с –1 (Гц).

Период и частота – взаимно обратные величины:

Линейная скорость – это скорость, с которой тело движется по окружности.
Обозначение – ( v ) , единицы измерения – м/с.
Линейная скорость направлена по касательной к окружности:

Угловая скорость – это физическая величина, равная отношению угла поворота к времени, за которое поворот произошел.
Обозначение – ( omega ) , единицы измерения – рад/с .

Направление угловой скорости можно определить по правилу правого винта (буравчика).
Если вращательное движение винта совпадает с направлением движения тела по окружности, то поступательное движение винта совпадает с направлением угловой скорости.
Связь различных величин, характеризующих движение по окружности с постоянной по модулю скоростью:

Важно!
При равномерном движении тела по окружности точки, лежащие на радиусе, движутся с одинаковой угловой скоростью, т. к. радиус за одинаковое время поворачивается на одинаковый угол. А вот линейная скорость разных точек радиуса различна в зависимости от того, насколько близко или далеко от центра они располагаются:


Если рассматривать равномерное движение двух сцепленных тел, то в этом случае одинаковыми будут линейные скорости, а угловые скорости тел будут различны в зависимости от радиуса тела:


Когда колесо катится равномерно по дороге, двигаясь относительно нее с линейной скоростью ( v_1 ) , и все точки обода колеса движутся относительно его центра с такой же линейной скоростью ( v_1 ) , то относительно дороги мгновенная скорость разных точек колеса различна.

Мгновенная скорость нижней точки ( (m) ) равна нулю, мгновенная скорость в верхней точке ( (n) ) равна удвоенной скорости ( v_1 ) , мгновенная скорость точки ( (p) ) , лежащей на горизонтальном радиусе, рассчитывается по теореме Пифагора, а мгновенная скорость в любой другой точке ( (c) ) – по теореме косинусов.
[spoiler title=”источники:”]
http://sprint-olympic.ru/uroki/fizika/96625-formyla-skorosti-oboznachenie-edinicy-izmereniia-i-primery-nahojdeniia.html
[/spoiler]















