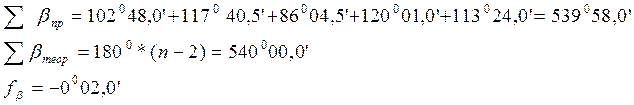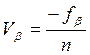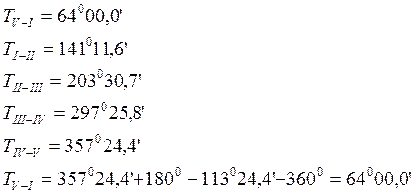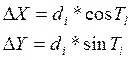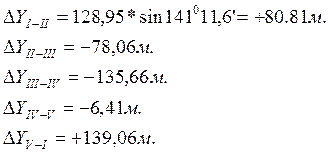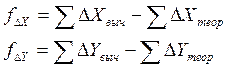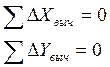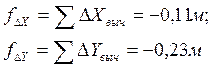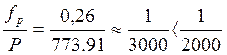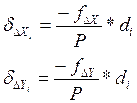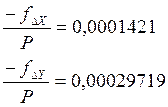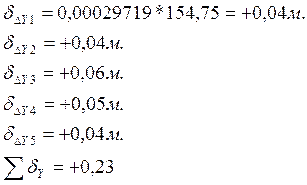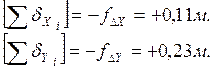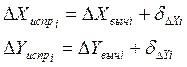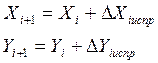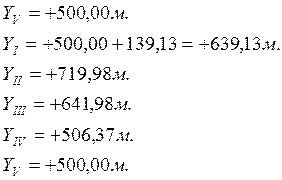Скачать с Depositfiles
4.1.4. Вычисление дирекционных углов сторон полигона
Определение дирекционных углов осуществляется по формуле
где — дирекционный угол некоторой i-й стороны полигона;
— дирекционный угол предыдущей (i — 1)-й стороны;
— исправленное значение угла, заключенного между этими
сторонами (левого по ходу).
Знак минус перед третьим членом в правой части формулы берут в том случае, когда сумма двух первых членов превышает 180°.
Если вычисленное по данной формуле значение дирекционного угла а. окажется больше 360°, то следует из него вычесть 360°, т.е. исключить полный оборот.
Дирекционный угол исходной стороны IV—I выдается преподавателем индивидуально каждому студенту. Пользуясь его значением и величиной угла , можно определить дирекционный угол следующей стороны I-II:
На основе полученного значения и угла
находим дирекционный угол стороны II—III:
Так, последовательно вычисляют дирекционные углы всех сторон полигона, включая и исходную сторону IV—I. Контролем вычислений дирекционных углов служит равенство вычисленного значения дирекционного угла исходной стороны IV—I заданному начальному значению этого угла.
4.1.5. Вычисление приращений координат
Приращения координат некоторой i-й стороны полигона представляют собой проекции этой стороны на координатные оси и вычисляются по следующим формулам:
где и
— приращения координат соответственно по осям Х и У;
— горизонтальное проложение длины i-й стороны;
— дирекционный угол i-й стороны полигона.
Вычисления приращений координат выполняются на микрокалькуляторе или же с помощью специальных таблиц.
При использовании микрокалькуляторов следует помнить о необходимости перевода значений дирекционных углов в десятичную систему счисления.
В микрокалькуляторах, имевших клавишу ° , » , такой перевод осуществляется автоматически: путем последовательного нажатия этой клавиши после набора на клавиатуре градусов, минут и секунд, составляющих значение дирекционного угла.
В микрокалькуляторах, не имеющих клавиши автоматического перевода минут и секунд в десятые доли градуса (например, БЗ-18А, МК-56 и др.), такой перевод осуществляется студентом самостоятельно. Алгоритм этого перевода прост и наглядно иллюстрируется следующим примером:
Пример: Перевести 128°37’45» в десятичную систему счисления.
Решение: (45″/60»+ 37′)/60’+ 128° = 128°,62916.
При табличном способе определения приращений координат могут быть попользованы таблицы: а) приращений координат; б) натуральных значений тригонометрических функций; в) логарифмов. Необходимо, чтобы любая из этих таблиц по точности была не ниже, чем пятизначная.
Наиболее простыми и удобными в работе являются таблицы приращений координат, однако следует помнить, что определение приращений координат в этих таблицах производится по значениям табличных, а не дирекционных углов. Значение табличного угла t для соответствующего ему дирекционного угла определяется в зависимости от координатной четверти, в которой находится данный дирекционный угол, по одной из известных формул приведения (табл. 4).
Таблица 4 Определение табличных углов и знаков приращений координат
|
Координатная четверть |
Дирекционный угол |
Формула приведения |
Знаки приращения |
|
|
I |
0° — 90° |
t = |
+ |
+ |
|
II |
90° — 180° |
t = |
_ |
+ |
|
III |
180° — 270° |
t = |
_ |
_ |
|
IV |
270° — 360° |
t = |
+ |
_ |
Значения приращений координат даны в таблицах для горизонтальных длин, равных соответственно 10, 20.…, 90 м, и для значений табличных углов, изменявшихся через 1. Для определения величин приращений координат, горизонтальное проложение длины стороны полигона раскладывают на слагаемые, состоящие из целого числа сотен, десятков, единиц метров и дробной части, а затем по таблицам находят значения приращений координат для каждого слагаемого и суммируют их. Знаки величин приращений координат берут в зависимости от координатной четверти, в которой находится дирекционный угол стороны (см. табл. 4). Ниже приведен пример, иллюстрирующий методику определения приращений координат по таблицам.
Пример: Найти приращения координат и
для стороны полигона, горизонтальное проложение которой равно 149,54 м, а дирекционный угол 329°07’45».
Решение: Дирекционный угол стороны находится в IV четверти. Следовательно, соответствующий ему табличный угол
t = 360° — 329°07’45» = 30°52’15» = 30°52′.
Величины и
будут равны:
|
|
|
|
|
100 |
85, 836 |
51, 304 |
|
40 |
43, 335 |
20, 522 |
|
9 |
7, 725 |
4, 617 |
|
0, 54 |
0, 46 |
0, 28 |
|
149, 54 |
128, 356 |
76, 723 |
Округляем значения приращений координат до сотых долей метра и присваиваем им соответствующий знак (см. табл. 4), Тогда
= 128,36 м;
= -76,72 м.
Вычисленные значения приращений координат записывают в графы 7 и вычислительной ведомости.
Скачать с Depositfiles
Обработка материалов теодолитного хода. Вычисление координат вершин замкнутого хода
Страницы работы
Содержание работы
Вычисление координат вершин
замкнутого хода
Исходные данные:
TV-I=640 00,0’
X5= +500,00 м.
Y5= +500,00 м.
|
Номера вершин |
Измеренные правые по ходу |
Горизонтальные проложения длин |
|
I |
1020 48,0’ |
|
|
II |
1170 40,5’ |
|
|
III |
860 04,5’ |
|
|
IV |
1200 01,0’ |
|
|
V |
1130 24,0’ |
|
|
I |
- Вычисление исправленных горизонтальных углов:
Угловая
невязка в замкнутом ходе определяется по формуле:
где -сумма
измеренных углов; -теоретическая сумма улов, при
этом -сумма внутренних углов
замкнутого многоугольника (n – число углов);
Допустимая
угловая невязка в замкнутом ходе определяется по формуле:
Условие выполняется, следовательно, угловую невязку
можно распределить на все углы поровну с округлением до 1’, отдавая предпочтение углам, образованным короткими сторонами.
Контроль вычисления поправок
|
Номера вершин |
Правые по ходу исправленные |
|
I |
1020 48,4’ |
|
II |
1170 40,9’ |
|
III |
860 04,9’ |
|
IV |
1200 01,4’ |
|
V |
1130 24,4’ |
Проверка
правильности вычислений:
Проверка
выполняется.
- Вычисление
дирекционных углов всех сторон хода по исправленным горизонтальным углам:
Дирекционный
угол Т-это угол, отсчитываемый от положительного (северного) направления
осевого меридиана до данного направления по ходу часовой стрелки. Он измеряется
от 00 до 3600.
Исходный
дирекционный задан , дирекционные углы последующих
сторон вычисляются по формуле:
Где
Тn+1-дирекционный угол последующей
стороны; Тn– дирекционный угол предыдущей
стороны; -правый по ходу исправленный угол между
этими сторонами.
Контролем
правильности вычислений служит равенство вычисленного значения дирекционного
угла исходной стороны его заданному значению.
Приращение
координат ∆X и ∆Y по дирекционным углам и горизонтальным проложениям
сторон теодолитного хода определяется по формулам:
где
di– горизонтальное проложение стороны
хода; Ti-дирекционный угол, соответствующие
данному направлению.
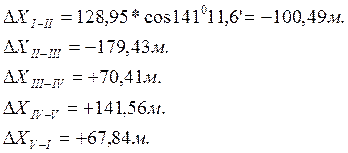
- Вычисление поправок к приращениям:
Невязки
приращения координат – это разности их вычисленного и теоретического значения
Так
как ход замкнут, то теоретические суммы приращений координат
и невязки
приращения координат равны вычисленным суммам приращений координат:
Абсолютная
невязка: м.
Относительная
невязка:
Относительная
невязка удовлетворяет указанному допуску, следовательно и
нужно распределить на каждое приращение с
обратным знаком пропорционально длине линии
где
и
-поправки
в приращениях с точностью 0,01 м; P
и di– длина периметра и соответствующей
стороны в сотнях метров.
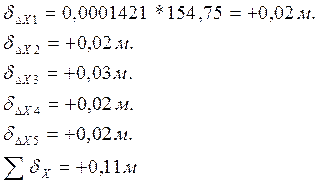
Проверка:
- Вычисление
исправленных приращений:
Исправленные
значения приращений координат для каждой линии вычисляется по формуле:
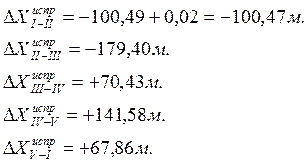
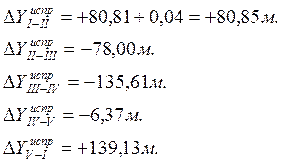
Контроль:
,
.
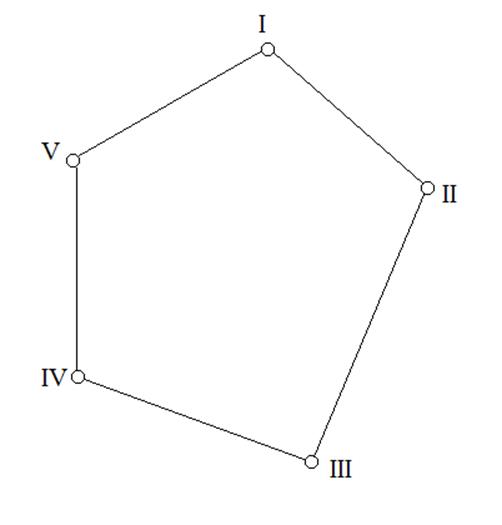
- Вычисление координат вершин замкнутого хода:
Координаты
X и Y вершин замкнутого хода определяются по формулам:
Контролем
правильности вычислений служит получение значений координат конечного исходного
пункта X1 и Y1
(он же – начальный пункт).
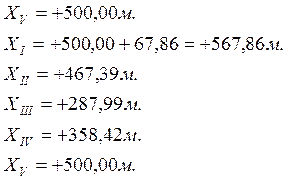
· Накладка вершин
углов теодолитного хода на план:
Накладка
теодолитного хода по координатам вершин на план в масштабе 1:2000 начинается с
построения координатной сетки. Для её построения применяются линейки Дробышева.
Это металлическая линейка с вырезами. Края вырезов скошены, на первом из них
нанесён индекс «0». Края других вырезов представляют дуги, описанные радиусами
10, 20, 30, 40, и 50 см; конец линейки представляет также дугу радиусом 70, 711 см, что соответствует гипотенузе треугольника с катетами 50х50 см.
На листе бумаги проводим диагонали,
от точки пересечения откладывают равные отрезки к углам листа, получая таким
образом вершины прямоугольника. Затем по сторонам прямоугольника откладывают
отрезки(10 см), величину которых определяют по масштабу. Соответствующие точки
на противоположных сторонах соединяют линиями, которые образуют сетку
квадратов. Контролируют построения по равенству диагоналей в каждом квадрате.
Расхождение диагоналей не должно превышать 0,2 мм. Затем полученная сетка квадратов оцифровывается так, чтобы весь ход оказался примерно в
середине листа, при этом +Х направляется вверх листа, а +У – вправо.
При нанесении на план точек по
прямоугольным координатам прежде всего определяют квадрат, в котором они
находятся. Построение производят с помощью циркуля-измерителя и масштабной
линейки. Каждую точку накладывают и обвожу кружком диаметром 1,5 мм с «усиками» длиной 0,5 мм, слева подписывают номера вершин. Правильность накладки проверяют,
сравнивая расстояния между точками с горизонтальным положением сторон в
масштабе плана. Допустимое расхождение ±0,6 мм.
Работу оформляют карандашом в
соответствии с образцом и условными знаками.
СГУПС
Кафедра «Инженерная
геодезия»
Расчетно-графическая
работа №1
«Обработка материалов
теодолитного хода»
Выполнил: ст.гр. У-215
Дмитрук А. А.
Проверил: Астраханцев В. Д.
Новосибирск 2010
План теодолитного хода
Похожие материалы
- Вычисление координат вершин замкнутого теодолитного хода, выполнение накладок точек на план
- Обработка результатов нивелирования трассы и составление профиля
- Обработка материалов и составление плана тахеометрической съемки. Решение задач по топографическому плану
Информация о работе
Тип:
Расчетно-графические работы
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание – внизу страницы.
По
известному дирекционному углу n
и по исправленным горизонтальным углам
испр
вычисляются дирекционные углы остальных
сторон теодолитного хода по формулам
для правых горизонтальных углов:
– дирекционный
угол последующей стороны равен
дирекционному углу предыдущей стороны
плюс 180
и минус исправленный горизонтальный
угол правый по ходу.
Величина
дирекционного угла не может превышать
360
и быть меньше 0.
Если величина дирекционного угла больше
360,
то из результата вычислений необходимо
вычесть 360
(см. пример).
Контроль
вычисления дирекционных углов. В
замкнутом теодолитном ходе в результате
вычислений получается дирекционный
угол исходной стороны.
Пример вычисления дирекционных углов: Дирекционный угол исходной стороны 1-2 равен 4545.
;
;
;
;
При
вычислении дирекционного угла получилось
значение 40545.
Из полученного значения вычитается
360.
.
Контроль
вычисления дирекционных углов получился.
Все
результаты вычислений заносятся в
таблицу «Ведомость вычисления координат»
(табл. 6).
3.3 Вычисление приращений координат
Вычисление
приращений координат выполняется по
формулам:
,
где
d
– горизонтальное проложение (длина)
линии;
– дирекционный угол этой линии.
Приращения
координат вычисляются с точностью два
знака после запятой.
Пример вычисления приращений координат:
;
;
;
;
.
;
;
;
;
.
Все
результаты вычисления заносятся
в табл. 6. Пример
вычисления тригонометрических функций
на калькуляторе приведен в
прил. 3.
3.4 Уравнивание линейных измерений
Разность
между суммой вычисленных приращений
координат и теоретической суммой
называется линейной невязкой хода и
обозначается fХ
и fY.
Уравнивание линейных измерений
выполняется по осям Х
и Y.
Линейная невязка
вычисляется по формулам:
.
Теоретическая
сумма приращений координат зависит от
геометрии хода. В замкнутом теодолитном
ходе она равна нулю, тогда невязка равна
.
Прежде,
чем распределять невязки в приращения
координат, необходимо убедиться в их
допустимости. Для чего вычисляется
абсолютная невязка хода fабс
и
относительная
,
где
Р
– периметр хода (сумма длин сторон), м.
Относительная
невязка сравнивается с допустимой
.
В
случае, когда полученная относительная
невязка допустима, т.е.
,
то вычисляются поправки в приращения
координат пропорционально
длинам сторон.
Невязки распределяются с обратным
знаком. Если
,
то проверяются вычисления в п.
3.3 и 3.4.
Поправки
в приращения координат X
и Y
вычисляются
по формулам с округлением до 0,01 м:
,
где
X
и Y
– поправка
в приращение по оси Х
и
Y,
соответственно, м; fX
и fY
–
невязки
по осям, м; Р
–
периметр
(сумма сторон), м; di
–
измеренная
длина (горизонтальное проложение), м.
Знак
у поправки противоположен знаку невязки.
Поправки записываются в «Ведомость
вычисления координат». В примере (табл.
6) поправки показаны красным цветом.
После
вычисления поправок следует сделать
проверку, т.е. сложить все поправки. Если
их сумма будет равна невязке с обратным
знаком, то распределение невязки
выполнено правильно. То есть:
.
Вычисляются
исправленные приращения.
Полученные
поправки алгебраически прибавляются
к соответствующим приращениям и
получаются исправленные приращения:
.
Контроль:
сумма исправленных приращений в замкнутом
теодолитном ходе должна равняться нулю,
т.е. должно выполняться равенство:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Актуальные цены на услуги геодезистов в Москве и Московской области в 2022 году.
Решение обратной геодезической задачи онлайн
Обратная геодезическая задача заключается в том, что при известных координатах точек А( XA, YA ) и В( XB, YB ) необходимо найти длину SAB и направление линии АВ: румб rAB и дирекционный угол αAB
Ниже представлена форма в которую можно ввести исходные значения и получить искомые данные. Это простое решение, которым может воспользоваться любой кому лень разбираться с формулами.
Если же говорить о сути решения задачи, то обратная геодезическая задача решается следующим образом.
Сначала находим приращения координат:
ΔX = XB – XA ;
ΔY = YB – YA .
Величину угла rAB определяем из отношения
По знакам приращений координат вычисляют четверть, в которой располагается румб, и его название. Используя зависимость между дирекционными углами и румбами, находим αAB.
Для контроля расстояние SAB дважды вычисляют по формулам:
Координаты – это величины, которые отображают местоположение конкретной точки в пространстве. Они определяются путем проведения геодезических измерений, к которым относится триангуляция, а также построение тахеометрического и теодолитного хода.
На плоскости координаты можно вводить неисчислимым количеством способов и через различные математические задачи создавать координатные системы. Благодаря вычислению координаты точек теодолитного хода на карту или план наносятся как эти самые пункты, так и жесткие объекты в зоне их видимости.
Содержание
- 1 Общие понятия о системах координат в геодезии
- 2 Исходные данные для расчетов
- 3 Уравнивание измерений
- 4 Вычисление дирекционных углов вершин
- 5 Решение прямой и обратной геодезической задачи
- 5.1 Создавайте будущее вместе с нами
- 6 Приращение координат и их увязка
- 7 Как вычислить координаты точек хода
- 8 Нанесение точек на план и его оформление
Общие понятия о системах координат в геодезии
Столь глубокие познания о строении и форме Земли, которые человек осваивал на протяжении веков, сегодня позволяют создавать невероятно точные координатные системы и картографические проекции.
Координатные системы заданы двумя направлениями на плоскости, а в пространстве – тремя. Осевые направления всегда перпендикулярны друг другу, а ориентированы горизонтально и вертикально. Их пересечение и определяет местоположение точки в заданной системе.
В геодезии координатные системы разделены на следующие две группы:
- Прямолинейные прямоугольные. К ним причисляют проекцию Гаусса-Крюгера, индивидуальные референцные и местные системы.
- Полярные. Это геодезические, географические, астрономические, а также геоцентрические и топоцентрические координаты.
Теодолитный ход можно считать самым распространённым плановым обоснованием. Он не требует дорогостоящего и высокоточного оборудования, но помогает создать надежную плановую основу на территориях со сложной местностью. Его развивают от пунктов государственных геодезических сетей (ГГС) и сетей сгущения с уже установленными координатами.
Вычисляются координаты точек замкнутого и разомкнутого теодолитного хода посредством нахождения дирекционных углов его сторон и решения прямой геодезической задачи. Но перед этим следует проверить, соответствуют ли измерения нормативным требованиям.
Исходные данные для расчетов
Теодолитный ход может быть проложен в виде замкнутой фигуры или ломаной линии. Это зависит от характера снимаемой местности. Он является отличной геодезической основой для многих инженерных изысканий.
По итогу проведенных измерений составляется план или карта местности, а все вычисления заносятся в специальные ведомости. В нее заносятся следующие данные:
– горизонтальные углы пунктов;
– измеренное расстояние между ними;
– координаты пункта ГГС или опорной сети;
– значение исходного дирекционного угла.
Для привязки хода к пункту ГГС или опорной сети необходимо определить местоположение одной его точки относительно этого пункта. Это можно сделать, измерив расстояние и горизонтальный примычной угол между ними. Такая процедура называется передачей координат и дирекционных углов.
Уравнивание измерений
Не существует еще методов, позволяющих без погрешностей выполнить измерения, но уравнивание позволит свести их к минимуму. Для замкнутого хода первым делом рассчитывается невязка:
(f_{beta}=sum beta _{изм}-sum beta_{теор})
где:
(sum beta _{изм}=beta _{1}+beta _{2}+…beta _{n}) – сумма углов пунктов;
(sum beta _{теор}) – теоретическая сумма, определяемая выражением:
(sum beta _{теор}=180^{circ}cdot (n-2))
(n) – количество углов.
Вычисленная невязка допустима, если соответствует требованию:
(beta _{испр}=pm 1,5sqrt{n})
Когда полученное значение не превышает допуск, то невязку разбрасываются между углами с противоположным знаком равномерно. Можно также распределить ее только между самыми короткими сторонами. Учитывая поправки и их знак, вычисляют исправленные углы:
(beta _{испр}=beta _{изм}+delta _{beta })
(delta _{beta }) – поправка.
Правильность уравнивания подтверждается следующим условием:
(sum beta _{теор}=beta _{испр})
Поскольку разомкнутый ход является ломаной линией, математические расчеты для него проводятся как для хода, в котором две исходные стороны и дирекционных угла. Для него применяют следующие выражения:
для левых углов:
(sum beta _{теор}=alpha _{кон}-alpha _{нач}+ncdot 180^{circ})
правых:
(sum beta _{теор}=alpha _{нач}-alpha _{кон}+ncdot 180^{circ})
Для упрощения дальнейших вычислений поправки могут быть распределены с целью округления десятых долей минут в углах до целых минут.
Вычисление дирекционных углов вершин
В геодезии за дирекционный угол ((alpha )) принимают угол, который начинают отсчитывать от северного направления осевого меридиана и до заданной стороны. Он измеряется от 0 до 360°. Вычислить его значение для правой стороны хода можно по формуле ниже:
(alpha _{n}=alpha _{n-1}+eta )
(eta=180^{circ} -beta _{пр.испр})
(a _{n}=alpha _{n-1}+180^{circ}-beta _{пр.испр})
Для левой стороны это выражение будет иметь такой вид:
(alpha _{n}=alpha _{n-1}+eta )
(eta=beta _{лев.исп.}-180^{circ} )
(a _{n}=alpha _{n-1}-180^{circ}+beta _{лев.исп.})
где:
(alpha _{n-1}) – дирекционный угол предыдущей стороны, а (n) – последующей;
(beta _{пр.исп.}) – значение правого исправленного угла между сторонами отрезка, а (beta _{лев.исп.})– левой стороны.
Вычисления выполнены верно при равенстве заданного α и начальной стороны теодолитного хода. Если дирекционный угол больше 360° или имеет отрицательное значение, то это говорит об ошибке в расчетах.
После дирекционных углов необходимо найти румбы – острые углы, отсчитываемые от 0 до 90°. Они берут свое начало от ближайшего окончания осевого меридиана до ориентирной линии.
| Четверть румба | Название четверти | Пределы изменения α | Формула румба | Знаки приращения | |
| ΔХ | ΔУ | ||||
| I | С.В. (северо-восток) | 0° – 90° | r = α | + | + |
| II | Ю.В. (юго-восток) | 90°-180° | r = 180° – α | – | + |
| III | Ю.З. (юго-запад) | 180°-270° | r = α – 180° | – | – |
| IV | С.З. (северо-запад) | 270°-360° | r = 360° – °α | + | – |
Таблица 1. Связь дирекционного угла и румба
Вычисление румбов и их знаков приращений зависит от четверти геодезических прямоугольных координат, в которой находится линия ориентирования.
Решение прямой и обратной геодезической задачи
Суть прямой геодезической задачи состоит в том, чтобы определить координатные значения вершины при заданных координатах соседней. Это возможно при известной горизонтальном проложении между ними и дирекционным углом линии. Для ее решения используются следующие формулы:
(Delta X=dcdot cos alpha )
(Delta Y=dcdot sin alpha )
где:
Создавайте будущее вместе с нами
Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.
(d)–расстояния между соседними пунктами.
(alpha ) – значение дирекционного угла.
Знаки приращений зависят от четверти, определяемой дирекционным углом направления. Координатные значения конечной точки линии равняется сумме координаты начальной и приращения между ними. Из этого следует следующие выражение:
(X_{2}=X_{1}+Delta X)
(Y_{2}=Y_{1}+Delta Y)
(X_{2}=X_{1}+d_{1-2}cdot cosalpha _{1-2})
(Y_{2}=Y_{1}+d_{1-2}cdot sinalpha _{1-2})
Стоит также упомянуть и обратную геодезическую задачу, которая позволяет определить дирекционный угол, румб и горизонтальное проложение при установленных координатах пунктов теодолитного хода. Вычисления имеют такую последовательность:
(Delta X=X_{2}-X_{1})
(Delta Y=Y_{2}-Y_{1})
определяется румб линии (r_{1-2}):
(tgr=frac{Delta Y}{Delta X})
из этого выходит, что:
(r=arctgfrac|{Delta Y}{Delta X}|)
По знакам приращения определяют четверть, в котором находится направление и по уже известному румбу вычисляют дирекционный угол. Определение горизонтального проложения будет завершающим этапом в решении обратной задачи:
(d=frac{Delta X}{cosalpha })
(d=frac{Delta Y}{sinalpha })
(d=sqrt{Delta X^2+Delta Y^2})
Приращение координат и их увязка
Приращением называют величины, на которые будут увеличены координаты предыдущей точки для вычисления последующей. В основу этих расчетов берется уже знакомая формула прямой задачи:
(Delta X=dcdot cos alpha )
(Delta Y=dcdot sin alpha )
Полученные значения также необходимо уровнять, чтобы равномерно распределить погрешности и получить наиболее точный результат. Начинают расчеты с определения невязок. Поскольку сумма проекций в сторонах многоугольной замкнутой фигуры равняется нулю, для вычисления невязок пунктов замкнутого хода используют следующую формулу:
(f_{X}=sum Delta X_{выч}-sum Delta X_{теор};sum Delta X_{теор}=0)
(f_{Y}=sum Delta Y_{выч}-sum Delta Y_{теор};sum Delta Y_{теор}=0)
(sum Delta X_{выч},sum Delta Y_{выч}) – суммы приращений, рассчитанные с учетом знаков для замкнутого и разомкнутого хода;
(sum Delta X_{теор},sum Delta Y_{теор}) – теоретические суммы приращений.
Если невязки не находятся в допуске, необходимы повторные расчеты, чтобы определить ошибку и устранить ее. В противном случае проводятся повторные измерения на участке.
Вследствие влияния погрешностей на ход, он будет разомкнут на величину , которая представляет собой абсолютную невязку в его периметре. По этому причине проверяется соответствие условию допустимости его невязок.
- Абсолютное значение:
(f_{p}=sqrt{f_{x}^2+f_{y}^2})
- Относительное
(f_{отн}=frac{f_{абс}}{P})
P – периметр хода, полученный суммированием всех его сторон.
Допустимая невязка должна удовлетворять условие 1/2000, а при соответствии выражению (|f_{отн}|leq |f_{доп}|) выполняют ее распределение с противоположным знаком. Однако перед этим рассчитывают поправки приращений, которые определяют для каждой стороны:
(delta _{x_{i}}=-frac{f_{x}d_{i}}{P});(delta _Delta {y_{i}}=-frac{f_{y}d_{i}}{P})
(delta _{x_{i}},delta _{y_{i}})– значения поправок в приращениях.
Чтобы упростить дальнейшие расчеты поправки, необходимо округлить их до 0,01 м.
Для разомкнутого хода за теоретическую сумму приращений берется разность между двумя соседними точками.
(f_{X}=sum Delta X_{выч}-sum Delta X_{теор}; sum Delta X_{теор}=x_{B}-x_{A})
(f_{Y}=sum Delta Y_{выч}-sum Delta Y_{теор}; sum Delta Y_{теор}=y_{B}-y_{A})
Для обоих ходов поправки имеют противоположный приращению знак. Уравнивание выполнено верно, если сумма исправленных приращений равна или максимально приближена к нулю.
Как вычислить координаты точек хода
Вычисляют значения координат вершин замкнутого и разомкнутого теодолитного хода сначала для опорного пункта, а потом уже для остальных его вершин.
Значение следующего пункта хода вычисляют суммированием предыдущего пункта и исправленного приращения. Это наглядно отображено в формуле:
(X_{n}=X_{n-1}+Delta X _{n-1(испр)})
(Y_{n}=Y_{n-1}+Delta Y _{n-1(испр)})
(X_{n-1},Y_{n-1}) – координатные значения предыдущего пункта
(Delta X_{теор}=x_{B}-x_{A},Delta Y_{теор}=y_{B}-y_{A}) – исправленные приращения.
В данных формулах применяется алгебраическая сумма, поэтому знаки также необходимо учитывать при расчетах. Если в конце вычислений получены координатные значения начальной точки, то они выполнены правильно.
Нанесение точек на план и его оформление
После завершения обработки измерений, которые были проведены на местности, составляется ее контурный или ситуационный план. Построение плана теодолитного хода происходит поэтапно и состоит из следующих этапов:
- Создание координатной сетки. Ход необходимо равномерно отобразить на плане, поэтому сначала определяют середину листа. Через весь лист проводят два диагональных отрезка, от которых и будет строиться сетка, состоящая из отрезков по 10 см. Допускается погрешность не более 0,2 мм. Определить их количество можно по формуле:
(N_{X}=(x_{max}-x_{min})/200)
(N_{Y}=(y_{max}-y_{min})/200)
(x_{max},y_{max}) – наибольшие значения координат, увеличенные до большего значения, которое кратное 200.
(x_{min},y_{min}) – наименьшее значение, но уменьшенное и кратное 200.
200 – длина стороны квадрата в метрах , которая в плане равна 10 см.
- Обозначение точек на плане. Лучше всего подходят для нанесения координат пунктов на план циркуль и масштабная линейка. Соседние вершины должны иметь такое же расстояние и дирекционный угол, как записано в ведомости.
- Нанесение ситуации на план. Участки снимаемой местности в процессе полевых работ отображают на специальном схематическом бланке – абрисе. В дальнейшем их используют для переноса контуров, линий и вершин точек. Ситуация изображается на планах и картах специальными обозначениями – условными знаками.
- Оформление плана в соответствии с требованиями. Все топографические материалы должны строго соответствовать нормативным документам. В частности, нужно выдерживать заданные очертания и их размеры. Должны присутствовать пояснительные надписи, легенда, а также указан масштаб.
Сегодня координаты замкнутого теодолитного хода вычисляются значительно проще, а создание всех графических материалов выполняется при помощи специализированных программ автоматически. Это значительно ускорило процесс выполнения геодезических работ и других инженерных изысканий.