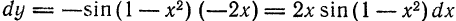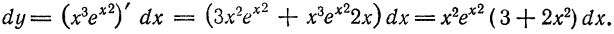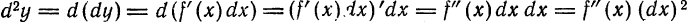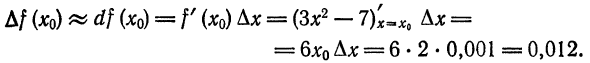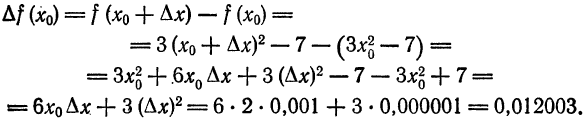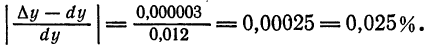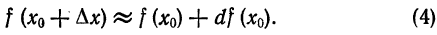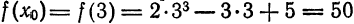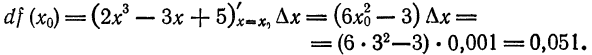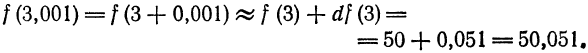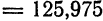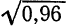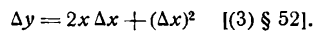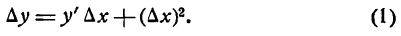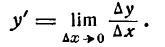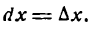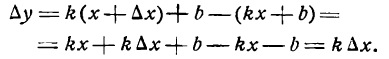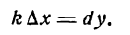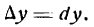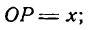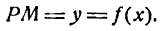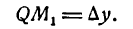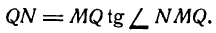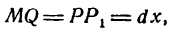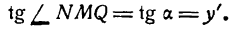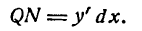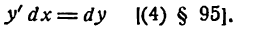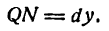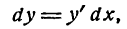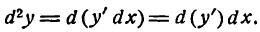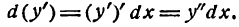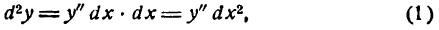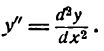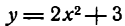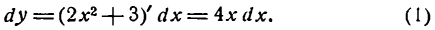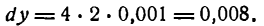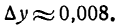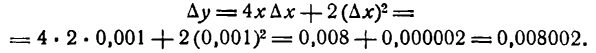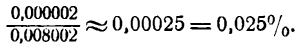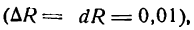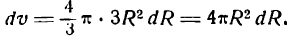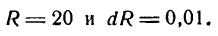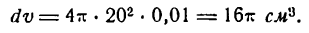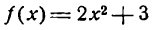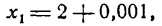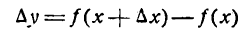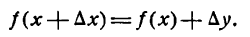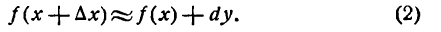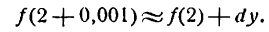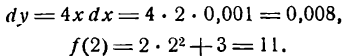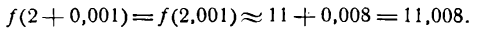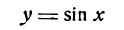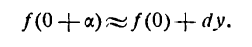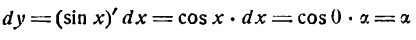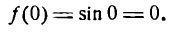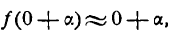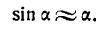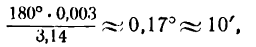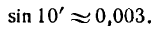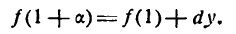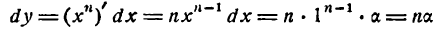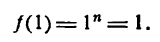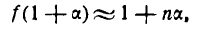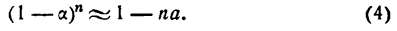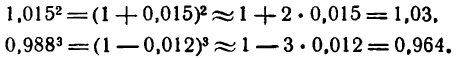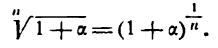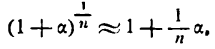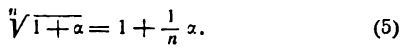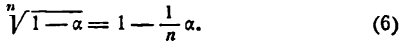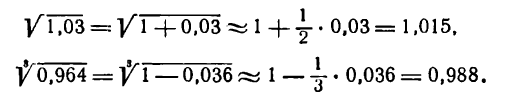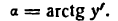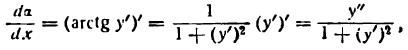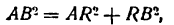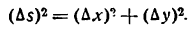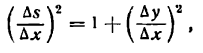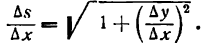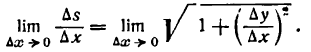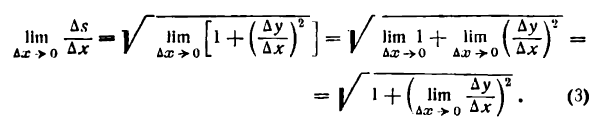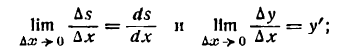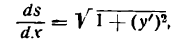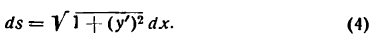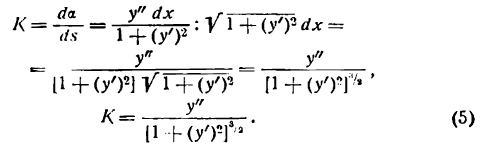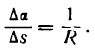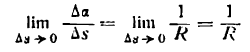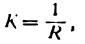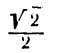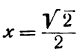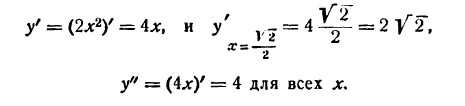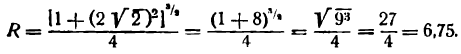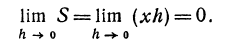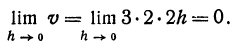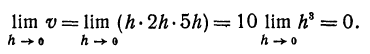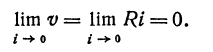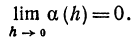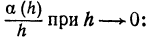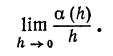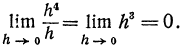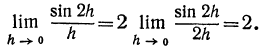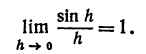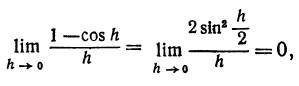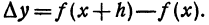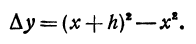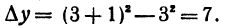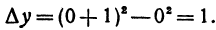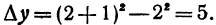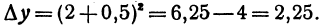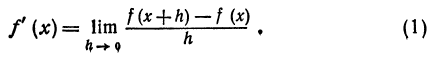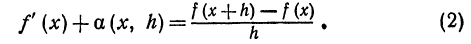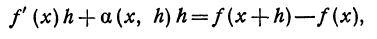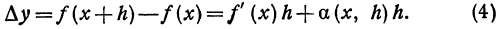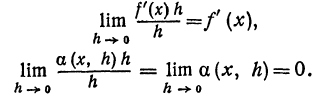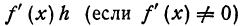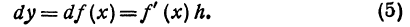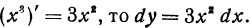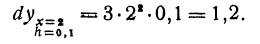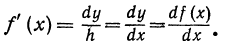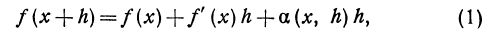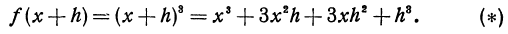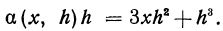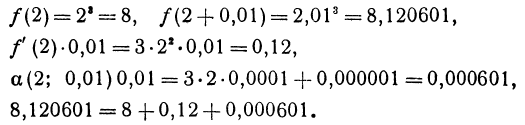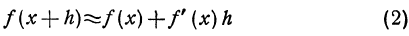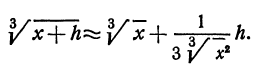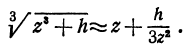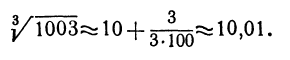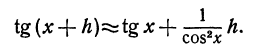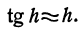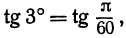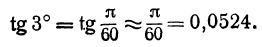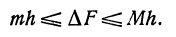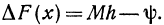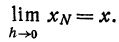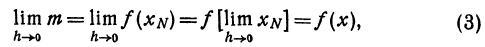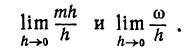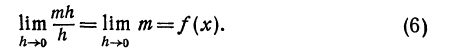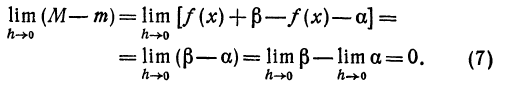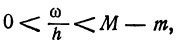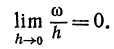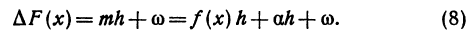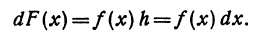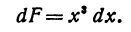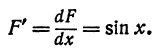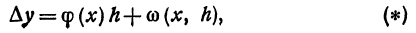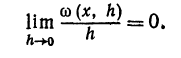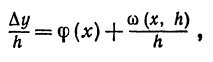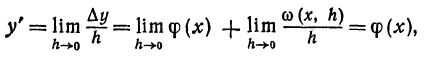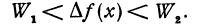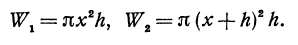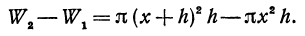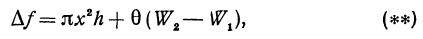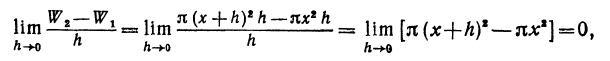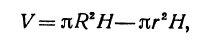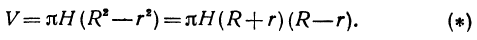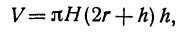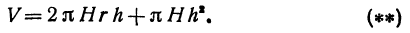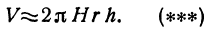Определение. Если переменная 



называется приращением величины 



Приращение постоянной величины равно нулю.
Пример. Начальное значение аргумента 



Решение. Так как 




Приращение функции есть 
Дата публикации: 09 апреля 2017.
Алгебра – 10 класс. Приращение аргумента, приращение функции
Урок на тему: “Приращение аргумента, приращение функции”
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:
Приращение аргумента, приращение функции (PDF)
Что будем изучать:
1.Определение приращения аргумента, приращения функции.
2. Непрерывная функция и приращение.
3. Примеры.
Определение приращения аргумента и приращения функции
Ребята, мы с вами научились находить пределы функции в точке. Важным остается вопрос, как изменяется значение функции при изменении значения аргумента около этой точки?
Математики ввели такое понятие – приращение аргумента и функции. Давайте запишем определение.
Определение: Пусть функция $y=f(x)$ определена в точках $x_0$ и $x_1$. Разность $x_1-x_0$ называют приращением аргумента, а разность $f(x_1)-f(x_0)$–приращением функции.
Иначе говоря, узнаем прирост точки $x_0$ в точке $x_1$. Приращение аргумента обозначают как $Δx$, читается как дельта x.
Приращение функции обозначают, как $Δy$ или $Δf(x)$.
Из нашего определения следует: $x_1-x_0=Δx$ => $x_1= Δx+x_0$ и $f(x_1)-f(x_0)=Δy$. Тогда получаем важное равенство: $Δy=f(x_0+ Δx)-f(x_0)$.
Приращение функции может быть как положительным, так и отрицательным.
Давайте рассмотрим пример.
Найти приращение функции $y=х^3$ при переходе от $x_0=2$ к точке:
а) $x=2,1$; б) $x=1,9$.
Решение:
Обозначим $f(x)=х^3$.
Имеем: $f(2)=2^3=8$.
а) Воспользуемся формулой $Δy=f(x_0+ Δx)-f(x_0)$.
Нам надо найти значение $f(2,1)$.
$f(2,1)=2,1^3=9,261$.
$Δy= f(2,1)- f(2)= 9,261-8=1,261$.
б) $f(2)=8$.
$f(1,9)=1,9^3=6,859$.
$Δy= f(1,9)- f(2)= 6,859-8=-1,141$.
Ответ: а) $1,261$; б) $-1,141$.
Непрерывная функция и приращение
Ребята, давайте вернемся к определению непрерывной функции, и посмотрим на него с помощью приращений.
Вспомним определение непрерывной функции.
Определение. Функцию $y=f(x)$ называют непрерывной в точке $x=a$, если выполняется тождество:
[lim_{x rightarrow a}f(x)=f(a)]
Обратим внимание: $x →a$, тогда $(x-a) →0$ т.е. $Δx → 0$.
Также заметим: $f(x) → f(a)$ , значит $f(x) – f (a) → 0$ т.е. $Δy → 0$.
Определение непрерывности функции в точке можно записать так.
Функция $y=f(x)$ непрерывна в точке $x=a$, если в этой точке выполняется следующее условие:
если $Δx→0$, то $Δy → 0$.
Примеры
1. Для функции $y=kx+b$ найти:
а) приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$;
б)предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Решение:
а) $f(x)= kx+b$.
$f(x+ Δx)=k(x+Δx)+b$;
$Δy= f(x+ Δx)-f(x)= k(x+Δx)+b-( kx+b)= kx+kΔx+b – kx-b= kΔx$.
б) Найдем требуемый предел: $lim_{Δx rightarrow 0}frac{Δy}{Δx}=lim_{Δx rightarrow 0}frac{kΔx}{Δx}=lim_{Δx rightarrow 0}k=k$.
2. Для функции $y=x^3$ найти:
а) приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
б)предел отношения приращения функции к приращению аргумента при условии, что приращение аргумента стремится к нулю.
Решение:
а) $f(x)= x^3$.
$f(x+ Δx)=(x+Δx)^3=x^3+3x^2Δx+3xΔx^2+Δx^3$.
$Δy= f(x+Δx)-f(x)= x^3+3x^2Δx+3xΔx^2+Δx^3-x^3=3x^2Δx+3xΔx^2+Δx^3$.
б) Найдем требуемый предел: $lim_{Δx rightarrow 0}frac{Δy}{Δx}=lim_{Δx rightarrow 0}frac{3x^2Δx+3xΔx^2+Δx^3}{Δx}=lim_{Δx rightarrow 0}(3x^2+3xΔx+Δx^2)=3x^2$.
Задачи для самостоятельного решения:
1) Найти приращение функции $y=x^4$ при переходе от $x_0=3$ к точке:
а) $x=3,2$;
б) $x=2,8$.
2) Для функции $y=3x+5$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
3) Для функции $y=x^2$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
4) Для функции $y=2x^3$ найти приращение функции при переходе от фиксированной точки $x$ к $x+ Δx$.
Понятие дифференциала функции:
Известно, что если функция 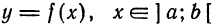
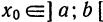
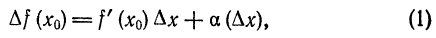
где функция 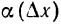
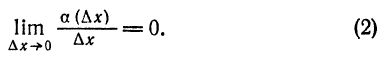
Слагаемое 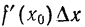
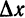
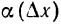
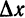
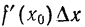
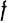
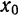
Определение:
Дифференциалом функции 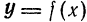
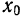
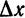
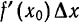
Дифференциал функции обозначается 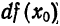
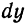
Таким образом,
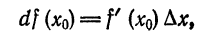
или

Пример:
Найти дифференциал функции 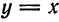
Решение:
По формуле (3) имеем:
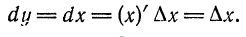
Итак, дифференциал 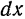
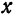
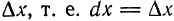

Пример:
Найти дифференциал сложной функции 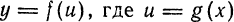
Решение:
По формуле (4) находим:
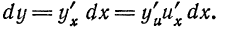
Но — 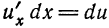

Таким образом, форма дифференциала не зависит от того, является аргумент данной функции независимой переменной или функцией другого аргумента. Это свойство дифференциала сложной функции называется инвариантностью формы дифференциала.
Пример:
Найти дифференциал функции
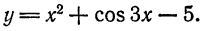
Решение:
По формуле (4) находим:
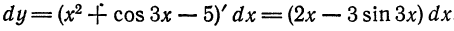
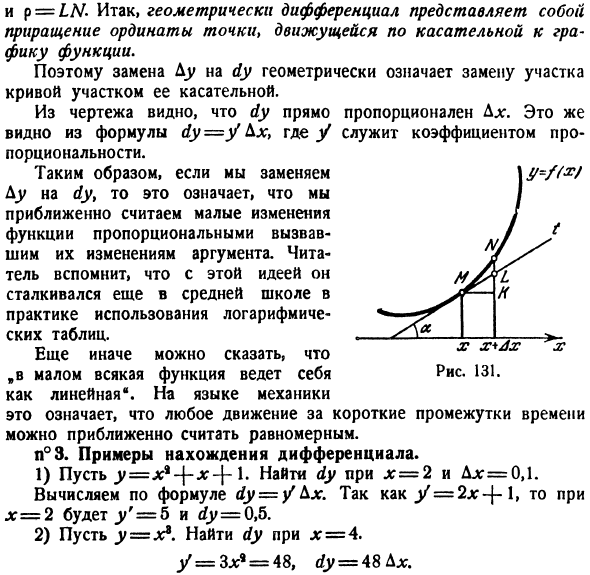
Геометрический смысл дифференциала
Пусть 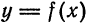
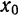
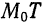
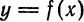
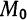
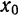
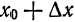
Из прямоугольного треугольника 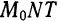
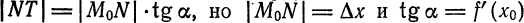
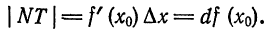
Таким образом, дифференциал функции 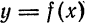
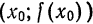
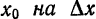
Можно показать, что этот вывод не зависит от расположения графика функции и касательной на координатной плоскости.
Дифференциал может быть как меньше приращения функции (см. рис. 74), так и больше (рис. 75). Однако при достаточно малых приращениях 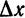
принять 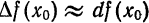
Вычисление дифференциала
Мы установили, что дифференциал функции 

т. е. дифференциал функции 
По формуле (1) можно вычислить дифференциал любой дифференцируемой функции. Так, например;
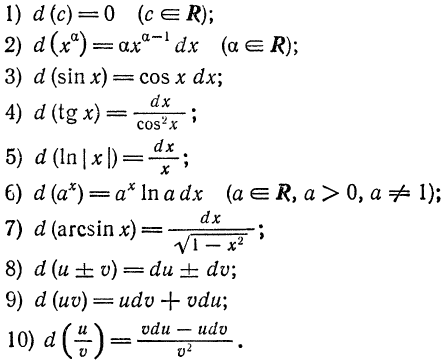
Аналогично, каждой из основных формул дифференцирования можно сопоставить соответствующую формулу для вычисления дифференциала.
Пример:
Найти дифференциал функции
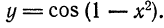
Решение:
По формуле (1) находим:
Пример:
Найти дифференциал функции
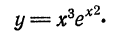
Решение:
Находим:
Дифференциалы высших порядков
Из формулы 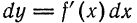
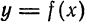
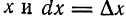
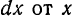
Рассмотрим дифференциал 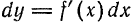
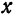
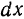
Дифференциал от дифференциала функции 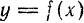
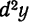
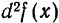
Таким образом,
Принято скобки при степенях 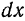

Аналогично определяются дифференциалы третьего порядка:
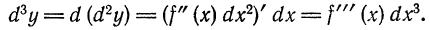
Вообще, дифференциалом п-го порядка называется дифференциал от дифференциала 
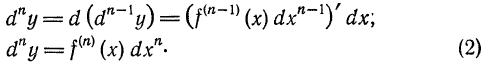
Таким образом, для нахождения дифференциала п—го порядка функции 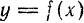
Пример:
Найти дифференциалы первого, второго и третьего порядка функции
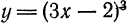
Решение:
Находим соответствующие производные
от данной функции:
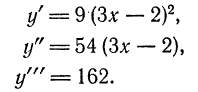
Следовательно,
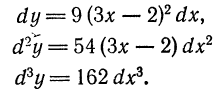
Приложение дифференциала приближенным вычислениям
Рассмотрим функцию 
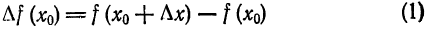
и дифференциал
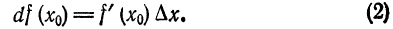
Выше (§ 2) было установлено, что при достаточно малых 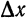

Так как вычислять 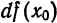
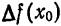
Вычисление приближенного значения приращения функции
Пример:
Найти приближенное значение приращения функции 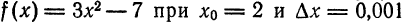
Решение:
Применив формулу (3), получим:
Посмотрим, какую погрешность мы допустили, вычислив дифференциал данной функции вместо ее приращения. Для этого найдем истинное значение приращения:
Далее, находим абсолютную погрешность приближения:
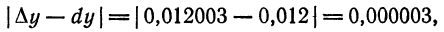
а затем и относительную погрешность:
Погрешность приближения оказалась довольно малой, что еще раз подтверждает целесообразность применения формулы (3).
Вычисление приближенного числового значения функции
Из формулы (1) имеем
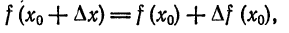
или
Пример:
Найти приближенное значение функции 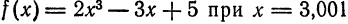
Решение:
Представим 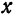
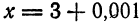
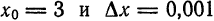
Следовательно,
Приближенное вычисление степеней
Рассмотрим функцию 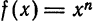
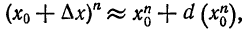
или
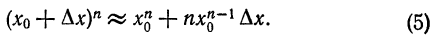
По этой формуле наводят приближенное значение степеней.
Пример:
Найти приближенное значение степени 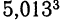
Решение:
Представим данную степень в виде 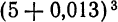
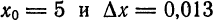
(5) найдем: 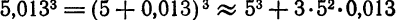
Приближенное извлечение корней
При 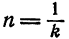
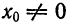
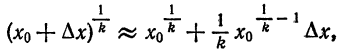
или
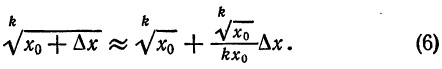
Формула (6), известная и по школьному курсу, дает возможность найти приближенные значения различных корней.
Пример:
Найти приближенное значение корня
Решение:
Представим данный корень в виде 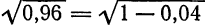
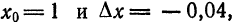
Дополнение к дифференциалу
Смотрите также:
Предмет высшая математика
Понятие о дифференциале в высшей математике
Сравнение бесконечно малых величин между собой
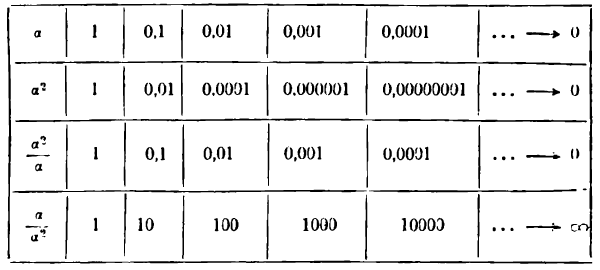
I. Мы рассмотрели действия над бесконечно малыми величинами и показали, что в результате сложения, вычитания и умножения их получаются также бесконечно малые величины. Однако частное от деления двух бесконечно малых друг на друга может быть не только бесконечно малой величиной, но и бесконечно большой и конечной.
В самом деле, пусть, например, а — бесконечно малая, тогда 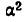
1) отношение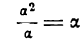
2) отношение 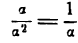
3) отношение 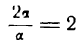
Первое отношение показывает, что бесконечно малая 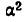
Второе отношение указывает на то, что а, неограниченно уменьшаясь, остается значительно больше, чем 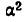
Сказанное можно иллюстрировать следующей таблицей:
Принято бесконечно малую 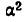
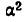
Что касается третьего отношения, то из него следует, что бесконечно малые 2а и а стремятся к нулю с одинаковой скоростью, так как при их изменении отношение 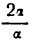
Таким образом, частное от деления двух бесконечно малых величин позволяет сравнивать их между собой. Это сравнение особенно полезно в приближенных вычислениях, где отбрасывание бесконечно малых высшего порядка приводит к значительному упрощению вычислений.
II. Возьмем функцию 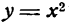
Множитель при 
Сравним изменение величины обоих слагаемых правой части равенства (I) с уменьшением 
х = 2 и, следовательно, у’ = 4, составим следующую таблицу значений этих слагаемых:
Как видно из таблицы, слагаемые у’
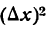


Покажем, что то же самое справедливо для любой дифференцируемой функции f(x).
Пусть дана функция у = f(х). Ее производная
Согласно определению предела переменной имеем:
где а—бесконечно малая величина при 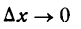
И здесь при уменьшении 



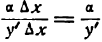
малая величина при 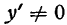



Определение:
Главная часть у’
Дифференциал функции у = f(х) принято обозначать символом dу. Таким образом
Дифференциал аргумента dх принимают равным приращению аргумента 
Поэтому равенство (3) можно переписать в следующем виде:
т. е. дифференциал функции равен произведению производной функции на дифференциал аргумента. Из формулы (4) следует:
Равенство (5) показывает, что производная функции есть отношение дифференциала функции к дифференциалу аргумента. На этом основании производную функции часто выражают в виде 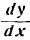
III. Заменив в равенстве (2)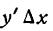
Как было показано выше, 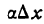
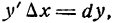
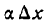
В практических вопросах часто используют формулу (7), т. е. берут дифференциал функции вместо ее приращения, делая при этом незначительную ошибку и тем меньшую, чем меньше 
Примечание:
В случае линейной функции 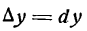
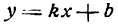
Множитель 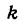
Итак, в случае линейной функции
Геометрическое изображение дифференциала
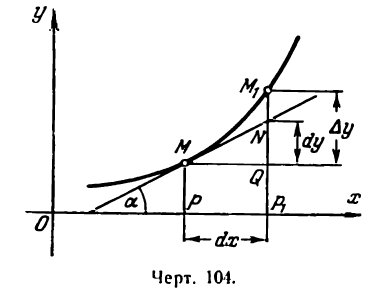
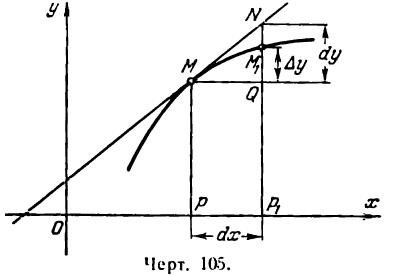
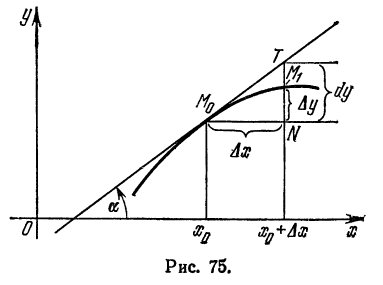
Возьмем функцию у = f(x), график которой изображен на рис. 104.
Пусть абсцисса точки М
тогда ордината ее
Дадим аргументу х приращение 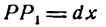
Проведем в точке М касательную к кривой; полученный при этом отрезок QN, равный приращению ординаты точки М, движущейся по касательной, называется приращением ординаты касательной. Из прямоугольного треугольника МQN имеем:
Но
а, согласно геометрическому смыслу производной,
Поэтому
Но
Следовательно,
Таким образом, если в точке М кривой у = f(х) провести касательную, то дифференциал функции у = f(х) в этой
точке изобразится приращением ординаты касательной, соответствующим приращению ее абсциссы на dx.
Дифференциал функции в данной точке может быть как меньше приращения ее (рис. 104), так и больше (рис. 105).
Дифференциал второго порядка
Дифференциал dy функции у = f(x), называемый первым дифференциалом или дифференциалом первого порядка, представляет собой также функцию x, а потому и от него можно найти дифференциал, который называют вторым дифференциалом или дифференциалом второго порядка. В этом случае пишут d(dy) или короче 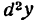
Найдем выражение дифференциала второго порядка от функции через ее производную. Для этого продифференцируем по х равенство.
считая dx постоянным множителем (так как dx не зависит от х):
Но согласно формуле (4)
Поэтому
т. е. дифференциал второго порядка равен произведению второй производной функции на квадрат дифференциала аргумента.
Из равенства (1) следует
Это дает основание для выражения второй производной
функции в виде отношения 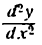
Приложение дифференциала к приближенным вычислениям
Рассмотрим несколько примеров использования дифференциала в приближенных вычислениях.
а) Определение приращения функции.
Пример:
Найти приближенно приращение функции
при х = 2 и 
Решение:
Так как приращение аргумента — величина малая, то согласно формуле (7) можем приращение функции заменить ее дифференциалом.
Дифференциал же данной функции
Заменив в равенстве (1) х и dх их значениями, получим:
Следовательно,
Посмотрим, какую ошибку мы делаем, беря дифференциал вместо приращения. Для этого найдем точное значение приращения функции:
Сравнивая полученное точное значение 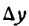
Ошибка оказалась очень малой.
Пример:
Шар радиуса R = 20 см был нагрет, отчего радиус его удлинился на 0,01 см. Насколько увеличился при этом объем шара?
Решение:
Объем шара определяется по формуле
Каждому значению R по закону, заданному этой формулой, отвечает одно определенное значение v, т. е. v есть функция от R. Следовательно, наша задача сводится к определению приращения функции v при заданном приращении аргумента R. Так как приращение аргумента мало
то мы можем приращение функции заменить ее дифференциалом.
Находим дифференциал функции v.
Но
Поэтому
б) Нахождение числового значения функции. Пусть требуется найти приближенное значение функции
при x1 = 2,001, т. е. найти величину f(2,001). Представим х1 в виде суммы
где 0,001 будем рассматривать как приращение аргумента. Из формулы для приращения функций
найдем:
Полагая 
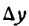
Применив равенство (2) к данному примеру, можем написать:
По
Поэтому
Равенство (2) может служить формулой для приближенного вычисления значения функции.
в) Вычисление по приближенным формулам. Пользуясь формулой (2), выведем приближенные формулы для вычисления некоторых выражений. 1) Возьмем функцию
и положим, что угол х, равный нулю, получает весьма малое приращение а. Применим формулу (2), полагая в ней х = 0 и dx = а. Получим:
Но
и
Поэтому
или
Отсюда следует, что синус очень малого угла приближенно равен самому углу; при этом нужно помнить, что угол должен быть выражен в радианной мере. Так, например, sin 0,003 
а
2) Возьмем функцию 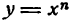
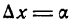
Но
и
Поэтому
или
Точно так же можно вывести равенство
По формулам (3) и (4) можно быстро найти приближенную степень числа, близкого к единице; например:
3) Выведем формулу для приближенного вычисления выражения 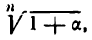
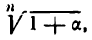
Но по формуле (3)
или
Аналогично выводится формула
По формулам (5) и (6) можно легко найти приближенное значение корня из числа, близкого к единице; например:
Кривизна кривой
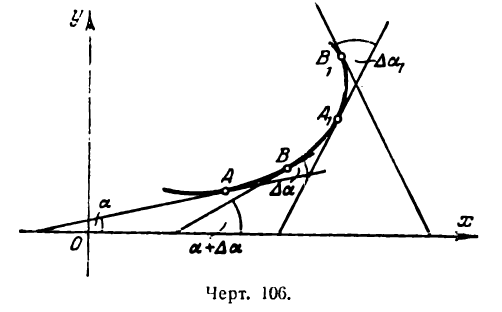
Пусть дана кривая, определяемая уравнением у = f(х) (рис. 106).
Возьмем на ней две точки А и В и проведем в них касательные к кривой. При переходе от точки А к точке В касательная меняет угол наклона к положительному направлению оси абсцисс на некоторую величину. Если обозначим угол наклона касательной в точке А к оси Ох через а, то угол наклона касательной в точке В к той же оси, получив приращение 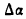
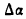
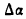
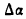
Разделив 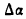
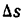
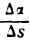
Средняя кривизна кривой на разных ее участках может быть различной.
Допустим теперь, что точка В, двигаясь по кривой, неограниченно приближается к точке А и 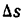
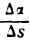
Определение:
Кривизной кривой в данной ее точке А называется предел, к которому стремится средняя кривизна дуги АВ при неограниченном приближении точки В к А.
Согласно определению производной
поэтому
Преобразуем правую часть этого равенства, выразив dа. и ds через производные данной функции у =f(x).
Согласно геометрическому смыслу производной имеем
где а — угол наклона касательной к кривой у =f(х) в точке А к положительному направлению оси абсцисс (рис. 106); отсюда
В этом равенстве аrctg у’ — функция от функции, так как аrctg у’ зависит от у’, a у’ зависит от х. Продифференцируем последнее равенство по аргументу х; получим:
отсюда
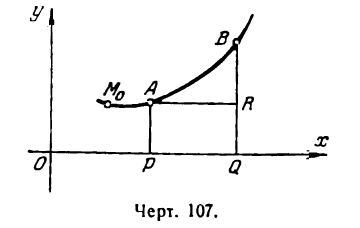
Найдем выражение ds через производную функции у =f(x). Для этого возьмем снова тот же участок АВ кривой (рис. 107).
Будем рассматривать длину АВ как приращение дуги 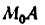

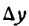

или
Разделив обе части равенства на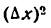
отсюда
Положим, что 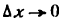
Применяя теоремы о пределе корня, суммы и степени , получим:
Но
поэтому равенство (3) примет вид
откуда
Подставив значение da и ds в выражение (1), получим:
Формула (5) позволяет найти кривизну кривой, определяемой уравнением у = f(x), в любой ее точке.
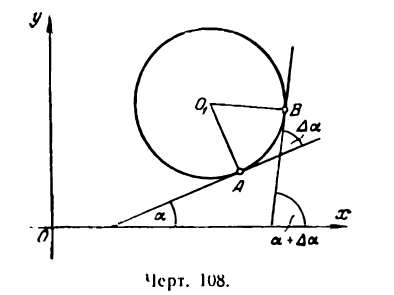
Кривизна окружности
Кривизну окружности можно определить по формуле (5) , но гораздо проще ее найти из следующих рассуждений.
Проведем касательные в двух точках А и В окружности (рис. 108).
Обозначив дугу АВ через 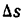
на этом участке; она выразится дробью 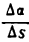
так как углы АО1В и 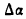
откуда
Ясно, что такой же вывод мы получим, взяв другой какой-либо участок окружности. Следовательно,
для любой точки окружности, т. е. кривизна окружности постоянна во всех ее точках и равна обратной величине ее радиуса.
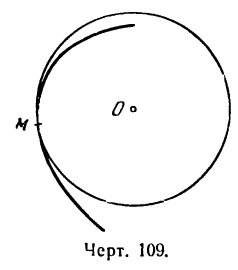
Радиус кривизны кривой
При изучении кривизны кривой подбирают такую окружность, кривизна которой равна кривизне кривой в той или иной ее точке. Центр этой окружнoсти называется центром кривизны кривой в соответствующей точке, радиус—радиусом кривизны кривой в этой точке, а сама окружность— окружностью кривизны (рис. 109).
Определение:
Окружностью кривизны в точке М кривой называется окружность, проходящая через точку М и имеющая с кривой одинаковую кривизну и общую касательную.
Заметим, что центр окружности кривизны всегда располагается со стороны вогнутости кривой.
Кривизна окружности, как мы знаем,
отсюда
Следовательно, и радиус кривизны кривой в точке ее определяется тем же равенством.
Заменив К его значением, взятым из равенства (5) , получим формулу для определения радиуса кривизны кривой в любой ее точке:
Применяя эту формулу к прямой линии, заданной, например уравнением 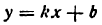
так как
Это значит, что прямую линию можно рассматривать как окружность бесконечно большого радиуса.
Пример:
Найти радиус кривизны кривой 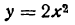
Решение:
Найдем сначала первую и вторую производные функции 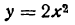
Подставив значения у’ и у» в формулу (1), получим:
Как найти дифференциал — подробная инструкция
Бесконечно малые величины
Бесконечно малые величины 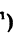
Определение:
Бесконечно малой величиной вблизи h = a называется функция, зависящая от h и имеющая предел, равный нулю при условии, что независимое переменное стремится к а.
Например, 
Бесконечно малые величины при условии, что независимое переменное стремится к нулю, будем называть «бесконечно малыми», не указывая, а только подразумевая условие 
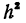

Приведем примеры геометрического и физического содержания.
Пример:
Площадь S прямоугольника со сторонами х и h является бесконечно малой при любых х, так как
Пример:
Объема прямоугольного параллелепипеда, ребра которого равны 3, 2 и 2h, является бесконечно малым, так как
Пример:
Объем v прямоугольного параллелепипеда, ребра которого равны h, 2h и 5h, является бесконечно малым, так как
Пример:
По закону Ома v = Ri, где v — напряжение, R — сопротивление и i — ток. Отсюда следует, что при постоянном сопротивлении напряжение является бесконечно малым относительно тока, так как
Пусть дана бесконечно малая величина а (h), т. е.
Рассмотрим предел отношения
Если этот предел существует и равен нулю, то бесконечно малая величина a (h) называется бесконечно малой более высокого порядка, чем h.
Если предел равен конечному числу 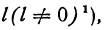
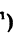
Пример:
Пусть 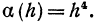
Пример:
Пусть а(h) = sin 2h; а(h) — бесконечно малая того же порядка, что и h , поскольку
Пример:
а (h) = sin h —бесконечно малая, эквивалентная h , так как
Пример:
a( h ) = l — cos h . Так как
то 1—cos h есть бесконечно малая более высокого порядка, чем h .
В заключение параграфа рассмотрим функцию y = f(x). Пусть приращение независимого переменного равно А, тогда приращение функции равно
Так как приращение h независимого переменного х не зависит от величины х, то для вычисления 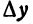
Пример:
Пусть дана функция 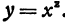
Если x = 3, а h =1, то
Если же x = 0 и по-прежнему h =1, то
Здесь h сохраняет значение 1, но, поскольку х меняется, изменяется и 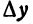
Если x = 2, а h = 1, то
Если же x = 2, а h = 0,5, то
Здесь х сохраняет значение 2, но h меняется, поэтому меняется и 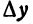
Если f(х)—функция непрерывная, то, по определению, ее приращение 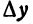
Дифференциал
Пусть дана непрерывная функция у = f(х), имеющая производную. Тогда, по определению производной,
Поэтому, если в правой части откинем знак предела, то получим ошибку, величина которой зависит и от x и от h. Обозначим эту ошибку через а( x , h ). Тогда вместо равенства (1) можно написать
Про ошибку а( x , h ) мы знаем, что
Это следует из равенства (1). Значит, ошибка а( x , h ) является бесконечно малой относительно приращения h независимого переменного.
Если умножим обе части равенства (2) на h , то получим
или
В левой части равенства (4) стоит приращение функции 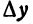
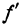
Очевидно, что первый член
одного порядка с h , т. е. является линейным относительно h , а второй член а(x , h)h является бесконечно малой величиной более высокого порядка относительно h .
Из равенства (4) получаем, что приращение функции с точностью до бесконечно малой высшего порядка равно f'(х)h ; это выражение называется дифференциалом функции.
Определение. Дифференциал есть та часть при-ращения функции 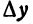
Дифференциал функции обозначают или dy, или df(x), так что
Для симметрии записей вводится определение дифференциала независимого переменного.
Определение:
Дифференциалом независимого переменного называется его приращение.
Дифференциал независимого переменного обозначается dx, так что имеем
Операция нахождения дифференциала называется дифференцированием.
Пример:
Найдем дифференциал функции у = sin х. Так как (sin х)’ = cos х, то dy = dsin х = cos х • h = cos xdx.
Пример:
Вычислим значение дифференциала функции 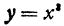
Так как
Подставляя сюда вместо х его значение 2, а вместо dx его значение 0,1, получим
Из определения дифференциала функции следует, что дифференциал функции одного переменного является функцией двух переменных. Из формул (5) и (6) следует, что
Таким образом, производная равна отношению дифференциала функции к дифференциалу независимого переменного.
С этого момента для обозначения производной будем пользоваться и знаком ( )’ и отношением дифференциалов.
Таблица дифференциал
Применение к приближенным вычислениям
Перепишем формулу (4) § 2 в следующем виде:
и для начала посмотрим на примере, как будут выглядеть отдельные ее члены при некоторых числовых значениях х и h.
Пример:
Пусть 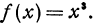
С другой стороны, применяя формулу (1) и зная, что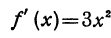
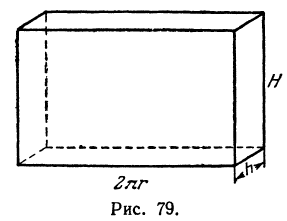
Сравнивая формулы (*) и (**), видим, что в левых частях стоит одно и то же, в правых же частях совпадают первые два члена, следовательно, третий член в формуле (**) равен двум последним членам в формуле (*), т. е.
Вычислим все члены, встречающиеся в этом примере, при указанных числовых значениях х и h:
Если бы мы захотели вычислить 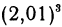
Аналогично в общем случае формулу (1) заменяют приближенной формулой, откидывая бесконечно малую высшего порядка, т. е. член а (x, h)h . Тогда получается приближенная формула
(знак 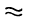
Приведем примеры применения формулы (2).
Пример:
Выведем приближенную формулу для вычисления кубического корня. Возьмем 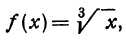
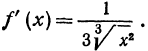
Если положить 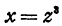
Отсюда видно, что если нам известен кубический корень из числа, то для близких чисел можно с удобством воспользоваться выведенной формулой. Например, зная, что 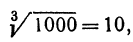
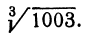
Сделаем проверку, возведя 10,01 в куб. Видим, что вместо 1003 получили число 1003,003001, т. е. ошибка меньше 0,005.
Пример:
Выведем приближенную формулу для вычисления тангенсов малых углов. Так как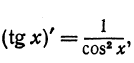
Зная, что tg 0 = 0 и cos 0=1, и полагая в предыдущей формуле x = 0, найдем
Напоминаем, что здесь h есть радианная мера угла. Например, вычислим tg3°. Переведем сначала градусную меру угла в радианную:
тогда
Дифференциал площади криволинейной трапеции
Определение:
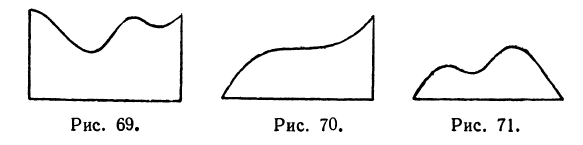
Криволинейной трапецией называется плоская фигура, ограниченная с трех сторон прямыми, а с четвертой стороны кривой. При этом две прямые параллельны между собой и перпендикулярны третьей, а кривая пересекается с любой прямой, параллельной боковым сторонам, в одной точке.
Не исключается случай, когда одна или обе боковые стороны обращаются в точку. На рис. 69, 70, 71 изображены криволинейные трапеции.
Все плоские фигуры, с которыми нам придется встречаться, могут быть представлены как совокупность криволинейных трапеций. Например, на рис. 72 фигура разбита на четыре криволинейные трапеции.
Конечная наша цель — определить площадь криволинейной трапеции, но пока эту задачу мы еще не можем решить. Однако мы сумеем найти дифференциал площади криволинейной трапеции. Решим эту задачу, предполагая, что трапеция расположена определенным образом.
Пусть дана криволинейная трапеция АВСD, ограниченная осью Ох, двумя прямыми, перпендикулярными этой оси, и кривой, заданной уравнением у=f(х) (рис. 73).
Будем считать, что прямая АВ неподвижна в процессе всех рассуждений, т. е. абсцисса точки А есть постоянная величина. «Прямую же СD будем двигать, т. е. абсцисса точки D будет переменной. Обозначим ее через х.
Ясно, что площадь криволинейной трапеции АВСD будет изменяться в зависимости от величины х, значит, площадь есть функция х. Обозначим ее F(х). Этой функции мы не знаем, но несмотря на это найдем ее дифференциал.
Дадим х приращение h = DК, тогда площадь F(x) получит приращение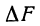
При изменении независимого переменного от величины х до х + h (от точки D) до точки К) функция f(х), т. е. ордината точки, лежащей на кривой, также изменяется и при этом достигает наибольшего значения М и наименьшего значения т. На рис. 73 QR = М и NР= т.
Рассмотрим прямоугольник с основанием DК и высотой QR = М , его площадь равна Т1= Мh. Прямоугольнике тем же основанием DK = h и высотой NР = т имеет площадь, равную T2 = тh.
Очевидно, что площадь второго прямоугольника Т2 меньше площади T1 первого на величину (М— т)h . Также очевидно, что площадь второго прямоугольника меньше приращения 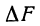
Следовательно, приращение 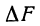
Обозначим разность между приращением 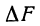
Величина 
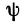
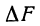
Остановимся на формуле (1) и проследим, как меняются ее члены при стремлении h к нулю.
Предварительно заметим, что, во-первых, всегда, т. е. при любых значениях x,
и, во-вторых, если 
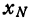

Функция f(х) предполагается непрерывной. В силу свойств непрерывной функции (см. гл. VI, § 6) находим
а это значит, что можно записать (см. начало § 2 этой главы)
где а—бесконечно малая относительно h. Также можно заключить, что
где 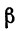
Исследуем порядок малости членов, стоящих в правой части равенства (1). Для этого найдем следующие пределы:
Первый предел находим непосредственно [применяя (3)]:
Чтобы найти второй предел, найдем сначала [используя (4) и (5)]
Так как 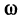
а в силу равенства (7)
Таким образом, установлено, что и mh и 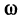
Учитывая все эти рассуждения и применяя равенство (4), можно переписать равенство (1) в виде
В правой части равенства (8) стоят три члена. Каждый из них является бесконечно малым относительно h первый из них линеен относительно h, а два других имеют высший порядок малости.
Применяя результаты § 2, заключаем, что приращение площади криволинейной трапеции равно f(x)h плюс величина высшего порядка относительно h , а поэтому дифференциал площади криволинейной трапеции равен f(x)h , т. е.
Этим результатом мы воспользуемся в следующих главах.
Пример:
Найдем дифференциал площади F криволинейной трапеции, ограниченной осью Ох, кривой, заданной уравнением 
Применяя только что полученный результат, будем иметь
Пример:
Найти производную от площади криволинейной трапеции, ограниченной осью Ох, кривой, заданной уравнением у = sin x, прямой х = 2 и подвижной прямой, параллельной оси Оу.
Находим дифференциал этой площади: dF = sin x dx, а следовательно и производную:
Применение дифференциала к различным задачам
Рассуждения не только приводят к понятию дифференциала, но в некоторых случаях позволяют найти производную. Предположим, что приращение некоторой функции представлено в виде
где 
Тогда
откуда
т. е. 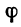
Пример:
Найти производную от функции f(x), определенной геометрически как объем, ограниченный:
1) поверхностью Р, полученной от вращения вокруг оси Ох дуги ОА, принадлежащей параболе 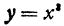
2) плоскостью П1, перпендикулярной оси Ох и отстоящей от начала координат на расстояние х (рис. 74).
Ясно, что объем зависит от величины х, т. е. является функцией х .
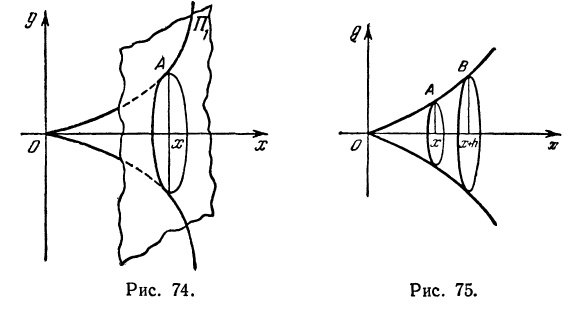
Возьмем произвольное число х. Соответствующее значение функции f(х) будет определяться объемом, ограниченным поверхностью Р и плоскостью П1 . Дадим х приращение h. Объем, т. е. функция f(x), в связи с этим получит приращение 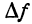
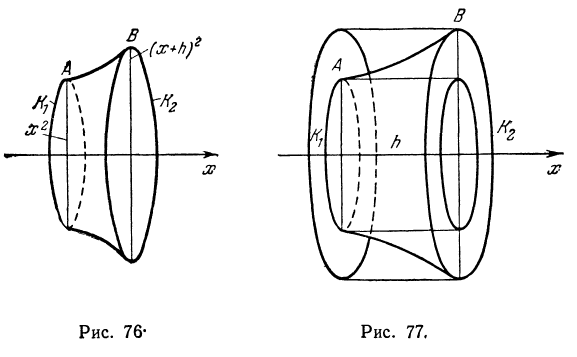
Рассмотрим два цилиндра: первый из них имеет основанием К1, образующую, параллельную оси Ох, и высоту h, второй имеет основанием К2 и образующую, также параллельную оси Ох (рис. 77).
Объем первого цилиндра обозначим через W1 второго — через W2 . Из чертежей ясно, что приращение функции 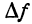
Но oбъемы W1 и W2 легко подсчитать:
Разность объемов W1 и W2 (т. е. объем цилиндрического кольца) равна
Приращение 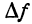
где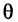
то член 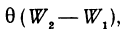
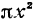
В этом примере следует обратить внимание на то, что функция f(х) была определена чисто геометрически, нам не была известна формула, определяющая эту функцию, однако производную мы нашли.
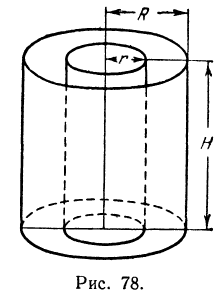
Пример:
Рассмотрим цилиндрическую трубу, у которой радиус внешней поверхности R, радиус внутренней поверхности r, высота H. Найдем объем V материала, из которого сделана эта труба (рис. 78).
Будем называть этот объем объемом цилиндрического слоя. Поскольку объем внешнего цилиндра равен 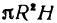
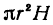
или
Если стенка трубы тонкая, то r и R мало отличаются друг от друга. Обозначим их разность через h (h = R — r). Тогда формула (*) примет вид
или
Второй член, стоящий в правой части равенства (*), второго порядка относительно h. Поэтому при 
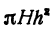
Интересно отметить еще один способ получения этой формулы (рис. 79).
Если разрезать трубку вдоль ее образующей и развернуть на плоскость, то получим «почти» прямоугольный параллелепипед с измерениями 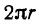
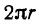
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Содержание:
- Приращение аргумента и функции
- Определение производной
- Дифференцирование функции
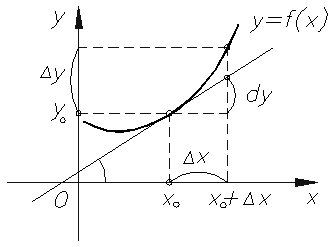
Пусть задана некоторая функция $y=f(x)$. Возьмем какое-нибудь
значение $x_{0}$ из области определения этой функции:
$x_{0} in D[f]$ . Соответствующее значение функции в этой точке
будет равно $y_{0}=fleft(x_{0}right)$ .
Приращение аргумента и функции
Определение
Приращением аргумента называется разность между двумя значениями аргумента: “новым” и “старым”.
Обычно обозначается как $Delta x=x_{1}-x_{0}$ .
Пример
Задание. Найти приращение аргумента $x$, если он переходит от значения 3 к значению 3,2.
Решение. Искомое приращение: $Delta x=3,2-3=0,2$ .
Ответ. $Delta x=0,2$
Зададим аргументу $x_{0}$ приращение
$Delta x$. А тогда значение функции в новой точке
$fleft(x_{0}+Delta xright)$.
Определение
Приращением функции $y=f(x)$ в точке
$x_{0}$, соответствующее приращению аргумента
$Delta x=x-x_{0}$, называется величина:
$Delta y=fleft(x_{0}+Delta xright)-fleft(x_{0}right)$

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти приращение функции $y=2 x^{2}$
при $x_{0}=3$ и
$Delta x=0,1$
Решение. Подставляя в формулу, получаем, что приращение функции:
$Delta y=y(3+0,1)-y(3)=2 cdot(3+0,1)^{2}-2 cdot 3^{2}=1,22$
Ответ. $Delta y=1,22$
Определение производной
Определение
Производной $y^{prime}(x)$ от функции
$y=f(x)$ в точке
$x_{0}$ называется предел отношения
приращения функции $Delta y$ к приращению аргумента
$Delta x$ :
$frac{Delta y}{Delta x}$ при
$Delta x rightarrow 0$, если он существует, то есть:
$y^{prime}left(x_{0}right)=f^{prime}left(x_{0}right)=lim _{Delta x rightarrow 0} frac{Delta y}{Delta x}=lim _{Delta x rightarrow 0} frac{fleft(x_{0}+Delta xright)-fleft(x_{0}right)}{Delta x}$
или
$y^{prime}left(x_{0}right)=lim _{x rightarrow x_{0}} frac{f(x)-fleft(x_{0}right)}{x-x_{0}}$
Пример
Задание. Найти производную функции $y=x^{2}+3 x$
в точке $x_{0}=0$.
Решение. Найдем приращение заданной функции в точке $x_{0}$ :
$Delta y=y(0+Delta x)-y(0)=y(Delta x)-y(0)=$
$=(Delta x)^{2}+3 Delta x-0=Delta x(Delta x+3)$
Тогда
$y^{prime}(0)=lim _{Delta x rightarrow 0} frac{Delta x(Delta x+3)}{Delta x}=lim _{Delta x rightarrow 0}(Delta x+3)=0+3=3$
Ответ. $y^{prime}(0)=3$
Дифференцирование функции
Определение
Операция нахождения производной функции называется дифференцированием этой функции.
Функция $y=f(x)$ имеет производную на интервале
$(a ; b)$ или называется дифференцируемой в этом
интервале, если производная $f^{prime}(x)$ существует в каждой точке этого интервала.
Функция $y=f(x)$ имеет в точке
$x$ бесконечную производную, если в этой точке
$f^{prime}(x)=lim _{Delta x rightarrow 0} frac{Delta y}{Delta x}=infty$ .
Теорема
(О непрерывности функции в точке)
Если функция $y=f(x)$ имеет конечную производную в
точке $x_{0}$ , то она непрерывна в этой точке.
Замечание. Обратное заключение не всегда верно: если функция $y=f(x)$
непрерывна в некоторой точке $x_{0}$ , то она может
и не иметь производной в этой точке.
Определение
Функция $y=f(x)$ называется дифференцируемой
в точке $x$, если приращение функции,
соответствующее приращению аргумента, можно представить в виде:
$Delta y=A cdot Delta x+alpha(Delta x) cdot Delta x$
где $A$ – число, не зависящее от
$Delta x$,
$alpha(Delta x)$ – б.м. функция при
$Delta x rightarrow 0$.
Теорема
(О необходимом и достаточном условии дифференцируемости)
Для того чтобы функция $y=f(x)$ была дифференцируемой
в точке $x$, необходимо и достаточно,
чтобы $y=f(x)$ имела в этой точке конечную производную.
Теорема устанавливает, что для функции $y=f(x)$
дифференцируемость в данной точке $x$ и существование конечной производной в этой точке – понятия равносильные.
Читать дальше: односторонние производные.
Лекция 9. Экономические задачи, решаемые методами
дифференциального исчисления. Приращение величины, аргумента,
функции. Скорость изменения функции
Дифференциальное
экономического
анализа
исчисление
–
широко
математический
аппарат.
применяемый
Базовой
для
задачей
экономического анализа является изучение связей экономических величин,
записываемых в виде функций. В каком направлении изменится доход
государства при увеличении налогов или при введении импортных пошлин?
Увеличится или уменьшится выручка фирмы при повышении цены на ее
продукцию? В какой пропорции дополнительное оборудование может заменить
выбывающих работников? Для решения подобных задач должны быть
построены функции связи входящих в них переменных, которые затем
изучаются с помощью методов дифференциального исчисления.
В экономике очень часто требуется найти наилучшее, или оптимальное
значение того или иного показателя: наивысшую производительность труда,
максимальную прибыль, максимальный выпуск, минимальные издержки и т.д.
Каждый показатель представляет собой функцию одного или нескольких
аргументов. Например, выпуск можно рассматривать как функцию затрат труда
и капитала (как это делается в производственных функциях). Таким образом,
нахождение оптимального значения показателя сводится к нахождению
экстремума (максимума или минимума) функции одной или нескольких
переменных. Подобные задачи порождают класс экстремальных задач в
экономике,
решение
которых
требует
использования
методов
дифференциального исчисления. Если экономический показатель y нужно
максимизировать или минимизировать как функцию другого показателя x
(например, задача на максимум прибыли как функции объема выпуска), то в
оптимальной точке (т.е. в точке максимума) приращение функции y на
приращение аргумента x должно стремиться к нулю, когда приращение
аргумента стремится к нулю. Иначе, если такое приращение стремится к
некоторой положительной или отрицательной величине, рассматриваемая точка
не является оптимальной, поскольку увеличив или уменьшив аргумент x,
можно
изменить
величину
в
y
нужном
направлении.
В
терминах
дифференциального исчисления это означает, что необходимым условием
=
экстремума функции
является равенство нулю ее производной.
В экономике часто приходится решать задачи на экстремум функций
нескольких переменных, поскольку экономические показатели обычно зависят
от многих факторов. Такие задачи хорошо изучены теорией функций
нескольких
переменных,
исчисления.
Многие
(минимизируемую)
использующей
задачи
функцию,
включают
но
и
методы
не
дифференциального
только
ограничения
максимизируемую
(скажем,
бюджетное
ограничение в задаче потребительного выбора). Это – задачи математического
программирования, для решения которых разработаны специальные методы,
также опирающиеся на дифференциальное исчисление.
Важный раздел методов дифференциального исчисления, используемых в
экономике, называется методами предельного анализа. Предельный анализ в
экономике – совокупность приемов исследования изменяющихся величин
затрат или результатов при изменениях объемов производства, потребления и
т.п. на основе анализа их предельных значений. Предельный показатель
(показатели) функции
=
– это ее производная (в случае функции одной
переменной) или частные производные (в случае функции нескольких
переменных).
В
экономике
широко
используются
средние
величины:
средняя
производительность труда, средние издержки, средний доход, средняя прибыль
и т.д. Но часто требуется узнать, на какую величину вырастет результат, если
будут увеличены затраты или, наоборот, насколько уменьшится результат, если
затраты сократятся. С помощью средних величин ответ на этот вопрос
получить невозможно. В подобных задачах требуется определить предел
отношения приростов результата и затрат, т.е. найти предельный эффект.
2
Следовательно,
для
их
решения
необходимо
применение
методов
дифференциального исчисления – нахождения производной в случае функции
одной переменной и частных производных, если функция зависит от
нескольких аргументов.
Так, например, если задана производственная функция:
где
=
,…,
,…,
– объем затрачиваемого i-го ресурса
,
= 1, … ,
, y – максимальный
объем выпуска, который можно получить, затрачивая ресурсы соответственно в
объемах
,…,
,…,
, то предельный эффект от использования i-го ресурса
определяется следующим образом:
,…,
=
+ ∆ ,…,
−
∆
,…,
,…,
.
равна дополнительному объему выпуска, который
Здесь величина
получается в результате затраты дополнительной единицы ∆
i-го ресурса при
неизменных объемах остальных ресурсов.
Показатель
предельного
эффекта
в
оптимизационных
моделях
применяется для нахождения оптимального объема производства при заданных
ресурсах, а также для определения оптимального распределения ограниченных
ресурсов по различным направлениям их использования. Если максимальный
показатель (например, прибыль) есть разность результата и издержек (в данном
случае результат представлен выручкой), то в оптимальной точке предельная
выручка должна равняться предельным издержкам. Такое равенство должно
выполняться по каждому из факторов, определяющих выручку и издержки, что
вытекает из необходимости равенства нулю частных производных прибыли по
всем этим факторам.
Необходимые
и
достаточные
условия
оптимума
во
многих
экономических задачах записываются с помощью частных производных и
дифференциалов.
Так,
если
решается
задача
на
максимум
выпуска,
описываемого с помощью приведенной выше производственной функции, при
наличии ограничения по общему расходу денежных средств на используемые в
3
производстве ресурсы, то в оптимальной точке должны быть равны между
собой отношения предельных производительностей ресурсов
и их цен.
Иными словами, для всех ресурсов должен быть одинаков предельный эффект
в расчете на единицу дополнительно расходуемых на эти ресурсы денежных
средств.
В
задаче
потребительского
выбора
отношение
предельных
полезностей благ должно быть равно отношению их цен. Иначе говоря,
предельная полезность в расчете на одну денежную единицу должна быть в
оптимальной точке одинакова по всем благам; в противном случае бюджет
потребителя мог бы быть перераспределен с увеличением его благосостояния.
Таким образом, методы дифференциального исчисления позволяют не только
решить различные экономические задачи, но и записать необходимые или
достаточные условия оптимума в этих задачах, которые позволяют дать ответ
на те или иные конкретные вопросы.
Широко используется в экономическом анализе понятие дифференциала,
или главной линейной части приращения функции. Так, если некоторая
и
величина y есть функция двух аргументов
, то с использованием
дифференциала легко рассчитать предельную норму замены между этими
аргументами, т.е. величину, показывающую, сколько нужно фактора 2 для
замены одной единицы фактора 1 с сохранением значения функции y.
Предельная норма замены важна в задачах потребительского выбора
(взаимозаменяемость
благ),
в
задачах
оптимизации
производства
(взаимозаменяемость труда и капитала) и в ряде других задач. Пусть
,
=
. Если мы хотим сохранить значение функции y неизменным, то это
означает, что приращение y, а значит и его главная линейная часть должны
быть равны нулю. Иным словами, 0 =
предельная норма замены −
=
=
∙
+
∙
. Отсюда
, т.е. равняется отношению частных
производных функции y по первому и второму факторам.
Методы дифференциального исчисления широко применяются не только
для анализа взаимодействия отдельных экономических факторов, определения
4
их взаимозаменяемости или оптимального сочетания, но и в сложных моделях
экономики,
в
частности
в
моделях
экономической
динамики.
Дифференциальное исчисление – это не только аппарат, позволяющий
находить решения таких моделей, но и необходимый составной элемент для их
построения. Динамические модели применяются для решения таких задач, как
определение
оптимальной
или
равновесной
траектории
развития
экономической системы, ее состояний в заданные моменты времени, анализ
системы на устойчивость, анализ структурных сдвигов и т.п.
Из
рассмотренных
направлений
применения
дифференциального
исчисления в экономике важнейшим является вопрос нахождения и анализа
взаимосвязей экономических переменных, определяющих функционирование
экономического объекта или протекание экономического явления, который мы
сейчас рассмотрим более подробно.
Анализ взаимосвязей экономических показателей
Анализируя взаимосвязи экономических показателей, мы должны
последовательно ответить на четыре вопроса. Какие факторы определяют
интересующий нас экономический показатель? Каков знак этой зависимости?
Какова степень этой зависимости? Каково числовое (функциональное)
выражение соответствующей зависимости?
Рассмотрим возможные ответы на эти вопросы на примере простейшей
экономической зависимости – функции спроса.
От чего зависит (от каких факторов)?
В ответ на этот вопрос надо перечислить все факторы, определяющие
исследуемый экономический показатель. В частности, величина спроса
!
на
какой-либо товар определяется ценой этого товара p, доходом потребителей I,
ценами на другие товары (дополняющие (C) или заменяющие (S) данный
товар), ожидаемыми ценами и ожидаемым доходом. Сокращенно это можно
записать так:
5
!
=
, “, #,
$
,
%
,
&
, “& , … .
Как зависит (положительно или отрицательно)?
В ответ на этот вопрос надо определить характер взаимосвязи.
Исследуемый показатель связан с каким-либо фактором положительно, если
его значение возрастает при увеличении фактора, и отрицательно, если его
значение уменьшается при увеличении фактора. В частности, величина спроса
!
на какой-либо товар уменьшается при увеличении его цены p, увеличивается
(для нормальных товаров) или уменьшается (для некачественных товаров) при
увеличении дохода потребителей I, уменьшается при увеличении цен на
дополняющие товары и увеличивается при увеличении цен на заменяющие
данный товар товары, увеличивается при ожидании повышения цен или
доходов. Сокращенно это можно записать так:
!
=
) ±
+
+ ±
( , ,$ , ,% , ,& , “(&
” ,#
‘( , (
+ )
, … -.
Какова степень зависимости?
Для ответа на этот вопрос надо определить, насколько чувствителен
исследуемый экономический показатель к изменению определяющих его
факторов. Другими словами, какова степень его изменения при заданном
абсолютном или относительном изменении факторов.
∆ =∈, ∆
!
=? или ∆” =∈, ∆
!
=?
Имеются два подхода к анализу чувствительности зависимости
Приростной подход ∆ ⟹ ∆ .
=
.
Прирост фактора ⟹ прирост исследуемого показателя
(изменение x) ⟹ (изменение y)
Мера “абсолютной” чувствительности – скорость изменения функции
(средняя (отношение изменений) или предельная (производная)):
∆
∆
→ lim
≡
∆ →8 ∆
∆
Темповый подход %∆ ⟹ %∆ .
≡
.
Темп прироста фактора ⟹ темп прироста исследуемого показателя
6
(процентное изменение x) ⟹ (процентное изменение y)
Напомним, что процентное изменение какой-либо переменной – это
отношение изменения этой переменной к первоначальному ее значению:
%∆ =
∆
=
−
.
Например, если цена буханки хлеба увеличилась с 200 до 300 рублей, то
процентное изменение цены:
300 − 200
= 50%.
200
Мера “относительной” чувствительности – эластичность функции
%∆ =
(средняя
(отношение
процентных
изменений)
или
производной)):
%∆
∆ /
%∆
→ lim
≡ lim
≡
%∆ →8 %∆
∆ →8 ∆ /
%∆
∙
≡
предельная
∙
( ≈
.
Каково функциональное выражение зависимости?
Для ответа на этот вопрос надо указать конкретное функциональное
выражение исследуемой зависимости (в виде формулы, графика или таблицы).
Эту зависимость можно получить либо из теоретической модели или из
эконометрического (эмпирического) исследования. Например, функция спроса
на какой-либо товар может определяться следующим выражением:
!
=
8
−@∙
−A∙
или изображаться прямой линией на графике.
$
+B∙
%
Другим не менее важным направлением дифференциального исчисления
является его применение к принятию оптимальных решений.
Принятие оптимальных решений
Пусть, например, монополист, зная (из маркетинговых исследований)
функцию спроса на свой товар, решает, сколько ему производить и по какой
цене продавать свой товар.
7
Если он установит достаточно высокую цену, то потребители за
определенный период купят у него не слишком много товара. Если он будет
производить больше, то ему придется понизить цену, чтобы распродать все
выпускаемое им количество за определенный период времени. При этом
выручка увеличится за счет увеличения объема продаж (выигрыш) и
одновременно уменьшится за счет уменьшения цены (потери). Результат будет
зависеть от того, что окажется большим: выигрыш или потери. Как же все-таки
монополист может определить зависимость выручки (или прибыли, если
учитывать издержки выпуска) от объема выпуска C ∙ D
=
∙
−E
=D
−E
=
и определить, при каком объеме выпуска прибыль
будет максимальна.
Из фундаментальных разделов теории математического анализа известно,
что задача определения максимума функции решается с помощью понятия
производной. Для этого надо знать ответы на два вопроса:
1. Как находить производные произвольных функций?
2. Как применять производные к исследованию функций?
Ответы на эти вопросы будут подробно освещены в следующей лекции.
Для ответа на первый вопрос мы рассмотрим определение и геометрический
смысл производной, формулы для нахождения производных нескольких
простейших
(элементарных)
функций
и
правила
дифференцирования,
позволяющие находить производные от любых комбинаций элементарных
функций.
Для ответа на второй вопрос мы рассмотрим связь знака и величины
производной с возрастанием, убыванием функций и определим необходимые и
достаточные условия экстремума (максимума или минимума) функций.
Приращение величины, аргумента, функции. Скорость изменения
функции
8
Приращение величины, аргумента, функции. Пусть величина z
меняется от значения F (начальное значение) до значения F
значение). Тогда величина ∆F
величины
z.
Приращение
F
F
Fкон
возрастающей
(конечное
Fнач называется приращением
величины
Fкон L Fнач
будет
положительно: ∆F L 0, а приращение убывающей величины Fнач L Fкон будет
отрицательно: ∆F M 0 . Если величина z не изменилась Fнач
приращение будет равно нулю: ∆F
Пусть дана функция
0.
и два значения аргумента
соответствуют два значения функции
∆
Fкон , то ее
и
называется приращением аргумента, а ∆
и
. Им
. Разность
∆
– приращением функции.
, ∈ NO; QR . Возьмем произвольную точку
Рассмотрим функцию
8
∈ NO; QR . Для любого
аргумента x в точке
8
8
8
8
называется приращением
и обозначается ∆ . Таким образом, ∆
∆ . Разность
и обозначается ∆
∈ NO; QR разность
8
8
называется приращением функции
(или ∆ , или ∆
8,
в точке
. Геометрическая интерпретация
этих величин показана на рис. 1.
9
Следовательно,
∆
=
8
−
8
=
8
+∆
В этих терминах можно сказать, что функция
−
8
непрерывна в точке
тогда и только тогда, когда приращение функции в точке
если приращение аргумента стремится к нулю.
.
8
8
стремится к нулю,
Скорость изменения функции на интервале (средняя скорость).
Если рассмотреть две разных, но монотонно возрастающих функции
(например, y1 = √
и y2 = T ), то можно отметить по их графикам, что
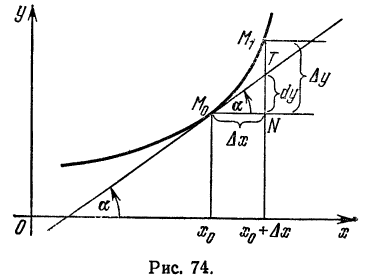
значения каждой из них меняется при изменении аргумента на величину
∆ =
−
8.
Из графиков видно, что вторая функция меняется (возрастает)
сильнее, чем первая, на интервале
8;
.
Для сравнения величин изменения различных функций при одинаковом
изменении аргумента вводится понятие скорости (быстроты) изменения
функции на интервале
изменения
функции,
8;
(средней скорости), определяемой как отношение
вызванного
изменением
соответствующему изменению аргумента.
Скорость изменения функции на интервале
8;
=
ее
аргумента,
к
Изменение функции
Изменение аргумента
Обозначая скорость буквой v, запишем это соотношение в виде:
de
8; ∆
=
∆
∆
8
=
+∆
∆
−
8
=
−
−
8
8
.
Из этого соотношения вытекает, что если при равных изменениях
аргумента f∆
=∆
g одна из функций меняется сильнее f∆
>∆
g,
то и скорость изменения второй функции на рассматриваемом интервале будет
больше, чем первой hd 2 > d 1 i.
Геометрический смысл скорости изменения функции на интервале
8;
(средней скорости) заключается в том, что она численно равна тангенсу угла
наклона отрезка, соединяющего две точки графика функции, соответствующих
10
значениям аргумента
8
и x. Недостаток такого определения скорости состоит в
том, что эта скорость зависит не только от точки
8,
относительно которой
рассматривается изменение аргумента, но и от самой величины изменения
аргумента, т.е. от величины интервала ∆ , на котором определяется скорость.
Для устранения этого недостатка вводится понятие скорости изменения
функции в точке (мгновенной скорости).
Скорость изменения функции в точке (мгновенная скорость).
8
Для определения скорости изменения функции в точке
точки x и
8,
сближают
устремляя интервал ∆ к нулю. Изменение непрерывной функции
при этом будет также стремиться к нулю. При этом отношение стремящегося к
нулю изменения функции к стремящемуся к нулю изменению аргумента дает
8
скорость изменения функции в точке
(мгновенной скорости), точнее, на
8
бесконечно малом интервале относительно точки
de
8
= lim
∆ →8
∆
∆
8
+∆
= lim
∆ →8
∆
−
Именно эту скорость изменения функции
производной функции
в точке
8.
8
= lim
→ j
в точке
8
−
−
8
8
.
и называют
Геометрический смысл скорости изменения функции в точке
8
(мгновенной скорости) в том, что она численно равна тангенсу угла наклона
касательной к графику функции в точке
8.
Это непосредственно следует из ее
определения, поскольку при сближении точек
8
и x точки пересечения графика
функции прямой линией также сближаются и сливаются в одной точке, в
которой линия и касается графика функции.
11