Бетон и арматура,
хотя и работают совместно, но имеют
разные модули упругости: при одинаковых
деформациях в них возникают разные
напряжения. Чтобы подсчитать их, сечения
приводят к одному материалу (обычно к
бетону) через коэффициент приведения
= Еs
/ Eb, гдеЕsиЕb– модули упругости арматуры и бетона
(начальный). Такие сечения называют
приведенными. Поясним примером.
Требуется определить
напряжения в бетоне преднапряженного
элемента, обжатого осевой силой Р =
spAsp,
гдеАsp– площадь сечения
напрягаемой арматуры. После обжатия
элемент упруго укорачивается на величинуl, илиb
= l/
l(рис. 23,а), причем вместе с бетоном
укорачивается и напрягаемая арматура:sp
= b.
Усилие в ней падает на величинуР
= spAsp
= spEsAsp.
Поскольку sp
= b,
аЕs = Еb,
тоsp=
spEs
= bEb
= (bp/Eb)Eb=
=bp,гдеbp
– установившееся напряжение в
бетоне. Условие равновесия:Р – Р
= Nbp, илиР = Nbp +
P, гдеNbp=bpAbусилие, воспринимаемое
бетоном,Аb– площадь
бетонного сечения,Р
= spAsp
=bpAsp.
ОтсюдаР = bpАb
+bpAsp
= bpAred,
гдеАred =Аb +
Aspплощадь приведенного
сечения. Тогда bp
= P/Ared.
Следовательно,
чтобы вычислить напряжения в бетоне
при обжатии, вовсе не обязательно
учитывать упругое укорочение арматуры
и падение в ней усилия Рдостаточно первоначальное значениеРподелить на площадь приведенного
сечения.
В более сложных
случаях одной площади недостаточно.
Например, чтобы вычислить bp
в любой точке приведенного сечения
при внецентренном обжатии (рис. 23,б)
требуется знать статический моментSred(для нахождения центра
тяжести приведенного сечения) и момент
инерцииJred. Тогдаbp
= Р/Ared Peopy/Jred, гдеy– расстояние от
центра тяжести до интересующей точки.
50. Чем отличаются стадии работы обычных и преднапряженных железобетонных элементов?
Рассмотрим работу
центрально растянутого элемента (рис.
24) с обычной (а) и напрягаемой (б) арматурой.
У элемента с обычной арматурой до
приложения внешней нагрузки напряжения
отсутствуют (если пренебречь влиянием
усадки) – стадия 1. С приложением внешней
силы N в бетоне и арматуре появились
растягивающие напряжения (стадия 2),
причем из условия совместности деформаций
в арматуре напряжения враз больше, чем в бетоне:bt
= s;
bt =
Ebb;
s =
Ess,
откудаs =
btEs/Eb=
bt.
По мере ростаNбетон достигает
предела прочности на растяжение (bt
=Rbt), а напряжения в
арматуре составляютs
= 2Rbt,
где цифра 2 учитывает удвоение, по
сравнению с упругой частью, деформаций
в бетонеbtк моменту его разрыва (см. диаграмму
на рис.1). Внешняя силаNна момент
образования трещин (разрыва бетона)
составляетNcrc = = Nbt
+ Ns = RbtAb
+ 2RbtAs
= Rbt (Ab + 2As),
гдеАb и As– площади сечения соответственно бетона
и арматуры. После образования трещин
вся нагрузка воспринимается арматурой
(стадия 3):N = sAs.

Рис. 34
У элемента с
напрягаемой арматурой на стадии 1
арматура натянута и закреплена на
упорах, в ней проявились первые потери
(кроме потерь от быстронатекающей
ползучести). Стадия 2 – натяжение
отпущено, бетон обжат силой Р1
= sp1Asp,
напряжения в немbp1
= P1 /Ared,
напряжения в арматуре уменьшились за
счет быстронатекающей ползучести и
упругого укорочения бетона и составилиsp1
– bp1.
Стадия 3 – проявляются вторые потери,
сила обжатия уменьшается до величиныР2, напряжения в бетоне –
до величиныbp2
= P2 /Ared,
а напряжения в арматуре – до величиныsp2
– bp2.
Стадия 4 – приложена внешняя нагрузкаN, по мере роста которой напряжения
в бетонеbp2падают до нуля, а напряжения в арматуре
растут на величинуbp2– сила обжатия бетонаР2погашена, элемент возвращается в исходное
положение на стадии 1, но с одной
существенной оговоркой: в бетоне
проявились деформации усадки и ползучести,
а в арматуре безвозвратно потеряна
часть напряжений. Условие равновесия:N = P2 = sp2Asp.
Стадия 5 – бетон растягивается до
напряженийbt
= Rbtпри нагрузке
Ncrc. Условие равновесия:
Ncrc =
Nbt
+ Ns,гдеNbt
= RbtAb,
Ns = P2 + Nsp
= sp2Asp
+ 2RbtAsp.
Окончательно:Ncrc= P2
+ Rbt (Ab+ 2Asp).
Стадия 6 – после образования трещин
бетон выключается из работы и всю
нагрузку воспринимает одна арматура
(так же, как элемент с обычной арматурой
на стадии 3).
Таким образом,
трещиностойкость (т.е. усилие образования
трещин Ncrc) преднапряженного
элемента по сравнению с обычным выросла
на величину силы обжатияР2(рис. 24,в). Подобные же стадии работы и у
изгибаемых элементов, только с более
сложными эпюрами напряжений.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
312014Авг
0
Приведенное сечение
Чтобы определить напряжения в сечениях предварительно напряженных железобетонных элементов в стадии до образования трещин, рассматривают приведенное бетонное сечение, в котором площадь сечения арматуры заменяют эквивалентной площадью сечения бетона. Исходя из равенства деформаций арматуры и бетона, приведение выполняют по отношению модулей упругости двух материалов.
Содержание
- Расчет ребристой плиты понедельным состояниям второй группы
- РАСЧЕТ И ПРОЕКТИРОВАНИЕ СБОРНЫХ ЖЕЛЕЗОБЕТОННЫХ ПЛИТ ПЕРЕКРЫТИЙ
- 2.1.8 Расчет ребристой плиты по предельным состояниям второй группы
- 2.1.9 Определение геометрических характеристик сечения
- 2.1.10 Определение потерь предварительного натяжения арматуры
Расчет ребристой плиты понедельным состояниям второй группы



Геометрические характеристики приведенного сечения определим по формулам (11.28) — (11.32). Отношение модулей упругости v =Еs /Eb=190 000/30000=6,35. Площадь приведенного сечения Ared=A+vA,=116*5+14*25+6,35*4,02=955 см 2 . Статический момент площади приведенного сечения относительной нижней грани Sred=116*5*27,5+14*25*12,5+6,35*4,02*3=20402 см 3 . Расстояние от нижней грани до центра тяжести приведенного сечения y0=Sred/Ared=20402/1060=22 см. Момент инерции приведенного сечения Ired=116*5/12+116*5*5,5 2 +14*25 3 /12+14*25*9,5 2 +6,35*4,02*19 2 =76700 см 4 .
Момент сопротивления приведенного сечения по нижней зоне Wred=Ired/y0=76700/22= 3500 см 3 .
Момент сопротивления приведенного сечения по верхней зоне Wred =Ired/(h-y0) = 76700/ (30-22) =9600 см’.
Расстояние от ядровой точки, наиболее удаленной от растянутой зоны (верхней), до центра тяжести приведенного сечения, согласно формуле (VII.31), r=φn(Wred/Ared)=0,85(3500) /1060)=2,8 см; то же, наименее удаленной от растянутой зоны (нижней) rinf=0,85 (9600/1 060) =7,7 см; здесь φn=1,6-σb/Rb,ser= 1,6- 0,75= 0,85.
Отношение напряжения в бетоне от нормативных нагрузок и усилия обжатия к расчетному сопротивлению бетона для предельных состояний второй группы предварительно принимаем равным 0,75.
Упругопластический момент сопротивления по растянутой зоне, согласно формуле (VII.37), Wpt = y*Wred= 1,75*3500=6125 см 3 ; здесь γ=1,75 — для таврового сечения с полкой в сжатой зоне.
Упругопластический момент сопротивления по растянутой зоне в стадии изготовления и обжатия элемента Wpl / =1,5*9600=14400 см 3 ; здесь γ=1,5 — для таврового сечения с полкой в растянутой зоне при bf/b>2 и hf/h 2 /8=1400 000 Нсм=14 кНм. Тогда

Потери от быстронатекающей ползучести при σbp/Rbp=4,8/12,5=0,39 100 МПа больше установленного минимального значения потерь. Усилие обжатия с учетом полных потерь
Расчет по образованию трещин, нормальных к продольной оси, производится для выяснения необходимости проверки по раскрытию трещин. При этом для элементов, к трещиностойкости которых предъявляются требования 3-й категории, принимаются значения коэффициента надежности по нагрузке γf=1; M=65,4 кНм. По формуле (VII. 3) М≤Мсrс.Вычисляем момент образования трещин по приближенному способу ядровых моментов по формуле (VII. 29): Mcrc=Rbt.serWpl+Mrp=1,6*6125(100)+2000000=352300 Нсм=35,23 кНм.
Здесь ядровый момент усилия обжатия по формуле (VII.30) при γsp=0,84 Mrp= Po2(eoP+r)=0,84*140000(19+3,35) =2000000 Нсм.
Поскольку М=65,4>MСГС=35,23 кН-м, трещины в растянутой зоне не образуются. Следовательно, расчет по раскрытию трещин не нужен.
Проверим, образуются ли начальные трещины в верхней зоне плиты при ее обжатии при значении коэффициента точности натяжения γsp=1.16. Изгибающий момент от веса плиты М=15 кНм. Расчетное условие
P1(e0p-rinf)-M≤RbtpWpl / = 1.16*140000(19-9.2)-1400000 = 1400000 Hсм / =27-0.5*5=24.5 см – плечо внутренней пары сил; esN=0, так как усилие обжатия Р приложено в центре тяжести площади нижней напрягаемой арматуры; Ws=Asz1=4,02*24.5 =98,49 см 3 – момент сопротивления сечения по растянутой арматуре.
Приращение напряжений в арматуре от действия полной нагрузки σs=(65400000-140000*24.5)/98,49(100)=163 МПа.
ширина раскрытия трещин от непродолжительного действия всей нагрузки

здесь μ=Аs/bh0=4,02/14*27=0.0106;δ=1; η=1; φi=1; d=16 мм – диаметр продольной арматуры;
ширина раскрытия трещин от непродолжительного действия постоянной и длительной нагрузок  ;
;
ширина раскрытия трещин от постоянной и длительной нагрузок 
Непродолжительная ширина раскрытия трещин acr=acrc1-аcrc2+аcгс3=0,12-0,07+0,105=0,16 мм / +ξ)bh0=bf / hf / =136*5=680 см 2 в соответствии с формулой (VII. 87) при a’s =0 и допущением, что ξ=hf / /ha.Вычисляем прогиб по формуле (VII. 131):

Понравилась статья? Добавь ее в закладку (CTRL+D) и не забудь поделиться с друзьями: 


Источник
РАСЧЕТ И ПРОЕКТИРОВАНИЕ СБОРНЫХ ЖЕЛЕЗОБЕТОННЫХ ПЛИТ ПЕРЕКРЫТИЙ
Сборные железобетонные плиты перекрытия целесообразно проектировать опертыми по двум сторонам (работающими на изгиб в одном направлении). При этом соотношение между сторонами плиты должно быть l/b>2 (где l длинная сторона, b − короткая).
При длине плиты l ≥ 6м плита проектируется предварительно напряженной. При длине l 2 перекрытия (см. табл. 3.1).
| Нагрузки на 1 м 2 сборного междуэтажного перекрытия | |||
| Вид нагрузки | Нормативная нагрузка, Н/м 2 | Коэффициент надежности по нагрузке, γf | Расчетная нагрузка, Н/м 2 |
| Постоянная: -от конструкции пола -от собственного веса плиты | … … | 1.35 1.35 | … … |
| Итого | qk=… .. | — | q=… |
| Временная: кратковременная длительная | … … … | 1.5 1.5 1.5 | … … |
| Итого | … | — | … |
Примечание: вес конструкций пола определяется умножением плотности материала ρ на объем (1м 2 на толщину слоя t); вес плиты перекрытия — аналогично, причем в качестве толщины t плиты используют приведенную толщину плиты:
Подбор сечения плиты
Перед определением высоты плиты необходимо предварительно задаться классом бетона, продольной (рабочей) и поперечной арматуры и определить необходимые прочностные характеристики.
Для изготовления сборных железобетонных плит перекрытия класс бетона принимается в зависимости от условий эксплуатации [прил. 3], но не ниже С 12 /15.
Прочность бетона на осевое сжатие fc, растяжению fct, модуль упругости Ес, коэффициент условий работы бетона γb2 можно принять согласно СНБ [прил. 7].
В качестве продольной рабочей (ненапрягаемой) арматуры целесообразно принимать арматуру класса S500 или S400, в качестве поперечной арматуры — арматуру класса S240, либо проволоку класса S500. Сварные сетки в верхней и нижней полках панели можно принимать: также из проволоки класса S500
Сопротивление арматуры сжатию (растяжению) fyk, в зависимости от класса и диаметра стержня, модуль упругости арматуры Es можно принять согласно СНБ (прил. 7).
Требуемая высота сечения плиты определяется по формуле:
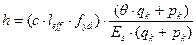 , , |
(3.2.1) |
с — коэффициент, принимаемый по табл. 2
Ө — коэффициент увеличения прогибов при длительном действии нагружения. принимаемый по табл. 3.2;
leff— расчетный пролет плиты;
qk — длительно действующая нормативная нагрузка на 1м 2 плиты;
Рк — кратковременно действующая нагрузка на 1м 2 .
согласно СНБ (прил. 7).
| Коэффициент | Θ | c |
| для пустотных плит | 18-20 | |
| для ребристых плит (с полкой в сжатой зоне) | 1,5 | 30-34 |
| Коэффициент | Θ | c |
| для пустотных плит | 18-20 | |
| для ребристых плит (с полкой в сжатой зоне) | 1,5 | 30-34 |
Для предварительно напряженных плит высоту можно принять равной h=l0/30 (для пустотных плит), или h = leff / 20 (для ребристых плит).
Вычисленную высоту сечения окончательно принимаем округленной до 10 мм. В зависимости от высоты сечения, принимаем остальные размеры (диаметр пустот и т.д.), т.е. конструируется реальное сечение плиты (см. рис. 3.2.)


Рис. 3.2. Сечение многопустотной плиты с круглыми пустотами
Для того, чтобы выполнить расчет, необходимо привести это сечение к одному из «элементарных» сечений (прямоугольник, тавр с полкой в верхней или нижней зоне, двутавр, . ).
Приведенное сечение для пустотной плиты представляет собой двутавр (см. рис. 3.3.), для ребристой — тавр (см. рис. 3.4.).

Рис. 3.3. Приведенное сечение для многопустотной плиты
Здесь h −высота сечения плиты; heff −рабочая высота сечения; а − защитный слой; hf` −толщина верхней полки двутавра; hf −толщина нижней полки двутавра; bf` −ширина верхней полки двутавра; принимается равной полной ширине плиты, при этом проверяется условие: при малой толщине сжатой полки (т.е. когда hf`/h
Лучшие изречения:
Наука — это организованные знания, мудрость — это организованная жизнь. © Иммануил Кант
==> читать все изречения. 171 —  | 158 —
| 158 — 
Источник
2.1.8 Расчет ребристой плиты по предельным состояниям второй группы
При эксплуатации конструкций в закрытом помещении и применении стержневой арматуры класса A600 к трещиностойкости предъявляются требования 3-й категории:
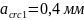

2.1.9 Определение геометрических характеристик сечения
Рассматриваем приведенное сечение, в котором площадь сечения арматуры заменяем эквивалентной площадью бетона. Исходя из равенства деформаций бетона и арматуры приведение выполняем по отношению модулей упругости двух материалов 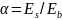 .
.
Отношение модулей упругости:
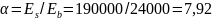 .
.
Площадь приведенного сечения:
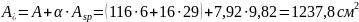 ,
,
где 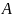 — площадь сечения бетона, см 2 .
— площадь сечения бетона, см 2 .
Статический момент приведенного сечения относительно нижней грани (оси 1-1):
 ,
,
где 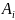 — площадь i-той части сечения;
— площадь i-той части сечения;
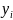 — расстояние от центра тяжести i-той части сечения до оси 1-1.
— расстояние от центра тяжести i-той части сечения до оси 1-1.
Расстояние от центра тяжести приведенного сечения до нижней грани:
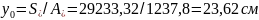 .
.
Момент инерции приведенного сечения относительно оси, проходящей через центр тяжести приведенного сечения:
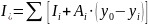 ,
,
где 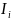 — момент инерции i-той части сечения, относительно оси, проходящей через центр тяжести этой части сечения.
— момент инерции i-той части сечения, относительно оси, проходящей через центр тяжести этой части сечения.
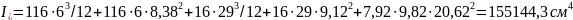
Момент сопротивления приведенного сечения по нижней грани:
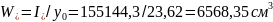
По верхней грани:
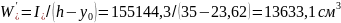
Расстояние от ядровой точки наиболее удаленной от растянутой зоны до центра тяжести приведенного сечения:

От наименее удаленной:
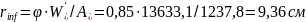
Здесь коэффициент, учитывающий влияние неупругих деформаций бетона сжатой зоны:

где 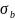 — максимальное напряжение в сжатом бетоне от внешней нагрузки и усилия предварительного обжатия. Отношение напряжения в бетоне от нормативных нагрузок и усилия обжатия к расчетному сопротивлению бетона для предельных состояний второй группы предварительно принимаем равным 0,75.
— максимальное напряжение в сжатом бетоне от внешней нагрузки и усилия предварительного обжатия. Отношение напряжения в бетоне от нормативных нагрузок и усилия обжатия к расчетному сопротивлению бетона для предельных состояний второй группы предварительно принимаем равным 0,75.
Упругопластический момент сопротивления приведенного сечения по растянутой зоне в стадии эксплуатации:
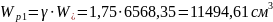
здесь коэффициент  учитывает влияние неупругих деформаций бетона растянутой зоны,
учитывает влияние неупругих деформаций бетона растянутой зоны,  для таврового сечения с полкой в сжатой зоне.
для таврового сечения с полкой в сжатой зоне.
Упругопластический момент сопротивления по растянутой зоне в стадии изготовления и обжатия элемента:
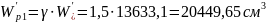
здесь 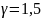 — коэффициент для таврового сечения с полкой в растянутой зоне при
— коэффициент для таврового сечения с полкой в растянутой зоне при 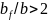 и
и  .
.
2.1.10 Определение потерь предварительного натяжения арматуры
При электротермическом способе натяжения арматуры на упоры следует учитывать:
1) Первые потери — от релаксации напряжений в арматуре; от быстронатекающей ползучести бетона.
2) Вторые потери — от усадки бетона; от ползучести бетона.
1. Потери от релаксации напряжений в арматуре при электротермическом способе натяжения.

2. Потери от быстронатекающей части ползучести бетона, подвергнутого тепловой обработке.
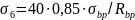 при
при 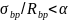
где 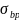 — напряжение обжатия в бетоне на уровне центра тяжести напрягаемой арматуры;
— напряжение обжатия в бетоне на уровне центра тяжести напрягаемой арматуры;
— передаточная прочность бетона;
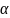 — коэффициент, принимаемый равным
— коэффициент, принимаемый равным 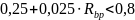 .
.
Определяем усилие предварительного обжатия бетона с учетом предыдущих потерь напряжения:
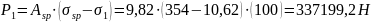
Усилие 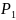 приложено по линии, проходящей через центр тяжести напрягаемой арматуры. Эксцентриситет этого усилия относительно центра тяжести приведенного сечения:
приложено по линии, проходящей через центр тяжести напрягаемой арматуры. Эксцентриситет этого усилия относительно центра тяжести приведенного сечения:
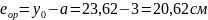
Максимальное сжимающее напряжение в бетоне при обжатии на уровне крайнего сжатого волокна определяется по формуле:
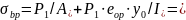

Устанавливаем величину передаточной прочности бетона из условия 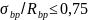 .
.
 B20 — 10 МПа; принимаем
B20 — 10 МПа; принимаем 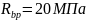 .
.
Вычисляем сжимающее напряжение в бетоне на уровне центра тяжести напрягаемой арматуры от усилия обжатия и с учетом изгибающего момента от веса плиты:
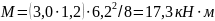
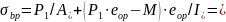
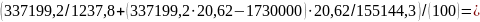
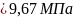
Определяем потери напряжения арматуры от быстронатекающей ползучести при
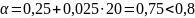
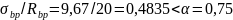
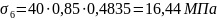
Первые потери составляют:
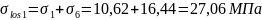 .
.
Уточняем значение усилия обжатия с учетом первых потерь 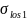 :
:
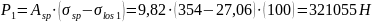
Определяем сжимающее напряжение в бетоне на уровне центра тяжести напрягаемой арматуры:
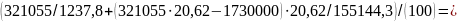
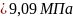
3. Потери от усадки бетона, подвергнутого тепловой обработке при атмосферном давлении 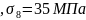 (для тяжелого бетона класса В35 и ниже).
(для тяжелого бетона класса В35 и ниже).
4. Потери от ползучести бетона при определяются по формуле
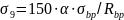
где — коэффициент, равный для бетона, подвергнутого тепловой обработке, 0,85;
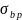 — то же, что и при определении
— то же, что и при определении  , но с учетом потерь . При
, но с учетом потерь . При  ;
;
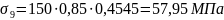 .
.
Вторые потери составляют:
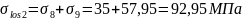 .
.
 (больше установленного в нормах минимального значения потерь).
(больше установленного в нормах минимального значения потерь).
Определяем усилие обжатия с учетом полных потерь:
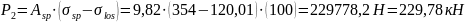 .
.
Источник
Adblock
detector
Железобетон
Приведенное сечение
Чтобы определить напряжения в сечениях предварительно напряженных железобетонных элементов в стадии I до образования трещин, рассматривают приведенное бетонное сечение, в котором площадь сечення арматуры заменяют эквивалентной площадью сечення бетона. Исходя нз равенства деформаций арматуры н бетона, приведение выполняют по отношению модулей упругости двух материалов V=Es/Eb. Площадь приведенного сечення элемента составит (рнс. II.7, б)
ARed = A + VASp + VAS + VASp + VAS> <“-28)
Где А — площадь сечения бетона за вычетом площади сечения каналов и пазов.
Статический момент приведенного сечення относительно осн /—/, проходящей по нижней грани сечення:
Sred — 2At У І, (11.29)
Где At — площадь части сечения; yi— расстояние от центра тяжести І-Й части сечения до оси I—/.
Расстояние от центра тяжести приведенного сечення до осн 1-І
Y0 = Sred/Ared■ (“-30)
Момент инерции приведенного сечення относительно оси, проходящей через центр тяжести приведенного сечення:
/гЄ£г = 2[/г + Лг(у0-«/г)2]. (11.31)
Где U — момент инерции І-Й части сечення относительно оси, проходящей через центр тяжести этой части сечения.
Расстояние до верхней н нижней границы ядра сечения от центра тяжести приведенного сечення составят:
Г= Ітей/Ared Уо‘ RTn1 = Lredl[Ared (Л —J/0)l – (11.32)
Напряжения в бетоне при обжатии
При обжатнн в бетоне развиваются неупругне деформации, эпюра нормальных напряжений приобретает криволинейное очертание. В упрощенной постановке напряжения в бетоне при обжатнн определяют в предположении упругой работы сечення и линейной эпюры напряжений
ОЬР = PIAred ± Ре0р Ytlred• (11-33)
В зависимости от дели расчета напряжения в бетоне определяют в разных по высоте сечения уровнях:
А) при установлении контролируемого напряжения в арматуре, натягиваемой на бетон, напряжения в бетоне определяют в уровне усилий в напрягаемой арматуре:
СТьр = P/Ared + Ре0р У$р/IreS (11.34)
°ЪР = P/ARed – Р% У Spared’ (” • 35)
Где Р определяют с учетом первых потерь при у«Р=1.
Б) при проверке предельных напряжений при обжатии напряжения в бетоне определяют в уровне крайнего сжатого волокна
0Ьр = PIAred + Ре ОР У о/1 Red– (11.36)
Здесь Р определяют с учетом первых потерь (без потерь ов) при Y»p=l.
В) при расчете потерь о6 от быстронатекающей ползучести и <т9 от ползучести напряжения в бетоне определяют на уровне центра тяжести напрягаемой арматуры по формулам (11.34) и (11.35).
7. Последовательность изменения предварительных напряжений в элементах после загружения внешней нагрузкой
Центрально-растянутые элементы. При изготовлении элемента арматуру натягивают до начального контролируемого напряжения Осоп на упоры форм, производят бетонирование, тепловую обработку и выдерживают в форме до приобретения бетоном необходимой передаточной прочности Rbp. В этом состоянии 1 произошли первые потери oiosi в основной их части (рис. II.8). Затем при освобождении с упоров форм и отпуске натяжения арматуры благодаря сцеплению материалов создается обжатие бетона, развиваются деформации быстронатекающей ползучести и происходят потери ов— состояние 2. Предварительное напряжение в арматуре с учетом упругого обжатия бетона равно осоп—От—v<r&p, здесь aiosi— без потерь <Тз, <Т4, поскольку последние учитываются в (Тсоп-
С течением времени происходят вторые потери Olos2, Соответственно уменьшаются и упругие напряжения в бетоне — состояние 3. Предварительное напряжение в арматуре с учетом полных потерь и упругого обжатия бетона в этом состоянии равно оС0П—ош—хоьрі.
После загружения элемента при постепенном увеличении внешней нагрузки напряжения в бетоне от предварительного обжатия погашаются — состояние 4. Предварительное напряжение в арматуре с учетом потерь на уровне нулевого напряжения в бетоне в этом состоянии равно: Os–P = Ocon—Oi0S–
Дальнейшее увеличение нагрузки приводит к появлению в бетоне предельных растягивающих напряжений Rbtn — состояние 5, т. е. конец стадии I напряженно-деформированного состояния.
Приращение напряжений в растянутой арматуре после погашения обжатия в бетоне исходя из предельной растяжимости бетона Eubt=-2Rbtn/Eb и совместности деформаций двух материалов
As = 8S Es = Eubt Es = (2Rbtn/Eb) Es = 2VRbtn.
6m~6to$i Бсап’^іоі
-f –
Состояние 2
ВыгиГ4- ж -6Losi. Щ Соствяние 3
Напряжение в напрягаемой растянутой арматуре перед образованием трещин равно Asp + 2VRbtn■ Оно превышает соответствующее на- Состояние I Пряжение в элементах без — предварительного напряже – , Ния на Gap, что повышает со-
Противление образованию трещин. После образования трещин в стадии II напряженно-деформированного состояния растягивающее усилие воспринимается арматурой. По мере увеличения нагрузки трещины раскрываются. При дальнейшем увеличении нагрузки напряжения в арматуре становятся предельными н происходит разрушение — стадия III.
, При натяжении арматуры на бетон последовательность напряженных состояний аналогичная. Отличие в период изготовления и до загружения элемента внешней нагрузкой заключается в том, что начальное контролируемое напряжение арматуры определяют с учетом обжатия бетона.
Изгибаемые элементы. При натяжении на упоры форм верхнюю и нижнюю арматуру натягивают на величину начальных контролируемых напряжений <тс<т, оСоп (рис. II.9). Обычно принимают оСоп = оСоп – После бетонирования и твердения в процессе тепловой обработки происходит основная часть первых потерь предварительных напряжений в арматуре — состояние 1. После приобретения бетоном необходимой прочности арматура освобождается с упоров форм и обжимает бетон; предварительные напряжения в арматуре в результате быстронатекающей ползучести н упругого обжатия бетона уменьшаются — состояние 2. При этом вследствие несимметричного армирования Л5р >А sр и внецентренного обжатия элемент получает выгиб. С течением времени происходят вторые потерн напряжений арматуры aiosi—состояние 3. После загружения внешней нагрузкой погашаются напряжения обжатия в бетоне — состояние 4. Предварительное напряжение в арматуре на уровне нулевого напряжения в бетоне в зоне, растянутой от действия внешней нагрузки, в этом состоянии
<*Sp — Ocon — Olos– (11.37)
При увеличении нагрузки напряжения в бетоне растянутой зоны достигают предельных Rbtn — состояние 5. Это и будет концом стадии I напряженно-деформированного состояния при изгибе. В этой стадии напряжение в арматуре равно ASp + 2VRbtn■ При изгибе, как и прн растяжении, перед образованием трещин напряжение в растянутой арматуре превышает соответствующее напряжение в арматуре элементов без предварительного напряжения на Osp. Этим и определяется значительно более высокое сопротивление образованию трещин при изгибе предварительно напряженных элементов. При увеличении-нагрузки в растянутой зоне появляются трещины, наступает стадия II напряженно-деформированного состояния. С дальнейшим увеличением нагрузки растягивающие напряжения в арматуре и бетоне достигают предельных, происходит разрушение — стадия III. Напрягаемая арматура площадью сечения Asp, расположенная в зоне, сжатой от действия внешней нагрузки, деформируется совместно с бетоном сжатой зоны, при этом предварительные растягивающие напряжения в ней уменьшаются. При предельных сжимающих напряжениях в бетоне напряжения в напрягаемой арматуре этой зоны
A =R —а’. (11.38)
SC sc SP 1 ‘
Напряжение asp определяют с коэффициентом точности натяжения ysp>l и с учетом потерь. При Asp<Rsc Арматура площадью Asp сжата, а при ASp>RSc растянута и в этом случае несколько снижается несущая способность предварительно напряженного элемента.
§ II.5. ГРАНИЧНАЯ ВЫСОТА СЖАТОЙ ЗОНЫ. ПРЕДЕЛЬНЫЕ ПРОЦЕНТЫ АРМИРОВАНИЯ
1. Граничная высота сжа»той зоны –
В сечениях, нормальных к продольной оси элементов,— изгибаемых, внецентренно сжатых, внецентренно растянутых—при двузначной эпюре напряжений в стадии III характерно одно и то же напряженно-деформированное состояние (рис. 11.10). В расчетах прочности усилия, воспринимаемые сечением, нормальным к продольной оси элемента, определяют по расчетным сопротивлениям материалов с учетом коэффициентов условий работы. При этом принимают следующие исходные положения: бетон растянутой зоны не работает — сопротивление Rbt равно нулю; бетон сжатой зоны испытывает расчетное сопротивление Rb — эпюра напряжений прямоугольная; продольная растянутая арматура испытывает напряжения, не превышающие расчетное сопротивление Os^Rs’, продольная арматура в сжатой зоне сечения испытывает напряжение Osc. В общем случае условие прочности при любом из перечисленных внешних воздействий формулируется в виде требования о том, чтобы момент внешних сил не превосходил момента внутренних усилий. Запишем это условие относительно оси, проходящей через центр тяжести растянутой арматуры:-
+ (11.39)
Где М — в изгибаемых элементах момент внешних сил от расчетных нагрузок; во внецентренно сжатых н внецентренно растянутых элементах — момент внешней Продольной силы относительно той же осн, т. е. M=Ne (Е—расстояние от силы N до центра тяжести растянутой арматуры, см. рнс. 11.10); Ss— статический момент площади бетона сжатой зоны относительно той же оси; г, — расстояние между центрами тяжести растянутой н сжатой арматуры.
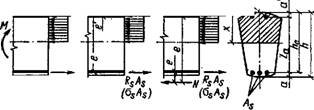
Ms
Рис. 11.10. К расчету прочности сеченнй любой симметричной формы
1 — изгибаемых; 2 — внецентренно сжатых; 3 — внецентренно растянутых
Напряжение в напрягаемой арматуре, расположенной в зоне, сжатой от действия нагрузок, Asc=Rsc—Osp определяют по значению, вычисленному при коэффициенте точности напряжения у3р, большем единицы. В элементах без предварительного напряжения ASc—Rsc–
Высоту сжатой зоны х для сечений, работающих по случаю 1, когда в растянутой арматуре и сжатом бетоне достигнуты предельные сопротивления, определяют из уравнения равновесия предельных усилий
RbAb + o„Atp-RtAtp±N = 0,
(П.40)
Где Аь — площадь бетоиа сжатой зоны, зависящая от высоты сжатой зоны; для прямоугольного сечення Аь — Ьх.
В уравнении (11.40) принимается знак «—» прн вне- центренном сжатии, знак « + » при внецентренном растяжении и yV=0 при изгибе.
Высоту сжатой зоны х для сечений, работающих по случаю 2, когда разрушение происходит пр сжатому бетону хрупко, а напряжения в арматуре предельного зна – I чення не достигают, также определяют из уравнения
. Но в этом^ случае расчетное сопротивление Rs Заменяют напряжением as.
На основе анализа результатов большого числа экспериментов установлено, что напряжение <т« зависит от относительной высоты сжатой зоны —xlho оно может определяться по эмпирической формуле
As = – lubh—(JL – i + asP. (11.41)
S 1 — (cd/1 ,1) V i SP ‘
В формуле (11.41) <A=X0/Ho— относительная высота сжатой зоны прн напряжении в арматуре as=aSp (или <Ts=0— в элементах без предварительного напряжения).
Поскольку при Os — Osp (или при <Ts=0) фактическая относительная высота сжатой зоны £ = 1, то со может рас – – сматриваться как. коэффициент полноты фактической эпюры напряжений в бетоне при замене ее условной прямоугольной эпюрой; при этрм усилие бетона сжатой зоны Nb=(j>bh0Rb (рис. 11.11). На основе опытных данных установлено, что для тяжелого бетона о>=0,85—0,008/?»; для бетонов на легких заполнителях со=0,8—0,008#г>.
Значение ©, вычисленное по этим опытным формулам, называется характеристикой двформативных свойств бетона сжатой зоны.
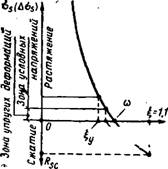
В формуле (П.41) первый член правой части представляет собой приращение напряжения Aas в напрягаемой арматуре или напряжение as в арматуре элементов без предварительного напряжения. Если относительная высота сжатой зоны £<со, напряжение <rs будет растягивающим, если же £>©,— сжимающим (рис. 11.12).
Граничная относительная высота сжатой зоны = —Xyjho, при которой растягивающие напряжения в арматуре начинают достигать предельных значений Os-+-Rs, Может быть найдена из зависимости (11.41)
Ъу = ю/[1 + (o-sl/o-s2)(l -(0/1,і), (11.42)
Где a<i=/?s — агр— напряжение в арматуре с фнзнческнм пределом текучести нли
O-Sl = Rs + 80,2 ES — Osp (II.43)
— напряжение в арматуре с условным пределом текучести с учетом накопившихся остаточных деформаций ео. г, поскольку в завнснмостн
Предполагается, что в арматуре развились только упругие деформации (рнс. 11.13).
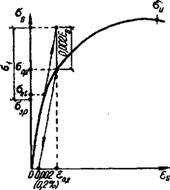
Рис. 11.13. К определению Oi — условного предельного напряжении в арматуре, не имеющей физического предела текучести
В расчетах сечений принимают е0,2£«=400 МПа; as2—RubEs — 400 МПа (исходя из предельной сжимаемости бетона 0,002); os2=eUbЈs = 500 МПа при коэффициенте условий работы бетона y&2<1 (когда при длительном действии нагрузки предельная сжимаемость бетона увеличивается и достигает 0,0025).
Если напряжения о*,’вычисленные по формуле (11.41) для арматуры, не имеющей физического предела текучести, превышают предел упругости 0«>=О,8 и находятся в интервале ase<Os^Rt, значение о* должно уточняться расчетом по формуле
= (11.44)
Для расчета прочности внецентренно сжатых элементов в нормах приводится другая упрощенная зависимость по определению граничной высоты сжатой зоны.
Таким образом, в общем случае расчет прочности сечения, нормального к продольной оси, производится в зависимости от значения относительной высоты сжатой зоны. Если Уг высота сжатой зоны определяется из уравнения (11.40), если же 1>1У, высота сжатой зоны определяется из совместного решения уравнения (11.40) и зависимости (11.41). При этом несущая способность в обоих случаях устанавливается по условию (11.39).
Напряжения высокопрочной арматуры as в предельном состоянии могут превышать’ условный предел текучести. По данным опытов, это может происходить, если относительная высота сжатой зоны, найденная из уравнения (11.40), меньше граничной, т. е. 1<1У. Превышение оказывается тем большим, чем меньше значение Опытная зависимость имеет вид
= 0,95 — (о,95 —^ — 1 ) . (11.45)
Rs 0(|,2 ст0,2 / 1у
В расчетах прочности сечений расчетное сопротивление арматуры RB умножают на коэффициент условий работы арматуры yse
Т* = Я-(Ч-1)(2Б/6,-1), (И-46)
Где г] —принимают равным:
TOC o “1-3” h z для арматуры классов A-IV, At-IVC 1,2
То же, A-V, Ат-V, B-II, Вр-ІІ, К-7, К-19 . … 1,15
» А-VI, At-VI 1,1
| определяют прн этом, полагая y»e= 1. *
Без надёжного фундамента невозможно возвести ни одно строительное сооружение. Монолитную базу (ленточный вариант) можно сделать из жидкого бетона, но это требует немалых затрат времени и финансов. К сведению тех, кто …
Железобетонные плиты перекрытия могут быть совершенно разных видов, но все они должны обеспечивать безопасную и долгую эксплуатацию здания. Даже при покупке бренда Ковальская плиты перекрытия очень важны для их долговечности …
Индустриальные технологии активно развивались в СССР еще с середины прошлого века, а развитие строительной индустрии требовало большого количество различных материалов. Изобретение сборного железобетона стало своеобразной технической революцией в жизни страны, …



