Как найти приведенную длину физического маятника - Сайт, где вы сможете решить свои вопросы

Физическим
маятником
называется твердое тело, закрепленное
на неподвижной горизонтальной ocи (оси
подвеса), не проходящей через центр
тяжести, и совершающее колебания
относительно этой оси под действием
силы тяжести.

Вывод
периода:

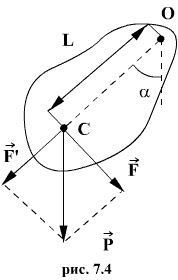
При небольших углах отклонения α (рис.
7.4) физический маятник так же совершает
гармонические колебания. Будем считать,
что вес физического маятника приложен
к его центру тяжести в точке С. Силой,
которая возвращает маятник в положение
равновесия, в данном случае будет
составляющая силы тяжести – сила F.

Знак
минус в правой части означает то, что
сила F направлена в сторону уменьшения
угла α. С учетом малости угла α

.
Используем основное уравнение динамики
вращательного движения

.
Момент силы: определить в явном виде
нельзя. С учетом всех величин, входящих
в исходное дифференциальное уравнение
колебаний физического маятника имеет
вид

.
Решение
этого уравнения

Определим
длину l математического маятника, при
которой период его колебаний равен
периоду колебаний физического маятника,
т.е.
или

.
Из этого соотношения определяем

.
Данная формула определяет приведенную
длину физического маятника, т.е. длину
такого математического маятника, период
колебаний которого равен периоду
колебаний данного физического маятника.

21.23.
Выведите уравнение колебательного
движения, являющегося суперпозицией
гармонических колебаний одного
направления с близкими частотами.
Изобразите результирующее колебание
на графике. Как называется такой вид
колебания?

Для
практики особый интерес представляет
случай, когда два складываемых
гармонических колебания одинакового
направления мало отличаются по частоте.
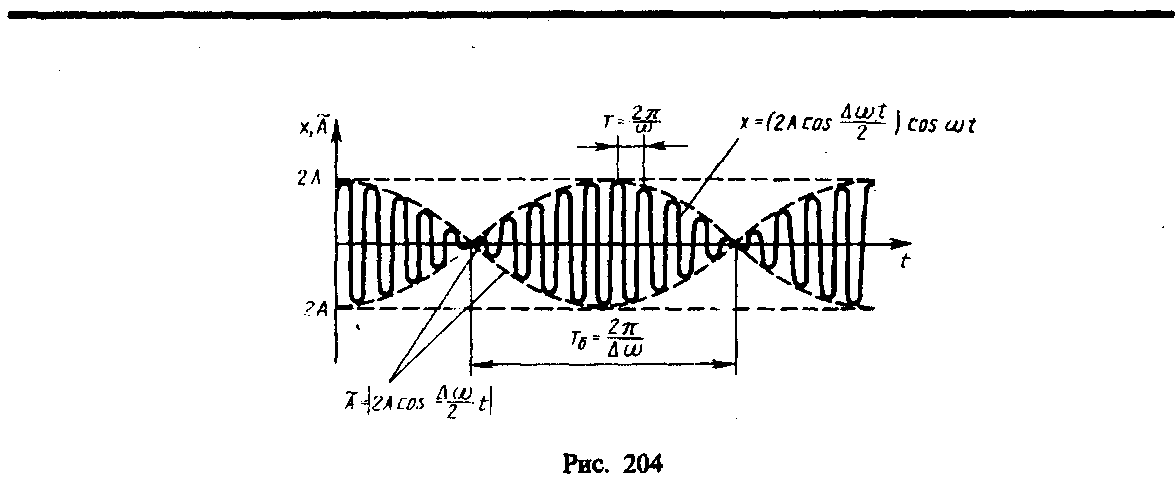
В результате сложения этих колебаний
получаются колебания с периодически
изменяющейся амплитудой. Периодические
изменения амплитуды колебания, возникающие
при сложении двух гармонических колебаний
с близкими частотами, называются
биениями. Пусть амплитуды складываемых
колебаний равны А, а частоты равны 
и +,
причем <<.
Начало отсчета выберем так, чтобы
начальные фазы обоих колебаний были
равны нулю:

Складывая эти выражения и учитывая, что
во втором сомножителе /2<<,
найдем

(144.3).
Результирующее колебание (144.3) можно
рассматривать как гармоническое с
частотой ,
амплитуда А_б,
которого изменяется по следующему
периодическому закону:

(144.4).
Частота изменения А_б
в два раза больше частоты изменения
косинуса (так как берется по модулю),т.
Е. частота биений равна разности частот
складываемых колебаний:

Период биений

22.Сложение
взаимно-перпендикулярных гармонических
колебаний. Получите уравнение траектории
частицы, колеблющейся по осям х и у с
одинаковой частотой. Каковы траектории
при колебаниях по взаимно перпендикулярным
осям с кратными частотами?

Рассмотрим
результат сложения двух гармонических
колебаний одинаковой частоты ,
происходящих во взаимно перпендикулярных
направлениях вдоль осей х и у. Для
простоты начало отсчета выберем так,
чтобы начальная фаза первого колебания
была равна нулю, и запишем

(145.1),
где 
— разность фаз обоих колебаний, А и В —
амплитуды складываемых колебаний.
Уравнение траектории результирующего
колебания находится исключением из
выражений (145.1) параметра t.
Записывая складываемые колебания в
виде

и заменяя во втором уравнении cost
на х/А и sint
на

,
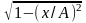
получим после несложных преобразований
уравнение эллипса, оси которого
ориентированы относительно координатных
осей произвольно:

(145.2)

Так
как траектория результирующего колебания
имеет форму эллипса, то такие колебания
называются эллиптически поляризованными.

25.
Какие силы называют квазиупругими?
Каков характер движения тела под
действием этих сил? Запишите дифференциальное
уравнение гармонических незатухающих
колебаний и его решение. Выведите формулу
для расчета периода.

КВАЗИУПРУГАЯ
СИЛА –
направленная к центру О сила. модуль
к-рой пропорционален расстоянию r от
центра О до точки приложения силы
(F=-cr),
где с –
постоянный коэф., численно равный силе,
действующей на единице расстояния. К.
с. является силой центральной и
потенциальной с силовой ф-цией U=-0,5cr².
Примерами К. с. служат силы упругости,
возникающие при малых деформациях
упругих тел (отсюда и сам термин “К.
с.”). Приближённо К. с. можно также
считать касательную составляющую силы
тяжести, действующей на матем. маятник
при малых его отклонениях от вертикали.
Для материальной точки, находящейся
под действием К. с., центр О является
положением её устойчивого равновесия.
Выведенная из этого положения точка
будет в зависимости от нач. условий или
совершать около О прямолинейные гармонич.
колебания, или описывать эллипс (в
частности, окружность).

Линейное
неоднородное дифференциальное уравнение:

(147.5)
Применяем
впоследствии его решение для вынужденных
колебаний конкретной физической природы
(x₀ в
случае механических колебаний
равно F₀/m, в
случае электромагнитных — U_m/L).

Решение
уравнения равно сумме общего решения

(146.5)
однородного уравнения

и
частного решения неоднородного уравнения.
Частное решение найдем в комплексной
форме. Заменим правую часть уравнения
(147.5) на комплексную величину х₀
:

(147.6). Частное
решение этого уравнения будем искать
в виде

Подставляя
выражение для s и
его производных
в
уравнение (147.6), получаем

(147.7). Так как это
равенство должно быть справедливым для
всех моментов времени, то время t из
него должно исключаться. Отсюда следует,
что h=w. Учитывая
это, из уравнения (147.7) найдем величину s₀ и
умножим ее числитель и знаменатель на

.
Это комплексное число удобно представить
в экспоненциальной форме:

,
где

(147.8);

(147.9)

Следовательно,
решение уравнения (147.6) в комплексной
форме примет вид

Его
вещественная часть, являющаяся решением
уравнения (147.5), равна

(147.10)

где А и j задаются
соответственно формулами (147.8) и (147.9).

Таким
образом, частное решение неоднородного
уравнения (147.5) имеет вид

(147.11). Решение
уравнения (147.5) равно сумме общего решения
однородного уравнения

(147.12). (см. (146.5)) и частного решения
(147.11). Слагаемое (147.12) играет существенную
роль только в начальной стадии процесса
(при установлении колебаний) до тех пор,
пока амплитуда вынужденных колебаний
не достигнет значения, определяемого
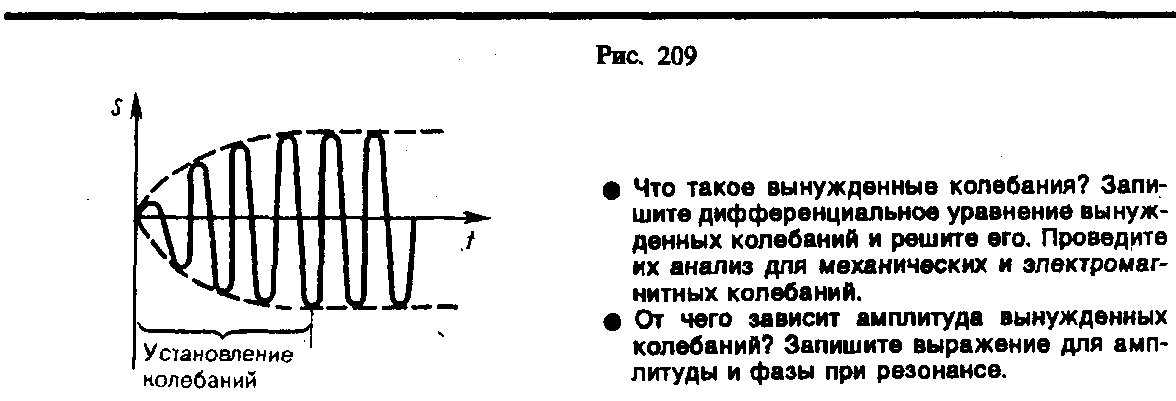
равенством (147.8). Графически вынужденные
колебания представлены на рис. 209.
Следовательно, в установившемся режиме
вынужденные колебания происходят с
частотой w и
являются гармоническими; амплитуда и
фаза колебаний, определяемые выражениями
(147.8) и (147.9), также зависят от w.

Выведите
формулу для расчета периода: используем
соотношение F=-kx (квазиупругая сила) ,
где k — жесткость пружины. В вертикальном
положении на груз на пружине действуют
сила тяжести и сила упругости пружины.
Под действием силы тяжести пружина
растягивается на х1,
а затем мы отклоняем его от этого
положения на х. Тогда согласно второму
закону Ньютона, учитывая знаки проекций,
получим:
.
Но
,
тогда:
.

Или
–
ускорение тела, колеблющегося на пружине,
не зависит от силы тяжести, действующей
на это тело. Сила тяжести только приводит
к изменению положения равновесия.

Выразим
ускорение:
.
Сравним полученное уравнение с уравнением
колебательного движения
.
Видно, что
или
–
циклическая частота при колебаниях
пружинного маятника. Период
колебаний
или
(формула
Гюйгенса).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 июля 2022 года; проверки требует 1 правка.

Физи́ческий ма́ятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

Дифференциальное уравнение движения физического маятника[править | править код]

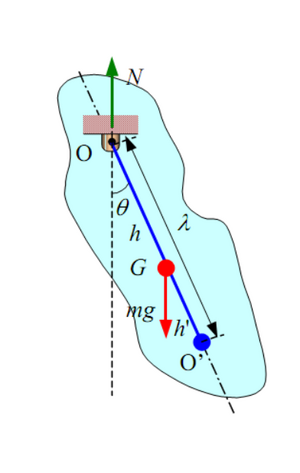
Момент инерции относительно оси, проходящей через точку подвеса, по теореме Штейнера:

${displaystyle I=I_{0}+mh^{2}=mleft(r^{2}+h^{2}right)}$

где I_0 — момент инерции относительно оси, проходящей через центр тяжести; — эффективный радиус инерции относительно оси, проходящей через центр тяжести.

Динамическое уравнение произвольного вращения твёрдого тела:

${displaystyle I{frac {d^{2}theta }{dt^{2}}}=-M_{s}}$

где M_s — суммарный момент сил, действующих на тело относительно оси вращения.

${displaystyle M_{s}=M+M_{f}}$

где — момент сил, вызванный силой тяжести; ${displaystyle M_{f}}$ — момент сил, вызванный силами трения среды.

Момент, вызванный силой тяжести, зависит от угла отклонения тела от положения равновесия:

Если пренебречь сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести:

$I{frac {d^{2}theta }{dt^{2}}}=-mghsin theta$

Если разделить обе части уравнения на и положить

${displaystyle lambda ={frac {r^{2}+h^{2}}{h}}={frac {r^{2}}{h}}+h}$

получим:

${displaystyle lambda {frac {d^{2}theta }{dt^{2}}}=-gsin theta }$

Такое уравнение аналогично уравнению колебаний математического маятника длиной lambda . Величина lambda называется приведённой длиной физического маятника.

Центр качания физического маятника. Теорема Гюйгенса[править | править код]

Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.

Поместим на луче, проходящем от точки подвеса через центр тяжести, точку на расстоянии lambda от точки подвеса. Эта точка и будет центром качания маятника.

Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром тяжести. Тогда момент инерции относительно оси подвеса будет равен ${displaystyle I=mlambda ^{2}}$ , а момент силы тяжести относительно той же оси . При этом уравнение движения не изменится.

Согласно теореме Гюйгенса,

Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.

Вычислим приведённую длину для нового маятника:

${displaystyle lambda _{1}={frac {r^{2}}{r^{2}/h}}+{frac {r^{2}}{h}}=h+{frac {r^{2}}{h}}=lambda }$

Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.

Период колебаний физического маятника[править | править код]

Наиболее общий случай[править | править код]

Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания.

Для этого умножим левую ${displaystyle lambda {frac {d^{2}theta }{dt^{2}}}=lambda {frac {d}{dt}}left({frac {dtheta }{dt}}right)}$ и правую часть этого уравнения на dtheta . Тогда:

${displaystyle lambda {frac {dtheta }{dt}}dleft({frac {dtheta }{dt}}right)=-gsin theta ,dtheta }$

Интегрируя это уравнение, получаем:

${displaystyle lambda left({frac {dtheta }{dt}}right)^{2}=2gcos theta +C}$

где — произвольная постоянная. Её можно найти из условия, что в ситуациях, когда , должно быть ${displaystyle {frac {dtheta }{dt}}=0}$ ( alpha — максимальный угол отклонения). Получаем:

Подставляем и преобразовываем получившееся уравнение:

${displaystyle {frac {dtheta }{dt}}=2{sqrt {frac {g}{lambda }}}{sqrt {sin ^{2}{frac {alpha }{2}}-sin ^{2}{frac {theta }{2}}}}.}$

Отделяем переменные и интегрируем это уравнение:

${displaystyle {sqrt {frac {g}{lambda }}}t=int limits _{0}^{frac {theta }{2}}{frac {dleft({frac {theta }{2}}right)}{sqrt {sin ^{2}{frac {alpha }{2}}-sin ^{2}{frac {theta }{2}}}}}}$

Удобно сделать замену переменной полагая $sin {frac {theta }{2}}=sin {frac {alpha }{2}}sin varphi$ . Тогда искомое уравнение принимает вид:

${displaystyle t={sqrt {frac {lambda }{g}}}int limits _{0}^{varphi }{frac {dvarphi }{sqrt {1-sin ^{2}{frac {alpha }{2}}sin ^{2}varphi }}}={sqrt {frac {lambda }{g}}}Fleft(varphi setminus alpha /2right).}$

Здесь — нормальный эллиптический интеграл Лежандра 1-го рода. Для периода колебаний получаем формулу:

${displaystyle T=4{sqrt {frac {lambda }{g}}},int limits _{0}^{pi /2}{frac {dvarphi }{sqrt {1-sin ^{2}{frac {alpha }{2}}sin ^{2}varphi }}}=4{sqrt {frac {lambda }{g}}},Kleft(sin {frac {alpha }{2}}right).}$

Здесь $Kleft(sin {frac {alpha }{2}}right)$ — полный нормальный эллиптический интеграл Лежандра 1-го рода. Раскладывая его в ряд, можно получить удобную для практических вычислений формулу:

${displaystyle T=2pi {sqrt {frac {lambda }{g}}}left{1+left({frac {1}{2}}right)^{2}sin ^{2}left({frac {alpha }{2}}right)+left({frac {1cdot 3}{2cdot 4}}right)^{2}sin ^{4}left({frac {alpha }{2}}right)+dots +left[{frac {left(2n-1right)!!}{left(2nright)!!}}right]^{2}sin ^{2n}left({frac {alpha }{2}}right)+dots right}.}$

Период малых колебаний физического маятника[править | править код]

Если — случай малых максимальных угловых отклонений от равновесия — то так как разложение синуса в ряд Маклорена ${displaystyle sin theta approx theta -theta ^{3}/3dots }$ и уравнения движения переходит в уравнение гармонического осциллятора без трения:

${displaystyle lambda {frac {d^{2}theta }{dt^{2}}}=-gtheta .}$

Период колебания маятника в этом случае:

${displaystyle T=2pi {sqrt {frac {lambda }{g}}}.}$

В иной формулировке: если амплитуда колебаний alpha мала, то корень в знаменателе эллиптического интеграла приближённо равен единице. Такой интеграл легко берётся, и получается хорошо известная формула малых колебаний:

${displaystyle T=2pi {sqrt {frac {lambda }{g}}}=2pi {sqrt {frac {I}{mgh}}}.}$

Эта формула даёт результаты приемлемой точности (ошибка менее 1 %) при углах, не превышающих 4°.

Следующий порядок приближения можно использовать с приемлемой точностью (ошибка менее 1 %) при углах отклонения до 1 радиана (≈57°):

${displaystyle Tapprox 2pi {sqrt {frac {lambda }{g}}}left(1+{frac {1}{4}}sin ^{2}left({frac {alpha }{2}}right)right)={frac {pi }{4}}{sqrt {frac {lambda }{g}}}left(9-cos {alpha }right).}$

См. также[править | править код]

Математический маятник
Маятник Дубошинского

Ссылки[править | править код]

маятник — статья из Большой советской энциклопедии.

Источник

Физическим маятником называется твердое тело, способное совершать колебания вокруг неподвижной точки, не совпадающей с его центром инерции (рис. 46а). В положении равновесия центр инерции С находится под точкой подвеса 0 маятника на одной с ней вертикали. При отклонении маятника от положения равновесия на угол j возникает вращательный момент сил, стремящийся вернуть маятник в положение равновесия. Этот момент равен

М = – mgl sinj,

где m – масса маятника, а l – расстояние между точкой подвеса и центром масс маятника. Знак “–” означает, что момент сил направлен против углового смещения. Уравнение вращательной динамики принимает вид:

b = М / I = – (mgl / I) sin j,

где I – момент инерции маятника относительно оси, проходящей через точку подвеса. В случае малых колебаний (j ≤ 5°) это уравнение переходит в дифференциальное уравнение собственных незатухающих колебаний:

решением которого является функция:

j = А cos (w₀t + a₀),

где через w₀ обозначена угловая частота колебаний:

w₀ = (mgl / I)^1/2.

Таким образом, при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, угловая частота w₀ которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром инерции маятника. Период колебаний физического маятника определяется выражением:

Из сопоставления формул и следует, что математический маятник с длиной l_пр = (I/ml) имеет такой же период колебаний, как и данный физический маятник. Величину l_пр = (I/ml) называют приведенной длиной физического маятника. Итак, приведенная длина физического маятника – это длина такого математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка 0′ на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения, называется центром качания физического маятника. По теореме Штейнера момент инерции маятника I может быть представлен в виде

I = I₀ + ml²,

где I₀ – момент инерции относительно оси, параллельной оси вращения и проходящей через центр инерции маятника.

Подставив I = I₀ + ml²в l_пр = (I/ml) , получаем: l_пр = (I₀/ml) + l, откуда следует, что приведенная длина l_пр всегда больше длины l, так что точка подвеса 0 и центр качания 0′ лежат по разные стороны от центра инерции С (центра масс). Подвесим маятник в центре качания 0′. Приведенная длина в этом случае будет равна: l_пр‘ = (I₀/ml‘) + l‘, где l‘ – расстояние между первоначальным центром качания и центром инерции маятника. Учитывая, что l‘ = l_пр – l , имеем:

l_пр‘ = I₀/m(l_пр – l) + l_пр – l = l_пр + [(I₀ + ml²) – ml_прl] /m(l_пр – l).

Выражение, стоящее в квадратных скобках, равно нулю, поскольку I₀ + ml² = I – это момент инерции относительно первоначальной оси вращения; этой же величине равно выражение ml_прl. Таким образом, мы приходим к выводу, что при подвешивании маятника в центре качания приведенная длина, а значит, и период колебаний будут теми же, что и вначале. Следовательно, точка подвеса 0 и центр качания 0′ обладают свойством взаимности: при переносе точки подвеса в центр качания прежняя точка подвеса становится новым центром качания.

На свойстве взаимности основано определение ускорения силы тяжести с помощью, так называемого оборотного маятника (рис. 46б). Оборотным называется такой маятник, у которого имеются две параллельные друг другу, закрепленные вблизи его концов опорные призмы П₁ и П₂, за которые он может поочередно подвешиваться. Вдоль маятника могут перемещаться и закрепляться на нем тяжёлые грузы – чечевицы А и В. Перемещением грузов добиваются того, чтобы при подвешивании маятника за любую из призм период колебаний был одинаков. Тогда расстояние между опорными ребрами призм будет равно l_пр. Измерив период колебаний маятника Т₀ и определив l_пр, при помощи формулы можно найти ускорение силы тяжести g:

Источник

Приведенная длина маятника, формула

Приведенной длиной физического маятника называется длина математического маятника с тем же периодом колебаний.

Если

l´	приведенная длина маятника,	метр
J_A	момент инерции тела относительно оси, проходящей через точку подвеса А,	кг · метр²
m	масса физического маятника,	кг
s	расстояние от точки подвеса А тела до его центра масс О,	метр

то в соответствии с формулами Математический маятник [4] и Физический маятник [4]

[
2πsqrt{frac{l´}{g}} = 2πsqrt{frac{J_{A}}{mgs}}
]

или

[
l´ = frac{J_{A}}{ms}
]

Вычислить, найти приведенную длину маятника, по формуле (2)

Приведенная длина маятника	стр. 548

Источник

19.
Физический маятник. Приведённая длина.

Физический
маятник – твердое тело, которое может
качаться вокруг неподвижной горизонтальной
оси. Точка А пересечения её с вертикальной
плоскостью, проходящей через центр масс
маятника, называется точкой подвеса
маятника. f
– угол отклонения от положения равновесия,
кинетическая энергия K=If’²/2,
I –
момент инерции относительно А.
Потенциальная энергия P=mgh,
h –
высота поднятия ц.масс над его нижним
состоянием. a
– расстояние между ц.масс и т.подвеса.
P=mga(1-cos
f)=2mga
sin²
(f/2),
для малых колебаний P=mgaf²/2.
Колебания маятника будут приблизительно
гармоническими с циклической частотой
w=V(mga/I)
и периодом T=2piV(I/mga).

Малые
колебания физического маятника изохронны,
т.е. не зависят от амплитуды.

Для
математического маятника a=l,
I=ml2,
где l
– длина маятника, по формуле получаем
T=2piV(l/g).
Физический маятник колеблется так же,
как математический маятник с длиной
l=I/ma.
Эта длина называется приведенной длиной
физического маятника.

Отложим
от точки подвеса A
вдоль прямой AC
отрезок AA’,
длина которого равна приведенной длине
физического маятника. Точка A’
– центр качания, т.е. математическая
точка, в которой можно сосредоточить
всю массу маятника, чтобы период его
колебаний остался неизменным. По т-ме
Гюйгенса-Штейнера I=I_c+ma²,
где I_c
– момент инерции маятника относительно
параллельной оси, проходящей через
ц.масс C.
Подставив значение l=I/ma,
получим l=a+I_c/ma.
Поэтому l>a,
причем всем точкам, одинаково удаленным
от ц.масс, соответствует одна и та же
длина.

Если
маятник подвесить за ц.качания, его
период не изменится и прежняя т.подвеса
станет новым ц.качания. Пусть a’=A’C,
при подвесе за т.A’
приведенная длина l’=a’+I_c/ma.
Но a’=l–a,
a’=I_c/(ma),
l’=I_c(ma)+a,
т.е. l’=l,
приведенная длина и период колебаний
не изменились.

Источник

Дифференциальное уравнение движения физического маятника[править | править код]

Центр качания физического маятника. Теорема Гюйгенса[править | править код]

Период колебаний физического маятника[править | править код]

Наиболее общий случай[править | править код]

Период малых колебаний физического маятника[править | править код]

См. также[править | править код]

Ссылки[править | править код]

Приведенная длина маятника, формула

Вычислить, найти приведенную длину маятника, по формуле (2)

Приведенная длина маятника

Вам также может понравиться

Как весам найти равновесие

Как найти девушку если ты анимешник

Как найти треугольник зная его высоту

Добавить комментарий Отменить ответ