Как найти приведенную массу молекулы - Сайт, где вы сможете решить свои вопросы

Приведённая масса — условная характеристика распределения масс в движущейся механической или смешанной (например, электро-механической) системе, зависящая от физических параметров системы (масс, моментов инерции, индуктивности и др.) и от её закона движения^[1].

Обычно приведенная масса определяется из равенства ${displaystyle T=mu v^{2},/2}$ , где — кинетическая энергия системы, а — скорость той точки системы, к которой приводится масса. В более общем виде приведённая масса является коэффициентом инерции $mu _{{ij}}$ в выражении кинетической энергии системы со стационарными связями, положение которой определяется обобщёнными координатами ${displaystyle r_{i}}$ :

${displaystyle 2T=sum _{i,,j=1}^{n}mu _{ij},{dot {r_{i}}}{dot {r_{j}}},,}$

где точка означает дифференцирование по времени, а ${displaystyle mu _{ij} }$ есть функции обобщённых координат.

Задача двух тел[править | править код]

В задаче двух тел, возникающей, например, в небесной механике или теории рассеяния, приведённая масса появляется как некая эффективная масса, когда задачу двух тел сводят к двум задачам об одном теле. Рассмотрим два тела: одно с массой ${displaystyle m_{1} }$ и другое с массой ${displaystyle m_{2} }$ . В эквивалентной проблеме одного тела рассматривают движение тела с приведённой массой, равной

${displaystyle mu ={1 over {{1 over m_{1}}+{1 over m_{2}}}}={{m_{1}m_{2}} over {m_{1}+m_{2}}} ,}$

где сила, действующая на эту массу, дается силой, действующей между этими двумя телами. Видно, что приведённая масса равна половине среднего гармонического двух масс.

Приведённая масса всегда меньше каждой из масс ${displaystyle m_{1} }$ или ${displaystyle m_{2} }$ или равна нулю, если одна из масс равна нулю. Пусть масса ${displaystyle m_{2} }$ значительно меньше массы $m_{1}$ ( ${displaystyle m_{2}ll m_{1}}$ ), тогда приближённое выражение для приведенной массы будет

${displaystyle mu ={frac {m_{2}}{1+m_{2}/m_{1}}}approx m_{2}(1-{frac {m_{2}}{m_{1}}})approx m_{mathrm {2} } .}$

Механика Ньютона[править | править код]

Используя второй закон Ньютона, можно найти, что воздействие тела 2 на тело 1 задаётся силой

${displaystyle mathbf {F} _{12}=m_{1}mathbf {a} _{1}.}$

Тело 1 оказывает влияние на тело 2 посредством силы

${displaystyle mathbf {F} _{21}=m_{2}mathbf {a} _{2}.}$

В силу третьего закона Ньютона эти две силы равны и противоположны по направлению:

${displaystyle mathbf {F} _{12}=-mathbf {F} _{21}.}$

Таким образом, имеем

${displaystyle m_{1}mathbf {a} _{1}=-m_{2}mathbf {a} _{2}}$

или

${displaystyle mathbf {a} _{2}=-{m_{1} over m_{2}}mathbf {a} _{1}.}$

Тогда относительное ускорение между двумя телами будет даваться выражением

${displaystyle mathbf {a} =mathbf {a} _{1}-mathbf {a} _{2}=left({1+{m_{1} over m_{2}}}right)mathbf {a} _{1}={{m_{2}+m_{1}} over {m_{1}m_{2}}}m_{1}mathbf {a} _{1}={mathbf {F} _{12} over mu }.}$

Тогда можно заключить, что тело 1 двигается относительно положения тела 2 (и в поле силового воздействия тела 2) как тело с массой, равной приведённой массе .

Механика Лагранжа[править | править код]

Задачу двух тел также можно описывать в лагранжевом подходе. Функция Лагранжа представляет собой разность кинетической и потенциальной энергий. В данной задаче это

${displaystyle L={1 over 2}m_{1}mathbf {dot {r}} _{1}^{2}+{1 over 2}m_{2}mathbf {dot {r}} _{2}^{2}-V(|mathbf {r} _{1}-mathbf {r} _{2}|)}$

где ${mathbf {r}}_{i}$ — радиус-вектор i-ой частицы с массой $m_{i}$ . Потенциальная энергия зависит от расстояния между частицами. Определим вектор

${displaystyle mathbf {r} =mathbf {r} _{1}-mathbf {r} _{2}}$

и пусть центр масс задаёт систему отсчёта

${displaystyle m_{1}mathbf {r} _{1}+m_{2}mathbf {r} _{2}=0}$

Тогда вектора положений масс $m_{i}$ переопределяются как

${displaystyle mathbf {r} _{1}={frac {m_{2}mathbf {r} }{m_{1}+m_{2}}},,,mathbf {r} _{2}={frac {-m_{1}mathbf {r} }{m_{1}+m_{2}}}.}$

Тогда новую функцию Лагранжа можно переписать в виде

${displaystyle L={1 over 2}mu mathbf {dot {r}} ^{2}-V(r),}$

откуда видно, что задача двух тел редуцировалась в задачу движения одного тела.

Применение[править | править код]

Приведенная масса может иметь отношение к более общим алгебраическим выражениям, которые задают взаимосвязь элементов системы и имеют вид

${displaystyle {1 over x_{text{eq}}}=sum _{i=1}^{n}{1 over x_{i}}={1 over x_{1}}+{1 over x_{2}}+cdots +{1 over x_{n}} ,}$

где ${displaystyle x_{i} }$ — характеристика i-го элемента системы (например, сопротивление резистора в параллельной цепи), ${displaystyle x_{eq} }$ — эквивалентная характеристика всей системы n элементов (например, полное сопротивление параллельного участка цепи). Такого рода выражения возникают во многих областях физики.

Понятие приведённой массы может встречаться в инженерных науках, например при расчётах конструкций на ударную нагрузку^[2].

Примечания[править | править код]

↑ С. М. Тарг. Приведённая масса // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 110. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
↑ А.И. Русаков Корректный расчет приведённых масс при ударе. Вестник РГУПС, №2, 2003. Дата обращения: 18 января 2010. Архивировано 19 февраля 2012 года.

Ссылки[править | править код]

Приведённая масса на HyperPhysics Архивная копия от 16 декабря 2006 на Wayback Machine

См. также[править | править код]

Задача двух тел

Источник

Меры количества компонентов в системе

За
меру количества принимают число
частиц компонента.

(k
= 1,…,k)
– число частиц k-компонентов
от 1 до k.

(k
= 1) – число
частиц компонента k.

На
практике обычно приходится иметь дело
с большими числами частиц компонентов,
порядка 10²³
единиц. Их оценку удобно производить
более крупной мерой, чем одна единица.
Роль такой меры играет 1 моль = 6,0210²³
единиц (частиц). Число единиц (частиц) в
1 моле называется числом Авогадро (N_А).
N_А
= 6,02310²³
моль^-1.

Эталоном
для воспроизводства 1 моля служит число
ядер в 0,012 кг (12 г) чистого изотопа С¹².

Очевидно,
что количество компонента «k»
n_k,
выраженное в молях, или число молей
данного компонента связано с числом
его частиц

соотношением:

. (1.1)

Отметим,
что 1 моль может служить мерой количества
не только компонентов, но и совокупности
любых других частиц (например, ядер,
электронов и др.) а также всяких дискретных
объектов, актов (например, элементарных
электрических зарядов, элементарных
актов химических реакций и т. д.)

Другая
мера количества k-компонента
– масса m_k
k-го
компонента:

, (1.2)

где
m_k
– масса компонента «k»;

–масса
всех частиц компонента «k»;

–масса
одной частицы;

–число
всех частиц.

Мольная
масса компонента M_k
в кг/моль в единицах СИ соответственно
равна

(1.3)

Из уравнения (1.2)
получим массу одной частицы:

. (1.4)

В
то же время из уравнения (1.3) следует,
что

. (1.5)

Совместное
решение уравнений (1.4) и (1.5) позволяет
получить уравнение связи между массой
m_kкомпонента
и его мольной массой M_k:

(1.6)

то
есть и

. (1.7)

Тогда
число молей компонентов может быть
определено (в дополнение к уравнению
(1.1))
из уравнения:

. (1.8)

Для
характеристики массы отдельных частиц
введена внесистемная углеродная единица
(у. е.), равная 1/12 массы чистого изотопа
С¹²:

1
у.е. =
= 1,6604410^-24
г = 1,660410^-27
кг.

Углеродная
единица массы и число Авогадро выбраны
таким образом, что мольная масса
компонента (г/моль) равна массе отдельной
его частицы, выраженной в углеродных
единицах. Например:

М(С₆Н₆)
=
(С₆Н₆)= (6_С
+ 6_H)
= 78 у.е.
6,02310²³
моль^-1
1,6604 10^-27
г/у.е.
= 78 г/моль

Частицы
компонентов состоят из еще более мелких
частиц, или субчастиц. Совокупность
таких мельчайших частиц одного и того
же вида называют субкомпонентом системы.
Если роль компонентов играют множества
одинаковых частиц атомной или молекулярной
природы, то субкомпонентами могут
служить, например, множества электронов
и одинаковых ядер, входящих в состав
упомянутых частиц. Приведенные выше
соотношения для компонентов распространяются
и на субкомпоненты.

Частицы,
составляющие компоненты, – химические
частицы (молекулы). Таким образом,
химические частицы – это ансамбли
физических частиц (атомных ядер,
электронов) и т. д. Частицы могут быть
простыми и сложными (одно- и многоядерными).

Классы химических частиц

Валентно-насыщенные
молекулы (Н₂, СО₂, Н₂О
и др.).

Молекулой
называется наименьшая нейтральная
частица данного вещества, обладающая
его химическими свойствами и способная
к самостоятельному существованию.
Различают одно- и многоатомные молекулы.

2. Ионы (катионы,
анионы).

Ион
– заряженная частица, представляющая
собой атом или группу химически связанных
с избытком электронов (анионы) или с
недостатком электронов (катионы). В
веществе положительные ионы существуют
вместе с отрицательными. Так как
электростатические силы, действующие
между ионами, велики, то невозможно
создать в веществе сколько-нибудь
значительный избыток ионов одного
знака.

3. Радикалы.

Свободными
радикалами называются частицы, обладающие
ненасыщенными валентностями (например,
СН₃
или NH₂)

В
обычных условиях свободные радикалы,
как правило, не могут существовать
длительное время. Другими словами –
свободные радикалы – это частицы,
обладающие высокой реакционной
способностью и содержащие неспаренные
электроны.

1.2. МИКРОСКОПИЧЕСКИЕ
СВОЙСТВА ВЕЩЕСТВА

Признаки,
характеризующие объект (компонент
системы) с качественной и количественной
стороны называют его свойствами.

Признаки,
характеризующие отдельные черты объекта
называются микроскопическими свойствами.
Для компонентов – это черты, характеризующие
строение вещества, т. е. распределение
масс и зарядов для частиц атомно-молекулярной
природы в пространстве. Эти свойства
определяются строением отдельных атомов
и характером их взаимодействия при
образовании химической связи. К числу
наиболее важных микроскопических
свойств следует отнести:

межъядерное
расстояние;

валентные
углы (углы связи);

моменты
инерции молекул;

дипольный
момент;

энергию связи.

Химическая
связь в основном осуществляется так
называемыми валентными электронами. У
s–
и p–элементов
валентными являются электроны внешнего
слоя, а у d–элементов
– электроны s–состояния
внешнего слоя и d–состояния
предвнешнего слоя. Как показывает
экспериментальные данные, при химическом
связывании атомов состояние электронов
внутренних слоев практически не меняется.

Химическая
связь образуется только в том случае,
когда при сближении атомов (двух или
большего числа) полная энергия системы
(сумма кинетической и потенциальной
энергий) понижается. Важнейшие сведения
о строении молекул вещества дают
зависимости потенциальной энергии
системы от расстояния между составляющими
ее атомами.

На
рис.1.1 в качестве примера приведена
кривая (1) потенциальной энергии для
системы из двух атомов водорода. По оси
абсцисс отложено расстояние между
ядрами водорода r,
а по оси ординат – потенциальная энергия
системы Е.

Характер
кривой можно объяснить следующим
образом. По мере сближения атомов
водорода между ними возникают
электростатические силы двух типов –
силы притяжения между ядром одного
атома и электроном другого и силы
отталкивания между ядрами и электронами
разных атомов. На больших расстояниях
начинают действовать в большей степени
силы притяжения и потенциальная энергия
системы понижается. Это понижение
продолжается до некоторого расстояния
r_e.
При дальнейшем уменьшении расстояния
между атомами начинают действовать
силы отталкивания, которые достигают
значительной величины при малых (меньше
r_e)
расстояниях между атомами.

Е,
кДж/моль

-400

800

Отталкивание

400

r, Å

Притяжение

E_св

r_e

Рис.
1.1 Изменение потенциальной энергии в
системе из двух атомов водорода в
зависимости от расстояния между ядрами:

1 – ;

2 – ;

3 – .

Минимум
на кривой потенциальной энергии отвечает
наиболее устойчивому состоянию системы
из двух атомов водорода – равновесному
межъядерному расстоянию r_e,
равному 0,74Ǻ,
т. е. образованию молекулы Н₂.
Указанное расстояние между ядрами
водорода в молекуле Н₂
заметно меньше суммы радиусов двух
свободных атомов водорода (1,06Ǻ).
Объясняется это тем, что возникновение
молекулы водорода из атомов водорода
сопровождается перекрыванием атомных
электронных облаков с образованием
молекулярного облака, которое окружает
два положительно заряженных ядра.
Расстояния между центрами ядер r_e
атомов в каждой отдельной молекуле
вещества представляет собой вполне
определенные величины – это те равновесные
расстояния, на которых силы притяжения
между ядрами уравновешиваются силами
отталкивания.

Мерой
прочности связи в молекуле может служить
как количество энергии, затрачиваемой
на ее разрыв, так и величина, которая
при суммировании по всем связям дает
энергию образования молекулы из атомов.

Для
двухатомных молекул энергия связи равна
величине энергии диссоциации молекул
на атомы и имеет положительные значения.
Энергия
образования связи Е_св
по величине та же, но имеет отрицательный
знак, поскольку образование молекулы
вещества сопровождается выигрышем
энергии. Последнее наглядно иллюстрируется
на рис.1.1, из которого видно, что на кривой
потенциальной энергии имеет место
минимум энергии, соответствующий
равновесному межъядерному расстоянию.

Геометрическая
характеристика двухсторонней молекулы
определяется межъядерным расстоянием.
Для многоатомной молекулы равновесную
конфигурацию можно описать межъядерным
расстоянием и углами между связями
(валентными связями).

Углы
связи –
определяются электронным строением
атомов и их взаимным расположением.

Пример:
молекула Н₂О

О₈Н₁

Рис 1.2

При
взаимодействии двух атомов кислорода
и одного атома водорода образуется
молекула воды

+

104,5^о

Рис. 1.3

В
процессе возникновения связи первоначальная
форма электронных облаков изменяется
и образуются новые орбитали одинаковой
формы. Это явление носит название
гибридизации
электронных
орбиталей. Угол при гибридизации близок
к 109^О.
Для молекулы воды НОН
= 104,5^о.

Обобщенной
геометрической характеристикой
двухатомных и многоатомных молекул
служат моменты
инерции молекул,
которые характеризуют распределение
масс отдельных ядер молекул в пространстве.

В
общем случае молекула может иметь
несколько ядер (несколько субкомпонентов)
с массами m_s,
удаленными от оси вращения на расстояния
r_s,
причем полное вращение можно разложить
на вращения вокруг трех взаимно
перпендикулярных осей (x,y,z).
Тогда момент инерции относительно
каждой оси.

(1.9)

Момент
инерции J_e
данной молекулы остается постоянным,
независимо от скорости и энергии
вращения, если пренебречь колебательным
движением ядер атомов (модель жесткого
ротатора).

Если
начало координат совпадает с центром
тяжести молекулы О^/,
то моменты инерции J_x,
J_y,
J_z,
называются главными
моментами инерции.

Т а б л и ц а 1.1

Классификация
многоатомных молекул по моментам инерции

	Тип молекулы	Момент инерции	Примеры
I	Линейная	J_x=0; J_y=J_z	CO, BrCl, NaCl многоат. HCN, N₂O, CO₂
II	Сферический волчок	J_x=J_y=J_z	CH₄, CCl₄ – тетраэдр, SF₆ –октаэдр
III	Симметричный волчок	J_x= J_y J_z	NH₃, PCl₃, CHCl₃, CH₃Cl, C₆H₆,CH₃C  CH
IV	Асимметричный волчок	J_x  J_y  J_z	H₂O, SO₂, CH₃OH, C₂H₃Cl, SO₃, CH₂O, CH₂Cl₂

I.
К первому типу относятся молекулы,
содержащие некоторые элементы II
группы (например, BeCl₂,
ZnBr₂,
CdJ₂).
Такой же конфигурацией обладают некоторые
молекулы с неодинаковыми межъядерными
расстояниями (в частности HCN).

II.
Тетраэдрическое строение типично для
углерода и его аналогов по IV
группе. Октаэдрическая структура –
SF₆,
HF₆.

III.
Пирамидальной формой обладает NH₃,
PCl₃
и другие соединения p–элементов
V
группы.

IV.
Многие соединения p–элементов
VI
группы (SO_2,,
H₂O
и др.). H₂S,
H₂Se,
H₂Te.

Рассмотрим
выше перечисленные типы молекул
подробнее.

Линейные
молекулы.
Наиболее
простые выражения моментов инерции
получаются для двухатомных молекул.
Для двухатомных молекул имеются два
равных по величине момента инерции
относительно двух взаимно перпендикулярных
осей z
и y,
не совпадающих с осью молекулы: J_z=J_y.
Момент инерции J_x
равен нулю из–за чрезвычайно малых
собственных размеров ядер.

Гомоядерная
двухатомная молекула (симметричная).

Пример:
молекула H₂

r₁
= r₂
, (1.10)

r_e
= r_H-H
= r₁
+ r₂
, (1.11)

J_e
= 2m_H
r₁²
, (1.12)

(

J_e=
m_H(r_e/2)²
+ m_H(r_e/2)²
= 1/2 m_Hr_e²

1.13)

Гетероядерная
двухатомная молекула (асимметричная).

Пример:
молекула СО

Центр тяжести
расположен так, что

r₁
m₁
= r₂m₂
. (1.14)

Так
как r_e
= r₁
+ r₂, то легко
видеть, что

r₁
= m₂/(m₁
+ m₂)
r_e
, (1.15)

r₂
= m₁/(m₁
+ m₂)
r_e
. (1.16)

Момент
инерции J_е
для двухатомной молекулы определяется
по уравнению:

J_e
= 
m_s
r_s²
= m₁r₁²
+ m₂r₂²
. (1.17)

J_e
= r_e²/(1/m₁+1/m₂)
= 
r_e²

одставляя уравнения (1.15) и (1.16) в
(1.17), получим:

, , (1.18)

где

– приведенная
масса молекулы

 =
m₁m₂/(m₁+m₂)
(1.19)

или

1/
= 1/m₁
+ 1/m₂
.

Приведенная
масса есть такая эквивалентная масса,
которая, будучи помещена на расстоянии
r_e
от оси вращения, приводит к той же
величине момента инерции, что и две
массы m₁
и m₂
на расстоянии r_e.

Смысл приведенной
массы поясняет рисунок

Для
практических расчетов удобно пользоваться
формулой:

1 у. е.


= 1,6610^-27
А₁А₂/(А₁+А₂)
, (1.20)

где

– приведенная масса, кг;

А₁
и А₂
– атомные массы ядер;

1,6610^-27
– численный
коэффициент – атомная единица (углеродная
единица) массы в кг.

Можно
выразить J_e
через приведенную массу, и для гомоядерной
двухатомной молекулы получаем

J_e=
1/2 mr_e²
= 
r_e².
(1.21)

Молекулы
типа сферического волчка. Для
этих молекул главные моменты инерции
относительно трех пространственных
осей равны J_x
= J_y
= J_z.
Сюда относятся молекулы тетраэдрического
строения.

П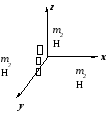ример:
молекула (СН₄)

Тетраэдр

J_x
= J_y
= J_z
= 8/3 m_H
r²_C_–_H

угол
при С
– 109^о28

r_1-2

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Состав веществ сложный, хотя образованы они крохотными частицами — атомами, молекулами, ионами. Молекулярное строение имеют многие жидкости и газы, а также некоторые твердые тела. Из атомов и заряженных ионов состоят металлы, многие соли. Все частицы обладают массой, даже самая крохотная молекула. Масса молекулы, если выразить ее в килограммах, получает очень маленькое значение. Например, m (Н₂О) = 30 • 10^-27 кг. Такие важнейшие характеристики вещества, как масса и размеры микрочастиц, издавна изучают физики и химики. Основы были заложены в трудах Михаила Ломоносова и Джона Дальтона. Рассмотрим, как изменились с тех пор взгляды на микромир.

Представления Ломоносова о «корпускулах»

Предположение о дискретном строении вещества высказывали ученые Древней Греции. Тогда же было дано название «атом» мельчайшей неделимой частице тел, «кирпичику» мироздания. Великий русский исследователь М. В. Ломоносов писал о ничтожно малой, неделимой физическими способами частице строения вещества — корпускуле. Позже в трудах других ученых она получила название «молекула».

Масса молекулы, а также ее размеры, определяются свойствами составляющих ее атомов. Долгое время ученым не удавалось заглянуть вглубь микромира, что тормозило развитие химии и физики. Ломоносов неоднократно призывал коллег изучать и в своей работе опираться на точные количественные данные — «меру и вес». Благодаря работам русского химика и физика были заложены основы учения о строении вещества, ставшие составной частью стройной атомно-молекулярной теории.

Атомы и молекулы — «кирпичики мироздания»

Даже микроскопически малые тела сложно устроены, обладают различными свойствами. Такие частицы, как атомы, образованы ядром и электронными слоями, отличаются по количеству положительных и отрицательных зарядов, радиусу, массе. Атомы и молекулы существуют в составе веществ не изолированно, они притягиваются с разной силой. Более заметно действие сил притяжения в твердых телах, слабее — в жидкостях, почти не ощущаются в газообразных веществах.

Химические реакции не сопровождаются разрушением атомов. Чаще всего происходит их перегруппировка, возникает другая молекула. Масса молекулы зависит от того, какими атомами она образована. Но при всех изменениях атомы остаются химически неделимыми. Но они могут войти в состав разных молекул. При этом атомы сохраняют свойства того элемента, к которому относятся. Молекула до своего распада на атомы сохраняет все признаки вещества.

Микрочастица строения тел — молекула. Масса молекулы

Для измерения массы макротел используются приборы, старейший из которых — весы. Результат измерения удобно получать в килограммах, ведь это основная единица международной системы физических величин (СИ). Чтобы определить массу молекулы в килограммах, надо сложить атомные массы с учетом количества частиц. Для удобства была введена специальная единица массы — атомная. Можно записать ее в виде буквенного сокращения (а.е.м.). Эта единица соответствует одной двенадцатой части массы углеродного нуклида ¹²С.

Если выразить найденное значение в стандартных единицах, то получаем 1,66 • 10^-27 кг. Такими малыми показателями для массы тел оперируют, в основном, физики. В статье приведена таблица, из которой можно узнать, чему равны массы атомов некоторых химических элементов. Чтобы узнать, чему равна масса одной молекулы водорода в килограммах, умножим на два приведенную в таблице атомную массу этого химического элемента. В результате получим значение массы молекулы, состоящей из двух атомов.

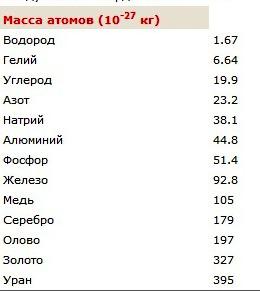
Относительная молекулярная масса

Трудно оперировать в расчетах очень маленькими величинами, это неудобно, приводит к затратам времени, к ошибкам. Что касается массы микрочастиц, то выходом из затруднительной ситуации стало применение относительных величин. Привычный для химиков термин состоит из двух слов — «атомная масса», его обозначение — Ar. Идентичное понятие было введено для молекулярной массы (то же самое, что масса молекулы). Формула, связывающая две величины: Mr = m(в-ва)/1/12 m(¹²C).

Нередко можно услышать, что говорят «молекулярный вес». Этот устаревший термин еще употребляется по отношению к массе молекулы, но все реже. Дело в том, что вес — это другая физическая величина — сила, которая зависит от географических координат тела. Напротив, масса служит постоянной характеристикой частиц, которые участвуют в химических процессах и перемещаются с обычной скоростью.

Как определить массу молекулы

Точное определение веса молекулы проводят при помощи прибора — масс-спектрометра. Для решения задач можно использовать сведения из периодической системы. К примеру, масса молекулы кислорода равна 16 • 2 = 32. Выполним несложные расчеты и найдем значение величины Mr(H₂O) — относительной молекулярной массы воды. По таблице Менделеева определим, что масса атома кислорода — 16, водорода — 1. Проведем несложные расчеты: M_r(H₂O) = 1 • 2 + 16 = 18, где M_r — молекулярная масса, H₂O — молекула воды, H — символ элемента водорода, О — химический знак кислорода.

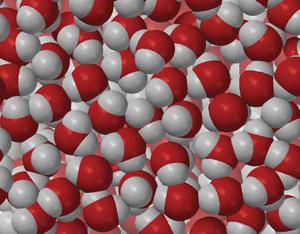
Массы изотопов

Химические элементы в природе и технике существуют в виде нескольких разновидностей атомов — изотопов. Каждый из них обладает индивидуальной массой, ее величина не может иметь дробное значение. Но атомная масса химического элемента чаще всего представляет собой число с несколькими знаками после запятой. При подсчетах учитывается распространенность каждой разновидности в земной коре. Поэтому массы атомов в периодической системе не всегда являются целыми числами. Используя такие величины для расчетов, мы получаем массы молекул, которые также не являются целыми числами. В некоторых случаях допускается округление значений.

Молекулярная масса веществ немолекулярного строения

Большинство неорганических веществ не имеет молекулярного строения. Металлы состоят из атомов, ионов и свободных электронов, соли — из катионов и анионов. Для веществ немолекулярного строения также подсчитывают массу условных молекул по брутто-формуле, отражающей простейший состав. Найдем значение Mr для вещества ионного строения — поваренной соли, формула которой NaCl. M_r = 23 + 35,5 = 55,5. Для некоторых видов расчетов требуется молекулярная масса воздуха — смеси газов. С учетом процентного содержания разных веществ в атмосфере молекулярная масса воздуха равна 29.

Размеры и масса молекул

На электронных микрофотографиях крупных молекул можно рассмотреть отдельные атомы, но они настолько малы, что в обычный микроскоп не видны. Линейный размер частицы любого вещества, как и масса, — это постоянная характеристика. Диаметр молекулы зависит от радиусов образующих ее атомов, их взаимного притяжения. Размеры частиц меняются с увеличением числа протонов и энергетических уровней. Атом водорода — самый маленький по размерам, его радиус составляет всего 0,5 • 10^-8 см. Атом урана в три раза больше атома водорода. Настоящие «великаны» микромира — молекулы органических веществ. Так, линейный размер одной из протеиновых частиц равен 44 • 10^-8 см.

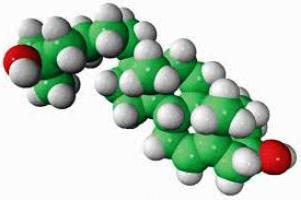
Подведем итог: масса молекул — это сумма масс атомов, входящих в их состав. Абсолютное значение в килограммах можно получить, умножив значение молекулярной массы, найденное в таблице Менделеева, на величину 1,66 • 10^-27 кг.

Молекулы ничтожно малы по сравнению с макротелами. Например, по своим размерам молекула воды Н₂О уступает яблоку во столько же раз, во сколько раз этот фрукт меньше нашей планеты.

Источник

Обычно приведенная масса mu , определяется из равенства , где T , — кинетическая энергия системы, а v , — скорость той точки системы, к которой приводится масса. В более общем виде приведённая масса является коэффициентом инерции $mu_{ij} ,$ в выражении кинетической энергии системы со стационарными связями, положение которой определяется s , обобщёнными координатами r_i : ,

$2T = sum^s_{i, , j = 1} mu_{ij}, dot{r_i} dot{r_j} , ,$

где точка означает дифференцирование по времени, а $mu_{ij}$ есть функции обобщённых координат.

Содержание

1 Задача двух тел
- 1.1 Движение тела с приведенной массой
2 Применение
3 Примечания
4 Ссылки
5 См. также

Задача двух тел

В задаче двух тел, возникающей, например, в небесной механике или теории рассеяния, приведённая масса появляется как некая эффективная масса, когда задачу двух тел сводят к двум задачам об одном теле. Рассмотрим два тела: одно с массой $m_{1}$ и другое с массой $m_{2}$ . В эквивалентной проблеме одного тела рассматривают движение тела с приведённой массой, равной

$mu = {1 over {{1 over m_1} + {1 over m_2}}} = {{m_1 m_2} over {m_1 + m_2}} ,$

Приведённая масса всегда меньше каждой из масс m_1 или m_2 или равна одной из них, если эта масса равна нулю. Пусть масса m_2 значительно меньше массы m_1 , (), тогда приближённое выражение для приведенной массы будет

$mu =frac{m_2}{1+m_2/m_1} approx m_2 (1- frac{m_2}{m_1})approx m_mathrm 2 .$

Движение тела с приведенной массой

Используя второй закон Ньютона, можно найти, что воздействие тела 2 на тело 1 задаётся силой

$F_{12} = m_1 a_1. !,$

Тело 1 оказывает влияние на тело 2 посредством силы

$F_{21} = m_2 a_2. !,$

В силу третьего закона Ньютона эти две силы равны и противоположны по направлению:

$F_{12} = - F_{21}.!,$

Таким образом, имеем

или

$a_2=-{m_1 over m_2} a_1. !,$

Тогда относительное ускорение между двумя телами будет даваться выражением

$a= a_1-a_2 = left({1+{m_1 over m_2}}right) a_1 = {{m_2+m_1}over{m_1 m_2}} m_1 a_1 = {F_{12} over mu}.$

Тогда можно заключить, что тело 1 двигается относительно положения тела 2 (и в поле силового воздействия тела 2) как тело с массой, равной приведённой массе mu , .

Применение

${1over x_text{eq}} = sum_{i=1}^n {1over x_i} = {1over x_1} + {1over x_2} + cdots+ {1over x_n} ,$

где x_i — характеристика i-го элемента системы (например, сопротивление резистора в параллельной цепи), $x_{eq}$ — эквивалентная характеристика всей системы n элементов (например, полное сопротивление параллельного участка цепи). Такого рода выражения возникают во многих областях физики.

Примечания

↑ «Физическая энциклопедия». В 5-ти томах. — М.: Советская энциклопедия, 1988. — ISBN 5-85270-034-7
↑ А.И. Русаков Корректный расчет приведённых масс при ударе. Вестник РГУПС, №2, 2003. Архивировано из первоисточника 19 февраля 2012. Проверено 18 января 2010.

Ссылки

Приведённая масса на HyperPhysics

См. также

Задача двух тел

Источник

Макеты страниц

Полное решение в общем виде допускает чрезвычайно важная задача о движении системы, состоящей всего из двух взаимодействующих частиц (задача двух тел).

В качестве предварительного шага к решению этой задачи покажем, каким образом она может быть существенно упрощена путем разложения движения системы на движение центра инерции и движения точек относительно последнего.

Потенциальная энергия взаимодействия двух частиц зависит лишь от расстояния между ними, т. е. от абсолютной величины разности их радиус-векторов. Поэтому лагранжева функция такой системы

Введем вектор взаимного расстояния обеих точек

и поместим начало координат в центре инерции, что дает:

Из двух последних равенств находим:

Подставляя эти выражения в (13,1), получим:

где введено обозначение

величина m называется приведенной массой. Функция (13,3) формально совпадает с функцией Лагранжа одной материальной точки с массой , движущейся во внешнем поле симметричном относительно неподвижного начала координат.

Таким образом, задача о движении двух взаимодействующих материальных точек сводится к решению задачи о движении одной точки в заданном внешнем поле . По решению этой задачи траектории каждой из частиц в отдельности (по отношению к их общему центру инерции) получаются по формулам (13,2),

Задача

Система состоит из одной частицы с массой Мил частиц с одинаковыми массами . Исключить движение центра инерции свести задачу к задаче о движении частиц.