Геометрия, 10 класс
Урок №9. Признак перпендикулярности прямой и плоскости
Перечень вопросов, рассматриваемых в теме.
- Доказательство признака перпендикулярности прямой и плоскости
Глоссарий по теме
Две прямые в пространстве называются перпендикулярными, если угол между ними равен 90º.
Прямая называется перпендикулярной к плоскости, если она перпендикулярная к любой прямой, лежащей в этой плоскости.
Лемма о перпендикулярности двух прямых к третьей прямой: если одна из двух параллельных прямых перпендикулярная к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
Теорема о параллельных прямых, перпендикулярных плоскости: если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Признак перпендикулярности прямой и плоскости: если прямая перпендикулярная к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости.
Обязательная литература:
Атанасян Л. С., Бутузов В. Ф. Кадомцев С. Б. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы: учеб. для общеобразоват. организаций: базовый и углубл. уровни. – 4-е изд. – М.: Просвещение, 2017. – 255 с.
Дополнительная литература:
Глазков Ю. А., Юдина И. И., Бутузов В. Ф. Рабочая тетрадь по геометрии для 10 класса. Базовый и профильный уровень. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения
Для того чтобы проверить перпендикулярность прямой к плоскости достаточно проверить перпендикулярность лишь к двум пересекающимся прямым, лежащим в этой плоскости.
Для доказательства рассмотрим прямую a, перпендикулярная к прямым p и q, лежащим в плоскости α и пересекающимся в точке О (рис. 1).

(Рис. 1)
Сначала рассмотрим случай, когда прямая a проходит через точку О (рис. 2). Проведем через точку О прямую l, параллельную прямой m. Если m проходит через точку О, то в качестве l возьмем саму m.
Отметим на прямой a точки A и B так, чтобы точка O была серединой отрезка AB. Затем проведем в плоскости α прямую, пересекающую прямые p, q и l соответственно в точках P, Q и L.

(Рис. 2)
Так как отрезок AO равен OB и прямая a перпендикулярна к прямым p и q, то p и q являются серединными перпендикулярами к отрезку AB. Поэтому отрезок AP равен BP и AQ равен BQ. Следовательно, треугольник APQ равен треугольнику BPQ по трем сторонам. Отсюда получаем, что угол APQ равен углу BPQ.
Треугольники APL и BPL равны по двум сторонам и углу между ними, так как отрезок AP равен BP, PL – общая сторона и угол APL равен углу BPL. Значит, отрезок AL равен BL. Значит, треугольник ABL – равнобедренный, а его медиана LO является и высотой, т.е. l перпендикулярна прямой a.
По лемме о перпендикулярности двух прямых к третьей прямой m будет перпендикулярна прямой a. Поэтому a перпендикулярна к любой прямой m плоскости α.
Теперь рассмотрим случай, когда прямая а не проходит через точку O (рис. 3). Проведем через точку O прямую a1, параллельную a. По лемме о перпендикулярности двух прямых к третьей, получим, что прямая a1 перпендикулярна прямым p и q. Поэтому по доказанному в первом случае a1 перпендикулярна плоскости α.

(Рис. 3)
По теореме о параллельных прямых, перпендикулярных плоскости a перпендикулярна к плоскости α.
Теорема доказана.
Примеры и разбор решения заданий тренировочного модуля
Пример 1. Докажем, что прямые CA1 и BD, проходящие через вершины куба ABCDA1B1C1D1, перпендикулярны (рис. 4).

(Рис. 4)
Рассмотрим плоскость ACC1 и прямую BD. Так как прямая BD перпендикулярна прямым AA1 и AC, то по признаку перпендикулярности прямой и плоскости, прямая BD перпендикулярна ACC1.
Следовательно, прямая BD перпендикулярна любой прямой в ACC1. В частности, прямая BD перпендикулярна прямой CA1. Что и требовалось доказать.
Тестовый вопрос №5. Верно ли, что если прямая перпендикулярна каким-нибудь двум прямым плоскости, то она перпендикулярна этой плоскости?
Решение. Воспользуемся признаком перпендикулярности прямой и плоскости: если прямая перпендикулярная к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна к этой плоскости. В нем сказано, что прямые в плоскости должны пересекаться. В условии подобного не сказано, поэтому утверждение неверно.
Ответ: неверно.
Тестовый вопрос №7. Треугольник АВС – равносторонний, CD – медиана, MD перпендикулярно плоскости ABC. AB = 2√3, MD = 4. Найти MC.
Решение. Рассмотрим треугольник ABC. Он равносторонний. Это означает, что его медиана так же является высотой и биссектрисой. Рассмотрим треугольник ADC. Он прямоугольный, т.к. DC медиана и высота. Сторона AD равна √3. По теореме Пифагора вычислим длину стороны DC:  .
.
Далее рассмотрим треугольник MDC, он прямоугольный, т.к. MD перпендикулярна плоскости ABC. Воспользовавшись теоремой Пифагора, найдем MC:  .
.
Ответ: 5.
Содержание:
Перпендикулярность в пространстве
В этом параграфе вы ознакомитесь с понятиями угла между прямыми в пространстве, угла между прямой и плоскостью, угла между двумя плоскостями; узнаете, что такое ортогональная проекция, изучите свойство ортогональной проекции многоугольника.
Угол между прямыми в пространстве
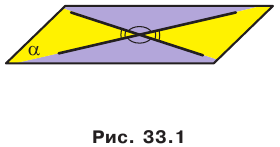
Поскольку две любые пересекающиеся прямые пространства лежат в одной плоскости, то угол между ними определим так же, как в планиметрии. Определение. Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает  (рис. 33.1).
(рис. 33.1).
Угол между двумя параллельными прямыми считают равным 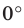 Следовательно, если
Следовательно, если 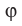 — угол между двумя прямыми, лежащими в одной плоскости, то
— угол между двумя прямыми, лежащими в одной плоскости, то 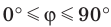 .
.
Введем понятие угла между скрещивающимися прямыми. Определение. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
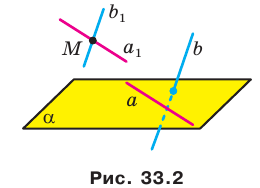
Пусть прямые  скрещивающиеся. Через точку М пространства проведем прямые
скрещивающиеся. Через точку М пространства проведем прямые 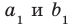 так, что
так, что 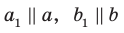 (рис. 33.2). По определению угол между скрещивающимися прямыми
(рис. 33.2). По определению угол между скрещивающимися прямыми 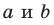 равен углу между пересекающимися прямыми
равен углу между пересекающимися прямыми 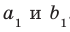 .
.
Возникает естественный вопрос: зависит ли угол между данными скрещивающимися прямыми 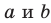 от выбора точки М ? Ответить на этот вопрос помогает следующая теорема.
от выбора точки М ? Ответить на этот вопрос помогает следующая теорема.
Теорема 33.1. Угол между двумя пересекающимися прямыми равен углу между двумя другими пересекающимися прямыми, соответственно параллельными данным.
Воспользовавшись теоремой 33.1, можно показать, что угол между скрещивающимися прямыми 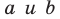 равен углу между пересекающимися прямыми
равен углу между пересекающимися прямыми 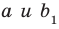 , где
, где 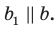
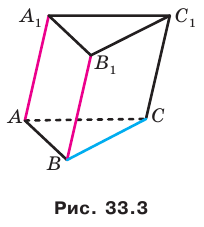
Например, на рисунке 33.3 изображена треугольная призма 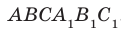 . Угол между скрещивающимися прямыми
. Угол между скрещивающимися прямыми 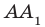 и ВС равен углу между пересекающимися прямыми
и ВС равен углу между пересекающимися прямыми 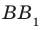 и ВС.
и ВС.
Определение. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.
Заметим, что перпендикулярные прямые могут как пересекаться, так и быть скрещивающимися.
Если прямые 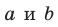 перпендикулярны, то записывают:
перпендикулярны, то записывают: 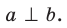 Два отрезка в пространстве называют перпендикулярными, если они лежат на перпендикулярных прямых.
Два отрезка в пространстве называют перпендикулярными, если они лежат на перпендикулярных прямых.
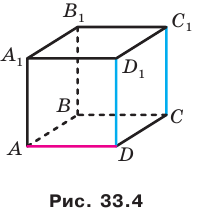
Например, ребра AD и 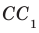 куба
куба 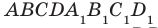 перпендикулярны (рис. 33.4). Действительно, поскольку
перпендикулярны (рис. 33.4). Действительно, поскольку 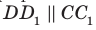 то угол между прямыми AD и
то угол между прямыми AD и 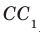 равен углу между прямыми AD и
равен углу между прямыми AD и 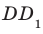 . Но
. Но 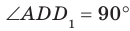 , поэтому
, поэтому 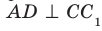 .
.
Пример:
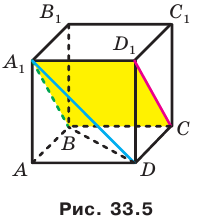
На рисунке 33.5 изображен куб 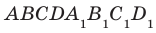 . Найдите угол между прямыми
. Найдите угол между прямыми 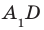 и
и 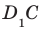 .
.
Решение:
Соединим точки 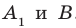 . Поскольку
. Поскольку 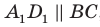 , то точки
, то точки 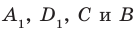 лежат в одной плоскости. Эта плоскость пересекает параллельные плоскости
лежат в одной плоскости. Эта плоскость пересекает параллельные плоскости 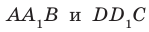 по параллельным прямым
по параллельным прямым 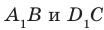 . Следовательно, угол между прямыми
. Следовательно, угол между прямыми 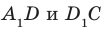 равен углу
равен углу 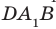 . Соединим точки В и D. Отрезки
. Соединим точки В и D. Отрезки 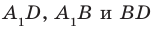 равны как диагонали равных квадратов. Следовательно, треугольник
равны как диагонали равных квадратов. Следовательно, треугольник 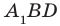 равносторонний. Тогда
равносторонний. Тогда 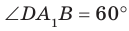 . Ответ : 60°.
. Ответ : 60°.
Перпендикулярность прямой и плоскости
В повседневной жизни мы говорим: флагшток перпендикулярен поверхности земли (рис. 34.1), мачты парусника перпендикулярны поверхности палубы (рис. 34.2), шуруп вкручивают в доску перпендикулярно ее поверхности (рис. 34.3) и т.п.



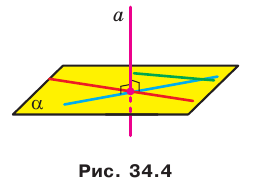
Эти примеры дают представление о прямой, перпендикулярной плоскости. Определение. Прямую называют перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости (рис. 34.4).
Если прямая 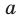 перпендикулярна плоскости
перпендикулярна плоскости 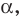 то записывают:
то записывают: 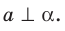 Также принято говорить, что плоскость
Также принято говорить, что плоскость 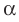 перпендикулярна прямой
перпендикулярна прямой 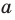 или прямая
или прямая 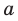 и плоскость
и плоскость 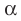 перпендикулярны.
перпендикулярны.
Из определения следует, что если прямая 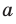 перпендикулярна плоскости
перпендикулярна плоскости 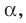 то она пересекает эту плоскость.
то она пересекает эту плоскость.
Отрезок называют перпендикулярным плоскости, если он принадлежит прямой, перпендикулярной этой плоскости.
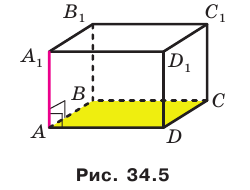
Например, интуитивно понятно, что ребро 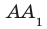 прямоугольного параллелепипеда
прямоугольного параллелепипеда 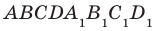 перпендикулярно плоскости АВС (рис. 34.5). Доказать этот факт нетрудно, воспользовавшись следующей теоремой.
перпендикулярно плоскости АВС (рис. 34.5). Доказать этот факт нетрудно, воспользовавшись следующей теоремой.
Теорема 34.1 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.
На рисунке 34.5 прямая 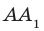 перпендикулярна двум пересекающимся прямым АВ и AD плоскости АВС. Следовательно, по признаку перпендикулярности прямой и плоскости
перпендикулярна двум пересекающимся прямым АВ и AD плоскости АВС. Следовательно, по признаку перпендикулярности прямой и плоскости 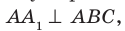 а значит, и ребро
а значит, и ребро 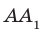 также перпендикулярно плоскости АВС.
также перпендикулярно плоскости АВС.
Теорему 34.1 часто используют на практике. Например, подставка для новогодней елки имеет форму крестовины. Если елку установить так, чтобы ее ствол был перпендикулярен направлениям крестовины, то елка будет стоять перпендикулярно плоскости пола (рис. 34.6).

Приведем теорему, которую можно рассматривать как еще один признак перпендикулярности прямой и плоскости.
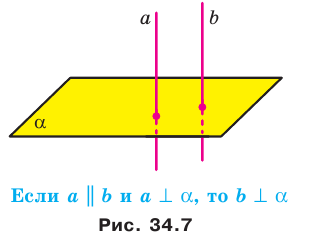
Теорем а 34.2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости (рис. 34.7).
Например, на рисунке 34.5 прямая 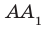 перпендикулярна плоскости АВС, а прямая
перпендикулярна плоскости АВС, а прямая 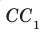 параллельна прямой
параллельна прямой 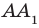 . Следовательно, по теореме 34.2 прямая
. Следовательно, по теореме 34.2 прямая 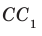 также перпендикулярна плоскости АВС. Сформулируем теорему, являющуюся признаком параллельности двух прямых.
также перпендикулярна плоскости АВС. Сформулируем теорему, являющуюся признаком параллельности двух прямых.
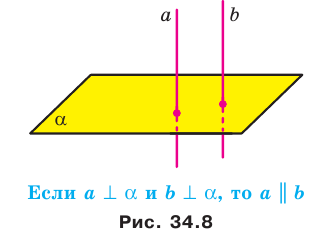
Теорем а 34.3. Если две прямые перпендикулярны одной и той же плоскости, то они параллельны (рис. 34.8). Справедлива и такая теорема.
Теорема 34.4. Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.
Пример:
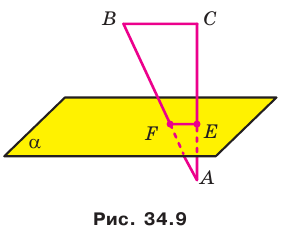
Плоскость  перпендикулярная катету АС прямоугольного треугольника АВС, пересекает катет АС в точке Е, а гипотенузу АВ — в точке F (рис. 34.9). Найдите отрезок EF, если АЕ : ЕС = 3 : 4, ВС = 21 см.
перпендикулярная катету АС прямоугольного треугольника АВС, пересекает катет АС в точке Е, а гипотенузу АВ — в точке F (рис. 34.9). Найдите отрезок EF, если АЕ : ЕС = 3 : 4, ВС = 21 см.
Решение:
Поскольку прямая АС перпендикулярна плоскости  то прямая АС перпендикулярна любой прямой этой плоскости, в частности прямой EF. Прямые EF и ВС лежат в одной плоскости и перпендикулярны прямой АС, поэтому
то прямая АС перпендикулярна любой прямой этой плоскости, в частности прямой EF. Прямые EF и ВС лежат в одной плоскости и перпендикулярны прямой АС, поэтому  . Из этого следует, что треугольники AEF и
. Из этого следует, что треугольники AEF и  подобны. Следовательно, можно записать: EF : СВ=АЕ : АС. Отсюда EF : 21 = 3 : 7, EF = 9 см. Ответ: 9 см.
подобны. Следовательно, можно записать: EF : СВ=АЕ : АС. Отсюда EF : 21 = 3 : 7, EF = 9 см. Ответ: 9 см.
Перпендикуляр и наклонная
Пусть фигура 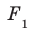 — параллельная проекция фигуры F на плоскость
— параллельная проекция фигуры F на плоскость 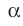 в направлении прямой
в направлении прямой 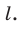 Если
Если 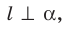 , то фигуру
, то фигуру 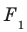 называют ортогональной проекцией фигуры F на плоскость
называют ортогональной проекцией фигуры F на плоскость 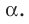
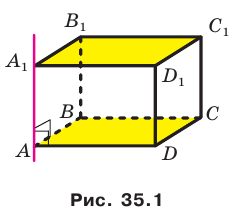
Например, основание ABCD прямоугольного параллелепипеда 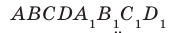 является ортогональной проекцией основания
является ортогональной проекцией основания 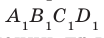 на плоскость АВС в направлении прямой
на плоскость АВС в направлении прямой 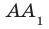 (рис. 35.1).
(рис. 35.1).
В дальнейшем, говоря о проекции фигуры, если не оговорено противное, будем иметь в виду ортогональную проекцию.
Пусть даны плоскость 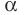 и не принадлежащая ей точка А . Через точку А проведем прямую
и не принадлежащая ей точка А . Через точку А проведем прямую 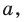 перпендикулярную плоскости
перпендикулярную плоскости 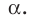 Пусть
Пусть 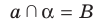 (рис. 35.2).
(рис. 35.2).
Отрезок АВ называют перпендикуляром, опущенным из точки А на плоскость 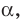 точку В — основанием перпендикуляра. Основание В перпендикуляра АВ — это проекция точки А на плоскость
точку В — основанием перпендикуляра. Основание В перпендикуляра АВ — это проекция точки А на плоскость 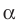 .
.
Отметим на плоскости 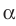 какую-нибудь точку С, отличную от точки В. Проведем отрезок АС (рис. 35.2). Отрезок АС называют наклонной, проведенной из точки А к плоскости
какую-нибудь точку С, отличную от точки В. Проведем отрезок АС (рис. 35.2). Отрезок АС называют наклонной, проведенной из точки А к плоскости 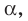 точку С — основанием наклонной. Отрезок ВС является проекцией наклонной АС.
точку С — основанием наклонной. Отрезок ВС является проекцией наклонной АС.
Теорема 35.1. Если из одной тонки проведены к плоскости перпендикуляр и наклонная, то наклонная больше перпендикуляра.
Пример:
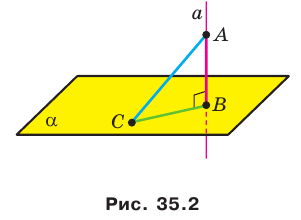
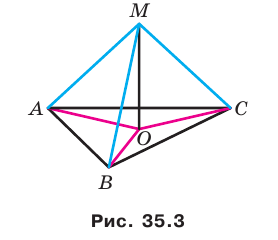
Докажите, что если точка, не принадлежащая плоскости многоугольника, равноудалена от его вершин, то проекцией этой точки на плоскость многоугольника является центр его описанной окружности.
Решение:
Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Пусть точка М не принадлежит плоскости АВС, причем МА = = МВ = МС. Опустим из точки М перпендикуляр МО на плоскость АВС (рис. 35.3). Докажем, что точка О — центр описанной окружности треугольника АВС. Поскольку 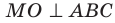 , то
, то 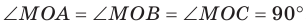 . В прямоугольных треугольниках МОА, МОВ, МОС катет МО — общий, гипотенузы равны, следовательно, эти треугольники равны по гипотенузе и катету. Из равенства данных треугольников следует, что ОА = ОВ = ОС, то есть точка О — центр описанной окружности треугольника АВС.
. В прямоугольных треугольниках МОА, МОВ, МОС катет МО — общий, гипотенузы равны, следовательно, эти треугольники равны по гипотенузе и катету. Из равенства данных треугольников следует, что ОА = ОВ = ОС, то есть точка О — центр описанной окружности треугольника АВС.
Заметим, что когда надо определить расстояние между двумя геометрическими фигурами, то стремятся найти расстояние между их ближайшими точками. Например, из курса планиметрии вы знаете, что расстоянием от точки, не принадлежащей прямой, до этой прямой называют расстояние от данной точки до ближайшей точки на прямой, то есть длину перпендикуляра, опущенного из точки на прямую. Теорема 35.1 показывает, что целесообразно принять следующее определение.
Определение. Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.
Пример:
Докажите, что если прямая параллельна плоскости, то все точки прямой равноудалены от плоскости.
Решение:
Пусть А и В — две произвольные точки прямой 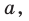 параллельной плоскости
параллельной плоскости 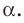 Точки
Точки 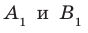 — основания перпендикуляров, опущенных соответственно из точек А и В на плоскость
— основания перпендикуляров, опущенных соответственно из точек А и В на плоскость 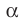 (рис. 35.4). Докажем, что
(рис. 35.4). Докажем, что 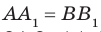 .
.
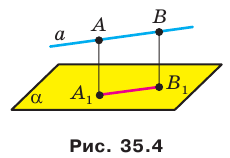
По теореме 34.3 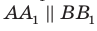 . Следовательно, точки
. Следовательно, точки 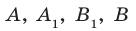 лежат в одной плоскости. Плоскость
лежат в одной плоскости. Плоскость 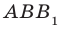 проходит через прямую
проходит через прямую 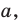 параллельную плоскости
параллельную плоскости 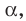 и пересекает плоскость
и пересекает плоскость 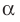 по прямой
по прямой 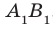 . Тогда по теореме 30.2 получаем:
. Тогда по теореме 30.2 получаем: 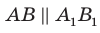 . Таким образом, в четырехугольнике
. Таким образом, в четырехугольнике 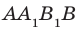 каждые две противолежащие стороны параллельны. Следовательно, четырехугольник
каждые две противолежащие стороны параллельны. Следовательно, четырехугольник 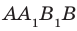 — параллелограмм. Отсюда
— параллелограмм. Отсюда 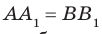 Так как точки А и В выбраны на прямой
Так как точки А и В выбраны на прямой 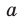 произвольно, то утверждение задачи доказано.
произвольно, то утверждение задачи доказано.
Доказанное свойство позволяет принять следующее определение. Определение. Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости. Используя результат, полученный в ключевой задаче 2, можно решить следующую задачу.
Пример:
Докажите, что если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости. Определение. Расстоянием между двумя параллельными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.
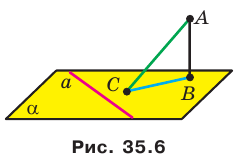
Результаты, полученные в ключевых задачах 2 и 3, часто используют в практической деятельности, например в строительстве (рис. 35.5).

Теорема 35.2 (теорема о трех перпендикулярах). Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.
Доказательство. Докажем первую часть теоремы.Пусть прямая 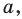 принадлежащая плоскости
принадлежащая плоскости 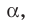 перпендикулярна проекции ВС наклонной АС (рис. 35.6). Докажем, что
перпендикулярна проекции ВС наклонной АС (рис. 35.6). Докажем, что 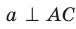 . Имеем:
. Имеем: 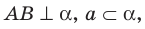 следовательно,
следовательно, 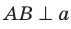 . Получили, что прямая а перпендикулярна двум пересекающимся прямым АВ и ВС плоскости АВС; следовательно,
. Получили, что прямая а перпендикулярна двум пересекающимся прямым АВ и ВС плоскости АВС; следовательно,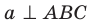 . Поскольку
. Поскольку 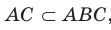 то
то 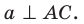 Доказательство второй части теоремы аналогично доказательству первой части.
Доказательство второй части теоремы аналогично доказательству первой части.
Пример:
Точка М не принадлежит плоскости выпуклого многоугольника и равноудалена от всех прямых, содержащих его стороны. Проекцией точки М на плоскость многоугольника является точка О, принадлежащая многоугольнику. Докажите, что точка О — центр вписанной окружности многоугольника.
Решение:
Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Опустим из точки О перпендикуляры ON, ОК и ОЕ соответственно на прямые АВ, ВС и СА (рис. 35.7). Соединим точку М с точками Е, К и N.
Отрезок ON является проекцией наклонной MN на плоскость АВС. По построению 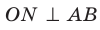 . Тогда по теореме о трех перпендикулярах получаем:
. Тогда по теореме о трех перпендикулярах получаем: 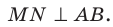
Аналогично можно доказать, что 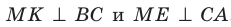 . Следовательно, длины отрезков MN, МК и ME — расстояния от точки М до прямых АВ, ВС и СА соответственно. По условию MN = МК = МЕ.
. Следовательно, длины отрезков MN, МК и ME — расстояния от точки М до прямых АВ, ВС и СА соответственно. По условию MN = МК = МЕ. 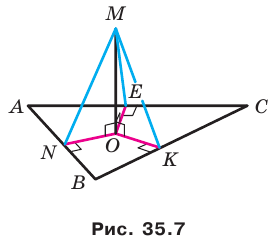
В прямоугольных треугольниках MON, МОК, МОЕ катет МО общий, гипотенузы равны; следовательно, данные треугольники равны по катету и гипотенузе. Из равенства этих треугольников следует, что ON = ОК = ОЕ.
Длины отрезков ON, ОК и ОЕ являются расстояниями от точки О до прямых, содержащих стороны треугольника АВС. Мы показали, что эти расстояния равны. Так как точка О принадлежит треугольнику АВС, то точка О — центр вписанной окружности треугольника АВС.
Угол между прямой и плоскостью
Вы знаете, что в давние времена путешественники ориентировались по звездам. Они измеряли угол, который образовывал с плоскостью горизонта луч, идущий от данной точки к небесному телу.
Сегодня человеку в своей деятельности также важно определять углы, под которыми наклонены к данной плоскости некоторые объекты (рис. 36.1). Эти примеры показывают, что целесообразно ввести понятие угла между прямой и плоскостью.

Определение. Если прямая параллельна плоскости или принадлежит ей, то считают, что угол меж ду такой прямой и плоскостью равен 0°.
Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен 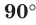 .
.
Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость (рис. 36.2).
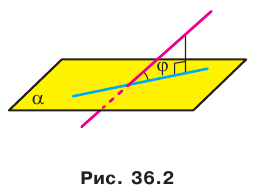
Из определения следует, что если 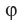 — угол между прямой и плоскостью, то
— угол между прямой и плоскостью, то 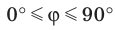 .
.
Также принято говорить, что прямая образует угол 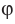 с плоскостью.
с плоскостью.
Углом между отрезком и плоскостью называют угол между прямой, содержащей этот отрезок, и плоскостью.
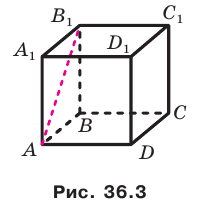
Например, рассмотрим куб 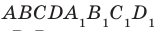 (рис. 36.3). Угол между диагональю
(рис. 36.3). Угол между диагональю 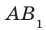 грани
грани 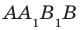 и плоскостью АВС равен 45°. Действительно, прямая АВ — проекция прямой
и плоскостью АВС равен 45°. Действительно, прямая АВ — проекция прямой 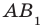 на плоскость АВС. Тогда угол между прямой
на плоскость АВС. Тогда угол между прямой 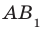 и плоскостью АВС равен величине угла
и плоскостью АВС равен величине угла 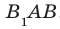 . Поскольку четырехугольник
. Поскольку четырехугольник 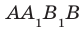 — квадрат, то
— квадрат, то 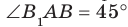 .
.
Пример:
Докажите, что если из одной точки к плоскости проведены наклонные, образующие равные углы с плоскостью, то проекция данной точки на плоскость равноудалена от оснований наклонных.
Решение:
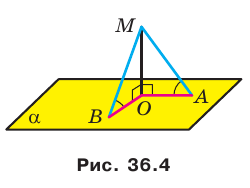
Пусть МЛ и М В — наклонные, образующие с плоскостью 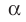 равные углы, отрезки ОА и ОВ — проекции этих наклонных (рис. 36.4). Докажем, что ОА = ОВ.
равные углы, отрезки ОА и ОВ — проекции этих наклонных (рис. 36.4). Докажем, что ОА = ОВ.
Прямая ОА является проекцией прямой МА на плоскость 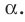 Так как угол МАО острый, то он равен углу между прямыми ОА и МА. Следовательно, величина угла МАО равна углу между наклонной МА и плоскостью
Так как угол МАО острый, то он равен углу между прямыми ОА и МА. Следовательно, величина угла МАО равна углу между наклонной МА и плоскостью 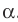 . Аналогично можно доказать, что величина угла МВО равна углу между наклонной МВ и плоскостью
. Аналогично можно доказать, что величина угла МВО равна углу между наклонной МВ и плоскостью 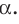 По условию
По условию 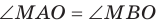 .
.
Поскольку 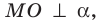 то
то 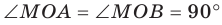 . Получаем, что прямоугольные треугольники МОА и МОВ равны по катету и противолежащему острому углу. Отсюда
. Получаем, что прямоугольные треугольники МОА и МОВ равны по катету и противолежащему острому углу. Отсюда 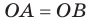 .
.
- Заказать решение задач по высшей математике
Двугранный угол. Угол между плоскостями
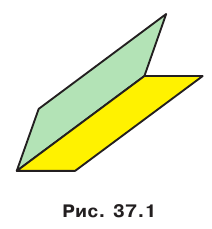
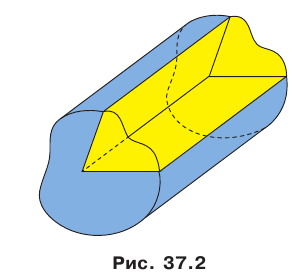
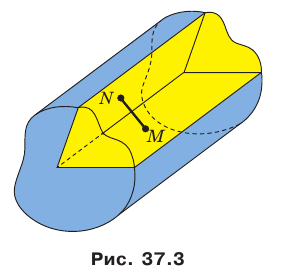
На рисунке 37.1 изображена фигура, состоящая из двух полуплоскостей, имеющих общую границу. Эта фигура делит пространство на две части, выделенные на рисунке 37.2 разными цветами. Каждую из этих частей вместе с полуплоскостями называют двугранным углом. Полуплоскости называют гранями двугранного угла, а их общую границу — ребром двугранного угла. Как видим, «желтый» и «синий» двугранные углы, изображенные на рисунке 37.2, существенно различаются. Это различие выражается следующим свойством. На гранях двугранного угла выберем произвольные точки М и N (рис. 37.3).
Отрезок MN принадлежит «желтому» двугранному углу, а «синему» двугранному углу принадлежат лишь концы отрезка. В дальнейшем, говоря «двугранный угол», будем подразумевать такой двугранный угол, который содержит любой отрезок с концами на его гранях («желтый» двугранный угол).
Наглядное представление о двугранном угле дают полуоткрытая классная доска, двускатная крыша, открытый ноутбук (рис. 37.4).

Двугранный угол считают пространственным аналогом угла на плоскости. Вы знаете, как определяют величину угла на плоскости. Научимся определять величину двугранного угла.
Отметим на ребре MN двугранного угла произвольную точку О. Через точку О в гранях двугранного угла проведем лучи ОА и ОВ перпендикулярно ребру MN (рис. 37.5). Угол АОВ, образованный этими лучами, называют линейным углом двугранного угла. Поскольку 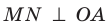 и
и 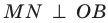 , то
, то 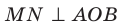 . Таким образом, если через произвольную точку ребра двугранного угла провести плоскость перпендикулярно ребру, то эта плоскость пересечет двугранный угол по его линейному углу.
. Таким образом, если через произвольную точку ребра двугранного угла провести плоскость перпендикулярно ребру, то эта плоскость пересечет двугранный угол по его линейному углу.
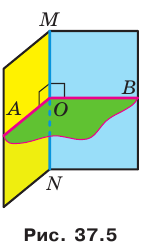
Определение. Величиной двугранного угла называют величину его линейного угла.
Двугранный угол называют острым, прямым, тупым или развернутым, если его линейный угол соответственно острый, прямой, тупой или развернутый.
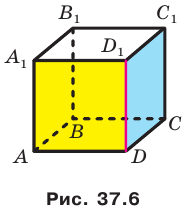
Например, рассмотрим куб 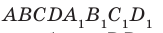 (рис. 37.6). Двугранный угол с ребром
(рис. 37.6). Двугранный угол с ребром 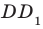 , грани которого принадлежат плоскостям
, грани которого принадлежат плоскостям 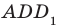 и
и 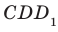 является прямым. Действительно, поскольку
является прямым. Действительно, поскольку 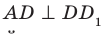 и
и 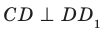 , то угол ADC — линейный угол двугранного угла с ребром
, то угол ADC — линейный угол двугранного угла с ребром 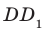 .
.
Угол ADC прямой.
При пересечении двух плоскостей образуются четыре двугранных угла, отличных от развернутого (рис. 37.7). Здесь возможны два случая:
- все четыре двугранных угла прямые (рис. 37.7, а);
- из четырех двугранных углов два равных угла острые и два равных угла тупые (рис. 37.7, б).
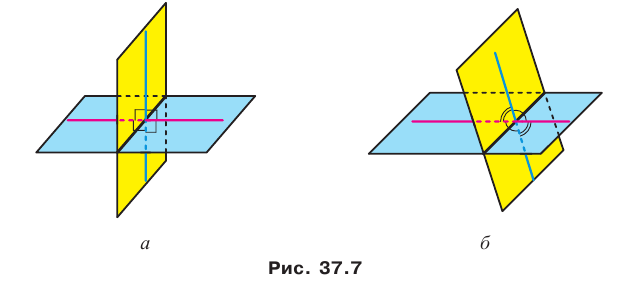
В обоих случаях из четырех двугранных углов найдется такой, величина которого не превышает 90°.
Определение. Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°. Угол между двумя параллельными плоскостям и равен 0°.
Углом между многоугольником и плоскостью, которой много угольник не принадлежит, называют угол между плоскостью, содержащей многоугольник, и данной плоскостью.
Углом между двумя многоугольниками, лежащими в разных плоскостях, называют угол между плоскостями, в которых лежат эти многоугольники.
Пример:
Прямоугольные треугольники 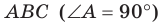 и АВМ
и АВМ 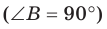 имеют общий катет АВ (рис. 37.8). Отрезок МВ перпендикулярен плоскости АВС. Известно, что МВ = 4 см, АС = 6 см, МС = 10 см. Найдите угол между плоскостями АВС и АМС.
имеют общий катет АВ (рис. 37.8). Отрезок МВ перпендикулярен плоскости АВС. Известно, что МВ = 4 см, АС = 6 см, МС = 10 см. Найдите угол между плоскостями АВС и АМС.
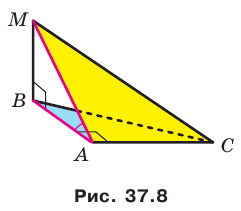
Решение:
Отрезок ВА является проекцией наклонной МА на плоскость АВС. Так как 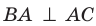 , то по теореме о трех перпендикулярах
, то по теореме о трех перпендикулярах 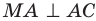 . Следователь но, угол МАВ — линейный угол двугранного угла с ребром АС, грани которого принадлежат плоскостям АВС и АМС. Поскольку угол МАВ острый, то угол между плоскостями АВС и АМС равен величине угла МАВ.
. Следователь но, угол МАВ — линейный угол двугранного угла с ребром АС, грани которого принадлежат плоскостям АВС и АМС. Поскольку угол МАВ острый, то угол между плоскостями АВС и АМС равен величине угла МАВ.
Для стороны AM прямоугольного треугольника АМС можно записать: 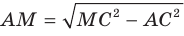 . Отсюда
. Отсюда 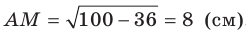 . Для угла МАВ прямоугольного треугольника МАВ запишем:
. Для угла МАВ прямоугольного треугольника МАВ запишем: 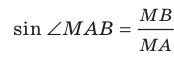 . Отсюда
. Отсюда 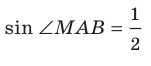 и
и 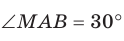 . Ответ: 30°.
. Ответ: 30°.
Имеет место теорема, устанавливающая связь между площадью данного многоугольника и площадью его проекции.
Теорема 37.1 (площадь ортогональной проекции многоугольника). Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где 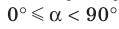 .
.
Определение. Две плоскости называют перпендикулярными, если угол между ними равен 90°.
Если плоскости 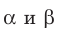 перпендикулярны, то записывают:
перпендикулярны, то записывают: 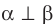 . Также принято говорить, что плоскость
. Также принято говорить, что плоскость 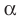 перпендикулярна плоскости
перпендикулярна плоскости 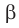 или плоскость
или плоскость 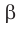 перпендикулярна плоскости
перпендикулярна плоскости 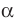 .
.
Наглядное представление о перпендикулярных плоскостях дают плоскости стены и потолка комнаты, плоскости двери и пола, плоскости сетки и теннисного корта (рис. 37.9).

Очевидно, что перпендикулярные плоскости при пересечении образуют четыре прямых двугранных угла (рис. 37.10).
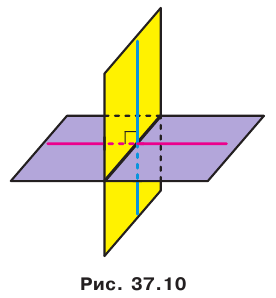
Теорема 37.2 (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
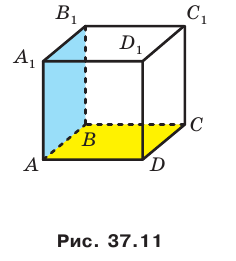
Например, плоскость грани 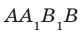 прямоугольного параллелепипеда
прямоугольного параллелепипеда 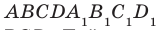 , (рис. 37.11) перпендикулярна плоскости грани ABCD. Действительно, плоскость
, (рис. 37.11) перпендикулярна плоскости грани ABCD. Действительно, плоскость 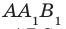 проходит через прямую
проходит через прямую 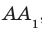 , перпендикулярную плоскости АВС.
, перпендикулярную плоскости АВС.
 ГЛАВНОЕ В ПАРАГРАФЕ 5
ГЛАВНОЕ В ПАРАГРАФЕ 5
Угол между прямыми в пространстве Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает 90°. Считают, что угол между двумя параллельными прямыми равен 0°. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.
Перпендикулярность прямой и плоскости
- Прямую называют перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
- Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.
- Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
- Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
- Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.
Ортогональная проекция фигуры
Пусть фигура 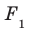 — параллельная проекция фигуры F на плоскость
— параллельная проекция фигуры F на плоскость 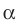 в направлении прямой
в направлении прямой 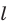 . Если
. Если 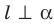 , то фигуру
, то фигуру 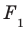 называют ортогональной проекцией фигуры F на плоскость
называют ортогональной проекцией фигуры F на плоскость 
Расстояние от точки до плоскости
Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.
Расстояние от прямой до параллельной ей плоскости
Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости.
Расстояние между двумя параллельными плоскостями
Расстоянием между двумя параллельными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.
Теорема о трех перпендикулярах
Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.
Угол между прямой и плоскостью
- Если прямая параллельна плоскости или принадлежит ей, то считают, что угол между такой прямой и плоскостью равен 0°.
- Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен 90°.
- Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость.
Величина двугранного угла
Величиной двугранного угла называют величину его линейного угла.
Угол между двумя пересекающимися плоскостями
Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°.
Площадь ортогональной проекции многоугольника
Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где 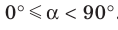
Перпендикулярные плоскости
Две плоскости называют перпендикулярными, если угол между ними равен 90°.
Признак перпендикулярности плоскостей
Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
- Векторы и координаты в пространстве
- Множества
- Рациональные уравнения
- Рациональные неравенства и их системы
- Предел числовой последовательности
- Предел и непрерывность числовой функции одной переменной
- Функции, их свойства и графики
- Параллельность в пространстве
План урока:
Перпендикулярность прямых
Перпендикулярность прямой и плоскости
Признак перпендикулярности прямой и плоскости
Задачи на перпендикулярность
Перпендикулярность прямых
Напомним, что планиметрии две прямые перпендикулярны, если угол между ними – прямой (то есть его величина составляет 90°).

Однако в стереометрии угол измеряется и между скрещивающимися двумя прямыми в пространстве, у которых общих точек нет. Если он составляет 90°, то прямые также именуются перпендикулярными.

Как же проверить, перпендикулярны ли скрещивающиеся прямые или нет? Для этого может быть использована специальная теорема, которую можно считать признаком перпендикулярности прямых.

Действительно, пусть есть прямые m, n и p, причем р||n и m⊥n. Требуется показать, что также m⊥p. Для этого выберем в пространстве какую-нибудь точку К и проведем через нее две такие прямые m’ и n’, что m’||m и n’||n:

По определению угла между прямыми из того факта, что m⊥n, вытекает, что и m’⊥n’. Так как p||n и n||n’, то в силу транзитивности параллельности, можно сделать вывод, что и р||n’. Но тогда угол между m’ и n’ одновременно является углом между m и p. А разm’⊥n’, то и m⊥p, ч. т. д.
Проиллюстрируем это правило на примере простого кубика:

Ребра ВС и AD параллельны как стороны квадрата АВСD. В свою очередь ВС⊥СG. Тогда по доказанной теореме можно утверждать, что и AD⊥CG.
Перпендикулярность прямой и плоскости
Из реальной жизни мы знаем, что палку в землю можно вставить так, что она будет стоять строго вертикально. В таких случаях говорят, что палка располагается перпендикулярно земле. Также гвоздь, «ровно» забитый в стену, оказывается перпендикулярным стене. Колонны, которые архитекторы используют при строительстве, также перпендикулярны плоскости пола в этих зданиях.

По аналогии и в геометрии прямая может быть перпендикулярна плоскости. На рисунке такая ситуация будет выглядеть так:

Сформулируем строгое определение:

Так, на следующем рисунке перпендикулярны прямая m и плоскость α. Это значит, что m перпендикулярна каждой прямым, находящимся в α:

Ясно, что прямая m, перпендикулярная плоскости α, должна пересекать ее. Действительно, если бы это было не так, то m либо полностью лежала бы в α, либо была бы ей параллельна. В обоих случаях в α можно было бы построить прямую n, параллельную m. В этом случае m и n уже не были бы перпендикулярны, а значит, что m уже не будет перпендикулярна к α.
Сформулируем две теоремы, связанные с перпендикулярностью прямой и плоскости.

Действительно, пусть есть прямые m и n, и m||n. Также есть плоскость α, и α⊥m. Проведем в α какую-нибудь прямую р:

По определению перпендикулярности (опр. 2) ясно, что m⊥p. Тогда по теор. 1 и n⊥p, ведь m||n. Прямая р была выбрана произвольно, поэтому получается, что n перпендикулярно любой произвольной прямой в α. Это как раз и значит, что n⊥α.
Теперь перейдем ко второй теореме, которая по сути обратна первой:

Для доказательства выберем на n точку К, не находящуюся в плоскости α. Через нее можно построить прямую р, параллельную m. Нам надо показать, что р и n – это одна и та же прямая. Пусть это не так, тогда р будет перпендикулярна α по теор. 2. Если n и р – различные прямые, то они должны пересекать α в разных точках, которые мы обозначим буквами Н и Т соответственно:

Прямая ТН будет перпендикулярна и n, и р. Тогда в ∆ТНК есть два прямых угла, ∠Н и∠Т, что невозможно. Значит, на самом деле прямые n и p совпадают. Так как p||m, то и n||m, ч. т. д.
Признак перпендикулярности прямой и плоскости
Заметим,что проверять перпендикулярность прямой и плоскости с помощью определения неудобно, ведь в любой плоскости находится бесконечно большое количество прямых. Поэтому на практике используется более простой признак перпендикулярности прямой и плоскости:

Доказательство. Пусть есть прямые m, n и р, причем m⊥n и m⊥p. При этом n и р пересекаются в какой-нибудь точке О, и через них проходит плоскость α.Надо продемонстрировать, что m также будет перпендикулярна и любой произвольной прямой k, принадлежащей α:

Если k||nили k||р, то k⊥m по теор. 1. Тогда надо рассмотреть случай, когда k пересекается с n и р. Проведем через О прямую k’, параллельную k.
Далее на прямой m отложим точки А и В так, чтобы ОА = АВ. Также проведем прямую s, пересекающую р, n, k’ в точках Р, L и Q соответственно:

В результате такого построения прямые n и р оказались серединными перпендикулярами для отрезка АВ. Тогда по свойству серединного перпендикуляра мы можем прийти к выводу, что

Теперь мы можем сравнить ∆АРQ и ∆BPQ, которые также оказываются равными:

Отсюда вытекает, что отрезки АQ и BQ одинаковы, поэтому ∆АВQ – равнобедренный. Теперь заметим, что в ∆АВQ отрезок OQ представляет собой медиану, ведь О – середина АВ. Но медиана в равнобедренном треугольнике – это ещё и высота, поэтому АВ⊥OQ. Это как раз и значит, что k’⊥m. Наконец, отсюда по теор. 1 выходит, что и k⊥m, ч. т. д.
Надо также рассмотреть и второй случай, когда изначально m НЕ проходит через О. В таком случае мы можем провести через О прямую m’, чтобы m’||m:

В этом случае по аналогии с предыдущим доказательством получаем, что m’⊥k. Тогда по теор. 1 и m⊥k, ч. т. д.
Покажем, как можно применить доказанный признак. Снова рассмотрим куб:

Докажем, что, например, ребро DH перпендикулярно грани АВСD. Действительно,DH⊥AD и DH⊥CD. Значит, в плоскости АВСD есть две пересекающиеся прямые (это AD и CD), каждая из которых перпендикулярна DH. По доказанному признаку (теор. 4) этого достаточно для того, чтобы DH⊥ABCD. Аналогично можно показать, что ребра BF, AE, СG также перпендикулярны АВСD.
Докажем ещё несколько важных и вместе с тем очевидных теорем.

Действительно, пусть есть прямая m и точка K. Здесь мы рассмотрим случай, когда K не находится на m. Тогда через m и K можно построить единственную плоскость α:

Дальше выполним следующие построения:
1) Проведем в плоскости α через К прямую n, такую, что n⊥m. Она пересечет m в какой-то точке Т.
2) Построим через m плоскость β, не совпадающую с α. То есть m окажется границей между α и β.
3) Через точку Т уже в плоскости β построим прямую р так, чтобы р⊥m.
4) Построим плоскость γ, проходящую пересекающиеся прямые р и n (эта плоскость будет единственной).
В итоге мы получили плоскость γ, в которой располагаются две прямые, р и n, каждая из которых перпендикулярна m. Тогда и вся плоскость γ будет перпендикулярна прямой m по теор. 4. То есть γ удовлетворяет условию теоремы.
В случае, когда точка К находится непосредственно на прямой m, плоскости α и β будут просто двумя различными плоскостями, проходящими через m. В каждой из них через К можно будет построить перпендикуляры к m, которые и будут играть роль прямых pи n.
Осталось убедиться, что γ – единственная плоскость, удовлетворяющая условию теоремы. В самом деле, пусть через некоторую точку К можно построить хотя бы две несовпадающие плоскости, перпендикулярные прямой m:

Обозначим буквами Т и Р точки, где m пересекает эти две плоскости. Тогда по опр. 2 получится, что РК⊥m и KT⊥m. Теперь рассмотрим ∆KPT. У него сразу два прямых угла – это ∠Р и ∠Т. Треугольник с двумя прямыми углами существовать не может, значит, на самом деле через K нельзя провести две плоскости, перпендикулярных m.
Прямым следствием из только что доказанной теоремы является следующее утверждение:

Действительно, пусть существуют такие плоскости α и β и прямая m, что m⊥α, m⊥β. Предположим, что α и β пересекаются по какой-нибудь прямой n. Тогда получается, что через каждую точку, принадлежащую n, проведены сразу 2 плоскости, перпендикулярные m, а это невозможно по теор. 5. Значит, α и β не пересекаются, то есть они параллельны.
Следующее утверждение часто называют теоремой о прямой, перпендикулярной плоскости:

Возьмем произвольные плоскость α и точку К. Далее в α выберем какую-нибудь прямую m. Мы можем провести через К такую плоскость β, что β⊥m (по теор. 5):

Прямую, по которой пересекутся α и β, обозначим буквой n. Теперь мы можем в плоскости β опустить перпендикуляр из К на n. Этот перпендикуляр обозначим буквой р.
Получается, что р⊥n,но также и р⊥m (ведь m⊥β, а р находится в β). Тогда по признаку перпендикулярности (теор. 4) получаем, что р⊥α, то есть р – это как раз искомая прямая.
Осталось показать, что р – единственная такая прямая. Действительно, пусть через К построили две прямых, каждая из которых перпендикулярна α. Тогда, по теореме 3, они окажутся параллельными. Но при этом у них будет общая точка K, а параллельные прямые общих точек не имеют. Поэтому р – единственная прямая, удовлетворяющая условию теоремы.
Задачи на перпендикулярность
Прежде, чем смотреть решение задач, постарайтесь решить их самостоятельно.
Задание. Ребра ВС и AD в тетраэдре АВСD перпендикулярны. M и N – это середины ребер АВ и АС. Докажите, что MN⊥AD.

Решение.MN по определению оказывается средней линией в ∆АВС. Это значит, что MN||ВС. Тогда, по теор. 1, можно утверждать, что и АD⊥MN, ч. т. д.
Задание. Диагонали квадрата, чья сторона имеет длина а, пересекаются в точке О. Через О проведена прямая ОК, перпендикулярная плоскости квадрата, причем отрезок ОК имеет длину b. Найдите расстояние от какой-нибудь вершины квадрата до точки К.
Решение.

Обозначим вершины квадрата буквами А, В, С и D. Найдем длину его диагонали, например, АС. Для этого используем теорему Пифагору и прямоугольный ∆АСD:

Точка пересечения диагоналей квадрата одновременно является серединой каждой диагонали, то есть отрезок ОС вдвое короче АС:

Теперь заметим, что если ОК перпендикулярна плоскости квадрата, то также ОК⊥ОС (опр. 2). Значит, ∆КОС – прямоугольный, и для него справедлива теорема Пифагора:

Аналогично можно показать, что расстояние и до других вершин вычисляется по такой же формуле.

Задание. В кубе найдите угол между прямыми АС и DH:

Решение. Заметим, что DH⊥АD и DH⊥CD, при этом AD и CD находятся в плоскости грани АВСD. Тогда по теор. 4 получаем, что DH перпендикулярна этой грани. В свою очередь из опр. 2 вытекает, что DH перпендикулярна любой прямой, принадлежащей грани, в том числе и АС. То есть угол между этими прямыми составляет 90°.
Ответ: 90°.
Задание. Ребро куба имеет длину, равную единице. Какова длина его диагонали FD?

Решение. Предварительно найдем длину диагонали FC (эта диагональ называется не диагональю куба, а диагональю грани ВСGF). Ее можно найти из прямоугольного ∆FCG:

Далее заметим, что СD⊥BC и CD⊥CG, то есть по теор. 4 ребро CD перпендикулярно всей грани BCGF. Это значит, что и ∠FCD– прямой, а ∆FCD – прямоугольный. Применим и к нему теорему Пифагора:

Задание. Какой угол в кубе с единичным ребром образуют диагональ куба и его ребро?

Решение. Используем рисунок предыдущей задачи и полученные в ней результаты. Нам надо найти ∠FDC. Мы уже рассчитали длины всех сторон в ∆FDC:

Тогда ∠FDC легко найти с помощью теоремы косинусов:

Примечание. Несложно показать, что ровно такой же угол диагональ куба образует и со всеми остальными ребрами куба. Также можно показать, что это угол никак не зависит от длины ребра.
Задание. Отрезок PQ и плоскость α параллельны. Через точку P и Q построены прямые, перпендикулярные α. Они пересекают α в точках Р1 и Q1. Докажите, что отрезки PQ и P1Q1 одинаковы.

Решение. По условию РР1⊥α и QQ1⊥α. Тогда по теор. 3 можно утверждать, что РР1||QQ1. Это значит, что отрезки РР1 и QQ1, в том числе и точки Р, Р1, Q, Q1 располагаются в одной плоскости. Тогда РQQ1P1– это плоский четырехугольник.
Заметим, что PQ||P1Q1, ведь если бы они пересекались, то точка их пересечения была бы общей для PQ и α, и тогда PQ и α не были бы параллельны. С учетом того факта, что и РР1||QQ1, получаем, что в четырехугольнике РQQ1P1 противоположные стороны параллельны. То есть он представляет собой параллелограмм.
Так как РР1⊥α и QQ1⊥α, то

Получается, что все углы в РQQ1P1 – прямые, то есть это прямоугольник. Из этого вытекает, что PQиP1Q1 – одинаковые отрезки, ч. т. д. Попутно мы также убедились, что также РР1 и QQ1 одинаковы.
Задание. Есть плоскости α и β, параллельные друг другу. Прямая m перпендикулярна α. Верно ли, что также m перпендикулярна и β?
Решение.

Пусть α и m пересекаются в точке Р. Заметим, что m обязательно должна пересекаться и с β в какой-нибудь точке М. Действительно, m не может полностью принадлежать β, ведь тогда бы точка Р также находилась в β, то есть существовала бы общая точка Р у параллельных плоскостей, что невозможно. Если бы m и β были параллельны, то тогда в β можно провести такую прямую m’, что m’||m. Раз m пересекает α, то и m’ должна пересекаться с α (по теор. 3 из этого урока). Но m’ с α не может пересечься, так как m’ находится в β и потому общих точек с α не имеет. Это противоречие показывает, что m пересекает β в точке, обозначенной нами как М.
Предположим, что утверждение в условии ошибочно и на самом деле β и m не перпендикулярны. Тогда через М можно провести третью плоскость γ, перпендикулярную m (по теор. 5). Проанализируем расположение плоскостей α, β и γ. Раз α⊥m и γ⊥m, то по теор. 6 можно утверждать, что α||γ. По условию α||β. Тогда в силу транзитивности параллельности и β||γ. Но это невозможно, ведь уβ и γ есть общая точка М. Значит, на самом деле β и m всё же перпендикулярны, ч. т. д.
Задание. Прямые AD, АС, АВ попарно параллельны. Известно, что
BC = 26
AB = 24
BD = 25
Найдите длину отрезка CD.

Решение. В задаче есть сразу три прямоугольных треугольника: ∆АВС, ∆АВD и ∆АСD. Для каждого из них можно записать теорему Пифагора, что позволит найти длины отрезков АС, АD и СD. Начнем с ∆АВС:

Теперь можно найти и длину CD c помощью ∆АСD:

Задание. На прямой m отмечена точка М. Через точку M проведены плоскость α и прямая n, причем m⊥α и m⊥n. Докажите, что n обязательно принадлежит α.
Решение. Так как m и n пересекаются, то через них можно построить плоскость β:

Так как у α и β есть общая точка М, то они должны пересекаться по некоторой прямой р. При этом р находится в α, а m⊥α, то m⊥n (по опр. 2). Тогда получается, что в плоскости β через точку M проходят две прямые, n и p, которые перпендикулярны m. Но в одной плоскости через точку прямой можно построить строго один перпендикуляр к ней. То есть n и p совпадают. Это значит, что n, как и p, полностью находится в α, ч. т. д.
Задание. Отрезок АВ не пересекает плоскость α, а отрезок СD принадлежит α. Известно, что отрезки АС и BD перпендикулярны α. Также известны длины:
AC = 3
BD = 2
CD = 2,4
Какова длина АВ?
Решение.

Если АС⊥α и BD⊥α, то АС||BD (по теор. 3). Это значит, что через АВ и СD можно провести плоскость, то есть АВСD – плоский четырехугольник. При этом∠С и ∠D прямые (по опр. 2). Построим отдельно этот четырехугольник и проведем некоторые построения:

Опустим из В перпендикуляр ВК на АС. Так как в четырехугольнике СDBK три угла прямые (∠С, ∠D и ∠K), то и четвертый угол также прямой, то есть СDBK – прямоугольник. Это значит, что

В ходе сегодняшнего урока мы узнали о перпендикулярных прямых в пространстве, а также о том, что перпендикулярны могут быть также прямая и плоскость. На основе простейших теорем о перпендикулярности возможно определять длину диагонали в кубе и углы, которые образует его диагональ с ребрами куба.
11
Авг 2013
Категория: Справочные материалы
Перпендикулярность прямых и плоскостей
2013-08-11
2013-08-12
Перпендикулярные прямые
Две прямые в пространстве называются перпендикулярными, если угол между ними составляет .
При этом прямые могут пересекаться,
а могут быть скрещивающимися: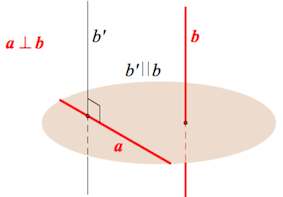
Перпендикулярность прямой и плоскости
Прямая называется перпендикулярной к плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
Признак перпендикулярности прямой и плоскости
Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Свойства перпендикулярных прямой и плоскости
1). Две прямые, перпендикулярные одной и той же плоскости, параллельны.


2). Прямая, перпендикулярная одной из двух параллельных плоскостей, перпендикулярна и другой плоскости.
3). Две плоскости, перпендикулярные одной и той же прямой, параллельны между собой
Перпендикулярность плоскостей
Пересекающиеся плоскости называются перпендикулярными, если третья плоскость, перпендикулярная прямой пересечения этих плоскостей, пересекает их по перпендикулярным прямым.

Признак перпендикулярности плоскостей
Если плоскость проходит через прямую перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Свойство перпендикулярных плоскостей
Если прямая лежит в одной из двух взаимно перпендикулярных плоскостей и перпендикулярна линии их пересечения, то эта прямая перпендикулярна второй плоскости.

Автор: egeMax |
комментария 3
Печать страницы
Перпендикулярность прямой и плоскости
В пространстве перпендикулярными могут быть:
- две прямые
- прямая и плоскость
- две плоскости
Давай для полного понимания рассмотрим не только перпендикулярность прямой и плоскости, а все три случая перпендикулярности в пространстве.
Все относящиеся к ним определения и формулировки теорем.
А потом обсудим очень важную теорему о трёх перпендикулярах.
И ты будешь знать о перпендикулярности в пространстве все!
Поехали!
Перпендикулярность в пространстве — коротко о главном
Перпендикулярность двух прямых
Две прямые в пространстве перпендикулярны, если угол между ними ( 90{}^circ ).
Перпендикулярность прямой и плоскости
Прямая перпендикулярна плоскости, если она перпендикулярна всем прямым в этой плоскости.
Перпендикулярность плоскостей
Плоскости перпендикулярны, если двугранный угол между ними равен ( 90{}^circ ).
Критерий перпендикулярности плоскостей
Две плоскости перпендикулярны тогда и только тогда, когда одна из них проходит через перпендикуляр к другой плоскости.
Теорема о трех перпендикулярах
Прямая ( a), не лежащая в плоскости ( alpha ), перпендикулярна прямой ( b), лежащей в плоскости ( alpha ), тогда и только тогда, когда проекция ( aprime ) прямой a перпендикулярна прямой ( b).
Перпендикулярность двух прямых
Определение:
Две прямые в пространстве перпендикулярны, если угол между ними ( displaystyle 90{}^circ ).
Ты можешь сказать: тоже мне, открыли Америку! Но вспомни, что в пространстве всё не совсем так, как на плоскости.
На плоскости перпендикулярными могут оказаться только такие прямые (пересекающиеся):
А вот перпендикулярность в пространстве двух прямых может быть даже в случае если они не пересекаются. Смотри:
Прямая ( displaystyle a) перпендикулярна прямой ( displaystyle b), хотя и не пересекается с нею. Как так?
Вспоминаем определение угла между прямыми: чтобы найти угол между скрещивающимися прямыми ( displaystyle a) и ( displaystyle b), нужно через произвольную точку ( displaystyle O) на прямой a провести прямую ( displaystyle {b}’parallel b).
И тогда угол между ( displaystyle a) и ( displaystyle b) (по определению!) будет равен углу между ( displaystyle a) и ( displaystyle {{b}’}).
Вспомнили? Ну вот, а в нашем случае – если окажутся перпендикулярны прямые ( displaystyle a) и ( displaystyle {{b}’}), то нужно считать перпендикулярными прямые ( displaystyle a) и ( displaystyle b).
Для полной ясности давай рассмотрим пример
Пусть есть куб ( displaystyle ABCD{{A}_{1}}{{B}_{1}}{{C}_{1}}{{D}_{1}}). И тебя просят найти угол между прямыми ( displaystyle AC) и ( displaystyle {{B}_{1}}{{D}_{1}}).
Эти прямые не пересекаются – они скрещиваются. Чтобы найти угол между ( displaystyle AC) и ( displaystyle {{B}_{1}}{{D}_{1}}), проведём ( displaystyle BD).
Из-за того, что ( displaystyle B{{B}_{1}}{{D}_{1}}D) — параллелограмм (и даже прямоугольник!), получается, что ( displaystyle {{B}_{1}}{{D}_{1}}parallel BD).
А из-за того, что ( displaystyle ABCD) – квадрат, выходит, что ( displaystyle ACbot BD). Ну, и значит ( displaystyle ACbot {{B}_{1}}{{D}_{1}}).
Перпендикулярность прямой и плоскости
Определение:
Прямая перпендикулярна плоскости, если она перпендикулярна всем прямым в этой плоскости.
Вот картинка:
Прямая ( displaystyle h) перпендикулярна плоскости ( displaystyle alpha ), если она перпендикулярна всем-всем прямым в этой плоскости: и ( displaystyle a), и ( displaystyle b), и ( displaystyle c), и даже ( displaystyle d)!
И ещё миллиарду других прямых!
Да, но как же тогда вообще можно проверить перпендикулярность в прямой и плоскости? Так и жизни не хватит!
Но на наше счастье математики избавили нас от кошмара бесконечности, придумав признак перпендикулярности прямой и плоскости.
Формулируем:
Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
Оцени, как здорово:
Если найдутся всего лишь две пересекающиеся прямые (( displaystyle a) и ( displaystyle b)) в плоскости ( displaystylealpha), которым перпендикулярна прямая ( displaystyle h), то эта прямая сразу окажется перпендикулярна плоскости ( displaystyle alpha ),
То есть всем прямым в этой плоскости (в том числе и какой-то стоящей сбоку прямой ( displaystyle c)).
Это очень важная теорема, поэтому нарисуем её смысл ещё и в виде схемы.
Что это за арка? Это значок «пересечение»! Хороший способ быстрее писать конспекты 🙂
Прямая перпендикулярна двум пересекающимся прямым!
И опять рассмотрим пример
Пусть нам дан правильный тетраэдр ( displaystyle ABCD).
Задача: доказать, что ( displaystyle BDbot AC).
Ты скажешь: это же две прямые! При чём же здесь перпендикулярность прямой и плоскости?!
А вот смотри:
Давай отметим середину ( displaystyle M) ребра ( displaystyle AC) и проведём ( displaystyle BM) и ( displaystyle DM).
Это медианы в ( displaystyle Delta ABC) и ( displaystyle Delta ADC).
Треугольники – правильные ( displaystyle Rightarrow BMbot AC) и ( displaystyle DMbot AC).
Вот оно, чудо: получается, что ( displaystyle ACbot BMD), так как ( displaystyle ACbot BM) и ( displaystyle ACbot DM).
И далее, ( displaystyle ACbot BMDRightarrow ACbot ) всем прямым в плоскости ( displaystyle BMD), а значит, и ( displaystyle ACbot BD).
Доказали.
И самым главным моментом оказалось именно применение признака перпендикулярности прямой и плоскости.
Перпендикулярность плоскостей
Определение:
Плоскости перпендикулярны, если двугранный угол между ними равен ( displaystyle 90{}^circ ).
То есть (подробнее смотри в теме «двугранный угол») две плоскости (( displaystyle alpha) и ( displaystyle beta)) перпендикулярны, если окажется, что угол между двумя перпендикулярами (( displaystyle a) и ( displaystyle b)) к линии пересечения этих плоскостей равен ( displaystyle 90{}^circ ).
И есть теорема, которая связывает понятие перпендикулярных плоскостей с понятием перпендикулярность в пространстве прямой и плоскости.
Теорема эта называется: Критерий перпендикулярности плоскостей.
Критерий перпендикулярности плоскостей
Давай сформулируем:
Две плоскости перпендикулярны тогда и только тогда, когда одна из них проходит через перпендикуляр к другой плоскости.
Как всегда, расшифровка слов «тогда и только тогда» выглядит так:
- Если ( displaystyle alpha bot beta ), то ( displaystyle alpha ) проходит через перпендикуляр к ( displaystyle beta ).
- Если ( displaystyle alpha ) проходит через перпендикуляр к ( displaystyle beta ), то ( displaystyle alpha bot beta ).
(естественно, здесь ( displaystyle alpha ) и ( displaystyle beta ) — плоскости).
Теорема о трёх перпендикулярах
Эта теорема – одна из самых важных в стереометрии, но, к сожалению, и одна из самых непростых в применении.
Так что нужно быть очень внимательным!
Итак, формулировка:
Прямая ( displaystyle a), не лежащая в плоскости ( displaystyle alpha ), перпендикулярна прямой ( displaystyle b), лежащей в плоскости ( displaystyle alpha ), тогда и только тогда, когда проекция ( displaystyle {{a}’}) прямой a перпендикулярна прямой ( displaystyle b).
И снова расшифровка слов «тогда и только тогда». Теорема утверждает сразу две вещи (смотри на картинку):
- ( displaystyle abot bRightarrow {a}’bot b)
- ( displaystyle {a}’bot bRightarrow abot b).
Давай попробуем применить эту теорему для решения задачи.
Задача: дана правильная шестиугольная пирамида ( displaystyle SABCDEF). Найти угол между прямыми ( displaystyle AS) и ( displaystyle CE).
Решение:
Из-за того, что в правильной пирамиде вершина при проекции попадает в центр основания, оказывается, что прямая ( displaystyle AD) — проекция прямой ( displaystyle AS).
Но мы знаем, что в правильном шестиугольнике ( displaystyle ADbot CE). Применяем теорему о трёх перпендикулярах:
( displaystyle ADbot CERightarrow ASbot CE)
И пишем ответ: ( displaystyle 90{}^circ ).
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
![]()
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
