Как найти призводную функции - Сайт, где вы сможете решить свои вопросы

Решать физические задачи или примеры по математике совершенно невозможно без знаний о производной и методах ее вычисления. Производная – одно из важнейших понятий математического анализа. Этой фундаментальной теме мы и решили посвятить сегодняшнюю статью. Что такое производная, каков ее физический и геометрический смысл, как посчитать производную функции? Все эти вопросы можно объединить в один: как понять производную?

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Геометрический и физический смысл производной

Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

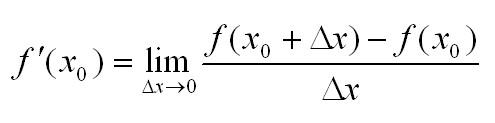
Иначе это можно записать так:

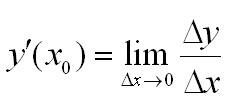
Какой смысл в нахождении такого предела? А вот какой:

Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:

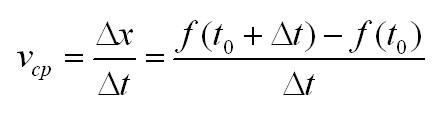
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:

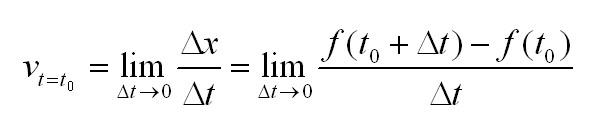
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.

Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:

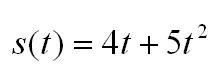
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:

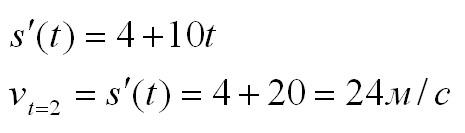
Правила нахождения производных

Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.

Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.

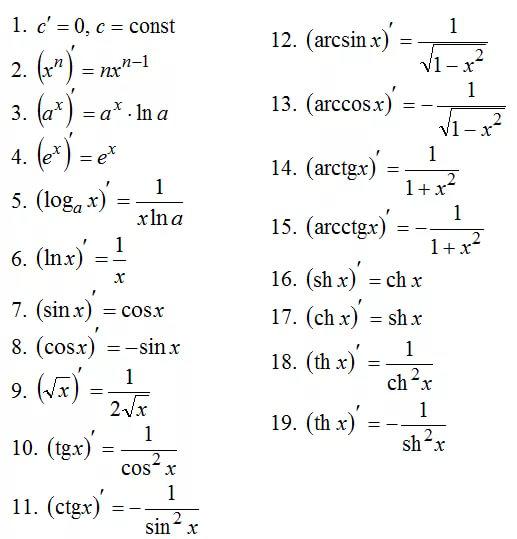
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правило первое: выносим константу

Константу можно вынести за знак производной. Более того – это нужно делать. При решении примеров по математике возьмите за правило – если можете упростить выражение, обязательно упрощайте.

Пример. Вычислим производную:

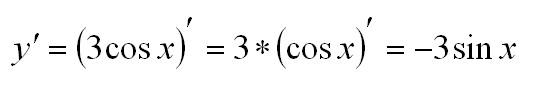
Правило второе: производная суммы функций

Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.

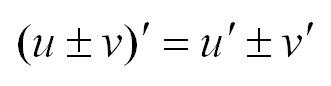
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.

Найти производную функции:

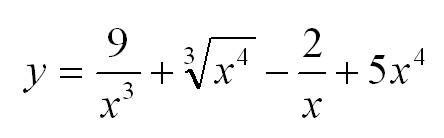
Решение:

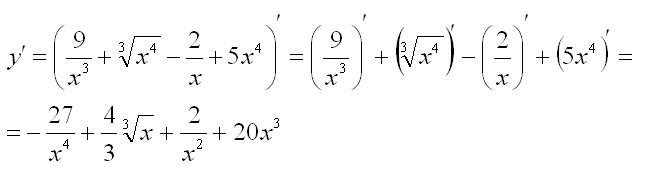
Правило третье: производная произведения функций

Производная произведения двух дифференцируемых функций вычисляется по формуле:

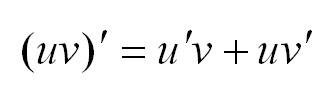
Пример: найти производную функции:

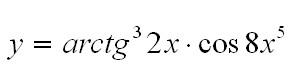
Решение: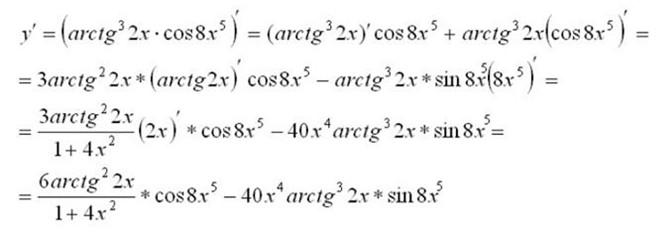

Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В вышеуказанном примере мы встречаем выражение:

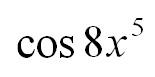
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.

Правило четвертое: производная частного двух функций

Формула для определения производной от частного двух функций:

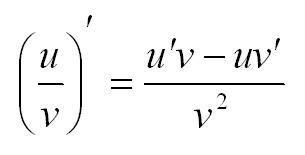
Пример:

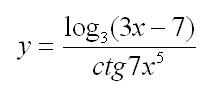
Решение:

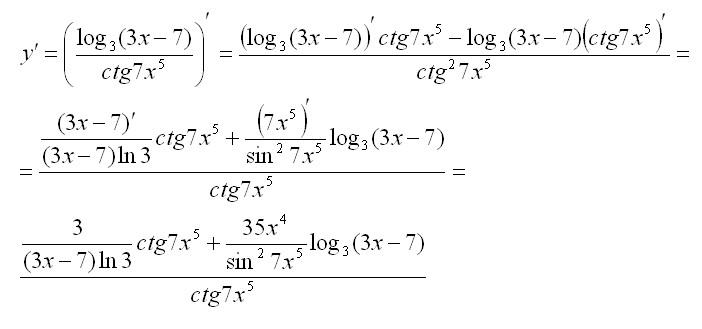
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.

С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.

Источник

Если вы ничего не смыслите в том, что такое производная и какими методами можно её вычислить, то совершенно невозможно решать примеры по математике или задачи по физике. Ведь такое понятие, как производная, является одним из самых важных в математическом анализе.

В этой статье мы расскажем вам, что является производной, какой она имеет геометрический и физический смысл. В общем, мы с вами попытаемся понять производную.

как найти производную онлайн?

Геометрический и физический смысл производной

Задаём функцию f(x) в интервале (a, b). А точки x и x0 этому интервалу принадлежат. Если изменится x, то и функция тоже изменится. Изменением аргумента является разность его значений x-x0. Записывается эта разность, как дельта икс и имеет название: приращение аргумента. Разность значений функций в двух точках называется приращением или изменением функции. Так каково определение производной?

Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.

Решение производной простыми словами: определение, как найти, примеры решений

Можно записать ещё следующим образом:

Встаёт вопрос, для чего нужно находить такой предел? Вот и ответ:

Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.

Ещё в школе нас учили тому, что скорость – это частное пути x=f(t) и времени (t). Вычисляем среднюю скорость за какой-то временной промежуток:

Для того чтобы нам узнать какова скорость движения в момент t0, необходимо вычислить предел:

Сейчас мы разберем один пример, который продемонстрирует вам применение производной на практике. Допустим, тело движется по закону:

Нам необходимо рассчитать скорость в момент времени t=2c. Вычисляем производную:

Правила нахождения производных

Дифференцирование – это процесс нахождения производной. А дифференцируемая функция – это функция, которая имеет производную в данной точке.

Каким образом нам найти саму производную? Нам необходимо составить отношения приращения функции и аргумента, а после вычислить предел при условии стремящегося к нулю приращения аргумента. Но практика показывает, что такой путь вычисления является очень долгим. Всё, что нам необходимо, уже посчитано. И специально для вас, мы подготовили таблицу с производными элементарных функций.

После таблицы мы рассмотрим правила по вычисления производных. Коснёмся мы и вычисления производных сложных функций. Подробно разберём всё на примерах.

Правило первое: выносим константу

Вынести константы можно за знак производной. Причём делать это необходимо! Когда вы решаете примеры по математике, то всегда помните правило – если есть возможность упростить выражение, то делайте это.

Для примера вычислил с вами производную:

Правило второе: производная суммы функций

Производная суммы двух функций равняется сумме производных этих функций. Это касается и производной разности функций.

Сейчас мы с вами на практике рассмотрим пример доказательства этой теоремы.

Найти производную функции:

Решение:

Правило третье: производная произведения функций

По следующей формуле мы сможем вычислить производную произведения двух дифференцируемых функций:

К примеру: необходимо найти производную функции:

Решение:

Необходимо сказать о том, каким образом вычисляются производные сложных функций.

Производная сложной функции равняется произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.

В примере, который указан выше, мы можем встретить выражение:

В этом примере промежуточным аргументом является 8x в пятой степени. Чтобы нам вычислить производную данного выражения, то для начала необходимо высчитать производную внешней функции по промежуточному аргументу, а после необходимо умножить на производную непосредственно сам промежуточный аргумент по независимой переменной.

Правило четвертое: производная частного двух функций

Ниже приведена формула для того, чтобы определить производную от частного двух функций:

Пример:

Решение:

В данной статье мы попытались рассказать о производных для тех, кто совершенно не знаком с этой темой. Когда вы будете решать примеры, то будьте очень внимательны, ведь в них часто можно встретить ловушки. Эта тема не так уж и проста, какой кажется на первый взгляд.

Вы можете обратиться в наш студенческий сервис по любым вопросам. Мы с удовольствием поможем решить для вас задачи любой сложности. А занимались вы раньше вычислением производных или нет, не имеет никакого значения. Мы помогаем всем!

Источник

урок 3. Математика ЕГЭ

Как найти производную от функции

Как считать производные?

Никто не использует определение производной, чтобы ее вычислить. Как же тогда ее посчитать?

Оказывается, существуют специальные формулы, с помощью которых производная от функции вычисляется достаточно просто.

Формулы производной

Выпишем теперь все формулы производной функции и порешаем примеры.

Производная от константы
Производная от любого числа всегда равна (0):
$$(const)^{/}=0;$$

Пример 1
$$(5)^{/}=0;$$

Производная от (x)
Производная просто от (x) равна (1):
$$x^{/}=1;$$

Производная от степени
$$(x^n)^{/}=n*x^{n-1};$$
Пример 2
$$(x^4)^{/}=4*x^{4-1}=4*x^{3};$$
$$(x^{10})^{/}=10*x^{10-1}=10*x^{9};$$
$$(x^{-3})^{/}=-3*x^{-3-1}=-3*x^{-4};$$
$$(x^{frac{1}{3}})^{/}=frac{1}{3}*x^{1-frac{1}{3}}=frac{1}{3}*x^{frac{2}{3}};$$

Производная от квадратного корня
$$(sqrt{x})^{/}=frac{1}{2sqrt{x}};$$
Тут полезно заметить, что формулу производной от квадратного корня можно не учить. Она сводится к формуле производной от степени:
$$(sqrt{x})^{/}=(x^{frac{1}{2}})^{/}=frac{1}{2}*x^{frac{1}{2}-1}=frac{1}{2}*x^{-frac{1}{2}}=frac{1}{2sqrt{x}};$$

Производная от синуса
$$sin(x)^{/}=cos(x);$$

Производная от косинуса
$$cos(x)^{/}=-sin(x);$$

Производная от тангенса
$$tg(x)^{/}=frac{1}{cos^{2}(x)};$$

Производная от котангенса
$$tg(x)^{/}=frac{-1}{sin^{2}(x)};$$

Производная от экспоненты
$$(e^x)^{/}=e^x;$$

Производная от показательной функции
$$(a^x)^{/}=a^x*ln(a);$$
Пример 3
$$(2^x)^{/}=2^{x}*ln(2);$$

Производная от натурального логарифма
$$(ln(x))^{/}=frac{1}{x};$$

Производная от логарифма
$$(log_{a}(x))^{/}=frac{1}{x*ln(a)};$$

Свойства производной

Помимо формул по вычислению производной еще есть свойства производной, их тоже надо выучить.

Вынесение константы за знак производной
$$(alpha*f(x))^{/}=alpha*(f(x))^{/};$$

Пример 4
$$(3*x^5)^{/}=3*(x^5)^{/}=3*5x^4=15x^4;$$
$$(10sin(x))^{/}==10*(sin(x))^{/}=10*cos(x);$$

Производная от суммы и разности двух функций
$$(f(x) pm g(x))^{/}=(f(x))^{/} pm (g(x))^{/};$$

Пример 5
$$(2x^4+x^3)^{/}=?$$
Тут (f(x)=2x^4), а (g(x)=x^3). Тогда по формуле производной от суммы:
$$(2x^4+x^3)^{/}=(2x^4)^{/}+(x^3)^{/}=2*(x^4)^{/}+(x^3)^{/}=2*4x^3+3x^2=8x^3+3x^2;$$

Пример 6
$$(ln(x)+cos(x))^{/}=(ln(x))^{/}+(cos(x))^{/}=frac{1}{x}-sin(x);$$

Пример 7
$$(x^6-e^x)^{/}=(x^6)^{/}-(e^x)^{/}=6x^5-e^x;$$

Производная от произведения двух функций
$$(f(x)*g(x))^{/}=(f(x))^{/}*g(x)+f(x)*(g(x))^{/};$$

Пример 8
$$(x^2*sin(x))^{/}=?$$
$$(x^2*sin(x))^{/}=(x^2)^{/}*sin(x)+x^2*(sin(x))^{/}=2x*sin(x)+x^2*cos(x);$$

Пример 9
$$(ln(x)*e^x)^{/}=(ln(x))^{/}*e^x+ln(x)*(e^x)^{/}=frac{1}{x}*e^x+ln(x)*e^x;$$

Производная от частного двух функций
$$left(frac{f(x)}{g(x)}right)^{/}=frac{(f(x))^{/}*g(x)-f(x)*(g(x))^{/}}{(g(x))^2};$$

Пример 10
$$left(frac{x^3}{sin(x)}right)^{/}=frac{(x^3)^{/}*sin(x)-x^3*(sin(x))^{/}}{(sin(x))^2}=frac{3x^2*sin(x)-x^3*cos(x)}{(sin(x))^2};$$

Примеры нахождения производной

Рассмотрим несколько примеров нахождения производной, чтобы разобраться, как применяются свойства и формулы производной на практике.

Пример 11
$$(5x^3+2cos(x))^{/}=(5x^3)^{/}+(2cos(x))^{/}=$$
$$=5*(x^3)^{/}+2*(cos(x))^{/}=5*3*x^2+2*(-sin(x))=15x^2-2sin(x);$$

Пример 12
$$left(-frac{3x^2}{2x^4+5x}right)^{/}=-frac{(3x^2)^{/}*(2x^4+5x)-3x^2*(2x^4+5x)^{/}}{(2x^4+5x)^2}=$$
$$=-frac{6x*(2x^4+5x)-3x^2*(8x+5)}{(2x^4+5x)^2}=-frac{12x^5-24x^3+15x^2}{(2x^4+5x)^2};$$

Пример 13
$$(2xsqrt{x})^{/}=(2x)^{/}*sqrt{x}+2x*(sqrt{x})^{/}=$$
$$=2*sqrt{x}+2x*frac{1}{2sqrt{x}}=2*sqrt{x}+frac{2x}{2sqrt{x}}=2*sqrt{x}+sqrt{x}=3sqrt{x};$$

Производная сложной функции

Сложная функция – это функция не от аргумента (x), а от какой-то другой функции: (f(g(x))). Например, функция (sin(x^2)) будет сложной функцией: «внешняя» функция синуса берется от «внутренней» функции степени ((x^2)). Так как под синусом стоит аргумент не (x), а (x^2), то такая функция будет называться сложной.
Еще примеры сложных функций:

$$ln(3x^4);$$
Внешняя функция: натуральный логарифм; Внутренняя функция: ((3x^4)).
$$cos(ln(x));$$
Внешняя функция: косинус; Внутренняя функция: ((ln(x))).
$$e^{2x^2+3};$$
Внешняя функция: экспонента; Внутренняя функция: ((2x^2+3)).
$$(sin(x))^3;$$
Внешняя функция: возведение в третью степень; Внутренняя функция: (sin(x)).

Чтобы посчитать производную от такой функции, нужно сначала найти производную внешней функции, а затем умножить результат на производную внутренней функции. В общем виде формула выглядит так:
$$f(g(x))^{/}=f^{/}(g(x))*g^{/}(x);$$
Скорее всего, выглядит непонятно, поэтому давайте разберем на примерах.

Пример 14
$$((cos(x))^4)^{/}=?$$
Внешней функцией тут будет возведение в четвертую степень, поэтому сначала считаем производную от степени по формуле ((x^n)^{/}=n*x^{n-1}). А потом умножаем результат на производную внутренней функции, у нас это функция косинуса, по формуле (cos(x)^{/}=-sin(x)):
$$((cos(x))^4)^{/}=underset{text{внешняя производная}}{underbrace{4*(cos(x))^3}}*underset{text{внутренняя производная}}{underbrace{(cos(x))^{/}}}=$$
$$=4*(cos(x))^3*(-sin(x))=-4*(cos(x))^3*sin(x);$$

Пример 15
$$(e^{2x^3+5})^{/}=?$$
Внешняя функция – это экспонента ((e^x)^{/}=e^x), а внутренняя функция – квадратный многочлен ((2x^3+5)):
$$(e^{2x^3+5})^{/}=e^{2x^3+5}*(2x^3+5)^{/}=e^{2x^3+5}*((2x^3)^{/}+5^{/})=e^{2x^3+5}*6x^2.$$

Пример 16
$$(ln((2x^2+3)^6))^{/}=?$$
Внешняя функция – это натуральной логарифм, берем производную от него по формуле ((ln(x))^{/}=frac{1}{x}), и умножаем на производную внутренней функции, у нас это шестая степень: ((x^n)^{/}=n*x^{n-1}). Но и на этом еще не все: под шестой степенью стоит не просто (x), а квадратный многочлен, значит еще нужно умножить на производную от этого квадратного многочлена:
$$ln((2x^2+3)^6)=frac{1}{(2x^2+3)^6}*((2x^2+3)^6)^{/}*(2x^2+3)^{/}=$$
$$=frac{1}{(2x^2+3)^6}*6*(2x^2+3)^5*(4x+0)=frac{1}{(2x^2+3)^6}*6*(2x^2+3)^5*4x=$$
$$=frac{6*(2x^2+3)^5*4x}{(2x^2+3)^6}=frac{24x*(2x^2+3)^5}{(2x^2+3)^6}=frac{24x}{(2x^2+3)^6}.$$

Вывод формул производной функции

Выведем некоторые из этих формул, чтобы было понимание, откуда они берутся. Но перед этим познакомимся с новыми обозначениями. Запись (f(x)) означает, что функция берется от аргумента (x). Например:
$$f(x)=x^3+sin(x);$$
На месте аргумента (x) может стоять все что угодно, например выражение (2x+3). Обозначение такой функции будет (f(2x+3)), а сама функция примет вид:
$$f(2x+3)=(2x+3)^3+sin(2x+3);$$
То есть, везде вместо аргумента (x) мы пишем (2x+3).

И несколько важных замечаний про (Delta f(x)) и (Delta x). Напомню, что значок (Delta) означает изменение некоторой величины. (Delta x) – изменения координаты (x) при переходе от одной точки на графике функции к другой; (Delta f(x)) – разница координат (y) между двумя точками на графике. Подробнее про это можно почитать в главе, где мы вводим понятие производной. Распишем (Delta x) для двух близких точек на графике функции (O) и (B):
$$Delta x=x_B-x_O;$$
Отсюда можно выразить (x_B):
$$x_B=x_O+Delta x;$$
Абсцисса (координата точки по оси (x)) точки (B) получается путем сложения абсциссы точки (O) и (Delta x).

Кстати, функцию (f(x)=x^3+sin(x)) от аргумента (x_B=x_O+Delta x) можно расписать:

$$f(x_B)=f(x_O+Delta x)=(x_O+Delta x)^3+sin(x_O+Delta x);$$

Рис.1. График произвольной функции

И распишем (Delta f):
$$Delta f(x)=f(x_B)-f(x_O)=f(x_O+Delta x)-f(x_O);$$
Тогда определение производной можно записать в виде:
$$f^{/}(x)=frac{Delta f(x)}{Delta x}=frac{f(x_O+Delta x)-f(x_O)}{Delta x} quad при quad Delta x to 0;$$

За (x_O) обычно обозначают точку, в окрестности которой берут производную. То есть, получается (x_O) – это абсцисса начальной точки, а (x_O+Delta x) – абсцисса конечной точки.

Нам это пригодится при выводе формул производной.

Производная квадратичной функции

Выведем теперь формулу производной от (f(x)=x^2), воспользовавшись определением производной:
$$f^{/}(x)=frac{Delta f(x)}{Delta x}=frac{f(x+Delta x)-f(x)}{Delta x} quad при quad Delta x to 0;$$
Распишем числитель (f(x+Delta x)-f(x)) с учетом, что (f(x)=x^2):
$$f(x+Delta x)-f(x)=(x+Delta x)^2-x^2=x^2+2xDelta x+(Delta x)^2-x^2=2xDelta x+(Delta x)^2;$$
Подставим в определение производной:
$$f^{/}(x)=frac{2xDelta x+(Delta x)^2}{Delta x}=frac{Delta x*(2x+Delta x)}{Delta x}=2x+Delta x;$$
Напоминаю, что (Delta x) это бесконечно малая величина:
$$(Delta x)^2 ll 0;$$
Поэтому этим слагаемым можно пренебречь. Вот мы и получили формулу для производной от квадратной функции:
$$f^{/}(x)=(x^2)^{/}=2x;$$

Производная от третьей степени

Аналогичные рассуждения можно провести для функции третьей степени:
$$f(x)=x^3;$$
Воспользуемся определением производной:
$$f^{/}(x)=frac{f(x+Delta x)-f(x)}{Delta x} quad при quad Delta x to 0;$$
$$f(x+Delta x)-f(x)=(x+Delta x)^3-x^3=(x+Delta x-x)((x+Delta x)^2+(x+Delta x)*x+x^2)=$$
$$=Delta x*(x^2+2x*Delta x+(Delta x)^2+x^2+x*Delta x+x^2)=Delta x*(3x^2+3xDelta x);$$
$$f^{/}(x)=frac{f(x+Delta x)-f(x)}{Delta x}=frac{Delta x*(3x^2+3xDelta x)}{Delta x}=3x^2+3xDelta x;$$
Так как при умножении на бесконечно малую величину получается бесконечно малая величина, то слагаемым (3xDelta x) можно пренебречь:
$$f^{/}(x)=(x^3)^{/}=3x^2;$$
Точно таким же способом можно вывести формулы производных для любых степеней:
$$(x^4)^{/}=4x^3;$$
$$(x^5)^{/}=5x^4;$$
$$…$$
$$(x^n)^{/}=n*x^{n-1};$$
Кстати, эта формула справедлива и для дробных степеней.

Вывод остальных формул делается похожим образом, только там может понадобиться знание пределов. Вывод всех формул разбирается в университетском курсе математического анализа.

Что такое производная функции простыми словами? Для чего нужна производная? Определение производной

Как решать задания №7 из ЕГЭ по математике. Анализ графиков при помощи производной. Графики производной и графики функции

Исследуем функцию с помощью производной. Находим точки минимума и максимума, наибольшее и наименьшее значение функции. Точки экстремума. Промежутки возрастания и убывания.

Связь коэффициента наклона и тангенса угла наклона касательной к функции и производной функции в точке касания. Задание №7 в ЕГЭ по математике.

Источник

Производная функции

Процесс нахождения производной функции называется дифференцированием. Производную приходится находить в ряде задач курса математического анализа. Например, при отыскании точек экстремума и перегиба графика функции.

Как найти?

Чтобы найти производную функции нужно знать таблицу производных элементарных функций и применять основные правила дифференцирования:

Вынос константы за знак производной: $$ (Cu)’ = C(u)’ $$
Производная суммы/разности функций: $$ (u pm v)’ = (u)’ pm (v)’ $$
Производная произведения двух функций: $$ (u cdot v)’ = u’v + uv’ $$
Производная дроби: $$ bigg (frac{u}{v} bigg )’ = frac{u’v – uv’}{v^2} $$
Производная сложной функции: $$ ( f(g(x)) )’ = f'(g(x)) cdot g'(x) $$

Примеры решения

Пример 1

Найти производную функции $ y = x^3 – 2x^2 + 7x – 1 $

Решение

Производная суммы/разности функций равна сумме/разности производных:

$$ y’ = (x^3 – 2x^2 + 7x – 1)’ = (x^3)’ – (2x^2)’ + (7x)’ – (1)’ = $$

Используя правило производной степенной функции $ (x^p)’ = px^{p-1} $ имеем:

$$ y’ = 3x^{3-1} – 2 cdot 2 x^{2-1} + 7 – 0 = 3x^2 – 4x + 7 $$

Так же было учтено, что производная от константы равна нулю.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ y’ = 3x^2 – 4x + 7 $$

Пример 2

Найти производную функции $ y = sin x – ln 3x $

Решение

По правилу производной разности:

$$ y’ = (sin x – ln 3x)’ = (sin x)’ – (ln 3x)’ = $$

По таблице интегрирования находим:

$$ (sin x)’ = cos x $$ $$ (ln x)’ = frac{1}{x} $$

С учетом того, что аргумент натурального логарифма отличен от $ x $, то нужно домножить ещё на производную самого аргумента:

$$ y’ = (sin x)’ – (ln 3x)’ = cos x – frac{1}{3x} cdot (3x)’ = $$

После упрощения получаем:

$$ = cos x – frac{1}{3x} cdot 3 = cos x – frac{1}{x} $$

Ответ

$$ y’ = cos x – frac{1}{x} $$

Пример 3

Найти производную функции $ y = (3x-1) cdot 5^x $

Решение

В данном примере стоит произведение двух функций, а производная произведения находится по формуле номер 3: $$ (u cdot v)’ = u’v + uv’ $$

$$ y’ = ( (3x-1) cdot 5^x )’ = (3x-1)’ 5^x + (3x-1) (5^x)’ = $$

Производная первой функции вычисляется как разность фунций:

$$ (3x-1)’ = (3x)’ – (1)’ = 3(x)’ – (1)’ = 3 $$

Вторая функция является показательной, производная которой находится по формуле: $ (a^x)’ = a^x ln a $: $$ (5^x)’ = 5^x ln 5 $$

Продолжаем решение с учетом найденных производных:

$$ y’ = (3x-1)’ 5^x + (3x-1) (5^x)’ = 3 cdot 5^x + (3x-1) 5^x ln 5 $$

Ответ

$$ y’ = 3cdot 5^x + (3x-1) 5^x ln 5 $$

Пример 4

Найти производную функции $ y = frac{ln x}{sqrt{x}} $

Решение

Производную дроби найдем по четвертой формуле. Положим $ u = ln x $ и $ v = sqrt{x} $. Тогда их производные по таблице основных элементарных функций равны:

$$ u’ = (ln x)’ = frac{1}{x} $$ $$ v’ = (sqrt{x})’ = frac{1}{2sqrt{x}} $$

Используя формулу №4 получаем:

$$ y’ = bigg ( frac{ln x}{sqrt{x}} bigg )’ = frac{ frac{1}{x} cdot sqrt{x} – ln x cdot frac{1}{2sqrt{x}} }{x} = $$

Выносим множитель $ frac{1}{2sqrt{x}} $ в числителе за скобку:

$$ y’ = frac{2-ln x}{2xsqrt{x}} $$

Ответ

$$ y’ = frac{2-ln x}{2xsqrt{x}} $$

Пример 5

Найти производную функции $ y = ln sin 3x $

Решение

Данная функция является сложной, потому производную будем брать по цепочке. Сначала от внешней функции, затем от внутренней. При этом выполняя их перемножение.

$$ y’ = (ln sin 3x )’ = frac{1}{sin 3x} cdot (sin 3x)’ = $$

Заметим, что аргумент синуса отличен от $ x $, поэтому тоже является сложной функцией:

$$ = frac{1}{sin 3x} cdot cos 3x cdot (3x)’ = frac{1}{sin 3x} cdot cos 3x cdot 3 $$

Учитывая определение котангенса $ ctg x = frac{cos 3x}{sin 3x} $ перепишем полученную производную в удобном компактном виде:

$$ y’ = 3ctg 3x $$

Ответ

$$ y’ = 3ctg 3x $$

Источник

У этого термина существуют и другие значения, см. Производная.

Данная статья описывает производные вещественных функций. О производной комплексных функций см. Комплексный анализ.

Иллюстрация понятия производной

Произво́дная функции — понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю (при условии, что такой предел существует). Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Процесс вычисления производной называется дифференци́рованием.
Обратный процесс — нахождение первообразной — интегрирование.

История[править | править код]

В классическом дифференциальном исчислении производная чаще всего определяется через понятие предела, однако исторически теория пределов появилась позже дифференциального исчисления. Исторически производная вводилась кинематически (как скорость) или геометрически (определяясь по сути наклоном касательной, в разных конкретных формулировках). Ньютон называл производную флюксией, обозначая точкой над символом функции, школа Лейбница предпочитала в качестве базового понятия дифференциал^[1].

Русский термин в форме «производная функция» впервые употребил В. И. Висковатов, переведя на русский язык соответствующий французский термин dérivée, используемый французским математиком Лагранжем^[2].

Определение[править | править код]

Пусть в некоторой окрестности точки $x_{0}in mathbb{R}$ определена функция $fcolon U(x_{0})subset mathbb{R} to mathbb{R} .$ Производной функции называется такое число , что функцию в окрестности $U(x_{0})$ можно представить в виде

$f(x_{0}+h)=f(x_{0})+Ah+o(h)$

если существует.

Определение производной функции через предел[править | править код]

Пусть в некоторой окрестности точки $x_{0}in mathbb{R}$ определена функция $fcolon U(x_{0})subset mathbb{R} to mathbb{R} .$ Производной функции в точке $x_{0}$ называется предел, если он существует,

${displaystyle f'(x_{0})=lim limits _{xto x_{0}}{frac {f(x)-f(x_{0})}{x-x_{0}}}=lim _{Delta xto 0}{frac {f(x_{0}+Delta x)-f(x_{0})}{Delta x}}=lim limits _{{Delta x}to 0}{frac {Delta {f(x)}}{Delta x}}.}$

Общепринятые обозначения производной функции y = f(x) в точке x₀[править | править код]

$f'(x_{0})=f'_{x}(x_{0})={mathrm {D}}!f(x_{0})={frac {df}{dx}}(x_{0})=left.{frac {dy}{dx}}rightvert _{{x=x_{0}}}={dot {y}}(x_{0}).$

Заметим, что последнее обычно обозначает производную по времени (в теоретической механике и физике, исторически часто тоже).

Таблица производных[править | править код]

Производные степенных функций	Производные тригонометрических функций	Производные обратных тригонометрических функций	Производные гиперболических функций
${displaystyle left(cright)^{(n)}=0}$	${displaystyle left(sin xright)^{(n)}=sin(x+{dfrac {pi n}{2}})}$	$left(arcsin xright)'={dfrac {1}{{sqrt {1-x^{{2}}}}}}$
${displaystyle left(x^{a}right)^{(n)}={dfrac {a!}{(a-n)!}}x^{a-n}}$	${displaystyle left(cos xright)^{(n)}=cos(x+{dfrac {pi n}{2}})}$	$left(arccos xright)'=-{dfrac {1}{{sqrt {1-x^{{2}}}}}}$
${displaystyle left(a^{x}right)^{(n)}=a^{x}ln ^{n}a}$	${displaystyle left(operatorname {tg} xright)'=sec ^{2}x}$	${displaystyle left(operatorname {arctg} xright)'={dfrac {1}{1+x^{2}}}}$	${displaystyle (tanh x)'=operatorname {sch} ^{2}x}$
${displaystyle left(log _{a}xright)^{(n)}={dfrac {(-1)^{n-1}(n-1)!}{x^{n}ln a}}}$	${displaystyle left(operatorname {ctg} xright)'=-csc ^{2}x}$	${displaystyle left(operatorname {arcctg} xright)'=-{dfrac {1}{1+x^{2}}}}$	${displaystyle (coth x)'=-operatorname {csch} ^{2}x}$
		${displaystyle left(operatorname {arcsec} xright)'={frac {1}{\|x\|{sqrt {x^{2}-1}}}}}$	${displaystyle (mathrm {sch} x)'=-{frac {sinh x}{cosh ^{2}x}}}$
		${displaystyle left(operatorname {arccosec} xright)'=-{frac {1}{\|x\|{sqrt {x^{2}-1}}}}}$	${displaystyle (mathrm {csch} x)'=-{frac {cosh x}{sinh ^{2}x}}}$

$left(e^{{x}}right)^{{left(nright)}}=e^{{x}}$
${displaystyle (ln {x})^{(n)}={dfrac {(-1)^{n-1}(n-1)!}{x^{n}}}}$

Дифференцируемость[править | править код]

Производная $f'(x_{0})$ функции в точке $x_{0}$ , будучи пределом, может не существовать или существовать и быть конечной или бесконечной. Функция является дифференцируемой в точке $x_{0}$ тогда и только тогда, когда её производная в этой точке существует и конечна:

$fin {mathcal {D}}(x_{0})Leftrightarrow exists f'(x_{0})in (-infty ;infty ).$

Для дифференцируемой в $x_{0}$ функции в окрестности $U(x_{0})$ справедливо представление

${displaystyle f(x)=f(x_{0})+f'(x_{0})(x-x_{0})+o(x-x_{0})}$

при $xto x_{0}.$

Замечания[править | править код]

Геометрический и физический смысл производной[править | править код]

Тангенс угла наклона касательной прямой[править | править код]

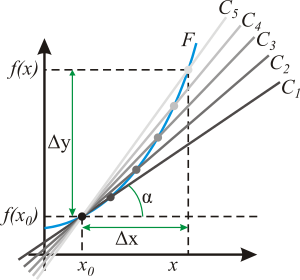
Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точки x₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C₅). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C₅ — C₁). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Если функция $fcolon U(x_{0})to mathbb{R}$ имеет конечную производную в точке x_0, то в окрестности $U(x_{0})$ её можно приблизить линейной функцией

$f_{l}(x)equiv f(x_{0})+f'(x_{0})(x-x_{0}).$

Функция $f_{l}$ называется касательной к в точке $x_{0}.$ Число ${displaystyle f'(x_{0})}$ является угловым коэффициентом (угловым коэффициентом касательной) или тангенсом угла наклона касательной прямой.

Скорость изменения функции[править | править код]

Пусть s=s(t) — закон прямолинейного движения. Тогда $v(t_{0})=s'(t_{0})$ выражает мгновенную скорость движения в момент времени t_0 . Новая функция также имеет производную. Эта т. н. вторая производная, обозначается как , а функция $a(t_{0})=s''(t_{0})$ выражает мгновенное ускорение в момент времени $t_{0}.$

Вообще производная функции y=f(x) в точке $x_{0}$ выражает скорость изменения функции в точке $x_{0}$ , то есть скорость протекания процесса, описанного зависимостью y=f(x).

Анимация, дающая первоначальное интуитивное представление о производной, как о «размахе» изменения функции при изменении аргумента (нажмите для воспроизведения).

Производные высших порядков[править | править код]

Понятие производной произвольного порядка задаётся рекуррентно. Полагаем

$f^{{(0)}}(x_{0})equiv f(x_{0}).$

Если функция дифференцируема в $x_{0}$ , то производная первого порядка определяется соотношением

$f^{{(1)}}(x_{0})equiv f'(x_{0}).$

Пусть теперь производная -го порядка $f^{{(n)}}$ определена в некоторой окрестности точки $x_{0}$ и дифференцируема. Тогда

$f^{{(n+1)}}(x_{0})=left(f^{{(n)}}right)'(x_{0}).$

В частности, вторая производная является производной от производной:

${displaystyle f''(x_{0})=(f'(x))'|_{x=x_{0}}}$

Если функция имеет в некоторой области D частную производную по одной из переменных, то названная производная, сама являясь функцией от может иметь в некоторой точке $(x_{0},y_{0},z_{0})$ частные производные по той же или по любой другой переменной.
Для исходной функции эти производные будут частными производными второго порядка (или вторыми частными производными).

${displaystyle u''_{x^{2}}=f''_{x^{2}}(x_{0},y_{0},z_{0})}$

или ${displaystyle {frac {partial ^{2}u}{partial x^{2}}}={frac {partial ^{2}f(x_{0},y_{0},z_{0})}{partial x^{2}}}}$

${displaystyle u''_{xy}=f''_{xy}(x_{0},y_{0},z_{0})}$

или ${displaystyle {frac {partial ^{2}u}{partial xpartial y}}={frac {partial ^{2}f(x_{0},y_{0},z_{0})}{partial xpartial y}}}$

Частная производная второго или более высокого порядка, взятая по различным переменным, называется смешанной частной производной. Например,

${displaystyle u''_{xy}=f''_{xy}(x_{0},y_{0},z_{0})}$

Класс функций, у которых производная -порядка является непрерывной, обозначается как ${displaystyle C^{(n)}}$ .

Способы записи производных[править | править код]

В зависимости от целей, области применения и используемого математического аппарата используют различные способы записи производных. Так, производная n-го порядка может быть записана в нотациях:

Лагранжа $f^{{(n)}}(x_{0})$ , при этом для малых n часто используют штрихи и римские цифры:

$f^{{(1)}}(x_{0})=f'(x_{0})=f^{I}(x_{0}),$

$f^{{(2)}}(x_{0})=f''(x_{0})=f^{{II}}(x_{0}),$

$f^{{(3)}}(x_{0})=f'''(x_{0})=f^{{III}}(x_{0}),$

$f^{{(4)}}(x_{0})=f^{{IV}}(x_{0}),$

и т. д.

Такая запись удобна своей краткостью и широко распространена; однако штрихами разрешается обозначать не выше третьей производной.

Лейбница, удобная наглядной записью отношения бесконечно малых (только в случае, если — независимая переменная; в противном случае обозначение верно лишь для производной первого порядка):

${frac {d^{n}!f}{dx^{n}}}(x_{0})$

Ньютона, которая часто используется в механике для производной по времени функции координаты (для пространственной производной чаще используют запись Лагранжа). Порядок производной обозначается числом точек над функцией, например:

${dot {x}}(t_{0})$

— производная первого порядка

по

при $t=t_{0}$

, или ${ddot {f}}(x_{0})$

— вторая производная

по

в точке $x_{0}$

и т. д.

Эйлера, использующая дифференциальный оператор (строго говоря, дифференциальное выражение, пока не введено соответствующее функциональное пространство), и потому удобная в вопросах, связанных с функциональным анализом:

${mathrm {D}}^{n}!f(x_{0})$

, или иногда $partial ^{n}!f(x_{0})$

Конечно, при этом необходимо не забывать, что служат все они для обозначения одних и тех же объектов:

${displaystyle f^{(n)}(x_{0})={frac {d^{n}!f}{dx^{n}}}(x_{0})={overset {overbrace {cdot cdot ldots cdot } ^{n {text{раз}}}}{f}}(x_{0})=mathrm {D} ^{n}!f(x_{0})=f{underbrace {_{xxldots x}} _{n {text{раз}}}}vert _{x=x_{0}}.}$

Примеры[править | править код]

Пусть . Тогда

$f'(x_{0})=lim limits _{{xto x_{0}}}{frac {x^{2}-x_{0}^{2}}{x-x_{0}}}=lim limits _{{xto x_{0}}}{frac {(x-x_{0})(x+x_{0})}{x-x_{0}}}=lim limits _{{xto x_{0}}}(x+x_{0})=2x_{0}.$

$f'(x_{0})=operatorname{sgn} x_{0},$

где обозначает функцию знака. А если $x_{0}=0,$ то
$f'_{+}(x_{0})=1,;f'_{-}(x_{0})=-1,$
а следовательно $f'(x_{0})$ не существует.

Теоремы, связанные с дифференцированием[править | править код]

Для непрерывных функций f,g на отрезке [a,b] , дифференцируемых на интервале (a,b) справедливы:

Лемма Ферма. Если принимает максимальное или минимальное значение в точке и существует , то f'(c)=0 .

Теорема о нуле производной. Если принимает на концах отрезка [a,b] одинаковые значения, то на интервале (a,b) найдётся хотя бы одна точка, в которой производная функции равна нулю.

Формула конечных приращений. Для найдётся точка , такая что ${frac {f(b)-f(a)}{b-a}}=f'(c)$ .

Теорема Коши о среднем значении. Если не равна нулю на интервале (a,b) , то найдётся такая точка , что ${frac {f(b)-f(a)}{g(b)-g(a)}}={frac {f'(c)}{g'(c)}}$ .

Правило Лопиталя. Если ${displaystyle lim _{xto c}f(x)=lim _{xto c}g(x)=0}$ или infty , причём для всякого из некоторой проколотой окрестности и существует ${displaystyle lim _{xto c}{frac {f'(x)}{g'(x)}}}$ , то ${displaystyle lim _{xto c}{frac {f(x)}{g(x)}}=lim _{xto c}{frac {f'(x)}{g'(x)}}}$ .

Правила дифференцирования[править | править код]

Операция нахождения производной называется дифференцированием. При выполнении этой операции часто приходится работать с частными, суммами, произведениями функций, а также с «функциями функций», то есть сложными функциями. Исходя из определения производной, можно вывести правила дифференцирования, облегчающие эту работу.
Если — постоянное число и — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

^[4]

$left({frac {C}{g}}right)'=-{frac {Cg'}{g^{2}}}$ (g ≠ 0)
Если функция задана параметрически:

$left{{begin{matrix}x=x(t),\y=y(t),end{matrix}};;tin left[T_{1};T_{2}right]right.$ , то
$y'_{x}={frac {dy}{dx}}={frac {dy}{dt}}cdot {frac {dt}{dx}}=y'_{t}cdot t'_{x}={frac {y'_{t}}{x'_{t}}}$

${frac {d}{dx}}f(g(x))={frac {df(g)}{dg}}cdot {frac {dg(x)}{dx}}=f'_{g}g'_{x}$
Формулы производной произведения и отношения обобщаются на случай n-кратного дифференцирования (формула Лейбница):

$(fg)^{{(n)}}=sum limits _{{k=0}}^{{n}}{C_{n}^{k}f^{{(n-k)}}g^{{(k)}}},$

где $C_{n}^{k}$

— биномиальные коэффициенты.

Следующие свойства производной служат дополнением к правилам дифференцирования:

Таблица производных некоторых функций[править | править код]

Функция	Производная	Примечание
${displaystyle x^{alpha }}$	${displaystyle alpha cdot x^{alpha -1}}$	Доказательство Фиксируем , придадим приращение аргументу . Вычислим приращение функции: $Delta y=(x+Delta x)^{alpha }-x^{alpha }=x^{alpha }((1+{frac {Delta x}{x}})^{alpha }-1)$ , т.о $(x^{alpha })'=lim _{{Delta xto 0}}{{frac {Delta y}{Delta x}}}=lim _{{Delta xto 0}}{{frac {x^{alpha }((1+{frac {Delta x}{x}})^{alpha }-1)}{Delta x}}}=$ См. $=lim _{{Delta xto 0}}{frac {alpha cdot x^{alpha }cdot {frac {Delta x}{x}}}{Delta x}}=alpha cdot x^{{alpha -1}}$
$a^{x}$	${displaystyle a^{x}cdot ln {a}}$	Доказательство Фиксируем , придадим приращение аргументу . Вычислим приращение функции: ${displaystyle Delta y=a^{x+Delta x}-a^{x}=a^{x}(a^{Delta x}-1)}$ , т.о $(a^{x})'=lim _{{Delta xto 0}}{{frac {Delta y}{Delta x}}}=lim _{{Delta xto 0}}{{frac {a^{x}(a^{{Delta x}}-1)}{Delta x}}}=$ См. $=lim _{{Delta xto 0}}{frac {a^{x}cdot Delta xcdot ln {a}}{Delta x}}=a^{x}cdot ln {a}$
${displaystyle log _{a}{x}}$	${displaystyle {frac {1}{xcdot ln {a}}}}$	Доказательство ${displaystyle (log _{a}x)'={frac {1}{ln {a}}}cdot (ln {x})'}$ Узнаем производную через производную обратной функции: ${displaystyle y_{x}=ln {x}Rightarrow x_{y}=e^{y},}$ ${displaystyle y_{x}'=(ln {x})'={frac {1}{(e^{y})'}}={frac {1}{e^{y}}}={frac {1}{x}}}$ Получаем: ${displaystyle (log _{a}{x})'={frac {1}{xcdot ln {a}}}}$
		Доказательство Фиксируем , придадим приращение аргументу . Вычислим приращение функции: ${displaystyle Delta y=sin(x+Delta x)-sin(x)=2sin({frac {x+Delta x-x}{2}})cdot cos({frac {x+Delta +x}{2}})=2sin({frac {Delta x}{2}})cdot cos(x+{frac {Delta x}{2}})}$ , т.о ${displaystyle lim _{Delta xto 0}{frac {Delta y}{Delta x}}=lim _{Delta xto 0}{frac {2sin({frac {Delta x}{2}})cdot cos(x+{frac {Delta x}{2}})}{Delta x}}=lim _{Delta xto 0}{frac {sin({frac {Delta x}{2}})cdot cos(x+{frac {Delta x}{2}})}{frac {Delta x}{2}}}=lim _{Delta xto 0}{frac {sin({frac {Delta x}{2}})}{frac {Delta x}{2}}}}$ ( См.) ${displaystyle cdot lim _{Delta xto 0}{cos(x+{frac {Delta x}{2}})}=cos(x)}$
		Доказательство Фиксируем , придадим приращение аргументу . Вычислим приращение функции: ${displaystyle Delta y=cos(x+Delta x)-cos(x)=-2sin({frac {x+Delta x+x}{2}})cdot sin({frac {x+Delta -x}{2}})=-2sin(x+{frac {Delta x}{2}})cdot sin({frac {Delta x}{2}})}$ , т.о ${displaystyle lim _{Delta xto 0}{frac {Delta y}{Delta x}}=lim _{Delta to 0}{frac {-2sin(x+{frac {Delta x}{2}})cdot sin({frac {Delta x}{2}})}{Delta x}}=lim _{Delta to 0}{frac {-sin(x+{frac {Delta x}{2}})cdot sin({frac {Delta x}{2}})}{frac {Delta x}{2}}}=lim _{Delta xto 0}{frac {sin({frac {Delta x}{2}})}{frac {Delta x}{2}}}}$ ( См.) ${displaystyle cdot lim _{Delta xto 0}{-sin(x+{frac {Delta x}{2}})}=-sin(x)}$
	${displaystyle {frac {1}{cos ^{2}{x}}}}$	Доказательство 1 Фиксируем , придадим приращение аргументу . Вычислим приращение функции: ${displaystyle Delta y=tg(x+Delta x)-tg(x)={frac {sin(x+Delta x-x)}{cos(x+Delta x)cdot cos(x)}}={frac {sin(Delta x)}{cos(x+Delta x)cdot cos(x)}}}$ , т.о. ${displaystyle lim _{xto 0}{frac {Delta y}{Delta x}}=lim _{Delta xto 0}{frac {frac {sin(Delta x)}{cos(x+Delta x)cdot cos(x)}}{Delta x}}=lim _{Delta xto 0}{frac {sin(Delta x)}{Delta x}}cdot }$ ( См.) ${displaystyle lim _{Delta xto 0}{frac {1}{cos(x+Delta x)cdot cos(x)}}={frac {1}{cos^{2}(x)}}}$ Доказательство 2 ${displaystyle (tgx)'=({frac {sin(x)}{cos(x)}})'={frac {(sin(x))'cdot cos(x)-sin(x)cdot (cos(x))'}{cos^{2}(x)}}={frac {cos(x)cdot cos(x)-sin(x)cdot (-sin(x))}{cos^{2}(x)}}={frac {cos^{2}(x)+sin^{2}(x)}{cos^{2}(x)}}={frac {1}{cos^{2}(x)}}}$
	${displaystyle -{frac {1}{sin ^{2}{x}}}}$	Доказательство ${displaystyle (ctgx)'=({frac {cos(x)}{sin(x)}})'={frac {(cos(x))'cdot sin(x)-cos(x)cdot (sin(x))'}{sin^{2}(x)}}={frac {-sin(x)cdot sin(x)+cos(x)cdot cos(x)}{sin^{2}(x)}}=-{frac {sin^{2}(x)+cos^{2}(x)}{sin^{2}(x)}}=-{frac {1}{sin^{2}(x)}}}$
		Доказательство ${displaystyle (sec(x))'=({frac {1}{cos(x)}})'={frac {(1)'cdot cos(x)-1cdot (cos(x))'}{cos^{2}(x)}}={frac {sin(x)}{cos^{2}(x)}}=sec(x)cdot tg(x)}$
		Доказательство ${displaystyle (cosec(x))'=({frac {1}{sin(x)}})'={frac {(1)'cdot sin(x)-1cdot (sin(x))'}{sin^{2}(x)}}=-{frac {cos(x)}{sin^{2}(x)}}=-coses(x)cdot ctg(x)}$
	${frac {1}{{sqrt {1-x^{2}}}}}$	Доказательство Найти производную арксинуса можно при помощи взаимно обратных функций. После чего мы должны взять производную этих обеих функций. Теперь мы должны выразить производную арксинуса. ${displaystyle (arcsin(x))'={frac {1}{cos(arcsin(x))}}}$ Исходя из тригонометрического тождества( ${displaystyle sin^{2}x+cos^{2}x=1}$ ) — получаем. ${displaystyle (arcsin(x))'={frac {1}{pm {sqrt {1-sin^{2}(arcsin(x))}}}}}$ Для того чтобы определить знак корня в знаменателе нужно взглянуть на область значений арксинуса. ${displaystyle E(arcsin(x))=[-{frac {pi }{2}};{frac {pi }{2}}]}$ Так как косинус находится в 1-й и 4-й четвертях, то косинус положительный. ${displaystyle (arcsin(x))'={frac {1}{sqrt {1-sin^{2}(arcsin(x))}}}}$ Отсюда ${displaystyle (arcsin(x))'={frac {1}{sqrt {1-x^{2}}}}}$
	$-{frac {1}{{sqrt {1-x^{2}}}}}$	Доказательство Найти производную арккосинуса можно при помощи данного тождества: ${displaystyle arcsin(x)+arccos(x)={frac {pi }{2}}}$ Теперь находим производную обеих частей этого тождества. ${displaystyle [arcsin(x)+arccos(x)]'=({frac {pi }{2}})'}$ Теперь выражаем производную арккосинуса. Получается. ${displaystyle (arccos(x))'=-{frac {1}{sqrt {1-x^{2}}}}}$
	${displaystyle {frac {1}{1+x^{2}}}}$	Доказательство Найти производную арктангенса можно при помощи взаимнообратной функии: Теперь находим производную обеих частей этого тождества. ${displaystyle {frac {1}{cos^{2}(arctg(x))}}cdot (arctg(x))'=1}$ Теперь мы должны выразить производную арктангенса: ${displaystyle (arctg(x))'=cos^{2}(arctg(x))}$ Теперь на помощь нам придет на помощь тождество( ${displaystyle cos(x)={frac {1}{sqrt {1+tg^{2}(x)}}}}$ ): ${displaystyle (arctg(x))'=({frac {1}{sqrt {1+tg^{2}(arctg(x))}}})^{2}}$ Получается. ${displaystyle (arctg(x))'={frac {1}{1+x^{2}}}}$
	${displaystyle -{frac {1}{1+x^{2}}}}$	Доказательство Найти производную арккотангенса можно при помощи данного тождества: ${displaystyle arctg(x)+arcctg(x)={frac {pi }{2}}}$ Теперь находим производную обеих частей этого тождества. ${displaystyle [arctg(x)+arcctg(x)]'=({frac {pi }{2}})'}$ Теперь выражаем производную арккотангенса. Получается. ${displaystyle (arcctg(x))'=-{frac {1}{1+x^{2}}}}$
	${displaystyle {frac {1}{\|x\|{sqrt {x^{2}-1}}}}}$	Доказательство Найти производную арксеканса можно при помощи тождества: ${displaystyle arcsec(x)=arccos({frac {1}{x}})}$ Теперь находим производную обеих частей этого тождества. ${displaystyle (arcsec(x))'=(arccos({frac {1}{x}}))'}$ ${displaystyle (arcsec(x))'=-{frac {1}{sqrt {1-{frac {1}{x^{2}}}}}}cdot (-{frac {1}{x^{2}}})}$ ${displaystyle (arcsec(x))'={frac {1}{x^{2}{sqrt {frac {x^{2}-1}{x^{2}}}}}}}$ ${displaystyle (arcsec(x))'={frac {1}{x^{2}{frac {sqrt {x^{2}-1}}{\|x\|}}}}}$ Получается. ${displaystyle (arcsec(x))'={frac {1}{\|x\|{sqrt {x^{2}-1}}}}}$
	${displaystyle -{frac {1}{\|x\|{sqrt {x^{2}-1}}}}}$	Доказательство Найти производную арккосеканса можно при помощи данного тождества: ${displaystyle arccosec(x)+arcsec(x)={frac {pi }{2}}}$ Теперь находим производную обеих частей этого тождества. ${displaystyle [arccosec(x)+arcsec(x)]'=({frac {pi }{2}})'}$ Теперь выражаем производную арккосинуса. Получается. ${displaystyle (arccosec(x))'=-{frac {1}{\|x\|{sqrt {x^{2}-1}}}}}$
		Доказательство ${displaystyle (operatorname {sh} {x})'=left({frac {e^{x}-e^{-x}}{2}}right)'={frac {1}{2}}cdot (e^{x}-e^{-x})'={frac {1}{2}}cdot (e^{x}-(-1)cdot e^{-x})={frac {e^{x}+e^{-x}}{2}}=operatorname {ch} {x}}$
		Доказательство ${displaystyle (operatorname {ch} {x})'=left({frac {e^{x}+e^{-x}}{2}}right)'={frac {1}{2}}cdot (e^{x}+e^{-x})'={frac {1}{2}}cdot (e^{x}+(-1)cdot e^{-x})=left({frac {e^{x}-e^{-x}}{2}}right)=operatorname {sh} {x}}$
	${displaystyle {frac {1}{mathrm {ch} ^{2} x}}}$	Доказательство ${displaystyle (th(x))'=({frac {sh(x)}{ch(x)}})'={frac {(sh(x))'cdot ch(x)-sh(x)cdot (ch(x))'}{ch^{2}(x)}}={frac {ch(x)cdot ch(x)-sh(x)cdot sh(x)}{ch^{2}(x)}}={frac {ch^{2}(x)-sh^{2}(x)}{ch^{2}(x)}}={frac {1}{ch^{2}(x)}}}$
	${displaystyle -{frac {1}{mathrm {sh} ^{2} x}}}$	Доказательство ${displaystyle (cthx)'=({frac {ch(x)}{sh(x)}})'={frac {(ch(x))'cdot sh(x)-ch(x)cdot (sh(x))'}{sh^{2}(x)}}={frac {sh(x)cdot sh(x)-ch(x)cdot ch(x)}{sh^{2}(x)}}={frac {sh^{2}(x)-ch^{2}(x)}{sh^{2}(x)}}=-{frac {1}{sh^{2}(x)}}}$
	${displaystyle -{frac {operatorname {sh} (x)}{operatorname {ch} ^{2}(x)}}}$	Доказательство ${displaystyle (sch(x))'=({frac {1}{ch(x)}})'={frac {(1)'cdot ch(x)-1cdot (ch(x))'}{ch^{2}(x)}}=-{frac {sh(x)}{ch^{2}(x)}}}$
	${displaystyle -{frac {operatorname {ch} (x)}{operatorname {sh} ^{2}(x)}}}$	Доказательство ${displaystyle (csch(x))'=({frac {1}{sh(x)}})'={frac {(1)'cdot sh(x)-1cdot (sh(x))'}{sh^{2}(x)}}=-{frac {ch(x)}{sh^{2}(x)}}}$
	${displaystyle {frac {1}{sqrt {x^{2}+1}}}}$	Доказательство ${displaystyle (arsh(x))'=(ln {(x+{sqrt {x^{2}+1}})})'={frac {1}{x+{sqrt {x^{2}+1}}}}cdot (x+{sqrt {x^{2}+1}})'={frac {1}{x+{sqrt {x^{2}+1}}}}cdot ((x)'+({sqrt {x^{2}+1}})')={frac {1}{x+{sqrt {x^{2}+1}}}}cdot (1+({sqrt {x^{2}+1}})')={frac {1}{x+{sqrt {x^{2}+1}}}}cdot (1+{frac {1}{2{sqrt {x^{2}+1}}}}cdot (x^{2}+1)')={frac {1}{x+{sqrt {x^{2}+1}}}}cdot (1+{frac {2x}{2{sqrt {x^{2}+1}}}})={frac {1}{x+{sqrt {x^{2}+1}}}}cdot ({frac {x+{sqrt {x^{2}+1}}}{sqrt {x^{2}+1}}})={frac {x+{sqrt {x^{2}+1}}}{(x+{sqrt {x^{2}+1}})cdot ({sqrt {x^{2}+1}})}}={frac {1}{sqrt {x^{2}+1}}}}$
	${displaystyle {frac {1}{sqrt {x^{2}-1}}}}$	Доказательство ${displaystyle (arch(x))'=(ln {(x+{sqrt {x^{2}-1}})})'={frac {1}{x+{sqrt {x^{2}-1}}}}cdot (x+{sqrt {x^{2}-1}})'={frac {1}{x+{sqrt {x^{2}-1}}}}cdot ((x)'+({sqrt {x^{2}-1}})')={frac {1}{x+{sqrt {x^{2}-1}}}}cdot (1+({sqrt {x^{2}-1}})')={frac {1}{x+{sqrt {x^{2}-1}}}}cdot (1+{frac {1}{2{sqrt {x^{2}-1}}}}cdot (x^{2}-1)')={frac {1}{x+{sqrt {x^{2}-1}}}}cdot (1+{frac {2x}{2{sqrt {x^{2}-1}}}})={frac {1}{x+{sqrt {x^{2}-1}}}}cdot ({frac {x+{sqrt {x^{2}-1}}}{sqrt {x^{2}-1}}})={frac {x+{sqrt {x^{2}-1}}}{(x+{sqrt {x^{2}-1}})cdot ({sqrt {x^{2}-1}})}}={frac {1}{sqrt {x^{2}-1}}}}$
	${displaystyle {frac {1}{1-x^{2}}}}$	Доказательство ${displaystyle ({displaystyle mathrm {arth} x})'={biggl (}{frac {1}{2}}cdot ln {biggl (}{frac {1+x}{1-x}}{biggl )}{biggl )}'={frac {1}{2}}cdot {frac {1-x}{1+x}}cdot {biggl (}{frac {1+x}{1-x}}{biggl )}'={frac {1}{2}}cdot {frac {1-x}{1+x}}cdot {frac {(1+x)'(1-x)-(1+x)(1-x)'}{(1-x)^{2}}}={frac {1}{2}}cdot {frac {1-x}{1+x}}cdot {frac {2}{(1-x)^{2}}}={frac {1}{1-x^{2}}}}$
	${displaystyle {frac {1}{1-x^{2}}}}$	Доказательство ${displaystyle ({displaystyle mathrm {arcth} x})'={biggl (}{frac {1}{2}}cdot ln {biggl (}{frac {x+1}{x-1}}{biggl )}{biggl )}'={frac {1}{2}}cdot {frac {x-1}{x+1}}cdot {biggl (}{frac {x+1}{x-1}}{biggl )}'={frac {1}{2}}cdot {frac {x-1}{x+1}}cdot {frac {(x+1)'(x-1)-(x+1)(x-1)'}{(x-1)^{2}}}={frac {1}{2}}cdot {frac {x-1}{x+1}}cdot {frac {-2}{(x-1)^{2}}}={frac {1}{1-x^{2}}}}$
	${displaystyle -{frac {1}{x(x+1){sqrt {frac {1-x}{1+x}}}}}}$
	${displaystyle -{frac {1}{x(x+1){sqrt {1+{frac {1}{x^{2}}}}}}}}$

Производная вектор-функции по параметру[править | править код]

Определим производную вектор-функции по параметру:

${frac {d}{dt}}{mathbf {r}}(t)=lim _{{hto 0}}{frac {{mathbf {r}}(t+h)-{mathbf {r}}(t)}{h}}$

Если производная в точке существует, вектор-функция называется дифференцируемой в этой точке. Координатными функциями для производной будут .

Свойства производной вектор-функции (всюду предполагается, что производные существуют):

Способы задания производных[править | править код]

Производная Джексона^[5]:

$D_{{x}}^{{q}}f(x)={frac {f(qx)-f(x)}{(q-1)x}}.$

Вариации и обобщения[править | править код]

Обобщения производных
- Дробная производная
- Производная Пеано
- Частная производная

См. также[править | править код]

Таблица производных
Производная (математика)
Дифференцирование сложной функции
Производная обратной функции
Дифференцируемая функция
Основная теорема анализа
Геометрический смысл производной
Производная по направлению

Примечания[править | править код]

↑ Колмогоров А. Н., Абрамов А. М., Дудницын Ю. П. Алгебра и начала анализа. Учебник для 10-11 классов средней школы. — М., Просвещение, 1994. — ISBN 5-09-006088-6. — C. 155—156
↑ Комков Г. Д., Левшин Б. В., Семенов Л. К. Академия наук СССР. Краткий исторический очерк (в двух томах). — 2-е изд. — М.: Наука, 1977. — Т. 1. 1724—1917. — С. 173.
↑ Производная суммы равна сумме производных
↑ Отсюда, в частности, следует, что производная произведения функции и константы равна произведению производной этой функции на константу
↑ A.I. Olemskoi, S.S. Borysov,a, and I.A. Shuda. Statistical field theories deformed within different calculi. Дата обращения: 21 апреля 2014. Архивировано 21 сентября 2017 года.

Литература[править | править код]

Виленкин Н., Мордкович А. Что такое производная // Квант. — 1975. — № 12.
В. Г. Болтянский, Что такое дифференцирование?, «Популярные лекции по математике», Выпуск 17, Гостехиздат 1955 г., 64 стр.
В. А. Гусев, А. Г. Мордкович «Математика»
Г. М. Фихтенгольц «Курс дифференциального и интегрального исчисления», том 1
В. М. Бородихин, Высшая математика, учеб. пособие, ISBN 5-7782-0422-1

Ссылки[править | править код]

Определение производной. Физический смысл производной
Правила дифференцирования
Онлайн калькулятор производных с подробным пошаговым решением на русском языке
Таблица производных
«Что такое производная — на примере с банковским счётом» — перевод статьи Understanding Calculus With A Bank Account Metaphor | BetterExplained (англ.)

Источник

Геометрический и физический смысл производной

Правила нахождения производных

Правило первое: выносим константу

Правило второе: производная суммы функций

Правило третье: производная произведения функций

Правило четвертое: производная частного двух функций

Геометрический и физический смысл производной

Правила нахождения производных

Правило первое: выносим константу

Правило второе: производная суммы функций

Правило третье: производная произведения функций

Правило четвертое: производная частного двух функций

Как найти производную от функции

Как считать производные?

Формулы производной

Свойства производной

Примеры нахождения производной

Производная сложной функции

Вывод формул производной функции

Производная квадратичной функции

Производная от третьей степени

Производная функции

Как найти?

Примеры решения

История[править | править код]

Определение[править | править код]

Определение производной функции через предел[править | править код]

Общепринятые обозначения производной функции y = f(x) в точке x0[править | править код]

Таблица производных[править | править код]

Дифференцируемость[править | править код]

Замечания[править | править код]

Геометрический и физический смысл производной[править | править код]

Тангенс угла наклона касательной прямой[править | править код]

Скорость изменения функции[править | править код]

Производные высших порядков[править | править код]

Способы записи производных[править | править код]

Примеры[править | править код]

Теоремы, связанные с дифференцированием[править | править код]

Правила дифференцирования[править | править код]

Таблица производных некоторых функций[править | править код]

Производная вектор-функции по параметру[править | править код]

Способы задания производных[править | править код]

Вариации и обобщения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Ссылки[править | править код]

Вам также может понравиться

Котел протерм гепард ошибка f62 как исправить

Как найти данные своего паспорта ссср

Как найти гибель титаника

Добавить комментарий Отменить ответ

Общепринятые обозначения производной функции y = f(x) в точке x₀[править | править код]