Задание
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
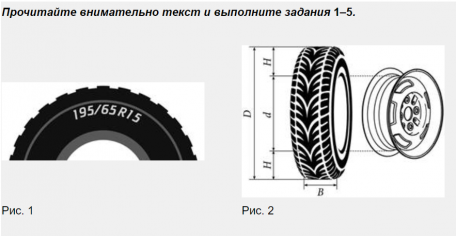
Для маркировки автомобильных шин применяется единая система обозначений. Например, (displaystyle 195/65, mathrm R15)(рис. 1). Первое число (число (displaystyle 195) в приведённом примере) обозначает ширину шины
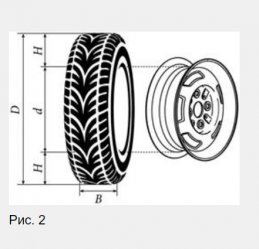
в миллиметрах (параметр (displaystyle B) на рисунке 2).
Второе число (число (displaystyle 65) в приведённом примере) – процентное отношение высоты боковины (параметр (displaystyle H) на рисунке 2) к ширине шины, то есть (displaystyle 100 cdot frac {H}{B}{small .})
Последующая буква обозначает тип конструкции шины. В данном примере буква (displaystyle mathrm R) означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса (displaystyle d) в дюймах (в одном дюйме (displaystyle 25{,}4) мм). Таким образом, общий диаметр колеса (displaystyle D) легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки (displaystyle 185/60, mathrm R14{small .})
Завод допускает установку шин с другими маркировками.
На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки (displaystyle 205/50, mathrm R16{small ?}) Результат округлите до десятых.
Решение
Требуется определить, на сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки (displaystyle 205/50, mathrm R16{small .})
Заметим, что пробег автомобиля при одном обороте колеса равен длине внешней окружности колеса (displaystyle L{small .})
|
Правило Длина окружностиДлина окружности (displaystyle L) равна произведению её диаметра (displaystyle D) на число (displaystyle pi{small :}) (displaystyle L=pi cdot D{small .}) |
Введём обозначения:
- (displaystyle D_{1}) и (displaystyle L_{1}) – диаметр и длина внешней окружности соответственно колеса, устанавливаемого на заводе;
- (displaystyle D_{2}) и (displaystyle L_{2}) – диаметр и длина внешней окружности соответственно колеса с шинами маркировки (displaystyle 205/50, mathrm R16{small .})
Требуется определить, на сколько процентов (displaystyle L_{2}) больше, чем (displaystyle L_{1}{small .})
Примем длину окружности (displaystyle L_{1}) за (displaystyle 100%) и определим, сколько процентов составляет длина (displaystyle L_{2}{small :})
- (displaystyle L_{1}=color {red}{pi cdot D_{1}})мм и это (displaystyle 100%{small .}) Тогда один мм составляет (displaystyle frac{100}{color {red}{pi cdot D_{1}}}) процентов.
- (displaystyle L_{2}=color {green}{pi cdot D_{2}})мм. Значит, в процентах это составляет (displaystyle color {green}{pi cdot D_{2}}cdot frac{100}{color {red}{pi cdot D_{1}}}=frac{color {green}{D_{2}}}{color {red}{D_{1}}}cdot 100) процентов.
Таким образом, для ответа на вопрос задачи нам достаточно найти диаметры колёс.
1. Найдём диаметр колёс, устанавливаемых на заводе.
Диаметр колеса, устанавливаемого на заводе, равен (displaystyle color{red}{D_{,1}=577{,}6})мм
2. Найдём диаметр колёс с шинами маркировки (displaystyle color{orange}{205}/color{green}{50}, mathrm Rcolor{magenta}{16}{small .})
Диаметр колеса, используемого для замены, равен (displaystyle color{green}{D_{,2}=611{,}4})мм
3. Найдём, сколько составляет длина (displaystyle L_{2}) в процентах от (displaystyle L_{1}{small.}) Ответ требуется дать с точностью до десятых, поэтому расчёты выполняем с точностью до сотых, а затем округляем до десятых:
(displaystyle L_{2}=frac{color{green}{D_{2}}}{color {red}{D_{1}}}cdot 100=frac{color{green}{611{,}4}}{color {red}{577{,}6}}cdot 100=frac{611400}{5776}≈105{,}85 …≈105{,}9{small.})
Значит, при замене колёс, установленных на заводе, колёсами с шинами маркировки (displaystyle 205/50, mathrm R16) пробег автомобиля при одном обороте колеса увеличится на
(displaystyle 105{,}9-100=5{,}9) процентов.
Ответ: (displaystyle 5{,}9)
#хакнем_математика 👈 рубрика, содержащая интересный, познавательный контент по математике как для школьников, так и для взрослых 🥳
Здравствуйте, уважаемые читатели канала Хакнем Школа!
По многочисленным просьбам читателей в комментариях к статье с задачами из ОГЭ по математике на «мобильную связь» публикуем статью с решением задач «с шинами».
Обращаю внимание читателей (особенно тех, кто не знаком с этими задачами) на то, что есть общее условие к заданиям №№ 1- 5, и к каждому заданию есть отдельное условие, будьте внимательны. Задачи взяты с сайта СтатГрад 2020 − 2021 уч. г.).
Но прежде, чем решать задачи, давайте выпишем из условия все величины и формулы, которые нам понадобятся. Итак,
По условию шина с завода имеет маркировку 175/70 R12:
В (первое число) — обозначает ширину шины, в мм, В = 175 мм;
Н (второе число) — высота боковины, при этом Н/В×100 % = 70 % ,
70 % = 0,70, отсюда можно выразить Н = В × 0,70
d — диаметр диска в дюймах, d = 12 дюймов, 1 дюйм = 25,4 мм
D — диаметр колеса, в мм, из рис. 2 видно, что
D = 2H + d. Итак, приступаем к решению задач.
Задание 1
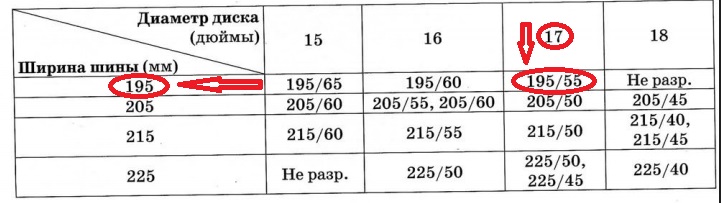
Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
Шины какой наибольшей ширины можно устанавливать на автомобиль, если диаметр диска равен 13 дюймам? Ответ дайте в миллиметрах.
Решение:
Эта задача не требует даже никаких вычислений. Ширина шины (в мм) это B — первое число в обозначении маркировки шины. Если диаметр диска равен 13 дюймам, мы видим из таблицы, к нему допускается ширина шины 175,185,195 мм. И наибольшее из них число — 195. Это и есть искомое число.
Ответ : 195.
Задание 2
Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
Решение
Итак, требуется найти диаметр колеса D из условия: 175/70 R12. Напомню, что D = 2H + d. Таким образом, нам нужно прежде всего найти H и d .
1) Из условия значение d = 12 дюймов, переведём его в мм (по условию 1 дюйм = 25,4 мм).
d = 12× 25,4 = 304,8 мм;
2) Найдём Н (помним, что В = 175 мм , Н = В×0,70)
Н = 175×0,7 = 122,5 мм;
3) Найдём D = 2H + d = 2×122,5 + 304,8 = 549,8 мм.
Ответ : 549,8 мм.
По сути своей, эта задача содержит всего 3 действия на вычисления десятичных дробей, фактически это задача для 5-го класса.
Задание 3
На сколько миллиметров радиус колеса с шиной маркировки 185/60 R 13 меньше, чем радиус колеса с шиной маркировки 175/65 R 13 ?
Решение
Это задание практически повторяет задание 2, только во 2 задании мы находили диаметр колеса D, а в этом нужно найти радиусы. Но все мы помним, что r = D / 2 .
Усложнена задача только тем, что нужно найти r колеса с маркировкой 185/60 R 13 и сравнить его с радиусом колеса с завода с маркировкой 175/65 R 13.
1) Найдём r колеса с маркировкой 185/60 R 13 (B = 185 мм, Н = В×0,60, d = 13 дюймов или 13 дюймов = 13 × 25,4 = 330,2 мм).
H = 185 × 0,60 = 111 мм.
D = 2H + d = 2 × 111 + 330,2 = 552,2 мм
r = 552,2 / 2 = 276,1 мм.
2) Найдём r колеса с маркировкой 175/65 R 13 (В = 175 мм и H = B × 0,65, d тот же и равен 330,2 мм). Ход решения тот же:
H = 175 × 0,65 = 113,75 мм.
D = 2H + d = 2 × 113,75 + 330,2 = 557,7 мм
r = 557,2 / 2 = 278,85 мм.
3) Найдём разницу между полученными радиусами:
278,85 – 276,1 = 2,75 мм.
Ответ : 2,75.
Задание 4
На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 195/60 R13?
Решение
Ход рассуждения, аналогичен задаче № 3. Кроме того, D колеса с завода мы находили в задаче № 2, воспользуемся её данными: D = 549,8 мм.
1) Найдём диаметр колеса D с шиной маркировки 195/60 R13:
H = 195 × 0,60 = 117 мм;
d = 13 дюймов или 330,2 мм (находили в задаче 3);
D = 2H + d = 2 × 117 + 330,2 = 564,2 мм.
2) Найдём разницу:
564,2 – 549,8 = 14,4 мм.
Ответ : 14,4.
Задание 5
На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 175/65 R 13? Результат округлите до десятых.
Решение
В этой задаче мы должны применить свои знания из курса геометрии, ну и задачи на проценты.
Что такое 1 оборот колеса? Это длина окружности (колеса) .
Длина окружности вычисляется по формуле: С = 2π r, где r — радиус колеса, D = 2 r , и формулу длины окружности можно записать как: С = Dπ
1) Диаметр колеса, установленного на заводе, мы находили в задаче
№ 2, D = 549,8 мм.
Тогда, оборот 1 колеса равен: C = Dπ = 549,8π (не спешите умножать на 3,14, нам это не понадобится).
2) Диаметр колеса с маркировкой 175/65 R 13 возьмём из задачи 3:
D = 557,7 мм,
тогда, оборот 1 колеса равен: C = Dπ = 557,7π.
3) Итак,
549,8π — 100 %
557,7π — x %
Составим и решим уравнение:
549,8πx = 557,7π×100
х = 101,4 (приближенно до десятых)
2) Найдём изменение 101,4 %– 100 % = 1,4 %.
Ответ : 1,4 .
Итак, мы прорешали с Вами 5 из 25 задач из ОГЭ по математике. Напоминаю читателям о том, что каждое из заданий №№ 1-5 оценивается по 1 баллу.
НО! Хочу напомнить, что для прохождения аттестационного порога необходимо набрать не менее 8 баллов, из которых не менее 2-х баллов должны быть получены за решение задач по геометрии (задания 15 – 19, 23 – 25).
Кроме первой, во всех задачах наше решение «крутилось» вокруг диаметра колеса D, и вычисления были очень похожи. К сожалению, надо отметить, что именно вычисления и пугают девятиклассников, ведь даже, если вы хорошо считаете, вычисления достаточно объёмные и требуют значительных временных затрат, ну и конечно достаточно объёмное первоначальное условие к задачам. Если вы не можете решить все 5 заданий (хотя бы из-за отсутствия времени), решите для начала 3, потом можно к ним вернуться.
Если Вы прорешаете хотя бы 2-3 таких варианта заранее, я уверена, вы справитесь с ними и на экзамене! Удачи в подготовке! И я надеюсь, моя статья Вам в этом поможет!
Читайте наш канал в телеграм – по этой ссылке
Автор: #ирина_чудневцева руководитель канала Хакнем Школа, 42 года, город Ярославль
Похожие статьи автора:
Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине. Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис.1). Первое число (число 195 в приведенном примере) обозначает ширину шины в миллиметрах (параметр В на рисунке 2). Второе число (65 в приведенном примере) – процентное отношение высоты боковины (параметр Н на рисунке 2) к ширине шины, то есть 100•НВ . Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идет число, указывающее диаметр d диска колеса в дюймах ( в 1 дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит внедорожники определенной модели и устанавливает на них колеса с шинами маркировки 215/65 R16.
📜Теория для решения:
Посмотреть решение
Задание №1. Завод допускает установку шин с другими маркировками. В таблице показаны разрешенные размеры шин.
| Ширина шины (мм) | Диаметр диска (дюймы) | ||
| 16 | 17 | 18 | |
| 215 | 215/65 | 215/60 | – |
| 225 | 225/65; 225/60 | 225/55 | – |
| 235 | 235/60 | 235/55; 235/50 | 235/50 |
Шины какой наибольшей ширины можно устанавливать на автомобиль, если диаметр диска равен 17 дюймам? Ответ дайте в миллиметрах.
Решение
Смотрим по таблице на столбец, где указан диаметр диска – 17 дюймов. Движемся по столбцу вниз и просматриваем первые числа (ширину шины) в маркировках, нам надо найти наибольшую, в последней строке – это число 235. Значит наш ответ 235.
Ответ: 235
Задание №2. На сколько миллиметров радиус колеса с шиной маркировки 215/55 R17 меньше, чем радиус колеса с шиной маркировки 275/50 R17?
Решение
Прежде всего мы должны понимать, что высота колеса (диаметр колеса D) состоит из высоты шины Н, а их две, а также из диаметра диска . Если изобразить это в виде геометрического рисунка, то он будет выглядеть так, как показано на рисунке 2:
Значит, D=2H + d. Для удобства и последовательного решения задачи лучше составить таблицу, в которой и будем всё решать. В верхней строке записаны данные из условия. В первом столбце выписаны все параметры, которые будем находить.
Таблица 1
| 1 колесо
215/55 R17 |
2 колесо
275/50 R17 |
|
| Высота Н | ||
| Диаметр диска d | ||
| Диаметр колеса D | ||
| Радиус колеса | ||
| Разница в радиусах |
Теперь начинаем заполнять каждую строчку для 1 и 2 колеса, проводя вычисления.
| 1 колесо
215/55 R17 |
2 колесо
275/50 R17 |
|
| Высота Н | Запоминаем: для нахождения высоты выражаем второе число десятичной дробью и умножаем на первое число (так как второе число – процентное отношение высоты боковины к ширине шины). Чтобы выразить число % десятичной дробью, надо разделить его на 100! | |
| 55/100∙215=0,55∙215=118,25 | 50/100∙275=0,5∙275=137,5 | |
| Диаметр диска d | Так как диаметр диска дан в дюймах, то надо умножить последнее число маркировки шины (17) на количество дюймов в 1 мм, т.е. на 25,4 | |
| 17∙ 25,4=431,8 | 431,8 | |
| Диаметр колеса D | В начале решения нашей задачи, мы выяснили как найти диаметр колеса, это надо запомнить! D=2H + d. Находим диаметр в каждом случае, используя данные, которые нашли выше. | |
| 2∙118,25 + 431,8=668,3 | 2∙137,5 + 431,8=706,8 | |
| Радиус колеса | Помним, что радиус, это половина диаметра | |
| 668,3:2=334,15 | 706,8:2=353,4 | |
| Разница между радиусами | Для того, чтобы ответить на вопрос задания, надо найти разность между найденными радиусами | |
| 353,4 – 334,15=19,25 |
Ответ: 19,25
Задание №3. На сколько миллиметров увеличится диаметр колеса, если заменить колеса, установленные на заводе, колесами с шинами маркировки 235/50 R18?
Решение
Решение данного задания будем строить по принципу задания 2, так как требуется найти разницу в диаметрах между шинами заводской маркировки (смотрим в условии) 215/65 R16 и шинами маркировки 235/50 R18.
Сделаем таблицу, аналогичную таблице 1 (до строки диаметр колеса) и заполним её. Объяснения смотрим по заданию 2.
| 1 колесо
215/65 R16 |
2 колесо
235/50 R18 |
|
| Высота Н | 0,65∙215=139,75 | 0,5∙235=117,5 |
| Диаметр диска d | 16∙ 25,4=406,4 | 18∙ 25,4=457,2 |
| Диаметр колеса D | 2∙139,75 + 406,4=685,9 | 2∙117,5 + 457,2=692,2 |
| Разница между диаметрами колеса | Для того, чтобы ответить на вопрос задания, надо найти разность между найденными диаметрами | |
| 692,2 – 685,9=6,3 |
Ответ: 6,3
Задание №4. Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
Решение
С данными про колесо автомобиля, выходящего с завода (215/65 R16) мы встретились в задании 3. Надо найти диаметр, он найден в этом же задании 3 (смотрим таблицу с решением этого задания и находим соответствующее значение диаметра). Это значение равно 685,9.
Ответ: 685,9
Задание №5. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колеса, установленные на заводе, колесами с шинами маркировки 225/65 R16? Результат округлите до десятых.
Решение
Пробег автомобиля при одном обороте колеса – это длина окружности колеса. Значит, необходимо найти длину окружности, зная формулу l=2πR (данная формула есть в справочном материале ОГЭ). Зная, что диаметр – это два радиуса, формулу можем записать короче l=πD. Значение числа π не обязательно подставлять в формулу при решении задачи, удобнее использовать буквенное выражение.
Итак, нам надо найти диаметры двух колес, затем найти длины окружностей этих колес и сравнить их в процентном отношении. С маркировкой заводского колеса мы встречались, а данные ко второму колесу нужно найти. Итак, составим таблицу, аналогичную таблице 1, впишем в нее уже найденные значения заводского колеса (из задания 3) и найдем недостающие про «новое» колесо.
| 1 колесо (заводское)
215/65 R16 |
2 колесо
225/65 R16 |
|
| Высота Н | 139,75 | 0,65∙225=146,25 |
| Диаметр диска d | 406,4 | 406,4 (одинаковый с заводским) |
| Диаметр колеса D | 685,9 | 2∙146,25+406,4=698,9 |
| Длина окружности l=πD | 685,9π | 698,9π |
Итак, имеем две длины окружности, теперь надо найти, на сколько процентов увеличится пробег автомобиля при одном обороте колеса.
Заводское колесо 685,9π – 100%
Колесо на замену 698,9π – х %
Найдем значение х, используя правило пропорции: 698,9π ∙100685,9π=101,895…При решении числа π сократились, а значение % будет приближенное. Теперь найдем разницу между длинами окружностей 100% – 101, 895%=1,895%, округлим его, как сказано в условии – до десятых, получим 1,9 %. Наш ответ 1,9%.
Ответ: 1,9%
Общие советы и рекомендации по данному виду задач
Главное, с чем мы работаем в условии данной задачи, это маркировка шины.
Помните о том, что высота колеса – это его диаметр, состоящий из двух высот и одного диаметра диска (внутренняя металлическая часть колеса). Формулой D=2H+d придется пользоваться на протяжении нескольких заданий.
Для нахождения высоты переводим второе число маркировки в десятичную дробь (разделив на 100) и умножить его на первое число.
Используйте для решения таблицу, чтобы не запутаться при нахождении каких-либо данных.
Желаем удачи!
Ответ: см. решение
Алла Василевская | Просмотров: 11.5k
Версия для печати и копирования в MS Word
На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 175/60 R14? Результат округлите до десятых.
Автомобильное колесо, как правило, представляет собой металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине.
Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65 R15 (рис. 1). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рисунке 2). Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины (параметр на рисунке 2) к ширине шины, то есть
Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции.
За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины.
Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры.
Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 165/70 R13.
Спрятать решение
Решение.
При одном обороте колесо проходит расстояние, равное длине окружности радиусом, равным половине общего диаметра колеса D: Найдем этот диаметр
для каждого из колес. Для шины с маркировкой 165/70 R13 получаем:
тогда
а значит, Для шины с маркировкой 175/60 R14 имеем:
откуда
Следовательно, расстояние, проходимое за один оборот колеса, увеличилось на
Ответ: 0,8 %.
1
Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
| Ширина шины (мм) | Диаметр диска (дюймы) | ||
|---|---|---|---|
| 13 | 14 | 15 | |
| 165 | 165/70 | 165/65 | — |
| 175 | 175/65 | 175/65; 175/60 | — |
| 185 | 185/65; 185/60 | 185/60 | 185/55 |
| 195 | 195/60 | 195/55 | 195/55; 195/50 |
Шины какой наименьшей ширины можно устанавливать на автомобиль, если диаметр диска равен 15 дюймам? Ответ дайте в миллиметрах.
2
На сколько миллиметров радиус колеса с шиной маркировки 205/55 R14 больше, чем радиус колеса с шиной маркировки 165/65 R14?
3
Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
4
На сколько миллиметров увеличится диаметр колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 195/50 R15?
5
Дмитрий планирует заменить зимнюю резину на летнюю на своём автомобиле. Для каждого из четырёх колёс последовательно выполняются четыре операции: снятие колеса, замена шины, балансировка колеса и установка колеса. Он выбирает между автосервисами А и Б. Затраты на дорогу и стоимость операций даны в таблице.
| Автосервис | Суммарные затраты на дорогу | Стоимость для одного колеса | |||
|---|---|---|---|---|---|
| Снятие колеса | Замена шины | Балансировка колеса | Установка колеса | ||
| А | 210 руб. | 60 руб. | 250 руб. | 200 руб. | 60 руб. |
| Б | 380 руб. | 55 руб. | 220 руб. | 180 руб. | 55 руб. |
Сколько рублей заплатит Дмитрий за замену резины на своём автомобиле, если выберет самый дешёвый вариант?
Прочитайте внимательно текст и выполните задания 1 — 5.
Для маркировки автомобильных шин применяется единая система обозначений.

Рекомендации для решения заданий про автомобильные шины
После прочтения текста, нужно составить схему, которая облегчит решение практико-ориентированных заданий.
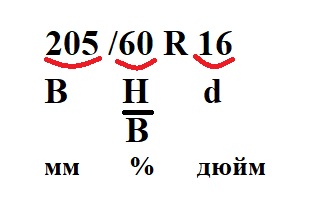
B — ширина шины, H/B — отношение высоты боковины к ширине шины, d — диаметр внутреннего отверстия в шине.
Используя рисунок шины, составляем формулу для нахождения диаметра колеса D: D = d + 2H.
Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен 17 дюймам? Ответ дайте в миллиметрах.
Решение: Используя таблицу, находим столбик с диаметром диска 17 дюймов. Выбираем строчку с наименьшим первым числом, которое показывает наименьшую ширину шины автомобиля (смотрите рисунок ниже).
Ответ: 195.
Задание 2 (ОГЭ 2021 маркировка автошин)
На сколько миллиметров радиус колеса с маркировкой 195/55 R17 больше, чем радиус колеса с маркировкой 225/45 R17?
Решение: У данных колес одинаковые диаметры внутренних отверстий шин, поэтому для нахождения разности радиусов колес, достаточно найти разность высот боковин шин.
Колесо с маркировкой 195/55 R17. B = 195 мм, d = 17 дюймов.
H/B = 55% или H/B = 0,55.
H/195 = 0,55,
H = 0,55 ⋅ 195 = 107,25 (мм).
Колесо с маркировкой 225/45 R17. B = 225 мм, d = 17 дюймов.
H/B = 45% или H/B = 0,45.
H/225 = 0,45,
H = 0,45 ⋅ 225 = 101,25 (мм).
Разность радиусов колес : 107,25 — 101,25 = 6 (мм).
Ответ: 6.
Задание 3 (ОГЭ 2021 маркировка автошин)
Найдите диаметр D колеса автомобиля, выходящего с завода. Ответ дайте в сантиметрах.
Решение: Маркировка шины с завода указана в таблице.

Для нахождения диаметра колеса понадобится формула : D = d + 2H.
d = 16 ⋅ 25,4 мм = 406,4 мм.
H/B = 60% или H/B = 0,6.
H/205 = 0,6.
H = 0,6 ⋅ 205 = 123 (мм).
D = 406,4 + 2 ⋅ 123 = 406,4 + 246 = 652,4(мм) = 65,24(см).
Ответ: 65,24.
Задание 4 (ОГЭ 2021 маркировка автошин)
На сколько миллиметров уменьшится диаметр D колеса, если заменить шины, установленные на заводе, шинами маркировкой 225/40 R18?
Решение: Найдем диаметр D колеса с шинами 225/40 R18.
B = 225 мм, H/B = 0,4.
H/225 = 0,4.
H = 0,4 * 225 = 90 (мм).
d = 18 * 25,4 = 457,2 (мм).
D = 457,2 + 2 * 90 = 457,2 + 180 = 637,2(мм) — диаметр колеса 225/40 R18.
Диаметр заводской шины найден в задании 3 — 652,4 мм.
Найдем на сколько мм уменьшится диаметр колеса, если заменить шины, установленные на заводе, шинами маркировкой 225/40 R18.
652,4 — 637,2 = 15,2 (мм).
Ответ: 15,2.
Задание 5 (ОГЭ 2021 маркировка автошин)
На сколько процентов уменьшится пробег автомобиля при одном обороте колеса, если заменить шины, установленные на заводе, шинами с маркировкой 225/40 R18? Округлите результат до десятых.
Решение: Пробег автомобиля при одном обороте колеса — это длина окружности, которая вычисляется по формуле: C = 2ПR или C = ПD, D — диаметр колеса.
Колесо с шиной, установленной на заводе (диаметр колеса находили в задании 3). C = 65,24П.
Колесо с шиной 225/40 R18 ( диаметр колеса находили в задании 4).
C = 63,72П.
Разность между пробегами: 65,24П — 63,72П = 1,52П.
Узнаем на сколько процентов уменьшится пробег автомобиля при одном обороте колеса. Пусть оборот колеса с заводской шиной составляет 100%. Х % — на сколько % уменьшится пробег. Составим пропорцию:
65,24П — 100%
1,52П — Х%
Найдем неизвестный член пропорции.
х = (1,52П * 100) / 65,24П= 2,3286 (%) ≈ 2,3% ( округляем до десятых, используя правила округления).
Ответ: 2,3.
Разбираем практико-ориентированные задания 1 — 5 ОСАГО из ОГЭ по математике 2021.